Abstract
We present a noninvasive method for characterizing the refractive index (RI) and thickness distribution in biological tissues using a combined multiphoton microscopy (MPM) and optical coherence tomography (OCT) system. Tissue layers are distinguished by the MPM and OCT images, and the RI and thickness of each layer are determined by analyzing the co-registered MPM and OCT images. The precision of this method is evaluated on four standard samples which are water, air, immersion oil and cover glass. Precision of within ~1% error compared to reference values is obtained. Biological tissue measurement is demonstrated on fish cornea. Three layers are detected, which are identified as the epithelium and stroma I and II of the cornea. The corresponding RI of each layer is measured to be ~1.446–1.448, 1.345–1.372, and 1.392–1.436, respectively. The difference of RI in the three layers correlates with the tissue compositions including cells in epithelium, large collagen fiber bundles in stroma I, and small collagen fibers in stroma II. The combined MPM/OCT technique is shown to be able to distinguish tissue layers through biochemically specific contrasts and measure RI and thickness of tissue layers at different depths.
OCIS codes: (180.4315) Nonlinear microscopy, (170.4500) Optical coherence tomography, (120.5710) Refraction
1. Introduction
The refractive index (RI) of biological tissue is a key parameter for characterizing the light-tissue interactions [1,2]. Knowledge of the tissue RI plays an important role in many biomedical applications. In optical diagnostics, malignant tissues can be distinguished from normal tissues by measuring and comparing their RI [3–5]. In laser eye treatments, the RI and thickness of cornea are important indicators of cornea states, such as cornea hydration and intraocular pressure, before and after laser surgery [6–9].
Several methods have been reported for measuring RI in tissues. One method was based on total internal reflection where it used a semicylindrical lens to determine the critical angle and therefore the RI of biological tissues [10–12]. It required direct contact with sample and only the RI of the layer in contact with the optics was measured. Wang et al. employed a phase contrast microscopy to quantitatively determine the spatial fluctuation of RI of tissues [5]. The phase contrast microscopy provided the optical pathlength of tissue. To obtain the RI, the physical thickness of the sample was determined by slicing the sample into a thin section. Choi et al. reported a method for quantitative three-dimensional (3D) mapping of refractive index in live cells and tissues using a phase-shifting laser interferometric microscope based on a Mach–Zehnder interferometer and multi-angle scanning [13]. This method required complicated 3D reconstruction algorithms and could only work for very thin tissues. Dirckx et al. devised a method based on a confocal microscope by measuring the optical thickness which was related to the RI and the physical thickness of a sample [14]. Complicated sample preparation was needed to section and sandwich the sample between two glass slides. Therefore, those methods are not suitable for noninvasive measurement of thick tissues because of the complicated sample preparation and requirement for thin or sectioned tissues.
Focus-tracking has been reported for RI measurement in tissues noninvasively [1,15–18]. This method employed low-coherence interferometry, such as optical coherence tomography (OCT), combined with translation stages. RI was obtained by taking the ratio between the optical pathlength measured by OCT and the focus shift resulted from translating the focus of an objective lens inside biological tissues [1]. This method required focusing the laser beam onto the front and rear surfaces of a sample. Determining the front and rear surfaces were based on reflected light, which could be difficult in biological tissues. Moreover, this method measured the RI along one axial line in tissue at a time, which made it difficult to determine the distribution of RI within tissues. Kim et al. reported measurement of RI and thickness by combining low coherence interferometry and confocal optics [19]. The confocal optics was used to determine the focus shift within a sample, which was similar to the focus-tracking method. Zvyagin et al. demonstrated a bifocal optical coherence refractometry system which was capable of creating two foci in the sample simultaneously [20]. The optical pathlength difference between the two foci was used to determine the RI of the sample. The limitation of this method was the requirement of exogenous contrast agents such as polystyrene spheres to increase image contrast for less scattering samples. For the low coherence interferometry and confocal based methods which rely on reflected or backscattered light as contrast, distinguishing tissue layers can be difficult in multilayered and heterogeneous tissue structures because the reflection or scattering contrast is non-specific to tissue compositions.
Cornea is a fairly complex structure which consists of five layers, epithelium, Bowman’s membrane, stroma, Descemet’s membrane and endothelium [21]. Epithelium is the outmost layer of cornea which is only 5-6 cell layers thick. Epithelial cells are densely packed and normally there is very little extracellular space between individual cells. Stroma is the thickest layer which mainly consists of collagen fibrils that run parallel to each other. Bowman’s membrane and Descemet’s membrane lie above and below stroma respectively, and consist mainly of collagen fibrils. Endothelium is only a single layer of cells. For cornea RI measurement, Kim et al. [22] and Lin et al. [23] measured the overall RI of cornea by focus tracking. Meek et al. measured the RI change in stroma when cornea swells [24] and Patel et al. measured the RI change in stroma before and after laser eye surgery [9] with Abbe refractometer. Abbe refractometer is based on the measurement of refraction angle and requires direct contact of cornea with two prisms. In all the above references, only the average value of cornea RI or a single layer such as the stroma of cornea RI has been reported. To the best of our knowledge, there has been no report on the characterization of RI variations among the multiple layers of cornea.
In this paper, we present a new method which can measure the RI and thickness of multiple tissue layers simultaneously in thick biological tissues noninvasively. It is based on a combined multimodal multiphoton microscopy (MPM) and OCT system. MPM and OCT are powerful tools for noninvasive functional and structural imaging of tissues. Derived from the Michelson interferometer, OCT can generate a cross-sectional view of tissues using the interference between the reflected light from a sample and a reference arm. MPM is a nonlinear microscopy which detects two-photon excited fluorescence (TPEF) and second harmonic generation (SHG) in tissues when excited by a femtosecond laser. TPEF signal originates from intrinsic sources such as nicotinamide adenine dinucleotide phosphate (NADPH) or exogenous fluorophores, while SHG signal comes from non-centrosymmetric molecules such as collagen, a common structural protein [25]. Thus, the highly specific contrasts in MPM can better distinguish tissue layers based on their biochemical compositions. In our experiment, OCT cross-sectional images and MPM 3D images of tissues at the same sample location are taken successively. Optical pathlength and physical thickness can be derived from those images, respectively. The RI is obtained by taking the ratio between the optical pathlength and the physical length. This method requires no sample preparation and is non-contact. It can measure the thickness and RI distribution of multiple tissue layers through a single measurement. Furthermore, the technique also provides visualization of cellular and extra-cellular matrix structures for characterizing multiple layers of biological tissues.
In Section 2, the principle of the method is explained. In Section 3, the measurement precision is first validated on four standard samples, water, air, immersion oil and cover glass. Then the capability of the system to measure RI and thickness of multilayered biological tissues is demonstrated on fish corneas. Section 4 discusses the sources of measurement errors and Section 5 concludes the paper.
2. Principles
OCT is an optical interference technique where interference happens only when the optical pathlengths of sample and reference arms are matched within the coherence length of a light source. Therefore, the thickness of a sample obtained from OCT images is the optical pathlength, which is the product of the physical thickness of the sample and its group index. In this paper, we assume the group index is equivalent to the RI of a sample. Thus, for a sample with a thickness of t and a RI of n, the corresponding optical pathlength Lp is
| (1) |
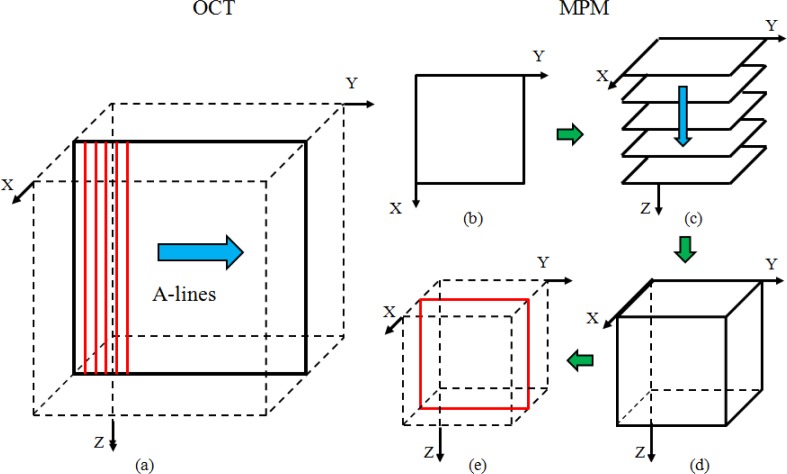
In our spectral domain OCT system, a spectrometer records the interference fringes which are processed by non-uniform fast Fourier transform (NUFFT) [26] to obtain a depth profile (A-line) in the Z direction. Cross-sectional view of the sample is obtained by scanning the laser beam in the Y direction and acquiring multiple A-lines as shown in Fig. 1(a) . The optical pathlength Lp can be measured from the OCT cross-sectional image.
Fig. 1.
Illustration of the OCT/MPM image acquisition procedure. (a) The solid rectangle denotes the OCT cross-sectional image which is reconstructed from 512 A-lines. (b) MPM en face image. (c) A stack of MPM en face images. (d) The reconstructed MPM 3D matrix from the MPM stack. (e) MPM cross-sectional image (solid rectangle) is sectioned from the MPM 3D matrix.
MPM is a nonlinear optical imaging technique where two photons are absorbed simultaneously to excite a fluorescence photon as in TPEF or two photons are converted to a harmonics photon at twice the energy as in SHG. A focused laser beam is raster scanned and nonlinear signals such as TPEF and SHG are acquired pixel by pixel. By scanning the laser beam in the XY plane, an en face view MPM image (Fig. 1(b)) is obtained from the focal plane. By further scanning the focal plane of an objective, a stack of en face MPM images can be acquired as shown in Fig. 1(c). From the MPM volume data, 3D reconstruction and subsequent cross-sectional view of the sample can be obtained as shown in Figs. 1(d) and 1(e).
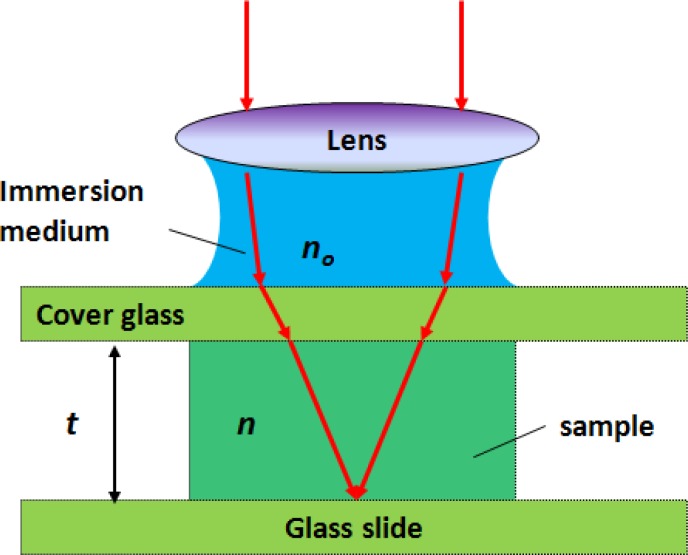
Although the MPM stack is obtained by scanning a microscope objective in the Z direction, the thickness of the sample obtained from the MPM cross-sectional image is not exactly the physical thickness due to the multilayer refractions in the sample arm. Figure 2 shows how refraction happens in a multilayered sample preparation. The sample (e.g. fluorescent dye solution) is held between two glass plates and the objective is immersed in water. Refraction occurs at the interfaces between the immersion water, the top glass plate and the sample.
Fig. 2.
Schematic of the optical phantom for validation. t and n are the physical thickness and RI of the sample, no is the RI of the immersion medium.
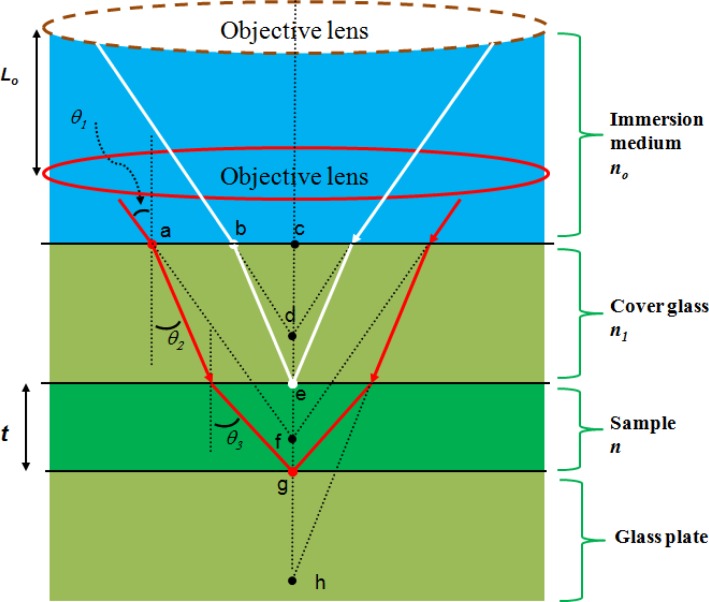
Figure 3 shows the ray optics diagram for a multilayered refraction case. The beam is first focused onto the top surface of the sample (point e). Then the objective is moved downward by a distance of Lo so that the beam is focused onto the bottom surface of the sample (point g). Here Lo is referred as the optical thickness of the sample which is related to RI. From Snell’s law, we have
Fig. 3.
The multilayer refraction of laser beam in sample arm. t and n are the physical thickness and RI of the sample. no is the RI of the immersion medium (water), n1 is the RI of the glass plate, θ1 is the incident angle, θ2 and θ3 are the refractive angles. Lo is the distance of the objective lens moved during imaging.
| (2) |
where no, n1 and n are the RI of the immersion medium (water), cover glass and sample, respectively, θ1 and θ2 are the incident angle and refractive angle on the boundary between immersion medium and cover glass, and θ3 is the refractive angle on the boundary between cover glass and sample.
By analyzing the triangle relationships in Fig. 3, we can get the relationship among n, t and Lo (see Appendix A for more details of the derivation):
| (3) |
For the MPM system using high NA objective, spherical aberration needs to be considered. Since the objective is corrected for spherical aberration, the effect is mainly from the index mismatch between the immersion medium, cover glass and sample [27]. Equation (3) shows that the Lo and t relationship depends on the incident angle. However, when the index mismatch between the immersion medium (water, n0) and the sample (n) is small, as in the case for tissue imaging, the effect of spherical aberration is very small. It has also been reported that spherical aberration is much smaller in two-photon systems than in one-photon systems [28]. In the next calculations, marginal beams will be used because of their contribution to the tight focusing in MPM, for which
| (4) |
and
| (5) |
Based on the two relationships (Eq. (1) and Eq. (5)), the physical thickness and the RI of the sample can be calculated:
| (6) |
| (7) |
In this paper, a water immersion 40 × objective (NA = 0.8, n0 = 1.33) is used for the MPM imaging. The optical thickness Lo can be measured from the MPM cross-sectional image and the optical pathlength Lp can be measured from the OCT image. From Lp and Lo, the thickness t and refractive index n can be determined.
3. Experiment and results
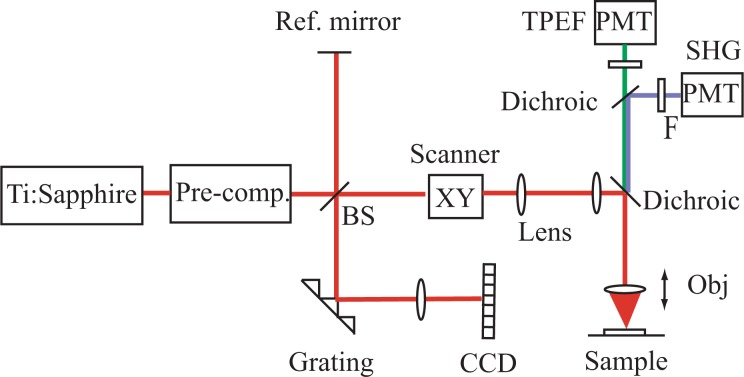
The schematic of the experimental setup is shown in Fig. 4 . A femtosecond Ti:sapphire laser with a centre wavelength of 800 nm and a spectral bandwidth of 120 nm is shared by MPM and OCT. A beam splitter splits the laser beam into a sample and a reference arm. The interference fringes of the backscattered beam from the sample arm and the reflected beam from the reference arm are recorded by a custom-built spectrometer. The OCT system can acquire cross-sectional images with a field-of-view of a few millimeters in the transverse direction and ~600 µm in depth at a speed of ~100 frames/s. MPM consists of two channels, TPEF and SHG, which are separated by a dichroic mirror and received by different photomultiplier tubes (PMTs) respectively. The MPM system can acquire en face images with a field-of-view of a few hundred microns at a speed of ~0.4 frames/s. The XY scans are controlled by two galvanometer mirrors. The depth scan (Z axis) of MPM is controlled by a piezo objective scanner. Two objectives are used in the MPM/OCT imaging, a 10 × objective (MPlanFL N, Olympus, NA = 0.3) for the OCT imaging and a water immersion 40 × objective (LUMPlanFL N, Olympus, NA = 0.8) for the MPM imaging. The OCT lateral resolution is ~2 µm and its axial resolution is ~2.8 µm (in air). The MPM lateral resolution is ~0.6 µm and its axial resolutions is ~1.5 µm. A detailed description of the setup can be found in our previous work [25].
Fig. 4.
Schematics of the combined MPM/OCT system. BS: beam splitter; F: filter; Obj: Objective; PMT: photomultiplier tube [25].
In the experiment, firstly, a cross-sectional OCT image as in Fig. 1(a) is obtained. The dimension of the OCT image in the Z direction is determined by the spectrometer design and is calibrated to be 600 µm by moving the reference mirror with a micrometer. From the OCT cross-sectional image, Lp can be measured. Secondly, a stack of several hundred MPM en face images are acquired and then reconstructed into a 3D matrix. Afterwards, the MPM cross-sectional image is sliced from the 3D volume as shown in Fig. 1(e). The dimension of the MPM image in the Z direction is determined by the number of frames in the image stack and the step size between the frames which is controlled by the piezo objective scanner. From the MPM cross-sectional image, Lo is derived. Finally, the RI and thickness are calculated based on Eqs. (6) and (7). The OCT and MPM cross-sectional images are co-registered and represent slightly different information about the optical pathlength and the optical thickness of the tissue respectively [25].
3.1 System validation
Four standard samples, water, air, immersion oil (Nikon, type A) and cover glass (Fisher, 12-542C), are used to evaluate the performance of this technique. The measurement for the RI of water is given as an example. A sandwiched phantom, as shown in Fig. 2, is prepared for the experiment. Fluorescent dye solution of very low concentration is used instead of pure water to generate TPEF contrast. The thickness of the solution layer is designed to be around 250 μm so that it is neither too thin to increase the measurement error nor too thick to go beyond the image depth of OCT (600 μm) and MPM (400 μm). Firstly, an OCT cross-sectional image of the phantom is obtained with the 10 × objective. Then the objective is switched to the 40 × objective without moving the phantom. Next, a stack of 400 MPM images are acquired at 1 µm step size. Based on the data volume, 3D visualized MPM image is reconstructed and a MPM cross-sectional image corresponding to the OCT image is generated.
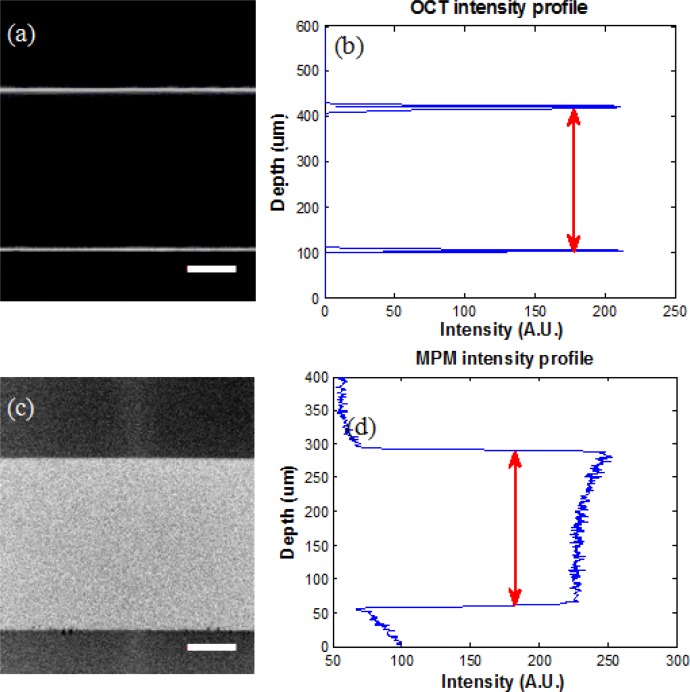
Figure 5(a) shows the OCT image of the phantom. The two bright lines denote the top and bottom boundaries of the solution layer. The intensity profile of the OCT image along the centre line is plotted in Fig. 5(b). The optical pathlength of this layer can be directly acquired by measuring the distance between the two peaks in Fig. 5(b). Since the fluorescent dye solution generates no SHG signal, only the TPEF image is obtained and shown in Fig. 5(c). The bright area denotes the solution layer while the dark area shows the top and bottom glass plates. Similarly, the central intensity profile of the TPEF image is plotted and shown in Fig. 5(d). The optical thickness of the solution layer in MPM is then acquired by getting the full width half maximum (FWHM) of the peak in Fig. 5(d). With these two parameters, the physical thickness and RI of the solution can be obtained according to Eqs. (6) and (7). Assuming the low concentration fluorescent dye contributes little change in the optical refraction of water, the RI of water can be determined from this experiment.
Fig. 5.
MPM/OCT images of the phantom. (a) Cross-sectional view of OCT. (b) The intensity profile along the central line of OCT cross-sectional image. (c) Reconstructed cross-sectional view of MPM. (d) The intensity profile along the central line of MPM cross-sectional image. Scale bars are 50 μm.
RI measurements for air, oil and cover glass are also performed. For the air and oil measurement, we designed a phantom similar to the one shown in Fig. 2 but replaced the dye solution with air or oil. Since cover glass can generate weak TPEF signal, this contrast is used to detect the top and the bottom surfaces of the air and oil gap. For the glass measurement, the TPEF signal from the glass itself is used as the contrast. All the experiments are conducted at room temperature and are repeated three times.
The experimental results, the reference values from literature and the errors with respect to the reference values are summarized in Table 1 . The measured results are presented in the form of average value plus standard deviation. For water, our measured RI is 1.336 ± 0.003, which matches well with the reference value of 1.329 (calculated from Sellmeier equation for wavelength 800 nm, temperature 20°C) [29]. The small standard deviation indicates that the measurement is highly repeatable. For air, the measured RI is 1.005 ± 0.003 which is close to the reference value 1.0003 (wavelength 800 nm, temperature 15C) [30]. For immersion oil, our result is 1.515 ± 0.004, which matches with the reference value 1.515 obtained from product specification (Nikon type A immersion oil, temperature 23°C). For cover glass, our result is 1.576 ± 0.002. The reference value is 1.56 ± 0.01, which is measured using the focus tracking method [1]. Although the average RIs obtained by the two methods are very close, our method has a much smaller standard deviation. No error is calculated for the cover glass because our result could have a better precision than the reference value obtained by focus tracking. From above, the results show that the technique is highly precise and repeatable. Our measurements are in agreement with reference values within ~1% error range. Thus the measurement of the standard samples proves the efficacy of this technique.
Table 1. The measurement of RI of standard samplesa.
| Meas | Ref | Err | |
|---|---|---|---|
| Water | 1.336 ± 0.003 | 1.329 [29] | ~1% |
| Air | 1.005 ± 0.003 | 1.0003 [30] | ~1% |
| Oil | 1.515 ± 0.004 | 1.5151 | ~1% |
| Cover glass | 1.576 ± 0.002 | 1.56 ± 0.012 | — |
aMeas: measured value (average ± standard deviation); Ref: reference value; Err: error with respect to the reference value. The error has already taken into account the standard deviation. 1: From Nikon type A immersion oil specification (23°C). 2: The RI of cover glass is measured using the focus tracking method [1].
3.2 Biological tissues
The application of this technique to biological tissues is tested on fish cornea. Fish cornea is similar to human cornea and generally consists of the five layers, epithelium, Bowman’s membrane, stroma, Descemet’s membrane and endothelium. Some species may contain more or less of the above layers [31]. In our experiment, black tilapia fish are obtained from a local vendor and fresh fish eyes are imaged under the microscope. In the tissue imaging, no sample preparation is required. The OCT cross-sectional image of fish cornea is acquired and shown in Fig. 6(a) . After that, a stack of en face MPM images are acquired and the representative images at different depths are shown in Figs. 6(c)-6(g). The reconstructed MPM cross-sectional view of the cornea is shown in Fig. 6(b). In Fig. 6, the MPM images are color coded with TPEF in red and SHG in green.
Fig. 6.
MPM/OCT images of fish cornea. (a) Cross-sectional view of OCT. (b) Reconstructed cross-sectional view of MPM. (c)-(g) MPM en face view at depths 80, 200, 316, 370 and 387 µm, respectively. TPEF is in red and SHG in green. Scale bars are 50 μm.
The co-registered MPM and OCT cross-sectional images clearly display the multilayer structure of the fish cornea. From Figs. 6(a) and 6(b), three layers can be distinguished in the fish cornea, which are denoted as L1, L2 and L3. The fine structures of each layer are provided by the high resolution en face MPM images. In Fig. 6(c), the clearly visible cellular structures which are shown by the TPEF contrast indicate that the top layer is the epithelium. Figures 6(d)-6(f) show mainly SHG signals from collagen fibers with different orientations and densities, which is an indication of the stroma layer. In Figs. 6(d) and 6(e), collagen fibers are observed to form large bundles and the bundles line up inside the plane but change orientation between planes. In Fig. 6(f), the SHG intensity decreases significantly and the collagen fibers seem to be smaller in diameter. Figure 6(g) shows the end of the cornea where weak autofluorescence is detected, which indicates the endothelium layer. From the en face MPM images, we can identify that L1 is the epithelium, L2 is the first layer of stroma and L3 is the second layer of stroma (possibly including the endothelium layer). The Bowman’s membrane and Descemet’s membrane are not distinguished from stroma in our study likely because they are very thin and mainly consist of collagen fibrils, similar as stroma.
Once the MPM and OCT images of fish cornea with clear structures are acquired, the thickness and RI can be calculated. Clearly, this method cannot only measure the overall RI of the whole cornea, but also measure the RI of each layer for a multilayered sample as cornea. Moreover, from the two co-registered cross-sectional images, the thickness variation and the RI distribution along the transverse direction of a few hundred micrometers can also be obtained.
Two sets of data acquired from different specimens are summarized in Table 2 . For each layer of the cornea, the RI and thickness at five different locations are calculated and averaged. The overall RI and thickness of the full cornea are also computed. For specimen one, the RI for epithelium (L1), stroma I (L2) and stroma II (L3) are 1.448 ± 0.015, 1.345 ± 0.002 and 1.436 ± 0.009 respectively. For specimen two, the RI for the respective layers are 1.446 ± 0.011, 1.372 ± 0.005 and 1.392 ± 0.012. Although there are some variations between the two specimens, the results show two common features. First, the epithelium has the highest RI among the three layers. From the high-resolution MPM images, the epithelium is observed to be composed of multiple layers of cells. The membrane structures of cells and cell nuclei tend to have high RI because of their lipid and DNA compositions. Second, the posterior layer of the stroma (II) has higher RI than that of the anterior layer of the stroma (I). From the SHG en face images, we found stroma I (Figs. 6(d)-6(e)) is composed of large collagen fiber bundles while stroma II (Fig. 6(f)) is made of small collagen fibers. Stroma I also shows higher SHG signal intensity than stroma II. The difference of the RI between stroma I and II correlates well with the collagen fiber structures and the SHG signal intensities. The variations between the two specimens are possibly due to the individual differences and the hydration levels of the corneas [9,24]. The thickness of each layer of the cornea is also listed in Table 2.
Table 2. RI and thickness of fish cornea.
| |
Specimen one |
Specimen two |
|||
|---|---|---|---|---|---|
| Layer | Refractive index | Average Thickness [μm] | Refractive index | Average Thickness [μm] | |
| Epithelium (L1) | 1.448 ± 0.015 | 43.8 | 1.446 ± 0.011 | 33.5 | |
| Stroma I (L2) | 1.345 ± 0.002 | 252.9 | 1.372 ± 0.005 | 219.0 | |
| Stroma II (L3) | 1.436 ± 0.009 | 41.2 | 1.392 ± 0.012 | 39.9 | |
| Overall | 1.370 ± 0.004 | 337.9 | 1.386 ± 0.005 | 292.4 | |
In the literature, the RI distribution in different cornea layers has not been reported. For human cornea, the average RI of the full cornea is reported to be ~1.37-1.39 [23,32]. In our result, the overall RI for the two specimens is 1.370 ± 0.004 and 1.386 ± 0.005 respectively, which are close to the reported number for human cornea. Our technique can further identify multiple layers in cornea and measure the RI and thickness distribution of tissue layers at different depths.
4. Discussion
The axial resolutions of OCT and MPM as well as the physical thickness of a sample are important factors in determining the measurement precision of this method. To estimate the error, we can rewrite Eq. (6) in the form of
| (8) |
According to the error propagation theory [33], the relative error of n is
| (9) |
Here △Lp and △Lo are the measurement errors of Lp and Lo respectively. The bar symbol means average.
Thus, we get
| (10) |
Based on Eq. (10), there are two ways to reduce the relative error. One is to increase the optical pathlength Lp and thickness Lo. Since Lp and Lo are proportional to the physical thickness t, the increase of t can give rise to the increase of Lp and Lo. In our experiments, the phantoms are specially designed so that they can make full use of the imaging depth and minimize the relative error. In tissue measurement, the sample thickness will be limited by the nature of the tissues. The other way is to reduce the measurement errors ΔLp and ΔLo, which are determined by the OCT and MPM axial resolutions. In Fig. 6, the optical pathlength Lp and the optical thickness Lo are measured from the intensity profile of the images. Since the detection of the boundary of the layers directly depends on the system resolving ability, a higher axial resolution will provide better measurement precision. In our system, the OCT axial resolution (2.8 μm in air) can potentially be improved to reach the source limited resolution (2.35 μm in air). To further improve the OCT resolution, a source with shorter center wavelength and/or broader bandwidth will be needed. For MPM, a higher axial resolution can potentially be achieved by using objectives with higher NA. Besides axial resolution, speckle noise in OCT and spherical aberration in tight focusing optics may also affect the measurement precision. Speckle noise is inherent in OCT due to the interference of coherent light [34]. Speckle noise makes it more difficult to identify the boundaries in OCT images. Spherical aberration is mainly caused by the index mismatch between the immersion medium and the sample [27,28]. For water and fish cornea measurements, the effect of spherical aberration is very small. For air and oil measurements, the effect of spherical aberration is expected to be higher. Considering the three factors above, the measurement precision of our system is estimated to be around ~1%, which matches with the error calculation in Table 1.
The experiment on fish corneas demonstrates the advantages of this method. Based on the tissue structures determined by OCT and MPM cross-sectional images, the RI and tissue thickness can be obtained. Furthermore, the high resolution en face TPEF and SHG images show the compositions of each tissue layer which can provide information on why RI varies among the different layers. This method works well for multilayered inhomogeneous samples. With a single measurement, the distribution of the RI and thickness within a sample can be obtained. Furthermore, by comparing the OCT and MPM images in the cornea data, the MPM image shows better identification of the different layers because the compositions of the epithelium and stroma are highly different which can be distinguished by the TPEF and SHG respectively. The scattering contrast in OCT shows no identification of the tissue compositions. Therefore, by using combined MPM/OCT, the tissue layers can be better distinguished during RI and thickness measurement, compared to techniques based on low coherence interferometry or confocal.
The MPM/OCT technique is noninvasive and requires no sample preparation. Therefore, it could be applied for in vivo characterization of RI and thickness of tissues. For in vivo imaging, the MPM acquisition speed needs to be increased which can be achieved by scanning the MPM image in cross-sectional mode directly.
5. Conclusion
We have presented a technique for characterizing the RI and thickness of biological tissues noninvasively using combined MPM/OCT. For standard samples, high precision measurements (~1% error) have been achieved. In fish cornea measurement, three layers in cornea are identified and the RI and thickness of each layer are obtained simultaneously. The results demonstrate that this technique is especially suitable for biological tissue characterization where the multilayered and heterogeneous structures of tissues can be distinguished through the MPM/OCT imaging and the RI and thickness distribution can be derived simultaneously.
Acknowledgments
This project is supported by the Natural Sciences and Engineering Research Council of Canada and the Canada Foundation for Innovation.
Appendix A
Based on Eq. (2) and the triangle relationships in Fig. 3, we can derive
| (A.1) |
| (A.2) |
We can combine Eq. (A.1) and Eq. (A.2) into
| (A.3) |
Similarly, we have
| (A.4) |
Multiply Eq. (A.3) with Eq. (A.4),
| (A.5) |
Notice that
| (A.6) |
and
| (A.7) |
By combining Eqs. (A.5)–(A.7), we can get the relationship among n, t, and Lo:
| (A.8) |
References and links
- 1.Tearney G. J., Brezinski M. E., Southern J. F., Bouma B. E., Hee M. R., Fujimoto J. G., “Determination of the refractive index of highly scattering human tissue by optical coherence tomography,” Opt. Lett. 20(21), 2258–2260 (1995). 10.1364/OL.20.002258 [DOI] [PubMed] [Google Scholar]
- 2.Wilson B. C., “Modeling and measurement of light propagation in tissue for diagnostic and therapeutic applications,” Laser Syst. Photobiol. Photomed. 252, 13–27 (1991). 10.1007/978-1-4684-7287-5_3 [DOI] [Google Scholar]
- 3.Motamedi M., Rastegar S., Lecarpentier G., Welch A. J., “Light and temperature distribution in laser irradiated tissue: the influence of anisotropic scattering and refractive index,” Appl. Opt. 28(12), 2230–2237 (1989). 10.1364/AO.28.002230 [DOI] [PubMed] [Google Scholar]
- 4.Arridge S. R., Hebden J. C., “Optical imaging in medicine: II. Modelling and reconstruction,” Phys. Med. Biol. 42(5), 841–853 (1997). 10.1088/0031-9155/42/5/008 [DOI] [PubMed] [Google Scholar]
- 5.Wang Z., Tangella K., Balla A., Popescu G., “Tissue refractive index as marker of disease,” J. Biomed. Opt. 16(11), 116017 (2011). 10.1117/1.3656732 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Borasio E., Stevens J., Smith G. T., “Estimation of true corneal power after keratorefractive surgery in eyes requiring cataract surgery: BESSt formula,” J. Cataract Refract. Surg. 32(12), 2004–2014 (2006). 10.1016/j.jcrs.2006.08.037 [DOI] [PubMed] [Google Scholar]
- 7.Patel S., Alió J. L., Artola A., “Changes in the refractive index of the human corneal stroma during laser in situ keratomileusis. Effects of exposure time and method used to create the flap,” J. Cataract Refract. Surg. 34(7), 1077–1082 (2008). 10.1016/j.jcrs.2008.03.022 [DOI] [PubMed] [Google Scholar]
- 8.Lohmann C. P., Güell J. L., “Regression after LASIK for the treatment of myopia: the role of the corneal epithelium,” Semin. Ophthalmol. 13(2), 79–82 (1998). 10.3109/08820539809059822 [DOI] [PubMed] [Google Scholar]
- 9.Patel S., Alió J. L., Pérez-Santonja J. J., “Refractive index change in bovine and human corneal stroma before and after lasik: a study of untreated and re-treated corneas implicating stromal hydration,” Invest. Ophthalmol. Vis. Sci. 45(10), 3523–3530 (2004). 10.1167/iovs.04-0179 [DOI] [PubMed] [Google Scholar]
- 10.Bolin F. P., Preuss L. E., Taylor R. C., Ference R. J., “Refractive index of some mammalian tissues using a fiber optic cladding method,” Appl. Opt. 28(12), 2297–2303 (1989). 10.1364/AO.28.002297 [DOI] [PubMed] [Google Scholar]
- 11.Lai J. C., Li Z. H., Wang C. Y., He A., “Experimental measurement of the refractive index of biological tissues by total internal reflection,” Appl. Opt. 44(10), 1845–1849 (2005). 10.1364/AO.44.001845 [DOI] [PubMed] [Google Scholar]
- 12.Ding H. F., Lu J. Q., Jacobs K. M., Hu X. H., “Determination of refractive indices of porcine skin tissues and intralipid at eight wavelengths between 325 and 1557 nm,” J. Opt. Soc. Am. A 22(6), 1151–1157 (2005). 10.1364/JOSAA.22.001151 [DOI] [PubMed] [Google Scholar]
- 13.Choi W., Fang-Yen C., Badizadegan K., Oh S., Lue N., Dasari R. R., Feld M. S., “Tomographic phase microscopy,” Nat. Methods 4(9), 717–719 (2007). 10.1038/nmeth1078 [DOI] [PubMed] [Google Scholar]
- 14.Dirckx J. J., Kuypers L. C., Decraemer W. F., “Refractive index of tissue measured with confocal microscopy,” J. Biomed. Opt. 10(4), 044014 (2005). 10.1117/1.1993487 [DOI] [PubMed] [Google Scholar]
- 15.Haruna M., Ohmi M., Mitsuyama T., Tajiri H., Maruyama H., Hashimoto M., “Simultaneous measurement of the phase and group indices and the thickness of transparent plates by low-coherence interferometry,” Opt. Lett. 23(12), 966–968 (1998). 10.1364/OL.23.000966 [DOI] [PubMed] [Google Scholar]
- 16.Knüttel A., Boehlau-Godau M., “Spatially confined and temporally resolved refractive index and scattering evaluation in human skin performed with optical coherence tomography,” J. Biomed. Opt. 5(1), 83–92 (2000). 10.1117/1.429972 [DOI] [PubMed] [Google Scholar]
- 17.Maruyama H., Inoue S., Mitsuyama T., Ohmi M., Haruna M., “Low-coherence interferometer system for the simultaneous measurement of refractive index and thickness,” Appl. Opt. 41(7), 1315–1322 (2002). 10.1364/AO.41.001315 [DOI] [PubMed] [Google Scholar]
- 18.Wang X. Y., Zhang C. P., Zhang L. S., Xue L. L., Tian J. G., “Simultaneous refractive index and thickness measurements of bio tissue by optical coherence tomography,” J. Biomed. Opt. 7(4), 628–632 (2002). 10.1117/1.1501887 [DOI] [PubMed] [Google Scholar]
- 19.Kim S., Na J., Kim M. J., Lee B. H., “Simultaneous measurement of refractive index and thickness by combining low-coherence interferometry and confocal optics,” Opt. Express 16(8), 5516–5526 (2008). 10.1364/OE.16.005516 [DOI] [PubMed] [Google Scholar]
- 20.Zvyagin A., Silva K. K., Alexandrov S., Hillman T., Armstrong J., Tsuzuki T., Sampson D., “Refractive index tomography of turbid media by bifocal optical coherence refractometry,” Opt. Express 11(25), 3503–3517 (2003). 10.1364/OE.11.003503 [DOI] [PubMed] [Google Scholar]
- 21.Klintworth G. K., “The cornea--structure and macromolecules in health and disease. A review,” Am. J. Pathol. 89(3), 718–808 (1977). [PMC free article] [PubMed] [Google Scholar]
- 22.Kim Y. L., Walsh J. T., Jr, Goldstick T. K., Glucksberg M. R., “Variation of corneal refractive index with hydration,” Phys. Med. Biol. 49(5), 859–868 (2004). 10.1088/0031-9155/49/5/015 [DOI] [PubMed] [Google Scholar]
- 23.Lin R. C., Shure M. A., Rollins A. M., Izatt J. A., Huang D., “Group index of the human cornea at 1.3-microm wavelength obtained in vitro by optical coherence domain reflectometry,” Opt. Lett. 29(1), 83–85 (2004). 10.1364/OL.29.000083 [DOI] [PubMed] [Google Scholar]
- 24.Meek K. M., Dennis S., Khan S., “Changes in the refractive index of the stroma and its extrafibrillar matrix when the cornea swells,” Biophys. J. 85(4), 2205–2212 (2003). 10.1016/S0006-3495(03)74646-3 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Tang S., Zhou Y. F., Chan K. K. H., Lai T., “Multiscale multimodal imaging with multiphoton microscopy and optical coherence tomography,” Opt. Lett. 36(24), 4800–4802 (2011). 10.1364/OL.36.004800 [DOI] [PubMed] [Google Scholar]
- 26.Chan K. K. H., Tang S., “High-speed spectral domain optical coherence tomography using non-uniform fast Fourier transform,” Biomed. Opt. Express 1(5), 1309–1319 (2010). 10.1364/BOE.1.001309 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.J. Pawley, Handbook Of Biological Confocal Microscopy, 3rd ed. (Springer, 2006). [Google Scholar]
- 28.Ganic D., Gan X., Gu M., “Reduced effects of spherical aberration on penetration depth under two-photon excitation,” Appl. Opt. 39(22), 3945–3947 (2000). 10.1364/AO.39.003945 [DOI] [PubMed] [Google Scholar]
- 29.Daimon M., Masumura A., “Measurement of the refractive index of distilled water from the near-infrared region to the ultraviolet region,” Appl. Opt. 46(18), 3811–3820 (2007). 10.1364/AO.46.003811 [DOI] [PubMed] [Google Scholar]
- 30.R. David, Lide, Handbook of Chemistry and Physics, 93th ed., CRC Press (2012). [Google Scholar]
- 31.B. G. Kapoor and T. J. Hara, Sensory Biology of Jawed Fishes: New Insights, Science Publishers, Inc (2001). [Google Scholar]
- 32.Patel S., “Refractive index of the mammalian cornea and its influence during pachometry,” Ophthalmic Physiol. Opt. 7(4), 503–506 (1987). 10.1016/0275-5408(87)90085-8 [DOI] [PubMed] [Google Scholar]
- 33.S. L. Meyer, Data Analysis for Scientists and Engineers (Peer Management Consultants, 1992). [Google Scholar]
- 34.Schmitt J. M., Xiang S. H., Yung K. M., “Speckle in optical coherence tomography,” J. Biomed. Opt. 4(1), 95–105 (1999). 10.1117/1.429925 [DOI] [PubMed] [Google Scholar]