Spectral Label Fusion

Abstract

We present a new segmentation approach that combines the strengths of label fusion and spectral clustering. The result is an atlas-based segmentation method guided by contour and texture cues in the test image. This offers advantages for datasets with high variability, making the segmentation less prone to registration errors. We achieve the integration by letting the weights of the graph Laplacian depend on image data, as well as atlas-based label priors. The extracted contours are converted to regions, arranged in a hierarchy depending on the strength of the separating boundary. Finally, we construct the segmentation by a region-wise, instead of voxel-wise, voting, increasing the robustness. Our experiments on cardiac MRI show a clear improvement over majority voting and intensity-weighted label fusion.

1 Introduction

Label fusion has gained much popularity in medical image segmentation. It benefits from prior information in a form of images previously labeled by experts. Instead of summarizing the data as a probabilistic atlas [2], label fusion algorithms maintain and use all the labeled images [6,9,11]. In various comparisons, label fusion outperforms alternative atlas-based segmentation strategies when the anatomical variability is too large to be represented by mean statistics [6,9].

In computer vision, spectral techniques, such as normalized cuts [12], are commonly employed for segmentation. Central to these methods is the quantification of pairwise similarities between points in the image, which serve as weights for the graph Laplacian. Earlier work computed the similarity by comparing intensity values [12]. Further studies introduced intervening contours, which relate the similarity between two locations to the existence of a boundary separating them [5]. In order to extract the boundary, image edges and textons are calculated to combine contour and texture cues [8]. The spectral framework constructs a globally optimal partitioning based on these local measures. In a recent comparison [1], a multiscale version of normalized cuts outperformed other contour detectors and produced excellent segmentation results on natural images.

The mentioned spectral algorithms, as well as active contour and level set techniques, obtain impressive results by solely considering image cues. In contrast, label fusion segmentation is mainly based on intensity differences between the images, but the contour information in the test image is rarely exploited. Our method addresses exactly this issue and closes the gap between label fusion techniques and spectral segmentation approaches. We combine image contour cues and label information in the graph Laplacian to produce contours that jointly depend on the atlas and the test image. Fig. 1 illustrates that this is beneficial. Intensity-weighted label fusion [11] leads to an undersegmentation of the left atrium of the heart (Fig. 1(a)). We observed this behavior in many cases. Using image contours only faces challenges in identifying the correct boundaries, especially for smooth intensity transitions (Fig. 1(b)). As a result, certain parts are oversegmented while others, e.g., the veins, are cut off. The segmentation with spectral label fusion, which fuses image and label information, leads to the most accurate segmentation. The proposed algorithm constitutes a novel approach to integrate prior information in spectral segmentation and leverages state-of-the-art contour and region extraction methods to enhance label fusion.

Fig. 1.

Example segmentations of the left atrium of the heart. Automatic segmentation is shown in yellow, expert labeling is shown in red.

1.1 Clinical Motivation

The proposed approach is well suited for delineating structures of high variability, which are challenging to segment with atlas-based techniques due to difficulties of inter-subject registration. With the integration of local image cues, the method is less prone to alignment errors. We focus on the left atrium of the heart, which exhibits large variations in the shape of the cavity and in the number and location of pulmonary veins [4]. Its segmentation is of significant clinical relevance, because one of the most common heart conditions is atrial fibrillation [4]. In atrial fibrillation, the left atrium no longer pumps blood into the left ventricle efficiently but instead quivers in an abnormal way. The common treatment is radio-frequency catheter ablation of ectopic foci [7]. Accurate segmentation of the left atrium and its pulmonary venous drainages on contrast-enhanced magnetic resonance angiography (MRA) images is essential for planning and evaluating ablation procedures.

1.2 Related Work

In addition to prior work reviewed above, our work is also related to a relatively new approach for brain image segmentation based on non-local means filtering [3,10]. The method compares image patches between the test subject and the atlas images, with voting that depends on intensity differences between these patches. In our application this technique seems less promising because we work with contrast-enhanced MRA images, characterized by substantial intensity variations. In [14], a local search on patches is performed to improve the results after the atlas-based segmentation. Instead of refining the segmentation through the integration of image information in a post-processing step, we consider image and label information jointly in the graph Laplacian. Moreover, we work on image contours that have advantages over comparing intensities [5].

Recently, an algorithm based on graph cuts has been demonstrated for the refinement of atlas propagation [13,15]. In contrast to this method, we apply techniques from spectral clustering and combine gradient and texture cues, leading to a region-based voting on an oversegmentation of the image. In [7], the segmentation of the left atrium is obtained by extracting the blood pool with intensity thresholding, which is sensitive to intensity variations. Intensity-weighted label fusion achieved accurate results for the segmentation of the left atrium in [4]. We therefore treat this label fusion technique as a baseline for comparison.

2 Method

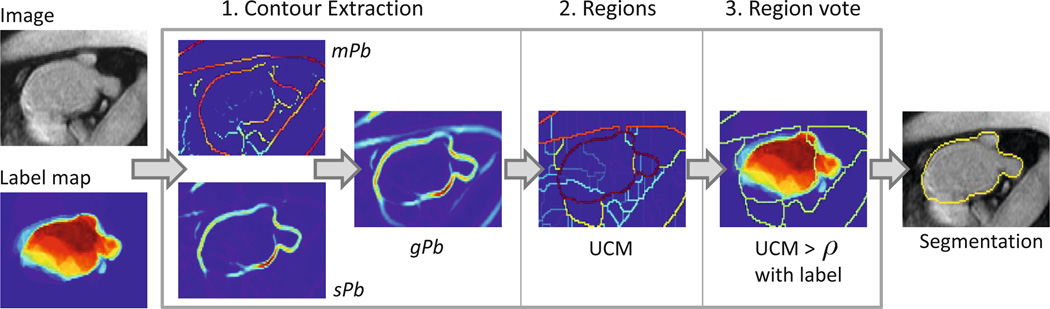
Spectral label fusion consists of three steps, as illustrated in Fig. 2. The first step extracts the boundaries from the image and label map, joins them in the spectral framework, and produces weighted contours. In the second step, these contours give rise to regions, partitioning the image. In the third step, we assign a label to each region based on the input label map, producing the final segmentation. We formulate segmentation as a binary labeling problem; for a multi-label problem the same procedure is repeated for each label.

Fig. 2.

Overview of spectral label fusion

2.1 Input Data

The new image I to be segmented and the probabilistic label map L̂ are the inputs to the algorithm. Any atlas-based approach, parametric or non-parametric, can be employed to create the label map, which serves as atlas-based label prior. In this work, we adapt the label fusion approach and register each of the images in the training set to image I with a variant of the diffeomorphic demons algorithm, iteratively fitting a polynomial transfer function to compensate for intensity differences in the MRA images [4]. We use ℐ = {I₁,…, I_n} to denote the transformed and intensity corrected training images. We apply the estimated warps to the labels, leading to propagated labels ℒ = {L₁,…, L_n}. Following the formulation in [4,11], we compute the MAP labeling at location x:

$$\mathrm{L̂}(x)=\text{arg}\underset{l}{\text{max}}p(L(x)=l,I(x)|ℒ,ℐ)=\text{arg}\underset{l}{\text{max}}{\displaystyle \sum _{i=1}^n}p(L(x)=l|L_i)·p(I(x)|I_i).$$ (1)

The label likelihood $p(L(x)=l|L_i)\propto \text{exp}(\kappa D_i^l)$ serves as soft vote, weighted by the image likelihood $p(I(x)|I_i)\propto \text{exp}(-\frac{{(I(x)-I_i(x))}^2}{2{\sigma }^2})$. $D_i^l$ is the signed distance transform of label l in the warped label map L_i. We set κ = 1.5 and σ² = 1.

2.2 Contours

We employ the concept of intervening contours to calculate the weights in the graph Laplacian, which leads to better results than the comparison of intensity values [5]. The first step is to estimate the probability Pb(x) of a contour in each slice of the image I at location x. We choose to employ the oriented gradient signal [1]. The method robustly estimates the image gradient by calculating the χ² distance between the histograms of two half-discs at each location for various orientations. Depending on the size of the disc, we obtain gradient estimates on multiple scales. To quantify the texture in the image, we calculate textons by convolving the image with 17 Gaussian derivative and center-surround filters [8]. We obtain 64 different textons with a K-means clustering in the 17-dimensional space. The image and texton gradients of multiple scales are added, resulting in the multiscale contour probability mPb(x) [1], as illustrated in Fig. 2. We use mPb to calculate weights between points i and j in the image, following the concept of intervening contours by identifying the maximum along the line $\overline{\mathit{\text{ij}}}$:

$$W_{\mathit{\text{ij}}}^I=\text{exp }(-\underset{x\in \overline{\mathit{\text{ij}}}}{\text{max}}\{\mathit{\text{mPb}}(x)\}).$$ (2)

Analogously, we estimate the probability of a contour in the label map L̂, denoted by lPb, and derive the weights

$$W_{\mathit{\text{ij}}}^L=\text{exp }(-\underset{x\in \overline{\mathit{\text{ij}}}}{\text{max}}\{\mathit{\text{lPb}}(x)\}).$$ (3)

For computational efficiency the weights are only calculated within a radius r = 5, yielding sparse matrices [1].

Once the image and label weights are computed, we combine them in the joint weight matrix

$$W=W^I+W^L.$$ (4)

The generalized eigenvalue decomposition (D − W)v = λDv gives rise to eigenvectors v_k that partition the image based on image and label cues, with D_ii = ∑_i W_ij. We consider the 16 eigenvectors corresponding to the smallest non-zero eigenvalues λ_k. Instead of performing a K-means clustering in the 16 dimensional space [12], which tends to break up uniform regions [1], we obtain the spectral boundary sPb by summing up the gradients of the eigenvectors $\mathit{\text{sPb}}={\displaystyle {\sum }_{k=1}^{16}}\frac{1}{\sqrt{{\lambda }_k}}·\nabla {\mathbf{v}}_k$. While mPb contains responses to all edges, sPb only shows the most salient structures in the image. The global contour is obtained by combining both maps to take advantage of the two characteristics, i.e., gPb = mPb + γ · sPb, where γ is a weighting constant.

2.3 From Contours to Regions

In the second step, we use the extracted contours gPb to partition the image into regions. These regions form an oversegmentation of the image. Consequently, the left atrium and veins do not correspond to one but several regions. The size of these regions is subject to a trade-off. Large regions provide stability in the face of registration errors, but they are also more likely to miss the actual organ boundary. To enable adaptive region size selection, we use the strength of the extracted boundaries to build a hierarchical segmentation. At the lowest level, we have the finest partition of the image, and the higher levels contain larger regions implied by stronger contours.

Specifically, we use the oriented watershed transform to create the finest partition [1]. We experimented with the watershed in 2D and 3D. For the 3D watershed, we apply a 3D closing operation of the contours to prevent leakage in out-of-plane direction. Next, we employ the ultrametric contour map (UCM) [1] to represent the hierarchical segmentation, illustrated in Fig. 2. We clearly see that the strong boundary of the atrium appears in the UCM. We select the segmentation scale in the hierarchy by thresholding with parameter ρ.

2.4 Voting on Regions

One of the limitations of the current label fusion framework [11] is the assumption of independence of voxel samples, which is generally not justified for medical images. It is more appropriate to consider independence with respect to a local neighborhood, applying the Markov property in the derivation. Crucial is the selection of image-specific neighborhoods that capture the relevant information. The regions constructed in the previous step can naturally serve as such neighborhoods. We obtain the region-based MAP estimation by considering the location x as random variable and marginalizing over it

$${\mathrm{L̃}}^R=\text{arg}\underset{l}{\text{max}}{\displaystyle \sum _{x\in R}}p(L^R=l|ℒ,x)p(I^R|ℐ,x)p(x)$$ (5)

$$=\text{arg}\underset{l}{\text{max}}{\displaystyle \sum _{x\in R}}{\displaystyle \sum _{i=1}^n}\text{exp }(\kappa D_i^l(x)-\frac{{(I(x)-I_i(x))}^2}{2{\sigma }^2}),$$ (6)

where L^R and I^R denote the region R in the label map and the intensity image, respectively. Since we aggregate the voting information over the entire region, the resulting method is more robust to registration errors and noise than a voxel-based approach.

3 Experiments

To evaluate the proposed method, we automatically segment the left atrium of the heart in a set of 16 electro-cardiogram gated (0.2 mmol/kg) Gadolinium-DTPA contrast-enhanced cardiac MRA images (CIDA sequence, TR=4.3ms, TE=2.0ms, θ = 40°, in-plane resolution varying from 0.51mm to 0.68mm, slice thickness varying from 1.2mm to 1.7mm, 512 × 512 × 96, −80 kHz bandwidth, atrial diastolic ECG timing to counteract considerable volume changes of the left atrium). The left atrium was manually segmented in each image by an expert. For all the experiments we set γ = 2.5, giving higher weight to the spectral component. We set ρ = 0.2 for the 2D and ρ = 0 for the 3D watershed after inspecting the UCM. We perform leave-one-out experiments by treating one subject as the test image and the remaining 15 subjects as the training set. We use the Dice score and the modified (average) Hausdorff distance between the automatic and expert segmentations as quantitative measures of segmentation quality. We compare our method to majority voting (MV) and intensity-weighted label fusion (IW) [11].

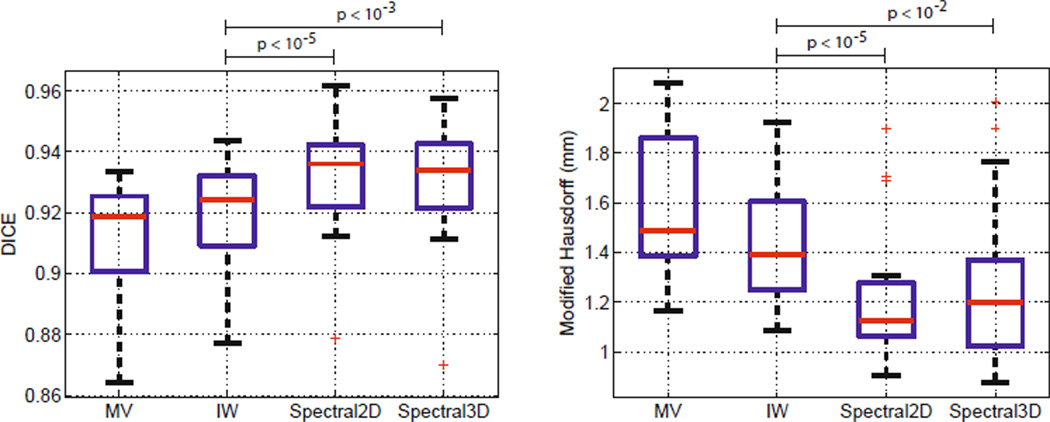
We apply a median filter in a 5 × 5 × 5 window to the spectral segmentations. In-plane filtering has little effect; filtering improves the consistency and closes holes in out-of-plane direction. The application of the filter on MV and IW segmentations led to a deterioration on all subjects. We therefore present unfiltered results for these cases. Fig. 1 illustrates the results of IW and the 2D spectral label fusion, together with an approach that considers only image contours, W = W^I. Fig. 3 presents dice volume overlap and modified Hausdorff distance for each algorithm. The improvements in segmentation accuracy between the proposed method and IW are statistically significant (p<10⁻⁵). At first glance, it may seem surprising that the 2D algorithm leads to better results than the 3D version. The anisotropic resolution of the data presents a challenge for extracting meaningful 3D regions. A further inspection of the results in each subject reveals that the values for IW are always better than the ones for MV, and the values of the 2D spectral method are consistently better than the ones for IW.

Fig. 3.

Dice volume overlap (left) and modified Hausdorff distance (right). Red line indicates median, the boxes extend to the 25^th and 75^th percentiles, and the whiskers reach to the most extreme values not considered outliers (red crosses). Significance was evaluated using a single-sided paired t-test with IW as baseline.

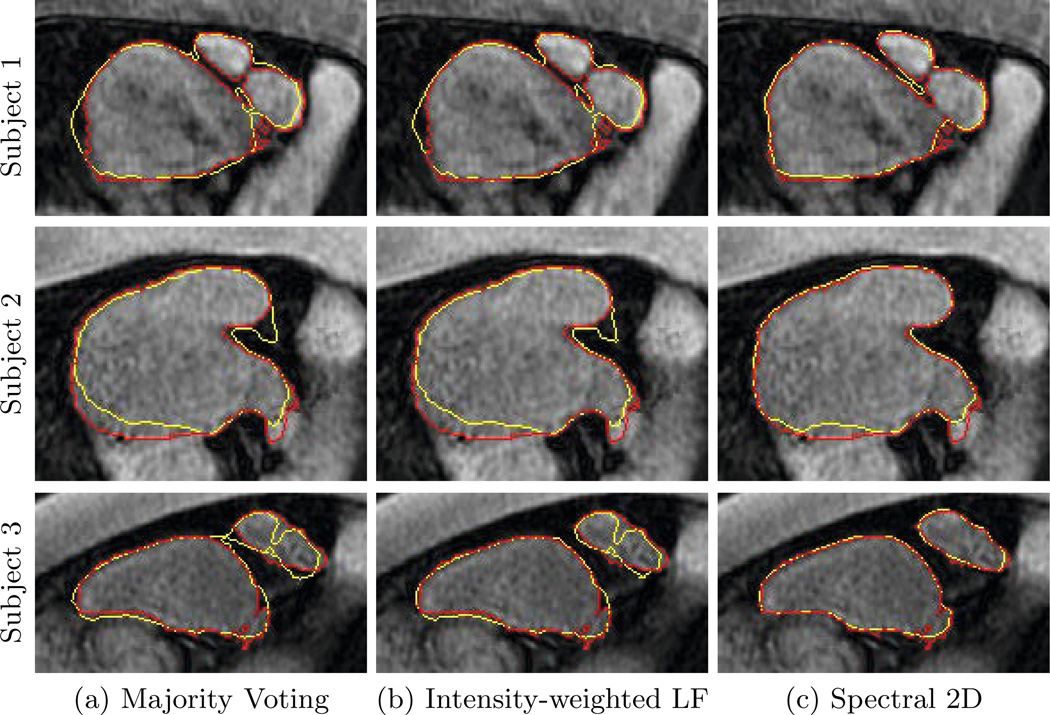
Fig. 4 illustrates the segmentation results for MV, IW, and 2D spectral fusion for several subjects. We see that spectral fusion better captures the organ boundary. This is supported by the clearly lower Hausdorff distances in Fig. 3. On the images for Subject 1 in Fig. 4, we observe that spectral label fusion achieves a better separation between the veins and atrium. This case is particularly challenging because the gap is small and registration errors of misaligning either the vein or the atrium lead to a closure. By integrating the image cues and voting on regions, we achieve a more accurate segmentation.

Fig. 4.

Examples of automatic segmentation results for different subjects are shown in yellow. Manual delineations are shown in red.

4 Conclusion

We presented spectral label fusion, a new approach for multi-atlas image segmentation. It combines the strengths of label fusion with advanced spectral segmentation. The integration of label cues into the spectral framework results in improved segmentation performance for the left atrium of the heart. The extracted image regions form a nested collection of segmentations and support a region-based voting scheme. The resulting method is more robust to registration errors than a voxel-wise approach.