Insights from in situ analysis of TCR–pMHC recognition: response of an interaction network

Summary

Recognition of peptide presented by the major histocompatibility complex (pMHC) molecule by the T-cell receptor (TCR) determines T-cell selection, development, differentiation, fate, and function. Despite intensive studies on the structures, thermodynamic properties, kinetic rates, and affinities of TCR–pMHC interactions in the past two decades, questions regarding the functional outcome of these interactions, i.e. how binding of the αβ TCR heterodimer with distinct pMHCs triggers different intracellular signals via the adjacent CD3 components to produce different T-cell responses, remain unclear. Most kinetic measurements have used surface plasmon resonance, a three-dimensional (3D) technique in which fluid-phase receptors and ligands are removed from their cellular environment. Recently, several two-dimensional (2D) techniques have been developed to analyze molecular interactions on live T cells with pMHCs presented by surrogate antigen presenting cells or supported planar lipid bilayers. The insights from these in situ analyses have provided a sharp contrast of the 2D network biology approach to the 3D reductionist approach and prompted rethinking of our current views of T-cell triggering. Based on these insights, we propose a mechanochemical coupled triggering hypothesis to explain why the in situ kinetic parameters differ so much from their 3D counterparts yet correlate so much better with T-cell functional responses.

Introduction

The basis for much of our immune system occurs as the cells comprising an immune response interact among themselves via molecules integrated and displayed on their plasma membranes. T cells, for example, express hundreds of such proteins on their surface. Some are receptors for soluble ligands, such as growth factors and cytokines. Others bind ligands anchored to the surface of another cell or extracellular matrix, such as adhesion receptors, immune receptors, and costimulatory molecules. To understand how the immune system works thus requires analysis of molecular interactions in the context of the cellular functions. The key factor in controlling how a T cell functions in its environment is the interaction of the T-cell receptor (TCR) with peptide bound to major histocompatibility complex (pMHC) molecule. Specific recognition of peptides is required to trigger developmentally appropriate responses at the distinct stages of T-cell maturation. For example, developing T cells in the thymus differ from peripheral T cells in that they possess substantially fewer TCRs on the surface, express both the CD4 and CD8 co-receptors, and make use of thymic epithelial cells to present self-antigens for at least the positive selection events. Furthermore, peripheral T cells interact with several types of antigen-presenting cells (APCs) and target cells expressing antigens as they mature into specific effector and memory cells. Thus, the same clonal TCR can lead to a range of T-cell responses and different cell fates depending on the context of interaction with antigen.

The outcome of a T-cell response is determined by the basic biochemical parameters of the TCR–pMHC interaction, since the TCR is the only molecule on the T-cell surface that senses antigen. Overall many characteristics of the TCR–pMHC interaction have been analyzed, including structural features (1–5), thermodynamic properties (6–8), rupture forces (9), affinity, and kinetic on-/off-rates. Of these parameters, the most extensively studied have been the TCR–pMHC affinity and kinetics, which are typically carried out using purified recombinant proteins and often analyzed by surface plasmon resonance (SPR) (10–17). In SPR, ligand binding is measured in solution as protein flows over a sensor chip coated with a recombinant receptor or vice versa. These measurements are considered to be three-dimensional (3D) binding because the soluble molecule is transported in a 3D space. Kinetic analysis of TCR–pMHC binding by SPR has provided useful information on the intrinsic physical chemistry of this interaction. In general, the best 3D parameter correlated to antigen potency and T-cell response has been the half-life of the TCR–pMHC bond, with progressively lesser degrees of correlation with the 3D affinity and on-rates. However, numerous outlier TCR–pMHC interactions have been observed (1, 10, 15, 16, 18–20) in which antigen potency did not equate to the 3D binding parameters. This is most readily apparent with antagonist altered peptide ligands (10, 15, 16, 19).

TCR binding measured in 3D by SPR is very different from how it occurs on real cells, which takes place at the interface of two apposing membranes. Instead of a simple biochemical analysis of purified proteins in 3D, TCR–pMHC interactions take place in different membrane environments between cells in the presence of other molecules that can affect the kinetic measurements in potentially unexpected ways. This is considered as two-dimensional (2D) binding because the cross-junctional gap spanned by the interacting proteins is negligibly small compared to the other two dimensions of the contact area formed between T-cell and APC membranes. This fundamental difference between 2D kinetic rates and their 3D counterparts is apparent in the units associated with the kinetic rates. The 2D affinity and on-rate units reflect the properties and limitations of the apposing membranes and are expressed in terms of surface density of the interacting molecules (per area, µm⁻² and per area per time, µm⁻² s⁻¹), whereas the 3D equilibrium dissociation constant (K_d) and on-rate units with which most immunologists are familiar are expressed in units of their volumetric concentration (molarity) and per concentration per time (M⁻¹ s⁻¹). Examinations of the 2D chemistries at work are still in their infancy, but the resulting kinetic rates (k_on and k_off) and the binding affinity (K_a, reciprocal of K_d) are beginning to reveal novel insights into antigen-specific triggering of T cells. Importantly, recent in situ measurements suggest that the 2D kinetic parameters more accurately reflect the biological outcome associated with antigen recognition by T cells (1, 21–24). Of note, there has been minimal success at transposing 2D to 3D kinetic rates or vice versa making this a highly relevant area of future research.

Several recent reviews have highlighted the importance of in situ 2D measurements of TCR–pMHC interactions. Those reviews summarized recent 2D data, discussed the advantages of new 2D methods over traditional 3D methods, pointed the differences and potential bridges between 2D and 3D parameters, indicated impacts of the new 2D data on existing models of T-cell discrimination and suggested how the in situ 2D kinetics may contribute to the understanding of T-cell antigen recognition at live cell membrane, including sensitivity, specificity, and speed (25–27). This review mostly focuses on the biological differences between SPR 3D measurements, a reductionist approach, and in situ 2D analyses, which require an understanding of the protein interactions at a systems level. We provide an overview of the 2D measurement techniques, followed by comparison of the 2D and 3D parameters of the same interactions for several systems as well observations made and insights gained from the new 2D data to T-cell biology. We then discuss how to take advantage of the complexity of the in situ measurements to analyze the T cell with a systems approach based on a model we termed mechanochemical coupled triggering. We also present an example for such analysis that involves signaling-dependent cooperative binding of pMHC by the TCR and CD8.

2D TCR binding kinetics within a network of interactions

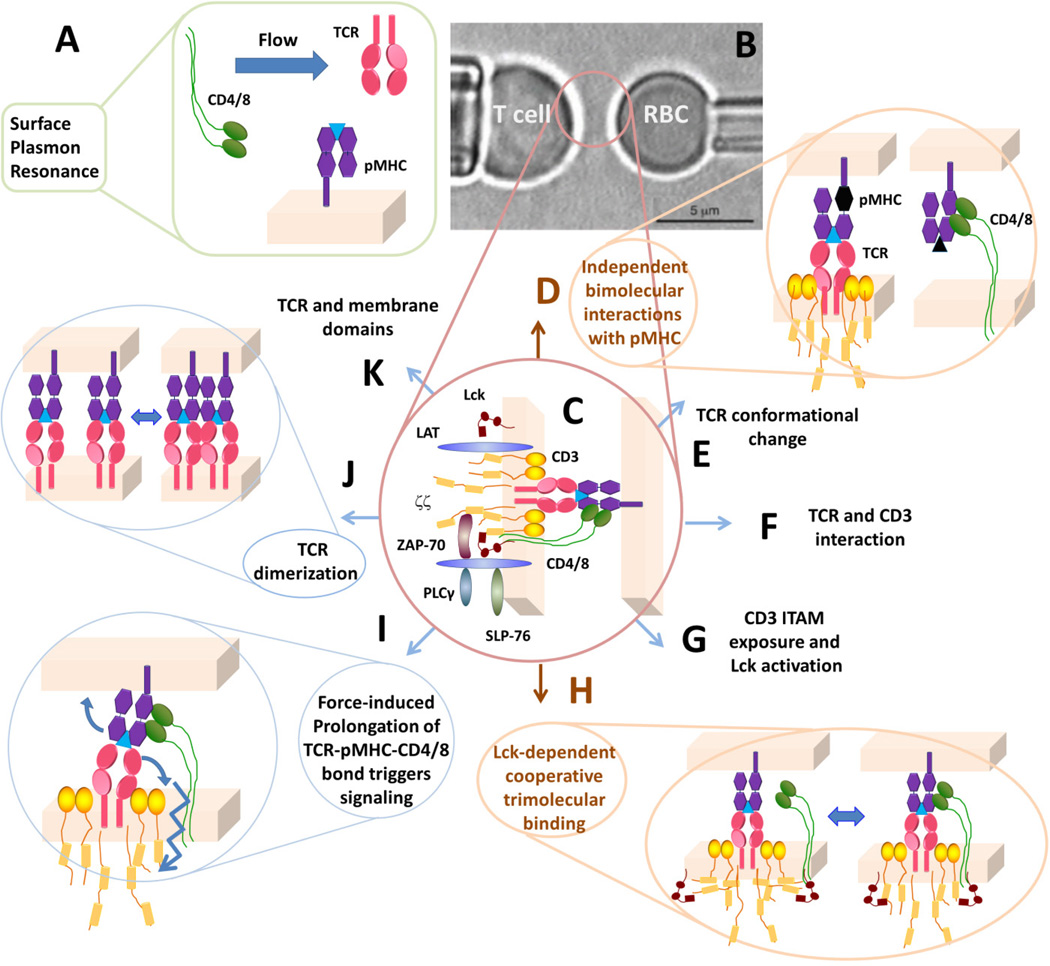
When one is assessing the response of membrane associated proteins, there is an obvious difference between the context of assessing receptor–ligand binding kinetics using purified proteins like in SPR (Fig. 1A) as opposed to a similar analysis of the same proteins in their proper context within the membrane (Fig. 1C). Molecular interactions on living cells are coupled with other biological processes, which are not accounted for in analysis of purified proteins (compare Fig. 1A and C). Without doubt, these biological differences would impact the measured results, but they have not been sufficiently recognized, understood, or appreciated. On the T-cell membrane, the TCR-CD3 complex includes not only the pMHC-binding αβ chains but also the CD3γε, δε, and ζζ dimeric signaling chains. The T-cell triggering converts pMHC-binding events by the TCR into immunoreceptor tyrosine-based activation motif (ITAM) phosphorylation and downstream signaling events. Thus, interactions among the subunits of the TCR-CD3 complex are necessary for the signal of TCR recognition to transit from outside to inside the cell. The TCR-CD3 complex additionally interacts with other structures at and beneath the plasma membrane, including CD4/8 co-receptor, Lck, ζ-associated protein of 70 kDa (ZAP-70), linker of activation of T cells (LAT), SH2 domain-containing leukocyte protein of 76 kDa (SLP-76), phospholipase Cγ (PLCγ), actin cytoskeleton, etc. (Fig. 1C). These form a network of interactions of which the TCR–pMHC is an integral part (28).

Fig. 1. Analysis of molecular interactions at the T-cell surface.

(A) Traditionally, TCR–pMHC and pMHC–CD4/8 interactions are analyzed in 3D by SPR using soluble molecules. (B) In the micropipette adhesion assay, live T cell is probed by a pMHC-coated RBC. (C) The interaction network being probed by the pMHC, including the TCR-CD3 complex, co-receptor, proximal signaling complexes formed after TCR ligand recognition. (D) Using mutant MHC to abolish co-receptor binding or null peptide to abolish TCR binding, independent TCR–pMHC and pMHC–CD4/8 bimolecular interactions can be analyzed separately. (E–G) Possible kinetic steps leading to TCR triggering. (H) Signaling-dependent cooperative binding among TCR, pMHC, and CD8. (I) Possible regulatory role of mechanical force. (J, K) Possible molecular organizations of the TCR in the membrane.

The reductionist approach inherent in 3D analyses breaks down the network into individual elements for independent study. For analysis of specific pMHC and TCR interactions, the focus is on probing the distal end of the TCRαβ chains by selected pMHCs. Analysis of purified proteins is useful when the binding kinetics of the selected receptor–ligand chains are negligibly impacted from associated proteins. In this case, SPR clearly provides intrinsic parameters describing the physical chemistry of the non-covalent interactions of the TCR–pMHC binding, but they provide very limited information regarding the interplay of binding events as part of a larger network of interactions. The a priori assumption fundamental to the SPR and other experiments employing cell-free systems is that the interactions defined with purified proteins accurately describe the binding events. The significant differences between 2D and 3D kinetics raise issues as to the validity of this assumption for TCR–pMHC interactions. In contrast, 2D methods analyze the whole cell as a system without exclusive limitation to the ligand–binding site, but inclusive of the entire network of interactions regulating access and orientation of the proteins (Fig. 1C). As such, the response to in situ 2D measurements should be considered as the systemic response of the network.

A recent comprehensive study making use of the 42F3 TCR system analyzed TCR binding to pMHCs by crystal structures, 3D SPR, 2D micropipette, pMHC tetramers, TCR tetramer, and functional responses to provide insights into requirements for T cell triggering (1). The results were consistent with the previous findings by our group and others in that the 2D affinities of the 42F3 TCR for a panel of pMHC ligands measured in situ correlated with the peptide potencies, but the 3D affinities measured by SPR with purified proteins did not (1). Interestingly, the 42F3 TCR tetramer pattern of interactions with APCs presenting different peptides mimicked the SPR 3D kinetic data, which did not predict peptide potency and T-cell functional response. These data reveal that removal of the TCR from the cell surface environment to probe pMHC interactions fails to correlate with T-cell response regardless of whether the TCR is used as purified monomeric or tetrameric protein. By comparison, keeping the TCR in the cell surface environment produces binding parameters that correlate with T-cell response, regardless of whether the in situ analysis is done with pMHC coated in a 2D surface or flowing in 3D as a tetramer. The different behaviors of the soluble 42F3 TCR from the cell surface TCR highlight the importance of analyzing TCR–pMHC interaction on the T-cell surface.

Overview of the 2D techniques

In 2010, two groundbreaking studies reported in situ analyses of different TCRs interacting with their respective antigens and panels of variant pMHCs (21, 22). Both show that the 2D parameters correlate with peptide potencies to activate T-cell effector functions better than their 3D counterparts. Two types of 2D methods have been developed: mechanical based (22) and fluorescent based (21). These methods probe the protein interactions in the context of the membrane environment but differ in how the interacting TCR–pMHC molecules are brought in contact, the time scales, the environments in which interactions occur, and how molecular interactions are measured. As the 2D methods differ, the description of the techniques provides information as to their respective strengths and weaknesses necessary for interpretation of the results. For example, the mechanical assays have high sensitivity to assess single-bond formation and dissociation over a short time frame but do not allow time for adhesion to be fully developed and strengthened. The fluorescence-based assays measure molecular interactions directly in an immunological synapse with mostly established contact areas. They can work at the level of single molecule or population of molecules and incorporate membrane diffusion of the interacting proteins. Overall the mechanical and fluorescent methods differ in the cellular environments where molecular interactions are measured, which have substantial impacts on the 2D parameter values. The end result is an enormous gap between the absolute affinity and on-rate values measured by the two classes of methods. Nonetheless, relative comparisons among different molecular interactions within each class of 2D techniques are consistent. More importantly, the 2D measurements differ from their 3D counterparts in a similar fashion regardless of whether they are measured by mechanical or fluorescent methods. Table 1 lists some of the technical aspects of the existing 2D methods.

Table 1.

Summary of the 2D methods

	2D Assays	Strengths	Weaknesses
Mechanical-based 2D Assays	The adhesion frequency assay	Single-bond detection sensitivity; Allows live cell measurements; Allows to probe first seconds of interaction; Ease to transpose to different receptor-ligand systems; Can be combined with force and lifetime measurements; Determines effective affinity and zero force off-rate with mathematical model; Higher sensitivity than tetramer binding.	Low throughput; Require extended models to extract kinetics parameters for interactions of more than one receptor-ligand species.
	The thermal fluctuation assay	Same strengths as 1–5 for adhesion frequency assay; Higher temporal and spatial resolution; More accurate kinetic parameters; Determines on- and off-rates at zero force.	Same weakness as the adhesion frequency assay; Technically challenging for both experiment and data analysis.
	The flow chamber assay	Same strengths as 1–4 for adhesion frequency assay; High throughput; Determines off-rates at a range of forces.	Unable/difficult to measure on-rate.
The population-based 2D fluorescent assays	Zhu-Golan Plot	Allows live cell measurements; Controls ligand presentation by glass-supported planer bilayer; Mimic immunological synapse; Determines 2D affinity for mobile molecules (equilibrium analysis).	Requires established contact area; Lower than single molecule resolution.
	Contact Area FRAP assay	Same strength as 1–3 for Zhu-Golan Plot; Determines 2D kinetic rates; Determines retarded diffusion and non-recoverable fraction in a stable contact area.	Same weakness as 1–2 for Zhu-Golan Plot; High non-recoverable fraction complicates analysis.
The single molecule-based 2D fluorescent assay	Single molecule FRET	Single-bond detection sensitivity; Allows live cell measurements; Direct visualization; Mimic immunological synapse.	High technical barrier for reagents design and generation; Requires fine-tuned optics.

Mechanical based 2D methods

The mechanical methods were originally developed to analyze adhesion receptor-ligand interactions, such as binding selectins and integrins with their corresponding ligands, because binding links the cells surfaces, making it amenable for mechanical measurements. Of the available mechanical methods, three have so far been used to study TCR–pMHC interactions: the micropipette adhesion frequency assay (1, 22–24), the thermal fluctuation assay (1, 22), and the flow chamber assay (29).

The micropipette adhesion frequency assay uses a human red blood cell (RBC) to present pMHC at a desired density (22, 30). This surrogate APC is aspirated by a micropipette, aligned opposite to a T cell aspirated by another micropipette and viewed laterally by an inverted microscope (Fig. 1B). To enable interaction, the two cells are driven into contact such that the onset, termination, and area of contact are precisely controlled. Here, the RBC serves as an ultrasensitive adhesion sensor as its soft membrane would be elongated by pico-newton force pulling at its apex, which is smaller than the force required to rupture a single TCR–pMHC bond (9). Although the outcomes of individual contacts are random, the likelihood or probability of adhesion (P_a) can be estimated from the adhesion frequency by averaging the binary adhesion scores (1 for adhesion and 0 for no adhesion) of many contacts. The adhesion frequency is measured over a range of contact times to generate kinetic information, which is then interpreted in terms of TCR–pMHC binding kinetics using a mathematical model.

The thermal fluctuation assay uses an advanced version of the micropipette system by attaching a pMHC-coated glass bead to the RBC apex to form a biomembrane force probe (BFP) (31). This allows the use of real-time image analysis to track the bead position precisely and rapidly with a nanometer spatial and sub-millisecond temporal resolution (32), sufficient to monitor the thermal fluctuation of the sensor probe in real-time. Such thermal fluctuations are damped by formation of a bond that connects the bead to the T cell, allowing the experimenter to identify the bond formation and dissociation events and measure lifetimes of individual bonds (33). The lifetime distribution is then interpreted using a model of first-order irreversible dissociation of single bonds (22).

The flow chamber assay uses fluid flow to separate freely flowing cells or functionalized microspheres from those bound to the chamber floor (29). An on-rate of cell or microsphere binding is determined from the tether rate, i.e. the ratio of the number of moving receptor-bearing cells or microspheres tethered to the ligand-coated chamber floor to the total number of microspheres flowing in the same focal plane per unit of time (34). In this assay, it is difficult to calculate the TCR–pMHC association on-rate from this cell or microsphere on-rate, because such calculation requires information for the frequency and duration of contacts between a flowing cell or microsphere and a stationary surface (34). Unfortunately, these parameters cannot be directly measured from the top view observation down to the chamber floor. Nevertheless, the microsphere on-rate can be used as a relative metric to compare 2D TCR on-rates for different pMHC ligands (29).The flow chamber assay derives off-rate from lifetime distribution of the tethers (assuming the microsphere is tethered by a single bond) in the same way as the thermal fluctuation assay derives off-rate from bond lifetime distribution. A single exponential decay lifetime distribution would support the model of first order irreversible dissociation of single bonds, enabling off-rate to be calculated from the decay rate or average of lifetime. An advantage of the flow chamber assay is that it measures tether lifetimes at different levels of wall shear stresses, enabling determination of off-rate as a function of force (29). By comparison, the micropipette adhesion frequency assay and the BFP thermal fluctuation assay measure off-rate in the absence of pulling force.

Fluorescence-based 2D methods

The fluorescence-based methods use a glass-supported bilayer reconstituted with lipid anchored ligands as surrogate APCs on which T cells form immunological synapses. The TCR and/or some of the ligands are conjugated with fluorescent tags of different colors to allow optical visualization and quantitation of molecular densities. Two fluorescence-based assays have been developed, one analyzes binding of a population of a large number of interacting molecules (35–40), the other analyzes single molecules (21).

The population-based 2D fluorescent assay uses a receptor (e.g. CD2) expressing cell (e.g. Jurkat) to form a contact area with a phospholipid bilayer by binding its ligand (e.g. CD58 for human or CD48 for mouse). Binding depletes the free ligand in the contact area, which drives its diffusion from outside to inside the contact area. This results in an accumulation of fluorescence, as measured by the differential fluorescent intensity from inside to outside of the contact area, which is proportional to the density of bonds. Just like in an SPR experiment, the equilibrium bond density increases with the free ligand density in the bilayer when ligand density is low, but reaches saturation when ligand density is sufficiently high. Fitting an equilibrium binding model to this Langmuir isotherm or its linear transformation, the 2D Scatchard plot (35) or Golan-Zhu plot (36, 40), allows for evaluation of the 2D affinity.

The above equilibrium analysis was later extended to a kinetic analysis by developing a contact area fluorescence recovery after photobleaching (FRAP) method, which measures the recovery of fluorescence in the contact area after it is bleached by a strong laser (38). Such a recovery results from a turnover of fluorescent bonds due to dissociation of bleached bound ligands from the cell surface receptors and their rebinding by unbleached ligands. The recovery curve thus contains information about both the diffusion of the ligand on the lipid bilayer and the kinetics of its interaction with the receptor on the cell. The kinetic parameters are extracted by fitting the experimental data with a coupled diffusion-reaction model (39).

The single molecule-based 2D fluorescent assay uses single-molecule fluorescence resonance energy transfer (FRET) and single molecule microscopy to measure 2D off-rate and affinity (21). In contrast to the aforementioned population-based method in which only the ligand is conjugated with fluorescence, in the single molecule-based method both the TCR on the T cell and the pMHC embedded in the planar lipid bilayer are respectively labeled with a pair of FRET donor and acceptor fluorophores. For intermolecular FRET to occur when TCR and pMHC bind, it requires that the two fluorophores be respectively attached to proper locations of the two interacting molecules. The choice of the locations was guided by the co-crystal structure of a monoclonal antibody Fab complexed with the Cβ region of a TCR. Based on structural analysis, a single-chain variable fragment (scFv) of this antibody was constructed with mutations that could be fluorescently labeled at sites of close proximity (4.1 nm) to the C-terminus of a peptide bound to a MHC to which the other fluorophore is attached. By monitoring the appearance and disappearance of single-molecule FRET signal, lifetimes of individual TCR–pMHC bonds are measured, which are analyzed the same way as single-bond lifetimes measured by BFP and flow chamber assays.

Huppa et al. (21) determined the 2D TCR–pMHC affinity by two methods. In the first method, the densities of TCR, pMHC, and TCR–pMHC bond were measured by dividing the intensity of the TCR fluorophore (Cy3) bulk fluorescent image (after acceptor bleaching), of the bulk pMHC fluorophore (Cy5) channel (before acceptor bleaching) and of the corrected FRET channel (before acceptor bleaching) through the average single-molecule intensity of the corresponding channel and by adjusting molecule numbers for the effective pixel size. With these densities a 2D K_a was calculated for each point over the entire immunological synapse. This method works only when the TCR could be quantitatively labeled by fluorescent scFv. When fast dissociation of the scFv underestimated the TCR density, the 2D affinity was determined by a second method using TCR occupancy, which is proportional to the FRET yield as determined through donor recovery after acceptor ablation. This method enables measurement of 2D affinities when a substantial proportion of the fluorescently labeled scFv has dissociated.

2D ligand–receptor off-rates are substantially faster than 3D counterparts

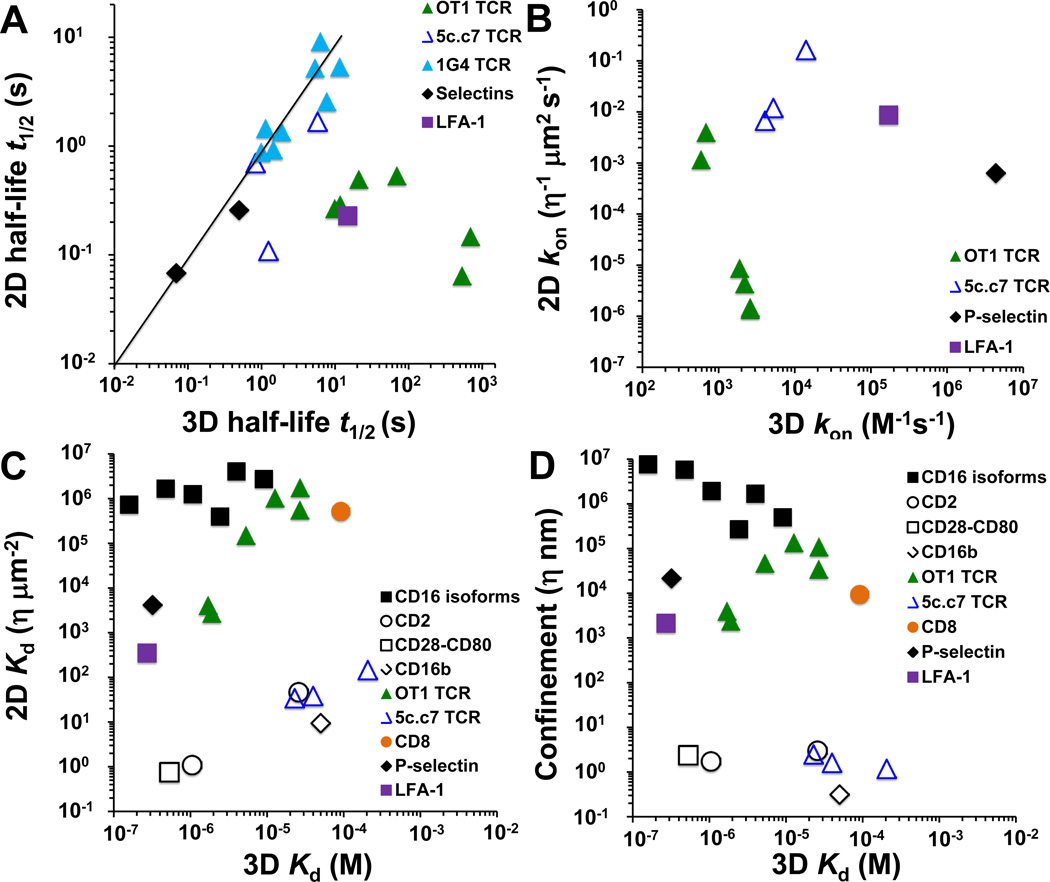
To gain insights into why the 2D parameters of TCR–pMHC interactions measured in situ better correlate with T-cell functions, it seems informative to compare 2D and 3D parameters of the same molecular interactions (Fig. 2). We begin with a comparison of off-rates, because this parameter has the same units of measure (time) regardless of 2D or 3D analysis. Fig. 2A plots the available half-life data for three TCRs: OT1 TCR on primary naive T cells from transgenic mice (22), 5c.c7 TCR on T-cell blasts (21), and soluble 1G4 TCR coated on microspheres (29). These interact with their respective antigens – ovalbumin, moth cytochrome c, and cancer testis antigens – and corresponding panels of variant pMHC ligands. Also plotted for comparison are half-lives of P-selectin glycoprotein ligand 1 (PSGL-1) bonds with P- and L-selectin on a cell-free system (33) and of intercellular adhesion molecule 1 (ICAM-1) bond with lymphocyte function-associated antigen 1 (LFA-1) on Jurkat cells (41). The 2D data obtained by mechanical (closed symbols) and fluorescent (open symbols) assays are indicated by different symbols. All 3D half-lives were measured by SPR (15, 16, 21, 42–45).

Fig. 2. Comparison of 2D and 3D binding parameters.

Half-life t_1/2 (A), on-rate k_on (B), equilibrium dissociation constant K_d (C), and confinement length (D) plots are shown for indicated molecular systems. 2D data obtained using living cells (unless otherwise stated) by the fluorescent and mechanical methods are shown with open and closed symbols, respectively. Data for TCR–pMHC interactions are shown as open or closed triangles. (A) 2D data for 1G4 TCR interacting with a panel of pMHCs () (29) and PSGL-1 interacting with P- and L-selectin (♦) (33) were measured using cell-free systems by the flow chamber and BFP thermal fluctuation assays, respectively. (B) k_on was calculated from the data in (A) and (C) by k_on = 0.693/(K_d × t_1/2). (C, D) Black symbols are from (46), including micropipette data for CD16 isoforms interacting with IgG of different species (■) (72), and Golan-Zhu plot data for CD2 interacting with CD58 and CD48 (○) (36), CD28–CD80 (□) (73), and CD16b-IgG (◊) (74) interactions.

When the data is plotted comparing 2D and 3D half-lives, the cell-free systems align with the diagonal line of a unit slope (Fig. 2A, line), regardless of whether they are for TCR–pMHC or selectin–PSGL-1 interactions. In other words, the 2D and 3D off-rates measured using the same recombinant molecules are in good agreement, regardless of whether one of the interacting partners is in the fluid phase (as in SPR) or both are linked to surfaces (as in flow chamber). Our own unpublished data obtained by respectively coating soluble 42F3 TCR and pMHC on two apposing surfaces for 2D assay (Liu B, Chen W, Adams JJ, Garcia KC, Zhu C) match the 3D data by SPR and by TCR tetramer (1), again indicating that removal of the TCR from the cell surface environment results in similar 2D and 3D results. These agreements between 2D and 3D results obtained using the same molecules in cell-free systems support the previous assertion based on biophysical considerations that off-rate is governed by the physical chemistry local to the binding interface of the interacting molecules, which is indifferent to whether the bonds are formed in 2D or 3D (46).

Strikingly, the data measured with living cells fall below the diagonal line, regardless of whether they are for TCR–pMHC or LFA-1–ICAM-1 interactions (Fig. 2A). This means that these 2D half-lives are shorter than their 3D counterparts. In other words, the 2D off-rates measured using living cells are faster than the 3D off-rates measured using soluble molecules. In the case of the OT1 TCR dissociating from agonist pMHCs, the 2D off-rates are up to three orders of magnitude more rapid than their 2D counterparts. For the 5c.c7 TCR, the 2D off-rates are 4–12-fold faster. For the LFA-1–ICAM-1 interaction, the 2D off-rate is 65-fold faster than the 3D off-rate. The underlying mechanism for these much faster off-rates is not clear but likely results from biological regulations of bond dissociation in situ. These possible factors are discussed further below, but elucidating biological mechanisms regulating off-rates will be an important area of future studies.

The correlation of TCR–pMHC half-life to the extent of response gives different results among the various model systems. In general, 3D half-lives of TCR–pMHC bonds correlate best with overall potency of responses (47–49). Because of their positive correlation with the 3D half-lives, the 2D half-lives of the 5c.c7 and 1G4 TCR bonds with their corresponding panels of pMHCs, respectively measured by single-molecule FRET and flow chamber, also equated to response levels. For the OT1 TCR, the most potent antigens yielded the shortest bond half-lives by the micropipette 2D analysis. This negative correlation with peptide potency is surprising, because it is opposite to the prediction of the popular kinetic proofreading model (50, 51). The negative correlation between 2D and 3D half-lives are also counter-intuitive, as it cannot be explained by any known biophysical considerations. We note that this is not an isolated case, as our recent data have provided another example in which short half-lives equate to more potent ligands (Liu B, Zhong S, Krogsgaard M, Zhu C., unpublished data). As discussed, this negative correlation with peptide potency can be corrected by replacing the lifetime of a single OT1 TCR by the lifetimes of all TCRs that a T cell accumulated in a unit time, which is related to the 2D affinity (22). For the 1G4 TCR, too long of half-lives also inhibited overall potency, arguing for an optimal half-life to maximize serial engagement of several TCRs by limited pMHC antigens (29). Correlation to peptide potency can be improved by incorporating the effects of both on- and off-rates to account for the total time when a TCR–pMHC pair stays together during binding and rebinding (42). Therefore, the seemingly different outcomes with the different 2D and 3D measures may relate to the assay used and the optimal half-life for serial engagement for the different antigens. A further complicating factor for understanding TCR–pMHC half-life and off-rate is the presence or absence of force. The flow chamber measures lifetimes of the 1G4 TCR bonds with pMHCs in a range of forces to extrapolate half-lives at zero force based on the Bell model (52). Huppa et al. (21) believed that the 2D half-lives of 5c.c7 TCR bonds were shortened by actin cytoskeleton-driven forces as treatment with actin depolymerizating agent latrunculin A lengthened half-lives. The importance of force in T-cell activation has been suggested by several reports (53–60). Unpublished work from our laboratory similarly suggests that force may regulate TCR–pMHC dissociation (Chen W, Liu B, Evavold BD, Zhu C, unpublished data).

Rapid and broadly ranged TCR 2D on-rates for pMHCs

In contrast to the off-rate that only depends on physical chemistry local to the TCR–pMHC interface, on-rate is thought to strongly depend on factors that regulate the space in which molecules are required to find their binding partners (46). Fig. 2B plots the on-rates for the OT1 and 5c.c7 TCRs interacting with their respective panels of pMHCs along with those for P-selectin–PSGL-1 and LFA-1–ICAM-1 associations. Previously, the high 2D affinity of the P-selectin–PSGL-1 interaction was attributed to its fast 2D on-rate, interpreted as a functional requirement for P-selectin–PSGL-1 interaction to capture flowing leukocytes on endothelium during brief encounters when they collide with the vessel wall (46). Interestingly, the 2D on-rates of the 5c.c7 TCR for all three pMHCs and of the OT1 TCR for two agonist pMHCs are even faster than that of P-selectin for PSGL-1 (Fig. 2B). More strikingly, the 3D on-rates of these TCR–pMHC interactions are orders of magnitude smaller than that of the P-selectin–PSGL-1 interaction. Furthermore, for their corresponding panels of pMHCs, the dynamic ranges of the TCR 2D on-rates are far broader than their 3D on-rates, as evident from the steep slopes of the 2D vs. 3D on-rate plots (Fig. 2B). For the OT1 system, the corresponding 3D on-rates are compacted in a narrow range of merely five-fold differences and show a slightly negative correlation with the peptide potencies. In sharp contrast, the 2D on-rates cover a huge 4-log range and correlate well with the peptide potencies. The 5c.c7 system is less dramatic, but the 2.7-fold range of 3D on-rates also corresponds to a much broader 13.7-fold range of 2D on-rates. It is currently unknown how the TCR–pMHC interactions achieve such broad 2D on-rate ranges with agonist pMHCs binding so fast despite that their 3D on-rates are compressed in low ranges, but the findings seem very compatible for the functional environment in which a TCR operates. For T-cell triggering to occur, the TCR must find antigen pMHC among the many other self-pMHC molecules presented by an APC. Intuitively, a much more rapid on-rate for antigen than self-pMHCs would be necessary for this process.

2D affinities depend on the environment where the molecular interactions occur

Affinity represents a balance between the dissociation off-rate constant and association on-rate to determine the equilibrium concentration (in 3D) or density (in 2D) of bonds per unit concentrations or densities of free receptors and ligands. Fig. 2C shows the K_d data (reciprocal affinity) for OT1 and 5c.c7 TCRs interacting with their respective antigens and corresponding panels of variant pMHC ligands (21, 22). These are compared to those of CD2, CD28, CD16, CD8, P-selectin, and LFA-1 interacting with their respective ligands (some receptors have multiple isoforms and/or multiple ligands). The 2D data were obtained from the micropipette adhesion frequency assay (closed symbols), population-based fluorescence assay (black open symbols), and single molecule-based fluorescence assay (blue open triangles).

A motivation for comparing the 2D and 3D K_d data is to look for ways to relate one metric to the other. However, no correlation seems apparent from Fig. 2C. To define an ‘in situ’ 3D K_d to replace the 2D K_d in the y-axis, the contact area may be multiplied by the gap distance between the two apposing membranes to calculate a reaction volume for the interacting molecules (46). For example, in situ 3D K_ds were calculated using a 13.4 nm gap distance for fully extended TCR–pMHC bonds (21). Even with different gap distances for different bonds, the in situ 3D K_d vs. solution 3D K_d plot would still exhibit a similar pattern.

A separate issue relates to the huge difference in the 2D K_d measured by the two classes of 2D assays. A 2001 review presented micropipette data of CD16–IgG Fc binding (Fig. 2C, ■) with five orders of magnitude lower 2D affinities than those measured by the Golan-Zhu plot analysis (Fig. 2C, ○, □ and ◊), despite their comparable 3D affinity ranges (46). We previously proposed a self-assembly hypothesis to explain this tremendous difference between the two 2D methods (39). For the population-based fluorescent method, it was suggested that cooperation of a large number of receptor–ligand interactions over an extended time smoothens the cell membranes and produces a uniform gap distance in the immunological synapse. This would favor efficient interaction and results in high 2D affinity from the Golan-Zhu analysis. By comparison, the mechanical assays probe a small number of receptor–ligand interactions in the first seconds of contact. The membranes remain rough, which does not favor efficient interaction and results in low 2D affinity. The increase of 2D affinity over time with increasing number of bonds participating in adhesion may represent a mechanism of adhesion maturation and strengthening, the mechanism of which should be further studied. The potential differences in affinities as they relate to the respective 2D assays are important to understand since it influences the interpretation of the results.

Instead of using an estimated gap distance between the interacting cell membranes to determine an in situ 3D K_d from the 2D K_d, a confinement length can be calculated in each assay from the experimentally derived 3D and 2D K_d values (35, 61)(Fig. 2D). Confinement length has been suggested to reflect the size of the search space where molecules find their binding partners and serve as a measure of the orderliness of the two apposing membranes (46). For example, the confinement lengths for CD2, CD28, and CD16b are smaller than the gap distance (Fig. 2D, ○, □ and ◊), suggesting that the Golan-Zhu plot measures ‘matured’ interactions between aligned membranes where the search spaces are very small because binding partners are readily accessible. By comparison, the confinement lengths for the CD16 isoforms are 5-logs larger (Fig. 2D, ■), suggesting that the micropipette assays ‘nascent’ interactions in disordered membranes where the interacting molecules have to search a huge volume to find each other.

Higher 3D affinities may not correlate to higher 2D affinities across all receptor–ligand pairs. This was observed in the 2001 data, where P-selectin had a 2D affinity two orders of magnitude higher than those of other systems measured by the mechanical method (Fig. 2C, compare ♦ to ■). But its confinement length is still tens of microns (Fig. 2D, ♦) because of the relatively high 3D affinity of the P-selectin–PSGL-1 interaction (43). Remarkably, the 2D affinities for two agonist pMHC ligands recognized by the OT1 TCR (Fig. 2C, lowest two ) are also 2–3 orders of magnitude higher that the 2D affinities of CD16-isoforms (Fig. 2C, ■). However, the 3D affinities of these two TCR–pMHC interactions are lower than some of those of the CD16 isoforms. Thus, these 2D TCR–pMHC affinities are similar to the respective 2D affinities of P-selectin for PSGL-1 and ICAM-1 for high-affinity LFA-1 (in Mn²⁺), despite that the 3D TCR–pMHC affinities are an order of magnitude lower than the 3D P-selectin–PSGL-1 (43) and LFA-1–ICAM-1 (44) affinities. Their confinement lengths are comparable to that of the LFA-1–ICAM-1 interaction and smaller than that of the P-selectin–PSGL-1 interaction (Fig. 2D).

By comparison, the 2D affinities of OT1 TCR (Fig. 2C, ) for weak pMHC ligands and of CD8 for H2-K^b MHC (Fig. 2C, ) (62) align with the previous low affinity data of the CD16 isoforms. Because of their lower 3D affinities, however, their confinement lengths are shorter than those of the CD16 isoforms (Fig. 2D). Note that these 2D data were all measured by the micropipette method using living cells. They show that the low affinity TCR–pMHC interactions in 3D (K_d in the 1–100 µM range) can translate to high affinity bonds in 2D.

Using the same notation as the 2001 paper (46), the y-axis variables in Fig. 2B–D are presented in units of η × µm⁻² s⁻¹, η × µm⁻² and η × nm, respectively, where η = A_c/A_c^* is the ratio of effective to apparent contact area. When a T cell makes contact with a surrogate APC (RBC or lipid bilayer) of an apparent area A_c^*, only a fraction of this is close enough to form molecular contact. The area where molecules can reach their interacting partners is the effective area A_c. In the respective 2D models for analysis of the micropipette and Golan-Zhu plot data, the 2D affinity and effective contact area are combined into a single parameter, A_cK_a (in µm⁴), termed effective 2D affinity. The ratio η of effective to apparent contact area depends on the 2D method used for measurement. It may be close to 1 for the fluorescence method (46) but was estimated to be only a few percent for the mechanical methods because a bond formed in the first seconds of contact between a T cell and a RBC likely occurs at the tip of a microvillus (30). The two orders of magnitude difference in the η values helps to bridge the respective differences in 2D affinity and confinement length between the OT1 and 5c.c7 TCRs for their corresponding agonist pMHCs (Fig. 2C,D, and the lowest ). The affinities are within one log despite the fact that they were independently measured by different mechanical and fluorescent methods, respectively. Additional measurements for the same TCR–pMHC interactions by different methods will help further understand the inherent differences in each.

The data obtained from fluorescence-based measurements are clustered along a line, regardless of the molecular systems involved and regardless of whether they are measured by the single molecule-based (Fig. 2C, ) or population-based (Fig. 2C, ○, □, and ◊) assay, suggesting correlation between 2D and 3D affinities for this group of data. By comparison, the data obtained by the micropipette assay are more scattered. For each TCR system a linear trend seems apparent but the slope differs from one system to another, suggesting that there is no universal conversion between 2D and 3D affinities. The linear trend for the OT1 system (Fig. 2C, ) has a steep slope because the one-log difference in the 3D affinities of this TCR for a panel of pMHC ligands corresponds to three-log difference in 2D affinities. It has been suggested that this tremendous expansion in the dynamic range of affinity helps discriminate the peptides of a broad range of potencies (22).

Unexpectedly, the 2D affinity values could be significantly reduced by agents that disrupt the membrane and cytoskeleton structures. This has been observed for TCR–pMHC interactions measured by both mechanical (22) and fluorescent (21) methods and for CD8–MHC interactions (62). These tell observations emphasize that 3D affinities depend on the environment where molecular interactions occur.

Lck-dependent TCR–pMHC–CD8 trimolecular interaction

To determine the 2D parameters of pMHCs for the OT1 TCR (Fig. 2) and CD8 (Fig. 2C, D), a mutant H2-K^bα3A2 that abolishes CD8 binding (22) and null peptides or anti-TCR that abrogates TCR binding (62) were used to isolate the bimolecular interaction of interest (Fig. 1D). The 2D data for the 5c.c7 system (Fig. 2) also represent TCR–pMHC bimolecular interactions as addition of anti-CD4 had no effect on the measured values (21). Using recombinant proteins in SPR studies, Garcia et al. (63) found that CD8 enhances the TCR–pMHC interaction by reducing the off-rate, but Wyer et al. (64) found that TCR and CD8 bind to pMHC independently and with distinct kinetics. Notwithstanding these discrepant results, the reductionist approach depicted in Fig. 1A cannot represent the network interactions depicted in Fig. 1H well. This has been demonstrated by our recent 2D analysis of the network interactions that involves the TCR, CD8, and Lck (23), as summarized below.

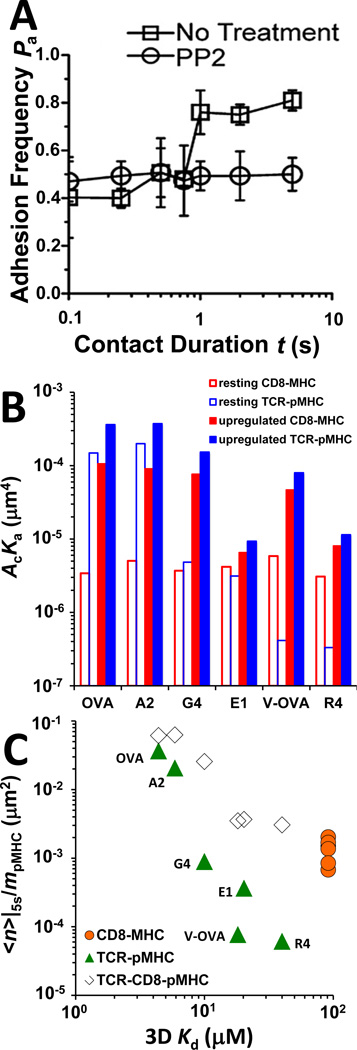
The minimum interaction network is depicted in Fig. 1H. Even when a single pMHC ligand species (e.g. agonist OVA:H2-K^b) is presented to the T cell, the adhesion frequency exhibits distinct behaviors depending on the contact time. At short contact times (<1 s), touching the T cell with OVA:H2-K^b and OVA:H2-K^bα3A2 results in indistinguishable adhesion frequencies. OVA:H2-K^b generates a step increase in the adhesion frequency as the contact time exceeds a threshold of ~1 s (Fig. 3A, □), but OVA:H2-K^bα3A2 produces the same adhesion frequency indifferent to the increasing contact time, indicating the increased adhesion is CD8 dependent, which is confirmed by anti-CD8 blocking experiments.

Fig. 3. Analysis of TCR–pMHC–CD8 trimolecular interactions.

(A) Two-stage adhesion frequency vs. contact time data of T cells from OT1 TCR transgenic mice interacting with OVA pMHC in the absence (□) and presence (○) of PP2. Reproduced from (23) with permission. (B) Bimolecular interaction affinities measured under conditions in which only bimolecular interactions were allowed (open bars, denoted by resting interactions) or calculated under the assumption that the increased adhesion in the second stage was due to upregulation of the chosen interaction with all other interactions unchanged (closed bars, denoted by upregulated interactions). (C) Plots of normalized bonds, defined as the average number of bonds <n> at 5-s contact time, calculated from adhesion frequency P_a by <n> = − ln(1 − P_a) and divided by the pMHC density, of TCR–pMHC () and MHC–CD8 () bimolecular interactions and of TCR–pMHC–CD8 (◊) trimolecular interaction for the indicated peptides are plotted against 3D K_d.

However, the 2D affinity of OVA:H2-K^b for OT1 TCR (Fig. 3B, 1^st open blue bar) is >40-fold higher than that for CD8 (Fig. 3B, 1^st open red bar), predicting negligible contribution to adhesion from CD8, should its affinity remain unchanged. In other words, to account for the increased adhesion by CD8 binding alone would require a >30-fold increase in the CD8 affinity (Fig. 3B, 1^st closed red bar). Alternatively, assuming the same low CD8 affinity would require the TCR affinity to undergo a step increase of ~2.4 fold (Fig. 3B, 1^st closed blue bar). Other peptides with diverse binding kinetics would have to change the CD8 or TCR affinity differently (Fig. 3B).

The 2D affinities shown by the open bars in Fig. 3 are denoted as ‘resting’ values, because they were measured under the conditions where only one type of bimolecular interaction was allowed (Fig. 1D). The closed bars are denoted as ‘upregulated’ values because they are calculated based on the assumption that only the interaction in question had changed property, everything else would remain the same. This assumption implies that the TCR–pMHC and MHC–CD8 interactions were independent from each other. The dependence of the adhesion increase in the second stage on TCR–pMHC interaction has been shown by anti-TCR blocking, which completely abolished not only the first stage (<1 s) but also the second stage adhesions (23).

Therefore, the increased adhesion in the second stage can be better interpreted as cooperative TCR–pMHC–CD8 trimolecular interaction (Fig. 1H). We introduce the notion of normalized bonds <n>|_5s/m_pMHC, defined as the average number of adhesion bonds <n> at the second plateau (5 s) normalized by the pMHC density as a metric for binding propensity, because the conventional definition of affinity does not apply to the TCR–pMHC–CD8 trimolecular interaction. For the bimolecular TCR–pMHC and MHC–CD8 interactions, the normalized bonds are equal to their corresponding 2D affinities multiplied by the TCR and CD8 densities, respectively. It is evident from Fig. 3C that the normalized bonds for the trimolecular interaction (◊) is greater than the sum of the normalized bonds from the two bimolecular interactions ( and ) for each distinct peptide. Indeed, the degree of cooperativity or synergy is measured by the difference between the normalized trimolecular bonds and the sum of the normalized bimolecular bonds, denoted as Δ<n>/m_pMHC. Note that the normalized MHC–CD8 bonds (, ~10⁻³ µm²) contribute negligibly to the gaps between the normalized total and TCR–pMHC bonds; the stronger the peptide (~ 10⁻²–10⁻¹ µm²), the smaller the CD8 contribution. So the normalized total bonds are approximately equal to normalized TCR–pMHC–CD8 bonds. The synergy due to cooperation for each peptide is dominated by the value of the normalized TCR–pMHC–CD8 bonds, because the Fig. 3C y-axis uses log scale. It is evident that the more potent the peptide, the stronger the synergy. Thus, cooperation between TCR and CD8 for pMHC binding provides a second step amplification of peptide discrimination (23).

The two-stage adhesion frequency kinetics is interpreted in the above discussion in terms of pMHC binding to the ectodomains of TCR and CD8, but interactions of their cytoplasmic domains with Lck also have an impact. This is manifested as reduction of the second-stage adhesion to the first-stage level by treatment of the T cell with PP2, a Lck inhibitor (Fig. 3A, ○). Thus, 2D analysis enables us to assess binding by dual receptors TCR and CD8 and their cooperation. It also allows assessment of interactions that are not part of the direct instrument readout but can impact its value through the network connection. This would not have been possible should the TCR and CD8 be removed from their environment on the T-cell membrane. This example highlights the ability of 2D analysis to reveal new information not obtainable by the 3D SPR studies.

Complexity of 2D analysis

As illustrated by the example in the preceding section, understanding the rules of 2D chemistry is complicated. This complexity manifests at several levels. At a practical level, the experimental measurements and the mathematical models for extracting the binding parameters differ from one method to another. For example, long distance excursion of protein in and out of the contact area occurs in the fluorescent method but not in the mechanical method because of the different time scales involved in the two types of methods. Molecular diffusion is not considered in the mechanical-based methods but is accounted for in the population-based fluorescent method by a reaction-diffusion equation (39). The model appears valid for the CD2–CD58 interaction as fluorescence recovery can reach nearly the unbleached level (38). However, it may not be valid for interactions with a significant unrecoverable fraction of bleached fluorescence, suggesting that the ligands become immobile and/or their bonds with the receptors become stable over a much longer time (38). This seems to be the case for TCR–pMHC interactions in the central supramolecular activation cluster (cSMAC) as it has been observed that the pMHC-conjugated fluorescence accumulated in the center of the immunological synapse did not recover after photobleaching (37), suggesting that binding in the cSMAC obeys different rules.

Binding is modeled very differently in the immunological synapse by the two fluorescence methods: uniform in the population analysis but variable in the single-molecule analysis. Indeed, large variations (as much as 250-fold spread) in local 2D affinity were observed (21), only the median values are plotted in Fig. 2C. The data suggest that there were significant variations in molecular densities in the immunological synapse, especially in the peripheral supramolecular activation cluster (pSMAC) where microclusters were originated, which were not governed by the simple diffusion law but might reflect the heterogeneity of the synaptic microenvironment.

The presence of other molecular interactions may also affect the measurement of the interaction in question. For example, in contrast to the population-based method that uses a single ligand at high density to form an immunological synapse-like contact area, in the single molecule-based method a low density of fluorescently labeled ligand was used to enable single-fluorophore imaging. To form an immunological synapse at a low density of fluorescently labeled pMHCs, the planar lipid bilayer was additionally reconstituted with non-fluorescent ICAM-1 and costimulatory molecule CD80 (21). It has been well established that engagement of TCR would activate LFA-1 to increase its affinity for ICAM-1 (65). Whether and if so, how the presence of LFA-1–ICAM-1 and CD28–CD80 interactions would impact the TCR–pMHC interaction kinetics has not been reported, complicating the comparison with the 2D results obtained with mechanical methods.

At an operational level, the 2D analyses are further complicated by their relative nature. For example, the effective 2D affinity of H2-K^b is two orders of magnitude higher for CD8 expressed on TCR⁻ OT1 hybridoma (23) than on primary naive T cells from OT1 transgenic mice (62). Unpublished data from our laboratory indicate that the 2D binding kinetics of TCR for pMHC changes as the T cell develops and differentiates (Hong J, Evavold BD, Zhu C, unpublished data). The precise reasons for this phenomenon are unknown, but several mechanisms seem possible. Regardless of the underlying mechanisms, this gives the immune system another layer of control for tailoring the immune response. The same clonal TCR could easily possess differing 2D binding kinetics as the cell matures from a developing thymocyte to a naive T cell as well as during the T-cell differentiation process into the myriad of T-effector, memory, and regulatory cells. Moreover, the different cells capable of presenting pMHC antigens could influence the 2D interactions. One could expect that dendritic cells (DCs), macrophages, B cells, epithelial cells, and peripheral target cells can differ in the process of antigen display at both the level of protein orientation and clustering as well as posttranslational modifications of the pMHC molecules.

The fast on-rate of the P-selectin–PSGL-1 association was attributed to pre-clustering of PSGL-1 on the tips of microvilli in the 2001 review (46). This was suggested to form lateral order that can be established prior to contact to enhance apparent 2D on-rate. The same explanation seems applicable to the low 3D but high 2D affinity of TCR (Fig. 2C), which is pre-clustered on the T-cell surface and becomes more clustered upon activation (66–69). Clustering increases apparent 2D affinity if the interaction of a pMHC with one TCR enhances binding of other TCRs in the cluster (22). Although using a simple model of monomeric receptor–ligand binding to fit the fast and frequent adhesion data caused by multimeric cooperative binding would return high 2D on-rate and affinity values, these represent apparent parameters. They cannot be directly compared with intrinsic parameters that govern monomeric binding without cooperation, which is the case in most SPR studies.

Mechanochemical coupled triggering hypothesis

The differences between 2D and 3D binding can be conceptually separated into physical and biological differences. Several biophysical differences, including the differential entropic losses of 2D vs. 3D interactions and differential transport in 2D vs. 3D, have been discussed (46, 52, 61). A recent theoretical work has treated these effects using mathematical modeling with some degrees of success (70).

The mechanisms by which other proteins at or below the cell membrane affect TCR binding kinetics with pMHC are unknown. We propose a mechanochemical coupled triggering model based on structural arguments. It extends from the receptor deformation model (58–60) and includes the discussions from this review that highlight differences in TCR interaction with pMHC depending on whether the TCR is in isolation or is part of the network of proteins on a living cell.

The pMHC-binding site is at the membrane distal end of the TCR αβ chains ~7 nm above the membrane. The phosphorylation sites on the ITAMs of the CD3 signaling dimers are located no closer than the inner leaflet of the cell membrane (71), >10 nm away from the peptide contact interface of the TCR αβ chains on the other side of the membrane. Therefore, for the chemical event of pMHC binding to induce the chemical event of ITAM phosphorylation, a mechanical bridge between the two sites is required because no chemical coupling can act across such a wide spatial gap. Mechanical coupling has to be carried out via physical structures. The TCR-CD3 along with the co-receptor/Lck complex should be part of such physical structures, as revealed by our 2D analysis of the Lck-dependent TCR-CD8 cooperation for pMHC binding (23). Changes in the physical structure of the TCR and associated proteins would affect the mechanical coupling, manifesting as altered TCR–pMHC affinity and kinetic rates. For example, separating the TCR-CD3 complex, CD8 and Lck from their membrane environment and analyzing their binding by SPR is unlikely to reproduce results corresponding to those exemplified in Fig. 3. This may also explain why the measurements depicted by Fig. 1A may not correlate to those depicted by Fig. 1D, as revealed in Fig. 2.

Supporting evidence for this hypothesis has been obtained in our previous study measuring binding of human Fcγ receptor IIIA (CD16A) to Fc of IgG from different species (72). Like the TCR-CD3 complex, the ligand binding chain of CD16A associates non-covalently with a signaling dimer (γγ, ζζ, or γζ) on the cell membrane and mechanical coupling seems to be required to couple the IgG Fc binding event in the CD16A ectodomain to the phosphorylation event in the signaling dimer ITAMs beneath the membrane. We show that a chimeric molecule that replaces the transmembrane and cytoplasmic domains of CD16A with a glycophosphatidylinositol (GPI) anchor to express the molecule on cell surface without the signaling dimer binds ligands with different affinities from the wild-type CD16A in an IgG specie-specific fashion (72). Importantly, similar ligand-specific differential affinities are observed by using the micropipette adhesion frequency assay with IgG coated on RBCs and by a competitive inhibition binding assay with IgG in fluid phase. This suggests that the differences are caused by the distinct CD16 structures and not by using different methods to make measurement in different dimensions.

To extend our argument further, TCR is known to be able to discriminate peptides with only a single amino acid difference but generate drastically distinct levels of T-cell responses. The information encoding the differential responses must be embedded in the TCR affinity and kinetic rates for the ligands, which provides the motivation for kinetic analysis of TCR–pMHC interactions. The mechanical coupling between binding of the pMHC at the membrane distal site of the TCR αβ chains and phosphorylation of ITAMs at the CD3 signaling dimers at and beneath the plasma membrane communicate the information to trigger different signals for distinct T-cell responses. In other words, different peptides correspond to differing affinities and kinetic rates, which in turn correspond to different mechanical couplings. The dependency of TCR triggering on additional proteins explains the effect observed with the truncated TCR αβ chains purified and separated from the signaling subunits.

Although this mechanochemical coupled triggering hypothesis has not been tested experimentally for all of its elements, it offers a plausible explanation for the differences between the parameters measured in situ by using living T cells and the parameters measured by using soluble TCRs. The hypothesis also suggests a new framework to think about how mechanical force may provide a mechanism for TCR triggering that enhances antigen discrimination. Mechanical coupling between the pMHC-binding site and the ITAM phosphorylation sites can take several forms including force transmission, direct physical interactions among different TCR subunits, and propagation of deformation and conformational changes from one site to another. All can be affected by force. Different couplings may be regulated by force in different ways or by different degrees. Therefore, our hypothesis offers a model for TCR triggering based on force (53–60). Additional data from our laboratory suggest that force may regulate TCR–pMHC dissociation (Chen W, Liu B, Evavold BD, Zhu C, unpublished data).

It is our hope that this review has illustrated in situ analysis of molecular interactions as a highly relevant and promising area of study in immunology. We emphasize that we are just beginning to scratch the surface of these analyses, having analyzed to date only a few interactions for a limited number of antigen specific systems. We expect that the use of 2D approaches to study the network interactions at the T-cell surface will elucidate the mechanisms by which binding of the αβ TCR heterodimer with distinct pMHCs triggers different intracellular signals via the adjacent CD3 components to produce different T-cell responses.