Modeling physical growth using mixed effects models

Abstract

This paper demonstrates the use of mixed effects models for characterizing individual and sample average growth curves based on serial anthropometric data. These models are an advancement over conventional general linear regression because they effectively handle the hierarchical nature of serial growth data. Using body weight data on 70 infants in the Born in Bradford study, we demonstrate how a mixed effects model provides a better fit than a conventional regression model. Further, we demonstrate how mixed effects models can be used to explore the influence of environmental factors on the sample average growth curve. Analyzing data from 183 infant boys (aged 3 to 15 months) from rural South India, we show how maternal education shapes infant growth patterns as early as within the first six months of life. The presented analyses highlight the utility of mixed effects models for analyzing serial growth data because they allow researchers to simultaneously predict individual curves, estimate sample average curves, and investigate the effects of environmental exposure variables.

Longitudinal data are necessary to investigate the dynamic process of physical growth. With this opportunity comes the analytical problem of a hierarchical data structure where serial measurements are nested within individuals over time. Conventional general regression provides a single equation or growth curve for an entire sample and does not consider differences in growth between individuals. In fact, applying conventional regression to hierarchical data produces incorrect standard errors and potentially misleading p-values (Goldstein, 1986; Goldstein, 1989). Researchers used to have to painstakingly fit separate regression models for each individual in a sample (Deming, 1957; Marubini et al., 1972; Cameron et al., 1982). Mixed effects regression is a more sophisticated approach that can incorporate individual growth characteristics in a single model, which simultaneously estimates individual curves and a sample average curve (Goldstein, 2010).

In addition, mixed effects growth models can incorporate exposure variables in the same way conventional regression models can (Goldstein, 2010). They can be used to investigate the evolutionary, intergenerational, biocultural, and genetic factors that affect the expression of growth in a sample and thus have many applications for anthropological research. Many publications in anthropology journals have related environmental factors to size at discrete ages (e.g., Bogin and Loucky, 1997; Varela-Silva et al., 2009; Hadley et al., 2011), but few have used mixed effects growth models to explain why systematic differences in the actual pattern of growth exist (e.g., Buschang et al., 1988; Bhargava, 2000; Reyes-Garcia et al., 2010). Only with the latter approach is it possible to ascertain exactly when differences in growth emerge and how they progress over time.

Mixed effects growth models were largely developed in the 1980s and 1990s (Laird and Ware, 1982; Bryk and Raudenbush, 1987), yet they have not often been utilized in recent anthropology research. An accessible demonstration of mixed effects growth curve modeling in an anthropology journal is thus timely and would fill a gap in the literature. This paper provides a worked example of mixed effects growth curve modeling. We focus on the first 15 months of life, a critical period where infants demonstrate remarkable plasticity to their environment (Cameron and Demerath, 2002) and where responses to the environmental may have long term consequences for health (Gluckman et al., 2009; Godfrey et al., 2010). Our specific aims were 1) to develop a mixed effects model that accurately describes the growth of 70 boys participating in the Born in Bradford birth cohort study, UK and 2) to investigate the effect of maternal education on weight growth in 183 rural Indian boys and test whether any potential association is mediated by concurrently measured morbidity.

METHODS

Samples and data

The sample used for our first aim comprised 70 boys participating in the Born in Bradford birth cohort study (Raynor and Born in Bradford Collaborative Group, 2008) with birth weight and serial infant weight measurements up to age 15 months. These data were collected at non-standard assessment ages. In total, there were 612 observations, with an average of 8.7 observations per participant (range 3–20) over an average of 0.92 years (range 0.55–1.25).

The sample used for our second aim comprised 183 boys from an Indo-USA funded collaborative longitudinal study, hereafter called the Infant Feeding Study, on the efficacy of an integrated feeding and care intervention among 3- to 15-month-old infants in Andhra Pradesh, India. Weight was measured at three monthly intervals. The 183 boys had a total of 859 observations, with an average of 4.7 per boy (range 3–5) over an average of 10.81 months (range 5–12). Maternal education level was self-reported at recruitment and the number of morbidity events (i.e., fever, vomiting, coughing, diarrhea) in the prior week was recorded at the target three monthly assessments. 18 (9.8%) boys had no morbidity data, but the 165 (90.2%) boys with morbidity data had an average of 4.7 recordings out of a possible five.

Statistical analysis: modeling the growth of Bradford infants

A series of statistical models were applied to the weight data of Born in Bradford boys to provide a worked example of infant growth curve modeling. The first model was a conventional general linear regression:

$$\mathrm{y}={\mathrm{\beta }}_0+{\mathrm{\beta }}_1(\mathrm{x})$$ [Model 1a]

Where, y is weight, x is age, β₀ is the intercept, and β₁ is a regression coefficient.

This model describes the line of best fit between weight and age, which we would expect to provide a poor fit for the data because we know that infant growth does not occur at a constant pace. The shape of the infant growth curve is a decaying polynomial because it gradually departs negatively from a straight line as time increases (Cameron, 2002). To create such a curve, an age² term was added:

$$\mathrm{y}={\mathrm{\beta }}_0+{\mathrm{\beta }}_1(\mathrm{x})+{\mathrm{\beta }}_2({\mathrm{x}}^2)$$ [Model 1b]

Where, y is weight, x is age, β₀ is the intercept, and β₁ and β₂ are regression coefficients.

This model is a quadratic or second degree polynomial. It describes a curvilinear relationship between weight and age, but it is still a linear model because each separate parameter describes a linear association. The main limitation of this model is that it does not consider the hierarchical nature of serial data. It only describes a single curve with an average intercept and an average slope; the parameters are described as having fixed effects. An improvement to the conventional regression model is the mixed effects model because it allows any or all of the parameters to take different values for each infant (Baxter-Jones and Mirwald, 2004). Such parameters are described as having mixed effects because they consist of fixed effects (i.e., average parameter values for the entire sample) and also random effects that are different for each infant. A second degree polynomial function where all parameters had mixed effects was fitted next to allow us to demonstrate the need to incorporate individual characteristics when modeling growth:

$${\mathrm{y}}_{\text{ij}}={\mathrm{\beta }}_{0\mathrm{j}}+{\mathrm{\beta }}_{1\mathrm{j}}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{2\mathrm{j}}({{\mathrm{x}}_{\text{ij}}}^2)$$ [Model 1c]

$${\mathrm{\beta }}_{0\mathrm{j}}={\mathrm{\beta }}_0+{\mathrm{u}}_{0\mathrm{j}}{\mathrm{\beta }}_{1\mathrm{j}}={\mathrm{\beta }}_1+{\mathrm{u}}_{1\mathrm{j}}{\mathrm{\beta }}_{2\mathrm{j}}={\mathrm{\beta }}_2+{\mathrm{u}}_{2\mathrm{j}}$$

Where, y_ij is the weight of infant j at occasion i, x_ij is the corresponding age, β_0j is the intercept, and β_1j and β_2j are regression coefficients. β_0j - β_2j have mixed effects that comprise a sample average fixed effect (β) and a subject specific random effect (u_j).

In this model, the fixed effects together describe the sample average curve and the random effects are individual departures from the intercept and slope of that curve. The formula therefore describes the growth curve of every infant. Because each model parameter takes different values for each infant, each parameter demonstrates variance and there is covariance between parameters. The underlying variance- covariance structure of these data is described by a matrix:

$${\mathrm{\Omega }}_{\mathrm{u}}=\left(\begin{array}{ccc}{\mathrm{\sigma }}_{\mathrm{u}0}^2\hfill & \hfill & \hfill \\ {\mathrm{\sigma }}_{\mathrm{u}01}\hfill & {\mathrm{\sigma }}_{\mathrm{u}1}^2\hfill & \hfill \\ {\mathrm{\sigma }}_{\mathrm{u}02}\hfill & {\mathrm{\sigma }}_{\mathrm{u}12}\hfill & {\mathrm{\sigma }}_{\mathrm{u}2}^2\hfill \end{array}\right)$$

Where, ${\mathrm{\sigma }}_{\mathrm{u}0}^2,{\mathrm{\sigma }}_{\mathrm{u}1}^2,\text{and}{\mathrm{\sigma }}_{\mathrm{u}2}^2$ are the variances of the three random effects and σ_u01, σ_u12, and σ_u02 are the covariances between the random effects.

All mixed effects modeling software allow the user to specify the structure of the variance-covariance matrix. For growth models, it makes sense to select the unstructured option because it allows the variance-covariance estimates to be distinct. It does not make sense to use other options because the variances of the random effects are unlikely to be the same since they describe different aspects of the individual curves. The independent and identity options should definitely not be used during infancy because they set covariance estimates to zero, when we know that birth size and subsequent growth rate should co-vary.

We next fitted a mixed effects fractional polynomial to demonstrate an approach that offers researchers flexibility to find a function of age that best describes their data (Long and Ryoo, 2010). A fractional polynomial is an automated procedure that runs a large number of models to find the one that best describes the dimension being modeled as some unknown function of age. An a priori decision to include two age terms (i.e., a two degree fractional polynomial) was made and the choice of powers with which to raise each age term was −2, −1, −0.5, 0, 0.5, 1, 2, or 3. This approach therefore comprised 36 options and had the form:

$${\mathrm{y}}_{\text{ij}}={\mathrm{\beta }}_{0\mathrm{j}}+{\mathrm{\beta }}_{1\mathrm{j}}({{\mathrm{x}}_{\text{ij}}}^{\mathrm{p}1})+{\mathrm{\beta }}_{2\mathrm{j}}({{\mathrm{x}}_{\text{ij}}}^{\mathrm{p}2})$$ [Model 1d]

$${\mathrm{\beta }}_{0\mathrm{j}}={\mathrm{\beta }}_0+{\mathrm{u}}_{0\mathrm{j}}{\mathrm{\beta }}_{1\mathrm{j}}={\mathrm{\beta }}_1+{\mathrm{u}}_{1\mathrm{j}}{\mathrm{\beta }}_{2\mathrm{j}}={\mathrm{\beta }}_2+{\mathrm{u}}_{2\mathrm{j}}$$

Where, y_ij is the weight of infant j at occasion i, x_ij is the corresponding age, β_0j is the intercept, and β_1j and β_2j are regression coefficients. β_0j - β_2j have mixed effects that comprise a sample average fixed effect (β) and a subject specific random effect (u_j). p1 and p2 represent the choice of powers [−2, −1, −0.5, 0, 0.5, 1, 2, or 3] with which to raise each age term; when p1 or p2 = 0, ln(x)⁰; when p1 = p2, x^p1 and x^p2*x.

The best fitting option (age⁻² and age^−0.5) was used as the model with the lowest deviance (see next paragraph).

All models were fit in Stata IC10 (College Station, Texas). Model fit was compared using log likelihood, Akaike Information Criterion (AIC), and Bayesian Information Criterion (BIC) statistics (Akaike, 1974; Shwartz, 1978). The log likelihood is the natural logarithm of the likelihood function, a measure of the probability of observing the set of dependent variable values. The estimation method for linear mixed effects models (maximum likelihood estimation) is an iterative procedure that finds the parameter estimates that make the log likelihood as close to zero as possible. The −2 log likelihood statistic or deviance is equal to the sum of squared residuals (i.e., observed – fitted values). The AIC penalizes the −2 log likelihood for model complexity by adding twice the number of estimated parameters. The BIC provides a more penalized statistic by adding the number of estimated parameters multiplied by the natural logarithm of the number of observations. Likelihood ratio tests were used to compare to the difference between the log likelihoods of two consecutive models (Neyman and Pearson, 1928). A p-value of < 0.05 was used to denote statistical significance. The residuals from each model were plotted against age to allow visual comparison of model fit across the studied age range. The sample average curves were plotted in a single figure to allow comparison, with the exception of the curve of the conventional quadratic polynomial model (1b) because it was nearly identical to that of the mixed effects quadratic polynomial model and therefore would not be visible on the same figure (1c). Using the mixed effects fractional polynomial model (1d), the individual curves of three boys (selected at random) were plotted against their observed data and the sample average curve to demonstrate the ability of a mixed effects model to predict individual growth curves.

Statistical analysis: testing maternal education effects on the growth of Indian infants

As well as describing infant growth using mixed effects models, researchers may want to test hypotheses about the effect of different exposures on the pattern of growth depicted by a sample average curve. Here, we investigated the effect of maternal education on weight growth in rural Indian infants and tested whether any potential association was mediated by concurrent morbidity.

Maternal education was categorized as secondary or college, primary, or illiterate. Morbidity at each three monthly assessment was categorized for each boy as two or more events, one event, no events, or missing data. The Berkey-Reed (1987) 1^st order function of age was used to model growth because it is known to provide a good fit for the data of these Indian infants (Johnson et al., 2012). Unlike models 1a–1d, it is a structural growth model (Hauspie and Molinari, 2004) that imposes a particular form to the curve:

$$\mathrm{y}={\mathrm{\beta }}_0+{\mathrm{\beta }}_1(\mathrm{x})+{\mathrm{\beta }}_2\text{ln}(\mathrm{x})+{\mathrm{\beta }}_{3}1/(\mathrm{x})$$

Where, y is weight, x is age, β₀ is the intercept, and β₁ - β₃ are regression coefficients. β₀ is related to birth weight, β₁ to the linear component of growth, β₂ to the decrease in growth rate over time, and β₃ to the inflection point in the curve.

Three separate mixed effects Berkey-Reed 1^st order models were developed and fitted in Stata. In all instances, the final parameter (β₃) did not have mixed effects, because Stata could not make such a model converge. In the first model, systematic differences in the weight of infants of mothers in different maternal education groups were investigated by including maternal education as a main effect:

$${\mathrm{y}}_{\text{ij}}={\mathrm{\beta }}_{0\mathrm{j}}+{\mathrm{\beta }}_{1\mathrm{j}}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{2\mathrm{j}}\text{ln}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{3}1/({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_4({\mathrm{D}}_{\text{primaryj}})+{\mathrm{\beta }}_5({\mathrm{D}}_{\text{illiteratej}})$$ [Model 2a]

$${\mathrm{\beta }}_{0\mathrm{j}}={\mathrm{\beta }}_0+{\mathrm{u}}_{0\mathrm{j}}{\mathrm{\beta }}_{1\mathrm{j}}={\mathrm{\beta }}_1+{\mathrm{u}}_{1\mathrm{j}}{\mathrm{\beta }}_{2\mathrm{j}}={\mathrm{\beta }}_2+{\mathrm{u}}_{2\mathrm{j}}$$

Where, y_ij is the weight of infant j at occasion i, x_ij is the corresponding age, β_0j is the intercept, and β_1j, β_2j, and β₃ - β₅ are regression coefficients. β_0j - β_2j have mixed effects that comprise a sample average fixed effect (β) and a subject specific random effect (u_j). D_primaryj is a dummy variable coded 1 for primary maternal education and 0 for secondary or college or illiterate maternal education; D_illiteratej is a dummy variable coded 1 for illiterate maternal education and 0 for secondary or college or primary maternal education.

This model allows a different intercept for each maternal education group. β₄ and β₅ represent an up or down shift in the entire curve for infants born to primary educated or illiterate mothers, respectively, relative to the referent group of infants born to mothers with secondary or college education. In the second model, maternal education group was also included as an interaction with the three age terms:

$${\mathrm{y}}_{\text{ij}}={\mathrm{\beta }}_{0\mathrm{j}}+{\mathrm{\beta }}_{1\mathrm{j}}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{2\mathrm{j}}\text{ln}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{3}1/({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_4({\mathrm{D}}_{\text{primaryj}})+{\mathrm{\beta }}_5({\mathrm{D}}_{\text{illiteratej}})+{\mathrm{\beta }}_6({\mathrm{D}}_{\text{primaryj}})({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_7({\mathrm{D}}_{\text{illiteratej}})({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_8({\mathrm{D}}_{\text{primaryj}})(\text{ln}({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_9({\mathrm{D}}_{\text{illiteratej}})(\text{ln}({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_{10}({\mathrm{D}}_{\text{primaryj}})(1/({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_{11}({\mathrm{D}}_{\text{illiteratej}})(1/({\mathrm{x}}_{\text{ij}}))$$ [Model 2b]

$${\mathrm{\beta }}_{0\mathrm{j}}={\mathrm{\beta }}_0+{\mathrm{u}}_{0\mathrm{j}}{\mathrm{\beta }}_{1\mathrm{j}}={\mathrm{\beta }}_1+{\mathrm{u}}_{1\mathrm{j}}{\mathrm{\beta }}_{2\mathrm{j}}={\mathrm{\beta }}_2+{\mathrm{u}}_{2\mathrm{j}}$$

Where, y_ij is the weight of infant j at occasion i, x_ij is the corresponding age, β_0j is the intercept, and β_1j, β_2j, and β₃ – β₁₁ are regression coefficients. β_0j - β_2j have mixed effects that comprise a sample average fixed effect (β) and a subject specific random effect (u_j). D_primaryj is a dummy variable coded 1 for primary maternal education and 0 for secondary or college or illiterate maternal education; D_illiteratej is a dummy variable coded 1 for illiterate maternal education and 0 for secondary or college or primary maternal education.

This model allows the shape of the growth curve to be different for each maternal education group. By setting all the D_primaryj and D_illiteratej dummy variables to zero, the model represents the growth of infants born to mothers with secondary or college education; by setting all the D_primaryj dummy variables to one and all the D_illiteratej dummy variables to zero, the model represents the growth of infants born to mothers with primary education; and by setting all the D_primaryj dummy variables to zero and all the D_illiteratej dummy variables to one, the model represents the growth of infants born to illiterate mothers. Next we wanted to test whether morbidity mediated any effect of maternal education on infant growth. Morbidity was a time dependent variable and was therefore included as a main effect and also as an interaction with age to account for the fact that the effect of morbidity on weight may have been different at each assessment age:

$${\mathrm{y}}_{\text{ij}}={\mathrm{\beta }}_{0\mathrm{j}}+{\mathrm{\beta }}_{1\mathrm{j}}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{2\mathrm{j}}\text{ln}({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{3}1/({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_4({\mathrm{D}}_{\text{primaryj}})+{\mathrm{\beta }}_5({\mathrm{D}}_{\text{illiteratej}})+{\mathrm{\beta }}_6({\mathrm{D}}_{\text{primaryj}})({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_7({\mathrm{D}}_{\text{illiteratej}})({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_8({\mathrm{D}}_{\text{primaryj}})(\text{ln}({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_9({\mathrm{D}}_{\text{illiteratej}})(\text{ln}({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_{10}({\mathrm{D}}_{\text{primaryj}})(1/({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_{11}({\mathrm{D}}_{\text{illiteratej}})(1/({\mathrm{x}}_{\text{ij}}))+{\mathrm{\beta }}_{12}({\mathrm{D}}_{\text{morbidity}1\mathrm{j}})+{\mathrm{\beta }}_{13}({\mathrm{D}}_{\text{morbidity}>2\mathrm{j}})+{\mathrm{\beta }}_{14}({\mathrm{D}}_{\text{morbiditymissingj}})+{\mathrm{\beta }}_{15}({\mathrm{D}}_{\text{morbidity}1\mathrm{j}})({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{16}({\mathrm{D}}_{\text{morbidity}>2\mathrm{j}})({\mathrm{x}}_{\text{ij}})+{\mathrm{\beta }}_{17}({\mathrm{D}}_{\text{morbiditymissingj}})({\mathrm{x}}_{\text{ij}})$$ [Model 2c]

$${\mathrm{\beta }}_{0\mathrm{j}}={\mathrm{\beta }}_0+{\mathrm{u}}_{0\mathrm{j}}{\mathrm{\beta }}_{1\mathrm{j}}={\mathrm{\beta }}_1+{\mathrm{u}}_{1\mathrm{j}}{\mathrm{\beta }}_{2\mathrm{j}}={\mathrm{\beta }}_2+{\mathrm{u}}_{2\mathrm{j}}$$

Where y_ij is the weight of infant j at occasion i, x_ij is the corresponding age, β_0j is the intercept, and β_1j, β_2j, and β₃ – β₁₁ are regression coefficients. β_0j - β_2j have mixed effects that comprise a sample average fixed effect (β) and a subject specific random effect (u_j). D_primaryj is a dummy variable coded 1 for primary maternal education and 0 for secondary or college or illiterate maternal education; D_illiteratej is a dummy variable coded 1 for illiterate maternal education and 0 for secondary or college or primary maternal education.

The sample average curves from models 2b and 2c were plotted by maternal education group to allow visual comparison of the effects of maternal education before and after adjusting for morbidity. In addition, for both model 2b and 2c, the fixed and random effect estimates for each parameter were used to estimate individual weight data at three monthly intervals. The differences in these estimated data between maternal education groups at each age were tested using separate between-subjects analysis of variance (ANOVA) models, specifying a Bonferroni correction for multiple comparisons.

RESULTS

The growth of Bradford infants

The parameter estimates of the four growth models (1a–d) applied to the weight data of Born in Bradford boys are shown in Table 1 and the sample average curves are shown in Figure 1. Fit diagnostics improved with each consecutive step in development, even after penalization for increasing model complexity with the AIC and BIC. Allowing a conventional quadratic polynomial (model 1b) to have mixed effects (model 1c) drastically improved fit diagnostics, thereby providing a clear example of the need to incorporate individual characteristics when modeling growth. Deviance, for example, was reduced by more than 60% (i.e., 876/1398*100). Figure 2 also clearly demonstrates the effect of a mixed effects approach on shrinking residuals. There was some evidence that the mixed effects quadratic polynomial (model 1c) and fractional polynomial (model 1d) estimated individual curves too low at birth and too high immediately after birth. This may reflect the inability of these models to describe weight loss in the first two weeks of life. In fact, investigation of three individual curves from the mixed effects fractional polynomial model (1d) revealed one infant (boy X) with a typical pattern of neonatal weight loss whose individual curve failed to capture this phenomenon (Fig. 3). Nevertheless, Figure 3 does demonstrate the ability of a mixed effects model to describe the growth of three individuals with very different patterns of change over age.

Table 1.

Growth models^a of serial weight from birth to 15 months of age for 70 boys in the Born in Bradford birth cohort study.

		Model 1a conventional regression	Model 1b conventional quadratic polynomial regression	Model 1c mixed effects quadratic polynomial regression	Model 1d mixed effects fractional polynomial regression
	Notation	Beta (Standard Error) P-value	B (SE) P-value	B (SE) P-value	B (SE) P-value
Intercept	β0	3.884 (0.053) <0.001	3.355 (0.056) <0.001	3.328 (0.063) <0.001	21.662 (1.212) <0.001
Age (decimal years)	β1	6.641 (0.110) <0.001	11.367 (0.317) <0.001	11.303 (0.287) <0.001
Age2	β2		−4.821 (0.309) <0.001	−4.819 (0.262) <0.001
Age−2	β1				−2.938 (0.612) <0.001
Age−0.5	β2				−15.495 (1.782) <0.001
Variance (intercept)	${\mathrm{\sigma }}_{\mathrm{u}0}^2$			0.248 (0.047)	75.454 (17.880)
Variance (age)	${\mathrm{\sigma }}_{\mathrm{u}1}^2$			4.068 (0.974)
Variance (age2)	${\mathrm{\sigma }}_{\mathrm{u}2}^2$			2.657 (0.824)
Covariance (intercept, age)	σu01			−0.219 (0.159)
Covariance (intercept, age2)	σu02			0.145 (0.144)
Covariance (age, age2)	σu12			−2.680 (0.822)
Variance (age−2)	${\mathrm{\sigma }}_{\mathrm{u}1}^2$				16.993 (4.423)
Variance (age−0.5)	${\mathrm{\sigma }}_{\mathrm{u}2}^2$				156.281 (38.575)
Covariance (intercept, age−2)	σu01				32.236 (8.571)
Covariance (intercept, age−0.5)	σu02				−107.464 (26.159)
Covariance (age−2, age−0.5)	σu12				−49.011 (12.828)
Variance (residual)	${\mathrm{\sigma }}_{\mathrm{e}}^2$			0.059 (0.004)	0.047 (0.003)
Log Likelihood		−802	−699	−261	−214
−2 Log Likelihood (i.e., deviance)		1604	1398	522	428
Δ −2 Log Likelihood (P-value)b		--	−206 (<0.001)	−876 (<0.001)	−94 (not possiblec)
AICd		1608	1404	542	448
BICe		1617	1417	586	492

^aAll models were fit in Stata IC10 (College Station, Texas). Model formulae are shown in the methods section and the sample average curves are shown in Fig 1, with the exception of the curve of model 1b because if was nearly identical to that of model 1c.

^bΔ −2 Log Likelihood is the difference in the −2 Log Likelihood between the model and the model in the previous column. The p-value is a test of this difference using a likelihood ratio test (i.e., −2 log(likelihood for null model) + 2 log(likelihood for alternative model)).

^cModels 1c and 1d had the same number of estimated parameters (and thus the degrees of freedom did not differ), thereby making it impossible to calculate a p-value for the difference in −2 Log Likelihoods.

^dAkaike Information Criterion (AIC) = −2 Log Likelihood + 2(number of estimated parameters).

^eBayesian Information Criterion (BIC) = −2 Log Likelihood + number of estimated parameters*ln(number of observations).

Figure 1.

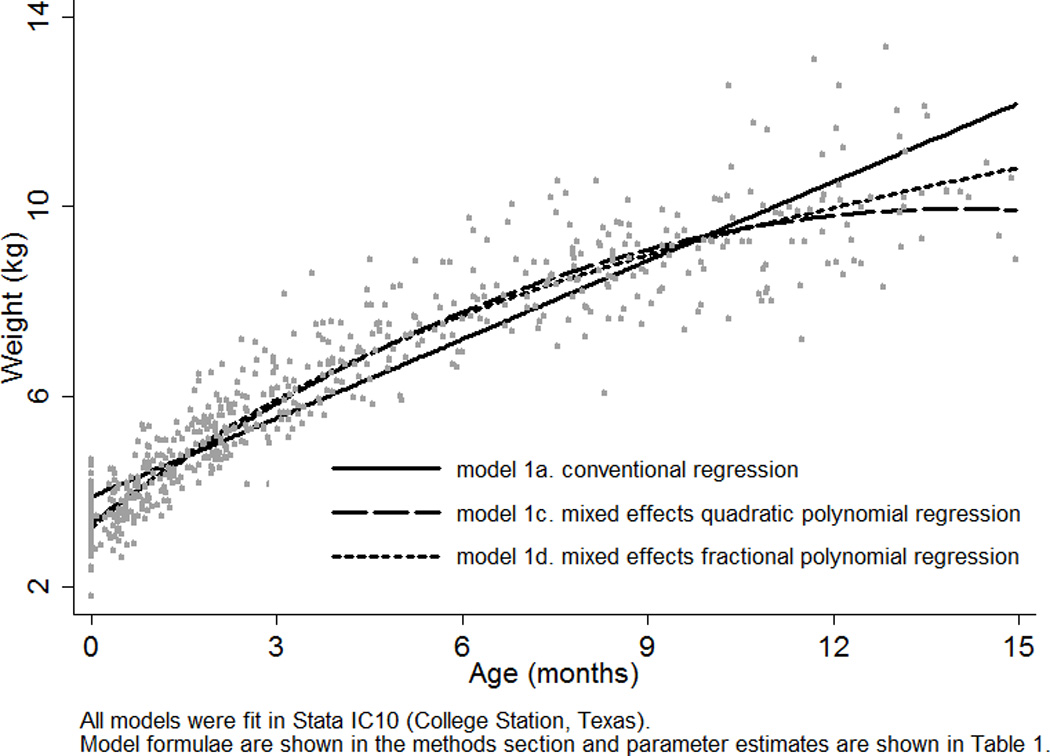
Sample average growth curves from three different statistical models (1a, 1c, 1d) applied to serial weight from birth to 15 months of age for 70 boys in the Born in Bradford birth cohort study.

Figure 2.

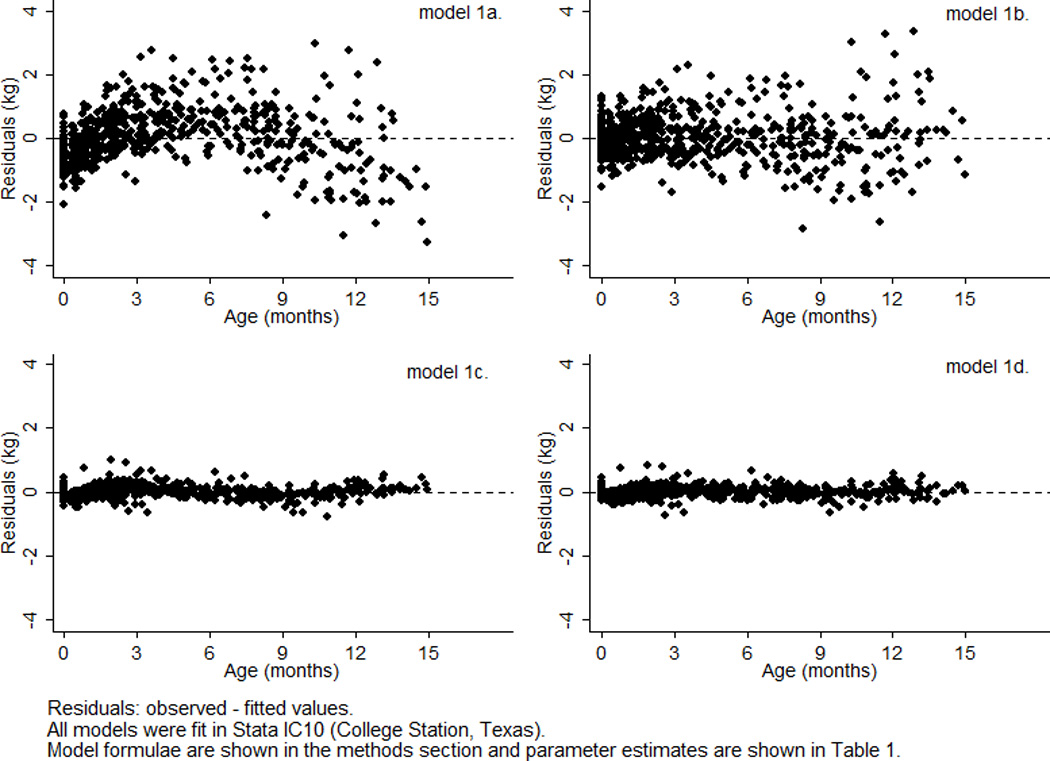
Residuals plotted against age for four different statistical models (1a–d) applied to serial weight from birth to 15 months of age for 70 boys in the Born in Bradford birth cohort study.

Figure 3.

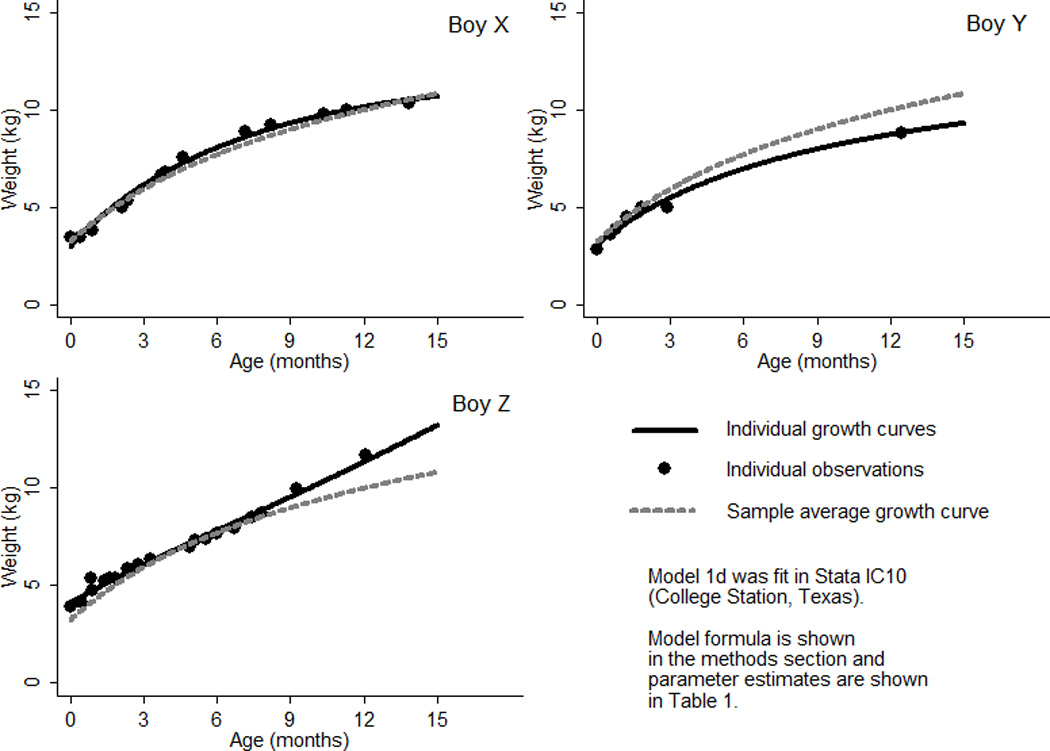
An example of individual growth curves of boys in the Born in Bradford birth cohort study: Estimated from a fractional polynomial mixed effects model (1d).

In addition to constructing a visual representation of growth, some of the model parameters in Table 1 provide useful information about the growth of the sample. In both the conventional and mixed effects quadratic polynomial models (1b and 1c), the intercept describes size at birth, the age term describes the gradient or rate of growth, and the age² term describes the multiplicative acceleration in weight that determines the shape of the curve. In model 1c, for example, average size at birth was 3.3 kg, infants gained an average of 11.3 kg/per year, and there was a decreasing growth rate over time because the solution to −4.819*age² becomes exponentially more negative (indicating a slowing down of growth or a less steep curve) as age increases. Therefore, the negative covariance between the intercept and the age term (i.e., σ_u01) indicates that infants who were lighter at birth demonstrated a faster rate of growth, the positive covariance between the intercept and age² term (i.e., σ_u02) indicates that infants who were heavier at birth had a slower declining rate of growth, and the negative covariance between the age and age² terms (i.e., σ_u12) indicates that infants with a steeper gradient had a faster declining rate of growth. The mixed effects fractional polynomial model (1d) provided the best fit for the data. The parameter estimates are, however, not discussed here because when multiplied by age⁻² and age^−0.5 the interpretation is not intuitive.

Maternal education effects on the growth of Indian infants

When maternal education was included only as a main effect in a mixed effects Berkey-Reed 1^st order model (2a), infants in the primary education group were consistently 16g heavier than those in the secondary or college education group, whereas the illiterate group were consistently 68g lighter than the secondary or college group (p-values 0.911 and 0.634, respectively) (Table 2). When, however, maternal education was included also as an interaction with the age terms in model 2b there was evidence that the shape of the growth curve for the illiterate group was significantly different to that for the secondary or college group (p-values for illiterate and illiterate-by-age, by-ln age, and by-inverse age <0.05). The curve for the illiterate group began to fall away from the secondary or college group after six months of age, resulting in a deficit of approximately 0.5kg at 15 months of age (Fig. 4). Separate ANOVA models, however, showed that at no one age were the differences between maternal education groups statistically significant (p-values >0.25).

Table 2.

The effects of maternal education and morbidity on the sample average weight growth curve of 183 Infant Feeding Study boys aged three to 15 months.

			Model 2a	Model 2b	Model 2c
	Notation	N (%)	Beta (Standard Error) p-value	B (SE) p-value	B (SE) p-value	% change in B from B in Model 2b
Berkey-Reed 1st order modela
Intercept	β0		10.189 (1.272) <0.001	5.099 (2.531) 0.044	6.192 (2.493) 0.013	+21.4
Age (months)	β1		0.228 (0.045) <0.001	0.069 (0.091) 0.449	0.129 (0.090) 0.151	+87.0
Ln(age)	β2		−1.480 (0.661) 0.025	1.117 (1.322) 0.398	0.481 (1.302) 0.712	−56.9
1/age	β3		−10.186 (2.062) <0.001	−2.027 (4.111) 0.622	−3.908 (4.049) 0.334	−92.3
Maternal education
Secondary or college (referent)		46 (25.1)	--	--	--	--
Primary	Β4	72 (39.3)	0.016 (0.141) 0.911	5.393 (3.267) 0.099	4.403 (3.208) 0.170	−18.4
Illiterate	Β5	65 (35.5)	−0.068 (0.144) 0.634	8.148 (3.248) 0.012	6.714 (3.199) 0.036	−17.6
Secondary or college*age (referent)				--	--	--
Primary*age	Β6			0.152 (0.117) 0.195	0.110 (0.115) 0.338	−27.6
Illiterate*age	β7			0.271 (0.117) 0.020	0.219 (0.115) 0.056	−19.2
Secondary or college*ln(age) (referent)				--	--	--
Primary*ln(age)	β8			−2.677 (1.704) 0.116	−2.132 (1.673) 0.203	+20.3
Illiterate*ln(age)	β9			−4.259 (1.695) 0.012	−3.510 (1.668) 0.035	+17.6
Secondary or college*1/age (referent)				--	--	--
Primary*1/age	β10			−8.711 (5.311) 0.101	−7.142 (5.217) 0.171	+18.0
Illiterate*1/age	β11			−13.072 (5.274) 0.013	−10.681 (5.197) 0.040	+18.3
Morbidity events in past week
0 (referent)		369 (43.0)b			--
1	β12	174 (20.3)b			0.203 (0.086) 0.018
≥2	β13	226 (26.3)b			0.112 (0.084) 0.181
Missing	β14	90 (10.5)b			0.002 (0.202) 0.994
0*age (referent)					--
1*age	β15				−0.024 (0.009) 0.006
≥2*age	β16				−0.026 (0.008) 0.002
Missing*age	β17				−0.004 (0.014) 0.785

^aAll models were fit in Stata IC10 (College Station, Texas). Model formulae are shown in the methods section and the sample average curves (by maternal education group) for models 2b and 2c are shown in Fig 4.

^bThe Ns for morbidity events in past week are given for observations not cases as this was a time dependent variable (i.e., data collected throughout the age period studied). This variable was also, therefore, included as an interaction with age to account for the fact that the effect of morbidity on weight may have been different at each assessment age.

Figure 4.

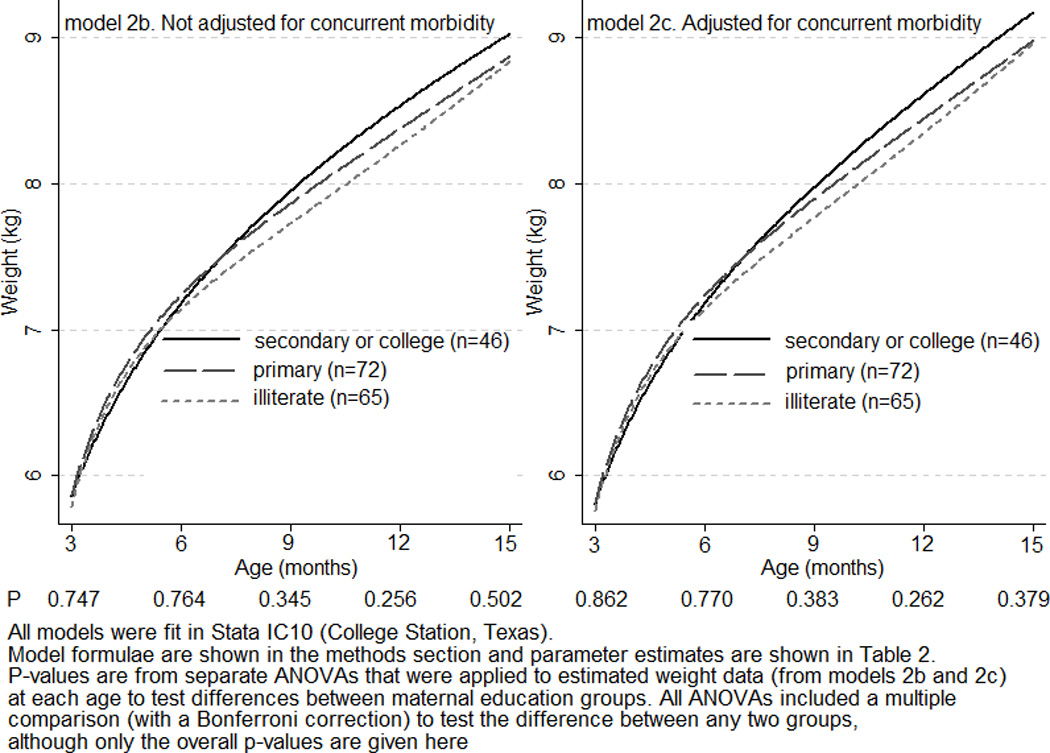
Sample average weight growth curves from three to 15 months of age, by maternal education group, in 183 rural Indian boys from the Infant Feeding Study: Estimated from separate mixed effects models (2b and 2c), the first not adjusted for concurrent morbidity and the second adjusted for concurrent morbidity.

In model 2c, we further adjusted for concurrent morbidity. The main effect of illiterate and also the illiterate-by-ln age and by-inverse age interactions retained significance, indicating that being born to an illiterate mother had effects on infant weight growth in this sample that were independent of concurrently measured morbidity. Because many of the parameter estimates, however, changed by more than 10% between models 2b and 2c, growth curves from model 2c were plotted (Fig. 4) to see whether adjusting for concurrent morbidity altered the effect of maternal education on weight growth. The three curves were slightly closer together and this was confirmed by marginally less significant p-values from ANOVA models.

DISCUSSION

The study of physical growth has long been a part of anthropological research. This paper provides an example of using mixed effects methods to analyze serial growth data. We demonstrate the principles of fitting individual curves and testing exposure variable effects on the average curve of a sample. The paper is neither a statistical treatise nor a how to guide to growth curve modeling, but it is a starting point for researchers with serial growth data that need analyzing (example code in online appendix). For simplicity, we only present linear parametric models, but the reader should be aware of other non-linear models (e.g., Jens and Bailey, 1937) and non-parametric approaches (e.g., splines and kernel estimators (Gasser et al., 2004)) that form part of a growth modeler’s toolbox.

To demonstrate the principles of mixed effects methods for growth analysis, we developed a robust statistical model to describe the weight growth of 70 infants in the Born in Bradford study. A mixed effects quadratic polynomial model (1c) provided a remarkably better fit for the data than a conventional quadratic polynomial model (1b), thereby providing a clear example of the need to incorporate individual characteristics when modeling growth. The overall residual standard deviation of a model provides a measure of average error in the original unit of measurement. It is calculated as the square root of the residual variance statistic we show in Table 1. The final mixed effects model (1d) in our example was a fractional polynomial with a residual standard deviation of 200g. Because this is larger than the technical error of measurement of infant weight data (Ulijaszek and Kerr, 1999), we would typically continue model development and test non-parametric approaches such as mixed effects cubic regression splines. In addition, after looking at a scatter plot of residual against age, there was some evidence that the final model was unable to describe the expected pattern of weight loss in the first two weeks of life. The development of a structural growth model that imposes a negative growth rate immediately after birth and an inflexion point around two weeks of age may be a worthy endeavor.

Before the advent of mixed effects growth modeling, researchers would have to fit separate models for each infant in a sample (Deming, 1957; Marubini et al., 1972; Cameron et al., 1982), and it was generally accepted that to do this the infant should have one more data point available than the number of parameters in the model (Baxter-Jones and Mirwald, 2004). In our analysis of data from Born in Bradford infants we demonstrate the ability of mixed effects growth models to combine all available data, regardless of the number and timing or serial observations, and estimate individual and sample average curves. Statistical packages efficiently handle non-consistently collected data using probability functions to describe the relative likelihood of each random effect occurring at a given point in the observation space (Rabe-Hesketh and Skrondal, 2008).

In our second worked example showing how to test the effects of an exposure variable on the sample average curve of a mixed effects model, we investigated the influence of maternal education on weight growth in rural south Indian boys. By fitting maternal education as a main effect (i.e., up / down shift in curve) and also an interaction with the age terms (i.e., change in shape of curve) in a Berkey-Reed (1987) 1^st order model, we were able to show that maternal education significantly influenced the shape of the weight growth curve of these rural south Indian boys. Despite maternal education influencing growth both before and after adjusting for concurrent morbidity, separate ANOVA models applied to estimated data at every three months of age showed that significant differences between maternal education groups at specific ages were not present. In this scenario, the advantage of producing growth curves for each maternal education group is that we can identify the beginning of infants falling short of their potential growth trajectories. A cross-sectional analysis would conclude that maternal education is not important for optimal infant growth, whereas this longitudinal analysis concludes that inequalities in infant growth due to maternal education may begin in infancy, which would be an important period to target for prevention of further growth faltering.

CONCLUSIONS

Growth curve modeling has many applications for anthropological research, yet mixed effects methods have not often been utilized in research in the field. This paper highlights the utility of mixed effects models for analyzing serial growth data because they allow researchers to simultaneously predict individual curves, estimate sample average curves, and investigate the effects of environmental exposure variables. A mixed effects fractional polynomial model best described the growth of Bradford, UK infants compared to other parametric options, but had the limitation that parameter estimates could not be easily interpreted. Indian infants of illiterate mothers started to deviate in their growth from those born to more highly educated mothers at approximately six months of age, thereby providing evidence that interventions targeting educational differences in growth in India should target the end of the exclusive breastfeeding period.