Dosimetric consequences of rotational errors in radiation therapy of pediatric brain tumor patients

Abstract

Purpose

To quantify the rotational offsets and estimate the dose effect of rotation on the target volume and normal tissues in children with brain tumor.

Methods

Twenty-one pediatric patients with brain tumors were included in this study. Cone-beam CT was performed before each treatment and at the end of every other treatment. Translational offsets were corrected before the treatment. An offline analysis was performed to quantify rotational errors. The treatment plans were altered and recalculated to simulate a rotation of 2° and 4°, and the dose changes were quantified.

Results

1016 CBCT datasets were analyzed for this report. The mean of the rotations were not meaningfully different from zero. 18.1% of the fractions had rotations with a magnitude ≥2°, 5.0% had rotations ≥3° and 0.9% had rotations ≥4°. For the 2° rotational simulation, the gEUD values of the PTV and critical structures changed by less than 2%. For the 4° simulation, parallel type normal structures had minor changes (<2%), but serial type normal structures and the PTV had changes of 10% and 5%, respectively.

Conclusions

The majority of rotational errors observed were less than 1°. A rotational error of 2° produced negligible changes in the gEUD to critical structures or target volumes. Rotational errors ≥4° produced undesirable results, therefore, at a minimum, errors >2° should be corrected.

In concept, the planning target volume (PTV) defines a space in which the prescribed dose of radiation will always be administered to the clinical target volume (CTV) despite uncertainties in patient positioning and variations in beam delivery. An improved understanding of these uncertainties and variations should enable a reduction in the PTV which is one possibility to reduce dose to normal tissues in children with brain tumors [1].

Spatial differences between the planned and actual position of the patient and targeted volume, also known as offsets or errors, may be translational and/or rotational. These differences are a major source of localization uncertainty when treating patients with external beam radiation therapy [2]. Numerous studies have reported on translational and rotational errors in adult patients treated for a variety of tumors, including prostate [3–6] and head and neck [7–9] cancer. Studies documenting localization uncertainty in pediatric patients are limited to the evaluation of translational errors [10–12] and their dosimetric impact [13,14].

We recently reported the first results of a clinical trial using cone-beam CT (CBCT) in conjunction with daily irradiation to evaluate set-up uncertainty in pediatric patients with brain tumors and tumors of the head and neck [10]. In our evaluation of 100 children, we found that when the daily pre-treatment CBCT was registered to the treatment planning CT to determine x, y, and z offsets, set-up uncertainty could be limited to less than 2 mm when the action threshold for correcting for translational offsets was an offset vector of 3 mm. We noted that there was some dependence on patient positioning (supine had less uncertainty than prone) and the use of general anesthesia (with GA has less uncertainty than without). We found that children who were not localized using CBCT had a set-up uncertainty as large as 4 mm. Because our ability to correct for positional uncertainty is limited to the cardinal plane movements of the standard linear accelerator treatment couch, we have now sought to determine the effect of rotational uncertainty calculated from the same CBCT datasets. Understanding the effect of rotational uncertainty, in combination with translational errors, may provide additional evidence that the margins used in the definition of the PTV are reasonable or that additional maneuvers are required to adapt treatment to maintain target volume coverage and spare normal tissues. In this report, we focus on describing rotational setup errors and their impact on target dose coverage in pediatric patients with intracranial tumors.

Materials and methods

Patient data

Data were collected from 21 pediatric brain tumor patients enrolled on an IRB approved daily localization protocol [10] which utilized an investigational low dose MV-CBCT system, called the imaging beam line (IBL) [15,16]. This investigational CBCT system delivers at most 1 cGy to the isocenter per CBCT. All of the patients were treated in the supine position, 11 were treated using daily general anesthesia administered IV. Each patient had a custom thermoplastic mask and neck rest for immobilization. The median age was 7.0 years (range 1–19 years). MV-CBCT was performed before each treatment (pre-CBCT) and after every other treatment (post-CBCT). The CBCT data were registered on-line to the treatment planning CT and translational offsets were corrected. If there was noticeable rotational offset, the patient was manually repositioned and another CBCT was acquired.

Image registration and evaluation of rotation

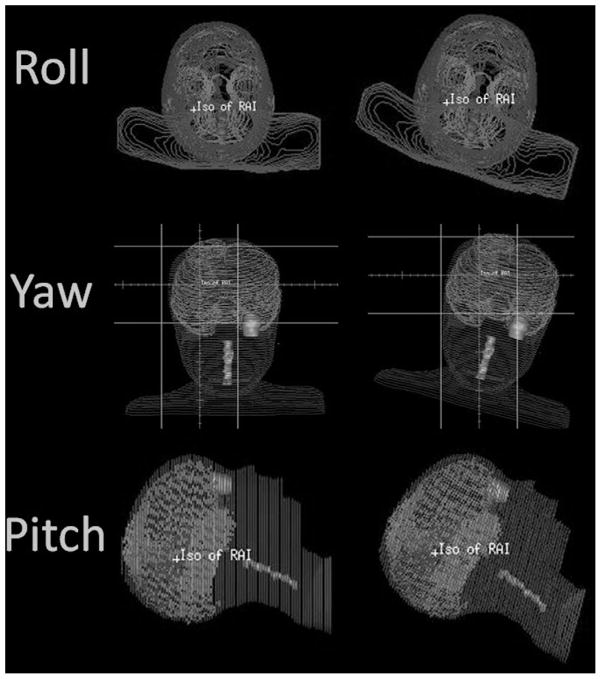
The offline rotation offset evaluation was performed with the Pinnacle treatment planning system (Phillips Medical Systems, Fitchburg, WI). All CBCT datasets were registered to the individual patient simulation CT dataset. A mutual information algorithm was used for the automatic registration. The auto registration was manually checked and adjusted if necessary. Special emphasis was placed on the boney anatomy close to the target. The registration matrix, which included the rotation component were recorded. The nomenclature used in this study was as follows: roll is a rotation about the superior–inferior axis, yaw is a rotation about the anterior–posterior axis, and pitch is a rotation about the right–left axis. Fig. 1 is a graphical representation of each rotation. The rotational offsets between the pre-CBCT and the simulation CT were calculated, giving the interfraction rotational error. The difference between the pre- and post-treatment CBCT was used to calculate intrafraction rotational change. The difference between the pre-CBCT and the pre-CBCT after patient re-positioning was used to calculate the effectiveness of manual repositioning to eliminate rotational offsets. Student’s t-test was used to compare rotational differences between those treated with IV general anesthesia and those who were not. In order to determine the precision of the registration and therefore estimate the minimum uncertainty, the first 10 CBCTs of five patients were registered five times each. This estimate was given by the root mean square of the standard deviation of these offsets.

Fig. 1.

The rotation nomenclature is shown. Roll is a rotation about the superior–inferior axis, yaw is a rotation about the anterior–posterior axis, and pitch is a rotation about the right–left axis. Each rotation shown is in the positive direction.

Rotation simulation

Rotation simulation was performed using the Plan UNC (University of North Carolina, Chapel Hill NC) treatment planning system (TPS). To calculate the machine parameters needed to represent rotational offsets it was necessary to convert the machine coordinates (collimator, table, and gantry) to the patient coordinate system (x, y, and z), apply the desired rotation offset and then convert back to the machine coordinate system. This maneuver provided the machine parameters representing rotational offset. This method was complicated because all patients were treated with non-coplanar beam arrangements. A detailed description of the rotation implementation is provided in the appendix of the article by Bose et al. [17]. MATLAB (MathWorks Inc., Natick, MA) was used to solve the matrix equations.

Dosimetric effects of rotation

The treatment plans from three patients with posterior fossa tumors treated using IMRT were re-calculated with +2° and +4° rotations about isocenter in each cardinal direction separately to determine the dosimetric effect of rotation on dose to critical normal tissue structures and the target volume coverage. In addition, a combined +2° rotation about each axis was simulated for the three patients. The posterior fossa location was chosen for this portion of the study because it is the most common pediatric brain tumor site treated with focal radiation therapy. The GTV to CTV margin was 5 mm and the CTV to PTV margin was 3 mm. Seven critical structures were examined in addition to the PTV: left and right cochlea, left and right optic nerve, optic chiasm, brainstem, and spinal cord. The generalized Equivalent Uniform Dose (gEUD) [18] for each structure was recorded.

Results

Rotational measurements

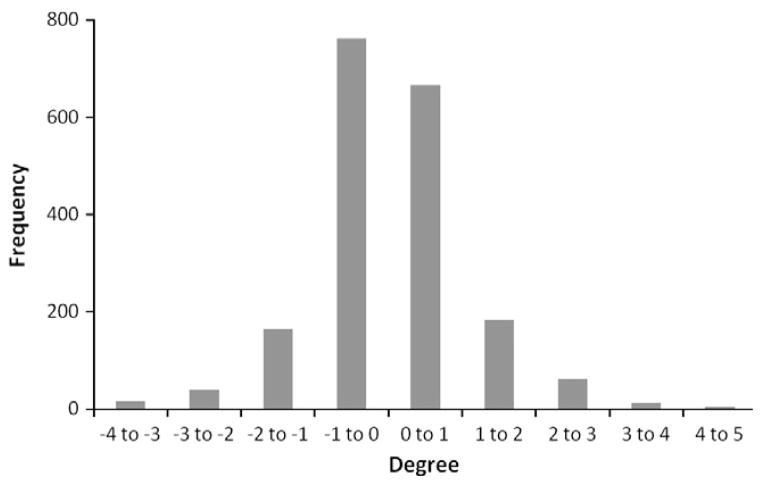
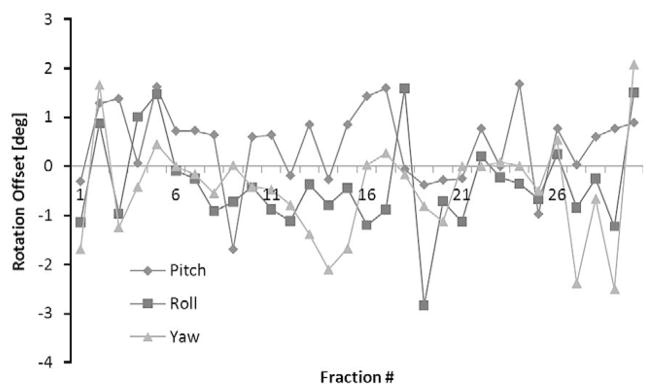
The number of CBCT studies pre-treatment and post-treatment was 637 and 320, respectively. There were 59 CBCT evaluations repeated to correct for observed rotation on the pre-treatment CBCT. In total, 1016 CBCT datasets were analyzed for this report. The mean ± standard deviation of the rotations were 0.37° ± 1.04° (pitch), −0.29° ± 0.96° (roll), and 0.03° ± 0.99° (yaw). The mean ± standard deviation difference between the pre- and post- CBCTs were 0.03° ± 0.73°, 0.12° ± 0.78°, and 0.06° ± 0.99°, respectively (Table 1). The distribution of rotational offsets in all direction is presented in Fig. 2. These data indicate that a systematic rotational error did not exist during setup for this group of patients. Fig. 3 displays the rotational offset in each direction for a single patient during the course of treatment. This patient had a wide variation in rotational offsets. The magnitude of rotation was calculated using the absolute value of the rotation. For example, a clockwise roll was normally positive and a counterclockwise roll negative, but for the magnitude calculation, they were both considered positive. This gives a more clinically useful metric. The mean ± standard deviation of the magnitude of rotations were 0.66° ± 0.89° (pitch), 0.72° ± 0.71° (roll), and 0.60° ± 0.79° (yaw).

Table 1.

Rotational offsets in children with brain tumors treated in the supine position.

	Pitch°	Roll°	Yaw°
Mean rotation	0.37 ± 1.04	0.29 ± 0.96	0.03 ± 0.99
Mean magnitude	0.66 ± 0.89	0.72 ± 0.71	0.60 ± 0.79
Difference pre/post	0.03 ± 0.73	0.12 ± 0.78	0.06 ± 0.99

Fig. 2.

Shown is a histogram of the rotational offset for all directions of all patients.

Fig. 3.

The rotational offset in each direction for an entire treatment of a patient that had a wide variance of rotational offsets is displayed.

Considering the entire dataset of pre-CBCT studies and rotation in at least one of the three cardinal planes, 18.1% had rotations with a magnitude ≥2°, 5.0% had rotations ≥3° and 0.9% had rotations ≥4°. In the setting where two pre-CBCTs (initial and repeat study to correct for observed rotation) were acquired, the mean ± standard deviation offset correction was 2.0° ± 1.2° and the mean offset after correction was 1.3° ± 1.0°.

There was no statistical difference when comparing the rotational errors of those treated with or without anesthesia for both the pre-treatment (interfraction) and pre- vs. post-treatment (intrafraction) CBCT data. Precision analysis of rotational registration gave 0.22° in pitch and roll, and 0.31° in yaw.

Rotation simulation

The treatment plans provided the machine settings for the collimator, table, and gantry positions for a particular field. The necessary transformations were applied to these settings to obtain new collimator, table and gantry positions for a particular rotational offset. Rotations were simulated for 2° and 4°. An example field setting is collimator at 90°, table at 270° and gantry at 66°. When a 2° roll is simulated, the collimator needs to be rotated by 2.19°, the gantry by 0°, and the table is rotated by 0.89° from their original positions.

Dosimetry effects of rotation

As noted in the methods section, the treatment plans of three patients with posterior fossa region tumors were recalculated with a 2° and 4° rotation about each individual axis. A total of 18 treatment plans were generated. A gEUD ‘a’ value of −10 was used for the PTV, +10 was used for serial type normal structures, and +2 was used for parallel type normal tissue structures [19]. For the 2° rotational simulation, the gEUD values of the PTV and critical structures changed by less than 2% in any directions (Table 2). For the 4° simulation, the parallel type normal structures had minor changes (<2%), but the serial type normal structures and the PTV had changes of 10% and 5%, respectively. For the combined 2° rotation, the results were similar to the single axis 2° rotations. The gEUD of the PTV and serial structures had minor changes (just under 2%), while the parallel type structures on average had a decrease in gEUD compared to the non-rotated case.

Table 2.

Dosimetric effects of rotational errors in children with posterior fossa tumors treated in the supine position.

	gEUD PTV	gEUD parallel	gEUD serial
2° Error	Δ< 2%	Δ< 2%	Δ< 2%
4° Error	Δ= 5%	Δ< 2%	Δ= 10%
2° Combined error	Δ ~2%	Δ< 2%	Δ ~2%

Discussion

In this report we have defined a range of rotational offsets for a cohort of children with brain tumor undergoing radiation therapy in the supine position with and without anesthesia. Although rotational offsets may be present, the majority are less than 1.3°. The most potentially consequential rotational differences appeared to be those measuring >4°; however, those were seldom observed, occurring in less than 1% of treatments. Rotational errors of 2° occurred 18% of the time and appeared to result in only minor dosimetry effects on critical structures or target volumes. We observed that relatively large rotational errors (>2°) are often apparent when utilizing CBCT and may be manually corrected by repositioning. If possible, noticeable rotations or rotations greater than 2° should be corrected. Dosimetricly, the combined 2° rotational errors had a similar impact as the single axis 2° error. We did not examine various combinations of rotations which may have a different impact the dosimetric results than the individual rotations or the one combined rotation examined. It is important to also note that the dosimetric study only looked at posterior fossa targets, and therefore the results are not directly applicable to targets in different locations. Having said that, it is reasonable to assume that the general results will hold true for other intracranial sites, given the target shape is not very complex or elongated. In a clinical setting, each case should be examined individual and the results stated here used only as a guide.

Careful examination of the mean rotational offset in each direction yields results comparable to zero. This tells us that there is no systematic rotational offset. The more clinically useful parameter is the magnitude of rotations; which, for the majority of cases, are inconsequential.

It is worth noting that in the dosimetric simulation, the rotations are simulated with gantry, table, and collimator rotations, not actually rotating the CT image. These rotations introduce an unwanted rotation that cannot be corrected. Looking at the example outlined previously; for a field setting of collimator at 90°, table at 270° and gantry at 66°, when a 2° roll is simulated, the collimator needs to be rotated by 2.19°, the gantry by 0°, and the table is rotated by 0.89° from their original positions. This introduces a pitch offset of 0.01°. In general, to simulate rotations of complex non-coplanar beam arrangements, an unwanted rotation offset is introduced, but this offset is generally much smaller than the rotation being simulated.

Based on these findings, pediatric patients with brain tumors, including posterior fossa tumors, being treated with IMRT may not require advanced rotational corrections including specialized treatment tables [20] or treatment machine-based corrections [21]. However, if margins are reduced, a more conformal therapy such as modulated arc therapy, or different modality such as proton therapy is used, these finding may not be valid. A system capable of reporting rotation offset would be helpful when determining if manual correction should be applied.

Conclusion

The majority of rotational errors observed were less than 1°. A rotational error of 2° produced negligible changes in the gEUD to critical structures or target volumes while rotational errors ≥4° produced undesirable results. Therefore, at a minimum, rotational errors >2° should be corrected.