A Multiple Object Geometric Deformable Model for Image Segmentation

Abstract

Deformable models are widely used for image segmentation, most commonly to find single objects within an image. Although several methods have been proposed to segment multiple objects using deformable models, substantial limitations in their utility remain. This paper presents a multiple object segmentation method using a novel and efficient object representation for both two and three dimensions. The new framework guarantees object relationships and topology, prevents overlaps and gaps, enables boundary-specific speeds, and has a computationally efficient evolution scheme that is largely independent of the number of objects. Maintaining object relationships and straightforward use of object-specific and boundary-specific smoothing and advection forces enables the segmentation of objects with multiple compartments, a critical capability in the parcellation of organs in medical imaging. Comparing the new framework with previous approaches shows its superior performance and scalability.

1. Introduction

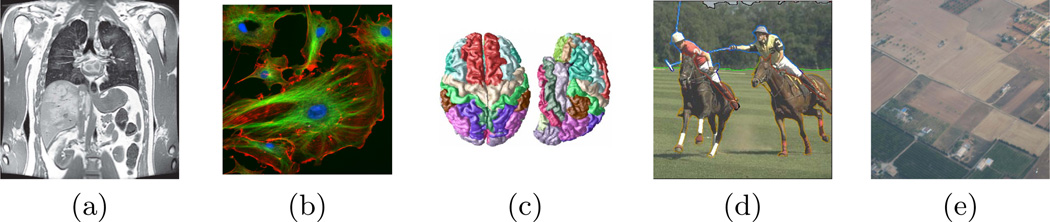
Image segmentation is one of the most fundamental problems in computer vision, with applications in scene reconstruction, motion tracking, content-based image retrieval, aerial imaging, etc. (see Fig. 1). Medical image analysis in particular has a growing need for the automatic segmentation of multiple organs and complex sub-structures from increasingly large data sets of multi-dimensional images [1–3]. The segmentation step often directly affects subsequent processing tasks such as quantification, registration, and visualization. In many cases, the segmentation of multiple objects should provide a complete parcellation of the image into components without overlaps and gaps between the segmented regions. When multiple regions meet, the boundary around a region often becomes heterogeneous in nature, e.g., where the image data provides little information, boundaries may need to be inferred based on a prior model, while image information can be relied upon elsewhere [2, 4]. Prior knowledge may also extend to the overall organization of the structures of interest and their spatial or topological relationships [1, 5, 6]. Finally, segmentation problems can easily involve large numbers of components or objects [7, 8], and the complexity of the applied methods must be taken into account for practical reasons.

Figure 1.

Various problems where images are to be segmented into multiple interacting objects: a) an MRI of the abdomen, showing many organs; b) fluorescent microscopy imaging involving complex interactions of multiple cells; c) a parcellation of the cortex into 78 gyral regions; c) images and videos of sporting events where the different players interact; d) aerial images of crops and farmlands. These examples were obtained from computer vision and medical imaging databases [3, 26, 27] or our own work (c) [28].

Parametric deformable models (PDMs)–i.e., active contours implemented by explicitly tracking points–have been widely used in computer vision to perform image segmentation [9]. An important property of this representation is its capability to represent boundaries at a sub-grid resolution as it is essential in the segmentation of thin structures (e.g., cortical sulci). Image-based “external forces” drive the contour toward desired features while contour-dependent “internal forces” regularize and smooth the boundary. Geometric deformable models (GDMs)–i.e., active contours implemented with level sets [10, 11]–permit flexible topological changes and yield contours with no self-intersections. In the GDM framework, “speed” functions describe the local movement of the contour and are analogs to the forces used in PDMs. With a single level set function, GDMs permit the segmentation of multiple isolated regions; but in their most basic implementation, they do not control the number of objects or their topology. Topology-preserving extensions [12–14] permit control of single object topology, but do not address topological relationships between objects or permit one to model boundaries between multiple objects at once.

A number of multiple object segmentation methods based on the level set framework have been proposed [15–24]. Most of these approaches use N level set functions to segment N objects and rely on coupling terms to avoid overlaps and gaps [18–20, 23, 25]. These methods have the advantage that each object can be independently specified in both its own topology and its internal and external speeds. However, coupling terms do not forbid certain object interactions, so these approaches can still produce overlaps and gaps in practice. As well, most are not formulated to consider the relationships between objects, and memory requirements become daunting as the number of objects to be segmented grows.

Vese and Chan [15] introduced the multiphase (MP) segmentation framework that represents N objects with log₂(N) level sets based on combination rules. This model permits multiple object boundaries, and guarantees no overlaps or gaps. As well, it substantially reduces the computational burden as the number of objects or compartments grows. However, this approach has three key limitations. First, its image-based external speed term is not easily generalized beyond the region-based model of Mumford and Shah [29]. This fact excludes a rich collection of external speeds that may be essential to solving many problems of practical importance. Second, the internal speeds in the multiphase framework—comprising a penalty on contour length—are applied to the level set functions rather than to the objects themselves. Thus, it is possible that while the lengths of the level set functions are minimized, it may not be so for the boundaries of the objects themselves. Third, the evolution/optimization can “get stuck” in situations where a pixel needs to acquire a label that can be reached only by changing two level set functions at the same time. The existing evolution strategy cannot resolve these situations, which are also more commonly found with an increasing number of objects. A remedy for this limitation involving a permutation of the level set combination rule used to represent a given label was proposed in [30]. As the number of level set functions increases, however, a greater number of permutations will need to be performed to ensure that transitions between all labels are possible.

Pohl et al. [21] proposed a probabilistic embedding to avoid overlaps and gaps by replacing the level set isocontours with a labeling of regions according to their maximum probability. In this case, however, the geometric properties of curvature associated with level set isocontours are no longer relevant, and the method still requires N − 1 level sets or N − 1 functions derived from level sets.

Brox et al. [24] presented a coupled curve evolution method where distinct objects are constrained through the coupling of the evolution equations rather than by changing the energy functional. Their coupled curve evolution shows that a pixel (or voxel) in one object competes with other objects, while additional terms help to discourage gaps. This approach deals with multiple objects, but it does not guarantee there are no overlaps or gaps, making relationships and other topology constraints difficult to enforce. The evolution requires N level set functions for N objects, increasing computational and storage burden as more objects are added.

Recent methods by Lie et al. [31] and Chung and Vese [32] formulate a “multilayer” method that represents multiple objects using a small number of nested level contours of a function. This approach is efficient with memory, requiring just two functions to represent triple junctions in 2D. However, it shares with the multi-phase approach a limitation in the types of speeds that may be applied, a lack of control of topology, and the interpretation of its regularization terms as minimizing level set length rather than object boundary length [15]. These representations also lose some of the computational advantages of using signed distance functions.

Much interesting work has gone into adapting the level set formalism for multiple object segmentation to account for prior shape information. Tsai et al. [22] developed a framework that constrains potential segmentation results using a parametric shape model based on principal component analysis. Uzunbas et al. [33] employed a similar framework, but built a statistical shape model using kernel techniques and furthermore modeled relative poses between objects. These methods used N level sets to represent N objects, and therefore, a heuristic approach was used in both to prevent overlaps. Vazquez-Reina et al. [34] used a shape model similar to [22], but used the MP level set representation of [15], rather than N level sets. This prevents overlap and gaps, and improves efficiency, but still suffers from some of the setbacks of the multiphase representation. Fussenegger et al. [35] extended [24] with a multi-object pose-invariant shape prior. These methods have been important contributions in constraining multiple object level set segmentation. However, none of these methods guarantee that single object topology, or topological relationships are preserved. The storage of N (or log₂(N)) level sets along with the shape priors may become burdensome as the number of objects increases.

Markov random fields (MRFs) are graphical models that have achieved great success in image segmentation. Classical algorithms such as iterated conditional modes (ICM) [36] can provide approximate solutions in the multiple label problem. Other methods have been proposed that efficiently and accurately solve the Potts model segmentation problem using advanced optimization techniques. Zach et al. [37] presented a method that efficiently solves a continuous relaxation of the Potts model. Lellmann et al. [38] solved a similar formulation using an operator splitting optimization framework. Bae et al. [39] performed optimization using a dual formulation. While these methods all perform very well for a variety of segmentation tasks, as presented they lack certain important capabilities that aid in segmenting specific objects in images rather than identifying image regions with similar features, (e.g., intensity). In particular, these methods, as proposed, might segment “high intensity” rather than “femur” in computed tomography. This specific identification is important in medical imaging, for example, where quantitative measurements of anatomy are often used for diagnosis or research purposes. High level information such as object topology, statistical priors, as well as partial volume functions have been instrumental in advancing this area of image segmentation. Furthermore, graph-based methods generally lack the sub-grid resolution offered by deformable models. The presentation of the above methods does not describe whether and how this information can be integrated in their respective frameworks, and such extensions appear far from trivial.

Another successful graphical model solver is the graph cuts framework, which provides a fast computational algorithm that is guaranteed to reach a global minimum for some categories of problems [40]. This technique can segment multiple objects by solving a sequence of binary segmentation problems [41], and a topology-preserving extension exists for single objects [42, 43]. However, the framework presently lacks the ability to model the topological relationships of objects, sub-grid boundaries, and different optimality criteria on different parts of boundaries.

In this paper, we present a multiple object geometric deformable model (MGDM) segmentation framework that 1) guarantees no overlaps or gaps, 2) evolves only a few level set-derived functions independently of the number of regions, 3) can apply any existing type of speed in the level set literature, 4) can enforce relationships and topological constraints on any or all objects and groups of objects if desired, and 5) can apply speeds that are different according to the specific object-to-object boundary. In this framework, the evolution of the level set functions representing any number of objects or compartments is recast into the evolution of a fixed, small number of distance functions and an equal number of corresponding label functions. Only two or three distance functions are needed for two-dimensional (2D) or three-dimensional (3D) problems, respectively. Since the number of functions is fixed, the computational penalty for increasing the number of objects is small.

MGDM is a multi-object extension to the conventional geometric level set formulation, and therefore one can apply all the conventional speeds that are useful and familiar to the community and can employ all the conventional fast computational methods such as fast marching and the narrow band method. The problem of object overlaps and gaps is automatically solved because the evolving functions directly provide a partition of the image. Object labels are specifically tracked within the evolution, enabling the straightforward implementation object-dependent speeds, including different speeds on different boundaries between specific objects or regions. The topology of objects and the relationships between groups of objects are preserved by using a multi-object simple point constraint directly on the new functions without having to reconstruct the level set function of individual objects. The description of MGDM we provide here is valid for both two-dimensional (2D) and three-dimensional (3D) images, and is generalizable to higher dimensions. Preliminary descriptions of 2D and 3D MGDM were presented in two conference papers [44, 45]. These methods described “homeomorphic level sets” which preserve the topology of each object as well as object relationships. The presentation here includes a complete mathematical framework describing the MGDM object decomposition, a new computationally efficient evolution strategy, a more complete description of the potential for object-specific speed and topology flexibility, comparisons with competing methods, new demonstration experiments, and additional measures of performance.

2. Notation and Definitions

Consider an image I defined on a domain Ω^d where d = 2 for 2D and d = 3 for 3D. We consider N objects (sets) O₁, O₂, …, O_N, each containing points from the domain x ∈ Ω^d such that these objects cover the whole domain with no overlaps or gaps. Formally, this means that ${\cup }_{i=1}^N{O}_i={\mathrm{\Omega }}^d\text{and}{O}_i\cap O_j=\mathrm{ø},\forall i\ne j$. In some applications, one of these objects might be identified as the background on which the other objects are segmented.

Object signed distance functions, denoted ϕ_i are commonly used in the level set literature for their desirable numerical properties. These functions are negative inside their respective objects, positive outside (cf. [10, 11]), and give the distance to the object boundary at every point x. Accordingly, ϕ_i(x) can be written as:

$${\varphi }_i(x)=\{\begin{array}{cc}\hfill -{\text{min}}_j{d}_x(O_j),& x\in O_i,\hfill \\ \hfill d_x(O_i),& x\notin O_i.\hfill \end{array}$$ (1)

where d_x(O_i) is the distance from a point x to object O_i,

$$d_x(O_i)=\underset{y\in O_i}{\text{min}}\Vert x-y\Vert .$$ (2)

If x is in O_i, then the closest boundary of O_i is the distance to the nearest other object O_j. Note that for a fixed x ∈ O_i there must exist at least one other object O_j such that ϕ_j(x) = −ϕ_i(x). In the following sections, we describe how to take advantage of this relationship in order to represent the collection of signed distances using a smaller number of functions. Now, we briefly describe how a locally optimal segmentation is found by evolving the objects’ signed distance functions. For now, we think of each object as having its own separate evolution; the efficient representation and computation strategy of MGDM will be described in the next section.

For each signed distance function, we seek an evolution of the level set functions according to speeds f_i, which can be written in the following general form [46]:

$$\frac{\partial {\varphi }_i}{\partial t}=({\alpha }_{1}p\kappa +{\alpha }_2{V}_p+{\alpha }_3\overrightarrow{\upsilon }·\frac{\nabla {\varphi }_i}{|\nabla {\varphi }_i|})|\nabla {\varphi }_i|=f_i|\nabla {\varphi }_i|$$ (3)

where

$$f_i={\alpha }_{1}p\kappa +{\alpha }_2{V}_p+{\alpha }_3\overrightarrow{\upsilon }·\frac{\nabla {\varphi }_i}{|\nabla {\varphi }_i|}.$$ (4)

This formulation includes spatially-varying potential functions p which can be used to drive the boundaries toward edges [47], a penalty on contour length κ which produces smoother curves [10, 11], conventional region-based balloon speeds V_p [48], and spatially-varying advection forces v⃗ such as gradient vector flow [49]. The relative contributions of these terms can be controlled by the weights given by the α’s. Any additional types of speeds that are formulated for conventional geometric deformable models, such as prior shape [50, 51], can be readily added if needed.

Although it is preferred for numerical reasons that the functions {ϕ_i} are signed distance functions (cf. [10]), they need only be level set functions—i.e., Lipschitz continuous, negative inside, and positive outside. In order to keep this distinction clear, we denote the more general level set functions, which are not necessarily signed distance functions with a “hat”, e.g., {ϕ̂_i}. We now describe how a decomposition of object level sets can be used to efficiently represent boundaries rather than objects.

3. Theory and Algorithm

3.1. Decomposition of multiple level sets

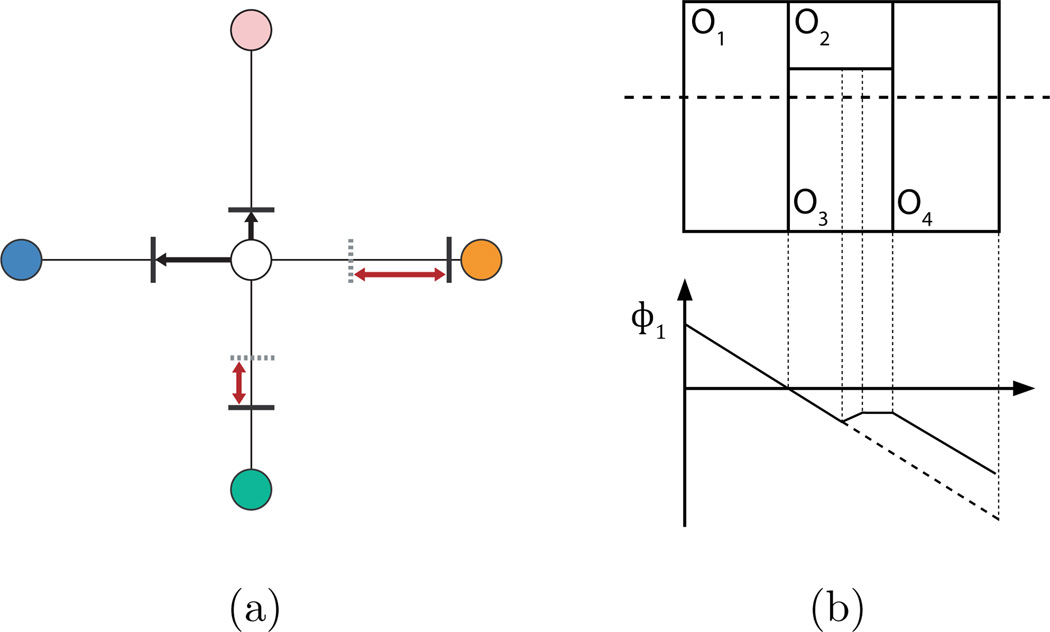
We define the set of label functions that describes the local configuration of neighboring objects at x as follows:

• DEFINITION 3.1. (Label functions)

  $$\begin{array}{cc}{\forall }_x,\hfill & L_0(x)=i\mathit{\text{iff}}{\varphi }_i(x)<0\hfill \\ \hfill & L_1(x)={\text{arg min}}_{j\ne L_0(x)}{\varphi }_j(x)\hfill \\ \hfill & L_2(x)={\text{arg min}}_{j\ne \{L_0(x),L_1(x)\}}{\varphi }_j(x)\hfill \\ \hfill & ⋮\hfill \\ \hfill & L_{N-1}(x)={\text{arg min}}_{j\ne {\{L_k(x)\}}_{k=0,\dots ,N-2}}{\varphi }_j(x).\hfill \end{array}$$

The label functions L₀, L₁, …, L_N−1 give a detailed description of the configuration of the objects. In particular, L₀ is the current segmentation and the first-level label L₁ identifies the closest neighboring object at each point. The ϕ_j function gives the distance to the boundary of O_j, and hence, minimizing over j yields the nearest object. More generally, L_k(x) = i, 1 ≤ k ≤ N − 1, if and only if O_i is the kth closest neighbor to x. In the event of a tie, we assume a fixed ordering of the objects so that there is always a unique label for L_k(x) at each point x. The effects of this choice are discussed in Section 6.

Given the set of label functions, we define the related distance functions as follows:

• DEFINITION 3.2. (Distance functions)

  $$\begin{array}{c}{\forall }_{x,}{\phi }_0(x)={\varphi }_{L_1}(x)\hfill \\ {\phi }_1(x)={\varphi }_{L_2}(x)-{\varphi }_{L_1}(x)\hfill \\ {\phi }_2(x)={\varphi }_{L_3}(x)-{\varphi }_{L_2}(x)\hfill \\ ⋮\hfill \\ {\phi }_{N-2}(x)={\varphi }_{L_{N-1}}(x)-{\varphi }_{L_{N-2}}(x)\hfill \end{array}$$

Here, the particular level set functions that are used in the right hand side of this decomposition are determined by the labels L₁, L₂, …, L_{N − 1} which are also functions of x, but we have dropped the argument for brevity and simplicity of notation. These distance functions specify the additional distances one must travel to reach the succession of next-closest neighbors. For example, φ₀ is the distance from x to its first neighbor and φ₁ is the additional distance that must be traveled to get to the second neighbor, and so on. According to this definition, φ_k(x) ≥ 0, ∀x, k since ϕ_Li(x) ≤ ϕ_Lj(x), ∀i < j.

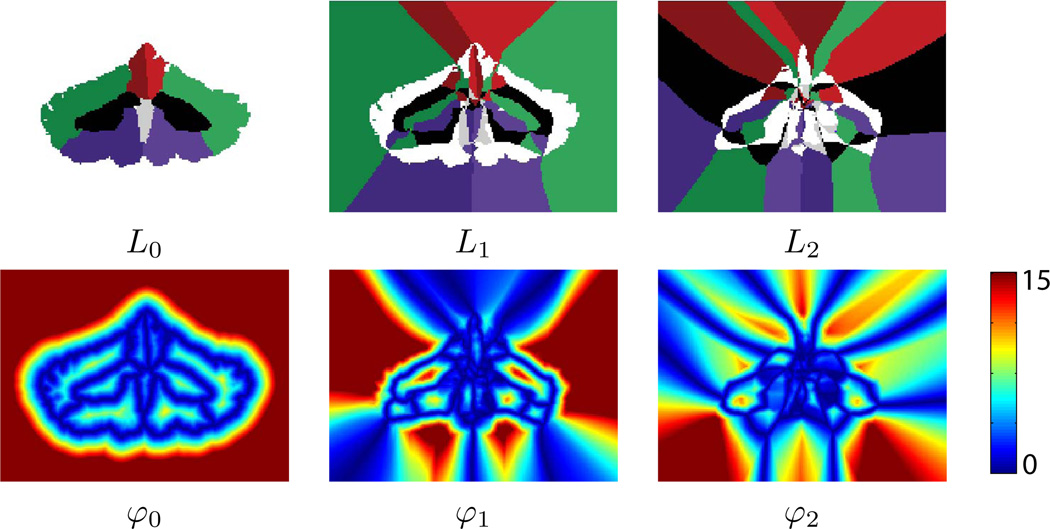
Figure 2 shows an example of this label-distance decomposition on a parcellated cerebellum for the first three label functions and their corresponding distance functions. An additional example of this decomposition can be found in a supplemental movie published with the electronic version of this manuscript.

Figure 2.

Illustration of a three-level label-distance decomposition of a parcellated cerebellum: The color used for each object’s label is identical for L₀, L₁, and L₂. The color scale for the distance functions have been compressed to the range [0, 15] to focus contrast around the boundaries. Here, blue pixels indicate points very close to a boundary, yellow pixels are more distant, and red are most distant.

3.1.1. Recovery of Signed Distance Functions

Given all the label and distance functions at a point x, the signed distance function of object i can be recovered as follows:

$${\varphi }_i(x)=\{\begin{array}{cc}-{\phi }_0(x),\hfill & i=L_0(x);\hfill \\ {\phi }_0(x),\hfill & i=L_1(x);\hfill \\ {\phi }_0(x)+{\phi }_1(x),\hfill & i=L_2(x);\hfill \\ {\phi }_0(x)+{\phi }_1(x)+{\phi }_2(x),\hfill & i=L_3(x);\hfill \\ ⋮\hfill & ⋮\hfill \\ {\displaystyle {\sum }_{j=0}^{N-2}{\phi }_j(x),}\hfill & i=L_{N-1}(x);\hfill \end{array}$$ (5)

We see that in order to recover all the signed distance functions, we require all the label and distance functions. Therefore, as it stands so far, there is apparently no advantage to the proposed decomposition, as it does not appear to lead to a compact representation or lower complexity.

The key to realizing the advantages of the label-distance decomposition is to observe that only signed distance values near object boundaries are required to accurately carry out the geometric level set computations. In fact, speeds at x should derive from the object L₀ to which x is assigned and the object L₁ that is closest to x—i.e., across the nearest boundary. Therefore, we do not need to keep the higher-order terms in this decomposition in order to carry out geometric deformable model computations. Accordingly, we can simply drop the “higher order” terms in (5) to get the following approximate signed distance functions:

• 2D:

  $${\hat{\varphi }}_i(x)=\{\begin{array}{cc}-{\phi }_0(x),\hfill & i=L_0(x)\hfill \\ {\phi }_0(x),\hfill & i=L_1(x)\hfill \\ {\phi }_0(x)+{\phi }_1(x)\hfill & i\ne L_{0,1}(x)\hfill \end{array}$$ (6)
• 3D:

  $${\hat{\varphi }}_i(x)=\{\begin{array}{cc}-{\phi }_0(x),\hfill & i=L_0(x)\hfill \\ {\phi }_0(x),\hfill & i=L_1(x)\hfill \\ {\phi }_0(x)+{\phi }_1(x),\hfill & i=L_2(x)\hfill \\ {\phi }_0(x)+{\phi }_1(x)+{\phi }_2(x),\hfill & i\ne L_{0,1,2}(x),\hfill \end{array}$$ (7)

where the notation i ≠ L_0,1(x) means i ≠ L₀(x) and i ≠ L₁(x) while i ≠ L_0,1,2(x) means i ≠ L₀(x) and i ≠ L₁(x) and i ≠ L₂(x). The functions ϕ̂_i(x) resulting from this truncated decomposition are negative inside and positive outside each object and are Lipschitz continuous. They are therefore legitimate level set functions despite being only approximations to the true signed distance functions.

The number of functions kept in the approximation is different for 2D and 3D because the functions encode the structure of the boundary between objects. In 2D, any boundary between neighboring objects is either a curve segment (between two objects) or a point (where three or more objects meet). In 3D, the boundaries are made of surface patches (between two objects), curve segments (between at least three objects), and points (between at least four objects). Therefore, in order to describe all the possible boundaries, we need to be able to describe these particular structures in their respective spaces. The curves are defined with one level set function in 2D, and the points joining them require two functions. Similarly, surfaces in 3D require one function, curves are defined as the intersection of at least two surfaces, and points require three surfaces. Nevertheless, as the truncated reconstruction is an approximation of the true signed distances, errors appear for objects that are not among those stored as neighbors (see Section 6 for details). The decomposition by its nature puts certain limitations on the evolution (see Section 3.2).

3.1.2. Alternate distance for topology control

In applications where the topology and relationships of segmented objects must be preserved, the above definitions can be modified to reflect the fact that objects that are not in contact will never meet at a boundary. Conversely, it means that the set of possible neighbors for a given object is restricted to the subset of the labels in contact with the object. This restriction can be enforced on the distance definition by setting d_x(O_j) to +∞ where it is undefined because the object O_j is not and should not be in contact with the object at x. If x ∈ O_i, this can be summarized as:

$$d_x^{\prime }(O_j)=\{\begin{array}{cc}{d}_x(O_j),\hfill & \text{if}{O}_i\text{and}{O}_j\text{are allowed to come in contact}\hfill \\ +\infty ,\hfill & \text{otherwise}\hfill \end{array}$$ (8)

This alternate definition ensures the correctness of algorithm evolution when topology constraints are required (see Section 3.3).

3.1.3. Computing the level set decomposition and reinitialization

Like conventional level set methods, MGDM requires an initialization of the labels to be segmented in order to compute the truncated MGDM decomposition. The initialization often takes the form of a voxel-wise segmentation (equivalent to L₀ in our notation), but can also make use of sub-grid information if level set functions of each object are provided.

In order to build the label and distance functions, the simplest approach consists of computing the signed distance functions for all N objects using fast marching, and then using Eqs. 3.1 and 3.2 to obtain L_k and φ_k for all k. We do not use this computationally intensive approach in practice and instead take advantage of the following efficient joint fast marching method: starting from the current segmentation L₀ (or boundary locations according to object level set functions), all the boundaries are set to march outward from each object. The first boundary to reach a voxel x gives the first neighbor L₁(x) and the distance function φ₀(x) = d_x(O_L1). When the second boundary reaches x, we get L₂(x) and φ₁(x) = d_x(O_L2) − φ₀(x). The marching is stopped in the voxels where φ₁ and L₂(x) have been set, and so the joint fast marching method needs only to go through the entire image twice in 2D, or three times in 3D (once for each φ).

The computational complexity of this re-initialization scheme is lower than that of both the N level set method and the multiphase level set method, and it is not dependent on the number of objects. As we will see in Section 3.2, our algorithm requires periodic re-initialization of the distance functions during evolution for reasons similar to classical level set methods. Efficient computation of the decomposition is particularly important as this re-initialization involves the entire image rather than just the narrow band.

3.2. Evolution

We now describe the deformable model evolution equations for the 2D case; analogous expressions are readily found for 3D and higher dimensions. Our objective is to recast the evolution of any individual level set function ϕ_i according to the overall speed f_i of O_i (i.e., $\frac{\partial {\varphi }_i}{\partial t}=f_i|\nabla {\varphi }_i|$, as presented in Eq. 3) into an evolution of φ₀, φ₁, L₀, and L₁. In general, the movement of the boundary between objects i and j depends on which region has a faster expanding speed; therefore, the evolution of φ₀ is given by

$$\frac{\partial {\phi }_0}{\partial t}=\frac{1}{2}(f_{L_0}|\nabla {\hat{\varphi }}_{L_0}|-f_{L_1}|\nabla {\hat{\varphi }}_{L_1}|),$$ (9)

where f_L0 is the speed of the object assigned to x and f_L1 is the speed of the closest neighboring object to x. The factor $\frac{1}{2}$ is introduced to preserve the overall scaling. Notice also that the evolution of the MGDM distance functions φ_i depends on the object level set functions ϕ_j. Since these are not stored during the evolution, the gradient of the object signed distance functions are computed using the signed distance functions reconstructed (locally and only when needed) using Eqs. 6 or 7.

The current segmentation at x is evolved by modifying the primary label function L₀(x) = i, the first neighbor label function L₁(x) = j, and the first distance function φ₀(x). A label change is necessary when the speeds would cause φ₀(x) to become negative (since the φ_i(x) functions are all positive and a negative value indicates that voxel x is no longer part of object O_i). This means that L₀(x) takes on the value of the former first neighbor, j, and the first neighbor L₁(x) takes the value of the former “current segmentation” label, i. Note that φ₀(x) remains positive since we have exchanged labels i and j and ϕ_i(x) = −ϕ_j(x), as noted in Section 2.

The above evolution equation describes how the first neighbor can become the current label via motion of the appropriate boundary, but this fact alone does not explain how arbitrary label changes can occur. MGDM accomplishes this by simultaneously moving all boundaries that are represented by the truncated decomposition. In fact, this amounts to evolving φ₁(x) and the higher-order distance functions which follow similar rules, i.e.,

$$\frac{\partial {\phi }_1}{\partial t}=\frac{1}{2}(f_{L_1}|\nabla {\hat{\varphi }}_{L_1}|-f_{L_2}|\nabla {\hat{\varphi }}_{L_2}|).$$ (10)

Let L₂(x) = k. Accordingly, when φ₁ is required to become negative, then the first neighbor L₁(x) must switch from j to k, and L₂(x) must switch from k to j. Equivalently, this means that the (i, k) boundary is now closer to x than the (i, j) boundary, or that object O_k is now closer to x than object O_j. In principle, if two label functions are stored, any object except i and j could be a candidate for L₂(x). We take advantage of the fact that in computing the K distance functions, we automatically obtain K + 1 neighbor functions (see Section 3.1.3). Therefore, the label k is stored as L₂(x) during the evolution so that the true second neighbor can take the place of the first neighbor when φ₁ would become negative. To compute the evolution of Eqs. 9 and 10, we follow a narrow band approach. The narrow band implementation produced an identical segmentation to a full field update with a mean difference in the φ₀ distance of 0.03 pixels for a 16 object experiment with reinitialization of the MGDM distance functions at least every five iterations. The mean difference in φ₀ was 0.00 pixels when reinitialization was forced after every iteration.

The algorithm performs the following steps at each updated point x at iteration t:

1. Set K = 2 for 2D (or K = 3 for 3D)

2. Compute the speeds $\frac{\partial {\phi }_K(x)}{\partial t}=\frac{1}{2}(f_{L_K}-f_{L_{K+1}})$ for all x in the narrow band.

3. Set ${\phi }_K^{t+1}(x)={\phi }_K^t(x)+\frac{\partial {\phi }_K(x)}{\partial t}$

4. If ${\phi }_K^{t+1}<0$, set

   $L_K^{t+1}(x)=L_{K+1}^t(x)$, (promote the K + 1 label)

   $L_{K+1}^{t+1}(x)=L_K^t(x)$, (demote the K label)

   ${\phi }_K^{t+1}(x)=-\left({\phi }_K^t(x)+\frac{\partial {\phi }_K(x)}{\partial t}\right)$ (ensure φ_K remains positive)

5. Repeat steps 2 through 4 for K − 1 to 0

6. If $L_{K+1}^{t+1}(x)=L_0^t(x)$, reinitialize (see Section 3.1.3).

Note that any label that is stored in the truncated label functions (i.e., {L₁(x) … L_K(x)} can become the current label by moving through the series of neighbor functions. This is because the neighbor boundaries are evolved before the current segmentation, therefore the second neighbor can become the first neighbor, and finally replace the current label. Labels that are not represented in this series are “far away” and so cannot immediately be assigned at x. These distant labels can appear in the L_i at reinitialization (since they are recomputed from the evolving segmentation boundaries) and can thereby be assigned to x at a later stage in the evolution. As we have noted previously, in 3D the evolution is extended to include a third distance function φ₂(x) and a third label function L₂(x). Analogously, L₃(x) is automatically obtained during the (re)initialization and may be stored so that the true third neighbor can replace L₂(x) when φ₂(x) would become negative. An example of the evolution of the MGDM functions can be found in a supplemental movie published with the electronic version of this manuscript.

3.2.1. Boundary-specific speeds

So far, the described framework has followed the classical approach where speeds are specified to act on objects (i.e., f_i is the speed of object O_i). Some segmentation tasks would benefit from the ability to specify speeds that act on different parts of an object. In particular, there are scenarios in which we would prefer to specify the speeds of contours/surfaces between objects rather than the objects themselves. In this way, different parts of a single object can behave differently because they belong to different boundary surfaces.

The MGDM framework is ideally suited to this task since it directly encodes specific boundaries within its decomposition. Because the closest boundary is immediately identified, boundary-specific speeds can be implemented without an expensive search for the closest boundary at each point. Specifically, at a voxel x, the distance of the nearest surface is immediately obtained from φ₀(x) (a convenient property of signed distance functions), and the objects separated by that surface are immediately available from L₀(x) and L₁(x). With this information, we are able to apply speeds specific to the nearest boundary.

To accommodate such boundary-specific speeds, Eq. 9 may be modified as follows:

$$\frac{\partial {\phi }_0}{\partial t}=f_{L_0}(x)|\nabla {\hat{\varphi }}_{L_0}|-f_{L_1}(x)|\nabla {\hat{\varphi }}_{L_1}|+f_{L_0,L_1}(x)|\nabla {\hat{\varphi }}_{L_0,L_1}|,$$ (11)

where f_L0(x) and f_L1(x) are speeds specified for objects O_L0 and O_L1, and f_L0,L1 is an additional speed acting on the boundary between objects O_L0 and O_L1. The expression |∇ϕ̂_L0,L1| = |∇ϕ̂_L0| = |∇ϕ̂_L1| describes the gradient magnitude of the level set functions of objects O_L0 and O_L1, and is equal to the gradient magnitude of the level set of either object (see the discussion following Eq. 1). Note that f_L0,L1(x) > 0 encodes expansion of the current label at point x, or equivalently, withdrawal of the (L₀, L₁) boundary away from point x. Likewise, f_L0,L1(x) < 0 describes advancement of the (L₀, L₁) boundary toward (or through) x. Note that the above interpretations depend on the convention that the level sets are negative inside the objects. If the opposite convention were used, than the signs of the speeds would need to be flipped in order to act in the same direction.

Despite the apparent simplicity of the above formulation, it is important to remember the richness of available speeds afforded by MGDM. These may stem from curvature, pressure, image intensities or membership functions, as well as gradient or advection vector fields. Furthermore, the weights associated with these speed types can also be controlled independently for different objects and boundaries.

3.3. Topology Control

Topology control is often desired in medical imaging applications since the topology of organs and their relationships are known from human anatomy. Other applications may also benefit from prior knowledge of topology and/or relationship information of objects in the image or scene. Most methods for handling topology only maintain or correct the topology for one object (or one object per level set function), but do not control the topological relationships between objects.

The concept of digital homeomorphism (an extension of the simple point criterion [52, 53] to multiple objects and groups of objects) introduced in [54] accounts for both single and multiple object constraints by controlling the topology of the boundary between objects. The level set decomposition we use intrinsically models boundary geometry, and so digital homeomorphism constraints are incorporated very naturally by modifying the evolution of φ₀as follows. Whenever φ₀ would change from positive to negative at a given point, the topology criterion for digital homeomorphisms is checked on the new segmentation L₀. If the criterion indicates a topological change, then the label is left unchanged and its associated distance-based function is set to a small value ε > 0, as proposed in [12] for single object topology-preserving level sets.

Multi-object topology preservation usually requires the use of a template with the desired topology when initializing the level set evolution. The template is then registered to the image of interest in order to provide a topologically correct initialization (see [6, 54]). With topology control, objects can only come in contact if they are adjacent in the original template. Thus, we can use the alternate distance definition of Eq. 8 in the algorithm, and make the evolution more efficient by only considering topologically consistent candidates at a given point. The reinitialization is also faster as the marching can stop when an object’s boundary reaches labels that are topologically invalid.

4. Experiments

4.1. Comparison with previous multiple geometric deformable models

We provide here a comparison of our algorithm (MGDM), the multiphase approach (MP) [15], and the N coupled level sets (CLS) of Brox et al. [24]. The MP method provides a compressed representation with no gaps or overlaps, while CLS uses the same intrinsic coupling as MGDM (as in Eq. 9) with N level sets. Rather than focusing on a specific application, we present here a generic problem for which all the methods should perform similarly given the same energy function. Accordingly, we consider a piecewise constant problem in which we minimize [29]:

$$E={\displaystyle {\int }_x\left[\alpha {\displaystyle \sum _{n}H({\varphi }_n(x)){\Vert I(x)-c_n\Vert }^2+\beta \Vert \delta ({\varphi }_n(x))\Vert }\right]}+\mu \left[1-{\displaystyle \sum _{n}H({\varphi }_n(x))}\right]dx$$ (12)

where I is the image to segment, c_n is the intensity of the n-th object and μ is the mean of the objects’ intensities. Note that overlaps incur a penalty since the data and length terms for both objects assigned at x contribute to the energy. The last term in this energy functional penalizes unassigned or “gap” pixels and is always zero for both MP and MGDM since they never form gaps during their evolutions. CLS, however, requires a “gap-filling” term (see [24] for details) that prevents the trivial solution comprising only gaps (and no objects). This last term therefore measures the impact of gaps during the CLS evolution, though it is exactly zero or close to zero upon convergence in most cases. We set the regularization parameter for the delta and Heaviside functions to ε = 1, as was used in [15]. The relative weights of the data and smoothness terms were set to α = 1, and β = 0.01.

We consider four images with N ∈ {4, 8, 16, 32} objects and 512 × 512 pixels (choosing N as a power of two simplifies the multiphase representation) comprising superpositions of circular shapes (see Figs. 3 and 4). Each unique intensity in the input image appears in a circle with a radius (r) inversely proportional to the number of objects to be segmented. The initialization consists of circles of fixed radii (4 pixels), whose labels cycle through the available labels. In both cases, circle centers are located at a distance 0.85r from one another. All circles in the initialization intersected at least one image circle with the corresponding intensity. All algorithms were given the same initialization and run until convergence or a maximum of 5000 iterations. Convergence is determined when 30 iterations pass without a change in the segmentation.

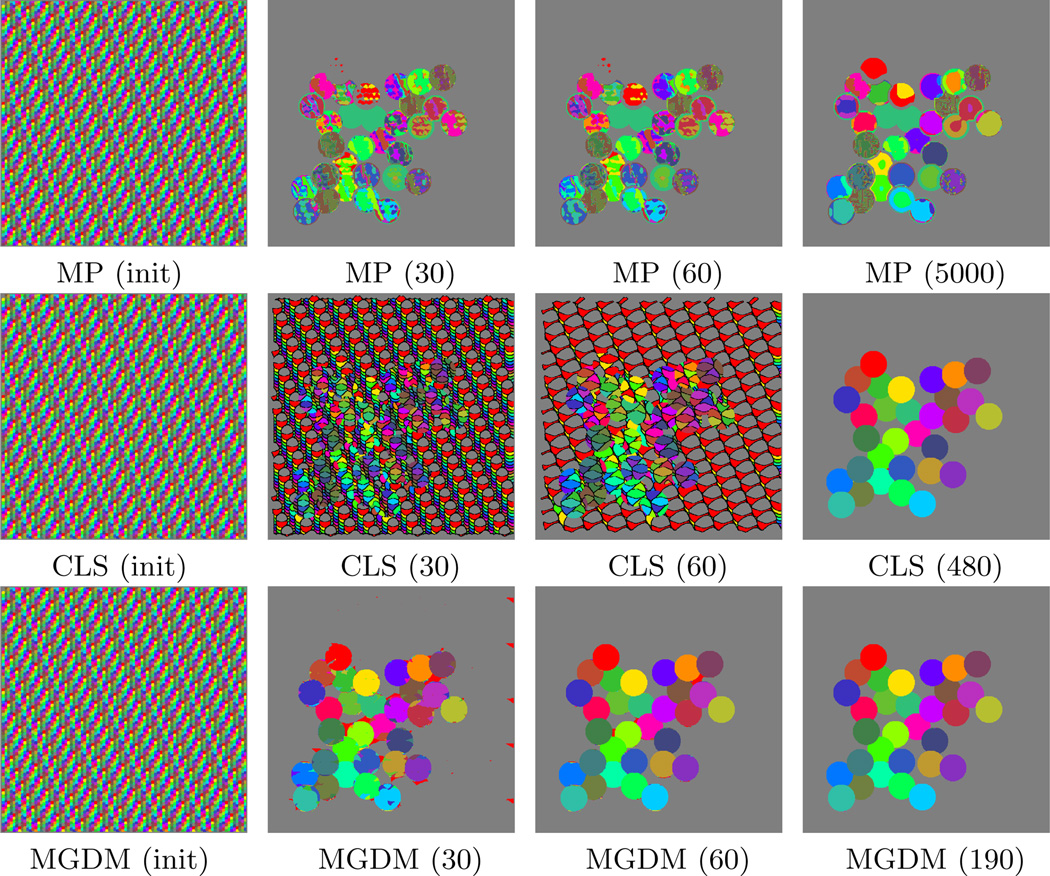
Figure 3.

Comparative experiments with four objects. The value in parenthesis indicates the iteration being shown. The rightmost column shows each algorithm’s result at convergence.

Figure 4.

Comparative experiments with 32 objects. The value in parenthesis indicates the iteration being shown. The rightmost column shows each algorithm’s result at convergence.

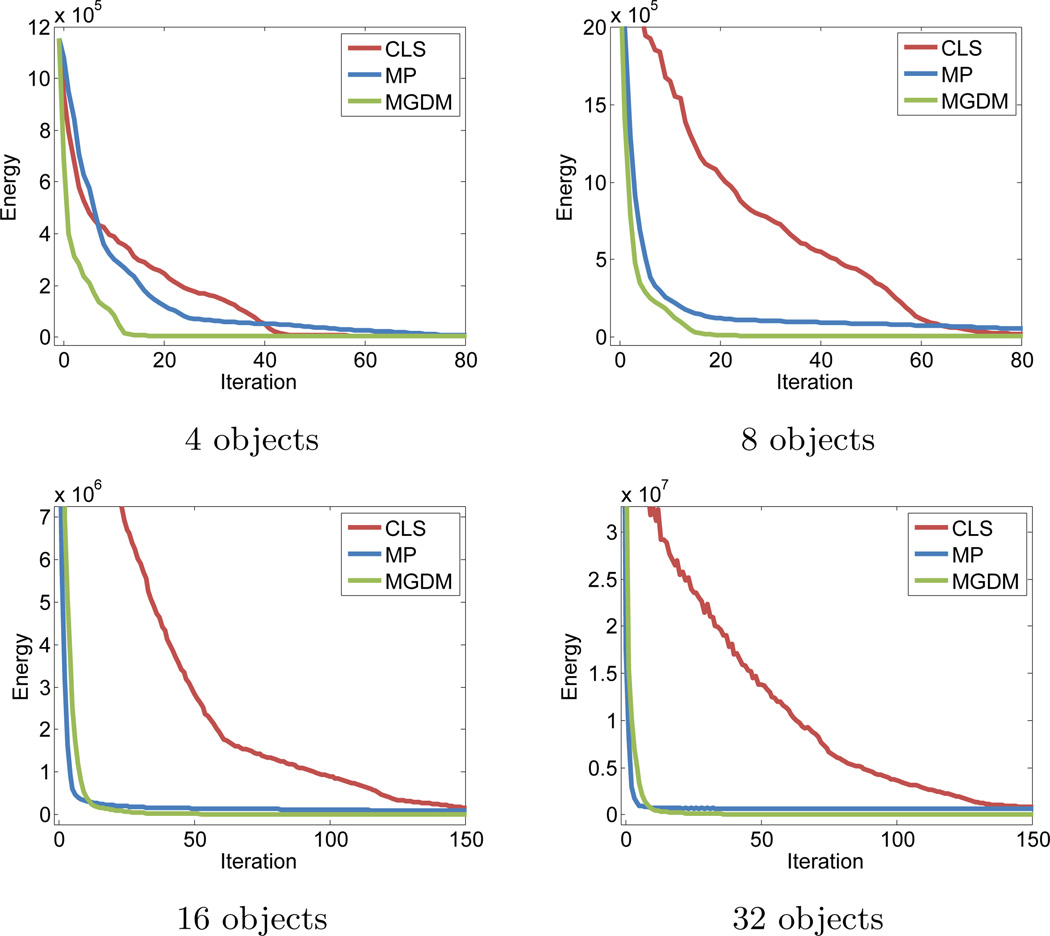
As shown in Table 1, all the methods converge correctly to the solution with four objects. When the number of objects increases, MP becomes quickly plagued by local minima in its optimization. This is because more objects increases the likelihood that multiple simultaneous sign changes are required in the multiphase representation in order to correctly switch labels. As a result, for large N, MP becomes trapped in a label configuration whose energy cannot be decreased by sign changes of a single level set function (see Fig. 4 for the case of 32 objects). The CLS method avoids this problem, maintaining high accuracy for even a large number of objects. There are no overlaps or gaps in any segmentation results of CLS, but gaps (shown in black) commonly appear over the course of the evolution (Fig. 4). MGDM remains stable with increasing numbers of objects, and also converges faster to the stable solution. This is evident by comparing the evolution of the energy function, as shown in Fig. 5. The presence of gaps in CLS slows the apparent decrease of energy, while the optimization scheme of MP prevents it from reaching an energy as low as MGDM or CLS.

Table 1.

Performance comparison for the three approaches on images with increasing numbers of objects. A full iteration is comprised of six iterations of level set evolution followed by reinitialization to ensure the stability of all methods. The first of these 30 iterations is reported as the iteration count for convergence. “DNC” indicates that the algorithm did not converge by the 5000th iteration. The misclassification rate counts gaps and overlaps as misclassified, and is computed after convergence.

	Objects	MP	CLS	MGDM
Convergence (full iterations)	4	223	105	33
	8	144	762	87
	16	DNC	459	142
	32	DNC	457	186
Memory usage (average, MB)	4	19	21	11
	8	22	29	11
	16	23	46	11
	32	26	78	11
Computation Time (average per iteration, ms)	4	54	236	51*
	8	81	593	32
	16	183	1143	34
	32	596	2840	35
Misclassification rate (%)	4	0.17	7.63E-4	1.91E-3
	8	0.93	7.63E-4	4.20E-3
	16	4.58	3.05E-3	4.65E-2
	32	14.3	8.01E-3	2.06E-2

Figure 5.

Evolution of the global energy function E for different numbers of objects.

Computationally, the MP approach is as memory efficient as MGDM for small problems, but has increasing storage requirements and slower convergence for larger problems (see Table 1 and Fig. 5). The poor convergence of MP with many objects is quite surprising, but outlines how apparently small limitations in the representation can lead to major problems with large numbers of objects. The computational and memory demands of the CLS method increase rapidly with the number of objects, while MGDM’s compact representation requires a constant amount of memory and lowers the computation times. Of the three methods, only MGDM maintains a high accuracy by avoiding local minima, prevents object gaps or overlaps, and remains efficient independently of the number of objects.

It is interesting to note that the computation time for MGDM iterations for four objects (marked by * in Table 1) is larger than that for larger numbers of objects. Also, the computation time for the MP method for eight objects is less than twice the time required for four objects. These behaviors are due to the narrow band implementation: the narrow band comprises a large number of pixels at early iterations due to the nature of the initialization, while it has fewer pixels at later iterations as the algorithm approaches convergence. The case with four objects converged after a small number of iterations, but the average time per iteration is high because most of those iterations operated on a large narrow band. In the case with many objects, the narrow band size decreases about as rapidly, but more iterations are performed before convergence with a small narrow band, decreasing the average iteration time.

4.2. Demonstration of boundary-specific speeds

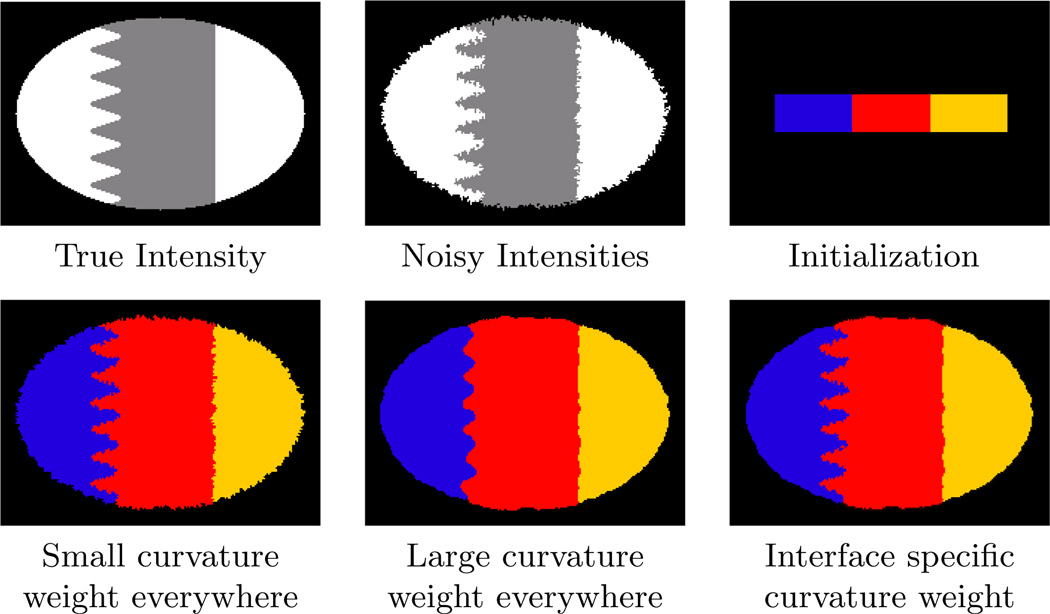
We next demonstrate MGDM’s ability to apply speeds on object boundaries rather than on the objects themselves. A “toy” image shows the benefits of designing speeds for boundaries rather than objects (see Fig. 6). The central (red) object here shares two boundaries with non-background objects. One of these boundaries has high curvature while one has low curvature. We would like to recover the locations of these boundaries after they are corrupted by “boundary noise” (described in [55]). If curvature terms are applied uniformly on the central object, either the low curvature boundary will be needlessly noisy (for uniform low weight curvature term), or the high-curvature boundary will be overly smoothed (for uniform high weight for the curvature term). When the curvature weights are allowed to vary, however, the influence of regularization and image terms can be balanced appropriately.

Figure 6.

A simple example demonstrating the benefits of applying different speeds on different boundaries. In this case, an intensity weight of 0.7 was applied in all cases. Curvature terms with weights of 0.1 and 1.0 were applied to all objects in the “Small curvature” and “Large curvature” cases. In the variable curvature experiment, a curvature weight of 0.1 was applied to the red-blue boundary, while all other boundaries had a curvature weight of 1.0. This allowed the high spatial frequencies of the true object to be captured on one boundary, while simultaneously and correctly smoothing noise on another.

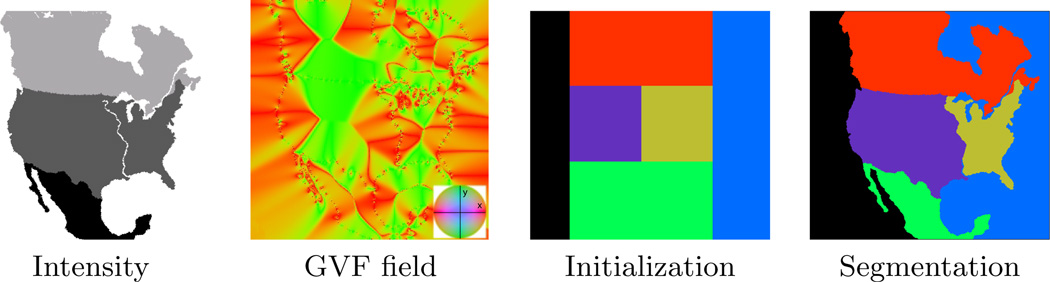
Figure 7 shows a synthesized example in which a cartoon version of North America’s geography is corrupted with “boundary noise”. The three countries and two oceans are able to be segmented based on their intensity contrast. The eastern and western United States, have the same image intensity, but can be separated by the narrow, high-intensity Mississippi river. An appropriate speed was designed by computing the gradient vector flow (GVF) [49] of the intensity image with a λ parameter of 0.2 and a maximum of 200 iterations. Most boundaries were regularized with moderate curvature terms, except along the eastern coast of Canada, where the St. Lawrence river and the Great Lakes define a more complex boundary. As we see in this simple example, the need for boundary-specific speeds arise quite naturally in many applications.

Figure 7.

A synthesized example showing the usage of different types of speeds (intensity and advection field). The x and y components of the GVF field are rendered in red and green, respectively. The eastern and western US are delineated by the GVF field despite having the same image intensity.

5. Application to cerebellum segmentation

We also explored applying MGDM in the segmentation and parcellation of the cerebellum from structural MRI. A magnetization prepared rapid gradient echo (MP-RAGE) image was acquired using a 3.0T MR scanner (Intera, Phillips Medical Systems, Netherlands) with the following parameters: 132 slices, axial orientation, 1.1mm slice thickness, 8° flip angle, TE= 3.9ms, TR= 8.43ms, FOV= 21.2 × 21.2cm, matrix 256 × 256 (voxel resolution 0.828125mm × 0.828125mm × 1.1mm). The cerebellum has a central white matter (WM) structure called the corpus medullare from which white matter branches sprout. These branches are covered in a sheet of gray matter (GM) and together, form the cerebellar lobes and lobules. A good delineation of the corpus medullare (WM) should be smooth and not contain branches of white matter, which suggests that a strong curvature term is required. The cerebellar gray matter surface, on the other hand, is highly convoluted and suggests that a curvature should play a minor role at the boundary of gray matter and cerebral spinal fluid (CSF). Furthermore, while image intensity can separate cerebellar gray matter, white matter and CSF, the lobes themselves have similar intensities and are separated by thin lines of lower intensity (the fissures). We found that voxels x for which the image Laplacian ∇²I(x) < 0 tended to belong to these fissures. This is because small fissures manifest as local intensity drops, and are therefore highlighted where the divergence of the gradient (Laplace operator) is negative. The GVF field of this thresholded image was found and used as an advection force in order to move the lobe boundaries into their correct positions.

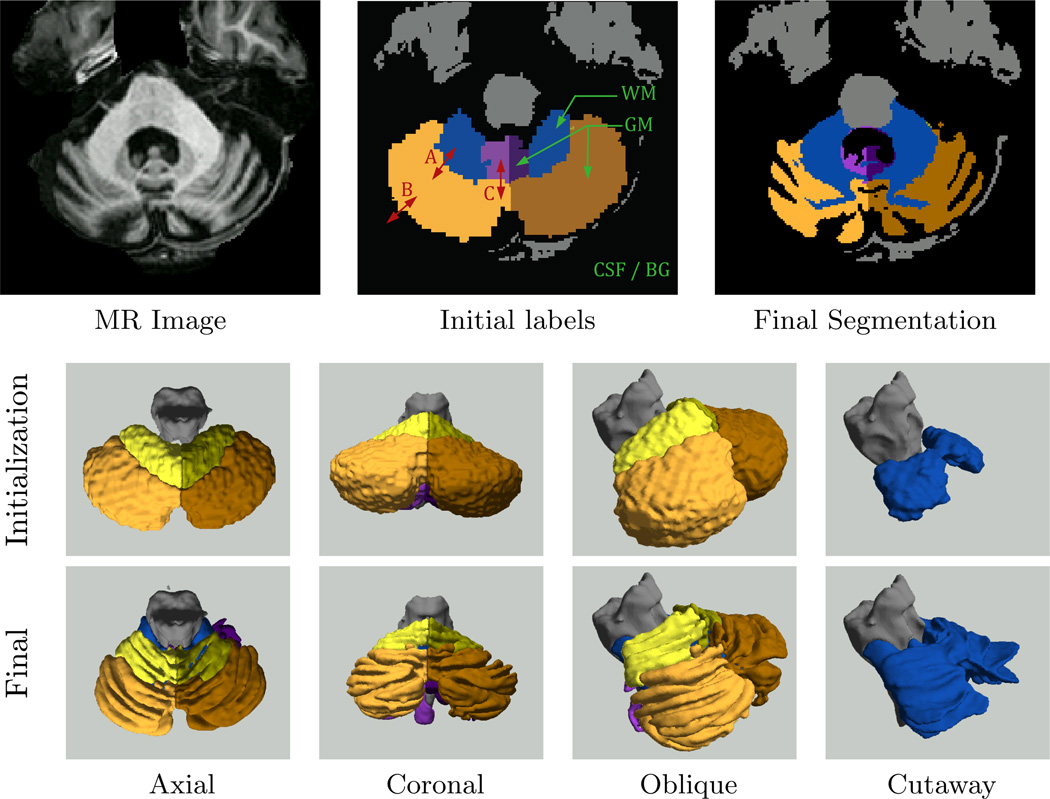
Figure 8 shows an example of a cerebellum parcellation using MGDM. We observe the effective delineation of the tissue classes based on intensity (membership functions). Note the simultaneous smoothness of the GM-WM boundary and roughness of the GM-CSF boundary. The lobe boundaries are also well aligned with the fissures under the guidance of GVF. The different boundary speeds are indicated with red letters on the initial labels in Fig. 8. These correspond to rows in Table 2, which summarizes speed types and their contributions to different tissue interfaces. In particular, the curvature weights and usage of region and GVF forces is different for different boundaries.

Figure 8.

Example of cerebellum segmentation results using MGDM. The top row shows 2D slices of the source image, initial labels, and final segmentation. The initial labels are annotated with tissue types (green) and boundary speed types (red). The GM-GM speeds (A), the WM-GM speeds (B), and the (GM-CSF) speeds are summarized in Table 2. The middle and bottom rows show 3D renderings of the initial labels and final segmentation, respectively. The gray matter labels were removed in the cutaway figure so that the white matter (rendered in blue) would be visible.

Table 2.

Summary of the speeds applied to different boundaries of the cerebellum parcellation experiment. The first column gives the boundary labels shown in Fig. 8.

	Interface	Curvature speed weight	Region speed weight	GVF weight
A	WM-GM	0.05	0.5	0.0
B	GM-CSF	0.5	0.5	0.0
C	GM-GM	0.2	0.0	0.5

6. Discussion

The MGDM decomposition and evolution combine the implicit coupling present in [24] with a compact representation. In particular, objects compete for image pixels according to the relative strengths of their expansion speeds. Furthermore, MGDM does not require a “gap-filling” term, since it evolves object boundaries (the object on the other side of any boundary immediately replaces the former object). This is possible because the novel level set decomposition stores a point’s nearest neighboring objects. A relatively small number of functions must be stored and correct computations are still achieved using approximate signed distance functions when far from an object’s boundary.

The approximation that is implicit in MGDM’s decomposition gives rise to potential limitations. The functions ϕ̂_i(x) (see Eqs. 6 and 7) are equal to the signed distance functions in the vicinity of the boundaries provided that the objects are not too thin and no more than three objects meet at a boundary point in 2D (and no more than four objects meet at a boundary point in 3D). Thin objects can be problematic when the evolution moves boundaries through them, and multiple objects meeting at boundaries present a slowly increasing error (see Fig. 9). In these cases, the difference between ϕ_i and ϕ̂_i(x) decreases to zero near any boundary, and is nearly zero in a narrow band around the zero level sets. For this reason, the proposed decomposition yields results exactly equivalent to N level set evolution in nearly all object configurations, but with substantial computational savings since the number of functions is independent of the number of objects. The error is nearly zero even in “undesirable” configurations, and can be reduced (at the expense of efficiency) by increasing the the number of label and distance functions that are computed and stored.

Figure 9.

Illustrations of the decomposition’s limitations assuming a two function approximation in 2D. In (a) the MGDM decomposotion can perfectly represent the distances to 3 different objects (including the current object) at a point, when 2 distance functions are used. The white object is the current label at the centerpoint. When one or two other object (blue and pink) are nearby, the true boundary locations (black lines) to those objects can be represented perfectly with two distance functions. However, when a third (green) or fourth (orange) object is nearby but further than the first two objects, MGDM approximates their distances (gray dotted lines) with the distance to the second neighbor and incurs errors, the magnitudes of which are indicated by the red arrows. The errors can be eliminated by storing additional levels of the decomposition. In (b), the 1D plot of the reconstructed level set function for object O₁ (along the dotted line), shows how approximations appear when we are further from the object’s boundaries than from other object’s boundaries.

The choice to enforce a strict ordering of labels when two labels are equidistant from a point (see Definition 3.1) rarely affects the evolution or final segmentation. First, the choice of the number of MGDM distance functions to store is made so that the object signed distance functions at triple points are exactly recoverable. This state of affairs is the most common situation in which this issue arises. This forced ordering could potentially affect results when one of the two equidistant labels is not stored due to the truncated decomposition (i.e., if the third and fourth neighbors are equidistant, and only the first three neighbors are stored, then the fourth neighbor will be discarded). This is unlikely to affect segmentation results very much for two reasons. First, the distance and label functions are recomputed at reinitialization, and the true neighbors will be stored (given evolution of the boundaries). Second, very distant neighbors do not often rapidly promoted to become the current label.

Our method is memory efficient, because the number of images that must be stored is independent of the number of objects, N. Note that the improved “multilayer” method with multiple level set embedding of [32] also uses two level set functions in 2D. For the evolution, we still have to compute the speeds for all objects in theory, making the overall complexity similar to the classical approaches (it is a requirement for the other methods as well). However, we can often remove unlikely objects at a given point x from the set of candidates in many practical applications. For instance, if the segmentation method were to use a statistical atlas, objects with low prior probability could be ignored. The algorithm variant with topology control can also make use of neighborhood information to reduce the set of candidates. The computational complexity for the level set evolution, on the other hand, is reduced relative to other methods as only two or three functions need to be updated, independently of the number of objects.

Topology preservation is an excellent method for constraining a segmentation when an a priori known topology can be asserted and a good initialization can be obtained. On the other hand, when the initialization is far from the true segmentation, the topology constraint can hinder a desirable evolution. Artifacts may also appear when topology is preserved as the constraint can restrict objects in taking on “strange” shapes. This is because topology constraints prevent object splitting or merging at erroneous boundaries while allowing unusual geometric deformations to appear in order to correct the errors.

MGDM is well-suited to many new and challenging segmentation problems since it accurately and efficiently can represent many objects. We demonstrated here its applicability in parcellating the cerebellum into seven sub-regions, and will explore a finer (34 object) parcellation in the future. We are currently applying MGDM to other problems such as cell segmentation and tracking, retinal layer segmentation from optical coherence tomography (OCT) images, and ultra-high resolution whole brain segmentation. We foresee MGDM providing a distinctive benefit in cell tracking/segmentation applications, where hundreds or thousands of cells need to be segmented and tracked. Employing topology priors would prevent cells that touch from merging labels, while simultaneously allowing cells that split to be tracked separately. This could be accomplished by allowing one type of topology change (a split) while preventing another (a merge), for instance, by following the approach of [13] with opposite rules.

7. Conclusion

In this paper, we introduced a multiple object level set representation, which guarantees no overlaps or gaps, can optionally preserve the topology of all objects and groups of objects, and may apply any existing type of speed in the level set literature with different weights on different parts of one object. The computational complexity in narrow band evolution and fast marching re-initialization schemes is reduced and largely independent of the number of objects to segment. Experiments on the fundamental problem of piecewise-constant image segmentation demonstrate the numerical stability and accuracy of the method for large numbers of objects. A challenging application to cerebellar parcellation in MRI illustrates how to exploit the various advantages of the representation.

Highlights.

We describe a multi-object level set segmentation framework called MGDM.

Our method efficiently represents an arbitrary number of objects.

Gaps and overlaps between objects are prevented.

Forces may be specified on object boundaries rather than on the objects themselves.