Abstract
Conventional mammillary models are frequently used for pharmacokinetic (PK) analysis when only blood or plasma data are available. Such models depend on the quality of the drug disposition data and have vague biological features. An alternative minimal-physiologically-based PK (minimal-PBPK) modeling approach is proposed which inherits and lumps major physiologic attributes from whole-body PBPK models. The body and model are represented as actual blood and tissue usually total body weight) volumes, fractions (fd) of cardiac output with Fick’s Law of Perfusion, tissue/blood partitioning (Kp), and systemic or intrinsic clearance. Analyzing only blood or plasma concentrations versus time, the minimal-PBPK models parsimoniously generate physiologically-relevant PK parameters which are more easily interpreted than those from mam-millary models. The minimal-PBPK models were applied to four types of therapeutic agents and conditions. The models well captured the human PK profiles of 22 selected beta-lactam antibiotics allowing comparison of fitted and calculated Kp values. Adding a classical hepatic compartment with hepatic blood flow allowed joint fitting of oral and intravenous (IV) data for four hepatic elimination drugs (dihydrocodeine, verapamil, repaglinide, midazolam) providing separate estimates of hepatic intrinsic clearance, non-hepatic clearance, and pre-hepatic bioavailability. The basic model was integrated with allometric scaling principles to simultaneously describe moxifloxacin PK in five species with common Kp and fd values. A basic model assigning clearance to the tissue compartment well characterized plasma concentrations of six monoclonal antibodies in human subjects, providing good concordance of predictions with expected tissue kinetics. The proposed minimal-PBPK modeling approach offers an alternative and more rational basis for assessing PK than compartmental models.
Keywords: PBPK, Mammillary model, Pharmacokinetics, Compartmental analysis
Introduction
Physiologically-based pharmacokinetic models (PBPK) are more mechanistic than ‘classical’ compartmental models as they incorporate anatomical and physiological knowledge into descriptions of pharmacokinetics (PK) [1]. Building such models, however, requires measurements of drug concentrations in numerous organs and tissues. When only blood or plasma data is available, the convention is to apply noncompartmental (NCA) and/or compartmental analysis [2]. However, mammillary models represent the body as a system of compartments that usually have limited physiologic or anatomic reality. They are highly dependent on the intensity of the blood collection schedule and make no prior use of the physiology of the organism [3, 4]. An intermediate perspective between full PBPK and compartmental models would be helpful. Recirculatory models offer a somewhat more physiologically realistic approach to describe PK in which flows to tissue spaces are considered [5]. These models usually require some empirical adjustments and are not often utilized as they are difficult to implement and interpret [6, 7].
‘Lumping’ is a commonly employed approach to reduce the dimensionality and complexity of whole body PBPK models placing tissues that show similar kinetics together to form fewer compartments [8, 9]. Whole body PBPK models are often successfully represented by a limited number of ‘lumped’ compartments. A PBPK model with only four organs was previously constructed for warfarin [10]. Some organs (muscle, fat, kidney) that exhibited similar kinetics could be further lumped in this model, and the time course of serum warfarin concentrations was mainly supported by nonlinear (liver) and linear tissue distribution components.
The concept of ‘hybrid-PBPK’ models has been utilized in previous studies by using plasma concentration functions with perfusion input to specific organs (mostly liver, kidney, brain, or tumor) [11–13]. This allows more detailed descriptions of drug exposures or disposition for specific tissues. Henthorn et al. [14] employed the term ‘minimal’ compartment model in constructing a parallel channel, lumped-parameter circulatory model for disposition of indocyanine green in dogs.
This report proposes a generalized minimal-PBPK modeling approach which represents the system as a substantially lumped PBPK model. The incorporation of physiological and anatomical knowledge into the minimal-PBPK models allows separation of system- and drug-specific parameters and permits consideration of known physicochemical and metabolic properties in determination of drug PK features (Fig. 1). Applications of the minimal-PBPK models will be shown by characterizing several types of drugs in different situations, revealing better PK insights than conventional mammillary models.
Fig. 1.
Paradigm for constructing PBPK models
Model structures
Figure 2 shows a minimal-PBPK model with two tissue compartments. The model is described using the differential equation structure similar to PBPK models:
| (1) |
| (2) |
| (3) |
where Cp is concentration of drug in Vp (blood or plasma volume), C1 and C2 are drug concentrations in tissue compartments 1 (V1) and 2 (V2), QCO is cardiac blood (or plasma) flow, fd1 and fd2 are fractions of QCO for V1 and V2, Kp1 and Kp2 are tissue partition coefficients, and CL is the systemic clearance.
Fig. 2.
Minimal-PBPK model with two tissue compartments. Symbols and physiological restrictions are defined with Eqs. (1–3). The blood compartment in the left box mimics the venous blood as in full PBPK models, but is not utilized in the present model
The key features of this model are the physiological restrictions where Vp is the designated blood or plasma volume, QCO is the assigned cardiac output, and:
This allows V2 to be treated as a secondary parameter with only estimation of V1.
The model was further extended by including the liver to describe oral dosing with hepatic first-pass as shown in Fig. 3. The modified model equations are:
| (4) |
| (5) |
| (6) |
| (7) |
where Qhep is portal vein blood flow, Chep is drug concentration in liver compartment (Vhep), CLintu and CLnon-hep are unbound hepatic intrinsic and non-hepatic clearances, and FG and ka are pre-hepatic bioavailability and the absorption rate constant. Other symbols represent the same parameters as in Fig. 2. The physiological restrictions of these parameters are:
Fig. 3.
Minimal-PBPK model extended with the hepatic compartment. Symbols and physiological restrictions are defined in Table 2
The extended model with a hepatic compartment (Fig. 3) can be related to clearance concepts of Rowland et al. [15] who proposed the well-stirred model:
| (8) |
which often works well for relating hepatic clearance (CLhep) to intrinsic clearance (CLintu), fraction unbound in plasma (fup), and extraction ratio (ER). With addition of FG and ka, the minimal-PBPK model can account for both oral and IV profiles. The extended model separates clearances by liver (CLintu) and other tissues (CLnon-hep). Hepatic clearance (CLhep) can be calculated from CLintu that is estimated based upon liver free concentration where 1/Kp is fraction unbound in the liver when fup = 1.
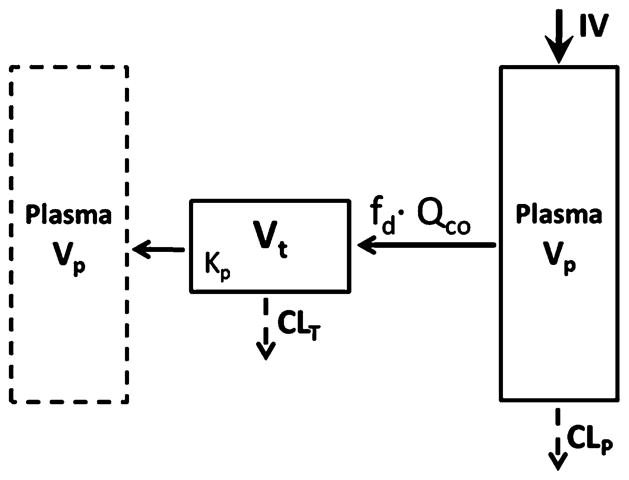
A basic model was applied to assess the PK of several monoclonal antibodies (mAb) as shown in Fig. 4. Since elimination of mAb mostly occurs in the tissue interstitial space [16], the clearance (CLT) was assigned to the tissue compartment (Model A) and compared with model with clearance (CLP) from plasma (Model B). The Model A equations are:
| (9) |
| (10) |
where QCO is specifically designated as plasma cardiac output for mAb and CLT was assumed to be relevant with total concentration of mAb in tissue. The physiological restrictions of relevant parameters are: fd ≤ 1 and Vt + Vp = BW:
Fig. 4.
Basic minimal-PBPK model assigning CL either from tissue (Model A) or plasma compartments (Model B). Symbols and physiological restrictions are defined with Eqs. (9) and (10)
Data analysis
The proposed minimal-PBPK models were applied to several PK data sets that were found in the literature: beta-lactam antibiotics [17–36], hepatic elimination drugs (dihydrocodeine [37], verapamil [38], repaglinide [39], and midazolam [40]), moxifloxacin PK in five species [41], and six mAbs PK in human subjects [42–47]. Concentration–time data were obtained via computer digitalization [48]. Alternative structures of the minimal-PBPK models were assessed such as numbers of tissue compartments, the same or different Kp values, and the same or different fdi values for multiple tissue spaces.
Moxifloxacin PK after intravenous dosing in five species was simultaneously described by integrating allometric scaling principles into the minimal-PBPK model with one tissue compartment. The integrated model was described by:
| (11) |
| (12) |
All species were assumed to have the same fitted fd and Kp value, while QCO and CL were allometrically scaled across species [49, 50] with two estimated parameters for CL (a and b)
Human PK profiles for 6 mAb after intravenous dosing were fitted and compared between minimal-PBPK models with CL from either tissue or plasma compartments (Fig. 4).
Fittings utilized the maximum likelihood method in ADAPT 5 [51]. The variance model was defined as:
| (13) |
where Vi is the variance of the response at the ith time point, ti is the actual time at the ith time point, and Y(ti) represents the predicted response at time ti from the model. Variance parameters σ1 and σ2 were estimated together with system parameters during fittings. The goodness-of-fit criteria included visual inspection of the fitted curves, sum of squared residuals, Akaike Information Criterion (AIC), Schwarz Criterion (SC), and Coefficient of Variation (CV) of the estimated parameters.
Results
General evaluation
The first physiological feature of the minimal-PBPK model is the assignment of blood (or plasma) volume as the initial distribution space as is done in full PBPK models. This has worked well in numerous instances and obviates a major problem in mammillary models where early time extrapolations are dependent on the timing and frequency of blood sampling [2, 3]. The assigned blood (or plasma) volume can be more specific with considerations of species, sex, and age differences [52]. The assumed blood volume for man was 5.2 L/70 kg [49].
The second feature is the employment of Fick’s Law of Perfusion for tissue distribution with the capability of tissue drug uptake and release to be either flow- or permeability-limited and limited to passive mechanisms. The fdi·QCO parameter, equivalent to distribution clearance, uses an assumed QCO (for man, 5.6 L/min) as do PBPK models. The fraction fdi allows for either multiple tissues and/or limitations in either capillary or cellular permeability. The structural or boundary limitation of fd1 + fd2 ≤ 1 is needed.
A key aspect of PBPK models is assessment of tissue/plasma partition coefficients by direct measurements. Mammillary models yield a tissue-average Kp value from Vss/BW [53]. The minimal-PBPK models incorporate one or more Kp values as fitted parameters.
Full PBPK models use actual organ and tissue weights in assessing overall distribution of drug, often requiring a carcass or ‘residual’ weight to account for unsampled sites. The minimal-PBPK models set BW or ECF = V1 + V2 + Vp. Here, the values of these parameters are assigned as physical volumes (or masses) of tissues (for man, BW = 70 kg). In certain cases, V1 (or V2) can be designated as a specific tissue. For instance, muscle accounts for 40–45 % of total body mass [49]; designating muscle as V1 (or V2) along with fd·QCO for its blood flow is feasible. In some situations (beta-lactams), the total distribution space is known to be ECF [54]. Of course, more specific values of all physiological parameters can be matched to actual subject characteristics.
The extended model with hepatic compartment allows separate estimates of CLintu and CLnon-hep. In certain cases, one clearance can be neglected if the other dominates. If the liver only slightly contributes to overall clearance, then including the hepatic compartment becomes futile and the extended model reduces to the basic model (Fig. 2).
It is feasible to incorporate hepatic intrinsic clearance and renal clearance as in full PBPK models. Tissue intrinsic clearances are easier to match to in vitro observations and have higher scaling potential to other species than systemic clearance [55]. A basic model assigning CL to the tissue compartment may reflect underlying mechanisms of drug elimination and permit estimates of an average tissue ‘intrinsic’ clearance.
Beta-lactam antibiotics
The PK of 22 beta-lactam antibiotics were found in the literature and their profiles were analyzed based on the proposed minimal-PBPK models. The final structural model was defined with the same Kp for two tissue compartments for 12 beta-lactam antibiotics. The remaining 10 drugs were described by a model with one tissue compartment. Total volume Vp + V1 + V2 was assumed to be ECF in this analysis (volume = 18.2 L) because beta-lactam antibiotics distribute mainly within extracellular fluid [54]. The fitted profiles are shown in Fig. 5 and the parameters are summarized in Table 1. All models captured the observed PK profiles quite well with reasonable CV % for the estimated parameters.
Fig. 5.
Pharmacokinetic profiles of 22 beta-lactams in human subjects
Table 1.
Final estimated pharmacokinetic parameters (CV %) for 22 beta-lactam antibiotics in human subjects
| Drugs [ref] | Dose (mg) | Dosing | Model | fup | Kp | fd1 | fd2 | V1 (L) | CL (L/min) | Vss (L) |
|---|---|---|---|---|---|---|---|---|---|---|
| Amoxicillin [17] | 1,000 | IV bolus | IIa | 0.82 | 0.785 (9.25) | 0.0180 (26.4) | 0.0737 (40.8) | 8.26 (14.5) | 0.298 (3.73) | 15.4 (6.13) |
| Ampicillin [18] | 1,000 | INF (30 min)b | II | 0.79 | 2.089 (95.08) | 0.00674 (45.8) | 0.419 (11.8) | 4.05 (19.9) | 0.235 (16.9) | 32.4 (79.8) |
| Cefatrizine [19] | 260 | INF (30 min) | Ic | 0.38 | 0.651 (7.89) | 0.0515 (14.5) | – | – | 0.231 (2.98) | 13.7 (4.88) |
| Cefazolin [20] | 2,000 | IV bolus | I | 0.11 | 0.494 (4.69) | 0.0229 (10.5) | – | – | 0.0747 (1.72) | 11.6 (2.59) |
| Ceforanide [20] | 2,100 | INF (30 min) | I | 0.19 | 0.484 (2.62) | 0.0321 (7.40) | – | – | 0.0576 (0.879) | 11.5 (1.43) |
| Dicloxacillin [21] | 2,000 | INF (30 min) | I | 0.04 | 0.162 (118) | 0.00208 (34.0) | – | – | 0.0812 (7.57) | 7.30 (34.0) |
| Flucloxacillin [22] | 1,000 | INF (5 min) | II | 0.05 | 0.445 (10.5) | 0.0988 (14.7) | 0.00409 (14.6) | 6.77 (8.97) | 0.141 (1.31) | 11.0 (5.53) |
| Mecillinam [23] | 700 | INF (15 min) | II | 0.78 | 0.568 (6.21) | 0.372 (95.6) | 0.00626 (24.2) | 8.42 (6.40) | 0.200 (2.19) | 12.6 (3.65) |
| Piperacillin [24] | 4,000 | INF (5 min) | II | 0.70 | 0.547 (4.97) | 0.416 (30.7) | 0.00311 (18.2) | 9.18 (2.83) | 0.190 (1.51) | 12.3 (2.87) |
| Temocillin [25] | 2,000 | IV bolus | II | 0.17 | 1.19 (4.86) | 0.0989 (26.4) | 0.0325 (9.97) | 2.11 (14.9) | 0.0396 (3.38) | 21.8 (3.77) |
| Mezlocillin [26] | 4,000 | INF (5 min) | II | 0.65 | 1.33 (131) | 0.895 (29.4) | 0.102 (18.8) | 12.7 (36.1) | 2.49 (18.7) | 22.5 (10.1) |
| Cloxacillin [27] | 1,000 | INF (5 min) | I | 0.05 | 0.280 (10.8) | 0.00798 (18.3) | – | – | 0.141 (3.48) | 8.84 (4.47) |
| Methicillin [28] | 1,050 | INF (15 min) | I | 0.65 | 1.93 (49.9) | 1.000 (0.0433) | – | – | 0.693 (42.2) | 30.3 (41.3) |
| Benzylpenicillin [29] | 600 | IV bolus | I | 0.32 | 0.479 (11.4) | 0.0351 (18.2) | – | – | 0.381 (3.67) | 11.4 (6.20) |
| Ticarcillin [30] | 2,000 | INF (30 min) | I | 0.60 | 1.60 (6.32) | 0.238 (17.6) | – | – | 0.391 (3.22) | 26.0 (5.06) |
| Carbenicillin [30] | 2,000 | INF (30 min) | I | 0.50 | 2.07 (29.3) | 1.000 (0.0264) | – | – | 0.479 (25.8) | 32.1 (24.5) |
| Azlocillin [32] | 4,160 | INF (20 min) | II | 0.70 | 0.517 (2.47) | 0.0415 (11.8) | 0.0755 (37.4) | 10.8 (4.66) | 0.125 (1.03) | 11.9 (1.39) |
| Cefamandole [33] | 2,000 | INF (30 min) | I | 0.20 | 0.146 (51.6) | 0.00143 (14.9) | – | – | 0.149 (4.01) | 7.10 (13.8) |
| Cefonicid [36] | 2,100 | IV bolus | II | 0.18 | 0.320 (13.9) | 0.00306 (20.4) | 0.148 (29.2) | 7.42 (6.88) | 0.0432 (1.26) | 9.36 (2.34) |
| Biapenem [31] | 300 | INF (30 min) | II | 0.96 | 1.94 (10.7) | 0.996 (–) | 0.00444 (8.11) | 4.72 (7.49) | 0.0998 (3.24) | 30.4 (8.91) |
| Cefoxitin [34] | 2,100 | IV bolus | II | 0.33 | 1.03 (21.6) | 0.362 (9.61) | 0.0160 (14.5) | 7.05 (20.4) | 0.390 (3.62) | 18.6 (15.6) |
| Nafcillin [35] | 500 | IV bolus | II | 0.16 | 1.24 (8.52) | 0.979 (0.0529) | 0.0203 (0.12) | 6.06 (9.00) | 0.512 (1.58) | 21.4 (6.45) |
Assumed 70 kg body weight. All symbols are defined in text
Minimal-PBPK model with two tissue compartments
Intravenous infusion (duration)
Minimal-PBPK model with one tissue compartment
For most beta-lactam antibiotics, tissue distribution rates were much lower than cardiac output (fd1 + fd2 <1); indicating permeability-limited uptake.
The Kp values were also calculated separately according to Kp = fup/fue using the relationship for fraction unbound in interstitial fluid (ISF):
| (14) |
where E/P is the ratio of protein concentrations for ISF: plasma and fue was approximated assuming albumin concentration in ISF being half that present in plasma [56]. The estimated Kp obtained by minimal-PBPK modeling correlated roughly (r2 = 0.319) with the calculated Kp (Fig. 6). This suggests that the unbound fraction only partly influences the degree to which beta-lactam antibiotics penetrate into interstitial fluids [57]. Other factors may also contribute such as ionization [58], transporters [59], or binding to other macromolecules such as penicillin-binding proteins [60]. Table 1 lists Vss values calculated by Vss = Vp + ΣKpi·Vti.
Fig. 6.
Correlation between estimated (Kp) and calculated partition coefficients Kp (fup/fue) for 22 beta-lactam antibiotics. The line of identity is shown
Hepatic elimination drugs
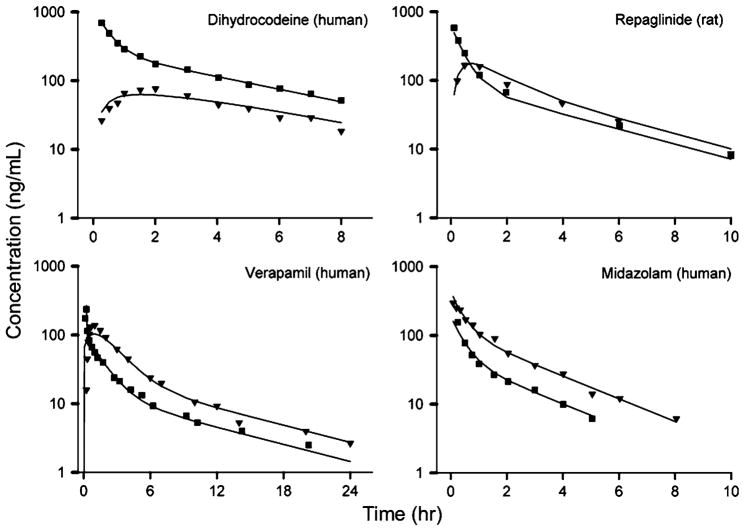
Four drugs with hepatic first-pass effects and incomplete apparent bioavailability (Bio) were selected for this analysis: dihydrocodeine [37], verapamil [38], repaglinide [39], and midazolam [40]. The data in the literature included both IV and oral administration. The extended model with the hepatic compartment and with typical Qhep and Vhep values [49] was used to analyze these data. The assumed Qhep was 1.45 L/min in man and 9.8 mL/min in rat [49]. As shown in Fig. 7, there is good agreement between the observed data and model-predicted profiles. The estimated parameters are listed in Table 2.
Fig. 7.
Pharmacokinetic profiles for four selected drugs after oral (triangle) and IV (square) dosing
Table 2.
Final estimated pharmacokinetic parameters (CV %) for hepatic extraction drugs
| Parameter (units) | Definition | Dihydrocodeine | Verapamil | Repaglinide | Midazolam |
|---|---|---|---|---|---|
| Species (Body Weight) | / | Man (70 kg) | Man (70 kg) | Rat (250 g) | Man (70 kg) |
| Oral dose | / | 30 mg | 120 mg | 0.5 mg/kg | 10 mg |
| IV dose | / | 30 mg | 15 mg (INF, 15 min)a | 0.2 mg/kg | 9.6 mg |
| fd1 | Fraction of QCO for V1 | 0.892 (3.77) | 0.903 (1.92) | 0.979 (0.00) | 0.692 (87.4) |
| fd2 | Fraction of QCO for V2 | 0.108 (NA) | 0.097 (NA) | 0.021 (NA) | 0.0842 (27.3) |
| Kp | Partition coefficient | 0.940 (4.32) | 3.96 (12.5) | 0.914 (8.74) | 0.655 (9.69) |
| ka (1/min) | Absorption rate constant | 0.00754 (10.3) | 0.0150 (12.6) | 0.0176 (12.1) | 0.218 (154) |
| CLintu (L/min or mL/min) | Hepatic intrinsic clearance | 0.424 (158) | 1.34 (59.0) | 1.70 (3.48) | 0.711 (8.20) |
| CLhep (L/min or mL/min) | Hepatic clearance | 0.328 | 0.696 | 1.45 | 0.477 |
| CLnon-hep (L/min or mL/min) | Non-hepatic clearance | NA | 0.214 (28.8) | NA | NA |
| ERb | Hepatic extraction ratio | 0.245 | 0.520 | 0.148 | 0.329 |
| V1 (L or mL) | Tissue compartment 1 | 46.2 (1.47) | 21.3 (13.0) | 53.5 (15.2) | 24.3 (14.4) |
| FG | Pre-hepatic bioavailability | 0.409 (6.21) | 0.553 (2.75) | 0.500 (0.236) | 0.742 (12.4) |
| Vss (L or mL) | Steady-state volume | 64.5 (3.97) | 346 (11.6) | 230 (8.23) | 46.5 (8.61) |
| Bioc | Bioavailability based upon NCA | 0.266 | 0.217 | 0.328 | 0.453 |
Intravenous infusion (duration)
ER, calculated according to Eq. (8)
calculated as (AUCoral/Doral)/(AUCiv/Div) with AUC from noncompartmental analysis (NCA)
Dihydrocodeine
The PK studies of dihydrocodeine were conducted in healthy subjects by Rowell et al. [37]. The extended model simultaneously captured the PK profiles following oral and IV dosing (Fig. 7). The finding that fd1 + fd2 = 1 indicates that dihydrocodeine rapidly diffuses into tissues with uptake restricted by blood flow. Hepatic intrinsic clearance is 0.424 L/min and CLhep = 0.328 L/min. The hepatic extraction ratio (ER) was calculated according to Eq. 8 as 0.245 and FG was estimated as 0.409. Thus, overall bio-availability would be about 0.309 based upon FG·(1-ER), near to the NCA Bio value of 0.266. Dihydrocodeine is known to be extensively metabolized in the liver and the modeling results support this with a negligible estimate of CLnon-hep. The separate estimates of different clearances allow quantitative assessment of their relative contributions to drug elimination and also support an identifiable FG.
Verapamil
Hepatic metabolism is the predominant route of elimination for verapamil and almost no intact drug is excreted according to previous studies [61]. The model supported this with a small estimate of CLnon-hep as 0.214 L/min. Figure 7 shows the fitted results. CLintu is 1.34 L/min, CLhep = 0.696 L/min, and ER was 0.520. High hepatic extraction resulted in low systemic bioavailability (26.6 %), in line with a previous study and the NCA Bio of 0.217 [62]. The high estimate of fd1 + fd2 indicates that the permeability of verapamil across capillary and cellular membranes was very high and distribution rate is primarily controlled by blood flow.
Repaglinide
This PK study of repaglinide was conducted in rats. Figure 7 shows the fitted results. A previous study indicated that repaglinide is mainly excreted via bile into feces and hepatic clearance dominates the overall elimination [63]. Our analysis confirmed this. The FG was 0.5, multiplying 1-ER (0.148), gives an overall bioavailability of 0.426. The high estimate of fd1 + fd2 suggested that distribution rate is mainly controlled by blood flow.
Midazolam
As a probe of CYP450 3A4/5, midazolam is subject to extensive first-pass metabolism in both intestine and liver [64]. Several approaches have evaluated the relative contributions of intestinal and hepatic metabolism to the overall first-pass effect [65, 66]. The fitted profiles are shown in Fig. 7. Our modeling gave estimates of their contributions. The FG was 0.742 and liver ER is 0.329, indicating comparable first-pass effects from intestine and liver. Such first-pass effect was also observed in previous studies [65, 66]. The Kp was about 0.655, consistent with an average PBPK literature value [67]. Hepatic and intestinal clearance accounts for most drug elimination as no other clearance was detected in our analysis.
Inter-species PK of moxifloxacin
As shown in Fig. 8, the PK of moxifloxacin in five species was assessed simultaneously by the integrated minimal-PBPK model. The estimated parameters are listed in Table 3. The low CV % values for the parameter estimates indicate good model performance although fittings for some of the digitized data are only approximate. Moxifloxacin appears to efficiently penetrate into tissues with blood flow as the rate-limiting step in the distribution process for the five species as shown by the high fd value of 1.0. The exponent (b) of the allometric equation for CL was 0.591, close to a reported value [68]. The Kp was 2.70, indicating moderate tissue partitioning and consistent with average tissue concentration in rats [69]. The initial misfit of the last several points for man observed in Fig. 8 may indicate that of CL does not precisely follow a conventional allometric relationship (Eq. 12). The fitting of human data was improved when b was increased. It is well appreciated that CL in man sometimes needs modifications from expectations of preclinical data. The main point of this case was to show a global mPBPK approach to assess fd and Kp, as well as scale CL across species.
Fig. 8.
Pharmacokinetic profiles for moxifloxacin in five species. The dotted line provides fitting with an adjusted b value for man
Table 3.
Pharmacokinetic parameters of moxifloxacin across five species
| Species | Body Wt, kg | Dose mg/kg |
|---|---|---|
| Mouse | 0.02 | 9.2 |
| Rat | 0.25 | 9.2 |
| Monkey | 5 | 2.8 |
| Dog | 10 | 2.8 |
| Man | 70 | 1.2 |
| Parameter | Definition | Value | CV% |
|---|---|---|---|
| fd | Fraction of QCO for V1 | 1.00 | < 0.01 |
| Kp | Partition coefficient | 2.70 | 7.57 |
| a | Normalization constant for CL | 0.014 | 5.75 |
| b | Scaling exponent for CL | 0.591 | 2.18 |
| bhum | Scaling exponent for CL in man | 0.691 | 3.07 |
Monoclonal antibodies
The clinical PK studies of six mAb were selected for this analysis: Hu12F6mu [42], lexatumumab [43], MEDI-528 [44], MEDI-563 [45], CR002 [46] and pateclizumab [47]. All mAb selected in this analysis showed linear PK that is usually analyzed with a 2CM mammillary model. The fitted profiles and simulated tissue concentrations are shown in Fig. 9 and the parameters are listed in Table 4 for models with tissue (Model A) versus plasma clearance (Model B). The models captured the observed PK profiles quite well with precise estimates of parameters. The tissue: plasma exposure ratios (AUC ratios) are reflected by the Kp values, which ranged 0.0475–0.0664 with Model A, and ranged 0.0330–0.0429 with Model B. Studies in mice have shown the muscle: serum AUC ratio of an antiplatelet antibody 7E3 to be 0.038, while other tissues had AUC ratios of 0.125 ± 0.036 [70]. Since muscle is about 60 % of BW, the mass-average AUC ratio should be about 0.07. A study in patients observed similar tissue: plasma AUC ratios of 111ln-labeled ZCEO25 IgG [71]. Thus, Model A appears somewhat superior to Model B. Both models yielded low estimates of fd, and Model A yielded fd in the range of 1.1–11.1 × 10−4. This gives a vascular permeability (fd·QCO) in the range of 0.017–0.17, close to a permeability value of 0.00567 L/h/70 kg (PSL + PSS) employed in a PBPK model by Baxter et al. [71]. mAbs are subject to extremely low capillary permeability [72] and net tissue uptake is further diminished by FcRn recycling [73]. Predictions of functional tissue concentrations of mAb should preferably employ interstitial fluid volume for Vt rather than BW − Vp owing to their limited cellular uptake except when a cellular target or receptor exists [71]. These models could be readily adapted to handle target-mediated disposition in plasma [74] or in tissue [75].
Fig. 9.
Pharmacokinetic profiles for six mAbs given to human subjects and simulated tissue concentrations
Table 4.
Pharmacokinetic parameters (CV %) for six monoclonal antibodies (mAb) in human subjects
| mAb [Ref] | Dosea | Model A: CL from tissue
|
Model B: CL from plasma
|
||||||
|---|---|---|---|---|---|---|---|---|---|
| fd (−) | Kp (−) | CLT (L/h) |
|
fd (−) | Kp (−) | CLP (L/h) |
|
||
| Hu12F6mu [42] | 10 mg | 0.00111 (15.3) | 0.0522 (8.86) | 0.412 (9.18) | 0.045 | 0.000936 (18.1) | 0.0429 (6.61) | 0.0187 (2.83) | 0.042 |
| Lexatumumab [43] | 10 mg/kg | 0.000692 (25.0) | 0.0475 (19.9) | 0.404 (24.6) | 0.037 | 0.000562 (26.8) | 0.0346 (15.2) | 0.0162 (7.62) | 0.032 |
| MEDI-528 [44] | 9 mg/kg | 0.000156 (10.9) | 0.0562 (9.62) | 0.126 (9.48) | 0.042 | 0.000123 (13.5) | 0.0330 (5.17) | 0.00553 (1.79) | 0.031 |
| MEDI-563 [45] | 3 mg/kg | 0.000398 (7.69) | 0.0519 (5.30) | 0.289 (3.80) | 0.041 | 0.000320 (9.56) | 0.0337 (3.56) | 0.0121 (1.45) | 0.033 |
| CR002 [46] | 30 mg/kg | 0.000110 (31.2) | 0.0664 (29.8) | 0.106 (23.1) | 0.046 | 0.0000779 (43.6) | 0.0333 (20.7) | 0.005 (6.58) | 0.031 |
| Pateclizumab [47] | 5 mg/kg | 0.000310 (14.5) | 0.0607 (12.6) | 0.241 (9.58) | 0.045 | 0.000231 (19.7) | 0.0368 (8.82) | 0.0112 (2.63) | 0.035 |
Assumed 70 kg body weight
AUCtissue: AUCserum ratio
Discussion
Full PBPK models use the modeling paradigm depicted in Fig. 1 melding all known body and drug properties to either simulate expected concentration–time profiles or perform fittings of available data. Blood flows and organ/tissue weights are largely taken from literature sources [49]. The PBPK models thus either confirm basic expectations about drug disposition or reveal further complexities where investigators add new model features based on experimental data and/or reasonable assumptions.
Minimal PBPK models offer similar possibilities with the constraints of only assessing blood or plasma concentration versus time data and yielding tissue-average drug concentrations. Our case studies with an array of drugs and disposition profiles allowed for reasonable fittings of data with model features predicated on the physicochemical and metabolic properties of a variety of drugs but providing outcomes with low dimensionality and ease of interpretation. As with full PBPK models, there is flexibility in adjusting major model components to accommodate specific drugs and conditions. The parameter estimates can be interpreted with more realism than compartmental models.
The purpose of this report is to demonstrate how minimal PBPK models can be envisioned and applied. The data were all digitized and thus analysis results will be imperfect. Owing to differences in assumptions, the fittings and parameters may differ somewhat from use of compartment models.
As with full PBPK models, blood or plasma volume, cardiac output, and total body space (BW or ECF) are assumed physiological components. For more extensive data sets, these parameters could be specified for subjects of varying ages, sexes, and body weights [76]. This provides freedom to allow the data to reveal fd, Kp, and CL values, parameters of special interest in PK. Most PK profiles are intrinsically bi- or tri-exponential allowing fitting of 4 or 6 parameters, both for compartmental models [2] as well as with minimal-PBPK models. Both approaches involve ‘lumping’ perspectives. When these models do not function well, there are likely added complexities which are not encompassed within the basic model structures and which need exploration.
Full PBPK, minimal-PBPK, and compartmental models have the expectation that CL = DoseIV/AUC when elimination occurs from blood or plasma. Compartmental models have the weakness that limited early blood sampling can miss high initial drug concentrations [77] and lead to deviations in estimates of the central compartment volume and cause bias of AUC prediction. For other clearance mechanisms, the minimal-PBPK models can easily include the liver for assessment of first-pass effects when jointly fitting oral and IV data (Fig. 3) or tissue clearance can be implemented (Fig. 4).
Compartmental models (with plasma CL) yield a whole-body distribution coefficient, Kp = Vss/BW [53]. The same parameter can be generated from both full and minimal PBPK models from Vss = Vp + ΣKpi · Vti. The minimal-PBPK models provide one or two Kp values depending on the number of exponential phases in the data. This number and value(s) are determined in a trial-and-error fitting approach. Of advantage for interpretation, this parameter is directly revealed as one of the primary ‘independent’ variables for each drug. These Kp values reflect either fractional tissue spaces [78] and/or plasma and tissue binding and can be compared among congeneric drugs (beta-lactams, Table 1) or among species (moxifloxacin, Table 3). Scaling of animal data to man is readily feasible with minimal-PBPK models using aspects of allometry for select model components as was done for moxifloxacin.
The minimal-PBPK models are attractive in utilizing the well-known Fick’s Law of Perfusion. The employment of the fractional distribution (fd) parameter not only accounts for organ/tissue ‘lumping’, but allows for inaccuracies or variability in QCO as well as flexibility for distribution to be controlled by permeability as revealed by small values of fd. The value of fd·QCO is equivalent to distribution clearance (CLD) as proposed by Stec and Atkinson [79] who adapted earlier concepts from the Kety–Renkin–Crone equation [80–83]:
| (15) |
where Q is blood flow and PS is a permeability/surface area coefficient. The function allows the value of CLD → Q when PS ≫ Q and CLD → PS when PS ≫ Q: Thus small values of fd depict permeability-limited tissue access and reflect operation of Fick’s Law of Diffusion. However, within the context of the minimal-PBPK paradigm, the fd values may represent either differing blood distribution to tissues/organs and/or flow/permeability. Of course, the presence of transporters will complicate such assessment [84].
It has been somewhat surprising that full PBPK models commonly work well with use of blood flow to various organs and tissues with occasional introduction of PS values for interstitial-cell water distribution [85]. It has been long appreciated that capillary permeability varies with molecular size producing very slow tissue access for large molecules such as plasma proteins [86, 87]. More frequent model assessment should be done based on permeability-limited access for various molecules. The minimal-PBPK models provide fd values allowing for a full range of PS and Q values to be operative for tissue distribution.
The parameters of minimal-PBPK models have a simple and logical basis allowing ease of fitting and interpretation. Preliminary NCA analysis can provide estimates of CL from Dose/AUC and Kp from Vss/BW = MRT·CL/BW where MRT is Mean Residence Time. Values of fd must fall between 0 and 1 and both fd and Kp are dimensionless. The value of V1 must fall with BW − Vp ≥ V1. Thus, most model parameters have natural physiological limits with restricted parameter spaces allowing for robust parameter estimates. The opposite extreme exists with finding rate constants in compartmental models which are non-intuitive and range widely.
The minimal-PBPK models are highly flexible allowing for most of the modeling adjustments found in applying full-PBPK models. An infusion rate constant or Bischoff g(t) input function [88] may be needed to mimic very early circulatory kinetics [6] rather than assuming Initial Conditions of Dose/Vp. The preferred organ perfusion medium is arterial rather than venous blood [1–3], although this is seldom feasible in human studies. Our modeling employed venous drug concentrations which is also not uncommon in enacting full PBPK models.
The model with hepatic clearance involved use of the well-stirred model and assumptions that the Kp value of liver was the same as other tissues and intrinsic clearance acts on unbound drug in liver. Thus the calculated parameters would differ if another hepatic model was applied (e.g. parallel-tube), if differential tissue binding occurs, and if facilitated uptake or nonrestrictive metabolism was present [89, 90]. Most of our conditions are commonly applied in full PBPK models.
The site of drug administration (IV, IM, SC, oral) can be more relevant than in compartmental models as shown with the extended model (Fig. 3). Nonlinearity in CL or Kp can be added when the range of doses, drug properties, and data profiles allow. As demonstrated with our cases, greater modeling flexibility is gained when studies include diverse dosing (Fig. 7), species (Fig. 8), or experimental conditions (Figs. 5, 9).
The present demonstration of various applications of minimal PBPK modeling utilized digitized data from various literature sources. Thus the parameter estimates are approximate but clearly reflect the feasibility of this modeling approach. However, as a fifth example of minimal-PBPK modeling with more comprehensive metrics, Grimsrud et al. [91] successfully applied a model similar to that in Fig. 2 to assess detomidine PK after IV and IM doses in horses using a population approach with specific physiological parameters for each horse. A physiologic muscle compartment was employed for V2 as the site of IM drug administration.
Application of full PBPK models remains the gold standard in PK, but requires physicochemical, physiologic, animal tissue, and in vitro metabolic measurements along with appreciable modeling efforts. Minimal-PBPK models offer a sensible compromise when only blood or plasma data are available. They allow the insightful pharmacokineticist great liberties in evaluating data and providing parameters of practical value.
Acknowledgments
This research was supported by the National Institutes of Health Grant GM57980, the University at Buffalo—Pfizer Strategic Alliance, and the UB Center for Protein Therapeutics. Review of this manuscript by Drs. Sihem Ait-Oudhia, Peter Bonate, Wilhelm Huisinga, Wojciech Krzyzanski, Donald E. Mager, and Marilyn E. Morris is appreciated.
Footnotes
Electronic supplementary material The online version of this article (doi:10.1007/s10928-012-9280-2) contains supplementary material, which is available to authorized users.
Contributor Information
Yanguang Cao, Department of Pharmaceutical Sciences, School of Pharmacy and Pharmaceutical Sciences, State University of New York at Buffalo, 404 Kapoor Hall, Buffalo, NY 14214-8033, USA.
William J. Jusko, Email: wjjusko@buffalo.edu, Department of Pharmaceutical Sciences, School of Pharmacy and Pharmaceutical Sciences, State University of New York at Buffalo, 404 Kapoor Hall, Buffalo, NY 14214-8033, USA
References
- 1.Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73. doi: 10.1146/annurev-pharmtox-010510-100540. [DOI] [PubMed] [Google Scholar]
- 2.Jusko WJ. Guidelines for collection and pharmacokinetic analysis of drug disposition data. In: Evans WE, Schentag JJ, Jusko WJ, editors. Applied pharmacokinetics: principles of therapeutic drug monitoring. 1. Applied Therapeutics Inc; Vancouver, WA: 1980. pp. 639–680. [Google Scholar]
- 3.Chiou WL. Potential pitfalls in the conventional pharmacokinetic studies: effects of the initial mixing of drug in blood and the pulmonary first-pass elimination. J Pharmacokinet Biopharm. 1979;7:527–536. doi: 10.1007/BF01062393. [DOI] [PubMed] [Google Scholar]
- 4.Riegelman S, Loo JC, Rowland M. Shortcomings in pharmacokinetic analysis by conceiving the body to exhibit properties of a single compartment. J Pharm Sci. 1968;57:117–123. doi: 10.1002/jps.2600570123. [DOI] [PubMed] [Google Scholar]
- 5.Vaughan DP, Hope I. Applications of a recirculatory stochastic pharmacokinetic model: limitations of compartmental models. J Pharmacokinet Biopharm. 1979;7:207–225. doi: 10.1007/BF01059739. [DOI] [PubMed] [Google Scholar]
- 6.Krejcie TC, Henthorn TK, Shanks CA, Avram MJ. A recirculatory pharmacokinetic model describing the circulatory mixing, tissue distribution and elimination of antipyrine in dogs. J Pharmacol Exp Ther. 1994;269:609–616. [PubMed] [Google Scholar]
- 7.Veng-Pedersen P, Freise KJ, Schmidt RL, Widness JA. Pharmacokinetic differentiation of drug candidates using system analysis and physiological-based modelling. Comparison of C.E.R.A. and erythropoietin. J Pharm Pharmacol. 2008;60:1321–1334. doi: 10.1211/jpp/60.10.0008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Nestorov IA, Aarons LJ, Arundel PA, Rowland M. Lumping of whole-body physiologically based pharmacokinetic models. J Pharmacokinet Biopharm. 1998;26:21–46. doi: 10.1023/a:1023272707390. [DOI] [PubMed] [Google Scholar]
- 9.Pilari S, Huisinga W. Lumping of physiologically-based pharmacokinetic models and a mechanistic derivation of classical compartmental models. J Pharmacokinet Pharmacodyn. 2010;37:365–405. doi: 10.1007/s10928-010-9165-1. [DOI] [PubMed] [Google Scholar]
- 10.Levy G, Mager DE, Cheung WK, Jusko WJ. Comparative pharmacokinetics of coumarin anticoagulants L: physiologic modeling of S-warfarin in rats and pharmacologic target-mediated warfarin disposition in man. J Pharm Sci. 2003;92:985–994. doi: 10.1002/jps.10345. [DOI] [PubMed] [Google Scholar]
- 11.Kawahara M, Sakata A, Miyashita T, Tamai I, Tsuji A. Physiologically based pharmacokinetics of digoxin in mdr1a knockout mice. J Pharm Sci. 1999;88:1281–1287. doi: 10.1021/js9901763. [DOI] [PubMed] [Google Scholar]
- 12.Rocci ML, Jr, Szefler SJ, Acara M, Jusko WJ. Prednisolone metabolism and excretion in the isolated perfused rat kidney. Drug Metab Dispos. 1981;9:177–182. [PubMed] [Google Scholar]
- 13.Gallo JM, Vicini P, Orlansky A, Li S, Zhou F, Ma J, Pulfer S, Bookman MA, Guo P. Pharmacokinetic model-predicted anticancer drug concentrations in human tumors. Clin Cancer Res. 2004;10:8048–8058. doi: 10.1158/1078-0432.CCR-04-0822. [DOI] [PubMed] [Google Scholar]
- 14.Henthorn TK, Avram MJ, Krejcie TC, Shanks CA, Asada A, Kaczynski DA. Minimal compartmental model of circulatory mixing of indocyanine green. Am J Physiol. 1992;262:H903–H910. doi: 10.1152/ajpheart.1992.262.3.H903. [DOI] [PubMed] [Google Scholar]
- 15.Rowland M, Benet LZ, Graham GG. Clearance concepts in pharmacokinetics. J Pharmacokinet Biopharm. 1973;1:123–136. doi: 10.1007/BF01059626. [DOI] [PubMed] [Google Scholar]
- 16.Lobo ED, Hansen RJ, Balthasar JP. Antibody pharmacokinetics and pharmacodynamics. J Pharm Sci. 2004;93:2645–2668. doi: 10.1002/jps.20178. [DOI] [PubMed] [Google Scholar]
- 17.Humbert G, Spyker DA, Fillastre JP, Leroy A. Pharmacokinetics of amoxicillin: dosage nomogram for patients with impaired renal function. Antimicrob Agents Chemother. 1979;15:28–33. doi: 10.1128/aac.15.1.28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Champoux N, Du Souich P, Ravaoarinoro M, Phaneuf D, Latour J, Cusson JR. Single-dose pharmacokinetics of ampicillin and tobramycin administered by hypodermoclysis in young and older healthy volunteers. Br J Clin Pharmacol. 1996;42:325–331. doi: 10.1046/j.1365-2125.1996.03967.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Pfeffer M, Gaver RC, Ximenez J. Human intravenous pharmacokinetics and absolute oral bioavailability of cefatrizine. Antimicrob Agents Chemother. 1983;24:915–920. doi: 10.1128/aac.24.6.915. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lee FH, Pfeffer M, Van Harken DR, Smyth RD, Hottendorf GH. Comparative pharmacokinetics of ceforanide (BL-S786R) and cefazolin in laboratory animals and humans. Antimicrob Agents Chemother. 1980;17:188–192. doi: 10.1128/aac.17.2.188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lofgren S, Bucht G, Hermansson B, Holm SE, Winblad B, Norrby SR. Single-dose pharmacokinetics of dicloxacillin in healthy subjects of young and old age. Scand J Infect Dis. 1986;18:365–369. doi: 10.3109/00365548609032348. [DOI] [PubMed] [Google Scholar]
- 22.Landersdorfer CB, Kirkpatrick CM, Kinzig-Schippers M, Bulitta JB, Holzgrabe U, Drusano GL, Sorgel F. Population pharmacokinetics at two dose levels and pharmacodynamic pro-filing of flucloxacillin. Antimicrob Agents Chemother. 2007;51:3290–3297. doi: 10.1128/AAC.01410-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gambertoglio JG, Barriere SL, Lin ET, Conte JE., Jr Pharmacokinetics of mecillinam in health subjects. Antimicrob Agents Chemother. 1980;18:952–956. doi: 10.1128/aac.18.6.952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Bulitta JB, Duffull SB, Kinzig-Schippers M, Holzgrabe U, Stephan U, Drusano GL, Sorgel F. Systematic comparison of the population pharmacokinetics and pharmacodynamics of piperacillin in cystic fibrosis patients and healthy volunteers. Antimicrob Agents Chemother. 2007;51:2497–2507. doi: 10.1128/AAC.01477-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hampel B, Feike M, Koeppe P, Lode H. Pharmacokinetics of temocillin in volunteers. Drugs. 1985;29(Suppl 5):99–102. doi: 10.2165/00003495-198500295-00020. [DOI] [PubMed] [Google Scholar]
- 26.Frimodt-Moller N, Maigaard S, Toothaker RD, Bundtzen RW, Brodey MV, Craig WA, Welling PG, Madsen PO. Mezlocillin pharmacokinetics after single intravenous doses to patients with varying degrees of renal function. Antimicrob Agents Chemother. 1980;17:599–607. doi: 10.1128/aac.17.4.599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Vinge E, Nergelius G, Nilsson LG, Lidgren L. Pharmacokinetics of cloxacillin in patients undergoing hip or knee replacement. Eur J Clin Pharmacol. 1997;52:407–411. doi: 10.1007/s002280050310. [DOI] [PubMed] [Google Scholar]
- 28.Yaffe SJ, Gerbracht LM, Mosovich LL, Mattar ME, Danish M, Jusko WJ. Pharmacokinetics of methicillin in patients with cystic fibrosis. J Infect Dis. 1977;135:828–831. doi: 10.1093/infdis/135.5.828. [DOI] [PubMed] [Google Scholar]
- 29.Rumble RH, Roberts MS, Scott AR. The effect of posture on the pharmacokinetics of intravenous benzylpenicillin. Eur J Clin Pharmacol. 1986;30:731–734. doi: 10.1007/BF00608225. [DOI] [PubMed] [Google Scholar]
- 30.Meyers BR, Hirschman SZ, Strougo L, Srulevitch E. Comparative study of piperacillin, ticarcillin, and carbenicillin pharmacokinetics. Antimicrob Agents Chemother. 1980;17:608–611. doi: 10.1128/aac.17.4.608. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kikuchi E, Kikuchi J, Nasuhara Y, Oizumi S, Ishizaka A, Nishimura M. Comparison of the pharmacodynamics of biapenem in bronchial epithelial lining fluid in healthy volunteers given half-hour and three-hour intravenous infusions. Antimicrob Agents Chemother. 2009;53:2799–2803. doi: 10.1128/AAC.01578-08. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Colaizzi PA, Polk RE, Poynor WJ, Raffalovich AC, Cefali EA, Beightol LA. Comparative pharmacokinetics of azlocillin and piperacillin in normal adults. Antimicrob Agents Chemother. 1986;29:938–940. doi: 10.1128/aac.29.5.938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Barza M, Melethil S, Berger S, Ernst EC. Comparative pharmacokinetics of cefamandole, cephapirin, and cephalothin in healthy subjects and effect of repeated dosing. Antimicrob Agents Chemother. 1976;10:421–425. doi: 10.1128/aac.10.3.421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Kampf D, Schurig R, Korsukewitz I, Bruckner O. Cefoxitin pharmacokinetics: relation to three different renal clearance studies in patients with various degrees of renal insufficiency. Antimicrob Agents Chemother. 1981;20:741–746. doi: 10.1128/aac.20.6.741. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Waller ES, Sharanevych MA, Yakatan GJ. The effect of probenecid on nafcillin disposition. J Clin Pharmacol. 1982;22:482–489. doi: 10.1002/j.1552-4604.1982.tb02639.x. [DOI] [PubMed] [Google Scholar]
- 36.Dudley MN, Shyu WC, Nightingale CH, Quintiliani R. Effect of saturable serum protein binding on the pharmacokinetics of unbound cefonicid in humans. Antimicrob Agents Chemother. 1986;30:565–569. doi: 10.1128/aac.30.4.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Rowell FJ, Seymour RA, Rawlins MD. Pharmacokinetics of intravenous and oral dihydrocodeine and its acid metabolites. Eur J Clin Pharmacol. 1983;25(3):419–424. doi: 10.1007/BF01037958. [DOI] [PubMed] [Google Scholar]
- 38.Krecic-Shepard ME, Barnas CR, Slimko J, Jones MP, Schwartz JB. Gender-specific effects on verapamil pharmacokinetics and pharmacodynamics in humans. J Clin Pharmacol. 2000;40:219–230. doi: 10.1177/00912700022008883. [DOI] [PubMed] [Google Scholar]
- 39.Li C, Choi DH, Choi JS. Effects of efonidipine on the pharmacokinetics and pharmacodynamics of repaglinide: possible role of CYP3A4 and P-glycoprotein inhibition by efonidipine. J Pharmacokinet Pharmacodyn. 2012;39:99–108. doi: 10.1007/s10928-011-9234-0. [DOI] [PubMed] [Google Scholar]
- 40.Heizmann P, Eckert M, Ziegler WH. Pharmacokinetics and bioavailability of midazolam in man. Br J Clin Pharmacol. 1983;16(Suppl 1):43S–49S. doi: 10.1111/j.1365-2125.1983.tb02270.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Siefert HM, Domdey-Bette A, Henninger K, Hucke F, Kohls-dorfer C, Stass HH. Pharmacokinetics of the 8-meth-oxyquinolone, moxifloxacin: a comparison in humans and other mammalian species. J Antimicrob Chemother. 1999;43(Suppl B):69–76. doi: 10.1093/jac/43.suppl_2.69. [DOI] [PubMed] [Google Scholar]
- 42.Li J, Zhou B, Shentu J, Du L, Tan M, Hou S, Qian W, Li B, Zhang D, Dai J, Wang H, Zhang X, Chen J, Guo Y. Phase I trial of a humanized, Fc receptor nonbinding anti-CD3 antibody, hu12F6mu in patients receiving renal allografts. MAbs. 2010;2:449–456. doi: 10.4161/mabs.2.4.12305. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Wakelee HA, Patnaik A, Sikic BI, Mita M, Fox NL, Miceli R, Ullrich SJ, Fisher GA, Tolcher AW. Phase I and pharmacokinetic study of lexatumumab (HGS-ETR2) given every 2 weeks in patients with advanced solid tumors. Ann Oncol. 2010;21:376–381. doi: 10.1093/annonc/mdp292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.White B, Leon F, White W, Robbie G. Two first-in-human, open-label, phase I dose-escalation safety trials of MEDI-528, a monoclonal antibody against interleukin-9, in healthy adult volunteers. Clin Ther. 2009;31:728–740. doi: 10.1016/j.clinthera.2009.04.019. [DOI] [PubMed] [Google Scholar]
- 45.Busse WW, Katial R, Gossage D, Sari S, Wang B, Kolbeck R, Coyle AJ, Koike M, Spitalny GL, Kiener PA, Geba GP, Molfino NA. Safety profile, pharmacokinetics, and biologic activity of MEDI-563, an anti-IL-5 receptor alpha antibody, in a phase I study of subjects with mild asthma. J Allergy Clin Immunol. 2010;125(1237–1244):e1232. doi: 10.1016/j.jaci.2010.04.005. [DOI] [PubMed] [Google Scholar]
- 46.Hawthorne T, Giot L, Blake L, Kuang B, Gerwien R, Smithson G, Hahne W, Mansfield T, Starling GC, Pochart P, Hoelscher D, Halvorsen YD. A phase I study of CR002, a fully-human monoclonal antibody against platelet-derived growth factor-D. Int J Clin Pharmacol Ther. 2008;46:236–244. doi: 10.5414/cpp46236. [DOI] [PubMed] [Google Scholar]
- 47.Emu B, Luca D, Offutt C, Grogan JL, Rojkovich B, Williams MB, Tang MT, Xiao J, Lee JH, Davis JC. Safety, pharmacokinetics, and biologic activity of pateclizumab, a novel monoclonal antibody targeting lymphotoxin alpha: results of a phase I randomized, placebo-controlled trial. Arthritis Res Ther. 2012;14:R6. doi: 10.1186/ar3554. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Rodionov N. Graph digitizer version 1.9. 2000 http://www.geocities.com/graphdigitizer.
- 49.Brown RP, Delp MD, Lindstedt SL, Rhomberg LR, Beliles RP. Physiological parameter values for physiologically based pharmacokinetic models. Toxicol Ind Health. 1997;13:407–484. doi: 10.1177/074823379701300401. [DOI] [PubMed] [Google Scholar]
- 50.Boxenbaum H. Interspecies scaling, allometry, physiological time, and the ground plan of pharmacokinetics. J Pharmacokinet Biopharm. 1982;10:201–227. doi: 10.1007/BF01062336. [DOI] [PubMed] [Google Scholar]
- 51.D’Argenio DZ, Schumitzky A, Wang XN. ADAPT V user’s guide: pharmacokinetic/pharmacodynamic system analysis software, biomedical simulations resource. Los Angeles: 2009. [Google Scholar]
- 52.ICRP Publication 89. Basic anatomical and physiological data for use in radiological protection: reference values. A report of age- and gender-related differences in the anatomical and physiological characteristics of reference individuals. Ann ICRP. 2002;32(3–4):5–265. [PubMed] [Google Scholar]
- 53.Jusko WJ, Chiang ST. Distribution volume related to body weight and protein binding. J Pharm Sci. 1982;71:469–470. doi: 10.1002/jps.2600710428. [DOI] [PubMed] [Google Scholar]
- 54.Cars O. Pharmacokinetics of antibiotics in tissues and tissue fluids: a review. Scand J Infect Dis Suppl. 1990;74:23–33. [PubMed] [Google Scholar]
- 55.Shiran MR, Proctor NJ, Howgate EM, Rowland-Yeo K, Tucker GT, Rostami-Hodjegan A. Prediction of metabolic drug clearance in humans: in vitro-in vivo extrapolation vs allometric scaling. Xenobiotica. 2006;36:567–580. doi: 10.1080/00498250600761662. [DOI] [PubMed] [Google Scholar]
- 56.McNamara PJ, Gibaldi M, Stoeckel K. Fraction unbound in interstitial fluid. J Pharm Sci. 1983;72:834–836. doi: 10.1002/jps.2600720735. [DOI] [PubMed] [Google Scholar]
- 57.Wise R, Gillett AP, Cadge B, Durham SR, Baker S. The influence of protein binding upon tissue fluid levels of six beta-lactam antibiotics. J Infect Dis. 1980;142:77–82. doi: 10.1093/infdis/142.1.77. [DOI] [PubMed] [Google Scholar]
- 58.Barza M, Weinstein L. Some determinants of the distribution of penicillins and cephalosporins in the body. Practical and theoretical considerations. Ann N Y Acad Sci. 1974;235:613–620. doi: 10.1111/j.1749-6632.1974.tb43295.x. [DOI] [PubMed] [Google Scholar]
- 59.Fujiwara K, Shin M. Immunocytochemistry for amoxicillin and its use for studying uptake of the drug in the intestine, liver, and kidney of rats. Antimicrob Agents Chemother. 2011;55(1):62–71. doi: 10.1128/AAC.01031-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Griaznova NS, Subbotina NA. Penicillin-binding proteins. Their enzymatic activity and properties. Antibiot Med Biotekhnol. 1986;31(7):487–498. [PubMed] [Google Scholar]
- 61.Hamann SR, Blouin RA, McAllister RG., Jr Clinical pharmacokinetics of verapamil. Clin Pharmacokinet. 1984;9:26–41. doi: 10.2165/00003088-198409010-00002. [DOI] [PubMed] [Google Scholar]
- 62.Eichelbaum M, Mikus G, Vogelgesang B. Pharmacokinetics of (+)-, (−)- and (±)-verapamil after intravenous administration. Br J Clin Pharmacol. 1984;17:453–458. doi: 10.1111/j.1365-2125.1984.tb02371.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Sjogren E, Bredberg U, Lennernas H. The pharmacokinetics and hepatic disposition of repaglinide in pigs: mechanistic modeling of metabolism and transport. Mol Pharm. 2012;9:823–841. doi: 10.1021/mp200218p. [DOI] [PubMed] [Google Scholar]
- 64.Lin YS, Dowling AL, Quigley SD, Farin FM, Zhang J, Lamba J, Schuetz EG, Thummel KE. Co-regulation of CYP3A4 and CYP3A5 and contribution to hepatic and intestinal midazolam metabolism. Mol Pharmacol. 2002;62:162–172. doi: 10.1124/mol.62.1.162. [DOI] [PubMed] [Google Scholar]
- 65.Tsunoda SM, Velez RL, von Moltke LL, Greenblatt DJ. Differentiation of intestinal and hepatic cytochrome P450 3A activity with use of midazolam as an in vivo probe: effect of ketoconazole. Clin Pharmacol Ther. 1999;66:461–471. doi: 10.1016/S0009-9236(99)70009-3. [DOI] [PubMed] [Google Scholar]
- 66.Thummel KE, O’Shea D, Paine MF, Shen DD, Kunze KL, Perkins JD, Wilkinson GR. Oral first-pass elimination of midazolam involves both gastrointestinal and hepatic CYP3A-mediated metabolism. Clin Pharmacol Ther. 1996;59:491–502. doi: 10.1016/S0009-9236(96)90177-0. [DOI] [PubMed] [Google Scholar]
- 67.Bjorkman S, Wada DR, Berling BM, Benoni G. Prediction of the disposition of midazolam in surgical patients by a physiologically based pharmacokinetic model. J Pharm Sci. 2001;90:1226–1241. doi: 10.1002/jps.1076. [DOI] [PubMed] [Google Scholar]
- 68.Cox SK. Allometric scaling of marbofloxacin, moxifloxacin, danofloxacin and difloxacin pharmacokinetics: a retrospective analysis. J Vet Pharmacol Ther. 2007;30:381–386. doi: 10.1111/j.1365-2885.2007.00886.x. [DOI] [PubMed] [Google Scholar]
- 69.Beckmann J, Kees F, Schaumburger J, Kalteis T, Lehn N, Grifka J, Lerch K. Tissue concentrations of vancomycin and moxifloxacin in periprosthetic infection in rats. Acta Orthop. 2007;78:766–773. doi: 10.1080/17453670710014536. [DOI] [PubMed] [Google Scholar]
- 70.Garg A, Balthasar JP. Physiologically-based pharmacokinetic (PBPK) model to predict IgG tissue kinetics in wild-type and FcRn-knockout mice. J Pharmacokinet Pharmacodyn. 2007;34:687–709. doi: 10.1007/s10928-007-9065-1. [DOI] [PubMed] [Google Scholar]
- 71.Baxter LT, Zhu H, Mackensen DG, Butler WF, Jain RK. Biodistribution of monoclonal antibodies: scale-up from mouse to human using a physiologically based pharmacokinetic model. Cancer Res. 1995;55:4611–4622. [PubMed] [Google Scholar]
- 72.Rippe B, Haraldsson B. Transport of macromolecules across microvascular walls: the two-pore theory. Physiol Rev. 1994;74:163–219. doi: 10.1152/physrev.1994.74.1.163. [DOI] [PubMed] [Google Scholar]
- 73.Junghans RP. Finally! The Brambell receptor (FcRB). Mediator of transmission of immunity and protection from catabolism for IgG. Immunol Res. 1997;16:29–57. doi: 10.1007/BF02786322. [DOI] [PubMed] [Google Scholar]
- 74.Hayashi N, Tsukamoto Y, Sallas WM, Lowe PJ. A mechanism-based binding model for the population pharmacokinetics and pharmacodynamics of omalizumab. Br J Clin Pharmacol. 2007;63:548–561. doi: 10.1111/j.1365-2125.2006.02803.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lammerts van Bueren JJ, Bleeker WK, Bogh HO, Houtkamp M, Schuurman J, van de Winkel JG, Parren PW. Effect of target dynamics on pharmacokinetics of a novel therapeutic antibody against the epidermal growth factor receptor: implications for the mechanisms of action. Cancer Res. 2006;66:7630–7638. doi: 10.1158/0008-5472.CAN-05-4010. [DOI] [PubMed] [Google Scholar]
- 76.Huisinga W, Solms A, Fronton L, Pilari S. Modeling interindividual variability in physiologically based pharmacokinetics and its link to mechanistic covariate modeling. Pharmacometrics Syst Pharmacol. 2012;1:e4. doi: 10.1038/psp.2012.3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Weiss M. Modelling of initial distribution of drugs following intravenous bolus injection. Eur J Clin Pharmacol. 1983;24:121–126. doi: 10.1007/BF00613938. [DOI] [PubMed] [Google Scholar]
- 78.Levitt DG. The pharmacokinetics of the interstitial space in humans. BMC Clin Pharmacol. 2003;3:3–14. doi: 10.1186/1472-6904-3-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Stec GP, Atkinson AJ., Jr Analysis of the contributions of permeability and flow of intercompartmental clearance. J Pharmacokinet Biopharm. 1981;9:167–180. doi: 10.1007/BF01068080. [DOI] [PubMed] [Google Scholar]
- 80.Kety SS. The theory and applications of the exchange of inert gas at the lungs and tissues. Pharmacol Rev. 1951;3:1–41. [PubMed] [Google Scholar]
- 81.Renkin EM. Effects of blood flow on diffusion kinetics in isolated, perfused hindlegs of cats; a double circulation hypothesis. Am J Physiol. 1955;183:125–136. doi: 10.1152/ajplegacy.1955.183.1.125. [DOI] [PubMed] [Google Scholar]
- 82.Renkin EM. Transport of potassium-42 from blood to tissue in isolated mammalian skeletal muscles. Am J Physiol. 1959;197:1205–1210. doi: 10.1152/ajplegacy.1959.197.6.1205. [DOI] [PubMed] [Google Scholar]
- 83.Crone C. The permeability of capillaries in various organs as determined by use of the ‘Indicator diffusion’ method. Acta Physiol Scand. 1963;58:292–305. doi: 10.1111/j.1748-1716.1963.tb02652.x. [DOI] [PubMed] [Google Scholar]
- 84.Watanabe T, Kusuhara H, Sugiyama Y. Application of physiologically based pharmacokinetic modeling and clearance concept to drugs showing transporter-mediated distribution and clearance in humans. J Pharmacokinet Pharmacodyn. 2010;37:575–590. doi: 10.1007/s10928-010-9176-y. [DOI] [PubMed] [Google Scholar]
- 85.Thompson MD, Beard DA. Development of appropriate equations for physiologically based pharmacokinetic modeling of permeability-limited and flow-limited transport. J Pharmacokinet Pharmacodyn. 2011;38:405–421. doi: 10.1007/s10928-011-9200-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Goldstein A, Aronow L, Kalman SM. Principles of drug action: the basis of pharmacology. Harper & Row; New York: 1974. p. 147. [Google Scholar]
- 87.Renkin EM. Multiple pathways of capillary permeability. Circ Res. 1977;41:735–743. doi: 10.1161/01.res.41.6.735. [DOI] [PubMed] [Google Scholar]
- 88.Bischoff KB, Dedrick RL, Zaharko DS, Longstreth JA. Methotrexate pharmacokinetics. J Pharm Sci. 1971;60:1128–1133. doi: 10.1002/jps.2600600803. [DOI] [PubMed] [Google Scholar]
- 89.Poulin P, Kenny JR, Hop CE, Haddad S. In vitro–in vivo extrapolation of clearance: modeling hepatic metabolic clearance of highly bound drugs and comparative assessment with existing calculation methods. J Pharm Sci. 2012;101:838–851. doi: 10.1002/jps.22792. [DOI] [PubMed] [Google Scholar]
- 90.Chiba M, Ishii Y, Sugiyama Y. Prediction of hepatic clearance in human from in vitro data for successful drug development. AAPS J. 2009;11:262–276. doi: 10.1208/s12248-009-9103-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Grimsrud KN, Ait-Oudhia S, Durbin-Johnson BP, Rocke DM, Mama KR, Rezende ML, Stanley SD, Jusko WJ. Population pharmacokinetic and pharmacodynamic analysis comparing diverse effects of detomidine, medetomidine and dexmedetomidine in the horse; Presented at the Annual Symposium of the Veterinary Science Training Program; University of California, Davis. March 2012.2012. [Google Scholar]