Functional dynamics in the active site of the ribonuclease binase

Abstract

Binase, a member of a family of microbial guanyl-specific ribonucleases, catalyzes the endonucleotic cleavage of single-stranded RNA. It shares 82% amino acid identity with the well-studied protein barnase. We used NMR spectroscopy to study the millisecond dynamics of this small enzyme, using several methods including the measurement of residual dipolar couplings in solution. Our data show that the active site of binase is flanked by loops that are flexible at the 300-μs time scale. One of the catalytic residues, His-101, is located on such a flexible loop. In contrast, the other catalytic residue, Glu-72, is located on a β-sheet, and is static. The residues Phe-55, part of the guanine base recognition site, and Tyr-102, stabilizing the base, are the most dynamic. Our findings suggest that binase possesses an active site that has a well-defined bottom, but which has sides that are flexible to facilitate substrate access/egress, and to deliver one of the catalytic residues. The motion in these loops does not change on complexation with the inhibitor d(CGAG) and compares well with the maximum k_cat (1,500 s⁻¹) of these ribonucleases. This observation indicates that the NMR-measured loop motions reflect the opening necessary for product release, which is apparently rate limiting for the overall turnover.

It has been inferred from the inspection of static structures that many enzymes sequester substrate or inhibitor from solution and release product by dynamically opening and closing their active site areas (1). Recently, NMR spectroscopy has become an important experimental method to obtain dynamic characterization for individual sites in proteins and nucleic acids (2). Here, we use several complementary NMR techniques—measurement of conformational exchange line broadening, measurement of residual dipolar couplings, and measurement of amide proton exchange—to characterize slower motions in the ribonuclease binase. This protein is a member of a family of homologous guanyl-specific ribonucleases that catalyze the cleavage of single-stranded RNA via a two-step mechanism involving trans-esterification with formation of a 2′,3′ cyclic phosphate intermediate followed by hydrolysis to yield 3′-phosphate. The residues His-101 and Glu-72 are involved in the acid-base catalysis of both of these steps (see Fig. 3 A and B and Refs. 3 and 4). Binase is expressed by Bacillus intermedius and is a 109-aa protein that differs in 17 residues and 1 deletion from the well-studied ribonuclease barnase (4). The substitutions are outside the active center and are mainly on the surface of the protein.

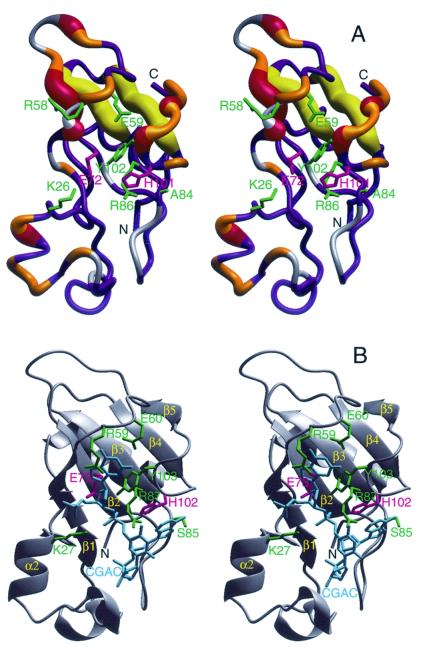
Figure 3.

(A) The crystal structure of binase (18) encoded with the ¹⁵N conformational exchange data obtained at 11.7 T (500 MHz ¹H). The width of the tube representing the backbone indicates the amount of conformational exchange broadening. The color coding is as follows: gray, no data; blue R_ex < 0.5 s⁻¹; orange, 0.5 s⁻¹ < R_ex < 1.5 s⁻¹; red and yellow, R_ex > 1.5 s⁻¹. The yellow coding indicates that the conformational exchange broadening for the β-strands β3 and β4 may be induced by the flexible loops hovering above it (see text). The side-chains of residues inferred to interact with substrate/inhibitor (see Fig. 3b) are indicated in green; the catalytic residues Glu-71 and His-101 in pink. (B) The crystal structure of barnase complexed with dC-G-A-C (PDB accession code 1BRN; ref. 30) in the same orientation. The DNA is in cyan; the active site residues that interact with this inhibitor are in green, the catalytic residues Glu-72 and His-102 are in pink (the barnase count deviates by one from binase for all these residues because of an insertion at the second residue). The figure was prepared with molmol (18).

Methods

Conformational Exchange Broadening: Theory.

The conformational exchange linebroadening R_ex contributes in the fast/intermediate limit to the ¹⁵N transverse relaxation rate R₂ as R₂ = R + R_ex, where R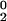 is the natural relaxation rate. In the free precession case, the broadening R_ex caused by conformational exchange at a rate τ 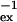between two sites A and B with fractions f_A and f_B, and a radial chemical shift difference Δω is given by (5)

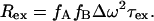1

The exchange contribution R_ex can be suppressed by a Carr-Purcell-Meiboom-Gill (CPMG) spin-echo sequence applied to the ¹⁵N spins. The residual exchange broadening R_ex is in the fast/intermediate exchange limit given by (6)

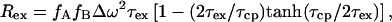2

where τ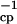 is the repetition rate of the spin echo. In the limit τ_cp ≪ τ_ex, all broadening disappears. A fast method to identify residues affected by exchange broadening is thus to compare the results of a free precession R₂ relaxation experiment for which R_ex is maximal and CPMG experiment with maximum repetition rate for which R_ex is minimal (or a T_1ρ measurement with maximum effective rf field strength). A pulse sequence that approaches the measurement of the free precession relaxation rate contains a single (composite) ¹⁵N π pulse in the center of the in-phase ¹⁵N R₂ relaxation period, and employs WALTZ proton decoupling to suppress ¹⁵N chemical shift anisotropy/¹⁵N–¹H dipole cross correlation, as well as the instantaneous ¹H-¹⁵N scalar coupling evolution. It has been stated that the use of a composite pulse sequence on the protons can interfere with the ¹⁵N spin-echo formation (7), but our results in Fig. 2a indicate that this effect is minimal. CPMG experiments were carried out as described in the literature (8). Our data on binase in Fig. 1 Top indicate that we would not have identified areas 65–70 and 85–100 to be affected by conformational exchange with the CPMG experiment alone. Estimations of the exchange rate parameters were obtained by varying the CPMG repetition rate as described (8, 9).

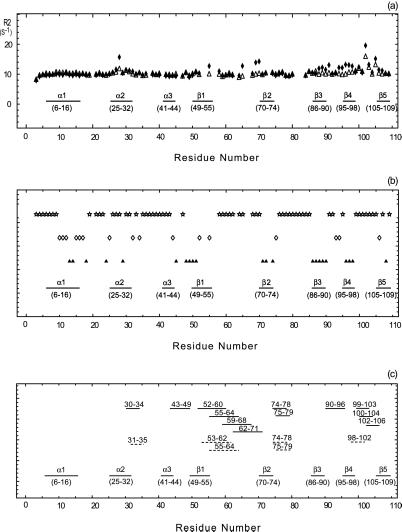
Figure 2.

(a) Conformational exchange in binase. The x axis indicates the amino acid sequence; elements of secondary structure are also indicated. The open triangles and filled diamonds give the ¹⁵N R₂ relaxation rate with and without a CPMG sequence, respectively. Large values of R₂ indicate conformational exchange broadening, caused by molecular motions at the ms-μs time scale. (b) Amide proton/deuterium exchange. A sample of 0.5 mM of ¹⁵N-labeled binase was lyophilized and dissolved in D₂O. ¹⁵N–¹H HSQC spectra were recorded with a repetition rate of 22 min. The open stars, open diamonds, and filled triangles give the fast, intermediate, and slow hydrogen exchange rates, respectively. The fastest exchange rate that could be measured was 22 min⁻¹; the slowest 96 h. Fast exchange indicates exposure/mobility. (c) Saupe tensor parameters, derived from residual ¹⁵N–¹H dipolar coupling parameters in binase, that deviate significantly from the average values, indicating either static or dynamic deviation of the solution conformation from the x-ray structure. Solid lines represent the axial and rhombic components whereas the dashed lines give the Euler angle beta. The numbers above these lines indicate the stretch where the five residues (quintets) are located.

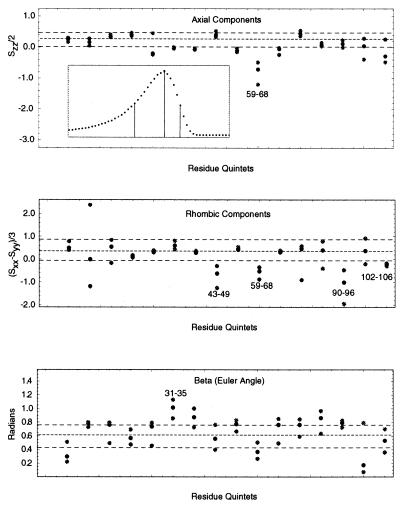
Figure 1.

Examples of Saupe order tensor elements in binase. The filled gray circles represent the flanks of the distribution corresponding to the half maximum height. The filled black circles represent the optimal values corresponding to the maximum heights of the distribution. Three dashed lines denote their average values over the entire protein sequence. These two flanking lines define the confidence limit. The numbers indicate the stretch (quintet) having the tensor values outside the confidence limits. (Top Inset) An example of a non-Gaussian distribution for quintet 102–106. Three vertical lines in the Inset indicate the maximum and its half heights. The x axes indicate the residue quintets used to calculate the tensor whereas the y axes indicate their corresponding values, for the top two panels in units of normalized order parameters (i.e., in units of the global ordering K^NHF).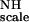

Sample quantum-mechanical calculations were carried out for a model β-sheet of three hydrogen-bonded N-methyl acetamide (NMA) molecules in the presence of the zwitterion Gly-Asp-acetate, using density functional theory with the B3LYP correlation functional (10) and the D95 basis set (11) for both the NMA trimer and Gly-Asp-acetate zwitterion as implemented in the program Gaussian98 (Gaussian, Carnegie, PA). The placement of the sidechain charge of the aspartate at 4, 6, and 8 Å approximately perpendicular above the NH moiety of the central NMA showed changes of 4, 1, and 0 ppm for the ¹⁵N isotropic shift and 0, 0, and 0 ppm for the ¹H isotropic shift of the central NMA, respectively.

Conformational Exchange Broadening: Experimental.

The ¹⁵N R₂ relaxation rates were measured by using a Bruker (Billerica, MA) Avance 500-MHz spectrometer at 30°C. The sample was uniformly ¹⁵N-labeled binase (12.3 kDa), with a concentration of about 1.0 mM (90:10 H₂O:D₂O, pH 6.4). Each two-dimensional data set contained 2048⋅128 complex points, with spectral widths of 8,333 Hz and 1,724 Hz for the ¹H and ¹⁵N dimensions, respectively. The proton decoupling during the relaxation period was achieved by WALTZ-16 for the R₂ measurement. In contrast, a sequence of π pulses was used to decouple the protons in the CPMG method. Pulse repetition rate (τ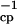) within the CPMG loop in Fig. 2 Top was 4 kHz. Relaxation delays were 5, 20, 35, 60, 85, 100, 110, 120, and 130 ms. The R₂ rates were determined by fitting the cross peak intensities in these two-dimensional spectra, to single exponential decay curves. The data were processed with nmrpipe (12) and analyzed with nmrview (13).

An average value of 300 μs for τ_ex was estimated from CPMG relaxation series with values of 0.4, 0.8, 1.2, and 1.6 ms for τ_cp and fitting the data to Eq. 2. The results are given in Table 1.

Table 1.

Conformational exchange rates for selective residues in binase^*

Residue	Conformational exchange rate, s−1
Gln-28	3.8  × 103 ± 600
Phe-55	2.4  × 103 ± 1,200
Trp-70	2.7  × 103 ± 200
Leu-97	2.7  × 103 ± 700
Tyr-102	4.7  × 103 ± 800
Ala-103	6.1  × 103 ± 1,200

^*The data were obtained by measuring the apparent ¹⁵N R₂ relaxation rate as a function of the CPMG repetition rate. 

d(CGAG) Titration.

A 0.3-mM sample of ¹⁵N,¹H-labeled binase in 20 mM NaPi (pH 6.3) was titrated with a 10 mM solution of d(CGAG) (Sigma Genosys, The Woodlands, TX) in the same buffer at the same pH. The concentrations were determined by NMR, using a 1-mM Ala solution as a standard.

Dipolar Couplings: Theory.

The dipolar interaction between two nuclei ¹⁵N and ¹H can be written as (14)

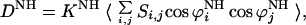3

where i,j = x′, y′, and z′ are three axes of the molecular frame, and 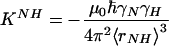is the dipolar interaction constant (22.956 kHz). The 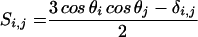(δ_i,j is the Kronecker delta) are elements of the traceless Saupe order matrix (14, 15) specifying the orientation of the molecule in the laboratory frame. The Saupe order matrix is sometimes called alignment tensor. The cosϕ_is are directional cosines defining the orientation of the internuclear vector between the ¹⁵N and ¹H in the molecular frame. The brackets represent the ensemble average. Assuming that the overall rotation of the whole molecule can be decoupled from internal motions of its internuclear vectors, then Eq. 3 can be separated into two independent parts

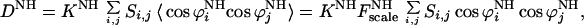4

where the parameter F represents the scaling of the dipolar interaction in weakly aligned proteins compared with the same interaction in solids.

With a known structure one derives from Eq. 4, the following system of linear equations for any group of five or more NH vectors with the same values for K^NH and F:

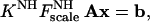5

where the vector b has as its components the five or more experimentally measured dipolar couplings and where the matrix A is constructed from the directional cosines of the corresponding vectors.

First, a global value of 30 Hz was obtained for K^NHF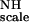 from a fit for all residues to Eq. 5 by using a simulated annealing program (available from the authors). This result gives an average ordering of 1.31 × 10⁻³ for F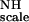. Subsequently, Eq. 5 was solved for individual groups of five vectors (quintets) by using the global value for K^NHF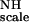, by lower-upper triangular decomposition and substitution (16). The solution vector x has as its components the five normalized independent elements of the normalized Saupe order matrix, which define in the lab frame the orientation of the quintet treated as a single unit. In other words, it specifies the orientation of the segment with respect to the lab frame, if we assume this segment itself is rigid.

The Saupe order tensor was subsequently diagonalized to yield the eigen values, S_zz, S_xx, and S_yy, which are here reported as the axial order (S_zz/2) and rhombic order [(S_xx − S_yy)/3] for compatibility with the literature (17). The eigen vectors give the three directions associated with the tensor. Beta is the Euler angle between the axial axis and the laboratory frame, and the Euler angles alpha and gamma describe the axis of the rhombic component.

Error propagation from input to the final elements of the diagonalized Saupe tensor was obtained as follows. Errors arise from the experimentally measured dipolar couplings and uncertainties in the input structure. We used as input structure an x-ray dataset for binase kindly provided by G. Dodson (University of York), with a resolution of 1.8 Å. Complete tensor determination and diagonalization was carried out for a distribution of input data where the former error range was modeled by adding Gaussian noise with a standard deviation 1.0 Hz to the dipolar couplings, and where the latter was modeled by adding Gaussian noise with a standard deviation of 0.15 Å to the (calculated) position of the amide H atom, resulting in a variable orientation of the NH vector in the molecular frame. We estimated this uncertainty by taking the nominal resolution of the x-ray structure (1.8 Å) and dividing this resolution by 6 to obtain an average coordinate precision. This number was then used to define the opening angle of the cone describing NH vector uncertainty. This measure of coordinate imprecision may be on the large side, but this increases the overall uncertainty of the tensor calculations, and hence the statistical significance of the outliers. In addition, by allowing a Gaussian distribution in the coordinates, the likelihood of collinear vectors is reduced, alleviating the associated problems of underdetermination of the order tensors. Fig. 1 shows some examples of the results obtained from the determination of the values of the diagonalized Saupe order tensor. For each set of five residues investigated, three data points are given: a center one that gives the optimal value as obtained from the center value of the measured dipolar coupling and the atomic coordinates, and the flanking ones indicating those values corresponding to the half-height of a distribution in the tensor value as calculated from a Gaussian distribution in estimated uncertainties of the measured dipolar couplings and atomic coordinates. Note that the calculated distribution in the tensor value and orientation is generally asymmetric and non-Gaussian, as shown in the Inset. The computation of the distribution in the tensor value established confidence limits for the tensor over the entire molecule, indicated by the horizontal lines in Fig. 1. This result in turn allows the identification of those residue quintets that have tensor eigen values and angles that lie outside of the confidence limits. Thus, in Fig. 1 Top, the axial ordering for a quintet of residues contained in the stretch 59–68 lies outside of the average, whereas, for instance, stretch 102–106 (the last points) does not, even though the center of its distribution lies outside the average. Similar identifications are made in Fig. 1 Middle for the amount of rhombic ordering and in Fig. 1 Bottom for the Euler angle beta. The analysis indicated that the distributions for the angles alpha and gamma, describing the orientation of the rhombic component, are too wide to identify outliers.

To scan the whole molecule, the groups of five NH vectors treated as single units were chosen sequentially along the amino acid sequence. The starting point is advanced during different rounds of calculations, resulting in a total of five series of calculations. The computer program developed to automate the scanning and computational procedure, including Monte-Carlo error estimation, as described above is available from the authors.

Our protocol to obtain the local Saupe order tensor from the dipolar couplings is similar to the singular value decomposition (SVD) method developed in the Prestegard laboratory (19). A critical innovation is that we have allowed for independent estimation of uncertainties in the atomic coordinates and in the determination of the dipolar couplings. This approach was necessary to obtain reliable (non-Gaussian) error margins in the Saupe matrix, which allowed the identification of the areas of molecular motion. The procedure can give reasonable criteria for selecting NH vectors for determining the orientation of the whole molecule. By averaging all of the elements of the Saupe matrices from different groups of five residues we obtained the average value for the whole molecule, in agreement with the value obtained for the global solution obtained from the simulated annealing program.

Dipolar Couplings: Experimental.

A lipid sample of a mixture of DMPC (dimyristoylphosphotidylcholine), DHPC (dihexanoylphosphotidylcholine), and CTAB (hexadecyltrimethylammonium bromide) at a ratio of about 30:10:1 was prepared following the published procedures (20, 21). The final aqueous bicelle medium contained about 9% (wt/vol) lipids, about 0.5 mM ¹⁵N uniformly labeled binase, 20 mM sodium phosphate, and 7% D₂O (pH 6.6). All spectra were acquired on a Bruker Avance 500 NMR spectrometer. One two-dimensional ¹H–¹⁵N heteronuclear single quantum correlation (HSQC) spectrum without ¹H decoupling during ¹⁵N evolution was acquired at 26°C where the bicelle medium is isotropic. Another similar HSQC spectrum was acquired at 33°C where the medium is oriented. One HSQC spectrum with the in-phase/anti-phase approach (22) was acquired for resolving the overlapping resonances in the overcrowded regions of the HSQC spectrum. The data were acquired with 2048⋅320 complex points in ¹H and ¹⁵N dimension, respectively. The spectral widths in both dimensions were the same as in the R₂ experiment. The data were processed with nmrpipe (12) and zero-filled to 4096⋅1024 real points. The processed data were analyzed with nmrview (13). For a majority of peaks, the differences in residual dipolar couplings from two independent experiments were less than 0.5 Hz, and no difference larger than 1 Hz was observed.

Results and Discussion

Conformational Exchange.

Fig. 2a shows the results of ¹⁵N T₂ NMR relaxation measurements for binase in solution, in absence of substrate or inhibitor. A CPMG experiment (6) and a sequence with a single ¹⁵N refocusing pulse (T₂) are compared. The differences between these experiments highlight those ¹⁵N nuclei for which the chemical shift is modulated by protein motions at a milli- to microsecond time scale. The data show that especially the loops 99–104 and 56–69 are greatly affected by such processes. Loop 99–104 contains one of the catalytic residues, His-101, whereas area 55–69 contains several residues (Phe-55, Arg-58, and Glu-59) that would be involved in the recognition of the guanosine base of the substrate. Although these findings are significant because these loops are involved in the enzyme's function, as is discussed in detail below, the fact that large external protein loops such as these are subject to dynamical processes may not come as a surprise from a biophysical point of view. It is surprising, however, that the α-helix 25–32 and the β-strands β3 and β4 show exchange line broadening as well.

Hydrogen/deuterium exchange data indicate that the amide protons in the α-helix 25–32 are labile (Fig. 2b), corroborating the mobility of this area. However, the amide protons in the β-strands β3 and β4 do not exchange even after 96 h. This observation indicates that this area is so immobile (or motionally correlated) that no hydrogen bond opening takes place, or that the area is inaccessible to the solvent. One of these possibilities is in apparent disagreement with the ¹⁵N R₂ data in Fig. 2a.

Local Structure Investigated with Residual Dipolar Couplings.

We further characterized the local disorder of binase by measuring residual ¹⁵N–¹H dipolar couplings. Residual dipolar couplings can be obtained for proteins or nucleic acids in solution if they are slightly oriented by their intrinsic anisotropic magnetic susceptibilities or by dissolution in dilute liquid crystalline media (17, 20, 23, 24). These methods have been mostly used to refine NMR solution structures (25), but recent studies also indicate their utility for the study of conformational exchange (26) and domain orientations and motions (27, 28). Here, we use amide nitrogen–hydrogen dipolar couplings to compare the local structure of binase dissolved in bicellar solution with that of binase as solved by x-ray crystallography (18). As detailed in the theory section, any five (quintet) dipolar couplings can be used to define the relative orientation of the molecular fragment containing these five groups with respect to the liquid crystal medium, provided that the three-dimensional structure for that fragment is known. The orientation of such a fragment is given by the three eigenvectors of the so-called Saupe order tensor (15) for that fragment computed from the input data. The motional restriction of that fragment (“amount” of orientation in the liquid crystal) is given by the two independent eigen values corresponding to the “axial” and “rhombic” component of the orientation. When the crystal structure and solution structure of the protein are identical and static, the computed tensor should be the same no matter which group of five couplings is chosen for analysis. All tensors should reflect the orientation and motional restriction of the entire protein in the liquid crystal matrix. If, in contrast, the local structures do differ in either static or dynamic ways, the results of the calculation will depend on which five residues are picked. Areas where such differences occur will show deviations of the Saupe tensor from the average (so-called “outliers”). Thus, one can use the Saupe-order matrix calculation to systematically “scan” the solution structure for compatibility with the crystal structure. More details are given in Methods.

Fig. 2c shows a compilation for the outliers of the Saupe tensor for binase. It is surprising that so many quintets can be identified as outliers, especially considering the very conservative analysis of the error ranges (see Methods). Several physical phenomena can give rise to the statistically significant outliers. First, there can be differences in the local structures of binase in solution and the coordinates of binase in the crystal. Such differences, if any, are expected to occur in surface loops of the protein. Here, one could distinguish between the case where the loop structure differences can be described by rigid body rotations such as hinge-like motions, and the case where the differences are within the loop structures themselves. In the former case, one may expect that the Saupe order tensor eigen values for these areas are not changed from the average, but that the orientation of the tensor is affected. In the latter case, both tensor eigen values and orientations should deviate from the average. A second cause that can give rise to the outliers is the presence of motion in the protein in solution. If the motion is hinge-like around the average (crystal) structure, one expects mainly change in the tensor eigen values but not much change in tensor orientation; if the motion is chaotic, both tensor and orientation should be affected.

Overall, the Saupe order tensor deviations in Fig. 2c correspond well with areas involved in milli/micro second conformational exchange (Fig. 2a). Very clear is the correspondence for the area 90–106, underscoring the conclusions derived above that this area is dynamic. The correspondence for area 52–71 identifies that the Saupe matrix deviations in this area are also caused by slower dynamical effects. Slow motions do not appear to contribute to the tensor deviations for the area 74–80. The fact that the conformational exchange broadening in the center of helix 25–32 is not observed as a deviation of the Saupe tensor indicates that the extent of the structural perturbation at that location is modest.

Induced Exchange Broadening?

Significantly, only one Saupe deviation is observed for the area spanned by β-strands β3 and β4, and this may reflect deviations in the intervening loop. In addition, the mass amide proton exchange is slow in this area. We conclude that the strands β3 and β4 are immobile at the time scales probed by the dipolar and deuterium exchange methods. For amide proton exchange, that is at the scale of seconds to days. Dipolar couplings would be affected by all motions faster than a typical residual dipolar coupling, e.g., faster than 5 s⁻¹. This conclusion is underscored by large ¹⁵N relaxation order parameters for strand β3, which appears thus well ordered (results not shown). The ¹⁵N relaxation order parameters data for strand β4 are more ambiguous; residue 97 has a significantly lower order parameter, indicating that high frequency motions are present, but which are apparently of insufficient magnitude to allow amide proton exchange or an average disturbance of structure as measured by the dipolar couplings (results not shown).

One must consider the possibility that the ¹⁵N NMR linebroadening is not caused by slow motions in the area itself, but by shift modulation because of motions of nearby residues. Although this is a general caveat in the interpretation of chemical exchange broadening, one must be especially careful in this case, because the dynamic loops 55–65 and 102–105 hover directly above the sheet (see Fig. 3A). For example, chemical shift modulation could be induced by changing ringcurrent shifts because of aromatic residues or by changing electrostatic fields (29) because of charged residues in these dynamic loops. Changing ringcurrent effects cannot be the cause of the ¹⁵N line broadening here, because the amide protons would become unobservable, but model quantum mechanical calculations indicate that there is a significant effect of a single electric charge within 6 Å on the chemical shifts of amide nitrogens, with a negligible effect on amide protons (see Methods). The ¹⁵N exchange broadening in strands β3 and β4 could thus be induced by the charged residues Arg-58, Glu-59, Arg-61, Arg-68, Asp-100, or His-101 on the dynamic loops 56–69 and 99–104.

Biological Significance.

Having analyzed the conformational exchange dynamics of binase in this way, we can discuss the biological implications of our findings. Fig. 3A shows the areas of binase affected by conformational exchange dynamics. Fig. 3B shows the crystal structure of barnase, complexed with the inhibitory tetranucleotide d(CGAC) (30). Comparison of the figures shows that the majority of conformational exchange dynamics in unligated binase occurs in the area that is involved in inhibitor binding in barnase. In particular, major broadening is observed for Phe-55, whose sidechain is in direct stacking interaction with the guanosine base in the barnase complex. Tyr-102 and His-101, the latter being one of the two catalytic residues, are located on the loop that folds over the scissile bond and are also showing much exchange broadening. At the other side of the bound nucleotide, one finds broadening for alpha helix α2, which contains Lys-26 that in the complex contributes to phosphate charge compensation.

In contrast, the “bottom” of the active site area, which contains the other catalytic residue, Glu-72 on β-strand β2, is dynamically silent, as one would expect for a well-formed β-sheet. Given the arguments above, the apparent slow motion of the β3 and β4 strands of the sheet may be caused by an induced effect, and they are likely also dynamically silent at the micro-/millisecond time scale.

By varying the repetition rate in the CPMG sequence, one obtains the rate of conformational exchange for these residues (8, 9). One expects the largest change in apparent broadening when the exchange and interpulse rates match. Fortunately, the exchange rates for the dynamic loops in binase occur at a time scale that lies within the technical range of the CPMG experiments: we observed large changes in apparent broadening when changing the interpulse delays from 0.4 to 1.6 ms. On quantitative analysis, we obtained an approximate rate constant of 3,000 ± 1,000 s⁻¹ for the conformational exchange dynamics in the three active site loops, with no significant difference between them (see Table 1). We interpret these dynamical processes as an interchange between open and closed conformations of the enzyme. This common rate constant compares favorably with the maximum turn-over rate for hydrolysis (k_cat) of any oligonucleotide by either barnase or binase (1,500 s⁻¹, see Ref. 31). Our data thus suggest that the opening of the enzyme may be rate limiting for product release and thus constitute the upper limit of the efficiency of these enzymes.

Intrigued by this idea, we carried out an R₂ and a single CPMG experiment with binase, in the presence of a 5:1 molar ratio of the inhibitor d(GCAG) over protein. This inhibitor was chosen following the example of the x-ray structural studies of barnase with this molecule by Fersht and coworkers (30). Many large chemical shift changes in the fast exchange regime for ≈50% of the signals were observed in the binase ¹⁵N–¹H HSQC spectrum on titration of the inhibitor, indicating that binding is taking place. We obtain a K_D between 50 and 100 μM from our titration data. This affinity compares favorably with the K_M of binase for oligoribonucleotides (between 100 and 400 μM for different substrates; ref. 31), suggesting that a functionally relevant binding is being monitored. The extent of the shift changes suggests that major structural rearrangements occur in the protein. Nevertheless, the dynamical behavior of the protein when fully saturated with the inhibitor is similar to the uncomplexed form; pronounced conformational exchange (excess) broadening occurs in the R₂ data for residues 28, 55, 70, 88, and 101 with values of 6, 20, 30, 6, and 11 s⁻¹, respectively. These locations are identical to the sites in the free protein (Fig. 2a). Although we have not yet carried out a detailed exchange rate determination, we note that the bulk of the broadening is suppressed in a CPMG sequence with a 0.5-ms repetition rate, suggesting similar kinetics as for the uncomplexed protein. The finding that the kinetics of loop rearrangement does not change (much) on binding of the ligand is fully consistent with the above hypothesis that the dynamics characterized for the uncomplexed state is the rate limiting step in product release from the bound state.

There are several other examples of enzyme structures in the protein database that contain active site areas that are guarded by surface loops. It is hypothesized that the functional reason for covering the active site is to generate a tight induced fit between substrate and enzyme, and possibly to expel solvent and hence increase the electrostatic interaction energies necessary for the catalytic process. An early example is the protein pepsin, which has a site-covering “flap” (32). More recent examples are numerous, e.g., flaps in HIV protease (33) and in the metallo-lactamase from Bacteroides fragilis (34). The fact that one of the catalytic residues, His-101 for binase, is located on a mobile loop is also not unprecedented: the tyrosine phosphatases of the P1B class, for instance, have a similar feature (35).

That slow dynamical processes are of importance to function has been recognized also for other systems: conformational exchange broadening was observed in the active site area of the enzyme oxalocrotonate tautomerase, both in the presence and absence of substrate analog. Although the time scale of these motions was not determined, it was suggested that they might be of importance to catalysis (36). Others investigated an intestinal fatty-acid binding protein and found that the binding cavity undergoes slow motions, likely necessary to accommodate the ligand (37). Slow motions in the substrate-binding site of adenylate kinase were suggested to originate from hydrogen-bond bifurcation dynamics (38). Biologically relevant slow dynamics were observed for the protein–protein recognition interface of the SpoOf response regulator protein factor (39), and in the signaling protein NtrC (40). A case that is very close to what we investigate here is that of slow movements in the flap area covering the catalytic site of HIV protease (33).

Conclusions

Although it has been suggested from inspection of the static structures that dynamical opening and closing processes need to take place to allow substrate access and product release, we present here one of the few cases where such processes are investigated in detail with several methods, and are quantitated. The following millisecond dynamic model presents itself for the active site area of the ribonuclease binase. The bottom of the site consists of a rigid β-sheet that contains one of the catalytic residues, Glu-72. This area is covered by two dynamic surface loops (56–69 and 99–104) that contain residues that would interact directly with substrate. The latter loop contains the second catalytic residue, His-101. A third contact with the substrate would be made by residue Lys-26, which is located on a dynamic helix. The loops move with a 3,000 s⁻¹ rate, which compares favorably with the maximum turn-over rate for hydrolysis (k_cat) of any oligonucleotide by either barnase or binase (1,500 s⁻¹). Because the rate does not change on complexation with an inhibitor, this indicates that the NMR-measured loop motions reflect the opening necessary for product release, which is apparently rate limiting for the overall turnover. Our observations directly underscore the importance of dynamical processes in biological function.

Abbreviations

CPMG

Carr-Purcell-Meiboom-Gill

NMA

N-methyl acetamide

HSQC

heteronuclear single quantum correlation