Testing the Calibration of Classification Models from First Principles

Abstract

The accurate assessment of the calibration of classification models is severely limited by the fact that there is no easily available gold standard against which to compare a model’s outputs. The usual procedures group expected and observed probabilities, and then perform a χ² goodness-of-fit test. We propose an entirely new approach to calibration testing that can be derived directly from the first principles of statistical hypothesis testing. The null hypothesis is that the model outputs are correct, i.e., that they are good estimates of the true unknown class membership probabilities. Our test calculates a p-value by checking how (im)probable the observed class labels are under the null hypothesis. We demonstrate by experiments that our proposed test performs comparable to, and sometimes even better than, the Hosmer-Lemeshow goodness-of-fit test, the de facto standard in calibration assessment.

Introduction

A large number of predictive modeling questions in biomedicine can be phrased as dichotomous classification problems. Examples of such questions are whether a particular combination of genetic markers is indicative of cancer, whether certain patterns in MRI images point to neurological anomalies, or whether patients with specific case histories are more likely than others to suffer from cardiovascular diseases. In each of these scenarios, a combination of findings is used to infer the probability that a patient belongs to one of two classes (say, the healthy and the diseased patients).

More formally, a classification model calculates the probability P (disease | x) of disease, given a vector x that summarizes the relevant patient information. The model construction process, mostly done with statistical or machine learning methods, requires a data set of patient information along with the correct class labels. The quality of a classification model is assessed by its ability to distinguish between the two classes (its discriminatory ability, usually measured by AUC, the area under the ROC curve), and by how well the predicted probability P (disease | x) matches the true probability of disease for this patient (its calibration, usually checked by applying a goodness-of-fit test).

Assessing the calibration of a model is not as straightforward as assessing its discrimination, because a patient’s true probability of disease is not readily available. Mostly, the term “true probability of disease” is interpreted as a relative frequency: If 55 out of 100 patients just like me will develop the disease, then my true probability of disease is 55%. This seemingly simple interpretation masks the problem that this information is hardly ever available in medical data sets: After all, when do we have 100 patients just like me? How do we even interpret the term “just like me”?

In light of these difficulties, the most widely-used way of assessing a model’s calibration is by the Hosmer-Lemeshow C-test,¹ which sidesteps the problems outlined above by grouping patients not by their similarity, but by similar model outputs (as probability estimates, all numbers between 0 and 1). Their method sorts the model outputs and then forms g equally-sized groups, with g =10 the most popular choice. The probabilities and true disease states in these groups are then checked by a χ² goodness-of-fit test, for which they empirically, using logistic regression models, observed the best fit at g − 2 degrees of freedom. As with any χ² goodness-of-fit test, the quality depends on a number of assumptions, most relevant of which are the large cell counts without which the test statistic does not follow a χ² distribution. There are several alternatives to the Hosmer-Lemeshow test which also do not rely on the assumption of large cell counts. A review of these measures can be found in the literature.^{2, 3}

We propose an entirely new way of assessing a model’s calibration that is based on the first principles of statistical hypothesis testing, and that does not rely on assumptions that may or may not be satisfied in practice. We consider only two entities—the model outputs and the correct class labels, without groupings or other aggregations—to test the null hypothesis that the model is correct.

Calibration testing from first principles

For our calibration assessment problem, we are given a trained model and a data set of n patient measurements along with the n-element vector of true class labels of these patients. The data set is used as test set to check the model’s calibration. Feeding the data set into the model, we obtain an vector p = (p₁,...,p_n) of probability outputs, one for each patient.

Our null hypothesis is that the model is correct, i.e., that the unknown true probabilities (π₁,...,π_n) are the probabilities (p₁,...,p_n) we obtained:

$$H_0=({\pi }_1=p_1\wedge \dots \wedge {\pi }_n=p_n).$$

We can then calculate the probability of any class label vector (c₁,...,c_n) under the null hypothesis via

$$P((c_1,\dots ,c_n)|(p_1,\dots ,p_n))=\prod _{i=1}^{n}P(c_i|p_i)$$

by noting that every label c_i can be seen as the realization of an independent Bernoulli random variable with parameter p_i, so that

$$P(c_i|p_i)=\{\begin{array}{ll}{p}_i\hfill & \text{if}\hspace{0.17em}{c}_i=1\hfill \\ (1-p_i)\hfill & \text{if}\hspace{0.17em}{c}_i=0.\hfill \end{array}$$

Thus, for example, with p = (0.2, 0.7, 0.3, 0.2, 0.8) and c = (1, 1, 0, 1, 1) we get

$$P((1,1,0,1,0)|(0.2,0.7,0.3,0.2,0.8))=0.2\times 0.7\times (1-0.3)\times 0.2\times (1-0.8)=\mathrm{0.00392.}$$

Note that under the null hypothesis that p =(0.2, 0.7, 0.3, 0.2, 0.8) is the correct model, the most likely vector of class labels is (0, 1, 0, 0, 1) with probability 0.8 × 0.7 × 0.7 × 0.8 × 0.8 = 0.251.

In hypothesis testing, we are not concerned only with the probability of the observed data, but with the probability of data that is at least as far from the most likely data as the observed data. We therefore need a notion of distance on binary class label vectors. The most widely used distance between two binary vectors v and w is their Hamming distance, defined as

$$H(v,w)=\left|\left\{i\right|v_i\ne w_i\}\right|,$$

i.e., the number of places at which the two vectors differ. The two example vectors above, (1, 1, 0, 1, 1) and (0, 1, 0, 0, 1), thus have Hamming distance 2.

The steps in our proposed new calibration test are then as follows:

1. State null hypothesis: (p₁,...,p_n) is the correct model.

2. Set a significance level α.

3. Calculate the most likely vector of class labels c^* as

   $$c_i^{*}=\{\begin{array}{ll}0\hfill & \text{if}\hspace{0.17em}{p}_i<0.5\hfill \\ 1\hfill & \text{if}\hspace{0.17em}{p}_i\ge \mathrm{0.5.}\hfill \end{array}$$

4. Calculate the Hamming distance d between c^* and the given vector c of class labels.

5. Calculate the probability of all the class label vectors with distance at least d from c^*.

6. If this probability is less than α, then reject the null hypothesis, otherwise do not reject.

All the steps above are straightforward, with the exception of step 5, which requires the calculation of a large number of probabilities — there are, after all, 2ⁿ different vectors of class labels.

Fortunately, the calculation of the probabilities at Hamming distances 0, 1, 2,...,n from c^* can be performed in O(n²) steps, which makes the computations feasible even for large n. The idea for this simplification utilizes the observation that the probability of two vectors of length k having Hamming distance exactly r can be written as

$$\begin{array}{l}(\text{the}\hspace{0.17em}\text{probability}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{first}\hspace{0.17em}k-1\hspace{0.17em}\text{components}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{vectors}\hspace{0.17em}\text{having}\hspace{0.17em}\text{distance}\hspace{0.17em}r-1)\times (\text{the}\hspace{0.17em}\text{probability}\hspace{0.17em}\text{that}\hspace{0.17em}\text{they}\hspace{0.17em}\mathit{do}\hspace{0.17em}\text{differ}\hspace{0.17em}\text{in}\hspace{0.17em}\text{position}\hspace{0.17em}k)\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\\ (\text{the}\hspace{0.17em}\text{probability}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{first}\hspace{0.17em}k-1\hspace{0.17em}\text{components}\hspace{0.17em}\text{of}\hspace{0.17em}\text{the}\hspace{0.17em}\text{vectors}\hspace{0.17em}\text{having}\hspace{0.17em}\text{distance}\hspace{0.17em}r)\times (\text{the}\hspace{0.17em}\text{probability}\hspace{0.17em}\text{that}\hspace{0.17em}\text{they}\hspace{0.17em}\mathit{do}\hspace{0.17em}\mathit{not}\hspace{0.17em}\text{differ}\hspace{0.17em}\text{in}\hspace{0.17em}\text{position}\hspace{0.17em}k)\end{array}$$

To implement this idea, we first need the probability f_i that a Bernoulli random variable with parameter p_i differs from $c_i^{*}$:

$$f_i=\{\begin{array}{ll}(1-p_i)\hfill & \text{if}\hspace{0.17em}{p}_i\ge 0.5,\text{thus}\hspace{0.17em}{c}_i^{*}=1\hfill \\ p_i\hfill & \text{if}\hspace{0.17em}{p}_i<0.5,\text{thus}\hspace{0.17em}{c}_i^{*}=0.\hfill \end{array}$$

We use the symbol a_r,k to denote the probability that the Hamming distance between the first k components of a Bernoulli binary vector with probabilities (p₁,...,p_n) and the first k components of c^* is exactly r. The values of a_r,k can be calculated recursively as follows:

1. Initialize a to an (n +1) × (n +1) matrix of all zeros.

2. Set a_0,0 = 1 and a_0,k = a_0,k−1 × (1 − f_k)    (for k = 1,...,n)

3. Set a_r,k = a_r−1,k−1 × f_k + a_r,k−1 × (1 − f_k)    (for 1 ≤ r ≤ k)

4. The values a_r,n (for r = 0,...,n) form the probability distribution of binary vectors with Hamming distances 0,1,...,n from c^*.

Note that the recursive formula in step 3 is precisely the implementation of the recursive idea given above.

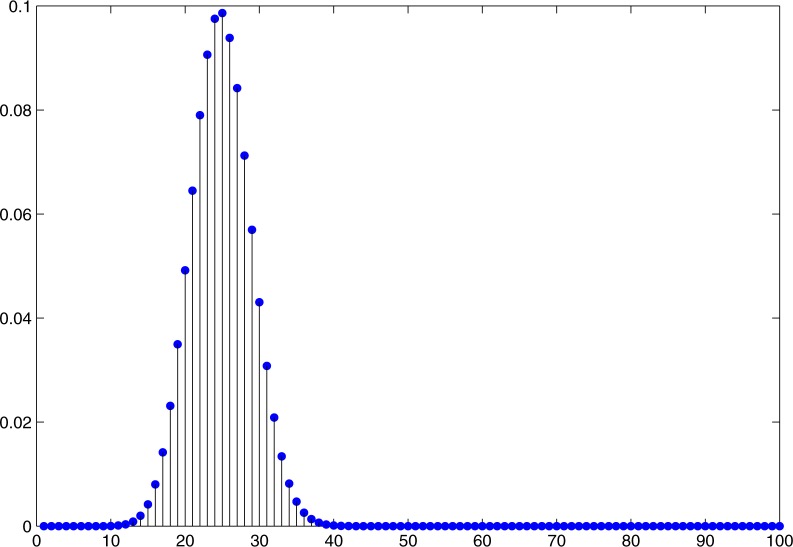
As an example, consider an arbitrary 100-dimensional vector p of Bernoulli probabilities. The probability distribution of the Hamming distances of all possible realizations of 100-dimensional Bernoulli random variables from c^* is shown in Figure 1. The rejection region for this particular distribution starts at 32: If the vector of class labels c has distance 32 or more from c^*, then the probability of obtaining a vector as far from c^* as c (if the null hypothesis is correct) is less than 5%. In these cases, we would thus reject the null hypothesis that the model is correct.

Figure 1.

Probability distribution of Hamming distances of realizations of independent Bernoulli random variables with parameters (p₁,...,p_n) from the most likely realization c^*.

Experiments

We compared our new proposed calibration test with the de facto standard in calibration testing, the Hosmer-Lemeshow goodness-of-fit test, on a series of artificial data sets as well as on a real-world data set on predicting myocardial infarction. For the Hosmer-Lemeshow test,¹ we used our own implementation in Matlab, with groupings of size 10 and thus 8 degrees of freedom.

Artificial data sets

We took samples of size n = 1000 from the standard multivariate normal distribution (μ = 0, Σ the identity matrix) in various dimensions. We then defined the correct model to be a logistic regression model with given β parameter vector (as unit vector) and slope factor s. Specifying a slope parameter allowed us to adjust the overlap in the two classes. The logistic regression model yielded a probability estimate for each data point; we took these as Bernoulli probabilities to generate the class labels at each data point. A larger slope parameter resulted in more “extreme” probabilities (closer to 0 and 1), and thus less overlap between the two classes.

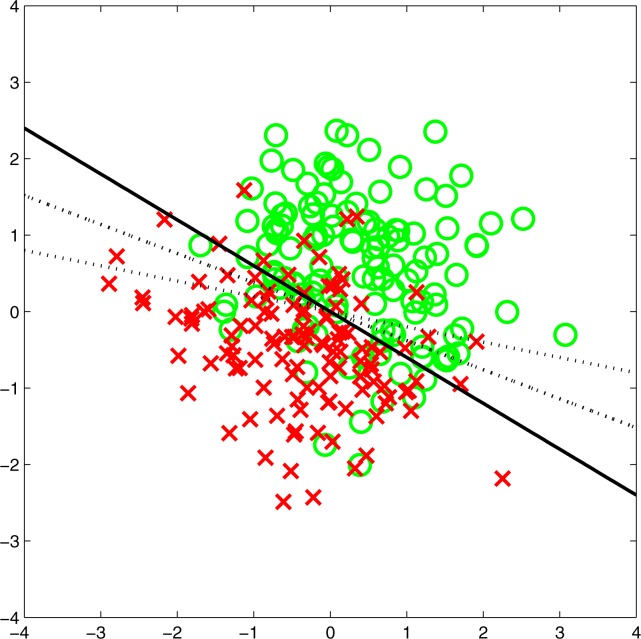
To investigate the performance of calibration tests, we then gradually worsened the model by changing the β and s parameters. For the β vector, we randomly generated candidate vectors until we found some that formed angles of about 10°, 20°, and 30° with the correct β vector. For the s parameter, we increased it in small percentage steps of the original value. A two-dimensional sample is shown in Figure 2.

Figure 2.

Synthetic data set in two dimensions. The two classes are labeled by crosses and circles, respectively. The solid line is the true separation line (with β = (0.51, 0.86)), and the dotted lines are the incorrect models with angles 10° and 20° from β. The slope parameter s = 2 resulted in an AUC of 0.86. For better visibility, only 250 data points are shown.

We performed two kinds of experiments on the artificial data set, where the correct model is known: First, we tested how often the calibration tests incorrectly rejected a correct model (type I error). Second, we tested how often the calibration tests failed to rejected incorrect models (type II error). These tests were run for dimensions 5, 10 and 20, with the incorrect models as specified above. We generated 1000 models for each parameter combination and used a χ² test to check whether the Hosmer-Lemeshow or our new test performed significantly better (that is, exhibited significantly lower type I or type II errors).

The results of these experiments for correct models are shown in Table 1. The slope parameter s was set to 2 to obtain average AUC values of about 0.85, because this reflects the common situation of good (but not great) discriminatory power. One can observe that our new calibration test has a type I error rate of 5% across all three chosen dimensions, which is only about half the error rate of the Hosmer-Lemeshow tests.

Table 1.

Performance comparison of Hosmer-Lemeshow (HL) and our new calibration test from first principles (FP). The null hypothesis that the model is correct is true. AUC denotes area under the ROC curve of the correct model. The p-value is for the comparison of HL vs. FP type I errors (^* denotes the test with significantly lower type I error at α level 0.05).

	data dimension
	5	10	20
average AUC	0.862	0.862	0.861
HL type I error	11.8%	12.1%	13.1%
FP type I error	5%*	5%*	5.2%*
p-value	< 0.001	< 0.001	< 0.001

The results of the various ways of specifying incorrect models are shown in Table 2. The left portion displays the results of gradually changing the parameter vector β of the logistic regression model. As before, the slope parameter was set to s = 2. It can be seen that out of the nine comparisons, the Hosmer-Lemeshow test is significantly better once, our new test is significantly better three times, and there is no significant difference in the remaining five comparisons.

Table 2.

Performance comparison of Hosmer-Lemeshow (HL) and our new calibration test from first principles (FP). The null hypothesis that the model is correct is false; the degree of incorrectness is given by the angles between the correct and incorrect β vectors (left portion) and the slope (right portion) of the logistic regression models. AUC denotes area under the ROC curve of the incorrect model. The p-value is for the comparison of HL vs. FP type II errors (^* denotes the test with significantly lower type II error at α level 0.05).

	angle incorrect model			increase in slope
	10°	20°	30°	10%	20%	30%
dim = 5:
average AUC	0.855	0.837	0.808	0.862	0.862	0.862
HL type II error	83.2%*	48.1%	2.8%	67.8%	28.4%	4.9%
FP type II error	87.5%	41.7%*	2.4%	69.0%	27.4%	5.2%
p-value	0.0065	0.004	0.574	0.5638	0.6181	0.7593
dim = 10:
AUC	0.856	0.836	0.807	0.862	0.862	0.862
HL type II error	87.5%	44.7%	2.2%	67.1	26.8	4.9
FP type II error	87.7%	39.2%*	1.7%	68.1	26.2	5.4
p-value	0.892	0.0127	0.4188	0.6328	0.7611	0.613
dim = 20:
AUC	0.855	0.835	0.805	0.861	0.861	0.861
HL type II error	84.8%	44.4%	1.8%	68.0%	25.8%	5.1%
FP type II error	86.6%	38.4%*	1.9%	67.2%	27.5%	6.6%
p-value	0.2503	0.0065	0.868	0.7023	0.3899	0.1530

The right portion of Table 2 shows the results of changing the slope parameter s. This parameter was again set to 2 for the correct model, and changed to 2.2, 2.4 and 2.6 for the incorrect models. As expected, this did not change the AUC, but only the calibration of the models. The experiments show that there is virtually no difference between the two methods, regardless of the dimensionality of the classification problem.

Myocardial infarction data set

This data set from the emergency department of the Edinburgh Royal Infirmary in Scotland consists of measurements from 1253 patients who presented with symptoms of acute myocardial infarction (AMI). 274 patients were diagnosed with AMI, which was ruled out in the remaining 979 patients. Of the 39 measurements taken, we discarded the 6 ECG measurements which would have made the diagnostic task too easy (as the gold standard diagnosis depends in part on these measurements). More details on this data set can be found in the original publication by Kennedy et al.⁴

We used ten-fold cross-validation for performance evaluation, with regularized logistic regression as classification models. The discriminatory power of the models was 0.858, similar to the AUC of the models of the artificial data sets. The Hosmer-Lemeshow goodness-of-fit test produced a test statistic of 15.74 (with a p-value of 0.046), and our new calibration test found that the class labels were at a distance of 216 (out of a maximum of 1253) from the most probable labeling c^*. This corresponded to a p-value of 0.0075. The use of our new test thus further confirmed the lack of model fit that was not as evident solely from the Hosmer-Lemeshow test.

Discussion

The Hosmer-Lemeshow test has become the standard test for assessing the goodness-of-fit of logistic regression models. As several authors have however pointed out, it is not without deficiencies. Bertolini et al. noted that calibration measures based on groupings of data are volatile in the sense that small changes in the assignment of cases to groups can have large effects on p-values, and thus on the calibration assessment of a model.⁵ Pigeon and Heyse observed that the test statistic might not follow a χ² distribution when the probabilities of the groups with lowest and highest predicted probabilities are very close to 0 or 1.⁶ This, unfortunately, is often the case for classification models, where the probabilities of easy-to-classify cases are indeed close to 0 or 1. Pigeon and Heyse subsequently developed a method to compensate for this.⁷

Our proposed new test approaches the problem of calibration assessment from an entirely different direction, and thus does not suffer from the drawbacks of the Hosmer-Lemeshow test outlined above. It allows us to answer the question of agreement or disagreement between model outputs (probabilities) and gold standard (class labels) by reducing it to a standard statistical hypothesis test. We calculate how likely or unlikely the class labels vector is, under the assumption that the model probabilities are indeed the correct probabilities. As such, the proposed test does not require any conditions or modeling assumptions to hold. In particular, it is not limited to assessing logistic regression models, but rather amenable to any probabilistic model that provides class-membership probabilities. Further empirical investigations will be required to determine whether the proposed test works better with some probabilistic models than with others.

We propose our new approach as a direct alternative, or compendium, to the Hosmer-Lemeshow test. Thus, we envision the test as a tool for model validation, to identify situations where the model does not represent the case distribution in the data sample sufficiently well (evidenced by the fact that the null hypothesis is rejected). In this case, it may even be possible to identify regions of poor model fit by analyzing subsets of the data.

Limitations

This is the first study using our proposed measure, and therefore necessarily limited in the scope of the experiments being conducted. The artificial data set used here provides only one particular way of specifying incorrect models; our proposed new test performed worse than the Hosmer-Lemeshow test when incorrectly using linear models where quadratic decision boundaries are appropriate (data not shown). At this preliminary stage of investigation, it is not yet clear under which conditions which of the two tests performs better.

Furthermore, given that it is only possible to calculate models that are guaranteed to be correct when the data generator is known, experiments using real-world data sets can only provide hints as to the applicability and validity of calibration methods.

Software

Implementations of the test for R, Matlab and Mathematica are available from the author’s website at http://staff.fh-hagenberg.at/sdreisei/CalibrationTesting.