Abstract
Association rule mining offers an automated approach for discovering new knowledge about diseases. A known challenge is how to constrain the search space to prevent an exponential explosion of rules while minimizing information loss. In this study, generalized association rule mining techniques were used to identify disease cooccurrences based on ICD-9-CM codes in a statewide hospital discharge data set. The Clinical Classifications Software (CCS) categorization scheme and the numerical hierarchy of ICD-9-CM were used to generalize the codes and produce generalized associations for comparison with associations generated from the raw data. By maintaining links between the raw and generalized data, associations lost in the generalization process, overlapping associations, and new associations were identified. In addition, preliminary results indicate that the concept hierarchy used for generalization may influence the associations found.
Introduction
Association rule mining has been well researched as a data mining method for discovering new and interesting knowledge and confirming existing knowledge about variables in large databases1. The question of how to appropriately constrain the search space to prevent an exponential explosion of rules continues to be an open research question. Constraining the search and rule space to reduce the number of association rules and using efficient unsupervised knowledge discovery methods to identify rules with high predictive accuracy and relevance within a domain (e.g., healthcare) becomes even more important as the amount of data increases2. Applying association rule mining to public health data sets, as was done in this study, has the potential to confirm existing knowledge regarding disease co-occurrences as well as to discover new disease relationships that could potentially lead to improved clinical care and health.
One technique to reduce the search space for association rule mining is to abstract the transaction data to a higher level, using domain knowledge of the relationships within the data. However, mining at the higher level of abstraction could result in information loss. If a concept hierarchy can be constructed using domain knowledge, then the patterns based on primitive data in the transactions can be abstracted to a higher concept level to create potentially more meaningful rules3. Using objective measures to set thresholds for constraining the search space has been used as a technique in association rule mining in the clinical domain4–7. The theoretical concept of using generalized data to create “actionable rules” from a concept hierarchy has been shown8. One area that has not been extensively studied is how different concept hierarchies influence the association rules discovered.
The objective of this study was to explore association rule mining techniques for generalizing diagnoses from a public health data set to identify disease co-occurrences, while maintaining links from the generalized data to the original raw data. The Clinical Classifications Software (CCS) categorization scheme and the numerical hierarchy inherent in the International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) were applied to generalize the data. Results indicate that generalizing the data may facilitate the identification of new associations as well as associations that could be flagged for potential removal, thus constraining the rule space. In addition, maintaining links from the generalized data to the original raw data appears to help minimize information loss. A preliminary comparison of the two concept hierarchies also indicates that use of different hierarchies can influence the disease co-occurrences found.
Background
Generalized Association Rule Mining
Association rule mining is a very popular data mining technique9 that tries to find interesting patterns in large databases10. Although developed in the context of market basket analysis11, it is easily applied to other domains. Defining appropriate search constraints to reduce the number of associations so that the associations found have a high predictive accuracy and are relevant within a domain2 is an important area of research. The Apriori algorithm was one of the earliest association rule mining algorithms. It exploits the downward closure property, which states that if an itemset is infrequent, all of its supersets must be infrequent. This can be used to eliminate itemsets from consideration, but presents a limitation when trying to mine for infrequent items. Each itemset has an associated statistical measure called support, denoted as supp. For an itemset X⊂I, supp(X) = s, if the fraction of transactions in the dataset D containing X equals s1. Setting a low support threshold to find infrequent items may cause a combinatorial explosion of itemsets. This dilemma is called the rare item problem12. The classic framework for association rule mining uses support and confidence as thresholds for constraining the search space. The confidence or accuracy of an association rule X=>Y in D is the conditional probability of having Y contained in a transaction, given that X is contained in that transaction: confidence(X=>Y) := P (Y | X)= supp(X∪Y)/supp(X)13.
Mining association rules at a higher level of abstraction is known as generalized association rule mining. A generalized association rule is an implication of the form X=>Y, where X⊂Z, Y⊂Z, X∪Y = ϕ, and no item in Y is an ancestor of any item in X14. If the thresholds for support and confidence are set low, too many rules are generated. Generalized association rule mining aims to help reduce the search space by making use of a concept hierarchy and assumes that such a hierarchy exists15–17. Abstracting rules to a higher level could lead to information loss if rules at all levels of the hierarchy are not generated and preserved18–21. As described in the original paper by Srikant14, mining at the leaf level of the hierarchy can generate many uninteresting rules, which motivated the introduction of the concept hierarchy into the mining process. The definition of interesting becomes an issue when using an objective measure to define a subjective threshold. The introduction of multilevel association rule mining in 1999 by Han22 helped this problem by applying different support thresholds set at different levels of abstraction. The problem still remains of having to select a threshold prior to the data mining process and possibly missing rare but interesting associations.
Mining Disease-Specific Associations
Interesting and previously unknown associations in the clinical domain have been found through the use of association rule mining in medical literature17, 23, showing the potential for knowledge discovery. Association rule mining has been used to find disease-disease, disease-finding, and disease-drug co-occurrences in electronic health record data24, 25, demonstrating the importance of finding disease co-occurrences. Association rule mining using objective measures and transitive inference for pruning has also been done in the clinical domain to find associations between medications and clinical problems using electronic health record data26, highlighting some of the challenges in identifying valid associations. The chi-square statistic has been used to find the measure of strength in associations between diseases and findings in a clinical data warehouse27, again highlighting the problem of setting thresholds. Mining clinical data to provide good coverage of all important patterns with a small number of association rules has been done by first examining more general associations rules and adding more specific rules, using statistical methods to ensure that the more specific rules are better predictors than the generalizations28, using the idea of generalizing data to get better coverage. Studies have demonstrated the feasibility of using a public health data set and diagnosis categories from the Clinical Classifications Software (CCS) for ICD-9-CM to build a classifier to predict disease risks29. Integrating a concept hierarchy, such as provided by the Unified Medical Language System (UMLS) from the National Library of Medicine, into association rule mining has been done to create a framework for reducing the number of association rules by creating a knowledge representation model for association rule analysis30. Other studies have involved generalizing the 5-digit ICD-9-CM codes to 3-digit category codes to create morbidity profiles16 and using CCS to reduce the number of ICD-9-CM codes for predicting heart failure31.
Although there are studies that use association rule mining and generalized data based on concept hierarchies for disease-specific knowledge, there are limited reports of examining the effect of generalization and use of different concept hierarchies. Leveraging linkages between the generalized and raw data could facilitate limiting the search space and the discovery of new associations.
Methods
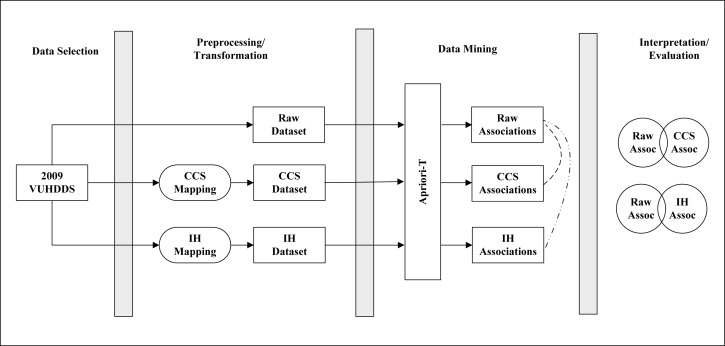
The overall approach used in this study follows the Knowledge Discovery in Databases (KDD)32 process to identify disease co-occurrences at different levels of abstraction from a public health dataset consisting of ICD-9-CM codes (Figure 1). This dataset was pre-processed and transformed to create three datasets for: (1) the raw transaction data, (2) generalized data using the CCS categorization scheme, and (3) generalized data using the ICD-9-CM hierarchy. Association rule mining techniques were then applied to each dataset to produce three sets of associations for interpretation and evaluation.
Figure 1:
Overview of Methods
Dataset
The data used in this study were from the 2009 Vermont Uniform Hospital Discharge Data Set (VUHDDS). This is a public dataset with de-identified inpatient and outpatient discharge data from 14 Vermont hospitals that are collected annually and administered by the Vermont Department of Banking, Insurance, Securities, and Health Care Administration (BISHCA)33. There are 334,409 rows in the dataset, where each row contains 75 values, including a unique admission identifier, hospital identifier, admission type, age group, zip code group, sex, and up to 20 diagnoses using ICD-9-CM codes for the coding. V and E codes (“supplementary classification of factors influencing health status and contact with health services” and “external causes of injury”) were excluded from the analysis.
Pre-Processing and Transformation
The pre-processing and data transformations included extracting ICD-9-CM codes from the 2009 VUHDDS files, creating links among the original and generalized datasets, and formatting each dataset for the data mining process. Using a set of Ruby scripts, the ICD-9-CM codes were mapped to CCS category codes and generalized ICD-9-CM codes to create the two generalized datasets. These scripts were also used to map the codes to integers from one to the number of unique codes in the respective dataset as required by the data mining software used in this study (further described below).
The original raw data extracted from the 2009 VUHDDS data file will be referred to as the Raw-Dataset. ICD-9-CM codes were extracted from the VUHDDS file corresponding to a row of the transaction data. There were 6,306 unique ICD-9-CM codes across the 334,409 records.
The Clinical Classifications Software (CCS) for ICD-9-CM is a diagnosis categorization scheme that was used to collapse the ICD-9-CM diagnosis codes from the Raw-Dataset into a smaller number of clinically homogenous clusters, called diagnosis categories. CCS for ICD-9-CM is a database developed as part of the Healthcare Cost and Utilization Project (HCUP), a Federal-State-Industry partnership sponsored by the Agency for Healthcare Research and Quality34. Every ICD-9-CM code has a corresponding diagnosis category and every category contains a set of ICD-9-CM codes. CCS provides both multi-level and single-level mappings. There are 12,562 unique ICD-9-CM codes (excluding ‘V’ and ‘E’ codes) mapped to 284 unique CCS categories (including one for invalid codes) in the single-level mappings. For example, ICD-9-CM code 414.00 (CORONARY ATHEROSCLEROSIS OF UNSPECIFIED TYPE OF VESSEL NATIVE OR GRAFT) and ICD-9-CM code 412 (OLD MYOCARDIAL INFARCTION) in the single-level mapping map to the same CCS category, 101 (CORONARY ATHEROSCLEROSIS AND OTHER HEART DISEASE). For this study, the single-level mapping for 2012 was downloaded from the CCS website34. The mapping of ICD-9-CM codes to the CCS category codes produced 252 unique CCS categories across the 334,409 records in the CCS-Dataset.
For the second hierarchy, the inherent structure of ICD-9-CM was used to collapse the specific ICD-9-CM diagnosis codes from the raw data into a smaller number of ICD-9-CM codes. The ICD-9-CM codes found in the raw data were modified to have the last digit of significance removed when the code in the raw data had more than three digits. For example, 414.00 (CORONARY ATHEROSCLEROSIS OF UNSPECIFIED TYPE OF VESSEL NATIVE OR GRAFT) was mapped to 414.0 (CORONARY ATHEROSCLEROSIS), 412 (OLD MYOCARDIAL INFARCTION) remained unchanged, and 305.1 (NONDEPENDENT TOBACCO USE DISORDER) was mapped to 305 (NONDEPENDENT ABUSE OF DRUGS). The mapping of ICD-9-CM codes using the ICD-9-CM Hierarchy (IH) produced 1,951 unique IH codes across the 334,409 records comprising the IH-Dataset.
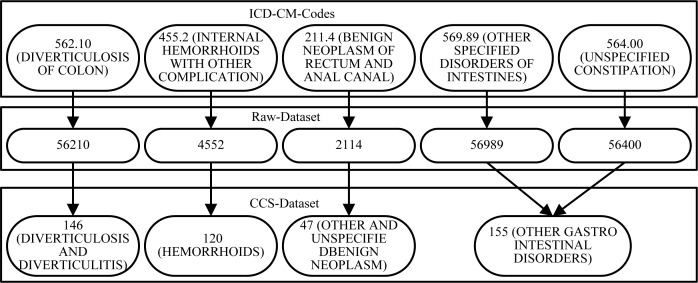
Each row of the transaction data was sorted into increasing order and any duplicate codes within the row were removed. The links between the Raw-Dataset and the two generalized datasets (CCS-Dataset and IH-Dataset) were stored for use in the evaluation. An example of the mappings from one row of the Raw-Dataset to one row of the CCS-Dataset is shown in the figure below (Figure 2). The row from the Raw-Dataset would look like “56210,4552,2114,56989,56400”, noting that the diagnosis codes in the original raw dataset were unformatted. Note that both 56400 and 56989 map to the same CCS category (155), which appears only once in the mapped data.
Figure 2:
Mapping Example
Data Mining
This study used the Apriori-T (Apriori Total)35 algorithm, a modified version of the Apriori1 algorithm. Apriori-T uses a T-tree (a balanced index tree data structure where both the index and the data can be kept in memory) to improve generation time and itemset storage requirements36. The Apriori-T algorithm requires the data be formatted so that each row of the transaction data is a set of integers sorted in increasing order, with any redundancy within the row removed. The integers represent the original transaction data by mapping the original data from one to the number of unique codes in the original data. The data are formatted in this manner to increase computing efficiency. The algorithm was implemented in Java. Several modifications were made to the Apriori-T algorithm as part of this study, such as using only support as a threshold filter for including a particular association in the output. In addition to the association rules, the Apriori-T algorithm was modified to output the values corresponding to the 2×2 matrix used to derive other objective measures, such as chi-square and confidence. These other objective measures calculated from the 2×2 matrix were applied in the post-processing step to measure the strength of each association. The code was also modified to generate only single item associations of the form {A}=>{B}; associations with more than one item in either the antecedent or consequent such as {A,B}=>{C,D} were not considered as part of this study. Post-processing included the association {A}=>{B} over {B}=>{A} based on the direction with the higher chi-square value.
Three sets of association rules (Raw-Associations, CCS-Associations, and IH-Associations) were produced for analysis. The Apriori-T algorithm was applied to the Raw-Dataset using a support value of 0.2, which was identified as a threshold in a preliminary study37. Removing the direction of the association produced 203 unique associations (e.g., A=>B and B=>A were counted once as A⬄B, where “⬄” is used to show an association where the direction has been removed). The Apriori-T algorithm was also applied to the generalized datasets (CCS-Dataset and IHDataset), starting with a support value of 0.5. The threshold was lowered in 0.05 increments to 0.2 on each run. The threshold of 0.2 was the cutoff value for the generalized datasets, as it was the largest support threshold that covered the raw data.
Post-Processing and Evaluation
The two sets of association rules based on the generalized data (CCS-Associations and IH-Associations) were compared with the Raw-Associations to examine the effects of generalization. The following four types of findings were examined (“⬄” is used to show an association where the direction has been removed and “→” is used to mean “maps to”):
An association in Raw-Associations of the form Raw1⬄Raw2 was covered if there was an association in the generalized results of the form Gen1⬄Gen2, where Raw1→Gen1 and Raw2→Gen2.
If an association in Raw-Associations of the form Raw1⬄Raw2 had mappings of the form Raw1→Gen1 and Raw2→Gen1, the association would be identified as an identity association and eliminated, as associations in the generalized data of the form Gen1⬄Gen1 would not be generated.
An association in the mapped data corresponded to an overlapping association if the generalized association was in the form Gen1⬄Gen2 where Map1’→Gen1, Map2’→Gen1, Map2’→Gen2, Map3’→Gen2. The overlap in the child codes (MapN’) was found by applying the same strategy used to generate the IH data, where the most significant digit was removed from the child ICD-9-CM code corresponding to the mapped code. Since the generalized Map2’ was a “child” of both Gen1 and Gen2, the association Gen1⬄Gen2 was considered an overlapping association.
If the child codes of the generalized association were not found as an association in the Raw-Associations, it was flagged as a new association. This way, associations in the generalized data could be mapped back to the raw data to determine if a generalized association covered an existing association or corresponded to a new, previously unseen association. For example, if Gen1⬄Gen2 represents an association in the generalized data and Raw1→Gen1, Raw2→Gen1, Raw3→Gen2, and Raw4→Gen2, if no association of the form Raw1⬄Raw3, Raw1⬄Raw4, Raw2⬄Raw3, or Raw2⬄Raw4 were found in Raw-Associations, it was flagged as a new association in the generalized data.
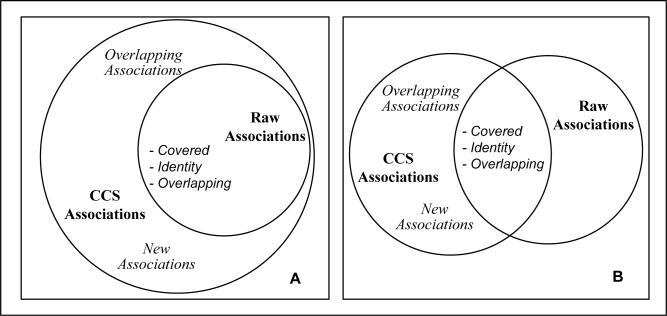
The figure below (Figure 3) summarizes the four types of associations, showing CCS-Associations and Raw-Associations as an example. The examples in the figure show complete coverage (A) and partial coverage (B). Covered, identity, overlapping, and new associations are shown. Overlapping associations are shown in two places, as they can be either inside the cover or outside. Similar relationships between IH-Associations and Raw-Associations pertain.
Figure 3:
Relationship between Covered, Identity, Overlapping, and New Associations
Results
Summary and Comparison of Associations
Results for the three datasets are shown in Table 1, which includes the distribution of covered, identity, overlapping, and new associations. At a support threshold of 0.5, CCS-Associations covered 138 and IH-Associations covered 97 of the 203 associations in Raw-Associations. Lowering the support to 0.2 for CCS and 0.2 for IH completely covered the raw data, taking into account the identity associations (192+11 and 199+4, respectively). At the lower levels of support, there were 446 unique CCS-Associations and 282 unique IH-Associations. The number of identity associations stayed constant across the varying support thresholds for CCS; IH went from 3 to 4 identity associations as the support threshold was lowered. Only CCS produced overlapping associations, with 31 at 0.2 support and 9 at 0.5 support. Based on how the IH-Dataset was constructed, there were no overlapping associations in IH-Associations. The CCS-Associations at support 0.2 included the most new associations, 302; IH-Associations included the fewest new association at support 0.5, one.
Table 1:
Result Summary (334,409 records)
| Source | Support | Unique Codes | Total Unique Associations | Covered | Not Covered | Identity Associations | Overlapping Associations | New Associations |
|---|---|---|---|---|---|---|---|---|
| Raw | 0.2 | 6306 | 203 | |||||
| CCS | 0.2 | 252 | 446 | 192 | 0 | 11 | 31 | 302 |
| CCS | 0.5 | 252 | 129 | 138 | 54 | 11 | 9 | 39 |
| IH | 0.2 | 1951 | 282 | 199 | 0 | 4 | 0 | 115 |
| IH | 0.5 | 1951 | 69 | 97 | 103 | 3 | 0 | 1 |
Comparing the new associations found across the two hierarchies at support 0.5 shows that the one new association found by IH-Associations was also found by CCS-Associations, and that the CCS hierarchy found an additional 38 associations not found in the associations based on the raw data. Both hierarchies covered the associations found in the raw data at support 0.2. With regards to new associations at 0.2 support, 302 (67.7% of the total 446 associations) were found with the CCS hierarchy and 115 (40.8% of the total 282 associations) with the IH hierarchy. In comparing the new associations, 278 out of the 302 (92.1%) associations were unique to CCS-Associations, 84 out of 115 (73.0%) unique to IH-Associations, and 24 (7.9%) and 31 (26.9%) associations were common to both relative to CCS-Associations and IH-Associations respectively. At support 0.5, the comparisons indicate that the CCS hierarchy better covered the raw data where 54 (26.6% of the 203 raw associations) of the raw data associations were not covered, compared with 103 (50.7% of the 203 raw associations) for the IH hierarchy. Further comparison of the hierarchies with respect to associations not covered revealed that 4 out of the 54 (7.4%) associations were unique to CCS-Associations, 53 out of 103 (50.7%) unique to IH-Associations, and 50 (92.5%) and 50 (48.5%) associations common to both relative to CCS-Associations and IH-Associations respectively. Overall, based on the measures considered, CCS better covered the raw data, finding more identity, overlapping, and new associations.
Identity Associations
Table 2 summarizes the eleven identity associations found in the CCS results. Generalizing the ICD-9-CM codes to the CCS categories, similar codes are found outside the strictly numerical hierarchy of ICD-9-CM. The associations shown, denoted in the column headings (CCS1, Raw1, Raw2) are of the form Raw1⬄Raw2 where Raw1→CCS1 and Raw2→CCS1. These would create an association of the form CCS1⬄CCS1 in the generalized data. The association Raw1⬄Raw2 could be flagged for removal in the Raw-Associations since it becomes an identity association in the generalized data. However, it would still be available if a reviewer was interested in the details of a particular category, reducing information loss.
Table 2:
Identity Associations for CCS
| CCS1 | CCS Description | Raw1 | ICD-9-CM Description | Raw2 | ICD-9-CM Description |
|---|---|---|---|---|---|
| 133 | OTHER LOWER RESPIRATORY DISEASE | 786.09 | RESPIRATORY ABNORMALITY OTHER | 786.2 | COUGH |
| 136 | DISORDERS OF TEETH AND JAW | 521 | DISEASES OF HARD TISSUES OF TEETH | 525.9 | DENTAL DISORDER UNSPEC |
| 101 | CORONARY ATHEROSCLEROSIS AND OTHER HEART DISEASE | 412 | OLD MYOCARDIAL INFARCTION | 414.00 | CORONARY ATHRSCL UNS VESSEL |
| 101 | CORONARY ATHEROSCLEROSIS AND OTHER HEART DISEASE | 412 | OLD MYOCARDIAL INFARCTION | 414.01 | CORONARY ATHEROSCLEROSIS OF NATIVE CORONARY ARTERY |
| 205 | SPONDYLOSIS; INTERVERTEBRAL DISC DISORDERS; OTHER BACK PROBLEMS | 722.52 | DEGENERATION OF LUMBAR OR LUMBOSACRAL INTERVERTEBRAL DISC | 724.4 | THORACIC OR LUMBOSACRAL NEURITIS OR RADICULITIS UNSPECIFIED |
| 211 | OTHER CONNECTIVE TISSUE DISEASE | 729.81 | SWELLING OF LIMB | 729.5 | PAIN IN LIMB |
| 53 | DISORDERS OF LIPID METABOLISM | 272.4 | HYPERLIPIDEMIA OT/UNSPEC | 272.0 | PURE HYPERCHOLESTEROLEM |
| 205 | SPONDYLOSIS; INTERVERTEBRAL DISC DISORDERS; OTHER BACK PROBLEMS | 724.8 | OTHER SYMPTOMS REFERABLE TO BACK | 724.2 | LUMBAGO |
| 205 | SPONDYLOSIS; INTERVERTEBRAL DISC DISORDERS; OTHER BACK PROBLEMS | 724.02 | SPINAL STENOSIS LUMBAR | 724.4 | THORACIC OR LUMBOSACRAL NEURITIS OR RADICULITIS UNSPECIFIED |
| 47 | OTHER & UNSPECIFIED BENIGN NEOPLASM | 211.4 | BENIGN NEOPLASM OF RECTUM & ANAL CANAL | 211.3 | BENIGN NEOPLASM OF COLON |
| 86 | CATARACT | 366.15 | CORTICAL SENILECATARACT | 366.16 | NUCLEAR SCLEROSIS |
Overlapping Associations
Table 3 summarizes the overlapping associations found in CCS-Associations at a support threshold of 0.5, where the CCS-Association had a link back to a Raw-Association. The overlap was found by looking at more generalized ICD-9-CM codes for each of the CCS categories. For each child code in the CCS category, where possible, the most significant digit of the child ICD-9-CM code was removed (similar to the method used to create the IH-Dataset). The more generalized child codes were then used to find overlapping codes across CCS categories. The ‘Overlap’ column indicates which codes from the CCS-Associations were found, where RawX’→CCS1, RawX’→CCS2 and where RawX’ is a generalization of either Raw1 or Raw2. Only four of the nine overlapping associations were of this form. Of these four, only one represents a mapping outside the numerical hierarchy (787.91⬄789). The other three overlaps could be derived directly from the ICD-9-CM numerical hierarchy.
Table 3:
Overlapping Associations for CCS at 0.5 support
| Raw1 | Raw1 Description | Raw2 | Raw2 Description | CCS1 | CCS1 Description | CCS2 | CCS2 Description | Overlap (RawX’) |
|---|---|---|---|---|---|---|---|---|
| 787.91 | DIARRHEA | 789 | OTHER SYMPTOMS INVOLVING ABDOMEN AND PELVIS | 155 | OTHER GASTRO INTESTINAL DISORDERS | 251 | ABDOMINAL PAIN | 789-ABDOMINAL SYMPTOMS |
| 787.01 | NAUSEA WITH VOMITING | 787.91 | DIARRHEA | 250 | NAUSEA AND VOMITING | 155 | OTHER GASTRO INTESTINAL DISORDERS | 787-SYMPTOMS DIGESTIVE SYSTEM |
| 787.03 | VOMITING ALONE | 787.91 | DIARRHEA | 250 | NAUSEA AND VOMITING | 155 | OTHER GASTRO INTESTINAL DISORDERS | 787-SYMPTOMS DIGESTIVE SYSTEM |
| 305.00 | NONDEPENDENT ALCOHOL ABUSE UNSPECIFIED DRINKING BEHAVIOR | 305.1 | TOBACCO USE DISORDER | 660 | ALCOHOL-RELATED DISORDERS | 663 | SCREENING AND HISTORY OF MENTAL HEALTH AND SUBSTANCE ABUSE CODES | 305-NONDEPENDENT ABUSE OF DRUGS |
New Associations
Table 4 summarizes the top ten of the 39 new CCS-Associations found at a support threshold of 0.5, based on their “interestingness”, sorted by chi-square value. These were highlighted in a review of the new associations by a clinical expert and require further investigation given the high level of generalization. This shows that using the generalized data even at a higher level of support will find new associations. In the table below, the number of ICD-9-CM codes comprising each CCS category, based on the raw data mapped to the CCS category, is shown in the ‘Child Counts’ column. By generalizing the data, ICD-9-CM codes that did not have enough support in the Raw-Dataset are grouped into the higher level CCS category, increasing the support so that new associations are found, even at the higher support threshold of 0.5.
Table 4:
New associations for CCS at 0.5 support
| CCS1 | CCS1 Description | CCS1 Child Counts | CCS2 | CCS2 Description | CCS2 Child Counts | X2 |
|---|---|---|---|---|---|---|
| 138 | ESOPHAGEAL DISORDERS | 20 | 53 | DISORDERS OF LIPID METABOLISM | 5 | 13216 |
| 136 | DISORDERS OF TEETH AND JAW | 81 | 663 | SCREENING AND HISTORY OF MENTAL HEALTH AND SUBSTANCE ABUSE CODES | 11 | 3559.8 |
| 101 | CORONARY ATHEROSCLEROSIS AND OTHER HEART DISEASE | 12 | 138 | ESOPHAGEAL DISORDERS | 20 | 3539.4 |
| 48 | THYROID DISORDERS | 27 | 138 | ESOPHAGEAL DISORDERS | 20 | 2940.9 |
| 127 | CHRONIC OBSTRUCTIVE PULMONARY DISEASE AND BRONCHIECTASIS | 13 | 53 | DISORDERS OF LIPID METABOLISM | 5 | 2713.3 |
| 49 | DIABETES MELLITUS WITHOUT COMPLICATION | 8 | 138 | ESOPHAGEAL DISORDERS | 20 | 2616.8 |
| 128 | ASTHMA | 13 | 138 | ESOPHAGEAL DISORDERS | 20 | 2528.3 |
| 146 | DIVERTICULOSIS AND DIVERTICULITIS | 6 | 53 | DISORDERS OF LIPID METABOLISM | 5 | 2423.9 |
| 47 | OTHER AND UNSPECIFIED BENIGN NEOPLASM | 103 | 53 | DISORDERS OF LIPID METABOLISM | 5 | 1486.8 |
| 204 | OTHER NON-TRAUMATIC JOINT DISORDERS | 140 | 53 | DISORDERS OF LIPID METABOLISM | 5 | 1451.1 |
Discussion
The goal of this preliminary study was to explore the impact of generalizing data and the effect of using different concept hierarchies in the association rule mining process. Using domain knowledge to create a concept hierarchy and incorporating the hierarchy into the data mining process by abstracting data to a higher level concept can help constrain the search space and enhance performance and results of the mining process. This study examined two concept hierarchies for generalization and involved maintaining links between the generalized and raw data. The results differed based on the concept hierarchy used for generalizing the data.
Once validated, disease-specific knowledge obtained using automated methods such as association rule mining could be used for applications such as quality of care, decision support, and hypothesis generation. The associations found in this study show the potential for discovering potentially new and interesting knowledge related to disease co-occurrences at different levels of abstraction. The identity associations found could help flag possible irrelevant disease co-occurrences and the new associations could serve as a starting point for further exploration. Established medical knowledge sources (e.g. biomedical literature) and more in depth review by domain experts (e.g. clinicians) will be done in future studies to determine the clinical validity of the new associations generated in this study. In addition, calculating other statistical or “interestingness” measures (e.g., interest and conviction) could be used to further assess the strength of each association. An important part of future analyses will also be to identify invalid and irrelevant associations.
Data mining at multiple levels of abstraction, known as multilevel association rule mining, was introduced in 1999 by Han22, where different support thresholds are set at different levels of abstraction. Multilevel association rule mining improves on the classic algorithms by using the concept hierarchy to allow for different thresholds at different levels of the hierarchy. Future studies will look at expanding from a single level of generalization to multiple levels of generalization, using varying support thresholds at each level, with links at each level back to the raw data. In this study, the data were generalized to one level of abstraction and different support thresholds were applied to various iterations of the process. Varying the support at each level of the hierarchy could be used to control the coverage, identity, overlapping, and new associations. By leveraging multiple levels, more granularity can be added to the generalized data. Expanding to multiple levels of the hierarchy, with multiple support thresholds and links across the multiple levels of the generalized data back to the raw data could create a much richer model for exploration and help to further assess the impact of using different concept hierarchies
Future studies will explore use of the multi-level CCS mappings, which contains 729 categories, with up to four levels per category. For example, ICD-9-CM code 414.00 (CORONARY ATHEROSCLEROSIS OF UNSPECIFIED TYPE OF VESSEL NATIVE OR GRAFT) maps to 7.2.4.4 (CORONARY ATHEROSCLEROSIS) and ICD-9-CM code 412 (OLD MYOCARDIAL INFARCTION) maps to 7.2.4.5 (OTHER FORMS OF CHRONIC HEART DISEASE) at the highest levels of the multi-level CCS mapping. In the single-level mapping, both ICD-9-CM codes mapped to the same CCS category, 101 (CORONARY ATHEROSCLEROSIS AND OTHER HEART DISEASE). Several of the new associations found in this study were of interest, but given the high level of generalization in the single level CCS categories, a more detailed review is needed. Using the multi-level CCS mapping will provide more granularity and allow for cross-level associations.
In addition to the multi-level CCS categories, other hierarchies (e.g., SNOMED CT and UMLS) will be explored in future studies to determine how they perform with regards to coverage, identity, overlapping, and new associations. The focus of this work and planned future studies will be to further evaluate the impact of selecting different concept hierarchies and how the different generalizations impact the outcome. Looking at temporal and sequential events38 could also be incorporated into future studies. In addition, multiple item associations from the Apriori-T algorithm could be included in future studies as well as using other association rule mining techniques from open source tools such as Hadoop. While ICD-9-CM codes in administrative datasets reflect billing with known reimbursement-based biases that can both overestimate and underestimate clinical findings, these datasets have been shown to be useful for studying general clinical knowledge39, 40 Other next steps include exploring health datasets that are less prone to these concerns in order to compare disease co-occurrences across datasets (e.g., administrative data vs. clinical data such as from electronic health records).
Conclusion
This study explored the use of generalized association rule mining for generalizing data to a higher level of abstraction in a public health dataset and compared disease co-occurrences at the different levels. The results suggest that maintaining links from the generalized data to the raw data may help constrain the search space and rule space, minimize information loss, and discover new associations. In addition, use of different concept hierarchies may have an impact on the outcome.
Acknowledgments
Hospital discharge data for use in this study were supplied by the VAHHS-NSO and BISHCA. All analyses, interpretations, or conclusions based on these data are solely that of the authors. VAHHS-NSO and BISHCA disclaim responsibility for any such analyses, interpretations, or conclusions. In addition, as the data have been edited and processed by VAHHS-NSO, BISHCA assumes no responsibility for errors in the data due to coding or processing by hospitals, VAHHS-NSO or any other organization, including the University of Vermont and Fletcher Allen Health Care.
References
- 1.Agrawal R, Srikant R. Fast algorithms for mining association rules. 20th VLDB Conference; Santiago, Chile. 1994. pp. 487–99. [Google Scholar]
- 2.Ordonez C. Association rule discovery with the train and test approach for heart disease prediction. IEEE Trans Inf Technol Biomed. 2006;10(2):334–43. doi: 10.1109/titb.2006.864475. Epub 2006/04/19. [DOI] [PubMed] [Google Scholar]
- 3.Chen M-S, Han J, Yu PS. Data mining: An overview from a database perspective. IEEE Trans on Knowl and Data Eng. 1996;8(6):866–83. [Google Scholar]
- 4.Brossette SE, Hymel PA., Jr Data mining and infection control. Clinics in Laboratory Medicine. 2008;28(1):119–26. doi: 10.1016/j.cll.2007.10.007. [DOI] [PubMed] [Google Scholar]
- 5.Cao H, Hripcsak G, Markatou M. A statistical methodology for analyzing co-occurrence data from a large sample. J Biomed Inform. 2007;40(3):343–52. doi: 10.1016/j.jbi.2006.11.003. Epub 2007/01/02. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Huang QR, Qin Z, Zhang S, Chow CM. Clinical patterns of obstructive sleep apnea and its comorbid conditions: A data mining approach. Journal of clinical sleep medicine : JCSM : official publication of the American Academy of Sleep Medicine. 2008;4(6):543–50. Epub 2008/12/30. [PMC free article] [PubMed] [Google Scholar]
- 7.Ordonez C, Ezquerra N, Santana C. Constraining and summarizing association rules in medical data. Knowl Inf Syst. 2006;9(3):259–83. [Google Scholar]
- 8.Li-Shiang T, Seunghyun I, editors. Mining generalized actionable rules using concept hierarchies. INC, IMS and IDC, 2009 NCM ‘09 Fifth International Joint Conference; 2009 25–27 Aug; 2009. [Google Scholar]
- 9.Borgelt C. Simple algorithms for frequent item set mining advances in machine learning ii. In: Koronacki J, Ras Z, Wierzchon S, Kacprzyk J, editors. Springer Berlin; Heidelberg: 2010. pp. 351–69. [Google Scholar]
- 10.Goethals B. Survey on frequent pattern mining. 2003.
- 11.Brin S, Motwani R, Silverstein C. Beyond market baskets: Generalizing association rules to correlations. Proceedings of the 1997 ACM SIGMOD international conference on Management of data; Tucson, Arizona, United States. ACM; 1997. pp. 265–76. 253327. [Google Scholar]
- 12.Liu B, Hsu W, Ma Y, editors. KDD-99. San Diego, CA: 1999. Mining association rules with multiple minimum supports. [Google Scholar]
- 13.Agrawal R, Imielinski T, Swami A. Mining association rules between sets of items in large databases. SIGMOD: ACM; 1993. pp. 207–16. [Google Scholar]
- 14.Srikant R, Agrawal R. Mining generalized association rules. Proceedings of the 21th International Conference on Very Large Data Bases 673304; Morgan Kaufmann Publishers Inc; 1995. pp. 407–19. [Google Scholar]
- 15.Painter J, Flowers N. Codeslinger: An interactive biomedical ontology browser. In: Combi C, Shahar Y, Abu-Hanna A, editors. Artificial intelligence in medicine. Springer Berlin; Heidelberg: 2009. pp. 260–4. [Google Scholar]
- 16.Schildcrout JS, Basford MA, Pulley JM, et al. An analytical approach to characterize morbidity profile dissimilarity between distinct cohorts using electronic medical records. Journal of Biomedical Informatics. 2010;43(6):914–23. doi: 10.1016/j.jbi.2010.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hristovski D, Stare J, Peterlin B, Dzeroski S. Supporting discovery in medicine by association rule mining in medline and umls. Stud Health Technol Inform. 2001;84(Pt 2):1344–8. Epub 2001/10/18. [PubMed] [Google Scholar]
- 18.Liu B, Hu M, Hsu W. Multi-level organization and summarization of the discovered rules. Proceedings of the sixth ACM SIGKDD international conference on Knowledge discovery and data mining; Boston, Massachusetts, United States. ACM; 2000. pp. 208–17. 347128. [Google Scholar]
- 19.Han J, Fu Y. Discovery of multiple-level association rules from large databases. Proceedings of the 21th International Conference on Very Large Data Bases 673134; Morgan Kaufmann Publishers Inc; 1995. pp. 420–31. [Google Scholar]
- 20.Davis DA, Chawla NV, Christakis NA, Barabási AL. Time to care: A collaborative engine for practical disease prediction. Data Min Knowl Disc; 2009. [Google Scholar]
- 21.Hripcsak G, Knirsch C, Zhou L, Wilcox A, Melton GB. Using discordance to improve classification in narrative clinical databases: An application to community-acquired pneumonia. Comput Biol Med. 2007;37(3):296–304. doi: 10.1016/j.compbiomed.2006.02.001. [DOI] [PubMed] [Google Scholar]
- 22.Han J, Fu Y. Mining multiple-level association rules in large databases. IEEE Transactions on Knowledge and Data Engineering. 1999;11:798–805. [Google Scholar]
- 23.Swanson DR. Medical literature as a potential source of new knowledge. Bull Med Libr Assoc. 1990;78:29–37. [PMC free article] [PubMed] [Google Scholar]
- 24.Chen ES, Hripcsak G, Xu H, Markatou M, Friedman C. Automated acquisition of disease drug knowledge from biomedical and clinical documents: An initial study. J Am Med Inform Assoc. 2008;15(1):87–98. doi: 10.1197/jamia.M2401. Epub 2007/10/20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hanauer DA, Rhodes DR, Chinnaiyan AM. Exploring clinical associations using ‘-omics’ based enrichment analyses. PLoS One. 2009;4(4):e5203. doi: 10.1371/journal.pone.0005203. Epub 2009/04/15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Wright A, Chen ES, Maloney FL. An automated technique for identifying associations between medications, laboratory results and problems. Journal of Biomedical Informatics. 2010 doi: 10.1016/j.jbi.2010.09.009. [DOI] [PubMed] [Google Scholar]
- 27.Cao H, Markatou M, Melton GB, Chiang MF, Hripcsak G. Mining a clinical data warehouse to discover disease-finding associations using co-occurrence statistics. AMIA Annu Symp Proc; 2005. pp. 106–10. Epub 2006/06/17. [PMC free article] [PubMed] [Google Scholar]
- 28.Batal I, Hauskrecht M, editors. Mining clinical data using minimal predictive rules. AMIA 2010 Symposium; Washington, D.C. 2010. [PMC free article] [PubMed] [Google Scholar]
- 29.Khalilia M, Chakraborty S, Popescu M. Predicting disease risks from highly imbalanced data using random forest. BMC Medical Informatics and Decision Making. 2011;11(1):51. doi: 10.1186/1472-6947-11-51. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Chen P, Verma RM, Meininger JC, Chan W, editors. Semantic analysis of association rules. Proceedings of FLAIRS 2008; Coconut Grove, Florida: Florida AI Research Society; 2008. [Google Scholar]
- 31.Phillips KT, Street WN, editors. Predicting outcomes of hospitalization for heart failure using logistic regression and knowledge discovery methods. AMIA Annu Symp Proc; 2005. [PMC free article] [PubMed] [Google Scholar]
- 32.Fayyad UM, Piatetsky-Shapiro G, Smyth P. Advances in knowledge discovery and data mining. American Association for Artificial Intelligence; 1996. From data mining to knowledge discovery: An overview; pp. 1–34. [Google Scholar]
- 33.BISHCA Available from: http://healthvermont.gov/research/hospital-utilization/RECENT_HOSP_REPORTS.aspx.
- 34.Clinical classifications software. Agency for Healthcare Research and Quality; 2012. Available from: http://www.hcup-us.ahrq.gov/toolssoftware/ccs/ccs.jsp. [Google Scholar]
- 35.Coenen F. The lucs-kdd apriori-t association rule mining algorithm. Department of Computer Science, The University of Liverpool, UK; 2004. http://www.csc.liv.ac.uk/~frans/KDD/Software/Apriori-T/aprioriT.html. [Google Scholar]
- 36.Coenen F, Leng P, Ahmed S. Data structure for association rule mining: T-trees and p-trees. Knowledge and Data Engineering, IEEE Transactions. 2004;16(6):774–8. [Google Scholar]
- 37.Kost R, Chen E, Littenberg B. Assessing disease co-occurrences using association rule mining and public health data sets. AMIA 2011 Annual Symposium; Washington, D.C.. 2011. p. 1841. [Google Scholar]
- 38.McCormick TH, Rudin C, Madigan D. A hierarchical model for association rule mining of sequential events: An approach to automated medical symptom prediction. Annals of Applied Statistics; 2011. [Google Scholar]
- 39.Tang PC, Ralston M, Arrigotti MF, Qureshi L, Graham J. Comparison of methodologies for calculating quality measures based on administrative data versus clinical data from an electronic health record system: Implications for performance measures. J Am Med Inform Assoc. 2007;14(1):10–5. doi: 10.1197/jamia.M2198. Epub 2006/10/28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Quan H, Parsons GA, Ghali WA. Validity of information on comorbidity derived rom icd-9-ccm administrative data. Medical care. 2002;40(8):675–85. doi: 10.1097/00005650-200208000-00007. Epub 2002/08/21. [DOI] [PubMed] [Google Scholar]