Comparing Predictive Models of Glioblastoma Multiforme Built Using Multi-Institutional and Local Data Sources

Abstract

The growing amount of electronic data collected from patient care and clinical trials is motivating the creation of national repositories where multiple institutions share data about their patient cohorts. Such efforts aim to provide sufficient sample sizes for data mining and predictive modeling, ultimately improving treatment recommendations and patient outcome prediction. While these repositories offer the potential to improve our understanding of a disease, potential issues need to be addressed to ensure that multi-site data and resultant predictive models are useful to non-contributing institutions. In this paper we examine the challenges of utilizing National Cancer Institute datasets for modeling glioblastoma multiforme. We created several types of prognostic models and compared their results against models generated using data solely from our institution. While overall model performance between the data sources was similar, different variables were selected during model generation, suggesting that mapping data resources between models is not a straightforward issue.

Introduction

The research community has increasingly adopted the practice of sharing data resources across multiple institutions to prospectively gather data on diseases, aggregating information into common databases. Compiling data across many sites improves the ability to gather a range of representative patient data that can often be difficult for institutions to gather individually. Increasing the amount of available data provides opportunities for creating models that can improve the understanding of diseases, leading to tools to aid physicians in decision making and the prediction of patient outcomes. Nevertheless, researchers have not fully explored the inherent problems of utilizing multi-institutional models created with shared data when applying them back at an institutional level. Data collection and clinical trials tasks focus efforts on testing the internal validity of data and models, exploring the ability of the model to predict consistently on test cases collected in the same manner as the training dataset. Testing models ability to generalize to cases outside the training population, or the model’s external validity, is not straight forward and often demonstrates a substantial drop in prediction accuracy. In addition, few papers presently provide results for both internal and external examinations, as outside datasets may not be available for an external comparison. Challenges related to external validation have been previously reported in epidemiology literature^13,14; in this paper, we examine the issue in the context of developing predictive models from publicly available repositories that aggregate clinical data from multiple academic medical centers.

A variety of issues exist that hinder the ability of researchers to apply a validated disease model constructed from a national data source to a local institution. First, differences in the new population being evaluated may reduce the accuracy of the original model’s predictions. There may be important disease characteristics for a target population that the model does not represent given a sampling bias. It has been standard in the past for each institution to generate a model from a dataset of their local population because their final model is not expected to be applicable elsewhere. But expecting all institutions to generate models from local data is an issue as many non-research hospitals will not realistically have access to datasets with sufficient statistical power to create their own model; and using a published model from a national dataset for predictions on their local patients may not be effective. Another issue is the amount of knowledge supplied concerning the design of the model and the required model inputs. Individual institutions currently have limited access to decisions such as the stratification techniques used during model creation by other groups unless they are reported in publications. These design considerations are important for preparing a new dataset to run with a published model. Imaging findings like tumor size measurement, for example, can differ between institutions based upon standard hospital practices and radiologist preferences. Similarly, model features are important because an institution may not perform the same types of tests or evaluations as the original researchers and will have large amounts of missing data to contend with, without foreknowledge of the model design. In this analysis, for example, TCGA data does not include a variable describing the amount of tumor removed during resections, and reduces the available predictive elements when compared to the other datasets examined. Collectively, these issues are known to place restrictions on the use and adaptation of models generated be separate research institutions. It is likely the same difficulties must be addressed when generating multi-institutional models in order for them to provide predictive capabilities back to not only the institutions which supplied data, but also to those that did not.

In this work we explore methods for evaluating and distinguishing the differences between multi-institutional models generated from shared data and single dataset models. Using publicly available data on glioblastoma multiforme patients from the National Cancer Institute’s (NCI) Rembrandt and The Cancer Genome Atlas (TCGA) initiatives, we have generated logistic regression and Bayesian belief models using clinical and imaging features. We examine the differences between the models related to their population differences, stratification techniques, and missing data concerns; and discuss the potential development of methods and tools to combat these issues when developing models in future work.

Background

Glioblastoma multiforme (GBM) is an aggressive malignant primary brain tumor, and accounts for almost half of the 45,000 newly diagnosed cases of adult brain tumor seen annually in the United States. Recent NCI SEER (Surveillance, Epidemiology, and End Results) data show that there has been no effective change in the survival of GBM patients during the last 20 years. The average survival time for GBM patients is between 12–24 months when receiving specialized care at academic centers; but for many patients, survival time is often much shorter. The treatment of brain cancer frequently includes a combination of surgical resection, chemotherapy, and radiation. The increasing numbers of available chemo- and adjunctive therapies makes it unclear which treatments will be effective for each individual. Moreover, genetic studies are making it clearer that despite similar diagnosis at outset, there are variations in tumor biology that may require different treatment responses^1,2. In addition, recent statistical papers covering GBM present differing results on what variables are relevant to the prediction of GBM outcomes^3–6. Our current understanding of this cancer and effective treatments are still limited; and working towards an integrative model of GBM can facilitate prognosis and treatment decisions in the clinic.

Present efforts to provide prospective observational databases containing brain cancer data include two projects form the NCI: the Repository for Molecular Brain Neoplasia Data (Rembrandt) Project, and TCGA. Rembrandt, available through caIntegrator, focuses specifically on the study of clinical, genetic, and proteomic correlates in gliomas^7,8. There are currently 639 total cases in its database, covering all glioma types (astrocytoma, GBM, mixed, oligodendroglioma) and a few unmatched non-tumor controls. TCGA is a large-scale effort to collect data on over 20 different cancers and is available through dbGaP⁹. The TCGA dataset contains primarily clinical and genomic (copy number, DNA methylation, gene expression, single nucleotide polymorphisms) data with ongoing efforts to make radiological and pathological images available. As of March 2012, the GBM subset of TCGA comprises 599 patients, with 582 downloadable tumor samples. The public availability of these data sources makes them prime candidates for use in developing predictive disease models. Both Rembrandt and TCGA include variables for demographics, clinical history, tumor diagnosis, performance status, treatments (chemotherapy, surgical, and radiotherapy), gene expression, and outcome. Both datasets combine cases submitted by institutions from across the United States. Notably, magnetic resonance imaging (MRI) for cases in Rembrandt and TCGA are available through the National Biomedical Imaging Archive, with a combined total of 302 unique patients with studies available. A set of 30 imaging features (e.g., multi-focality, satellites, proportion of contrast enhancement, etc.) have been defined for annotating imaging characteristics based on the NCI Vasari (Visually Accessible Rembrandt Images) effort. The In Silico Brain Tumor Research Center (ISBRTC) has reported on efforts to correlate radiologic imaging, pathology, and genetic data from TCGA to identify molecular variables that are strong prognostic indicators of overall survival¹⁰.

While national data repositories allow research hospitals to contribute disease information, patient data collection and medical decision-making process is ultimately performed in individual clinics governed by local protocols and practices. By way of illustration, the problems, findings, and attributes of neuro-oncology patients that are reported in clinical records may differ between institutions. And while each site may gather information on the same disease, there are variations in the study design and data collection which complicate the ability to integrate and compare subjects directly. Arguably, while the collaborative efforts spanning multiple institutions seek to pool data to improve statistical power and population metrics, the resulting knowledge and models of such an endeavor must be made applicable to any given site. As models are generated from federated collections of observational patient data, inter-site differences must be mapped and described so that additional patient data from other institutions will match the previous design or can be modified appropriately when collected under different methods. To begin to understand these challenges, we compared the process of constructing an array of different prognostic models from Rembrandt and TCGA relative to a local GBM dataset garnered from past work with the UCLA Neuro-oncology Program.

Methods

Prior to statistical analysis, the clinical and imaging variables from the three datasets (Rembrandt, TCGA, UCLA) were examined to determine which of the available variables were appropriate for analytic use. In order to make our initial analysis manageable, focus was placed on a small subset of the available variables. From the complex set of available variables presented in Table 1, we decided to focus on clinical, imaging and treatment variables. To simplify the analysis, genetic data was not used in the predictive modeling task due to the complexity of determining appropriate genetic markers to use as variables. In addition, complete Vasari imaging findings were only available for a small subset of each dataset; these imaging variables were therefore excluded until more data is available. An imaging summary variable was used in its place.

Table 1:

Partial list of potential predictive variables available from among the three data sources. Data sources: (T) TCGA; (R) Rembrandt; (U) UCLA

Category	Variable	T	R	U	Variable	T	R	U	Variable	T	R	U
Patient information	Demographics	•	•	•	Family & social history		•	•	Environmental exposure			•
	Presenting age	•	•	•
Tumor presentation	Tumor site	•	•	•	Tumor size	•	•	•
Histopathology	Tumor grade	•	•	•
Gene expression	VEGF	•	•	•	PTEN	•	•	•	MGMT	•	•	•
	EGFR VIII	•	•	•	TP53	•	•	•	DNA methylation	•	•	•
Chemotherapy	Drug name	•	•	•	Frequency/dosage	•	•	•	Number of cycles	•	•	•
Surgical resection	Type of procedure	•	•	•	Extent of resection	•	•	•
Radiation therapy	Type of radiation therapy	•	•	•	Fractionation	•	•	•	Total dosage	•	•	•
Steroids	Drug name	•	•	•	Frequency	•	•	•	Dosage	•	•	•
Other medications	Drug name	•	•	•	Frequency	•	•	•	Dosage	•	•	•
Neurological assessment	Karnofsky score	•	•	•	Other		•
Imaging assessment	Tumor volume	•	•	•	Non-contrast enhancing region	•	•	•	Mass effect	•	•	•
	Necrosis	•	•	•	Multi-focality	•	•	•	Satellites	•	•	•
	Contrast enhancement	•	•	•	Edema volume	•	•	•	ADC map			•
Outcomes	Time to progression (TTP)	•	•	•	Time to survival (TTS; death)	•	•	•

To make a determination on what clinical, imaging, and treatment variables to use, we first examined the availability of complete data for the available variables. Large amounts of missing data and cases of data not missing at random can make it impossible to use variables, even when using data imputation techniques. Within the Rembrandt data some of the participating institutions did not report clinical data for their subjects, leaving all fields blank. Cases with this characteristic were excluded from the dataset. Situations of non-reporting were also seen in the TCGA data and cases were excluded in the same fashion. In total, 70 (11%), 82 (15%), and 0 (0%) cases were excluded from the Rembrandt, TCGA, and UCLA datasets respectively due to this issue. In addition, variables concerning treatment with radiation and chemotherapy were divided based on prior- and on-study treatment events in the Rembrandt data. Reporting of these variables for on-study work was inconsistent and only covered a small subset of the total number of cases. In addition, the on-study variables cover events of recurrence and our model design targets prediction on first presentation. Therefore, only prior-study data was used from the Rembrandt dataset. Similarly, data related to the first appearance of tumor in patients was also selected for both the TCGA and Rembrandt datasets and follow-up data was avoided. Following these steps, any cases still missing values for two or more of the target variables were excluded under the assumption that their data were not reported correctly (rather than being left out at random). This caused the removal of an additional set of 343 (54%), 8 (1.5%), and 28 (14%) cases. In addition, 19 (3%), 0 (0%), and 0 (0%) of the remaining cases were only missing outcome data necessary for building and testing the predictive model were also excluded. Finally, the Rembrandt dataset contains cases for multiple grades of glioma and our predictive model targets only glioblastoma; therefore we excluded 109 (17%) cases of grade II and grade III gliomas from the dataset.

Following the removal of cases and variables for circumstances of non-random missingness, we selected the final set of modeling variables common to all three datasets. Demographic fields (e.g., gender, age) are typically straightforward to match. In addition, status variables such as Karnofsky performance score (KPS) are standardized and collected in the same way by all institutions. However, different naming schemes and a lack of documentation on data representations and formatting made it more difficult to determine when other variables were linked. For example, a general imaging status variable reported by the UCLA and Rembrandt teams was named differently between the datasets; and neither had documentation to indicate that both were using the same constraints for the scale value. Longitudinal collection of many of the variables also required a simplification for this analysis as most of the clinical variables (KPS, imaging, therapeutic interventions) were all recorded over time, and varied dependent on the number of follow-ups for a given patient and/or tumor recurrence. Variables with longitudinal data were therefore controlled for by pulling the closest follow-up to the halfway point of median survival time for each dataset.

Each ensuing dataset was then used to generate two predictive models: 1) a binary logistic regression model; and 2) a Bayesian belief network model. The end point for outcome was determined as survival past the mean survival time of the dataset. Logistic regression analysis was then performed using SPSS 20. The SPSS multiple imputation package generates missing values using an iterative Markov chain Monte Carlo (MCMC) method. The Bayesian belief network (BBN) predictive model was performed using BayesiaLab 5.0. For comparison, the prediction rates for a naïve Bayes classifier and “expert-derived” network were tested. Learning algorithms in BayesiaLab was also attempted, seeking to derive network connections from the data directly. The resulting network configurations, however, were not reasonable and some algorithms failed to produce a connected topology. Imputation for missing variables in these cases were computed by BayesiaLab using structural expectation maximization. Results from each of these methods were then compared to appreciate the differences in the datasets and the predictive rates possible based on the available data.

Results

After selecting a set of variables for evaluation and removing cases that did not have complete reporting, 98 Rembrandt cases, 467 TCGA cases, and 176 UCLA cases were available for the generation of predictive models. The final set of variables selected for model building in this analysis are presented below in Table 2. The chosen variables represent key clinical and treatment variables, and include an alternative imaging score variable as Vasari imaging variables were excluded. While, the selected variables were all available for the Rembrandt and UCLA datasets, the TCGA database did not contain alternative neurological and imaging scores and data on resection events did not indicate the amount of tumor removed. Radiation and chemotherapy treatments are coded into binary variables indicating if the prescribed treatment was received by the patient. Tumor resection is coded into four classes covering the extent of surgical resection: complete resection, partial resection, unknown result, and no reported resection. Given that the outcome for our model is survival of the patient past the median survival time for the population in the dataset, this selection resulted in a survival prediction at 18 months for Rembrandt; 12 months for TCGA; and 12 months for UCLA. Below we review the results found for each dataset using logistic regression and Bayesian belief network models.

Table 2.

Selected variables.

Variable	Range/Categorical Values	Data Source
		Rembrandt	TCGA	UCLA
Age	20–70	*	*	*
Survival past median	0 (No); 1 (Yes)	*	*	*
Karnofsky Score	0–100	*	*	*
Other neurological score	−2 – +2 (5-point scale)	*		*
Summary imaging score	−3 – +3 (7-point scale)	*		*
Radiation treatment	0 (No); 1 (Yes)	*	*	*
Temodar treatment	0 (No); 1 (Yes)	*	*	*
Other chemotherapy treatment	0 (No); 1 (Yes)	*	*	*
Amount of tumor resected	1 (Complete); 2 (Partial); 3 (Unknown); 4 (Not reported)	*		*

Rembrandt

Mean age of the patients was 50 (σ = 13). Patients survived for an average of 23 months (σ = 18) with a median survival time of 19 months. Missing data was present for the Karnofsky performance score, other neurological score, and imaging summary score variables. These variables were also measured for multiple patient follow-ups. To normalize the value used for analysis, the values collected closest to the 12 month follow-up examination were used. Five imputation groups were generated using the SPSS Multiple Imputation package to provide complete values for the regression algorithm. A binary logistic regression was then run with forward conditional selection. Variables were added to the model when reaching 95% significance. Models for each imputation group selected Karnofsky score, other chemotherapy treatment, and MRI exam score for the model. The predictive rates of outcome ranged from 65.7% to 69.2% for the five imputations. A full listing of results for each imputation run is provided in Table 3. The Rembrandt data was analyzed using two probabilistic models: a naïve Bayes classifier and a Bayesian belief network derived from an expert-derived topology of the selected GBM variables. The former method predicted patient survival outcome correctly at a rate of 76.53%. The expert model’s predictive success was 76.53%

Table 3.

Variables chosen for each dataset by logistic regression analysis.

	Run	Variables chosen				Constant	Accuracy (%)
Rembrandt	1	Karnofsky score	Other chemotherapy	MRI exam		−2.636	79.6
	2	Karnofsky score	Other chemotherapy	MRI exam		−2.803	74.5
	3	Karnofsky score	Other chemotherapy	MRI exam		−2.509	71.4
	4	Karnofsky score	Other chemotherapy	MRI exam		−2.040	74.5
	5	Karnofsky score	Other chemotherapy	MRI exam		−2.904	77.6
TCGA	1	Age	Karnofsky score	Radiation treatment	Other chemotherapy	−3.653	66.8
	2	Age	Karnofsky score	Radiation treatment	Other chemotherapy	−3.006	67.0
	3	Age	Karnofsky score	Radiation treatment	Other chemotherapy	−1.774	65.7
	4	Age	Karnofsky score	Radiation treatment	Other chemotherapy	−3.254	66.8
	5	Age	Karnofsky score	Radiation treatment	Other chemotherapy	−2.883	67.5
UCLA	1	Karnofsky score	Other chemotherapy			−5.062	71.0
	2	Karnofsky score	Other chemotherapy			−5.588	70.5
	3	Karnofsky score	Other chemotherapy			−5.087	69.9
	4	Karnofsky score	Other chemotherapy			−6.400	72.2
	5	Karnofsky score	Other chemotherapy			−6.300	69.9

TCGA

Patients from the TCGA dataset had a mean age of 53 (σ = 13). Average survival time was 16 months with a median time of 11 months. Only values for the Karnofsky performance score were missing for this dataset. Again, five imputations were generated from the available data. Selection for the TCGA dataset chose the same variables for all imputations: age, Karnofsky score, radiation treatment, and other chemotherapy treatment. Predictive rates of outcome ranged from 65.7% to 69.2% for the five imputations. Naïve Bayes prediction for the TCGA dataset was 67.45%. Performance from the expert model reached a success rate of 68.95%.

UCLA

Average age for patients seen at UCLA was 51 (σ = 13). Average survival time for patients was 14 months (σ = 12) with median survival falling at 11 months. Values were imputed to fill missing data for the Karnofsky performance score and other neurological score variables. All subjects in the UCLA dataset were prescribed treatment with temozolomide (Temodar). Therefore, Temodar treatment was not included for variable selection by the logistic regression analysis. Selected variables were consistent from the five generated imputations yielding Karnofsky score and other chemotherapy treatment as predictive variables for the model. Predictive rates of outcome ranged from 69.9% to 72.2% for the five imputations. Prediction of survival outcome for the UCLA dataset by the naïve Bayes model was 70.45%. Survival outcome prediction when applying the expert model reached 71.59%.

Following the generation of these models, prediction of UCLA outcomes was testing using the expert BBNs generated from Rembrandt and TCGA data. In both cases, the multi-institutional models were less accurate than the UCLA specific model. Prediction rates for the Rembrandt and TCGA models were 31% and 59% respectively. These results indicate additional considerations must be made in order to predict outcomes for patients from the local dataset beyond our efforts to control variable selection and model design.

Discussion

Our initial efforts to create a predictive model utilizing Rembrandt, TCGA, and UCLA data sources revealed several challenges related to data collection, representation, and analysis. We attempt to explain 1) the observed variability of the GBM datasets during the variable selection process despite their common disease ties; 2) the significant challenges related to the standardization and semantic representation of variables across these data sources; and 3) the issue of handling missing data. Finally, we describe future work aimed at understanding the nuances about combining study populations and applying theoretical approaches to address these issues.

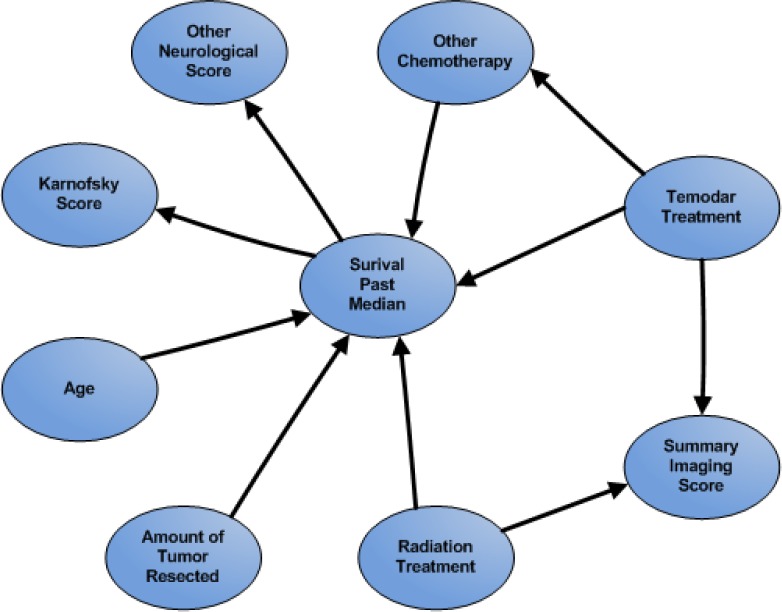
The logistic regression process tests the variables supplied for prediction and includes variables when they are deemed significant in their contribution to the decision making task. In our design, we attempted to choose a set of clinical variables that are common between the datasets. However, when the models were constructed, each regression equation was built around a different set of predictors. Some overlap exists between the resultant models, but the final selections cannot be considered equivalent. For the Bayesian models, the variable selection process assumed either full independence under naive Bayes or was dictated by an expert derivation of the topology. When we applied the UCLA data to expert Bayesian models generated using multi-institutional data, we found the final prediction rate fell below the observed rates seen using the UCLA-specific model. This pattern has been true for institution-specific models researchers are used to seeing in past research: they do not generalize well when used with data from a separate institution. When considering a multi-institutional model, researchers have anticipated that the diverse nature of the data resource might provide enough coverage of a population to create a generalizable model that could be supplied to many outside institutions.

It is apparent that simply matching the variable selection between datasets will not ensure that outside datasets can “plug-in” cases into another model to obtain predictions, even in the multi-institutional case. On the surface, even from a demographics perspective, the populations appear to be the same. Yet underlying differences in the population must be contributing to the inability to use the predictive information from a multi-institutional model to predict values from the local data. One potential cause of these issues is the coverage of the datasets used in model generation. For example, the standard Karnofsky score ranges from 0 to 100 in steps of 10. While scores in Rembrandt covered this full range, TCGA and UCLA data had minimum reported scores of 20 and 40 respectively. Similarly, while an instance of both 0 and 100 scores exist in Rembrandt, it is quite possible some scores are not represented in the training dataset or are underrepresented. When a future input from UCLA falls outside of the available training data, the prediction is more likely to be incorrect.

When working towards a working dataset for this study, concerns were also raised regarding the lack of standardization on the types of information collected within each dataset. Part of the difficulty is the lack of documentation associated with variables: a data dictionary that explicitly defines each variable or maps them to a controlled vocabulary would be a step in the right direction. Furthermore, it is important when working with public research data to understand contextual information such as the under what conditions were the data collected and what assumptions were made in recording the data (e.g., grading scale used). While TCGA provides a data dictionary with standardized terms (linked to the NCI Common Data Elements) and definitions, no equivalent resource is provided for Rembrandt data. In addition, while certain variables, such as Karnofsky score, are taken using a standardized scale, other variables nominal and ordinal variables are more difficult to interpret. For example, UCLA and Rembrandt have variables ranging from −3 to 3 that refer to a qualitative assessment of the patients imaging exam, “TumorStatus” and “MRIDesc” respectively, so the assumption was made that both variables were describing the same type of evaluation of imaging data (and, based on discussions with a practicing neuro-oncologist, this assumption is true). Similarly, for variables describing chemotherapy treatment, there was no indication if contributing institutions should report when no therapy was prescribed or if a blank entry in the database indicated this trait. Without documentation to describe the intended variable states it is left up to a researcher unfamiliar with the original design to make assumptions for facts such as scale variable ranges or when empty database entries imply no treatment or should be considered as an unreported fact. In addition, while Rembrandt data captures temporal ordering of certain variable measurements (e.g., Karnofsky performance score), no details about the number of days occurring between measurements and how the measurements relate to one another (e.g., are all temporally-dependent variables measured on the same day?); this information needs to be provided before meaningful temporal models can be built from the data.

The number of instances where data appears to be unreported in the Rembrandt and TCGA datasets further demonstrates the need for meta-documentation. In Rembrandt, for example, a few institutions contributed genetic data from their patients, but the remaining section on clinical data is empty except for information on end survival outcome (i.e., time to survival). Though the focus of the Rembrandt and TCGA initiatives is on genetic findings, clinical information is relevant to comparing cases for statistical analysis. Thus, when examining additional cases with partially complete clinical reporting, it became unclear if certain variables contained null values due to unreported facts missing at random; facts intentionally withheld based on some criteria; or were cases where the variable was not relevant because a particular treatment or reading was not performed on that patient. In handling missing data, it is important to understand the differences between when data is missing completely at random, missing at random, or missing not a random. There is no indication made if there are circumstances where this information is allowed to be excluded. Currently, we are removing cases from the datasets when it is unclear whether fields are empty due to data missing at random (MAR) or missing not at random (MNAR); however, this reduces the sample size of our cohort. If the data is MAR or MNAR, we potentially could use imputation techniques such as expectation maximization to estimate missing values. It is important for public data resources to document the expected format of submitted data since data is coming from many locations. Few research hospitals gather data in the same formats or with the same systems, meaning all data requires some amount of alteration or mapping for submission. Proper understanding of the data format and reporting can help indicate when missing values are due to an institution not having the appropriate data to submit.

Even if perfect documentation for all future resources were possible, some of these issues will still persist. Therefore, additional work must be done to examine methods which may examine these problems of external validly. Transportability theory provides a framework for determining under what circumstances integrating information from many different studies is possible¹¹. Since study populations differ, a level of generalization is required to make the data comparable. In traditional meta-analysis as well as our current analysis, this process is done by selecting studies based on some ad hoc criteria. Using the paradigm of transportability, one can use knowledge of the respective study designs and populations to bridge the gaps between study variables in order to compare and combine them in a principled way. Proper application of transportability rules describe the causal relations between the model variables and indicate where differences in populations will block the ability to generalize findings when predicting across populations. Therefore, applying this theory presents a challenge concerning how to translate our qualitative understanding of the data collection procedures into a causal model that explicitly describes the variables, relationships, and differences in populations. Within the theory, population differences for a variable are handled utilizing selection nodes which dictate when data is accessible from each differing group using the model for prediction. As part of future work, we intend to explore methods that would provide modelers with guidelines for applying transportability theory to a causal model and permit analysis of which model assumptions derived from one population are applicable to another without need to control for population differences. These guidelines require robust techniques for specifying the causal model and probabilities for each study population which is another open problem; we are currently exploring methods that utilize information reported in literature (e.g., randomized controlled trials) to provide estimates. Natural language processing (NLP) techniques are commonly employed to handle the task of matching data elements to controlled ontologies providing opportunities for term standardization. In addition, if elements of the data source are tied to a high level data source (e.g., neuroradiology reports, oncology results, labs), NLP tasks could be designed to pull relevant variable data from patient records directly to fill missing and unreported values and complete a dataset for an institution. Conventional statistical methods do not always make situations of bias obvious when working with observational data as gathered from our datasets. Using propensity scoring methods, we can more accurately test for potential bias across the large multi-institutional datasets and reconstruct our models accordingly¹². Finally, given the progression of disease in a patient, temporal aspects must be included in the design of future models. Dynamic belief networks (DBN) can be extended from baseline BBNs in order to model a disease progression over time.

Conclusion

This analysis is preliminary in examining the full scope of the relationships between these GBM resources. Results from the predictive analysis indicate that a selection of clinical variables is not powerful enough to predict outcomes for a clinical setting. Performance rates are similar between the different models and datasets, but variable selection in the models differs. This variation is expected to increase as more data is included to cover the entire scope of imaging and genetic variables. Therefore, additional work must be performed to understand the complex relationships between datasets and discover the proper techniques to relate evidence from individual institutions for use with multi-institutional models.

Figure 1.

Expert Bayesian Network