An Analysis of Multi-type Relational Interactions in FMA Using Graph Motifs with Disjointness Constraints

Abstract

The interaction of multiple types of relationships among anatomical classes in the Foundational Model of Anatomy (FMA) can provide inferred information valuable for quality assurance. This paper introduces a method called Motif Checking (MOCH) to study the effects of such multi-relation type interactions for detecting logical inconsistencies as well as other anomalies represented by the motifs. MOCH represents patterns of multi-type interaction as small labeled (with multiple types of edges) sub-graph motifs, whose nodes represent class variables, and labeled edges represent relational types. By representing FMA as an RDF graph and motifs as SPARQL queries, fragments of FMA are automatically obtained as auditing candidates. Leveraging the scalability and reconfigurability of Semantic Web Technology, we performed exhaustive analyses of a variety of labeled sub-graph motifs. The quality assurance feature of MOCH comes from the distinct use of a subset of the edges of the graph motifs as constraints for disjointness, whereby bringing in rule-based flavor to the approach as well. With possible disjointness implied by antonyms, we performed manual inspection of the resulting FMA fragments and tracked down sources of abnormal inferred conclusions (logical inconsistencies), which are amendable for programmatic revision of the FMA. Our results demonstrate that MOCH provides a unique source of valuable information for quality assurance. Since our approach is general, it is applicable to any ontological system with an OWL representation.

Introduction

Ontologies are shared conceptualizations of a domain represented in a formal language^[1]. They represent not only the concepts and classes used in scientific work, but just as importantly, the relationships between the concepts/classes. Ontologies have become a critical component in biomedical information management. They are used to handle terminological heterogeneity, facilitate system interoperability, and enable knowledge discovery. Familiar in their role in supporting application menus similar to those generated by MeSH Headings, ontologies are also becoming valuable for designing intuitive and novel interfaces to query, access, and visualize large sets of distributed biomedical datasets^[2,3,4]. Researchers are increasingly relying on biomedical ontologies as critical resources throughout their experimental work flows. In the last decade, more than 5,000 publications indexed by PubMed involved the use of ontologies. The Bio-Portal of the NCBO lists nearly 300 ontologies consisting of 5.3M terms used in a range of biomedical informatics applications from bench experiments to patient care at the bedside.

However, by their nature as formal representations of knowledge, ontologies are often incomplete, under-specified, and non-static. New applications are calling for new ontologies or expansion and enhancement of existing ones while many additional factors, such as manual editing, may introduce unintended defects. Thus Ontology Quality Assurance (OQA) has become an integral part of the ontology development life-cycle^[5,6]. Existing work includes the design of specific relational patterns for capturing circular, mutually exhaustive, redundant, and missed entries^[7], checking for lattice-violating fragments motivated by Formal Concept Analysis^[8], and logical^[9,10] lexical^[11], and content-based approaches^[12].

We introduce a novel method for OQA by exploiting the interaction of multiple types of relationships, called Motif Checking (MOCH). MOCH has a unique combination of features. It leverages antonyms to uncover the disjointness relation between concepts, not explicitly modeled in FMA; It combines the interaction of multiple times of relationships in the context of the disjointness property to achieve greater auditing specificity; It is computationally scalable, through the use of Semantic Web technology, so small graph motifs can be exhaustively enumerated and systematically checked; It has a strong rule-based flavor and is generally applicable to other ontological systems (not just FMA). The primary use case considered in this paper is the Foundational Model of Anatomy (FMA^[13]), which involves five main relational subtypes: subclass (is-a), part-of, regional-part-of, constitutional-part-of, and systemic-part-of. Such subtypes are explicitly supported by the Foundational Model Explorer (http://fme.biostr.washington.edu:8080).

The standard semantics for “part-of” is this following: class A is classified as part of class B if every instance of A has some instance of B as a part. This can be formally expressed in description logic^[15] as: A part-of B if and only if A ⊑ ∃pB, where p is the relation capturing the part-of relation at the instance level. By chaining of logical implications (i.e. X ⊑ Y and Y ⊑ Z implies X ⊑ Z), we obtain the following as a general principle, which we call subclass-partonomy mixing (Fig. 1): if A is-a B, and B is part-of C, then A is part-of C.

Figure 1:

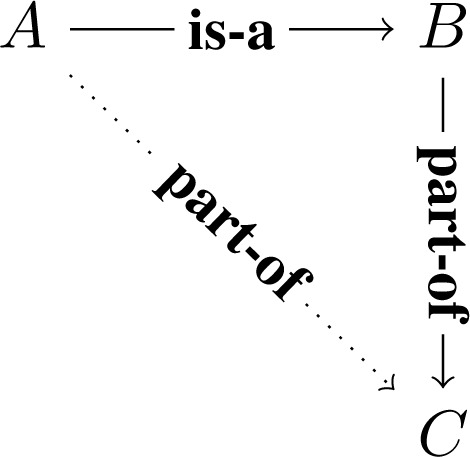
The subclass-partonomy mixing motif. Dotted line represents the inferred relation instance. This principle is sometimes called “relation dependence^[16].”

Does FMA conform to this? To answer this question, consider an example

• A = Male urinary system (FMA222947),

• B = Urinary system (FMA7159), and

• C = Female human body (FMA67812).

about which FMA asserted two relational instances:

1. Male urinary system (A) is a subclass of Urinary system (B), and

2. Urinary system (B) is a part of Female human body (C).

Therefore, we obtain “Male urinary system” is a part of “Female human body,” implying that the two classes should share instances, which is of course incorrect because Male urinary system and Female human body are disjoint classes. We know this based on external knowledge about canonical human anatomy, which is not represented in FMA. Therefore, such errors cannot be detected by checking logical consistency of FMA because it is under-specified with respect to disjointness.

The main objective of MOCH is to provide an exhaustive, computationally scalable approach to analyze the effect of interactions of multiple types of relations in ontological systems and provide a unique source of information valuable for quality assurance. This unique feature comes from the idea of “negative thinking:” motifs are designed to capture seemingly impossible configurations, aided by syntactic grounding on possible disjointness of concepts using antonyms in the names.

MOCH represents patterns of such interactions as small labeled sub-graph motifs, whose nodes represent class variables, and labeled edges represent the type of relationship. The motifs can be designed in such a way to deliberately capture “impossible” or “inconsistent” situations, such as the one on top of Fig. 2. If an actual subgraph is found which matches this motif, such as that shown in the lower part of Fig. 2, then it represents an auditing candidate. It invites us to re-examine the two asserted relational instances, Male urinary system is a subclass of Urinary system, and Urinary system is a part of Female human body, one of which is likely to be incorrect. In this particular example, the latter is incorrect because not all Urinary systems (male and female) are a part of Female human body.

Figure 2:

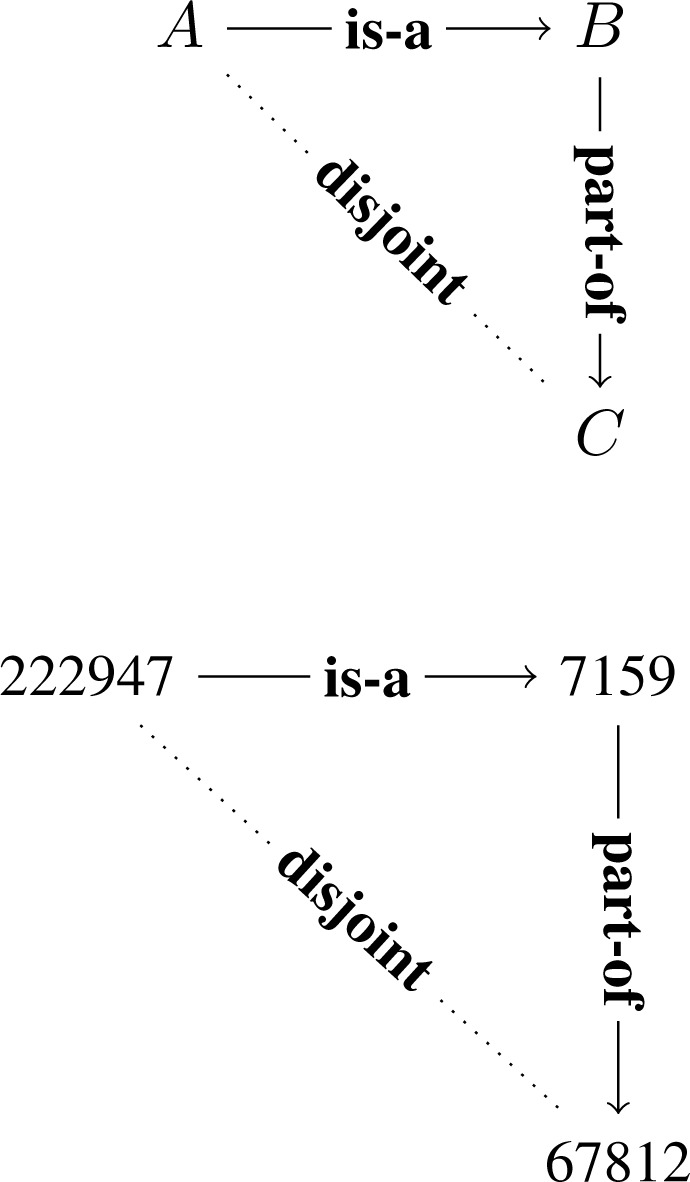
A disjoint open jaw motif (above) and a matching instance in FMA (below; numbers displayed are FMA ID).

This paper reports our implementation of MOCH for FMA in a Semantic Web (OWL, RDF, SPARQL) framework which is proven effective in lattice-based auditing of a different ontology^[8]. By representing FMA as an RDF data store and motifs as SPARQL queries, fragments of FMA satisfying the constraints expressed by the motifs are automatically obtained as auditing candidates. Leveraging the scalability and reconfigurability of RDF and SPARQL^[14], we performed exhaustive analyses of three two-node motifs, resulting in 638 matching FMA configurations; twelve three-node motifs, resulting in 202,960 configurations; and 755 root nodes with 4,100 respective descendants with opposing antonyms in their class names, for arbitrary-length motifs.

The analysis of such arbitrary-length motifs is achieved by an extension of MOCH, called Principal Ideal Explorer (PIE). PIE accounts for classes which may be vertically separated in the hierarchy by a sequence of mixed relationships. This achieves the ability to completely check arbitrary-length motifs by computationally manageable transitive closure operations. We found that the PIE extension can capture some situations not captured by MOCH alone, since the disjoint classes can be more than 8 steps away (i.e., requiring 8 relationship instances to reach from one end to the other). Although computationally more expensive, PIE is especially valuable since it would be very difficult to manually uncover errors following a long sequence of relations, particularly if one has to traverse different kinds of relations.

The rest of the paper is organized as follows. In Section 1 we review the background knowledge that our work draws from, such as FMA, RDF, SPARQL, and graph motifs. In Section 2 we describe the approach, computational pipeline, and the motifs studied. In Section 3 we present and discuss results obtained, and limitations. Concluding remarks are provided in the last section.

1. Background

Our methodology leverages two technological domains as a basis for analysis of the Foundational Model of Anatomy (FMA) ontology. The first technological domain we draw from is a subset of the Semantic Web technologies: the Web Ontology Language (OWL), the Resource Description Framework (RDF), and its associated query language SPARQL. The other technological domain is that of motif-based data mining. Below, we give an overview of these areas to explain the details of the methodology described in the subsequent sections. We begin with an overview of FMA.

1.1. The Digital Anatomist Foundational Model (FMA)

The FMA is both a theory of human anatomy and an ontology artifact^[13]. As a theory, it provides a unifying framework for the nature of the diverse entities that make up the bodily structure of biological organisms as well as the relationships between them. In particular, it is a theory of the canonical, phenotypic structure of the human organism at all biologically salient levels of granularity. As a theory of canonical anatomy, it ranges over those categories of entities which are idealizations of an organism’s body and its typical component parts. As a computational artifact, it is a formal representation of this theory, suitable for machine manipulation. The FMA is organized in a hierarchy of mutually-disjoint concepts^[16]. FMA modeling principles support the assumption that all the direct subclasses of a class are mutually disjoint. For example, Esophagus (FMA7131) and Stomach (FMA7148) are two direct subclasses of “Organ with organ cavity (FMA55672),” which are disjoint in the sense that an instance of “Esophagus” cannot be also an instance of “Stomach^[17].”

For the purpose of this work, since we are not working with direct sibling classes, we use implied disjointness property between classes using lexical information in class names. That is, we leverage antonyms for likely (but not always) disjointness, where disjointness of classes A and B means that no instance is both A as well as B; in set notation, A ∩ B =∅. For example, we infer that “Male urinary system” and “Female human body” are disjoint classes because their use of the antonym pair (male, female). (And indeed these are disjoint classes because an instance of “Male urinary system” cannot be also an instance of “Female human body”).

Table 1 includes common antonyms that may imply disjointness when used as pairs. We selected such anatomically relevant ones from a total of 400 common antonyms. Note that we listed only two lexicons, “first” and “second,” but of course this extends to subsequent numerals such as “third,” “forth,” etc. Strictly speaking, (first, second) are not antonyms.

Table 1:

A list of antonyms used in FMA class names which could, but not always, imply disjoint classes. The number represents the total number of FMA classes using the antonym in their class name.

Antonym	#FMA classes	Type
(male, female)	(165,155)	gender
(long, short)	(162, 116)	length
(left, right)	(19,494, 19,443)	lateral
(first, second)	(2,502, 2,902)	order
(simple, complex)	(16, 14)	order
(major, minor)	(346, 369)	order
(anterior, posterior)	(3,848, 5,519)	position
(upper, lower)	(1,423, 1,379)	position
(frontal(front), back)	(350(6), 120)	position
(horizontal, vertical)	(70, 44)	position
(outer, inner)	(89, 109)	position
(small, large)	(104, 78)	size

Note that classes using antonyms are not automatically disjoint. For example, it likely takes a domain expert to conclude that the class “Transitional myocyte of right branch of atrioventricular bundle (FMA263172),” containing the substring “right,” is disjoint from “Region of wall of left ventricle (FMA85471)” which contains the substring “left.” The heuristics we exploit is that in some cases, especially gender, such classes are indeed disjoint. Nonetheless, some gender specific information may not be explicitly reflected in class names, such as “Prostate (FMA9600),” a male only anatomical class which does not contain “male” in the label.

1.2. Semantic Web Technology: OWL, RDF and SPARQL

In the Semantic Web, RDF is used as a format to represent directed, labeled multi-graphs. It models entities in a triple structure consisting of a subject, predicate, and object^[18]. The Web Ontology Language (OWL^[19]) is a formal language for specifying the constraints of a particular domain, and is meant to govern the structure and meaning of the vocabulary used by RDF content. OWL ontologies are often distributed as RDF graphs in a document format.

The query language for RDF is called SPARQL^[20]. SPARQL queries are comprised of patterns and logical combinations thereof. The patterns in a SPARQL query also have a triple structure, but the terms can also use variables that represent wildcards. They are evaluated against an RDF database (a.k.a. RDF store) that is typically hosted on a remote server over a standard, web-based protocol. SPARQL queries result in matching subgraphs as solutions, which map variables in the query to the variable terms that comprise the triple structure of an RDF graph in the data store.

1.3. Networks, Graph Motifs, and Disjointness

Ontologies like the FMA can be represented in RDF as a directed, labeled graph. In such a graph, classes are RDF subjects and objects, semantic relationships between classes are RDF predicates interpreted as edge labels, and class labels are attached to class nodes via other triples using the RDF predicate rdf:type. This way, powerful results from network science, such as motif analysis^[21,22] in graph mining^[23], can be used to provide analytical characterizations of networks of different types and the distributions of the constituent small subgraph components, in ontologies.

Methods in both network science and graph mining are aimed almost exclusively at unlabeled graphs, either directed or undirected. But in semantic graphs like ontologies, the semantics are exactly carried by the label information in the semantic relation predicates and class labels, in addition to the directionality of the links (triples are not generally symmetric). We bring specifically methods in labeled and directed motifs to bear in MOCH and PIE to identify anomalous patterns within the FMA. Such patterns hinge upon the property of disjointness between classes. Although disjointness is not explicitly represented in FMA, we approximate it syntactically from antonyms (Section 1.1).

We use SPARQL queries to represent graph motifs. Such queries, when evaluated against an RDF store, will return a set of configurations satisfying the motif. Thus it is very natural to use RDF and SPARQL as the computational framework to implement our methods. We use Virtuoso, an implementation of RDF and SPARQL by OpenLink, for this study.

2. Methods

The MOCH approach for identifying FMA auditing fragments for review involves the following steps: 1) acquiring FMA data and generating RDF data store; 2) creating SPARQL queries to encode two-node, three-node motifs; 3) executing the motifs to obtain detected configurations.

2.1. Acquiring FMA Data

The model underlying the FMA is a frame-based representation with 78,977 concepts including macroscopic, microscopic and sub-cellular canonical anatomy. For our analysis, we used the legacy version of the OWL translation of FMA from the Open Biomedical Ontology (OBO) Foundry. The FMA OWL version from OBO foundry is distributed as an RDF/XML-based serialization that enables it to be stored in an RDF data store and made available to be queried via SPARQL over internet protocol.

2.2. Preparing SPARQL-based Motif Templates

SPARQL queries were created in three distinct categories corresponding to the three types of motifs we investigated: two-node motifs, three-node motifs, and arbitrary-length motifs. For single node, the motif would amount to checking cycles, which we have not found any in FMA, consistent with known-observations^[15].

Two-node Motif

A two-node motif is the smallest motif of interest. With one relationship instance between two class nodes, this become the basic building block of primitive asserted relationship instances. The following motifs are considered:

1. A is-a B and also A is a part-of B at the same time;

2. A is-a B, and A and B involve antonyms in their class names;

3. A is a part-of B, and A and B involve antonyms in their class names.

We were interested in this kind of motifs because such multiple types of relationships between the same classes looked counterintuitive at first.

Three-node Motif

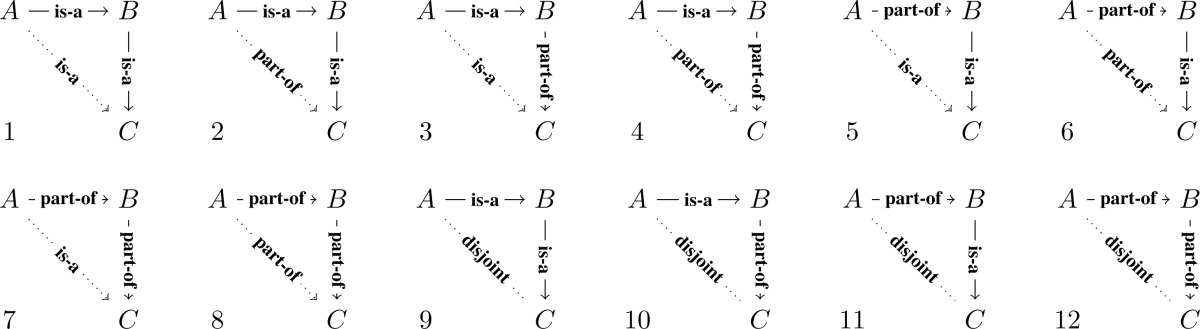
With a single edge relation linking three node classes, we considered 12 motifs as displayed in Table 2.

Table 2:

The first 8 motifs accounts for all possible combinations of two relational types, is-a and part-of, between any pair among three classes. The remainder 4 motifs (9–12) represent configurations that fix any two relationships between A, B and B, C, but leaves the third one, between A, C, to be possibly disjoint. Disjointness exists between opposing gender classes, but may not be automatically inferred from antonyms.

Principal Ideal Exploration

One of the limitations of three-node motifs is that the classes at the two ends are separated by precisely two links, i.e., two asserted relationship instances. We use Principal Ideal Explorer (PIE) to extend MOCH to account for situations where classes at the two ends are separated by an arbitrary number of links, exploiting the transitivity property of is-a and part-of. Thus PIE will extend motif analysis to principal ideals to achieve completeness of quality checking throughout the hierarchy.

The idea behind PIE is that properties that hold for more general (“ancestor”) classes in taxonomies and partonomies also hold for more specific (“descendant”) classes. If class A and class B are connected by a sequence of relational instances (is-a or part-of), in the same direction, then A and B should not be disjoint (otherwise it is not possible to inherit properties from the ancestor class). For an illustration, Fig. 3 depicts the class “Superficial fascia of male perineum (FMA20722),” which is linked to the class “Female body wall (FMA259159)” through a sequence of 5 links. What makes this situation incorrect is the disjointness of the class at one end (“Superficial fascia of male perineum”) with one at the other end (“Female body wall”).

Figure 3:

The class “Superficial fascia of male perineum (FMA20722)” is linked to the class “Female body wall (FMA259159)” through a sequence of five “is-a” and “part-of” relationship instances.

In order theory, the group of descendants of a class is called a “principal ideal.” The systematic calculation of principal ideals involves transitive closure, which is computational prohibitive when multiple types of relations are involved. Therefore, to achieve a feasible PIE motifs implementation using SPARQL, we perform the computation in two phases. The first phase transforms the FMA OWL/XML source file by converting every part-of relational instance to an is-a instance. A relation-type-ignorant RDF store is created from this transformed source which encapsulates structural, or hierarchical information only since directionality and linkage are maintained. The second phase involves look-ups, after interesting structural information is obtained, into a separate RDF store which faithfully encapsulates distinct relationships (which we use for two-node and three-node motifs). The second phase is used to query relational types necessary for detailed final results.

2.3. Implementation

The FMA OWL file was loaded into a Virtuoso RDF store, version 06.01.3127, hosted on a MacPro desktop machine with 32GB of RAM and one 2.8GHz Quad-Core Intel Xeon “Nehalem” processor, running Max OS X Snow Leopard. The motif-specific SPARQL queries patterns were executed against the Virtuoso store using a simple script.

The script executed the two-node and three-node motifs in SPARQL queries in a straightforward manner. For example, following SPARQL query retrieved the 9 results for motif 10 in Table 3, displayed in detail in Table 4.

Table 3:

Entry indicates the number of FMA configurations matching the corresponding motif. *: The details of the 9 configurations for Motif 10 are displayed in Table 4.

(a) Number of Cases for Motifs 1–8 in Table 2
Case	# (A,B), (B,C) instances	A is-a C	A part-of C
1&2	108,154	0	30
3&4	22,078	0	631
5&6	31,826	810	210
7&8	40,902	13	1,047
Total	202,960	823	1,918

(b) Number of Cases for Motifs 9–12 in Table 2
Antonym\Motifs	9	10	11	12
(male, female)	0	9	0	1
(left, right)	37	39	11	78
(anterior, posterior)	146	29	36	38
(upper, lower)	3	10	8	17
Total	186	87	55	134

Table 4:

All 9 fragments for Motif 10 are displayed, where A is a subclass of B, B is a part of C, with A, C involving opposite gender and B being gender-neutral.

A	B	C
Skin of male breast	Skin of breast	Female breast
Superficial fascia of male breast	Superficial fascia of breast	Female breast
Male nipple	Nipple	Female breast
Male areola	Areola	Female breast
Male urinary system	Urinary system	Female human body
Compartment of male thorax	Compartment of thorax	Female thorax
Compartment of male thorax	Compartment of thorax	Female body compartment
Compartment of female thorax	Compartment of thorax	Male thorax
Compartment of female thorax	Compartment of thorax	Male body compartment

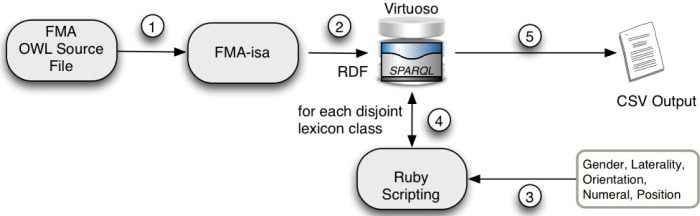
PIE was implemented in several steps (see Fig. 5): (1) convert all part-of relation to is-a relation in the XML data source, for computational efficiency when performing transitive closure; (2) create a relation-type-ignorant RDF store in Virtuoso from the converted data source; (3) feed antonyms and (4) perform SPARQL query for transitive closure against Virtuoso’s SPARQL API through a custom Ruby script; (5) output matching configurations in a csv file.

Figure 5:

PIE computational pipeline.

An independent set of length-specific SPARQL queries was created and executed to validate the result for the (male, female) antonym pair, for motif lengths ranging from 3 to 8, involving 4 to 9 nodes. In fact, Fig. 3 was a part of the result for a six-node PIE motif.

3. Results

The results are organized around the sizes of the motifs: two-node, three-node, and arbitrary-length motifs.

3.1. Two-Node Motifs

Ais-aBand alsoAis a part-ofB (Type (I)). We found 180 pairs (A, B) such that A is-a B and also A is a part-of B. For example, “White matter of right cerebral hemisphere” is both a subclass of, as well as a regional part of “Cerebral white matter.” All pairs involve continuous structures, such as “branch,” “surface,” “vessel,” “join,” and “layer.” All of the 180 cases, except one, involve the “regional-part-of” relation. The exception involves “Joint of head of rib” being a systemic part of “Costovertebral synovial joint,” in addition to being a subclass and a regional part of it.

Ais-aB, andAandBinvolve antonyms (Type (II)). We found no male-female anatomic pairs, but two upper-lower pairs: “Inferior margin of left upper lobe” is a subclass of “Inferior margin of lower lobe of lung,” and “Set of upper superficial inguinal lymph nodes” is a subclass of “Set of lymph nodes of lower limb.” These warrant further discussion on their validity. The remaining 34 cases of right-left, 15 cases of left-right, 151 cases of posterior-anterior and 128 cases of anterior-posterior pairs did not result in any apparent inconsistency. This is because both opposite antonyms appear in the same class name (in either one or both A and B), such as “Parenchyma of superior division of posterior part of right anterior bronchopulmonary subsegment.”

Ais a part-ofB, andAandBinvolve antonyms (Type (III)). We found no male-female anatomic pairs, but 7 lower-upper pairs, 17 left-right pairs, 33 right-left pairs, 40 posterior-anterior pairs, and 33 anterior-posterior pairs. Some left-right instances for case 2.3 are worth further discussion: “Tarsal gland of lower eyelid” is a regional part of “Skin of left upper eyelid;” “Cavity of interchondral joint of left 5th and 6th ribs” is a regional part of “Interchondral joint of right 5th and 6th ribs;” “Set of right subclavian lymphatic vessels” is a constitutional part of “Left subclavian lymphatic chain;” “Skin of lower inner quadrant of right breast” is a regional part of “Skin of left breast;” “Anterior lamina of splenorenal ligament” is a regional part of “Posterior wall of splenic part of lesser sac.” Such cases may indicate the challenges in precisely defining the meaning of “regional part of” and “constitutional part of,” both of which seem to refer to some larger anatomical contexts not explicitly specified.

3.2. Three-Node Motifs

With a single edge relation linking three node classes, we considered 12 motifs as displayed in Table 2. Table 3 summarizes the number of cases for each of the 12 motifs, with results for motifs 1–8 given in Table 3 (a) and motifs 9–12 in Table 3 (b). As indicated in Table 3 (a), Motif 1 and Motif 3 have no instances. This is reasonable because the transitivity for subclass (is-a) is implicitly assumed and rarely explicitly asserted. Motif 2 has 30 instances. As discussed in the two-node case, this reflects a small subset of anatomical structures that are recursive or continuous. Motif 7’s 13 instances represent similar situations. The remaining Motifs 4,5,6 and 8 have more instances.

Table 3 (b) summarizes results for the four remaining “disjoint open-jaw” Motifs (9–12). To capture “disjointness,” we use antonyms (Table 1) as filters to track down a subset of class pairs that are more likely to be disjoint. Each number in Table 3 (b) represents the number of instances of antonym concept pairs (A, C) for Motifs 9 - 12. Each case represents an unlikely or impossible configuration according to logic. For example, Table 4 lists the nine instances for Motif 10. Each instance here implies an incorrect assertion because of the disjointness implied by the antonyms (male, female), such as “Male urinary system” is a part of “Female human body.”

The remaining cases in Table 3 (b) are less clear as the (male, female) situation. Many FMA class names contain multiple antonyms in the same class. Among 78,977 FMA classes, the longest has 18 words, as in “Trunk of communicating branch of zygomatic branch of right facial nerve with zygomaticofacial branch of right zygomatic nerve.”

3.3. Arbitrary-length Motifs

The PIE method exploits transitivity to identify subgraph patterns with an arbitrary number of links (Section 2.2). We have tested and validated PIE on FMA and found results beyond those captured by MOCH. Table 5 displays the number of roots, as well as leaves of the opposing antonym. For example, there are a total of 11 roots involving “female” in their class names, nominating a total of 112 classes involving “male” in their class names. Similarly, there are a total of 21 roots involving “male” in their class names, nominating a total of 135 classes involving “female” in their class names.

Table 5:

Summary of results for arbitrary-length motifs. Numbers indicate the corresponding number of roots, as well as numbers of leafs involving the opposing antonym.

	(Female, Male)	(Left, Right)	(Anterior, Posterior)	(Lower, Upper)	Total
# Roots	(11, 21)	(132, 143)	(176, 239)	(16, 17)	755
# Opposite Descendants	(112, 135)	(876, 960)	(950, 875)	(98,94)	4,100

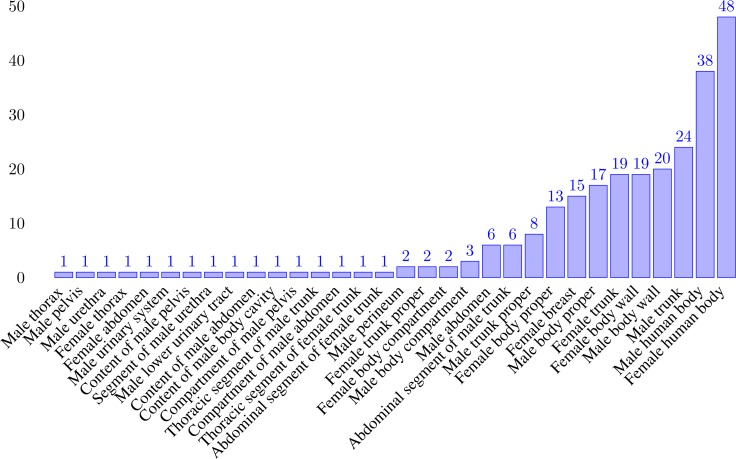
The details of the (11, 21) respective (Female, Male) root entry in Table 5 are plotted in Fig. 6. For example, “Skin of female thorax” is a descendant of “Male human body” through such is-a and part-of sequences: “Skin of female thorax” → “Skin of thorax” → “Skin of trunk proper” → “Skin of trunk” → “Skin of body proper” → “Skin” → “Integument” → “Integumentary system” → “Male human body.” Thus “Skin of female thorax” is one of the 38 classes in Fig.6, involving the female gender that fall under the subtree rooted at “Male human body.”

Figure 6:

The x-axis represents root class in the principal ideal, and the y-axis represents the number of descendants involving the opposite gender that are linked to the root class by a sequence of up to 8 links of subclass and part-of relationships.

All the chains in Fig. 6 involve a transition link where a gender neutral class is a direct descendant of a gender specific class, such as “Integumentary system” → “Male human body.” In most cases, such relationship instances are symmetric with respect to gender, i.e. if the instance “Integumentary system” → “Male human body” exists, the instance “Integumentary system” → “Female human body” also exists. Table 6 provides a sample of such relationship instances. We selected the cases that would fit a single line format, realizing that some FMA class names are quite long and will interfere with the illustration of the flavor of results found.

Table 6:

Sample classes that are both part-of a class associated with male, and a class associated with female.

Gender neutral class	part-of	Female gender class	Male gender class
Liver	constitutional-part-of	Compartment of female abdomen	Compartment of male abdomen
Neck	regional-part-of	Female body proper	Male body proper
Head	regional-part-of	Female human body	Male human body
Skin	constitutional-part-of	Female human body	Male human body
Diaphragm	constitutional-part-of	Female thorax	Male thorax
Coccyx	constitutional-part-of	Wall of female pelvis	Wall of male pelvis

3.4. Discussion

FMA

FMA is a large and complex ontological system, which currently consists of nearly 90,000 classes, over 174 spatio-structural relations, and about 2.4 million relationship instances. This paper only addresses one aspect of quality assurance, though using an innovative approach whose results would be difficult to uncover through manual means de novo. We found it quite impressive that only a very small fraction of the FMA suffers from inconsistency and errors using our systematic motif checking. Such errors seem correctable without too much effort. Indeed, the Structural Informatics Group at UW is working on correcting the inconsistencies identified in this study.

Semantics of Part-of

Formal modeling of the semantics of the different kind of partonomy relationships is a well-recognized intricate topic^[15]. It is especially challenging if logical reasoning is to be built on top of it^[16]. From what we can learn from the denotational semantics of programming languages^[25], there could be three general mechanisms to model the semantics of A is a part-of B at the class level: (a): A ⪯₁B if (∀x ∈ A)(∃y ∈ B) p(x, y), where p is a binary relation at the instance level representing “part-of;” (b): A ⪯₂B if (∀y ∈ B)(∃x ∈ A) p(y, x), where p(y, x) reads “y has-part x;” (c): A ⪯₃B if both A ⪯₁B and A ⪯₂B hold. In terms of the syntax of description logic, A ⪯₁B amounts to A ⊑ ∃pB; A ⪯₂B amounts to B ⊑ ∃p⁻A; and A ⪯₃B amounts to (A ⊑ ∃pB) ⊓ (B ⊑ ∃p⁻A), where p⁻ is the reverse of p. The outcome of this study hinged upon interpretation (a), a standard semantic interpretation for part-of. To differentiate the meaning of the different partonomy relationships, one might consider such different possible interpretations. However, any change in interpretation is likely to impact the rest of the structure as well^[15], and one needs to accept all logical consequences of any semantic commitment made.

Recommendation

If we take care of the incorrect cases in Table 4, then all the cases in Fig. 6 would disappear. There are two possible ways to amend the cases. One is to “relink,” the other is to “reinterpret.” One possible strategy would be to replace, for example, “Diaphragm” is a constitutional-part-of “Female thorax” and “Diaphragm” is a constitutional-part-of “Male thorax” simply by on assertion: “Diaphragm” is a constitutional-part-of “Thorax.” A new version of FMA already has reflected this strategy in part of the identified cases. Either way, it is important that in a single ontological system, the same semantic interpretation is maintained throughout the entire system.

3.5. Limitations

There are different versions of FMA and we did not systematically test our method on all of them for cross validation. FMA is originally represented in a frame-based structure^[17], which is not DL-based. Even though the OWL version of FMA we used is not semantically equivalent to its original representation, manual inspection with the version at http://fme.biostr.washington.edu:8080 shows that they share anomaly types identified here.

Our motif error detection method is most effective for disjoint classes. However, other than gender, using antonyms as a proxy for disjointness in other cases such as (left, right) turned out to be less reliable and had produce false positives based on limited manual inspection. In most cases, automatic methods need to be complemented by manual inspection and validation before any changes to take place.

We have not studied motifs of a more complex structure beyond 3 nodes, other than the arbitrary-length linear motifs through PIE. However, such an investigation is entirely feasible based on our approach, as long as the complex-structured larger motifs capture patterns of interest.

4. Conclusion

Using Semantic Web-based techniques, we have successfully implemented MOCH and PIE for ontology quality assurance of FMA, specifically targeting interaction of multiple types of relations captured as labeled graph motifs with disjointness constraints, in an exhaustive manner.

Our graph motif-based approach for ontology quality assurance has several unique aspects. First, arbitrarily sized motifs can be checked using PIE. Second, our approach has a rule-based, logical flavor, not only manifested in its implementation as “basic graph patterns” in SPARQL, but also in disjointness constraints between nodes. Third, our methodology and computational framework are completely general and are applicable to other ontological systems.

Gender induced disjoint classes allowed us to uncover a class of previous unidentified errors in FMA. With the help of Nature Language Processing techniques, it might be possible to extract more reliable disjoint classes based on the positions of a wider class of antonyms. Additionally, use of new advances in labeled motif analysis^[26] can help characterize the label assignments on the edges of structurally equivalent small graph patterns to represent the distribution of the semantic information in those subgraphs in terms of joint link pattern to identify other anomalous patterns within the FMA. Finally, the IHSTDO (http://www.ihtsdo.org) has launched a project for reconstructing the anatomical ontology. Our method should remain applicable if OWL is used as the main representation mechanism, or a translation to OWL can be readily achieved.

Figure 4:

Sample SPARQL query for a three-node motif with the male-female antonym.