Abstract
Privacy is becoming a major concern when sharing biomedical data across institutions. Although methods for protecting privacy of individual patients have been proposed, it is not clear how to protect the institutional privacy, which is many times a critical concern of data custodians. Built upon our previous work, Grid Binary LOgistic REgression (GLORE)1, we developed an Institutional Privacy-preserving Distributed binary Logistic Regression model (IPDLR) that considers both individual and institutional privacy for building a logistic regression model in a distributed manner. We tested our method using both simulated and clinical data, showing how it is possible to protect the privacy of individuals and of institutions using a distributed strategy.
Introduction
Data are increasingly being collected electronically in the field of biomedicine 2. A most prominent challenge for sharing these data is how to protect privacy. Although information exchange is critical in healthcare 3 and many people believe that the integration of data might lead to models that can help improve the quality of life 4–7, the prospect of inadvertently leaking sensitive patient information makes data custodians reluctant to share the data 8,9. To overcome such barriers and facilitate research 10, we have to systematically handle privacy concerns and mitigate the risk of inappropriate disclosure.
An interesting problem is how to train a global statistical model without sharing patient data from distributed local sites, which we have addressed in prior work 1. There are typically two types of studies, depending on how data are partitioned. The partition of patient sets is called a horizontal partition11. If attributes of each patient are split among data owners, we called this a vertical partition12. An early study 13 discussed how to train linear regression on both horizontally and vertically partitioned data. However, compared to the linear regression, the binary logistic regression 14 (LR) is more popular in biomedical informatics 15–19. Therefore, a model for training LR in a distributed and privacy-preserving manner is useful. Earlier work 20 by other authors showed how to estimate the coefficients of a LR model from distributed data concentrated on computing efficiency, but did not discuss the variance estimation, distributed ROC curves or distributed model fit test statistic calculations. Our recent approach, the GLORE model 1, which is based on the decomposition of patient data in the Newton-Raphson coefficient estimation procedure 21, provides a practical solution for training a LR model, conducting the Hosmer-Lemeshow goodness-of-fit test 22, and calculating the Area Under the ROC Curve (AUC) score 23. Although GLORE is a very useful privacy-preserving model for individuals, it requires that sites send their intermediary results to the central server without considering institutional privacy24, We define institutional privacy as the protection of important and sensitive information that, if leaked, can put an institution in disadvantage with respect to its peers or competitors. The goal in institutional privacy it so allow institutions to remain anonymous, so data cannot be traced back to a particular institution. This includes masking the provenance of information such as infection rates, complications, etc. It also includes masking the provenance of coefficients in a distributed logistic regression model. In this paper, we describe an algorithm that masks the ownership of the intermediary results (i.e., adjusted coefficients) sent to the central server, in an effort to promote institutional privacy.
Methodology
In GLORE, the distributed sites calculate coefficients for the LR model using their local data at each step or iteration, send these coefficients to the central site, and receive adjusted coefficients to start the next iteration. The central site can determine which site contributed each matrix of coefficients, and hence institutional privacy is not achieved. To overcome the shortcomings in GLORE, we propose Institutional Privacy-preserving Distributed binary Logistic Regression (IPDLR). The problem is how to combine necessary information from distributed sites into a central server in a privacy-preserving manner.
We developed the following algorithm, in which we assume that the central server needs to obtain the sum of matrices (i.e., each of size m1 × m2) from k local sites. This algorithm is inspired by Chen 9, who proposed a method for performing log-rank test in survival analysis in a distributed fashion.
Algorithm 1.
Secure summation
|
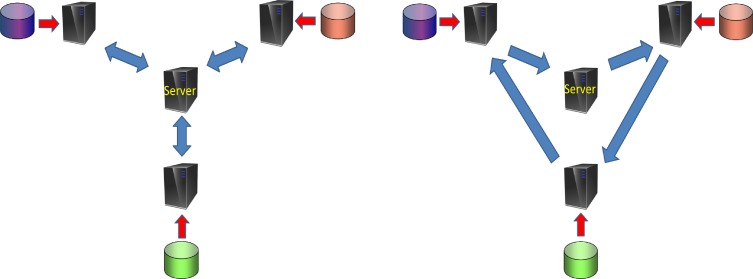
We can see that, by adopting Algorithm 1, the central server cannot recover the local matrix and each participating site is not able to infer local matrices from the other sites. Note that, in order to use Algorithm 1, the matrix sent to the server should be the sum of the matrices from all local sites. Figure 1 shows two different networks used for the basic GLORE model and for secure summation in IPDLR. Note that in the GLORE model only server-to-client communication is needed, while client-to-client communication is necessary in IPDLR.
Figure 1.
Two types of network for distributed computing. The left panel is the network used for base GLORE model, in which only communications between server and clients are needed. The right panel is the network used for Algorithm 1, in which communications between two clients are also necessary.
The innovations in the work described her refer to modification of GLORE to enable institutional privacy through secure summation, and a method to calculate ROCs in a distributed, privacy preserving fashion. In our previous work, we have only described an algorithm for AUC calculation in a distributed fashion.
Improvements in GLORE
IPDLR applies Algorithm 1 to various data integration steps involved in the GLORE model; including model coefficients estimation, variance-covariance estimation, and H-L test statistic computation. Specifically, the secure summation algorithm ensures the confidentiality in transmitting partial derivatives for coefficients, Fisher information for variance-covariance, and outcome distribution within each decile for H-L tests. This provides stronger security for local information in the distributed computation. In addition to these improvements, we developed a privacy-preserving way to obtain the ROC curve by leveraging the secure summation algorithm, which was not possible with the basic GLORE model.
Privacy-Preserving ROC curve
GLORE discusses how to compute the Area Under the ROC Curve (AUC) for model validation in a distributed, individual privacy-preserving fashion. However, the ROC curve supplies much more information than a single AUC score, since the ROC curve shows the one-to-one relationship between sensitivity and specificity. Some users may want to plot the ROC curve instead of getting a single AUC value. The ROC curve needs the contingency table, including true positive (TP), true negative (TN), false positive (FP) and false negative (FN) for each predicted probability. Please refer to Zou 23 for excruciating details on ROC analyses. For the overall contingency table, if all sites send their local table to the central server directly, the relationship between predictions and record labels (“one” or “zero”) for each site can be recovered in the central server. For example, if TP is increased by 4 between two adjacent rows, then the central server knows that there are 4 records with label “1” from a specific local site with a known predicted probability. Hence, a safer method is necessary for the ROC computation. Towards this goal Algorithm 1 is applied, and the local table information from each site is masked from the central server, which implies, according to our definition, that institutional privacy is preserved
To use secure summation, each site requires a local contingency table for all predictions from all sites. In fact, to create a local table each site only needs the rankings of its own predictions among the overall sorted (in descending order) prediction set, in addition to the size of the overall prediction set. Here, we present a method to get the local table elements (TP, TN, FP, FN) for the predictions from other sites. The four elements for a prediction with ranking is obtained using the following two rules when the prediction is from another site.
If i = 1, let TP = 0 and FP = 0, TN equals the number of local zero-labeled records, FN equals the number of local one-labeled records.
II. If i > 1, table elements are same as those for prediction with ranking i − 1.
IPDLR applies Algorithm 2 to obtain the overall contingency table. Once the central server has the contingency table, the ROC curve is plotted by the sensitivity ( ) against 1-specificity ( ) for each prediction.
Algorithm 2.
Overall contingency table calculation
|
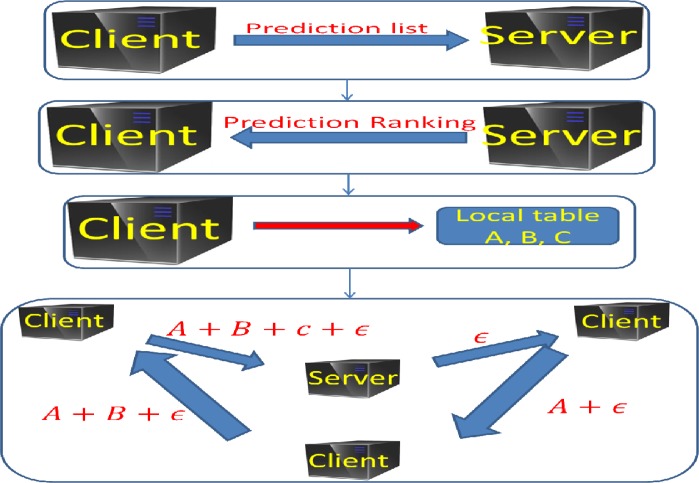
Figure 2 shows the flow chart for the main steps of plotting the ROC curve with three local clients. Next we use a simple artificial example to explain how Algorithm 2 works when there are only two local sites S1 and S2. Suppose site S1 has prediction set (0.9, 0.8, 0.5, 0.3, 0.2) and a corresponding class label set (1, 1, 0, 1, 0), and site S2 has prediction set (0.8, 0.7, 0.5, 0.3, 0.1) and a corresponding class label set (1, 0, 1, 0, 0).
Step 1 Both S1 and S2 send their prediction sets to the central server.
Step 2 The server sorts the combined sets in descending order to get A = (0.9, 0.8, 0.7 0.5, 0.3, 0.2, 0.1). The server sends prediction rankings R1 = (1, 2, 4, 5, 6) to S1 and sends prediction rankings R2 = (2, 3, 4, 5, 7) to S2. In addition, the server sends 7 (the size of A) to the two sites.
Step 3 (a) S1 creates the local contingency table for 7 predictions in A. First S1 finds table elements for its own predictions, which occupy the rows in R1. Then, using the two rules introduced previously, we fill out the missing parts in the table. Table 1 is the local contingency table for S1. The red colored cells in the table are filled based on the two rules.
Similarly Table 2 is the local contingency table created by S2.
Step 4 Algorithm 1 is adopted for the server to find the combined contingency table, as shown in Table 3.
Figure 2.
The flow chart for Algorithm 2 for ROC curve computation. Suppose there are three local clients with local contingency tables A, B and C. By the secure summation (Algorithm 1), the central server get the overall table A+B+C.
Table 1.
The local contingency table for S1
| prediction | rank | TP | FP | TN | FN |
|---|---|---|---|---|---|
| 0.9 | 1 | 1 | 0 | 2 | 2 |
| 0.8 | 2 | 2 | 0 | 2 | 1 |
| 3 | 2 | 0 | 2 | 1 | |
| 0.5 | 4 | 2 | 1 | 1 | 1 |
| 0.3 | 5 | 3 | 1 | 1 | 0 |
| 0.2 | 6 | 3 | 2 | 0 | 0 |
| 7 | 3 | 2 | 0 | 0 |
Table 2.
The local contingency table for S2
| prediction | rank | TP | FP | TN | FN |
|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | 2 | |
| 0.8 | 2 | 1 | 0 | 3 | 1 |
| 0.7 | 3 | 1 | 1 | 2 | 1 |
| 0.5 | 4 | 2 | 1 | 2 | 0 |
| 0.3 | 5 | 2 | 2 | 1 | 0 |
| 6 | 2 | 2 | 1 | 0 | |
| 0.1 | 7 | 2 | 3 | 0 | 0 |
Table 3.
The overall contingency table for plotting ROC curve
| TP | FP | TN | FN |
|---|---|---|---|
| 1 | 0 | 5 | 4 |
| 3 | 0 | 5 | 2 |
| 3 | 1 | 4 | 2 |
| 4 | 2 | 3 | 1 |
| 5 | 3 | 2 | 0 |
| 5 | 4 | 1 | 0 |
| 5 | 5 | 0 | 0 |
Experiments
We performed a simulation study and used two clinical data sets to validate the accuracy for IPDLR results. The computation was conducted using the R statistical language.
Simulation study
In the simulation study, we compared IPDLR (assuming data are evenly partitioned between 2 sites) and ordinary LR (combining all data for computation). We choose a total sample size of 1000 (500 for each site) and the feature (i.e., variable) number to be 9. First, we simulated all features from a standard normal distribution, then simulated the response from a binomial distribution assuming that the log odds of the response being 1 was a linear function of features (all coefficients were set to 1). We conducted the study on 100 runs to compare coefficient estimation difference between IPDLR and LR for the same simulated data. The study shows that the numbers of Newton-Raphson iterations to convergence are always 6 in this data set when 10−6 precision is set for the iteration stop criterion.
Table 4 shows the mean absolute difference (MAD) between 2-site IPDLR and LR estimations for all 10 coefficients (9 features plus 1 intercept), where the mean is for 100 runs. There are no substantial differences between IPDLR and LR estimations for all model coefficients.
Table 4.
Mean absolute difference (MAD) between a 2-site IPDLR and a centralized LR estimations
| Intercept | 5.30E-16 | Feature 5 | 2.11E-16 |
| Feature 1 | 3.87E-16 | Feature 6 | 4.88E-16 |
| Feature 2 | 7.99E-17 | Feature 7 | 3.19E-16 |
| Feature 3 | 1.21E-16 | Feature 8 | 7.55E-17 |
| Feature 4 | 8.77E-17 | Feature 9 | 9.21E-17 |
Clinical dataset experiments
Two real datasets are used to illustrate our IPDLR model. The first clinical dataset is related to myocardial infarction at Edinburgh, UK 15, which has 1,253 records with one binary outcome and 48 features. We picked nine non-redundant features in this data set and evenly split 1,253 records into two parts (627 vs. 626) to test IPDLR with 2 sites. The second dataset contains 141 records with 1 binary outcome denoting with cancer or not, and two biomarkers CA-19 and CA-125. The 141 records were split into 71 and 70 for two sites.
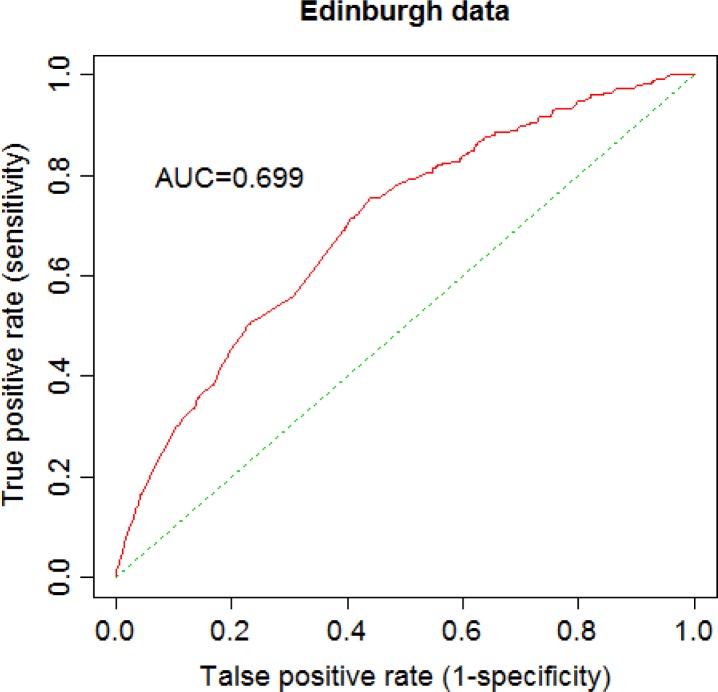
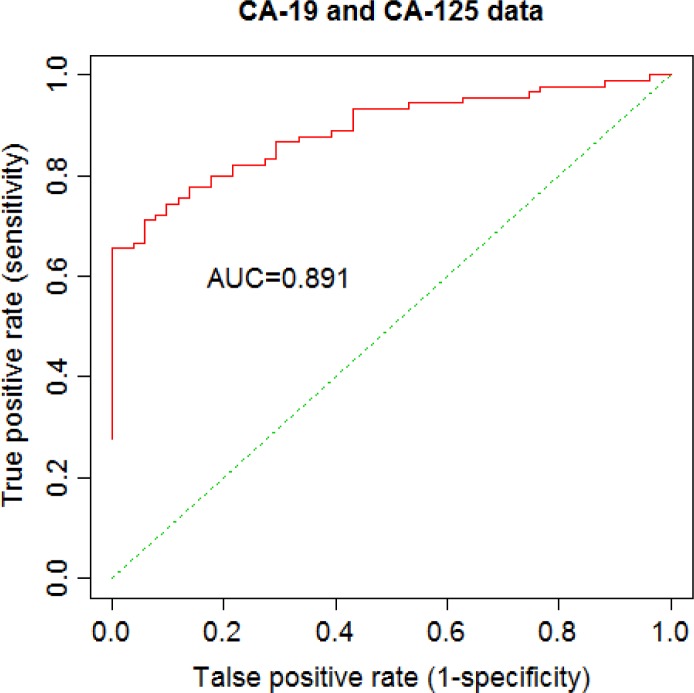
Tables 5 and 6 show results for fitting IPDLR including coefficient estimation and their standard errors, Z-test statistics and p-values for the Edinburgh data and for the CA-19 and CA-125 cancer marker data, respectively. When fitting IPDLR H-L test statistic equals 12.983 with a p-value 0.112 for the Edinburgh data, and H-L test statistic equals 3.510 with a p-value 0.898 for CA-19 and CA-125 data, which are no different from the results of fitting ordinary LR models. Moreover, there are 5 and 12 Newton-Raphson iterations needed for convergence with 10−6 precision for Edinburgh data and CA-19 and CA-125 data, respectively. In addition, AUC values for IPDLR are 0.699 and 0.891 for Edinburgh data and CA-19 and CA-125 data, respectively, which are no different from the results of ordinary LR models using all data. ROC curves for IPDLR were plotted as well. Figure 3 and Figure 4 are ROC curves generated by Algorithm 2 for the Edinburgh data and for CA-19 and CA-125 data, respectively. These ROC curves are exactly same as those produced from ordinary LR. Based on the H-L test and ROC curve (AUC) for the two clinical datasets, we see that LR fits CA-19 and CA-125 data very well.
Table 5.
Coefficient estimation for Edinburgh data for fitting 2-site IPDLR
| Estimation | Std. Error | Z-value | Pr(>|z|) | |
|---|---|---|---|---|
| Intercept | −1.0158 | 0.1940 | −5.2370 | 1.67E-07 |
| Smoker | 0.0799 | 0.1498 | 0.5331 | 5.94E-01 |
| Family history | 0.2939 | 0.1639 | 1.7933 | 7.29E-02 |
| Pain in left chest | −0.8456 | 0.2010 | −4.2074 | 2.58E-05 |
| Pain in right chest | −0.4011 | 0.2840 | −1.4126 | 1.58E-01 |
| Pain in back | 0.2864 | 0.2292 | 1.2494 | 2.12E-01 |
| Sharp pain | −1.2899 | 0.2344 | −5.5040 | 3.71E-08 |
| Tight pain | 0.1638 | 0.1621 | 1.0105 | 3.12E-01 |
| Previous angina | −0.4165 | 0.1485 | −2.8055 | 5.02E-03 |
| Sex | 0.2450 | 0.1559 | 1.5721 | 1.16E-01 |
Table 6.
Coefficient estimation for CA-19 and CA-125 data for fitting 2-site IPDLR
| Estimation | Std. Error | Z-value | Pr(>|z|) | |
|---|---|---|---|---|
| Intercept | −1.4645 | 0.3881 | −3.7739 | 1.61E-04 |
| CA19 | 0.0274 | 0.0085 | 3.2063 | 1.34E-03 |
| CA125 | 0.0163 | 0.0077 | 2.1008 | 3.57E-02 |
Figure 3.
ROC of a 2-site IPDLR for Edinburgh data
Figure 4.
ROC of a 2-site IPDLR for CA-(19,125) data
Discussion and Conclusion
The proposed IPDLR model was built on top of our GLORE model, but further improved it for institutional privacy, and added a mechanism to plot ROC curves in a distributed, institutionally-private fashion. In IPDLR, the provenance of original and derived data is masked. The core algorithm of IPDLR is secure summation. This algorithm is based on the creation of a random matrix and works when summation of partial information from all local sites is required in computation. To perform the secure summation, properties of the partial data could also be considered to improve the security. For example, the random matrix for the contingency table should only contain integer elements, and we could make the column that corresponds to the TP column also increasing. The central server also could perform error check before accepting the partial data, for example to verify whether the row sum is the same. IPDLR improves all distributed methods in GLORE, including coefficient estimation, variance-covariance matrix estimation, H-L test statistic calculation and AUC value calculation. Furthermore, IPDLR proposes a privacy-preserving method for calculating the ROC curve, which was not described in our previous work. IPDLR model improves the confidentiality of all participating clients and of the central server when the protocol is followed (i.e., all parties are trustful). However, it might still be possible to decrypt some patient information from the partial data while performing data analysis or data management. We plan to quantify the privacy risk within exchanged partial data using “differential identifiability”, a recent model proposed by Lee and Clifton 25, in future work. We will also improve the robustness and security of the system by developing quality control and error checking modules for received partial data. One idea for quality control is to filter out participants with low counts. For example, before the IPDLR model fitting starts, the central server will send the same computing algorithm (i.e., scripts or executable JAR files) to all sites and set a threshold to rule out sites with very low observation numbers.
Limitations:
Although IPDLR provides the opportunity of combining data for more statistic power, we need to decide whether fitting IPDLR with combined data will have added value (i.e., depending on the goodness-of-fit statistics at the local site as well as for the global model). We also need to perform data preprocessing for all local sites using same procedure before fitting IPDLR. The secure summation algorithm ensures institutional privacy. As a cost, the software design for IPDLR involves more complicated communications between parties as compared to what was needed for GLORE. We have also not addressed the problem of internal attacks that originate from within the communication network.
More work is needed to demonstrate the successful application of IPDLR in practice. However, this article presents the first steps towards a distributed logistic regression algorithm and its distributed evaluation that preserves the privacy of individuals as well as the privacy of institutions. We are currently working on a project making distributed models accessible and useful to data analysts, and we will use this opportunity to test and implement an IPDLR application in some clinical centers.
Acknowledgments
The authors were funded in part by the NIH grants R01LM009520, U54HL108460, R01HS019913, UL1RR031, 1K99LM011392-01.
References
- 1.Wu Y, Jiang X, Kim J, et al. Grid LOgistic REgression (GLORE): Building Shared Models Without Sharing Data. Journal of the American Medical Informatics Association (Accepted) 2012 doi: 10.1136/amiajnl-2012-000862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Wicks P, Vaughan TE, Massagli MP, et al. Accelerated clinical discovery using self-reported patient data collected online and a patient-matching algorithm. Nature biotechnology. 2011;29:411–414. doi: 10.1038/nbt.1837. [DOI] [PubMed] [Google Scholar]
- 3.McGraw D. Privacy and health information technology. The Journal of Law, Medicine & Ethics. 2009;37:121–149. doi: 10.1111/j.1748-720X.2009.00424.x. [DOI] [PubMed] [Google Scholar]
- 4.Mohammed N, Fung BCM, Hung PCK, et al. Centralized and Distributed Anonymization for High-Dimensional Healthcare Data. ACM Transactions on Knowledge Discovery from Data. 2010;4(18):1–18. 33. [Google Scholar]
- 5.Agrawal R, Grandison T, Johnson C, et al. Enabling the 21st century health care information technology revolution. Commun ACM. 2007;50:34–42. [Google Scholar]
- 6.Ramsey SD, Veenstra D, Tunis SR, et al. How comparative effectiveness research can help advance “personalized medicine” in cancer treatment. Health affairs (Project Hope) 2011;30:2259–68. doi: 10.1377/hlthaff.2010.0637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Informatics: H, Value LI to. Health Informatics: Linking Investment to Value. Journal of the American Medical Informatics Association. 1999;6:341–348. doi: 10.1136/jamia.1999.0060341. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.El Emam K, Hu J, Mercer J, et al. A secure protocol for protecting the identity of providers when disclosing data for disease surveillance. Journal of the American Medical Informatics Association. 2011;18:212–7. doi: 10.1136/amiajnl-2011-000100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Chen T, Zhong S. Privacy-preserving models for comparing survival curves using the logrank test. Computer Methods and Programs in Biomedicine. 2011;104:249–253. doi: 10.1016/j.cmpb.2011.04.004. [DOI] [PubMed] [Google Scholar]
- 10.Ohno-Machado L, Bafna C, Boxwala A, et al. iDASH. Integrating data for analysis, anonymization, and sharing. Journal of the American Medical Informatics Association. 2012;19:196–201. doi: 10.1136/amiajnl-2011-000538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kantarcioglu M. Privacy Preserving Data Mining. Springer US; 2008. A Survey of Privacy-Preserving Methods Across Horizontally Partitioned Data; pp. 313–335. [Google Scholar]
- 12.Vaidya J. A Survey of Privacy-Preserving Methods Across Vertically Partitioned Data. Privacy-Preserving Data Mining. 2008;34:337–358. [Google Scholar]
- 13.Sanil AP, Karr AF, Lin X, et al. Privacy preserving regression modelling via distributed computation. Proceedings of the tenth ACM SIGKDD international conference on Knowledge discovery and data mining; Seattle, WA: ACM; 2004. pp. 677–682. [Google Scholar]
- 14.Hosmer DW, Lemeshow S. Applied logistic regression. New York: Wiley-Interscience; 2000. [Google Scholar]
- 15.Kennedy RL, Burton a M, Fraser HS, et al. Early diagnosis of acute myocardial infarction using clinical and electrocardiographic data at presentation: derivation and evaluation of logistic regression models. European Heart Journal. 1996;17:1181–1191. doi: 10.1093/oxfordjournals.eurheartj.a015035. [DOI] [PubMed] [Google Scholar]
- 16.Hosmer DW, Lemeshow S. Confidence interval estimates of an index of quality performance based on Logistic Regression models. Statistics in medicine. 1995;14:2161–2172. doi: 10.1002/sim.4780141909. [DOI] [PubMed] [Google Scholar]
- 17.Seidling HM, Phansalkar S, Seger DL, et al. Factors influencing alert acceptance: a novel approach for predicting the success of clinical decision support. Journal of the American Medical Informatics Association. 2011;18:479–484. doi: 10.1136/amiajnl-2010-000039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Vest JR, Zhao H, Jasperson J, et al. Factors motivating and affecting health information exchange usage. Journal of the American Medical Informatics Association. 2011;18:143–149. doi: 10.1136/jamia.2010.004812. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ohno-Machado L. Modeling medical prognosis: survival analysis techniques. Journal of Biomedical Informatics. 2001;34:428–439. doi: 10.1006/jbin.2002.1038. [DOI] [PubMed] [Google Scholar]
- 20.Chu CT, Kim SK, Lin YA, et al. Map-reduce for machine learning on multicore. Advances in neural information processing systems. 2007;19:281–288. [Google Scholar]
- 21.Minka T. A comparison of numerical optimizers for logistic regression. CMU Technical Report. 2003;2003:1–18. [Google Scholar]
- 22.Hosmer DW, Hosmer T, Le Cessie S, et al. A comparison of goodness-of-fit tests for the Logistic Regression model. Statistics in Medicine. 1997;16:965–980. doi: 10.1002/(sici)1097-0258(19970515)16:9<965::aid-sim509>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- 23.Zou KH, Liu AI, Bandos AI, et al. Statistical evaluation of diagnostic performance: topics in ROC analysis. Boca Raton, FL: CRC Press Chapman & Hall; 2011. [Google Scholar]
- 24.Kantarcioglu M, Jin J, Clifton C. When do data mining results violate privacy?. Proceedings of the 2004 ACM SIGKDD international conference on Knowledge discovery and data mining - KDD ’04; New York, NY: ACM Press; 2004. p. 599. [Google Scholar]
- 25.Lee J, Clifton C. Differential Identifiability. ACM SIGKDD international conference on Knowledge discovery and data mining - KDD; 2012. (accepted) [Google Scholar]