Probabilistic Causal Models of Multimorbidity Concepts

Abstract

Multimorbidity, i.e., the presence of multiple diseases within one person, is a significant health-care problem for western societies: diagnosis, prognosis and treatment in the presence of of multiple diseases can be complex due to the various interactions between diseases. A literature review reveals that there is a variety of definitions that describe different concepts with respect to multimorbidity, both for the cause of multimorbidity as well as the implications of multimorbidity. To be able to aid computerized decision support systems within patient care, e.g. electronic clinical guidelines that can be personalized given the patient’s problems, these multimorbidity aspects need to be defined rigorously in a formal language. In this paper, we employ causal Bayesian networks to define and analyze a novel framework that can be used to model a spectrum of aspects related to multimorbidity. We conclude that this framework provides a solid basis for modeling interactions between multiple diseases.

Introduction

Epidemiological research indicates that more than two third of the elderly have two or more chronic diseases at the same time; this problem, one of the most challenging of modern medicine, is referred to as the problem of comorbidity or multimorbidity. Its focus has been increasing lately, and a large number of multimorbidity indices are available these days. A systematic literature research² emphasis on the heterogeneity of these indices, but also points out one important similarity, i.e. the focus is on diseases with a high prevalence and a severe impact on affected individuals, e.g. diabetes mellitus, cardiovascular diseases, and depression.

Although these indices show us the size, impact, and growth of the multimorbidity burden, they do not give much insight in underlying causal relationships between different chronic diseases that occur simultaneously within patients. The need for an integrated optimal management for a patient with multiple diseases, and the need to do so using decision support technology, implies the need for an integrated research methodology of multiple diseases. It is unlikely that such methodologies will be based upon traditionally statistical methods, e.g. logistic regression that focuses on the predictive power of specific variables for the presence or absence of one particular disease²⁶. In this paper, we will argue that probabilistic graphical models, e.g. Bayesian networks¹⁵, provide a good starting point for modeling interactions between multiple diseases. The edges of a graphical model represent statistical relationships between variables, which generalizes to multiple diseases in a natural way.

Some examples exist within clinical research that model specific diseases within a multimorbidity setting^17,20,25. However, to provide a more generic framework, we first need precise probabilistic definitions of the existing concepts related to multimorbidity. The contribution of this paper is therefore twofold. Firstly, we summarize existing classifications and terminologies used in definitions related of multimorbidity and point out their similarities and differences. Secondly, we will provide a rigorous probabilistic framework of multimorbidity concepts, using causal Bayesian networks, that fit these classifications and terminologies. Existing definitions of multimorbidity aspects are analyzed on the basis of this framework.

Background

Comorbidity and multimorbidity

In this paper, the principal focus is on the term multimorbidity, but since this is closely related to comorbidity, we also study the concepts related to the term comorbidity, which is most often defined in relation to a specific index condition, as in the seminal definition of Feinstein³. His interest was the prognosis of chronic somatic diseases and he defined comorbidity as any distinct additional entity that has existed or may occur during the clinical course of a patient who has the index disease under study. The term multimorbidity has been introduced in chronic disease epidemiology to refer to any co-occurrence of two but often more than two multiple chronic or acute diseases and medical conditions within a person^22,19. The introduction of this term indicates a shift of interest from a given index condition to the individuals who suffer from multiple diseases.

Much of the medical research relies on regression models which are applied to a single disease, and, thus, ignore the complexity of multimorbidity. Prevalence of multimorbidity has been studied in family practices^23,4, sometimes with clustering of specific diseases¹⁴, or a factor analysis to reveal patterns of co-occurrence of diseases¹⁸. These methods show that cardiovascular diseases often co-occur with metabolic diseases, and psychiatric diseases often co-occur with neurologic and somatic diseases causing chronic pain and disability.

These results illustrate the impact and complexity of multimorbidity, but give little insight into interactions between diseases. A systematic review on aging with multimorbidity¹³ identified twelve cross-sectional studies on multimorbidity, four on incidence and risk factors for multimorbidity, twenty-two on consequences of multimorbidity, nine on function status, six on quality of life, eight on health care utilization and six on models and quality of care. One of the major conclusions is that little is known about causality within multimorbidity.

Recently Valderas et al.²¹ summarized several conceptual problems. Differentiating the nature of conditions is critical to the conceptualization of comorbidity, e.g. conditions can be part of a certain syndrome and should perhaps not be classified as having comorbidity. The question of which condition should be designated as the index and which the comorbid condition is not self-evident and may vary in relation to the research question, the disease that prompted a particular episode of care, or of the specialty of the attending physician. In that respect, the sequence in which comorbidities appear may have important implications for genesis, prognosis, and treatment.

From a patient and physician’s point of view, multimorbidity is part of a bigger concept, i.e. the multimorbidity burden, which adds parameters such as polypharmacy, sex, age, frailty and other health-related individual attributes and the patient’s complexity (adding non-health related individual attributes). For polypharmacy, multiple definitions are utilized in the literature. Basically a certain minimum number of drugs has to be used, but additional definitions include the minimum time of subscription, regular daily consumption of multiple medications, and the use of high-risk medications and questionable dosing. A literature review on polypharmacy in the elderly⁵ stated that selecting appropriate limits for numbers of medications may be counterproductive in populations with multiple comorbidities.

Causal relations within multimorbidity

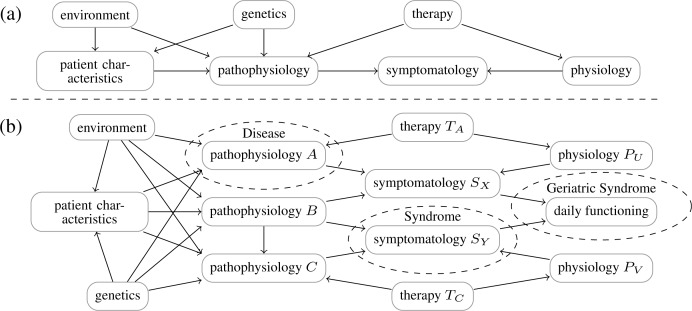
A part of the context of the multimorbidity burden is illustrated by Figure 1, which provides an abstract view on the problem. We make the assumption that a disease always corresponds with a particular pathophysiology, in contrast to syndromes. Syndromes represent a certain symptomatology which can be caused by several pathophysiologic processes. Furthermore, within gerontology certain combinations of diseases are defined as a geriatric syndrome, meaning a combined set of specific symptomatology that leads to impaired daily functioning. For example, the combination of polyneuropathy, impaired vision, and the usage of drugs that affect the patient’s consciousness (e.g., benzodiazepine), often leads to higher risks of falling, the latter being defined as a geriatric syndrome.

Figure 1:

Abstract model of a single disease (a) and multiple diseases (b).

A therapy does not necessarily have to act directly on the underlying pathophysiology of the disease intended to treat. In many cases another physiologic process is used to suppress the symptoms of the disease. For example, within hypertension diuretics use kidney function to lower the blood pressure, although the actual cause of the hypertension within a particular patient may be due to another pathophysiologic process. Another issues is that where a therapy typically acts on a designated (patho)physiology, it may also act on another physiologic processes, causing side effects. Accumulation of side effects due to polypharmacy can have a major impact on the quality of life.

Whereas the single disease model is fairly simple, mutual dependences within the multiple disease model may concern the pathophysiology, symptomatology, therapy, and prognosis. By modeling these interactions explicitly, better decisions can be made for patients who have multiple diseases. Moreover, single disease models often contain a lot of overlap; this redundancy may be avoided by integrating different disease models into a single model. For example, consider a physician facing a patient, with a history of multiple chronic diseases, now having a new problem. How could the physician tell if the problem is caused by either a new disease, existing morbidity, a side effect of existing pharmacotherapy, or just a natural phenomena due to aging or aging related stress factors? Treating it just as a new problem (whether introduced by existing diseases/treatments or not) is often the most pragmatic way. But with each newly introduced treatment the overall personal multimorbidity puzzle becomes more and more intractable.

As an example consider Diabetes Mellitus (DM), in which two types are recognized, i.e. impaired insulin production due to destruction of β-cells in the pancreas (type I), and insulin resistance of peripheral tissue (type II), both causing uncontrolled high blood glucose levels. Measuring this feature of the disease, i.e. high blood glucose levels, is the corner-stone of the diagnosis and pharmacological control of DM. The main consequences of sustained high blood glucose levels are neuropathy and blood vessel damage, the latter causing new diseases, e.g. retinopathy, renal failure, heart failure, impaired wound healing etc. So, a sustained pathophysiological condition caused by a chronic disease, which can be measured using a specific laboratory test, is often the cause of new diseases. In fact, we can do the same exercise for condition like a sustained high blood pressure (mostly of unknown cause) or high blood lipids (mostly of dietary cause). In general practice, the presence of such secondary diseases strengthens the diagnosis.

Methods

To model and analyze multimorbidity concepts, we will employ Bayesian networks, which are statistical models that have the ability to model more complex structures between disease variables in comparison to traditional regression models. While regression models can only represent models with just one dependent variable, e.g., a single disease, Bayesian networks allow for inference about multiple diseases at the same time. Moreover, it has been shown that in complex medical domains, Bayesian network can outperform the predictive power of regression models¹¹.

Formally, a Bayesian network is a tuple ℬ = (G, X, P), with G = (V, E) a directed acyclic graph (DAG), X = {X_v | v ∈ V} a set of random variables indexed by V, and P a joint probability distribution. In the remainder of this paper, all random variables will be binary with values true and false and we will denote x for X = true and x̄ for X = false. X is a Bayesian network with respect to the graph G if P can be written as a product of the probability of each random variable, conditional on their parent variables:

$$P(x_1,\dots ,x_n)=\prod _{v\in V}P\left(x_v|x_j\hspace{0.17em}\hspace{0.17em}\text{for all}\hspace{0.17em}\hspace{0.17em}j\in \pi \left(v\right)\right)$$

where π(v) is the set of parents of v (i.e. those vertices pointing directly to v via a single arc). As a convenience, we will often write V if we mean the random variable X_v that is associated to v. In Bayesian networks, the arcs between variables model dependences between variables which give rise to probabilistic conditional independence relationships. We say that a variable X and Y is independent given Z if it holds that P (X | Y, Z) = P (X | Z). These independences can also be read off the graph using a well-known criterion called d-separation¹⁵.

Causal Bayesian networks are Bayesian networks where the directed edges in G represent causal influences between variables¹⁶, i.e., an arc between C and E means that C is a cause of E. In these models, we can consider probability distributions after interventions, written as P(x₁, . . . , x_n | do(x_i)), e.g., a probability distribution after modifying a certain risk factor. This probability distribution can be computed by:

$$P\left(x_1,\dots ,{\widehat{x}}_i,\dots x_n|\mathit{do}\left(x_i\right)\right)=\{\begin{array}{ll}{\mathrm{\Pi }}_{v\in V,v\ne i}P\left(x_v|x_j\text{for all} j\in \pi \left(v\right)\right)\hfill & \text{if}\hspace{0.17em}{\widehat{x}}_i=x_i\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$

In order to represent qualitative relationships between variables, we use qualitative causal influences and synergies resembling those of qualitative probabilistic networks^27,6. The semantics of these qualitative signs is slightly different in order to express comorbidity and multimorbidity concepts. Concretely, if we have an arc C → E, then we say C causally positively influences E if:

$$P(e|\text{do}(c))>P(e|\text{do}(\overline{c}))$$

Negative causal influences can be defined similarly. We can also consider synergies, e.g., positive additive synergies expresses that the joint causal influence of C′ and C′ is greater than their separate influence on their child E, i.e.,

$$P\left(e|c,c^{\prime }\right)+P\left(e|\overline{c},{\overline{c}}^{\prime }\right)>P\left(e|c,{\overline{c}}^{\prime }\right)+P\left(e|\overline{c},c^{\prime }\right)$$

Finally, we define a causal product synergies that expresses how the value of one variable influences the probability of the values of another variable in view of a third variable. A negative product synergy of C and C′ on variable E with value e means that if C is the case, then this renders C′ less likely, which can be expressed by:

$$P\left(e|c,c^{\prime }\right)\cdot P\left(e|\overline{c},{\overline{c}}^{\prime }\right)<P\left(e|c,{\overline{c}}^{\prime }\right)\cdot P\left(e|\overline{c},c^{\prime }\right)$$

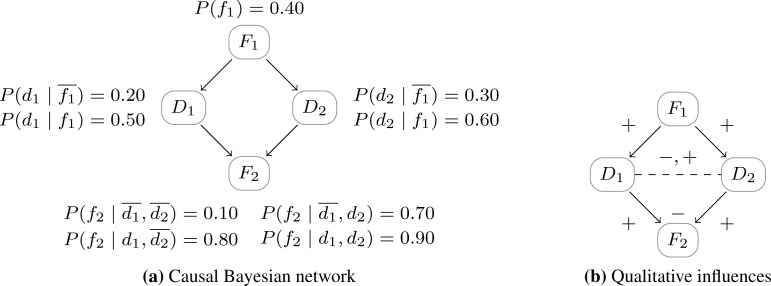
Similarly, negative additive and positive product synergies can be defined. See Figure 2, which illustrates a causal Bayesian network and the qualitative influences and synergies derived from the probability distribution.

Figure 2:

Example domain with two diseases and two features: F₁ causes D₁ and D₂; D₁ and D₂ both cause F₂. On the left a causal Bayesian network with its associated conditional probability distribution. On the right, the same network with its qualitative signs. All the influences between variables are positive, the additive synergy between D₁ and D₂ is negative and the product synergy between D₁ and D₂ is negative if f₂ and positive if $\overline{f_2}$.

Results

We will first list existing concepts with respect to comorbidity and multimorbidity from literature. Then we systematically discuss causal network structures with qualitative signs and provide an formal analysis with respect to these existing concepts.

Existing comorbidity and multimorbidity concepts

We searched the literature for possible relationships between comorbid and multimorbid diseases. The result of this search is summarized in Table 1. Each of these papers introduce concepts related to comorbidity and multimorbidity, which are sometimes mutually exclusive, but often overlapping.

Table 1:

Classification and terminology of comorbidity.

Author	Classification	Definition
Kraemer9	random	co-occurrence is completely random
	clinical	the response to a disease depends on the presence of another disease
	epidemiologic	there is a (un)known mechanism that bonds diseases together
	familial	the occurrence of diseases within a family is higher than one would expect purely based on epidemiological chance
Akkermans et al24	concurrent	the co-occurrence of an index condition with another health condition whether coincidental or not
	cluster	the co-occurrence of an index condition with another health condition at a significantly higher rate than expected by chance
	causal	the causal mechanism underlying the co-occurrence of an index condition and another health condition is known
Valderas et al21	non-etiological	there is no etiological association between diseases
	direct causation	one of the disease may cause the other
	associated	the risk factors for diseases are correlated
	heterogeneity	the risk factors are not correlated but affect both diseases
	independence	the presence of the diagnostic features of diseases is due to another distinct disease
Kaplan et al3,8	diagnostic	an associated disease can simulate symptoms of the index disease
	prognostic	diseases, in relation to an index disease graded according to their anticipated effects on therapy and life expectancy
	- cogent	comorbid ailments expected to impair a patient’s survival
	- noncogent	other ailments
Angold et al1	homotypic	diseases within a diagnostic grouping
	heterotypic	diseases from different diagnostic groupings
Piette et al7	concordant	diseases are part of the same pathophysiologic or management profile
	discordant	diseases that are not directly related in either pathogenesis or management and do not share an underlying predisposing factor

The classification made by Kraemer⁹, was one of the first classifications, classifying comorbidity into random, clinical (C-comorbidity), familial (F-comorbidity), and epidemiologic comorbidity (E-comorbidity). While clinical and familial comorbidity are defined, the focus of this paper is mostly on the measurement and interpretation of the types of comorbidity occurring in epidemiology (E-comorbidity). A further analysis of C-comorbidity and F-comorbidity is not given. The classification proposed by Van den Akker et al²⁴, based on categorization the of Schellevis¹⁹, is a hierarchical classification. Obviously, all instances of comorbidity fulfill the definition of concurrent comorbidity. Some of these comorbidities will occur in numbers greater than expected by chance and hence should be classified as cluster comorbidity. Some of those statistically significant comorbid associations represent known causal relationships and should be defined as causal comorbidity. This classification is taken significantly further in the work by Valderas et al²¹. In this paper there are three ways that lead to associations between diseases: by direct causation, by associated risk factors, or by heterogeneity in risk factors. In the direct causation model, the pathophysiology of one disease leads to another disease. In the associated risk factor model, risk factors are correlated (e.g., one causes another). Finally, in the heterogenic risk factor model, the risk factors are independent, but influence both diseases. For two given diseases, these models can occur at the same time.

Besides the mechanisms for the co-existence of multiple diseases, differences in implications for multimorbid diseases on clinical care is also relevant. For example, Kaplan et al^3,8 distinguished between diagnostic and prognostic comorbidity. In diagnostic comorbidity different diseases can share specific symptomatology, making the diagnosis harder. In prognostic comorbidity, comorbid diseases alter the prognosis of the patient (mostly negative), sometimes as expected (cogent), but sometimes also unexpected (non-cogent). Closely related to diagnostic comorbidity is the work done by Angold et al¹, who classified comorbidity into homotypic and heterotypic. These terms are typically used in psychiatric comorbidity, where in homotypic comorbidity, diseases belong to the same diagnostic group, e.g. depression and a dysthymic disease, and in heterotypic comorbidity, diseases belong to a different diagnostic group, e.g. depression and a personality disease. Finally, Piette et al⁷ classified multiple diseases into concordant and discordant. Concordant diseases are part of the same pathophysiology, e.g. cardiovascular diseases due to atherosclerosis, or share a specific therapy, e.g. β-blockers are used for both hypertension and cardiac arrhythmias. Discordant diseases do not share a part of the pathophysiology or similar types of management.

Etiological probabilistic models of multimorbidity

From a probabilistic point of view, there are only a few essential differences in the co-occurrence of multiple diseases. The first possibility is that the co-occurrence between diseases is random, which means that the co-occurrence of these diseases is exactly from what can be expected by chance. Adopting the standard probabilistic terminology, we will call this notion independent multimorbidity, and can be expressed in probability theory by:

$$P\left(d_1,d_2\right)=P\left(d_1\right)P\left(d_2\right)$$

Assuming the binary random variables D₁ and D₂ represent the occurrence of each disease, it follows that D₁ is independent of D₂, e.g., the absence of d₂ also will not have an influence on d₁ as

$$P\left(d_1|\overline{d_2}\right)=\frac{P\left(d_1,\overline{d_2}\right)}{P\left(\overline{d_2}\right)}=\frac{P\left(d_1\right)-P\left(d_1,d_2\right)}{1-P\left(d_2\right)}=\frac{P\left(d_1\right)-P\left(d_1\right)P\left(d_2\right)}{1-P\left(d_2\right)}=\frac{P\left(d_1\right)\left(1-P\left(d_2\right)\right)}{1-P\left(d_2\right)}=P\left(d_1\right).$$

This notion completely coincides with the notion of random co-occurrence⁹ and non-etiological associations²¹. In these models, there is no direct causation between diseases, nor are the causes of the diseases related. See Figure 3 for a simple example of non-etiological multimorbidity. In non-etiological multimorbidity models, it holds that D₂ is d-separated from D₁ by ∅. Therefore, it holds that D₁ and D₂ only occur because of independent multimorbidity.

Figure 3:

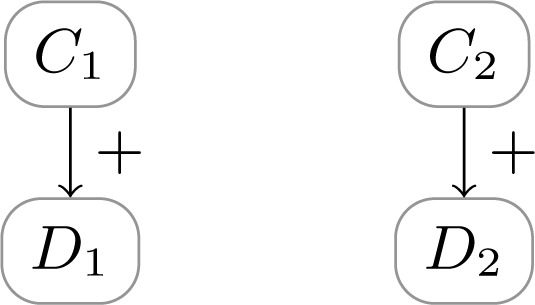
Non-etiological multimorbidity, where diseases D₁ and D₂ are caused by independent factors C₁ and C₂.

We propose to call the opposite of independent multimorbidity associative multimorbidity, which means that there is some relationship between two diseases which cause co-occurrence of diseases to be different than expected by chance. Formally speaking, in the terminology of Kraemer, this notion is called epidemiological comorbidity⁹. However, Kraemer requires that this association should also be epidemiologically measurable (making it independent from F-comorbidity, see below). Typically, one is interested in a positive associative multimorbidity, i.e., if

$$P\left(d_1,d_2\right)>P\left(d_1\right)P\left(d_2\right).$$

This coincides with what Akkermans et al. call cluster comorbidity, i.e., if d₁ is the index disease, then d₂ is more likely to occur than expected if d₁ and d₂ would have been independent. Negative associative multimorbidity can also occur, e.g., it seems that myopia is protective against diabetic retinopathy¹². For patients with diseases that are negatively associated, Akkermans et al. then speak of concurrent comorbidity as this co-occurrence is caused by ‘chance’ rather than the association.

The division into types of association according to Valderas et al²¹ is listed in Figure 4. The direct causation model coincides with the definition of causal comorbidity by Akkermans et al²⁴, whereas the other two (associated risk factor model and heterogenetic risk factor model) are considered cluster comorbidity. From the formal point of view, the focus in these models on risk factors, rather than causes of diseases could be considered problematic. For example, the authors write that if “the risk factors for 1 disease are correlated with the risk factor for another disease” (i.e., in the associated risk model) then this makes “the simultaneous occurrence of the diseases more likely”. However, this conclusion is only valid if the risk factors are of a causal nature as it is depicted in Figure 4. Consider, e.g., diabetes and familial hypercholesterolemia, which both causes elevated LDL cholesterol. While an elevated LDL cholesterol is a (non-causal) risk factor for both diseases, these diseases themselves are not associated.

Figure 4:

Example causal network structures of comorbidity relations as defined in by Valderas et al²¹ where diseases are associated. In the associated risk factor model, C₁ and C₂ can be associated by any causal mechanism.

Besides the way in which the association between diseases is structured, we can also consider which types of causes lead to a positive association between diseases. In Figure 1 we introduced an abstract framework with mechanisms that diseases can be related, which directly yields number of possibilities. In general, there are a large number of possible combinations of risk factors. Focusing on a single disease, there are three primary causal risk factors: environmental, genetic and those related to patient characteristics. Example models are given in Figure 5. In biomedical research, they play a distinct role: in practice, controlled studies are only performed to study influences of patient characteristics on diseases; environmental factors can only be studied well using epidemiological research; finally, genetic factors are often researched in observational studies using DNA samples, or twin studies.

Figure 5:

Primary classes of single risk factors inducing multimorbidity, with D_i diseases, C a patient characteristic, G a genetic factor, and E an environmental factor.

Each of the single risk factors causes associations between diseases. Nonetheless, as mentioned, Kraemer notes that familial comorbidity, i.e., comorbidity which has a genetic cause, is compatible with independent multimorbidity, i.e., familial comorbidity is compatible with the absence of epidemiological comorbidity. However, this is only true if in some families there is a positive association between diseases and in some other families there is a negative association between the same diseases. Further, the association may not be epidemiologically relevant if the particular gene causing an epidemiological comorbidity has a low prior probability. Consider for example a familial comorbidity between D₁ and D₂ caused by a genetic factor G. If P(g) ≈ 0 and P (D_i| ḡ) ≈ P(D_i), then:

$$\begin{array}{lll}P\left(D_1,D_2\right)\hfill & =\hfill & {\sum }_{G}P\left(D_1|G\right)P\left(D_2|G\right)P\left(G\right)\hfill \\ \hfill & \approx \hfill & P\left(D_1|\overline{g}\right)P\left(D_2|\overline{g}\right)P\left(\overline{g}\right)\approx P\left(D_1|\overline{g}\right)P\left(D_2|\overline{g}\right)\approx P\left(D_1\right)P\left(D_2\right).\hfill \end{array}$$

Clearly, familial comorbidity might not be epidemiologically measurable if the diseases are almost independent.

Probabilistic models for reasoning about clinical impact of multimorbidity

In practice, the impact of multimorbidity might be more relevant than the actual cause of the co-existence of multi-morbidity. The literature describes several dimensions in which interactions between diseases are relevant, namely if there are diagnostic, prognostic, or therapeutic interactions.

We say that there is a diagnostic multimorbidity problem if there are interactions between diseases that complicates the diagnosis of one of these diseases. In essence, making such a diagnosis involves the consideration of multiple diseases that might be the cause of the presented symptomatology within a patient. While in case of single disease management, eventually one disease from this set of diseases is considered to be the one and only cause of the presented symptomatology, in case of diagnostic multimorbidity it might be the case that more than one disease is involved in the presented symptomatology. Formally, given a sign or symptom S, the diagnostic value of S for a given disease D is typically defined by the so-called diagnostic odds ratio, i.e.,

$$\text{DOR}\left(s|d\right)=\frac{\text{odds}\left(s|d\right)}{\text{odds}\left(s|\overline{d}\right)}$$

Multimorbidity has an impact on the diagnostic value of S for D₁ in the presence of another disease D₂ if it alters its diagnostic odds-ratio, e.g., negatively, which can be expressed formally by

$$\frac{\text{odds}\left(s|d_1,d_2\right)}{\text{odds}\left(s|\overline{d_1},d_2\right)}<\frac{\text{odds}\left(s|d_1,\overline{d_2}\right)}{\text{odds}\left(s|\overline{d_1},\overline{d_2}\right)}$$

which can be shown to be equivalent to:

$$P\left(s|d_1,d_2\right)\cdot P\left(s|\overline{d_1},\overline{d_2}\right)<P\left(s|\overline{d_1},d_2\right)\cdot P\left(s|\overline{d_1},d_2\right)$$

i.e., a negative product synergy. Valderas et al²¹ gives an example of such a problem: patients with diabetes mellitus (dm) may have altered pain sensation, e.g. angina pectoris (ap), thereby interfering with and making it more difficult to diagnose coronary heart disease (chd). It thus holds that:

$$\frac{P\left(\mathit{ap}|\mathit{chd},\mathit{dm}\right)}{P\left(\mathit{ap}|\overline{\mathit{chd}},\mathit{dm}\right)}<\frac{P\left(\mathit{ap}|\mathit{chd},\overline{\mathit{dm}}\right)}{P\left(\mathit{ap}|\overline{\mathit{chd}},\overline{\mathit{dm}}\right)}$$

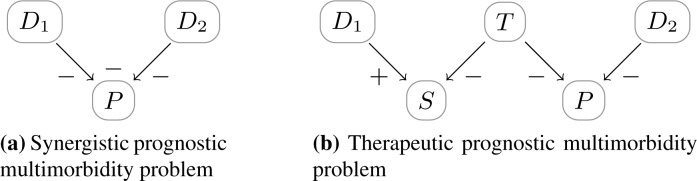
expressing that ap has less diagnostic value for chd in the presence of dm. Such diagnostic multimorbidity can be illustrated by a product synergy as shown in Figure 6.

Figure 6:

Diagnostic multimorbidity problem: D₁ and D₂ positively influence S. A diagnosis for D₁ negatively influences the diagnostic value of s for D₂, and vice versa.

A prognostic multimorbidity problem occurs if diseases have a (negative) influence on the prognosis of another disease, due to the anticipated effects on therapy and synergetic influence on prognostic factors such as quality adjusted life expectancy (QALYs). This definition is similar to the definition of prognostic comorbidity by Kaplan et al⁸. For example, diabetes mellitus (DM) and dyslipidemia (DL) contribute to biochemical processes that lead to vascular and Alzheimer dementia (AD). Moreover, there is a positive additive synergy between these two diseases on Alzheimer dementia¹⁰, i.e.,

$$P\left(\mathit{ad}|\mathit{dm},\mathit{dl}\right)-P\left(\mathit{ad}|\overline{\mathit{dm}},\mathit{dl}\right)<P\left(\mathit{ad}|\mathit{dm},\overline{\mathit{dl}}\right)-P\left(\mathit{ad}|\overline{\mathit{dm}},\overline{\mathit{dl}}\right)$$

Moreover, the prognosis of a disease can be influenced by therapeutic effects given for another disease. For example, using the example of Valderas et al²¹, corticosteroids (cs) prescribed for chronic obstructive pulmonary disease in the same patient will have an antagonistic effect on the prognosis of diabetes (p_DM), i.e., it is a negative causal influence:

$$P\left(p_{\text{DM}}|\text{do}\left(\mathit{cs}\right)\right)<P\left(p_{\text{DM}}|\text{do}\left(\overline{\mathit{cs}}\right)\right)$$

Examples of such models are illustrated in Figure 7.

Figure 7:

Two types of prognostic multimorbidity. In the synergistic prognostic multimorbidity problem, the negative effects on the prognosis P has an additional negative additive synergy, i.e., the prognosis is worse with multiple diseases compared to the effects of the single disease on the prognosis. In the therapeutic prognostic multimorbidity problem, the therapy given for D₁ – as it negatively influences the symptom S – has a negative impact on the prognosis P for D₂. The effect of T on S is mediated by either the pathophysiology of D₁ or by some other physiological process (cf. Figure 1).

A therapeutic interaction problem occurs when two therapies interact with each other. Agonistic and antagonistic effects can be modeled using qualitative causal influences (cf. Figure 8a and 8b), although the diseases that are intended to be treated could be independent from each other from a pathophysiologic point of view, i.e., independent multimorbidity. Sometimes, combinations of therapies can even induce new problems. For example, the combination of diuretics (as anti-hypertensive treatment) and NSAID’s (as treatment for some independent pain syndrome), can easily lead to dehydration within the elderly. Schematically, this is shown in Figure 8c. Hypertension, diuretics and blood pressure, are then represented with a D₁, T₁, and S₁ respectively. The same applies for the pain syndrome, represented with a D₂, T₂ and S₂. The node S₃ then represent a side effect of both T₁ and T₂, which prevalence can be even more then expected due to synergistic effects between T₁ and T₂.

Figure 8:

Therapeutic interactions between independent diseases. In (c) therapy T₁ is used to treat D₁; therapy T₂ is used to treatment D₂; T₁ and T₂ lead to synergetic side-effects (expressed in S₃).

Discussion

In this paper we reviewed existing terminologies within multimorbidity concepts and provided a framework using causal Bayesian networks that defines many of these concepts in a precise and formal manner. These results show that sometimes concepts are similar from a probabilistic point of view, and that sometimes concepts can be sub-categorized into different types of causal networks. The advantage of putting the multimorbidity concepts into a causal Bayesian network, is that we are able to model the true nature of dependency between multiple disease variables, which is crucial for developing decision support systems for managing multimorbidity patients. While in this paper we focused on multimorbidity with two diseases, we believe the results presented in this paper generalize to more complex situations, e.g., by also considering qualitative synergies in the presence of more than two causes.

Some concepts from literature are not explicitly modeled in this framework. Firstly, the definition of clinical comorbidity by Kraemer⁹ can be used to designate a variety of comorbid concepts. She states that any disease that has an altering effect on some kind of response to an index disease is of clinical importance. In this definition the response variable can be anything, e.g. age of onset, therapeutic response, prognosis, which, in a causal network framework, are special cases of prognostic and therapeutic multimorbidity problems, which is why this concept is not explicitly mentioned. This is similar for homotypic and heterotypic multimorbidity, which have their origin in psychiatric diseases and their corresponding diagnostic classifications, i.e. homotypic diseases are closer related to each other then heterotypic diseases from a diagnostic point of view. For homotypic diseases, this may lead to diagnostic multimorbidity problems. Finally, the concepts of cogent and non-cogent prognostic comorbidity can be considered concepts beyond causal or probabilistic meaning, as they rely on expectations of the medical researcher.

In future research, we will also consider cyclic models, e.g., when diseases contribute to each other’s pathophysiology. From a formal point of view, acyclic models can also be used for this purpose by modeling the progression and interaction of diseases over multiple time slices. Cyclic probabilistic graphical models¹⁶ may also be considered as an alternative for providing a succinct representation of such interactions.

In conclusion, the models presented in this paper provide insight in the different aspects of multimorbidity: both in the etiological relationships between multiple diseases as well as in the impact that multimorbidity has on the clinical practice. We believe that these results provide a foundation for probabilistic models of multimorbidity, which can be taken as a basis of computerized decision support systems for multiple diseases.