Abstract
Background:
The ability to identify the risk factors related to an adverse condition, e.g., heart failures (HF) diagnosis, is very important for improving care quality and reducing cost. Existing approaches for risk factor identification are either knowledge driven (from guidelines or literatures) or data driven (from observational data). No existing method provides a model to effectively combine expert knowledge with data driven insight for risk factor identification.
Methods:
We present a systematic approach to enhance known knowledge-based risk factors with additional potential risk factors derived from data. The core of our approach is a sparse regression model with regularization terms that correspond to both knowledge and data driven risk factors.
Results:
The approach is validated using a large dataset containing 4,644 heart failure cases and 45,981 controls. The outpatient electronic health records (EHRs) for these patients include diagnosis, medication, lab results from 2003–2010. We demonstrate that the proposed method can identify complementary risk factors that are not in the existing known factors and can better predict the onset of HF. We quantitatively compare different sets of risk factors in the context of predicting onset of HF using the performance metric, the Area Under the ROC Curve (AUC). The combined risk factors between knowledge and data significantly outperform knowledge-based risk factors alone. Furthermore, those additional risk factors are confirmed to be clinically meaningful by a cardiologist.
Conclusion:
We present a systematic framework for combining knowledge and data driven insights for risk factor identification. We demonstrate the power of this framework in the context of predicting onset of HF, where our approach can successfully identify intuitive and predictive risk factors beyond a set of known HF risk factors.
Introduction
Heart Failure (HF) has become increasingly prevalent and is among the most costly diseases for Medicare patients. The annual direct cost is $33 billion [1,2,3,4]. The prevalence and cost trends will continue to rise unless novel and cost-effective strategies are developed to better manage this disease. While hospital admissions and readmissions are being reduced, the cost benefit is modest, self-limiting, and too infrequently does little to improve patient quality of life. The persistent challenge is in the failure to detect HF at stage that is early enough to implement proven lifestyle and pharmacologic interventions that can delay and possibly even prevent disease progression. The ultimate goal of our study is to develop robust, valid, and practical means of early detection that can be applied in primary care practices that use electronic health records (EHR). To construct such predictive models, the key is to identify predictive risk factors and extract them from data.
Risk factors for HF have been previously studied [5] but with a stronger focus on primary prevention. EHRs typically document those relevant risk factors from clinical knowledge like literature, including Age, Hypertension, MI, Diabetes, Valvular heart disease, Coronary heart disease, and Chronic kidney disease. The advantage of this knowledge driven approach is the interpretability of the risk factors, which is grounded in established evidence and based on features that are reasonably well understood. This approach is also computationally appealing, since the number of features involved in the model is usually relatively small (e.g., in the order of 10 to 100). The disadvantage of this approach is that resulting models may not adequately represent the complex disease processes that underlie the insidious emergence of HF. Not all risk factors have been identified, and many predictive features are yet to be constructed and tested. Another subtlety is that most of knowledge driven risk factors describe high-level clinical concepts, which do not directly map to the underlying EHR data. To construct and deploy a model in the operational setting, one need to connect those knowledge driven risk factors to the EHR data by constructing appropriate features, which is not trivial.
Recognizing the limitation of a purely knowledge driven approach, we can use a data driven approach that systematically constructs and tests a large number of features. Our evaluation results indicate that a data driven strategy outperforms a knowledge driven strategy (e.g., over 20% improvement in the area under the ROC curve). However unlike the knowledge driven strategy, the data driven approach is often computationally demanding since a large number of features have to be constructed, selected and tested. Another limitation of the data driven strategy is with interpretability, since the resulting models often involve more features and more complex relations.
Knowledge driven and data driven strategies reflect two ends of the spectrum. More specifically, a knowledge driven approach is based on evidence of varying quality, guidelines, and experts’ opinions, while a data driven approach is solely based on the observational data. In this paper, we present a hybrid strategy that starts with prior knowledge, then extends to a more comprehensive model by selectively including an additional set of features that both optimize prediction and complement knowledge based features. We compare the hybrid approach to knowledge driven approaches to quantitatively judge the feasibility of combining two complementary strategies for model building. In particular, we extend a sparse feature selection method Scalable Orthogonal Regression (SOR) [6] to expand a set of knowledge driven risk factors with additional risk factors from data. Furthermore, the method is designed specifically to select less redundant features without sacrificing the quality, for which redundancy is measured by an orthogonality measure added as a penalty term in the objective function.
Our study utilizes EHR data extracted from Geisinger’s Enterprise data warehouse on all primary care patients. We construct 4,644 heart failure cases and 45,981 control patients, which in total consist of over 20 million EHR records from 2003 to 2010. The data contains diagnosis, medication, symptoms derived from clinical notes, and lab results. To showcase the power of the proposed method, we start with a set of known comorbidities to HF as the knowledge driven features, then extend them with a set of optimal data driven features from the EHR data. The evaluation metric is the area under the ROC curve (AUC) measure. Our evaluation confirms that by including additional data driven risk factors, classification performance is significantly improved with respect to the AUC measure in comparison to the knowledge driven baseline. Moreover, most of selected data driven features are clinically relevant to the development of HF, which further demonstrates the benefit of the proposed method.
Background
Feature selection
The purpose of feature selection is to identify a subset of K most informative features from a pool of candidates. There are two major problems in feature selection. One is the measurement of how informative a given subset of features is, and the other one is how to obtain the optimal subset of features. Given a measurement of the quality of features, the feature selection problem becomes a combinatorial optimization problem. Because of its computational complexity, finding the optimal subset is usually solved by an approximation or greedy search. In general, there are two types of feature selection methods in the literature: (1) filter methods [7] where the selection is independent of the classification or regression model and (2) wrapper methods [8] where the selection is tightly coupled with a specific model.
Filter methods evaluate features one by one and select the top K features according to their scores. This type of scheme can be interpreted as a greedy approach by iteratively selecting one feature from the remaining unselected feature set. Within this category, one can implement it using two approaches. Univariate filtering, e.g. Information Gain, or multivariate filtering, e.g. Minimum Redundancy-Maximum Relevance (mRMR) [9].
Wrapper methods provide an alternative way to obtain a subset of features by incorporating the classifiers, e.g. directly approximating the area under the ROC curve [10] or optimization of the Least Absolute Shrinkage and Selection Operator (LASSO) model [11,12].
Methodologies for learning of non-redundant features have also been discussed in literature. For example, mRMR explicitly prefers low redundancy features [9], and non-redundant codebook feature learning method was also proposed [13]. Beyond searching orthogonal features, our focus in this paper is to systematically address the redundancy between a preselected set of features (the knowledge driven features) and potential additional data driven features.
Heart failure risk factor identification
Several risk prediction models have previously been developed for HF. However, they are limited in that the populations used to develop the models included restricted, generally healthier populations enrolled in clinical trials or observational studies [14,15]. In addition the number of incident HF cases was relatively small with the largest including only 500 HF cases [16]. Also, the amount of data available to engineer features and develop the models was primarily limited to baseline variables captured at baseline. Our study includes nearly 10-fold more real-world patients routinely followed in a primary care setting with extensive longitudinal healthcare data. Therefore, feature selection is extremely important in our setting because of abundance of data and features that are potentially useful for predicting HF.
Methods
We propose a framework for identifying and combining risk factors from knowledge and operational data. We first introduce the components involved in this system, and then describe the computational core SOR feature selection method.
System Overview
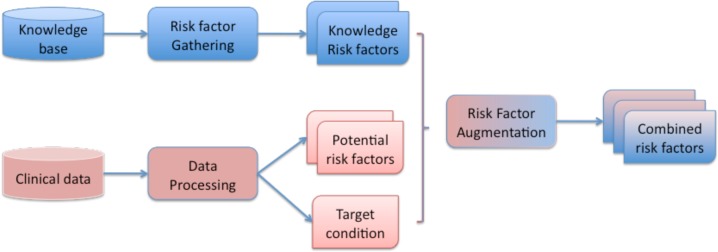
Our analytic system takes two different paths to identify risk factors, and merge them at the end to construct the combined set of risk factors. The system architecture, as illustrated in Figure 1, shows the analytic components and the required input and output. The blue path indicates the analytic process for obtaining knowledge driven risk factors. The red path indicates the analytic process for gathering potential data driven risk factors. Finally, through the risk factor augmentation module, both sets are merged into the combined set of risk factors. Next, we describe each component in more details.
Figure 1:
System Overview for Risk Factor Combination
Knowledge driven risk factor gathering
The objective here is to identify risk factors from knowledge base or experts for a given disease scenario, for example, HF prediction in our case. This can be achieved using two approaches. In the first approach, we take direct input from experts for a given disease condition through interviews. The expert inputs are compiled into a list of risk factor concepts, which are often high-level concepts of those relevant risk factors. These concepts are not yet risk factors that we can directly use for predictive modeling. We still need to map those concepts to the EHR data in order to extract the instances of those risk factor concepts. For example, hypertension is a risk factor concept for predicting heart failure. However, we need to map hypertension to diagnosis codes 401.x–405.x in diagnosis tables in the EHR database. We need to decide whether individual codes should be mapped to separate features (one-toone mapping) or aggregated into a single feature variable (many to one mapping). We found when sample size is large (i.e., the number of samples are much greater than the number of features), one-to-one mapping leads to better performance, since features are created at the finer diagnostic level and can often lead to better discriminating power. In this approach, ICD-9 codes 401.x will be treated as a set of different features from ICD-9 405.x. However, when sample size is small (i.e., the number of samples are smaller than the number of features), many-to-one mapping can lead to smaller number of features and better prediction results, since a simpler model is more robust against over-fitting. In this case, 401.x–405.x will be mapped to the same feature.
Another possible approach to obtaining knowledge based risk factors is to process medical guidelines and literature to extract known risk factors for a given disease condition. For example, some known HF risk factors are listed from published guidelines [5]. Again, we need to map them to actual EHR data so that they can be quantified and leveraged in the predictive models. In this study, we use the common comorbidities to HF as the knowledge driven features (see Table 1 for details). Moreover, Table 1 also presents the prevalence of those comorbidities in both cases and controls, where cases always have higher prevalence than controls.
Table 1:
HF Comorbidities among Cases and Controls (x is the wildcard character that indicates to include all the lower level ICD-9 codes)
| Comorbidity | ICD-9 codes | Cases | Controls |
|---|---|---|---|
| Hypertension | 401.x–405.x | 2874 (61.89%) | 24939 (54.24%) |
| Diabetes | 250.x | 1478 (31.83%) | 11037 (24.00%) |
| Prior Myocardial Infarction | 410.x | 34 (0.73%) | 192 (0.42%) |
| Known Coronary Disease | 413.x, 414.x | 1183 (25.47%) | 7240 (15.75%) |
| Peripheral Vascular Disease | 440.x–442.x | 190 (4.09%) | 1106 (2.41%) |
| Cerebrovascular Disease | 430.x–438.x | 460 (8.74%) | 3033 (6.60%) |
| Valvular Heart Disease | |||
| Aortic | 424.1 | 111 (2.39%) | 541 (1.18%) |
| Mitral | 424.0 | 83 (1.79%) | 427 (0.93%) |
| Chronic Obstructive Pulmonary Disease | 490.x–496.x | 855 (18.41%) | 5621 (12.22%) |
| Chronic Kidney Disease | 585.x, 403.x | 202 (4.41%) | 1243 (2.70%) |
Data driven risk factor construction
In addition to knowledge driven risk factors, there are rich sets of features that can be computed from EHR data. We systematically construct features from different data sources in EHR, recognizing that longitudinal data on even a single variable (e.g., blood pressure) can be represented in a variety of ways. The objective is to capture sufficient clinical nuances of heterogeneity of HF patients. A major challenge is in data reduction and in summarizing the temporal event sequences in EHR data into features that can differentiate cases and controls. In particular, we observe longitudinal sequences of measures based on diagnoses, medication, labs, vitals, and symptoms. The sparseness of the data will vary among patients and we expect the sequencing and clustering of what is observed to also vary. Different types of clinical events arise in different frequency and in different orders. We construct summary statistics for different types of event sequences based on the feature characteristics: For static features such as gender and ethnicity, we use a single static value to encode the feature. For temporal numeric features such as lab measures, we use summary statistics such as point estimate, variance, and trend statistics to represent the features. For temporal discrete features such as diagnoses, we use the event frequency (e.g., number of occurrences of a ICD-9 code).
Besides constructing potential risk factors as features, we need to identify a target variable. In this case, we use the indicator variable to represent whether a patient has been diagnosed with HF by a certain date.
The numbers of all features from different data sources can be large. For example, there are more than 9,000 distinct ICD-9 codes in our dataset, which could all become separate features. To focus on potentially relevant features for HF risk, we perform an initial feature filtering by discretizing the features, then using information gain to rank those discretized features with respect to the target indicator variable. We keep the features with information gain score of 10−3, which include 387 diagnosis features, 403 medication features, 294 lab features, 30 symptom features. Note that many of these features are not in the knowledge driven risk factors. Next we explain how to merge them systematically.
Risk Factor Augmentation
The goal here is to combine knowledge driven and data driven risk factors systematically so that the resulting risk factors are interpretable as well as predictive. We start with knowledge driven risk factors since they are more intuitive and well accepted for assessing the risk of target condition. From there, we search for additional risk factors from the data driven risk factors and extend Scalable Orthogonal Regression (SOR) model [19] to perform the merge. The SOR model is specifically designed to ensure that:
The additional risk factors are highly predictive of the adverse condition of interest.
There is little or no correlation between the additional risk factors from data and knowledge driven risk factors, so that additional risk factors indeed contribute to new understanding of the condition, which could lead to new potential treatment/management options.
There is little or no correlation among the additional risk factors from data, to further ensure quality of the additional factors
The SOR model achieves nearly linear scale-up with respect to the number of input features and the number of patients as shown in [19]. SOR is formulated as an alternative convex optimization problem with theoretical convergence and global optimality guarantee. In [19], we compare SOR with several existing feature selection methods to show its scalability and stability. In this paper, we focus on the SOR extension that searches for an optimal set of data driven features to augment knowledge driven risk factors.
Knowledge Driven Scalable Orthogonal Regression
Let Xd = [x1, x2,…, xp] ∈ Rn×p denote the data driven features, which contain n patients and p features. Each patient has a target variable, which in our case is whether patient is HF case or not. Let y ∈ Rn×1 denote the target vector. In our case, Xd contains features from diagnosis, medication, lab results and symptoms. In addition to the data driven features Xd, we have q knowledge driven features Xe = [xp+1, xp+2, …, xp+q] ∈ Rn×q. The entire features are represented as X = [Xd, Xe].
The goal is to select a set of features from Xd, which can help predict y and are also low-redundant to the existing knowledge driven features Xe. To achieve that the objective function has the following parts:
The reconstruction error and α is the regression coefficient. This term captures how accurate the data driven features can estimate the target variable through a regression model;
The regularization on coefficient ||α||1 is the L1 norm of α: , which enforces a sparse solution and features with nonzero coefficient are selected.
The redundancy among data driven features ;
The redundancy between data driven features and knowledge driven features: .
With the above terms, we define the following objective function:
where α is the regression coefficient, α ∈ Rp×1, β is model parameter. The corresponding gradient is
| (1) |
where G = XTX, A = ααT and ⊙ is the matrix Hadamard (elementwise) product.
The goal is to find the best α that minimizes ((f(α) + λ|| α||1). To do that, we apply the Lipschitz Auxiliary Function method [21] for the optimization, which is summarized in Algorithm 1. In terms of model parameter setting, we set λ and β to 1, and γ is a scaling parameter for increasing L when the Lipschitz condition is not satisfied and we set γ = 1.2.
Algorithm 1
|
Results
We first describe the EHR data and features used in this study. We then present the evaluation metric and results.
EHR data
Patient EHRs dating from 2003 to 2010 within the Geisinger Health System were utilized. The Geisinger Health System is an integrated health care system that provides health services in 31 counties of central and northeastern Pennsylvania and includes 41 Community Practice Clinics. Data for this study were derived from approximately 400,000 primary care patients served by these 41 clinics. From these EHRs, we identified 4,644 incident HF cases with a clinical HF diagnosis based on meeting at least one of the following criteria: (1) HF diagnosis appearing on the problem list at least once; (2) HF diagnosis appeared in the EHR for two outpatient encounters; (3) at least two medications prescribed with an associated ICD-9 diagnosis of HF; or (4) HF diagnosis appearing on one or more outpatient encounters and at least one medication prescribed with an associated ICD-9 diagnosis for HF. The diagnosis date was defined as the first appearance of a HF diagnosis in the EHR [20]. Approximately 10 eligible clinic-, sex-, and age-matched (in five-year age intervals) controls were selected for each incident HF case (45,981 group-matched controls). Primary care patients were eligible as controls if they had no history of HF diagnosis before December 31, 2010. Control patients were required to have had their first Geisinger Clinic office encounter within one year of the incident HF case’s first office visit and had at least one office encounter 30 days before or anytime after the case’s HF diagnosis date. For the purposes of this study, we extracted the outpatient diagnosis, problem list, medication orders and reconciliation list, lab results and Framingham related symptoms of these patients.
Feature construction
For each patient, we anchor an index date, and construct a feature vector from the observation window, which is defined as the fixed size time window right before index date. For a HF case patient, the index date is the diagnosis date, while for a control patient the index date is the diagnosis date of his/her matching case patient. In our study, we use two year observation windows.
The feature vector consists of statistical measures derived from the longitudinal clinical events during the observation window. Each clinical event becomes a feature as described in the System Overview section. In particular, feature values are derived from the corresponding EHR records from the observation window for this patient. For discrete events like diagnosis, medication and symptoms, we use the number of occurrences at the feature value. For continuous events such as lab measures, we compute the average of those measures in observation windows after removing invalid and noisy outliers.
The knowledge driven features are the diagnosis features described in Table 1. The distinct number of diagnosis codes in both outpatient data and problem list is 296. The data driven features are all remaining features, which is 12,320. To speed up the computation, we filter out the data driven features which have little correlation with the target variable. To do this, we discretize the data driven features into buckets and compute information gain between the discretized feature and the target variable. We filter out ones with information gain less than 10−4.
Evaluation
To quantitatively validate the performance of the selected features, we conduct 5-fold cross-validation on the entire dataset and use the area under the ROC curve (AUC) as the performance metric. Note that within each fold, feature selection only processes the training data and leave the testing data out for validation of the AUC. First, we compare the performance of different knowledge driven features. The goal here is to better understand the predictive power of existing risk factors. Second, we gradually add additional data driven features according to the feature ranking computed by the SOR algorithm. Here we showcase their impact on predictive performance, and also comment on their clinical relevancy.
Comparison among knowledge driven features
We pick three major sets of knowledge driven features (Hypertension, Diabetes and Coronary disease) based on their prevalence in HF cases. We also combine all knowledge driven features as listed in Table 1. The performance results are shown in Table 2. Note that hypertension features and coronary disease features perform better than diabetes features. Hypertension seems to perform relatively well despite that there are only 10 features, while there are 89 diabetes features and 129 coronary disease features. This observation confirms the biggest known risk factors of HF are hypertension related. The combination of all comorbidities performs better than the individual feature types as expected. However, absolute AUC measure of knowledge driven comorbidity features is not high, only 0.62 AUC, which further shows the need for augmenting data driven features.
Table 2:
Performance on the major knowledge driven features. Performance metric is AUC±stddev.
| Type | Cardinality | AUC |
|---|---|---|
| Hypertension | 10 | 0.57±0.0072 |
| Diabetes | 89 | 0.55±0.0038 |
| Known Coronary Disease | 129 | 0.58±0.0052 |
| All comorbidities in Table 1 | 296 | 0.62±0.0058 |
Combining knowledge driven and data driven features
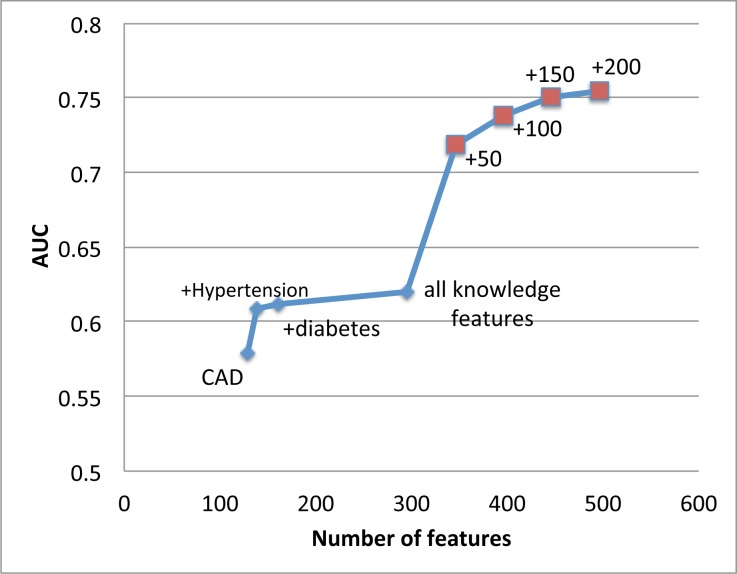
Based on the performance ranking in Table 2, as shown in Figure 2 we start with only coronary disease (CAD) and then add other sets of knowledge driven features such as hypertension and diabetes. The resulting AUC slowly increases. The largest jump by adding knowledge driven features comes from hypertension features. However, after adding hypertension features, there is a diminishing return on AUC by adding more knowledge driven features.
Figure 2:
AUC significantly improves as complementary data driven risk factors are added into existing knowledge based risk factors. A significant AUC increase occurs when we add first 50 data driven features.
However, still in Figure 2, when we start adding in carefully selected data driven features based on the ranking provided by the SOR algorithm, the AUC performance significantly improves from 0.62 to above 0.75. We observe a significant jump on AUC by adding only 50 data driven features. As more data driven features included, the AUC performance consistently improves. This confirms the power of the proposed feature augmentation process.
Table 3 shows the breakdown of the top-200 selected data driven features by type and by their relevancy to HF. The types consist of diagnosis, symptom, medication and lab. The relevancy to HF are judged by a cardiologist with categories: yes, possible, and no. About half of the top 200 features (48%) are considered relevant. 36% are considered possibly relevant. Only 15% are considered not directly relevant. Among the top 200 features, the relevant features are about equally spread across all four types, which illustrate the importance of leveraging heterogeneous data sources for building a predictive model. Note that the correlation between knowledge- and data-driven features still exists although small. The model objective function balances both model accuracy and feature correlation, in order to lead predictive features with small correlation.
Table 3:
The breakdown of top-200 data driven features by feature type and their relevancy to HF
| Type | Yes | Possible | No | Total |
|---|---|---|---|---|
| Diagnosis | 24 (12%) | 16 (8%) | 7 (3.5%) | 47 (28.5%) |
| Symptom | 20 (10%) | 0 | 0 | 20 (10%) |
| Medication | 27 (13.5%) | 24 (12%) | 9 (4.5%) | 60 (30%) |
| Lab | 27 (13.5%) | 32 (16%) | 14 (7%) | 73 (36.5%) |
|
| ||||
| Total | 96 (48%) | 72 (36%) | 30 (15%) | 200 |
Top 10 data driven features are listed in Table 4. Nine out of ten are considered relevant to HF, and one possibly relevant, which confirm the interpretability of the proposed method for expanding knowledge driven risk factors.
Table 4:
Top 10 data driven features among Cases and Controls
| Feature type | Feature name | Relevancy to HF |
|---|---|---|
| Diagnosis | DYSLIPIDEMIA | Yes |
| Medication | Thiazides and Thiazide-Like Diuretics | Yes |
| Medication | Antihypertensive Combinations | Yes |
| Medication | Aminopenicillins | Yes |
| Medication | Bone Density Regulators | Possible side effect, or maybe a surrogate for elderly women |
| Medication | NATRIURETIC PEPTIDE | Yes |
| Symptoms | Denial Rales | Yes |
| Medication | Diuretic Combinations | Yes |
| Symptoms | Denial S3Gallop | Yes |
| Medication | Nonsteroidal Anti-inflammatory Agents (NSAIDs) | Yes, contribute to fluid retention due to renal effects |
Limitation and discussion
One limitation is that we currently trust all knowledge driven features and include them all in the model. However, it is possible, as we observe in our application, that some of the knowledge driven features are not really predictive (due to various reason such as data quality). It can be valuable to quantify the predictive power of the knowledge driven features and eliminate the ones that are not predictive.
Another subtlety in the problem formulation is that we search for orthogonal features. As a result, the selected features have less redundancy among themselves, which is often a desirable feature of the method. However, because of little redundancy exists in the selected features, small perturbation of the data may lead to select different features. This is especially true if there are many correlated features. Intuitively, if feature A and B are two highly correlated features, it is unlikely to select both A and B. It is quite possible for the algorithm to select A initially, then change to B when rerun the algorithm on the updated dataset. In fact, this is a common characteristic of many feature selection methods with orthogonality constraints such as mRMR [9]. The way to alleviate the instability is to introduce some constraints in the optimization such that the previously selected features are preferred, which will be part of our future work.
Conclusion
We present a systematic framework for combining knowledge and data driven insights for risk factor identification. Our proposed method is based on a sparse learning formulation that balances the model accuracy and the redundancy between knowledge driven and data driven features. We demonstrate the power of this framework in the context of predicting onset of HF on a large dataset of 7-year longitudinal EHR data of over 50K patients. Our evaluation confirms that our method can improve knowledge driven features by adding predictive and meaningful data driven features to improve prediction performance. In our experiments, we achieve over 20% improvement in terms of AUC by adding data driven factors. Those selected data driven features are also clinically meaningful in the context of HF risk assessment.
References
- 1.Curtis LH, Whellan DJMHS, Hammill BG, et al. Incidence and Prevalence of Heart Failure in Elderly Persons, 1994–2003. Arch Intern Med. 2008;168:418–424. doi: 10.1001/archinternmed.2007.80. [DOI] [PubMed] [Google Scholar]
- 2.Teng TK, Finn JFRCNA, Hobbs, Michael BS, D.Phil, F.R.A.C.P., Hung JBS., F.R.A.C.P. Heart Failure: Incidence, Case Fatality, and Hospitalization Rates in Western Australia Between 1990 and 2005. Circulation: Heart Failure. 2010;3:236–243. doi: 10.1161/CIRCHEARTFAILURE.109.879239. [DOI] [PubMed] [Google Scholar]
- 3.Rosamond W, Flegal K, Friday G, et al. Heart disease and stroke statistics--2007 update: a report from the American Heart Association Statistics Committee and Stroke Statistics Subcommittee. [Erratum appears in Circulation. 2010 Jul 6;122(1):e9 Note: Kissela, Bret [corrected to Kissela, Brett]] Circulation. 2007;115:e69–171. doi: 10.1161/CIRCULATIONAHA.106.179918. [DOI] [PubMed] [Google Scholar]
- 4.Writing Group Members. Roger VL, Go AS, et al. Heart Disease and Stroke Statistics--2012 Update: A Report From the American Heart Association. Circulation. 2012;125:e2–e220. doi: 10.1161/CIR.0b013e31823ac046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Schocken DD, Benjamin EJ, Fonarow GC, et al. Prevention of heart failure: a scientific statement from the American Heart Association Councils on Epidemiology and Prevention, Clinical Cardiology, Cardiovascular Nursing, and High Blood Pressure Research; Quality of Care and Outcomes Research Interdisciplinary Working Group; and Functional Genomics and Translational Biology Interdisciplinary Working Group. Circulation. 2008;117:2544–2565. doi: 10.1161/CIRCULATIONAHA.107.188965. [DOI] [PubMed] [Google Scholar]
- 6.Luo D, Wang F, Sun J, Markatou M, Hu J, Ebadollahi S. SOR: Scalable Orthogonal Regression for Non-Redundant Feature Selection and its Healthcare Applications. SIAM Data Mining. 2012 [Google Scholar]
- 7.Langley P. Selection of relevant features in machine learning. AAAI Fall Symposium on Relevance; 1994. pp. 140–144. [Google Scholar]
- 8.Kohavi R, John GH. Wrappers for feature subset selection. Artificial Intelligence. 1997;(1–2):97. 273–324. [Google Scholar]
- 9.Peng H, Long F, Ding C. Feature selection based on mutual information: Criteria of max-dependency, max-relevance, and min-redundancy. IEEE Trans. Pattern Analysis and Machine Intelligence. 2005;27 doi: 10.1109/TPAMI.2005.159. [DOI] [PubMed] [Google Scholar]
- 10.Ma S, Huang J. Regularized roc method for disease classification and biomarker selection with microarray data. Bioinformatics. 2005;214356(24) doi: 10.1093/bioinformatics/bti724. [DOI] [PubMed] [Google Scholar]
- 11.Efron B, Hastie T, Johnstone I, Tibshirani R. Least angle regression. The Annals of statistics. 2004;32(2):407–499. [Google Scholar]
- 12.Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1996;58(1):267–288. [Google Scholar]
- 13.Zhang W, Surve A, Fern X, Dietterich T. Learning non-redundant codebooks for classifying complex objects. Proceedings of the 26th Annual International Conference on Machine Learning; ACM; 2009. pp. 1241–1248. [Google Scholar]
- 14.Butler J, Kalogeropoulos A, Georgiopoulou V, Belue R, Rodondi N, Garcia M, Bauer DC, Satterfield S, Smith AL, Vaccarino V, Newman AB, Harris TB, Wilson PWF, Kritchevsky SB. Incident Heart Failure Prediction in the Elderly. The Health ABC Heart Failure Score. Circ Heart Fail. 2008;1:125–133. doi: 10.1161/CIRCHEARTFAILURE.108.768457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lewis EF, Solomon SD, Jablonski KA, Rice MM, Clemenza F, Hsia J, Maggioni AP, Zabalgoitia M, Huynh T, Cuddy TE, Gersh BJ, Rouleau J, Braunwald E, Pfeffer MA. Predictors of Heart Failure in Patients With Stable Coronary Artery Disease. Circ Heart Fail. 2009;2:209–216. doi: 10.1161/CIRCHEARTFAILURE.108.820696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lee DS, Gona P, Vasan RS, Larson MG, Benjamin EJ, Wang TJ, Tu JV, Levy D. Relation of Disease Pathogenesis and Risk Factors to Heart Failure With Preserved or Reduced Ejection Fraction Insights From the Framingham Heart Study of the National Heart, Lung, and Blood Institute. Circulation. 2009;119:3070–3077. doi: 10.1161/CIRCULATIONAHA.108.815944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Xu H, Stenner SP, Doan S, Johnson KB, Waitman LR, Denny JC. MedEx: a medication information extraction system for clinical narratives. J Am Jed Inform Assoc. 2010;17:19–24. doi: 10.1197/jamia.M3378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.MetaMap http://metamap.nlm.nih.gov/
- 19.Luo D, Wang F, Sun J, Markatou M, Hu J, Ebadollahi S. SOR: Scalable Orthogonal Regression for Non-Redundant Feature Selection and its Healthcare Applications. SIAM Data Mining Conference; 2012. [Google Scholar]
- 20.Wu J, Roy J, Stewart WF. Prediction modeling using EHR data: challenges, strategies, and a comparison of machine learning approaches. Med Care. 2010;48:S106–13. doi: 10.1097/MLR.0b013e3181de9e17. [DOI] [PubMed] [Google Scholar]
- 21.Luo D, Ding C, Huang H. Towards Structural Sparsity: An Explicit l2/l0 Approach; ICDM; 2010. pp. 344–353. [Google Scholar]