Extracellular Sheets and Tunnels Modulate Glutamate Diffusion in Hippocampal Neuropil

Abstract

Although the extracellular space in the neuropil of the brain is an important channel for volume communication between cells and has other important functions, its morphology on the micron scale has not been analyzed quantitatively owing to experimental limitations. We used manual and computational techniques to reconstruct the 3D geometry of 180 μm³ of rat CA1 hippocampal neuropil from serial electron microscopy and corrected for tissue shrinkage to reflect the in vivo state. The reconstruction revealed an interconnected network of 40–80 nm diameter tunnels, formed at the junction of three or more cellular processes, spanned by sheets between pairs of cell surfaces with 10–40 nm width. The tunnels tended to occur around synapses and axons, and the sheets were enriched around astrocytes. Monte Carlo simulations of diffusion within the reconstructed neuropil demonstrate that the rate of diffusion of neurotransmitter and other small molecules was slower in sheets than in tunnels. Thus, the non-uniformity found in the extracellular space may have specialized functions for signaling (sheets) and volume transmission (tunnels).

The extracellular space (ECS) is an arena for signaling between neighboring cells on the nanometer and micron scale, and the geometry of the ECS affects this signaling. For example, the ECS provides a reservoir of ions used to support currents in electrically active neurons (Hodgkin and Huxley, 1952). During periods of high neuronal activity, change in extracellular ion concentration depends on local ECS volume (Moody et al., 1974; Bellinger et al., 2008). Activation of metabotropic receptors and extrasynaptic N-methyl-D-aspartate (NMDA) receptors occurs via diffusion of glutamate from the synapses (Scanziani et al., 1997; Chen and Diamond, 2002), and extrasynaptic dopamine receptors are activated by diffusion-based volume transmission of dopamine (Rice and Cragg, 2008). The extracellular volume fraction varies across the hippocampus (McBain et al., 1990; Sykova and Nicholson, 2008), and stimulus-induced drops of 20–50% have been observed in extracellular volume fraction driven by fluid and electrolyte movements into glial cells (Van Harreveld and Khattab, 1967; Dietzel et al., 1980; Ransom et al., 1985; Kroeger et al., 2010). The morphology of the ECS in vivo is dynamic and likely varies between different brain regions and during pathology, adjusting to network activity, synapse formation, osmolarity, and many other conditions.

Despite its importance for brain function, the morphology of the ECS on the micron scale is largely unknown. The ECS is tens of nanometers in width based on electron microscopy (EM) images (Wahl et al., 1996; Rusakov and Kullmann, 1998a; Thorne and Nicholson, 2006), below the resolution of light microscopy, and falls into a regime that poses significant challenges for in vivo measurement. However, in vivo measurements of the ECS have been available for two macroscopic properties, averaged over hundreds of microns of neuropil: First, the extracellular volume fraction captures the fraction of total tissue volume that lies outside of cells; Second, the total tortuosity accounts for the observed reduction in rate of diffusion of small molecules through the ECS compared with free diffusion due to geometric inhomogeneities and interactions with the extracellular matrix (Sykova and Nicholson, 2008). In early development the extracellular volume fraction is 40% and decreases with age (Fiala et al., 1998) and during periods of anoxia (Sykova and Nicholson, 2008). The extracellular volume fraction in the adult rat hippocampus is 20% and total tortuosity is 1.45, based on the diffusion of small probe molecules in the ECS (Nicholson and Phillips, 1981; Magzoub et al., 2009; Zheng et al., 2008).

To capture the morphology of the ECS on the micron scale, we generated a spatially accurate, geometrically and topologically consistent, 3D reconstruction of 180 μm³ of a volumetric, bounded neuropil region from adult rat hippocampal serial electron microscopy sections at nanometer resolution (see Materials and Methods and Online Movie at http://cnl.salk.edu/~jkinney/waltz/waltz.mp4). Ideally, the geometry of the reconstruction could be compensated for any tissue shrinkage that occurs during processing (Fig. 1), such as the 12.5% linear tissue shrinkage for the protocol used here (Kirov et al., 1999). However, direct measurements of shrinkage were not made on the tissue samples used here, and consensus in the literature is elusive, with values ranging from 4 to 50% (Hillman and Deutch, 1978; Diemer, 1982; Schuz and Palm, 1989). Additionally, it is unknown how the intracellular space (ICS) of neural tissue changes during preparation for EM.

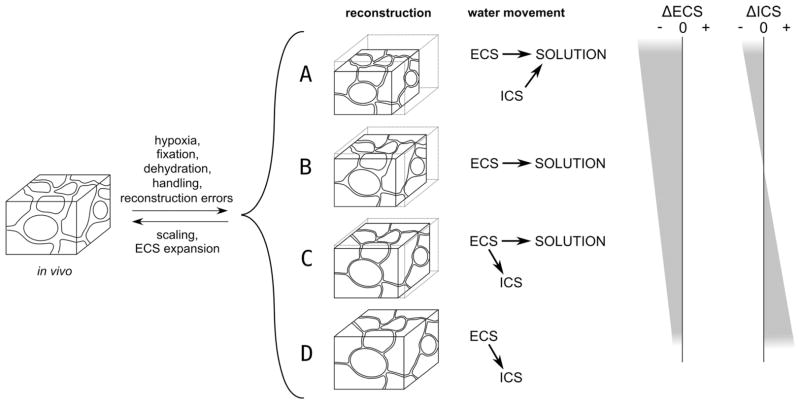
Figure 1.

Three models of water movement could explain the decrease of extracellular volume fraction and tissue shrinkage observed in the EM image stack and raw reconstruction. Morphological changes to the extracellular space (ECS) due to hypoxia, fixation, dehydration, handling, and reconstruction errors are evident. However, changes to the ICS are unknown, leading to four plausible accounts for tissue shrinkage. In all cases, the original morphology can be recovered by scaling the reconstruction by an amount equivalent to the volume of tissue shrinkage (which is 1.0 for D) and then expanding the ECS at the expense of the ICS, or vice versa. A: Water loss from the ECS and the ICS into the solution causes the extracellular and intracellular and total volume to decrease. B: Water loss from the ECS into the solution and no exchange with the ICS causes extracellular volume and total volume to decrease, leaving intracellular volume unchanged. C: Movement of water from the ECS into both the solution and the ICS causes the extracellular and total volume to decrease and the intracellular volume to increase. D: No change in overall tissue volume occurs, as water is simply transferred from the ECS to the ICS. This scenario is incompatible with the 33% volume shrinkage associated with our EM protocol.

To compensate for a range of possible volume shrinkages and in vivo variations, we explored quantitatively the range of physiological geometries of the ECS by rescaling the reconstruction (linearly along three orthogonal dimensions), and varied its lacunarity by collecting or dispersing the ECS using a bipartition of the space based on local topology. In all, we generated six possible models of the ECS, which span the range of geometries that could occur under normal conditions in vivo, and used the models to study the non-uniform distribution of subcellular structures relative to the ECS and the impact of the space morphology on diffusion of small molecules such as neurotransmitter. It is likely that each of the diverse geometries demonstrated here occurs somewhere in the brain at some time depending on local conditions.

MATERIALS AND METHODS

All the data and software tools described in this paper are available for download. The co-registered EM image stack, contours, and reconstructed surfaces can be found here: http://www.mcell.cnl.salk.edu/models/hippocampusecs-2012-1. The EM images were traced with RECONSTRUCT (http://synapses.clm.utexas.edu). The contours were converted into 3D surfaces with VolumeRover (http://cvcweb.ices.utexas.edu/cvcwp/?page_id=100).

Tissue source and electron microscopy conditions

The EM image stack used here is centered on a large apical dendrite of a CA1 neuron (Fig. 2A) and has been previously described (V3) by Mishchenko et al. (2010). All procedures were approved by the University of Texas at Austin Institutional Animal Care and Use Committee and the Institutional Biosafety Committee and followed the National Institutes of Health guidelines for the humane care and use of laboratory animals. No new animals were prepared for this study. The image stack came from hippocampal area CA1 of a perfusion-fixed brain that had previously been obtained from a male rat of the Long–Evans strain weighing 310 g (postnatal day 77; Harris and Stevens, 1989). It was located in the middle of s. radiatum about 150–200 μm from the hippocampal CA1 pyramidal cell bodies. A series spanning 160 sections was cut according to our published methods (Harris et al., 2006), 100 of which were used in this study. Briefly, a diamond-trimming tool (EMS, Electron Microscopy Sciences, Fort Washington, PA) was used to make small trapezoidal areas that were about 200 μm wide by 30–50 μm high. Serial thin sections were cut at ~45–50 nm on an ultramicrotome and then mounted on Pioloform on a Synaptek slot grid. The sections were counterstained with saturated ethanolic uranyl acetate, followed by Reynolds lead citrate, each for 5 minutes. Individual grids were placed in grid cassettes and stored in numbered gelatin capsules. The cassettes were mounted in a rotating stage to obtain uniform orientation of the sections on adjacent grids, and the series were photographed at 5,000× on a JEOL 1200EX electron microscope (JEOL, Peabody, MA).

Figure 2.

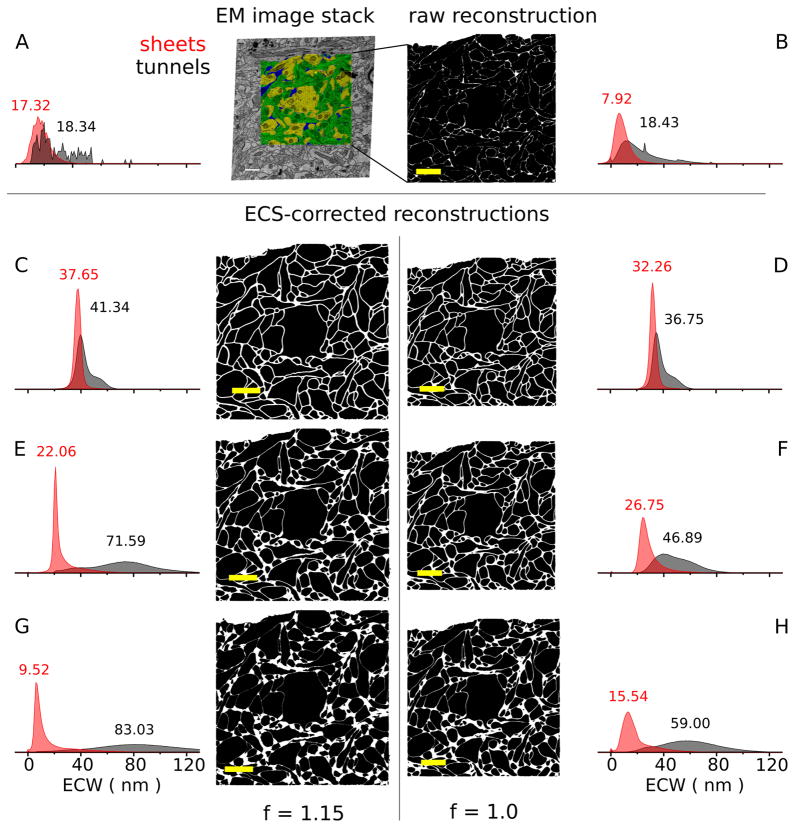
Sheet-and-tunnel model of extracellular space allows exploration of ECS lacunarity. A: Normalized histogram of extracellular width for sheets and tunnels, and arbitrary EM image from stack partially segmented with contours. Inset numbers represent median values of the distributions. The median extracellular width for tunnels was 17 nm (4,965 measurements) for sheets, and 18 nm (151 measurements) for tunnels, somewhat wider than the sheets, as observed by Van Harreveld et al. (1965). B: Virtual slice through the raw reconstruction with ICS rendered black and ECS as white. The median sheet extracellular width distribution was 8 nm (N = 1,756,847), smaller than observed in EM images, suggesting a bias in contour placement toward the extracellular side. All virtual slices in B–H are at the same location in the stack as A. C–H: Virtual slices through six reconstructions, built from the raw reconstruction, covering a range of ECS lacunarity values, but with nearly identical extracellular volume fraction of 0.2 (0.202 ± 0.003). C,E,G: Half of the reconstructions were scaled by 15% along three orthogonal axes to account for shrinkage associated with the tissue preparation protocol used here. The reconstructions in B–D had similar median values for sheet and tunnel extracellular width (ECW) distributions. These provide a lower bound on ECS lacunarity. Expanding the tunnel ECS volume (E–H) at the expense of the sheet ECS volume, to maintain constant extracellular volume fraction, increased the lacunarity of the ECS and broadened the tunnel extracellular width distributions. The integral of each sheet (red) and each tunnel (black) relative frequency histogram was normalized to one. Scale bar = 1 μm in A–H.

EM image stack registration

The 100 serial-section EM images of adult rat hippocampus (4,096 × 4,096 pixels, 2.3-nm resolution, gray-scale) were co-registered by using the software program RECONSTRUCT (Fiala, 2005), which is freely available from http://synapses.clm.utexas.edu. Images were optimized for brightness and contrast. Manual alignment was obtained by placing five or more fiducial points (e.g., cross-sectioned mitochondria or microtubules) that were in the same location on adjacent pairs of serial sections. The minimal algorithm (usually linear) was applied in RECONSTRUCT to perform section-to-section alignment while blending the adjacent images. Pixel size was calibrated relative to a diffraction grating replica (Ernest F. Fullam, Latham, NY) photographed with each series, and section thickness was computed by dividing the diameters of longitudinally sectioned mitochondria by the number of sections they spanned (Fiala and Harris, 2001; Harris et al., 2006). Every structure was then traced through serial sections and identified as a dendrite, spine, axon, glial process, synapse, etc. until the entire volume was complete (total = 180 μm³).

3D reconstruction of an EM image stack

The process for building 3D reconstructions of neuropil from electron microscopy images is described in detail by Kinney (2009). Briefly, the outer surface of the plasma membrane of every dendritic, axonal, and glial process in each section was manually traced from the micrographs to create contours at a resolution of 2.3 nm per pixel by using RECONSTRUCT software. The sets of contours for each process were stitched together by using the ContourTiler software, which generates 3D surfaces by constructing triangles between contours on pairs of adjacent sections (Bajaj et al., 1996, 1999). Because the tiling algorithm only operates on pairs of sections at a time, the program need only load a small amount of data into memory at any one moment, making the program easily extendable to the reconstruction of forests of neurons in the software program VolumeRover, a suite of tools for reconstruction, visualization, and analysis of high-quality meshes, (Edwards and Bajaj, 2011; http://cvcweb.ices.utexas.edu/cvcwp/?page_id=100).

The 3D computer model of neural tissue consists of water-tight, triangulated surfaces representing the outer surface of the lipid bilayer of each process in the volume. In Mishchenko et al. (2010) this EM image stack was studied with a focus on the location of synapses, and the ECS was 1 pixel wide by default following semiautomated reconstruction. Here we use the same EM image stack to investigate the morphology of the ECS.

Measurements of extracellular width in EM images

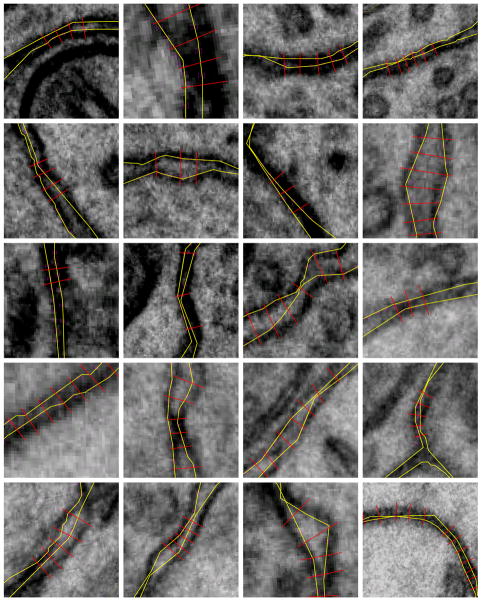
We chose to measure the extracellular width in EM images at places where plasma membranes lie orthogonal to the plane of section (Fig. 3). Such places were identified by using the aforementioned 3D computer model of the neural tissue. Specifically, regions of the EM images were chosen as candidates for extracellular width measurement if both opposing membranes of the ECS had normal vectors lying within 4.5 degrees of the plane of section. Of the more than 2.3 million vertices in the reconstruction, 10% were tagged as orthogonal. Furthermore, the candidate regions must have (upon inspection of the image) clearly delineated dark staining of the membranes with abrupt transitions to minimal staining of the cytoplasm.

Figure 3.

Contour location error accounts for one-quarter of ECS loss observed in raw reconstruction. In the raw reconstruction 8% of the total volume is ECS, compared with 20% in vivo. The discrepancy is partly explained by contour placement error during EM image tracing. Contour location error (yellow) was estimated by measuring the extracellular width (red) in regions where the cell membranes lies orthogonal to the plane of section. The raw reconstruction has a median sheet extracellular width of 7.92 nm, well below the EM image stack sheet median extracellular width of 17.32 nm (Table 1).

In the sheet regions of the ECS, the width was measured as the shortest perpendicular distance between the opposing membranes. Straight lines (red) were drawn from the intracellular edge of one membrane, across the membrane, across the ECS, to the intracellular edge of the opposing membrane. This approach was adopted to handle accurately cases in which the extracellular width was near zero. The extracellular width was calculated as the length of the measurement line minus twice the membrane width. The membrane width was measured to be 7.5 nm, consistent with the membrane staining width in EM images (Rosenbluth, 1962; Lehninger, 1968). In the tunnel regions of the ECS, the extracellular width was measured directly, because the tunnel width was always greater than zero. Extracellular width measurements were made on odd numbered EM images (50 in total) to distribute the measurements across the stack of 100 images.

Calculating the volume of ECS on the nanometer scale

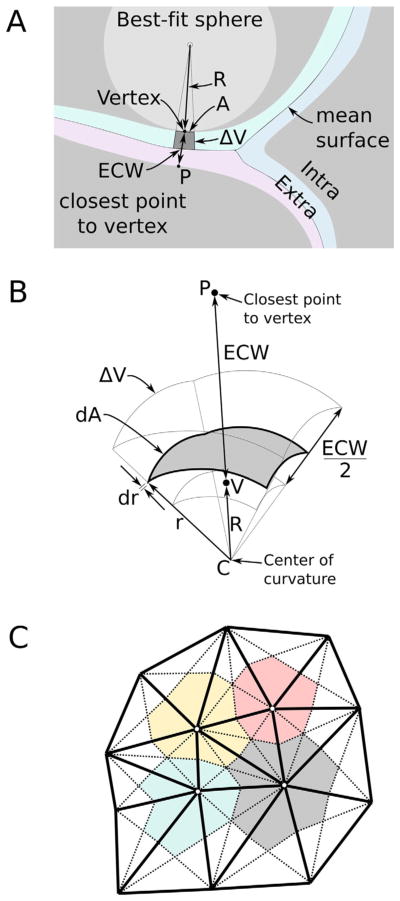
Here we describe a method to parcel the ECS into small, discrete subregions, associated with surface patches on neighboring cells. In this way, the heterogeneity of the ECS on the nanometer scale is measured. To begin, the ECS around each reconstructed object is imagined as a shell encapsulating the object (Fig. 4A). The total volume V_ECS of the ECS is the sum of all ECS shells (one shell per object for N objects): V_ECS = Σ_NV_shell,i. The volume V_shell,i of the shell of object i is calculated by summing the volume ΔV_j of small shell elements over the entire surface S of object i: V_shell,i = Σ_SΔV_j. Beginning from a small area A_j on the surface of the object, a shell element extends out radially a distance equal to one-half of the extracellular width ECW_j. The surface mesh of each reconstructed object is not entirely flat like a plane, but also includes some concave regions and other convex regions (Fig. 4B). On a small scale the curvature of the surface can be considered constant and modeled as the surface of a sphere with a radius R_j fit to the small patch of surface under the shell element. The volume ΔV_j of a shell element is calculated as an integral of differential elements shaped like spherical shells: ΔV_j = ∫dA_jdr. The area of a sphere of radius r is equal to 4πr². The area dA_j of the differential element is a fraction f_j of the total area of the sphere where 0 < f_j < 1: dA_j = f_j4πr². Because the shell element extends radially from the surface, f_j is constant for all differential elements in ΔV_j and is calculated from the surface area A_j of the shell element and the radius of curvature $R_j:f_j=A_j/4\pi R_j^2$.

Figure 4.

Accurate calculations of extracellular space volume using radial shell elements. A: The ECS volume is approximated as the sum of many small shell elements (one per vertex). The curvature of the element is estimated by fitting a sphere of radius R to the constellation of local vertices that describe the surface patch of area A under the element with volume ΔV. B: The extracellular width (ECW) is measured as the distance between the vertex V and closest point P. The shell element extends halfway across the extracellular width. C: A sample patch of a surface mesh illustrates how the surface was partitioned by using a median mesh into distinct domains around each vertex. Edges (solid black) connect vertices (white circles). Median lines (dashed) were drawn between vertices and the midpoint of the opposite edge. This particular construction divides the triangles into six smaller triangles with equal area. One-third of the area of each large triangle is assigned to its vertices. This method has three advantages. First, the surface domain (red, gray, blue, yellow) of each vertex surrounds the vertex. Second, the surface area of the domain is simply one-third the cumulative area of all neighbor triangles of the vertex. Third, the domains perfectly tile the surface. The shape of the shell element surface domain does not influence the calculation; only the scalar area is measured and used.

Finally, the volume ΔV_j of a shell element is calculated as follows:

$$\mathrm{\Delta }{V}_j={\int }_{R_j}^{R_j+{\mathit{ECW}}_j/2}d{A}_{j}dr=(A_j/3R_j^2)[{(R_j+{\mathit{ECW}}_j/2)}^3-R_j^3].$$

This expression for the volume ΔV_j of a shell element behaves well for all values of radius of curvature R_j. For shell elements over flat regions of the object surface (R_j → ±∞), the element volume reduces to the expression for a simple prism(A_jECW_j/2). It can also be shown that for convex surface regions where 0 < R_j < ∞ (e.g. R_j = ECW_j) the shell element volume is greater than the volume for a flat region as expected. Likewise, for concave surface regions where −∞ < R_j < 0, e.g. R_j = −ECW_j, the shell element volume is less than the volume for a flat region as expected. The local radius of curvature at each vertex was measured by generating the least-squares fitted sphere to the patch of surface around each vertex (Coleman et al., 2005). Specifically, each sphere was fit to the collection of the primary vertex and immediately adjacent vertices. The radius of the sphere was taken as the curvature measure.

To assess the accuracy of these equations, we compared the volume of the entire ECS in each reconstruction, computed by subtracting the ICS of each cell from the volume of bounding box of the reconstruction, to the volume calculated using these equations. An algorithm for calculating the volume of the ECS in reconstruction is to assign an ECS shell element to each vertex in the model:

$$V_{\mathit{ECS}}={\sum }_i{\sum }_j\left(A_j/3R_j^2\right)\left[{(R_j+{\mathit{ECW}}_j/)}^3-R_j^3\right].$$

For each vertex j in each object i, calculate 1) the local radius of curvature R_j, 2) the surface area A_j of the mesh region around the vertex (Fig. 4C), and 3) the extracellular width ECW_j between the vertex and its closest point. Use these three values to compute the volume contribution ΔV_j of the shell element over the vertex j to the entire ECS volume. Error associated with this algorithm should converge to zero as surface patch size shrinks, i.e., number of vertices increases in mesh for a given surface. This model had an ECS volume error fraction of 0.009 ± 0.015 (mean ± SD, max = 0.027) across all reconstructions. A planar model of ECS (assuming zero curvature) had an ECS volume error fraction of 0.108 ± 0.033 (mean ± SD, max = 0.162) and was not used.

Tortuosity

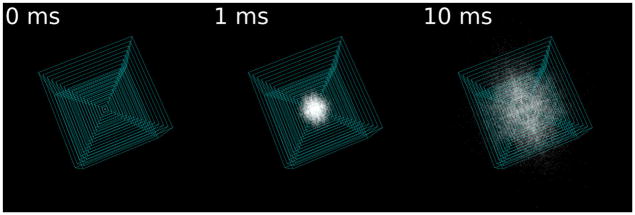
On the micron scale, the morphology of the ECS is dictated by the twisting and turning of the cell membranes. Looking much like a plate of spaghetti, the convoluted structure of neuropil hinders the rate of neurotransmitter diffusion by virtue of its constricted pore space and the farther distance between two locations in the ECS compared to a free environment, attributes that we refer to as micron-scale, or geometric, tortuosity (λ_g). The micron-scale tortuosity of each reconstruction was estimated by measuring the diminished rate of diffusion in MCell simulations (Stiles and Bartol, 2001) of molecules in the ECS. The effective rate of diffusion of 10,000 molecules through the ECS was recorded by using concentric sampling boxes centered on the release site (Tao and Nicholson, 2004). The largest sampling box (8.5 μm on a side) was located fully within the reconstruction. To minimize boundary effects, the MCell simulation ended when 4% of the molecules had diffused out of the largest sampling box (Fig. 5).

Figure 5.

Measuring micron-scale tortuosity in a reconstruction of a 5 × 6 × 6 μm volume of neural tissue. The diffusion of glutamate in the ECS was simulated with MCell to measure the diffusional impedance due to micron-scale geometry of each reconstruction. Seventeen concentric sampling boxes (cyan) recorded the time course of glutamate (white) concentration during diffusion through the reconstructed tissue (not shown). The largest sampling box is 8.5 μm on a side. The glutamate count in each sampling box over time was used to estimate a diminished rate of diffusion (Tao and Nicholson, 2004). The resulting estimate of micron-scale tortuosity (Fig. 8C,D) had a fairly tight confidence interval, suggesting that a tissue volume of 1,000 μm³ would yield similarly well-constrained estimates of tortuosity without mirroring (see Materials and Methods). Reconstructions smaller than this are not representative of the neuropil because the volume is too small to average out the heterogeneity seen in the cellular structure.

The particles must sample a large subset of the reconstruction geometry by diffusing several microns to yield accurate and precise estimates of the micron-scale tortuosity. However, the particular tissue volume used here contains a large apical dendrite centered in the volume, which precluded central glutamate release. Our only recourse was to release peripherally and use three mirror planes to artificially expand the size of the reconstruction eightfold around the site of glutamate release to improve the estimate of micron-scale tortuosity. Thus we effectively oversampled the data, possibly introducing biases into our estimates of micron-scale tortuosity. Anisotropy of micron-scale tortuosity was not explicitly measured in our reconstruction (because the tissue volume was so small); however, the presence of the large apical dendrite would likely bias the rate of diffusion to be faster in the direction of the dendrite’s medial axis. The site of molecule release was located 250 picometers away from the point of intersection of the three mirror planes so that the cloud of molecules underwent simulated diffusion as if from a single point source. We confirmed that our choice of time step (1.0 × 10⁻⁶ seconds) was sufficiently small to avoid diffusion artifacts by reducing the time step by 50 (to 0.5 × 10⁻⁹ seconds) after which only a small change in rate of diffusion was measured (data not shown).

The rate of molecule diffusion through the ECS is also diminished relative to a free environment due to macromolecules obstructing the diffusion path on the nanometer scale and drag effects from the membrane walls. The diffusion constant of a molecule in the ECS can be calculated from its free diffusion constant in water, e.g., 7.5 cm² per second at 25°C for glutamate (Longsworth, 1953), and the ratio of geometric to total tortuosity in the ECS, e.g., 1.45 for glutamate in rat hippocampal CA1 (Sykova and Nicholson, 2008):

$$D_{\mathit{ECS}}=D_{\mathit{free}}{({\lambda }_g/{\lambda }_t)}^2$$ (1)

Image postprocessing

Digital images were captured on the TEM and imported into the RECONSTRUCT software where contrast and brightness were optimized to visualize specific objects, such as postsynaptic densities and plasma membranes while tracing.

RESULTS

Reconstructed ECS has lower than expected volume

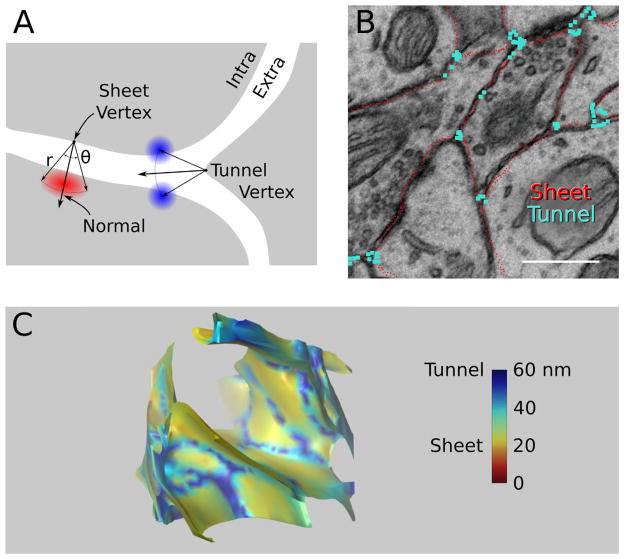
The measured extracellular volume fraction of the raw reconstruction was 8%, well below in vivo estimates of 20%. This was not entirely surprising, as tissue shrinkage is commonly attributed to insults from the process of preparing neural tissue for EM imaging (Fig. 1) including hypoxia, aldehyde fixation, and dehydration (Fox et al., 1985; Kirov et al., 1999). Nevertheless, the width of the ECS was measured in the stack of EM images to confirm that our EM data were consistent with published observations of extracellular width. The EM image measurements were collected in two distinct pools based on whether the measurement was made at the intersection of two membranes or at the intersection of three or more membranes (Fig. 6A,B). In the 3D reconstruction these become sheet-like and tunnel-like volumes, respectively (Fig. 6C). The distribution of extracellular widths at pairs of membranes had a median value of 17.32 nm (Fig. 2A), close to the conventional extracellular width value of 20 nm based on EM measurements (Rusakov and Kullmann, 1998a; Barbour, 2001; Wahl et al., 1996; Castejon, 2009), suggesting that our tissue preparation protocol was acceptable and the EM image stack reflected commonly reported ECS geometries.

Figure 6.

Topological analysis of the ECS reveals a patchwork of flat sheets separated by a network or tubular tunnels of larger extracellular width. A: Decomposition of the ECS into sheets and tunnels by local topological classification. ICS (gray) and ECS (white) are demarcated by the reconstructed outer surface of the lipid bilayer of cellular processes. Vertices in the reconstructed surface mesh were classified as having sheet-like or tunnel-like ECS nearby according to the number of neighboring objects (Experimental Procedures). Vertices with exactly one neighbor are labeled as “sheet” whereas vertices with two or more neighbors are labeled as “tunnel.” B: Cross section through the raw reconstruction showing approximate location of vertices identified as having tunnel-like (blue) and sheet-like (red) ECS nearby. The appearance of tunnel-labeled vertices in regions of the 2D cross section that resemble sheets is expected when only two of the three (or more) cellular processes forming the tunnel are captured in the slice and additional processes are visible only in adjacent slices. C: One cubic micron from the reconstruction shown in Figure 2F was rendered with the ECS as solid and ICS invisible. Coloring the ECS according to extracellular width reveals the interconnectedness of the tunnel network (blue). Extracellular widths are measured in nanometers in the color bar. Scale bar = 500 nm in B.

So, we investigated the process of converting the EM image stack into 3D surfaces as a cause of the diminished ECS in the raw reconstruction. Measuring the extracellular width in the raw reconstructions did reveal a small population of sites where neighboring objects collided, as evidenced by negative widths in the histogram (Fig. 2B). More importantly, errors in contour placement (Fig. 3) lead to a substantial decrease of the median extracellular width in the raw reconstruction (7.92 nm), compared to the EM images. Consequently, the raw reconstruction has a lower extracellular volume fraction than the EM image stack, because of a systematic bias of contour tracing toward the outside of the cell membranes. Inevitably, errors also arose when the plasma membrane was difficult to discern and the proper placement of contours is no longer obvious, which occurred when a process was cut obliquely along its medial axis. Assuming the raw reconstruction has pure sheet ECS (actual fraction is 0.6; Table 1), the tissue volume ascribed to contour error can be calculated as volume = 0.5 * (17.32–7.92) * surface_area. Dividing the contour placement error volume by the raw total tissue volume (also from Table 1), the extracellular volume fraction lost by contour error is estimated to be 3% of the total tissue volume. This implies that the extracellular volume fraction in the image stack was closer to 11%, still leading to the conclusion that the ECS geometry in the EM image stack is shrunken compared to in vivo.

TABLE 1.

Summary Statistics for Reconstructions¹

Recon	EVF	Sheet EVF	Tunnel EVF	Overall median ECW (nm)	Sheet median ECW (nm)	Tunnel median ECW (nm)
A	—	—	—	—	17.32	18.34
B	0.080	0.63	0.37	8.93	7.92	18.43
C	0.201	0.67	0.33	38.25	37.65	41.34
D	0.199	0.66	0.34	33.27	32.26	36.75
E	0.207	0.37	0.63	31.25	22.06	71.59
F	0.203	0.50	0.50	34.55	26.75	46.89
G	0.200	0.23	0.77	30.29	9.52	83.03
H	0.202	0.29	0.71	40.40	15.54	59.00

Recon	Total Area (μm2)	Sheet Area (μm2)	Tunnel area (μm2)	Geometric tortuosity	Diffusivity in ECS (μm2/ms)
A	—	—	—	—	—
B	2,343.62	1,843.46	485.46	1.42 ± 0.04	0.60 ± 0.04
C	2,575.47	1,868.90	704.49	1.22 ± 0.06	0.44 ± 0.05
D	1,940.06	1,389.01	549.57	1.22 ± 0.04	0.44 ± 0.03
E	2,494.80	1,459.41	1033.50	1.28 ± 0.06	0.49 ± 0.05
F	1,834.73	1,168.28	664.57	1.25 ± 0.04	0.47 ± 0.03
G	2,533.01	1,440.60	1090.81	1.41 ± 0.06	0.59 ± 0.05
H	1,866.52	1,042.14	823.09	1.33 ± 0.04	0.53 ± 0.03

¹Recon refers to reconstruction labels in Figure 2. ECW is the median width of the extracellular space (ECS) measured from each surface at a density equivalent to tiling the surface with equilateral triangles of side length 40 nm and then measuring the extracellular width from the barycenter of each triangle. Raw reconstruction has a total volume of 1.83347e+11 nm³. Nonscaled (f = 1) reconstruction has a total volume of 1.82012e+11 nm³. Scaled (f = 1.15) reconstruction total volume was assumed to be 50% more than the nonscaled volume. The square root of the ratio of total surface area of the scaled to nonscaled reconstruction should equal the scaling factor f. Given mean surface areas of 2,534.4 and 1,880.4 μm² for scaled and nonscaled reconstruction respectively, the calculated scaling factor is 1.16, close to the 1.15 used, suggesting that total surface area is insensitive to reconstruction lacunarity.

EVF, extracellular volume fraction.

To address the shrinkage, we expanded the ECS of both the raw reconstruction and a copy scaled by 1.15 (linearly along three orthogonal dimensions) to compensate for an estimated 33% volumetric shrinkage from our protocol (Kirov et al., 1999). Custom software iteratively manipulated the location of the surfaces on the nanometer scale in response to model forces controlling the width of the ECS (see Materials and Methods). The diminished extracellular volume fractions in the raw and scaled reconstructions were expanded to 0.2 while maintaining uniform extracellular width (Fig. 2C,D).

Quantitative topological analysis of the ECS

We performed a quantitative topological analysis of the ECS and decomposed the ECS into sheets and tunnels. There are a number of ways to do a comprehensive topological analysis, e.g., Morse graphs or stable manifolds (Shinagawa et al., 1996; Chazal and Lieutier; Goswami et al., 2006). Most of them essentially reduce to constructing and analyzing the medial axis set of the ECS. This is equivalent to skeletonizing a bounded volume with surface boundaries. For the ECS, the surface boundaries are surface patches of the axial/dendritic/glial membranes that come close together in the neuropil. The medial axis set is usually sheet-like when two surface patches of the ECS come close together, and when three or more such membrane boundaries come together in close proximity, they often induce a tubular or tunnel-like region, whose medial axis is curve-like and forms the axis path of the tunnel.

Using this decomposition, we classified a surface patch around each vertex in the surface meshes as belonging to either sheets or tunnels, according to the number of closest neighbor surface points each vertex had, 2 and 3+ respectively. The algorithm has several steps: For each vertex, an axis is defined through the vertex by averaging the normal vectors of the neighboring polygons. Around this axis, a cone of angle θ (e.g., 60 degrees) and radius r (e.g., 250 nm) is searched by ray tracing along the axis itself and eight evenly spaced rays along the perimeter of the cone. Intersection of the rays and any surface reveals the presence of a neighboring surface patch (Fig. 6A). The number and arrangement of the closest surface patch points determines the topological identity of the vertex and its neighborhood.

Manipulating the ECS on the nanometer scale

After the ECS was decomposed into sheets and tunnels, we varied the distribution of ECS between the two regions, allowing for the creation of a family of reconstructions, all with identical extracellular volume fraction but with different distributions of tunnel and sheet volumes (Fig. 2). Varying the lacunarity of the ECS according to topology, as such, is one way of introducing variance into the ECS distribution. However, this latter morphing process was underconstrained on the micron scale, so we made the simplifying assumption of uniform ECS width within the sheet region and within the tunnel region, and built this assumption into the morphing algorithm. However, in fact, the ECS width was never perfectly uniform in any of the reconstructions (Fig. 3); the spring model implicitly captured the lipid membrane’s resistance to bending, so the ECS width histograms of sheets and tunnels have some spread.

We wrote custom software to control the ECS by manipulating the location of the reconstructed surfaces on the nanometer scale. The software implements a simple model of forces on the membrane surface involving springs between neighboring regions on a surface and between surfaces on different neighboring processes. The collection of all springs describes a potential energy system, which is relaxed to determine the final location of the surfaces. The spring forces will tend to generate an ECS with uniform width controllable by a user-specified target value.

From the two corrected reconstructions (Fig 2C,D), four additional versions of the reconstruction were created by varying the allocation of the ECS volume between sheets and tunnels (Fig. 2E–H). All six of the new reconstructions had the same extracellular volume fraction (0.202 ± 0.003), but the uniformity of the extracellular width in the reconstructions varied dramatically. The distributions of extracellular width in the sheets and tunnels were nearly identical in the more uniform reconstructions (Fig. 2C,D; Table 1) but diverged as the sheet volume shrank and the tunnel regions expanded (Fig. 2E–H). The variances of the extracellular widths for sheets and tunnels increased along with their medians.

The sheets and tunnels were non-uniformly distributed

We examined the distribution of sheets and tunnels around axons, dendrites, and astrocytic processes and found that axons were surrounded by more tunnel-like spaces and astrocytes tended to be near sheet-like volumes (Fig. 7B). We attribute these findings to differences in cellular geometry: Axons have a smaller cross-sectional area than dendrites (Mishchenko et al., 2010), which promotes the formation of tunnels in the ECS. In contrast, the vellate structure of astrocytes is more conducive to having sheet-like ECS (Online Movie at http://cnl.salk.edu/~jkinney/waltz/waltz.mp4).

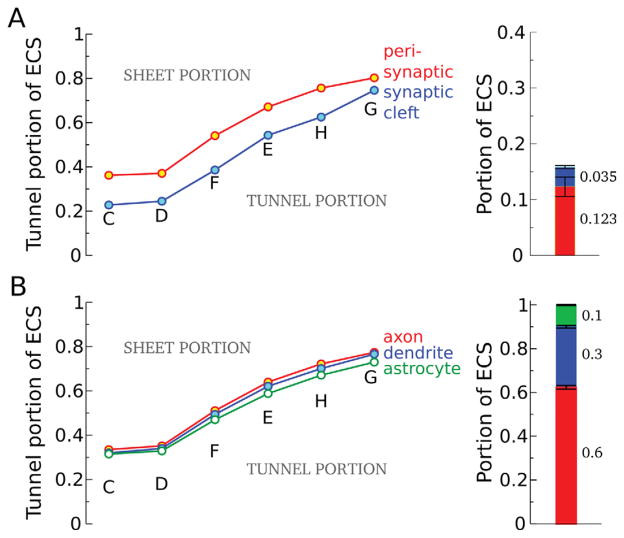
Figure 7.

Astrocytes and synapses were enriched with sheet-like extracellular space (ECS) and the perisynaptic region with tunnel-like ECS. The subcellular distribution of ECS volume was measured for each ECS-corrected reconstruction, including the fraction of ECS in synaptic clefts, perisynaptic regions, and surrounding axons, dendrites, and astrocytes. The relative amount of tunnel- and sheet-like volume in these functionally defined regions of ECS was also calculated. A: Perisynaptic regions have the highest fraction of ECS volume in tunnels. In contrast, synaptic clefts have an ECS more sheet-like than other regions of membrane. The perisynaptic region was defined to be twice as wide as synaptic clefts to adequately sample ECS around synapses. This implies the perisynaptic region will be eightfold larger than cleft area (assuming concentric, circular geometry). Perisynaptic regions and synaptic clefts accounted for 12.3% and 3.5% of the ECS volume, respectively. B: The ECS was also decomposed into three fractions corresponding to axonal, dendritic, and astrocytic regions accounting for 60%, 30%, and 10% of the ECS volume, respectively. Axonal regions of ECS are consistently more tunnel-like than dendrites and astrocytes. Conversely, the ECS around astrocytes is enriched with sheets.

By specifying exact patches of the reconstruction surface, both axonal and dendritic, as belonging to glutamatergic synaptic clefts and perisynaptic regions, the ECS volume belonging to these two groups was identified and measured (Fig. 7A). As expected, synaptic clefts were enriched with sheet-like ECS; indeed, the classical definition of a synapse as being an apposition of presynaptic and postsynaptic membrane matches our topological definition of sheet. The fraction of ECS volume in synaptic clefts in our reconstructions was 3.5% of the ECS, consistent with previous findings (Rusakov et al., 1998). Non-glutamatergic synapses accounted for less than 2% of all synapses and were excluded from the analysis.

The ECS in perisynaptic regions was more tunnel-like than all other membrane types, consistent with the fact that glutamatergic synapses in hippocampus occur on dendritic spines. The perisynaptic ECS volume fraction was 12.3% on average, fourfold larger than the synaptic cleft volume. It is generally accepted that the width of the synaptic cleft is tightly controlled in the 15–25-nm range (Savtchenko and Rusakov, 2007) owing to the high concentration of synaptic adhesion molecules in the cleft (Latefi and Colman, 2007). In our reconstructions the synaptic cleft width was not explicitly controlled, but instead was allowed to vary according to local topology of the neuropil. The mean synaptic cleft extracellular widths in the ECS-corrected reconstructions were 39.2, 33.8, 45.2, 34.4, 47.9, and 38.1 nm for reconstructions C–H, respectively.

To probe further the relationship between synapses and tunnels, we computed the mean straight-line distance from each vertex to the centroid of the nearest synapse (Table 2). In all models the tunnels were closer to the synapses than sheets: On average the tunnels were closer by 26.7 ± 4.7 nm. Coupled with the result that diffusion is faster in the tunnels than the sheets, this finding suggests that the ECS may be functionally organized into regions.

TABLE 2.

Tunnels Are Closer to Synapses Than Are Sheets¹

Recon	Mean distance (nm)	SEM (nm)	SD of distance (nm)	No. of vertices
C, sheet	728	0.47	454	922,397
C, tunnel	706	0.66	436	433,498
D, sheet	401	0.17	157	881,150
D, tunnel	385	0.21	146	467,270
E, sheet	743	0.59	465	615,596
E, tunnel	702	0.50	433	739,397
F, sheet	406	0.19	159	714,478
F, tunnel	383	0.18	145	630,458
G, sheet	746	0.61	469	595,424
G, tunnel	700	0.49	429	755,893
H, sheet	414	0.21	162	568,999
H, tunnel	381	0.16	145	774,364

¹Also see Figure 7. The straight-line distance from each vertex to the centroid of the closest synapse was measured. In all reconstructions, vertices facing tunnel ECS are closer to a synapse on average than vertices facing sheets. In Figure 7 we observed that perisynaptic ECS is tunnel-enriched. Together these results suggest that synapses are more closely associated with tunnels than sheets. Recon refers to reconstruction labels in Figure 2.

Monte Carlo diffusion simulations in the ECS

Because the diffusion of molecules in the ECS could be affected by the extracellular width distribution, the micron-scale tortuosity (see Materials and Methods) was calculated for each of the reconstructions by measuring the spread of 10,000 molecules in Monte Carlo simulations of diffusion using the MCell program (Stiles and Bartol, 2001; Kerr et al., 2008) (http://www.mcell.cnl.salk.edu). MCell simulates the diffusion of point particles (zero radius). Using space-filling particles to simulate molecular diffusion would effectively reduce the extracellular volume fraction and all extracellular widths proportionally with the diameter of the particle. In the case of glutamate, the Stokes–Einstein equation estimates a hydrodynamic diameter of less than 1 nm at 35°C (Thorne and Nicholson, 2006). As a consequence, the impedance to simulated diffusion of a sub-nanometer–diameter glutamate molecule should be slightly higher than we measured. Tao and Nicholson (2004) used simulations in a geometric model of the neuropil to show how changing the extracellular volume fraction affects the rate of neurotransmitter diffusion. We have confirmed this in the reconstructed neuropil and have shown in addition that for a fixed extracellular volume fraction, changing lacunarity also affects the rate of diffusion (Fig. 8A,B).

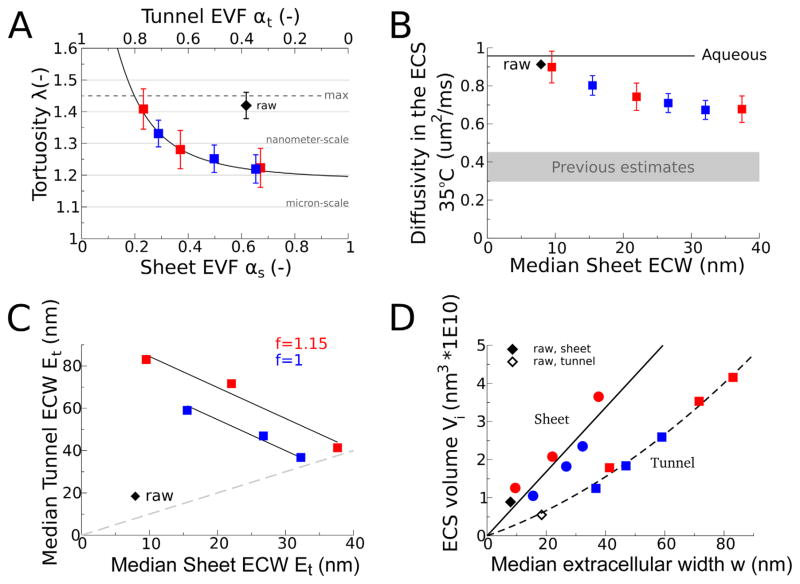
Figure 8.

Comparisons of the geometric properties among the shrinkage-corrected reconstructions. A: Sheet and tunnel extracellular volume fractions (EVFs) were correlated with micron-scale tortuosity, as measured by the impedance to simulated diffusion of point particles through the ECS of each reconstruction. As expected the estimated micron-scale tortuosities were above the minimum allowed value (1, corresponding to free space) and below the maximum expected value (1.45, corresponding to total tortuosity measured in vivo), and mostly fell between previous estimates from the literature (1.18, 1.35, 1.4 from Tao and Nicholson, 2004]; [Rusakov and Kullmann, 1998a]; and [Rusakov and Kullmann, 1998b, Zheng et al., 2008], respectively). The micron-scale tortuosity varies quadratically with sheet extracellular volume fraction over the range of extracellular volume fractions tested, ${\lambda }_g=0.8/(1+50{\alpha }_s^2)+1.18({\text{r}}^2=0.99)$, constrained to have a pure-sheet tortuosity of 1.18 as chosen from the Tao and Nicholson (2004) relationship between micron-scale tortuosity and extracellular volume fraction for uniform extracellular width (λ = [(3 − α)/2]^1/2) evaluated at extracellular volume fraction = 0.2. B: From the measured micron-scale tortuosities and Equation 1, we calculated the corresponding rate of diffusion through the ECS of each reconstruction that yields the observed effective rate of diffusion in vivo. The rate of free diffusion of glutamate in aqueous solution is 0.76 μm²/ms at 25°C (Longsworth, 1953), which sets an upper bound on the rate of diffusion in the ECS of 0.96 μm²/ms at 35°C, assuming a Q10 value of 1.26 (Zheng et al., 2008). Our estimates of glutamate diffusion constant in the ECS were higher than previous estimates (0.25, 0.3, 0.33, 0.45 from [Franks et al., 2002]; [Barbour, 2001, Savtchenko and Rusakov, 2004, and Stiles et al., 1996]; [Nielsen et al., 2004]; and [Zheng et al., 2008], respectively). C: Sheet and tunnel median extracellular widths (ECWs) were inversely correlated (r² = 0.98) for both scaled and nonscaled reconstructions. For the two regressions (constrained to have the same slope of 1.47), the median tunnel extracellular width extrapolated to zero sheet width is 99 and 84 nm, close to the scaling factor (15%) used on the scaled reconstructions. Similarly, the predicted uniform extracellular widths (when tunnel and sheet median width were equal) were 40 and 34 nm for f=1.15 and f=1.0, respectively. Perfect extracellular width uniformity lies along the line E_t =E_s (gray, dashed). D: Cumulative sheet extracellular volume in the reconstructions varied linearly with median extracellular width: V_s = 0.8w_s (r² = 0.9), consistent with a planar geometry of the sheets. In contrast, the cumulative tunnel extracellular volume increased with a combined linear and quadratic dependence on median extracellular width: $V_t=(2.8e-2)w_t+(2.8e-4)w_t^2({\text{r}}^2=0.99)$ , suggesting cylindrical geometry of the tunnels.

The micron-scale tortuosity was higher for reconstructions with low sheet extracellular volume fraction and high tunnel volume fraction (Fig. 8A). The range in micron-scale tortuosity across the reconstructions was 15%, even though the shortest paths through the neuropil did not change significantly. The main change was an overall reduction of cross-sectional area in sheet-like regions of the ECS, which hindered the rate of diffusion of the particles through the neuropil. When the sheet width was smallest, micron-scale tortuosity was greatest. The impedance due to tunnels was less than the diffusional hindrance of sheets, because the median sheet extracellular width was less than the median tunnel extracellular width (Fig. 8C).

The glutamate diffusion constants in the ECS required for a total tortuosity of 1.45, given the micron-scale tortuosity values in Figure 8A, were calculated by using Equation 1 (see Materials and Methods) and ranged from 0.7 to 0.9 μm²/ms at 35°C, greater than previous estimates (Barbour, 2001; Savtchenko and Rusakov, 2004; Nielsen et al., 2004; Stiles et al., 1996; Franks et al., 2002). We found that the rate of diffusion of small molecules like glutamate through the neuropil depended on the proportion of ECS in sheets and tunnels (Fig. 8B). Our highest estimates of glutamate diffusivity occurred in the reconstruction with the highest lacunarity (Fig. 2G,H) but not because of the lacunae. Instead, these reconstructions had smaller median sheet extracellular widths and higher micron-scale tortuosity, which required higher diffusion constants to achieve a total tortuosity of 1.45. In the literature, previous geometric models of neuropil morphology had ECS with a more uniform width. Our estimate of the glutamate diffusivity approached the values in the literature for large values of median sheet extracellular width (Figs. 2C,D, 4B), which had nearly uniform extracellular width.

The distribution of the ECS volume in the sheets and tunnels varied with the median extracellular width (Fig. 8D). The sheet-like ECS volume was approximately proportional to the sheet extracellular width, consistent with a model in which the two surfaces separate linearly. In contrast, the tunnel ECS volume had an additional term that scaled quadratically with tunnel extracellular width, consistent with a tubular model of the tunnel geometry.

DISCUSSION

Visual inspection of EM images of neuropil indicate that the ECS is not uniform in width, but is instead narrow between pairs of cell processes and grows wider at the junction of multiple cell processes (Fig. 2A). EM images from brain tissue prepared by rapid-freezing and freeze substitution, a process thought to preserve subcellular structure, confirm a high variance of the local size of the ECS in neuropil (Sosinsky et al., 2008). Inspired by these observations, we explicitly decomposed the ECS based on local topology, consistent with the mechanical properties of the cell membrane and cytoskeleton as a plausible physiological basis of wider ECS at the confluence of multiple cell processes (McMahon and Gallup, 2005).

We observed that subcellular features with small radii, e.g., axons, tend to have wider ECS in their vicinity (Fig. 7B; Van Harreveld and Khattab, 1965). Likewise, the presence of dendritic spines results in wider ECS surrounding the perisynaptic regions (Fig. 7A), as confirmed in recent findings using a cryogenically cooled knife that demonstrated large voids in the ECS, especially around synapses (Ohno et al., 2007). In contrast, large-diameter dendrites are preferentially surrounded by narrow ECS regions (Van Harreveld et al., 1965), as were the vellate wings of the astrocytes (Fig. 7B).

However, many aspects of tissue preparation for EM affect the volume of the ECS and ICS including hypoxia (Van Harreveld et al., 1965; but mitigated in our perfusion-fixation protocol), fixation (Quester and Schroder, 1997; Cragg, 1980; Van Harreveld and Khattab, 1967), and dehydration (Grace and Llinas, 1985; Schuz and Palm, 1989). In addition, the degree of tissue shrinkage varies by brain region (Grace and Llinas, 1985). Consequently, predicting changes in tissue volume for an arbitrary experiment based on the literature is difficult and prone to error. However, changes to the ICS and ECS observed after shrinkage can be characterized with two measurements: the EVF and total tissue volume (ECS+ICS). Here, we observed a reduction of extracellular volume fraction in both the EM image stack (11%) and raw 3D reconstruction (8%) compared to in vivo estimate (20%). However, little is known about changes to the ICS during tissue shrinkage. For instance, it is unclear whether the ICS shrinks, remains unchanged, or expands (Fig. 1).

Here we generated 3D reconstructions of rat hippocampal neuropil that covered a range of ECS distributions and that were compensated for tissue shrinkage and errors in the reconstruction process, in order to make quantitative measurements of the ECS morphology on the micron scale. Topological analysis of the raw reconstruction revealed that the ECS was composed of sheets with narrow extracellular widths surrounded by an interconnected network of tunnels with diameters significantly larger than the sheet width (Fig. 8C). Our sheet and tunnel model of the ECS in the 3D reconstructions can be approximated as a mixture of the tubular and sheet-like structures as proposed by Thorne and Nicholson (2006). Because the raw reconstruction, untouched by any morphing algorithm, had sheets and tunnels, our conclusions about the topology of the ECS are not simply artifacts of the morphing software. However, in the ECS-corrected reconstructions, the spring model potential energy system was relaxed under the assumption of uniform width of the ECS within sheets and tunnels. So, our results do not preclude the possibility of there being more tunnels nested in the sheets in vivo, in which case our tunnels represent a minimal network.

Reconstructions allow us to explore a broad range of plausible accounts for the inferred changes in the ECS and ICS (Fig. 1). On the one hand, significant shrinkage of both the ECS and ICS would lead to the most overall tissue volume loss (Figs. 1A, 2C,E,G), consistent with the 33% tissue volume loss for our EM protocol. On the other hand, no change in overall tissue volume implies that ICS increases at the expense of ECS (Figs. 1D, 2D,F,H). Between these two extremes are intermediate degrees of volume change. If the intracellular volume is unaffected by EM prep, then all tissue shrinkage is from ECS loss (Fig. 1B). Alternatively, the ECS may lose volume to both the ICS and solution (Fig. 1C).

Further evidence for tissue perturbation is found by looking for the ECS-corrected reconstruction that best matches the extracellular width histograms of the EM image stack (Fig. 2A). The sheet histogram in Figure 2H (red) is consistent with the image stack Figure 2A (red) but not the tunnels (black), suggesting that the tunnel ECS is preferentially lost during tissue shrinkage. In contrast, the reconstructions with more uniform extracellular widths (Fig. 2D,F) better reflect the significant overlap of the sheet and tunnel extracellular width distributions seen in the EM images, but at larger mean widths. No reconstruction matched the distribution of extracellular widths in the EM image stack, and the most parsimonious explanation is that our tissue did in fact shrink during preparation for EM imaging.

In the reconstructions, the diffusion of small molecules, such as glutamate, through the sheets was lower than through the tunnels, and the reconstruction with the narrowest sheets was also the most tortuous (Fig. 8A). However, no reconstruction could fully account for the reduced rate of diffusion as observed in vivo, based on micron-scale tortuosity alone. Dead-end pores have been posited as a contributor to diffusional impedance in brain tissue following ischemia and even in normoxia (Hrabe et al., 2004; Hrabetova and Nicholson, 2004). Our extracellular volume fraction-corrected reconstructions suggest that cellular geometry on the submicron scale (including many cases of glial ensheathment and a few dead-end concavities in axons) cannot account for observed tortuosity of small molecules like glutamate in vivo. We attribute the remaining diffusional impedance to interactions with extracellular matrix and cell membranes (Sykova and Nicholson, 2008). Diffusing particles experience anisotropic wall drag effects that hinder neurotransmitter mobility near the cell membranes (Beck and Schultz, 1970; Huang and Breuer, 2007). Whether extracellular matrix is distributed differentially in the sheets and tunnels is unknown. Of course, the reconstructions do not include the location and effect of ion channels, transporters, degradative enzymes, adherent junctions, extracellular matrix molecules, cell adhesion molecules, and a host of other molecular and structural players that might exert an even greater influence on diffusion.

Constraining the cleft width to 20 nm would involve a loss of synaptic ECS in our reconstructions. For instance, the synaptic ECS may actually account for less than 2% of ECS, compared to the 4% observed here. To correct the reconstructions, 2% of the ECS that is lost can be evenly distributed across the nonsynaptic space. Such a minimal perturbation of the ECS morphology is not expected to significantly affect the results. A reduction of synaptic cleft width will cause micron-scale tortuosity to increase slightly, but the contribution to tortuosity, either geometric or total, of a region of ECS is proportional to volume, which is small in the case of synaptic clefts.

We imagine that the compressed extracellular width distribution of sheets compared to tunnels could affect transient increases in the concentrations of small molecules in the two ECS regions. For example, release of a fixed number of molecules would produce a higher peak concentration in the narrower sheet regions than in the larger tunnel regions. Conversely, rapid release of fewer molecules in the sheets than in the tunnels would be needed to achieve the same peak concentration of molecules. Furthermore, because sheets have a higher surface-area-to-volume ratio than tunnels, the maximum rate of change of concentration, as seen by cell surface receptors, for example, in the sheets, would be higher than in the tunnels, whose larger volume acts as a low-pass filter on the concentration signal.

In principle, the larger median extracellular width of the tunnels compared to the sheets should allow the diffusion of larger molecules. The smaller median extracellular width of the sheets may pose a diffusion barrier to large molecules, thereby corralling them into the tunnels. The tunnels may also be the avenues for diffusion of large probe molecules, such as dextran and quantum dots in diffusion experiments (Thorne and Nicholson, 2006; Binder et al., 2004; Zador et al., 2008). If the tunnels are used for volume transmission of large signaling molecules, then the receptors for these molecules may be concentrated on the walls of the tunnels.

Previous reports that glia swelling may modulate extracellular volume fraction, combined with our observations that astrocytes preferentially lie near sheets and sheet extracellular volume fraction determines the rate of small molecule diffusion (Fig. 8A), suggest that glia are well positioned to regulate volume communication in neuropil (Ventura and Harris, 1999). The relative coverage of synaptic area by glia varied significantly within each reconstruction, implying a heterogeneous exposure of synapses to glial-induced changes in ECS.

In conclusion, decomposing the ECS according to the local topology revealed a patchwork of flat sheets separated by a network of tubular tunnels of larger extracellular width. The sheets and tunnels form an organized structure. Synapses and axons were surrounded by more tunnel-like ECS and astrocytes tended to be near sheets. Finally, the diffusion of neurotransmitter in the ECS was modulated by the extracellular width distribution in the sheets and tunnels even while maintaining a constant extracellular volume, raising the possibility that the ECS may be functionally specialized into regions that enhance signaling through concentration changes (sheets) and other regions that enhance volume transmission of large molecules (tunnels).