Large Local Analysis of the Unaligned Genome and Its Application

Abstract

We describe a novel method for the local analysis of complete genomes. A local distance measure called LODIST is proposed, which is based on the relationship between the longest common words and the shortest absent words of two genomes we compared. LODIST can perform better than local alignment when the local region is large enough to cover some recombination genes. A distance measure called SILD.k.t with resolution k and step t is derived by the integral LODISTs of whole genomes. It is shown that the algorithm for computing the LODISTs and SILD.k.t is linear, which is fast enough to consider the problem of the genome comparison. We verify this method by recognizing the subtypes of the HIV-1 complete genomes and genome segments.

1. Introduction

The approach to defining or extracting the similarity information between genomes is a major issue for computational biology because the suitable similarity can be used to obtain phylogenetic information, structure information, function information, and others. Many methods are served by this work (Mantaci et al., 2008; Vinga and Almeida, 2003).

Among those methods, character vector (CV) methods are well studied by many researchers (Jun et al., 2010; Sims et al., 2009). Before extracting similarity information between the genomes, a typical CV method attempts to extract features of each genome sequence first. For example, a fast CV method, the D2 statistic, compares sequences by using k-word content as the feature. To improve the accuracy of the comparison, Reinert et al. (2009) and Wan et al. (2010) suggest two variants of the D₂ word-count statistic, 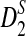and 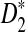, and show that the statistic is asymptotically normally distributed and not dominated by the noise in individual sequences. Aside from those, some researchers treat DNA sequences as Markov chains. Hence the Markov model is frequently employed to get information on the biological sequences (Dai et al., 2008; Kantorovitz et al., 2007; Pham, 2007; Pham and Zuegg, 2004). We deduce that character vectors are just one kind of representation of sequences. The comparison between two sequences is the one between their representations. From this point of view, graphical representations of sequences are another kind of CV method. There are some typical graphical representation methods (Liao et al., 2006; Randić, 2007; Yao et al., 2008; Yao et al., 2010; Zhang et al., 2003) that represent sequences in two-dimensional or three-dimensional space to realize the visualization. However, it is known that a feature can have a great effect on one situation but little effect on another. A family character can distinguish different families but cannot distinguish members in the same family. Hence, single representation cannot settle all problems.

Aside from the CV methods, there is another kind of method without the feature extraction step. This method involves putting the sequences together and computing the similarity score. The idea that two sequences are considered to be close if one sequence can be compressed significantly under the condition that the other sequence information is known, which is based on text compression technique, belongs to this kind of method and has been well-studied by many researchers (Ferragina et al., 2007; Li et al., 2001; Liu and Li, 2008; Otu and Sayood, 2003). The feature, compressing rate of one sequence, plays an important part in the comparison process, though it varies with the variation of the comparison object. The methods are called relative feature methods. Relative feature means that a character of one sequence depends on the compared objects. That is, once the compared object changes, so does the feature. Many comparison methods belong to the relative feature methods. The most widely used is the alignment method. The relative features of alignment are the ways of insertion, deletion, and substitution, which can convert one sequence to another at the lowest cost. However, although kinds of substitution matrices are used, the sequence alignment seems inadequate for measuring mutations that involve longer segments. Nevertheless, relative feature methods are efficient and powerful tools in the field of sequence analysis, and this work will amplify the toolbox of the relative feature method.

In this article, we take the large local analysis (LLA) problem that the local is large enough to cover some recombination gene segments in consideration, for which the alignment methods are not suitable. The method, one kind of relative feature method, is based on the longest common words and the shortest absent words of the two sequences studied by Haubold et al. (2005), Haubold et al. (2009), Pinho et al. (2009), and Ulitsky et al. (2006). We find that the sum of all the lengths of the longest common words is an index reflecting the degree of the local segments belonging to the reference sequence even though the segments cover some gene arrangements. Considering the relationship between the longest common words and the shortest absent words, we derive a local distance measure called LODIST, which means that the smaller sum implies the closer distance between the reference sequence, which is totally different from the idea proposed by Ulitsky et al. (2006). Experiments show that LODIST has good properties to solve the LLA problem. Furthermore, we propose a distance measure based on LODIST to compare the genomes and apply it to recognizing the HIV-1 complete genome subtypes. The high recognition rate shows that the method we propose is efficient and powerful.

2. Method

Let's consider the sequences defined on a given alphabet. That sequence S is called an n-complete sequence means that for any sequence lengthened, n is a subsequence of S.

If 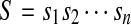, denote 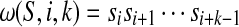and l(S) = n. Now we can define some sets as follows:

Definition 2.1

W(S) = {(S,i,k)|1 ≤ i + k − 1 ≤ l(S),i,k are postive integers}

CW(S,T) = {(S,i,k) ∈ W(S)|for some j,ω(T,j,k) = ω(S,i,k)}

AW(S,T) = W(S)\CW(S,T) = {(S,i,k) ∈ W(S)|for any j,ω(T,j,k) ≠ ω(S,i,k)}

LCW(S,T) = {(S,i,k) ∈ CW(S,T)|(S,i − 1,k + 1) ∈ W(S) implies (S,i − 1,k + 1) ∈ AW(S,T) and (S,i,k + 1) ∈ W(S) implies (S,i,k + 1) ∈ AW(S,T)}

SAW(S,T) = {(S,i,k) ∈ AW(S,T)|(S,i,k − 1) and (S,i + 1,k − 1) ∈ CW(S,T) or k = 1}

Here are the interpretations of the acronyms implied by definition 2.1. W(S) can be used to describe all the words of the sequence S. The representation of the word in S, instead of the alphabet string, is starting point (“i”) and length (“k”). Then CW(S,T) could be regarded as the set of the words in S, which also appear in the sequence T while AW(S,T) is the set of the words in S, called absent words of S in T, but not showing in the sequence T. Usually, the words we consider most are the longest common ones between S and T. Their starting points and lengths could be obtained by the elements of the LCW(S,T). Meanwhile, if we are interested in the shortest absent words of S in T, then the SAW(S,T) will be used. Next we will show the relationship between the longest common word set (LCW(S,T)) and the shortest absent word set (SAW(S,T)).

Proposition 2.1

If (S,i,k) ∈ CW(S,T), p ≥ i and p < p + q ≤ i + k, then (S,p,q) ∈ CW(S,T).

Proof

(S,i,k) ∈ CW(S,T) implies that there exists j such that ω(T,j,k) = ω(S,i,k), which means 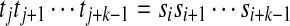. Since p ≥ i and 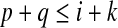, 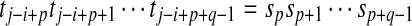. Hence, (S,p,q) ∈ CW(S,T).  ■

Proposition 2.2

If (S,i,k) ∈ AW(S,T), p ≤ i and p + q ≥ i + k, then (S,p,q) ∈ AW(S,T).

Proof

If (S,p,q) ∈ CW(S,T), then since i ≥ p and i + k ≤ p + q, (S,i,k) ∈ CW(S,T) according to proposition 2.1. That is a contradiction.  ■

Proposition 2.3

The following conditions are equivalent.

• (i) S is a subsequence of T;

• (ii) AW(S,T) = ∅;

• (iii) SAW(S,T) = ∅.

Proof

If S is a subsequence of T, then (S,1,l(S)) ∈ CW(S,T). For any (S,i,k) ∈ W(S), since i ≥ 1 and i + k − 1 ≤ l(S), the proposition 2.1 indicates (S,i,k) ∈ CW(S,T), which means W(S) ⊆ CW(S,T). Hence, AW(S,T) = ∅. Furthermore, SAW(S,T) = ∅.

On the other hand, if S is not a subsequence of T, then (S,1,l(S)) ∈ AW(S,T), which means AW(S,T) ≠ ∅. Pick 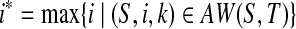and 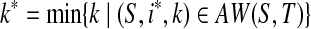. Clearly, (S,i*,k*) ∈ SAW(S,T), which means SAW(S,T) ≠ ∅.  ■

Proposition 2.4

The set LCW(S,T) can be ordered as 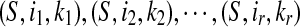where 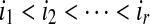. The set SAW(S,T) can be ordered as 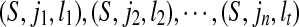where 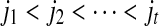. For any 1 ≤ p ≤ r − 1, we have i_p + k_p < i_p+1 + k_p+1.

Proof

Firstly, we will show that if (S,i,k) and (S,i,l) both belong to LCS(S,T) then k = l. If k > l, since (S,i,l) ∈ LCS(S,T) and i + k > i + l, (S,i,k) ∈ AW(S,T) according to the definition of LCW(S,T). That is a contradiction. The similar contradiction is due to the k < l. Hence, the set LCW(S,T) can be ordered as 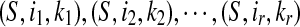where .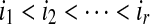

Secondly, we claim that if (S,j,k) and (S,j,l) both belong to SAW(S,T), then k = l. If k > l, since (S,j,k) ∈ SAW(S,T) and i + k > i + l, (S,i,l) ∈ CW(S,T) according to the definition of SAW(S,T). That is a contradiction. The similar contradiction is due to the k < l. Hence, the set SAW(S,T) can be ordered as 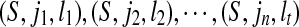where .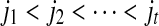

Finally, for any 1 ≤ p ≤ r − 1, i_p + k_p ≥ i_p+1 + k_p+1, i_p < i_p+1 and (S,i_p+1,k_p+1) ∈ LCW(S,T) imply that (S,i_p,k_p) ∈ AW(S,T) according to the definition of LCW(S,T). That is a contradiction. The contradiction implies i_p + k_p < i_p+1 + k_p+1.  ■

Proposition 2.5

Let LCW(S,T) and SAW(S,T) be ordered as proposition 2.4. If T is n-complete and n ≥ 1, then i_p+1 ≤ i_p + k_p.

Proof

That T is n-complete and n ≥ 1 implies (S,i_p + k_p,1) ∈ CW(S,T). Pick 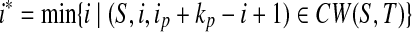and 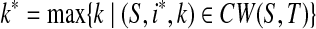. Clearly, (S,i*,k*) ∈ LCW(S,T). Since (S,i_p,k_p) ∈ LCW(S,T), (S,i_p,i_p + 1) ∈ AW(S,T). That indicates i_p < i* ≤ i_p + k_p. Hence i_p+1 ≤ i* ≤ i_p + k_p.  ■

Theorem 2.1

Let LCW(S,T) and SAW(S,T) be ordered as proposition 2.4. If T is n-complete and n ≥ 1, then i₁ = 1, t = r − 1 and for any 1 ≤ p ≤ t, j_p = i_p+1 − 1,l_p = i_p −i_p+1 + k_p + 2.

Proof

Since (S,1,1) ∈ CW(S,T) according to T is n-complete and n ≥ 1, we obtain 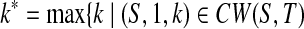. Clearly, (S,1,k*) ∈ LCW(S,T). Hence, i₁ = 1.

The proposition 2.5 implies to us that i_p − i_p+1 + k_p + 2 ≥ 2. We claim (S,i_p+1−1,i_p − i_p+1 + k_p + 2) ∈ SAW(S,T), which is supported by (S,i_p+1−1,i_p−i_p+1 + k_p + 1) ∈ CW(S,T) and (S,i_p+1,i_p−i_p+1 + k_p + 1) ∈ CW(S,T) according to the definition of SAW(S,T). In fact, it is known that i_p+1−1 ≥ i_p according to proposition 2.4, i_p+1−1 + i_p−i_p+1 + k_p + 1 = i_p + k_p and (S,i_p,k_p) ∈ CW(S,T), which stand for (S,i_p+1 − 1,i_p −i_p+1 + k_p + 1) ∈ CW(S,T) according to proposition 2.1. On the other hand, i_p+1 + i_p −i_p+1 + k_p + 1 = i_p + k_p + 1 ≤ i_p+1 + k_p+1 according to proposition 2.4, and (S,i_p+1,k_p+1) ∈ CW(S,T) implies (S,i_p+1,i_p −i_p+1 + k_p + 1) ∈ CW(S,T) according to proposition 2.1.

Last but not least, we need to show that for any (S,j,l) ∈ SAW(S,T), there exists p such that j = i_p+1 − 1. If not, then there exists p such that i_p − 1  < j < i_p+1 − 1. Since (S,i_p+1 − 1,i_p − i_p+1 + k_p + 2) ∈ SAW(S,T) and (S,j,l) ∈ SAW(S,T), j + l − 1  < (i_p+1 − 1) + (i_p −i_p+1 + k_p + 2) − 1 = i_p + k_p. In other words, j + l ≤ i_p + k_p. That is to say (S,j,l) ∈ CW(S,T) because (S,i_p,k_p) ∈ LCW(S,T) and proposition 2.1. It is a contradiction.  ■

Theorem 2.2

If T is n-complete and n ≥ 2 and LCW(S,T) and SAW(S,T) are ordered as proposition 2.4, then 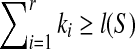and 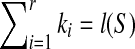if and only if S is a subsequence of T.

Proof

Because T is n-complete, l_p ≥ n + 1 which implies for any 1 ≤ p ≤ r − 1, i_p−i_p+1 + k_p + 2 ≥ n + 1 according to the Theorem 2.1. That is to say i_p+1 ≤ i_p + k_p−(n−1). Therefore, 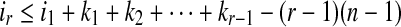. It is known that i₁ = 1 and i_r + k_r − 1 = l(S), which implies that 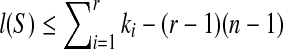. Since r ≥ 1 and 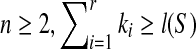. If 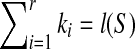, we have r = 1, which implies SAW(S,T) = ∅ according to Theorem 2.1. Hence, 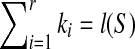implies S is a subsequence of T according to proposition 2.3. It is easy to check that S is a subsequence of T, which implies 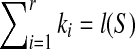. Therefore, 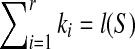if and only if S is a subsequence of T.

From this point, we assume that the difference between the 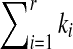and the l(S) can be used to represent the degree of the segment S belonging to sequence T. Considering the effect of the length of S, in this article, we utilize the relative difference between 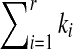and l(S) to represent the scale of segment S belonging to sequence T.  ■

Definition 2.2

The Local Distance between S and T: .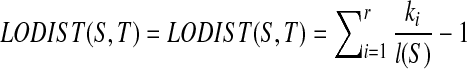

Theorem 2.3

If T is n-complete and n ≥ 2, then LODIST(S,T) ≥ 0. LODIST(S,T) = 0 if and only if S is a sub sequence of T.

LODIST(S,T) describes the scale of S belonging to T. We can apply it to local similarity analysis.

Now we find that there is an essential distinction between the distance measure proposed by Ulitsky et al. (2006) and our local distance measure, although both are based on the common word. The former measure is under the intuitive assumption that the longer the total length of the longest common prefixes [the longest common prefixes do not belong to the LCW(S,T); in this article, the longest common prefix is (S,i,k), belonging to CW(S,T) if (S,i,k + 1) does not belong to CW(S,T)], the more similarity the two sequences have. However, according to the local distance, the sum of all the longest common words implies the difference between the sequences. Some possible reasons are as follows: one is that the distance measure proposed by Ulitsky et al. (2006) reflects the similarity between the whole sequences while our local distance measure represents the scale of the segment S belonging to the sequence T. Another important reason is that one longest common word often produces many longest common prefixes. Hence, the inherent property of the total length of the longest common words is covered by the total length of the longest common prefixes.

2.1. Example and simple explanation of the main theorems

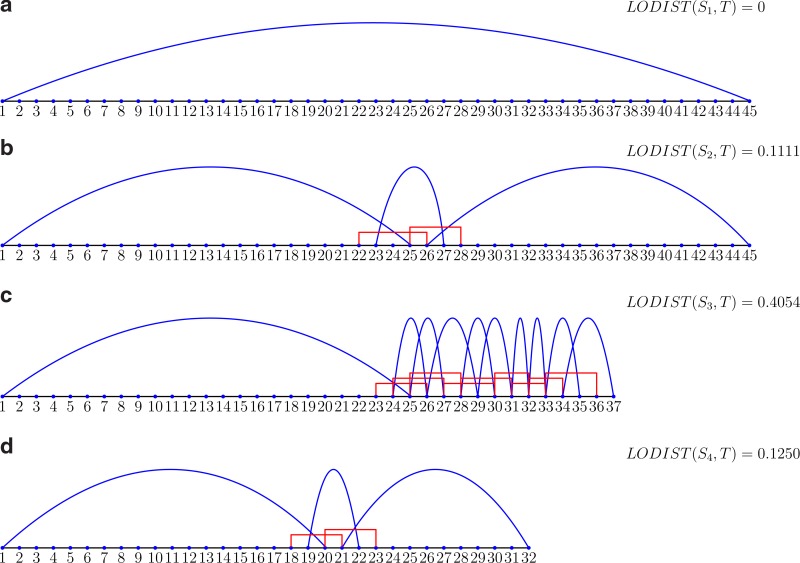
For example, let S = GATTGTGCGAGACAATGCTACCTTATTATGACGTTATTCTACTTT, and T = GCC TGGTCTTCGTTATGACGTTATTCTACTTTGATTGTGCGAGACAATGCTACCTTAAAGTTAGCA. The local alignment between S and T is shown in Figure 1b. LCW(S,T) ={(S,1,25),(S,23,5),(S,26,20)} and the SAW(S,T) = {(S,22,5),(S,25,4)}. LODIST(S,T) = (25 + 5 + 20)/45 − 1 = 1/9. We can represent LCW(S,T) and SAW(S,T) by a diagram. Put S on a line with integers representing the nucleotide. Given (S,i,k) ∈ LCW(S,T), we draw a curve connecting i and i + k − 1. For a (S,i,k) ∈ SAW(S,T), “ ⊓ ” connecting i and i + k − 1 is used. The diagram of the example is shown in Figure 2b. From the diagram, it is not difficult to find all the longest common words (the word under ”⌢”) and all the shortest absent words (the word under “ ⊓ ”). Moreover, the simple diagram can reflect the relationship of LCW(S,T) and SAW(S,T) as Theorem 2.1 indicates. Theorem 2.1 just implies that “ ⊓ ” crosses its neighbors. When we extend the crossing region on both sides, an absent word is obtained. The shortest absent word is the shortest extension.

FIG. 1.

Four examples of local alignments between S₁ = M + N, S₂ = N + M, S₃ = N + Q, S₄ = M + P, and the reference sequence T = O + M + N + P.

FIG. 2.

Four examples for LODISTs between S₁ = M + N, S₂ = N + M, S₃ = N + Q, S4 = M + P, and the reference sequences T = O + M + N + P.

2.2. The locality property and the integral local distance metric

Technically, we obtain the LCW(S,T) and SAW(S,T) by the suffix tree, which is a linear algorithm. Even so, when doing the local analysis, if we compute the LCWs of every local region by the suffix tree it will be time-consuming work due to the vast local regions. Fortunately, the set of SAW(S,T) has good local property that helps obtain the SAWs of every local region easily. Once the SAWs are obtained, the LCWs are obtained by Theorem 2.1.

Proposition 2.6

SAW(ω(S,p,q),T) = {(ω(S,p,q),i,k)|(S,i + p−1,k) ∈ SAW(S,T),p ≤ i + p − 1 ≤ i + p+ k − 2 ≤ p + q − 1}.

Proof

Let 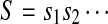and 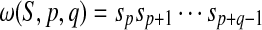. If p ≤ i + p − 1 ≤ i + p + k − 2 ≤ p + q−1, then 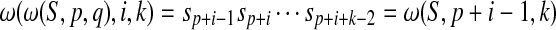. The proposition implies that 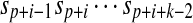is a shortest absent word of ω(S,p,q) with T if and only if it is a shortest absent word of S with T. Clearly, it is true.  ■

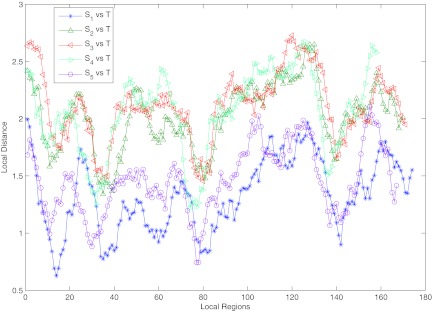
Now, given two genome sequences S and T, we utilize LODIST to show the local similarity between two genomes by the sliding window. First, compute the LCW(S,T) and the SAW(S,T) with the suffix tree or other methods. Then, after setting the size of the sliding window and the sliding step, we slide it through genome S and compute the LODIST of each local region according to proposition 2.6, Theorem 2.1, and Theorem 2.3. Figure 3 shows the LODISTs of five HIV-1 complete genomes and one reference HIV-1 complete genomes. S₁ and S₅ are subtype A; S₂,S₃, and S₄ are subtypes B, C and D, respectively. The reference sequence T is subtype A. The size of the sliding window is 500 and the sliding step is 50. From the figure, it is easy to locate the similarity region and estimate the similarity. LODISTs of S₁ and S₅ are lower than others, which answers the fact that S₁, S₅, and T are the same subtype A. Aside from those, we find that the trend of the five groups of LODISTs are almost the same, all of which deserve our further research.

FIG. 3.

The LODISTs of five HIV-1 complete genomes and one reference HIV-1 complete genome. S₁ and S₅ are subtype A; S₂, S₃, and S₄ are subtype B, C, and D, respectively. The reference sequence T is subtype A. The sliding window's size is 500 and the sliding step is 50.

Sometimes, we need to compare whole sequences instead of local regions. We do this by the simple but powerful idea that integrates all the LODISTs of local regions.

Definition 2.3

Let T be all n-complete sequence and n ≥ 2.

The Integral Local Distance between S and T with resolution k and step t:

.

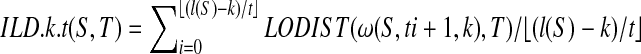The Symmetrical Integral Local Distance between S and T:

SILD.k.t(S,T) = min(ILD.k.t(S,T),ILD.k.t(T,S)).

Note that the resolution k and step t in the definition of ILD.k.t are respectively the size and step of the sliding window. Neither the ILD.k.t nor SILD.k.t are true distance measure because they do not satisfy the triangle inequality condition. However, they are of great influence in the comparison of the sequences.

3. The Comparison with the Alignment Method

3.1. The complexity of the algorithm

The alignment method is mainly based on dynamic programming, which is O(n₁n₂) time complexity where n₁,n₂ are the length of two sequences. It is tough to align two whole genomes whose lengths are too long. Often, the compromise among time, space, and accuracy is considered. However, it is O(n₁ + n₂) time complexity that computes the longest common words between two sequences using the generalized suffix tree. In practice, the suffix array is chosen as the data structure, which is O(nlog(n)) time-consuming but O(n) space-consuming. Moreover, the suffix tree or suffix array technique gives an excellent performance when we need to compute a pairwise distance matrix on a large data set (Ulitsky et al., 2006).

3.2. The locality of the algorithm

We show the difference of the local analysis between LODIST and the local alignment. For example,

M = TTATGACGTTATTCTACTTT;

N = GATTGTGCGAGACAATGCTACCTTA;

O = GCCTGGTCTTCG;

P = AAGTTAGCA;

Q = CGAGCGGGCAAT.

Assume that we do the local analysis between segments S₁ = M + N,S₂ = N + M,S₃ = N + Q,S₄ = M + P and reference sequence T = O + M + N + P shown in Figure 1. The similarity scores are 104.3333, 65.3333, 70.3333, and 52.3333, respectively. The alignment between S₁ and T gives the highest similarity score due to the identical part (M + N). However, the alignments give a lower score of S₂ than S₃ although there are two identical parts (N and M) existing in S₂, whereas one identical part (only N) in S₃. Although the two identical parts (M and P) are in alignment between S₄ and T, it is the lowest similar score. In fact, as is known, the alignment does not perform well when the “local” is large enough to cover some recombination gene segments. Especially, the alignment cannot afford different arrangements of gene segments. On the other hand, local analysis by LODIST is shown in Figure 2. The LODISTs are 0, 0.1111, 0.4054, and 0.1250, respectively. Since LODIST represents how much one segment belongs to the other, we conclude that segment S₁ belongs to T and segments S₂ and S₄ are closer to T than S₃. It is in anticipation.

Therefore, it is suggested that when we do local analysis, LODIST performs better than the local alignment method if the neighborhood considered is large enough to cover some recombination gene segments. Undoubtedly, LODIST is a powerful tool in large local analysis.

4. Application to recognizing the HIV-1 subtype

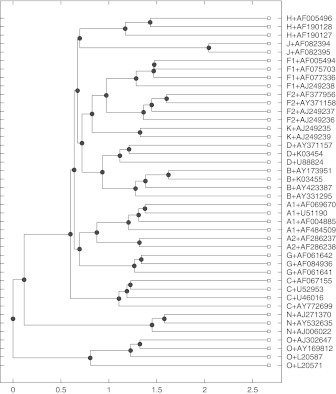
A set of 42 whole genomic sequences is used to test our method first. The set was carefully selected by considering several criterias (Leitner et al., 2005). Wu et al. (2007) pointed out that 42 HIV-1 reference sequences consist of 6 A subtypes (4 A1 and 2 A2), 4 B subtypes, 4 C subtypes, 3 D subtypes, 8 F subtypes (4 F1 and 4 F2), 3 G subtypes, 3 H subtypes, 2 J subtypes, 2 K subtypes, 3 N types and 4 O types. The distance matrix computed by setting the resolution at 500 and the step at 50 is used to construct the hierarchy tree by the UPGMA method illustrated in Figure 4, which is the same result obtained by Wu et al. (2007).

FIG. 4.

The hierarchy tree of 42 HIV-1 complete genomes by UPGMA method. The distance matrix is computed by SILD.500.50.

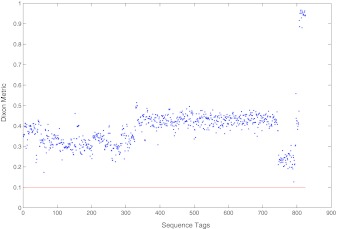
Furthermore, we treat the 42 reference sequences as a train set to classify 825 pure subtype HIV-1 whole genomes, which were also used in Wu et al. (2007). Among the 825 sequences, there are 64 A, 264 B, 415 C, 51 D, 2 F1, 10 G, 2 N, and 17 O. Wu et al. (2007) classify those sequences by the nearest neighborhood principle and obtain a 100% perfectly accurate rate, which is better than many commonly used methods. However, there is a flaw when using the Dixon metric to quantify the confidence. The Dixon metric is computed by (d₂−d₁)/(d₃−d₁), where d₁ and d₂ denote the shortest and the second-shortest average distances, respectively, and d₃ denotes the longest average distance. If the numerical confidence is greater than 0.1, then the confidence is high (Su et al., 2001). The flaw is that five of them are less than 0.1 among those prediction confidences. In this article, we do the same with Wu et al. (2007) and obtain the same perfectly accurate rate. Moreover, all the Dixon confidences shown in Figure 5 are greater than 0.1.

FIG. 5.

Subtype prediction confidence values (Dixon metric). All of them are greater than 0.1.

Finally, we confirm our method through the segments subtype recognition. We choose the DNA segments randomly from 825 HIV-1 whole genomes. Because the data set of the 825 sequences is bias, fixing segment length, we do that as follows:

• Step 1. Choose a subtype with equiprobability;

• Step 2. In the chosen subtype class, choose a sequence with equiprobability;

• Step 3. In the chosen sequence, choose a segment with equiprobability.

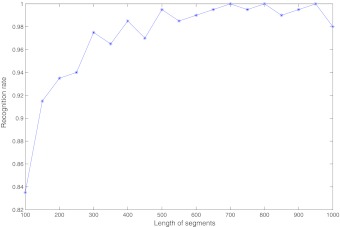
After obtaining adequate segments for the given length, we then change the length. We obtain 200 HIV-1 pure subtype segments of the length 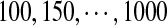, respectively. The recognition rates are shown in Figure 6. It can be seen that the LODIST metric has a good performance in recognizing the subtype of the HIV-1 DNA segments. It can also be seen that there is a higher recognition rate when the segment length gets longer. The recognition rate is high when the length is 500.

FIG. 6.

The recognition rates of the set of HIV-1 sequence segments.

5. Conclusions

A local analysis method that can solve the large local analysis problem for the genome is proposed. We use LODIST to describe the degree of a local region belonging to the reference sequence. LODIST performs well when the local region is large enough to cover some arrangements of genes. Based on LODIST, the distance measures ILD.k.t and SILD.k.t with resolution k and step t are derived to compare the genome. Since the algorithm is linear, the computation of LODIST, ILD, and SILD are fast even if the genome sequence is large. The choice of resolution k and step t is experimental. We suggest that resolution k should be large enough to cover much recombination information and not too large to avoid the effect of the noise. The step t is used to reflect the variation trend, and hence, is much smaller than the resolution. In this article, we utilize SILD.500.50 to classify the HIV-1 complete genome subtype. The accurate classification shows that our method is useful in genome comparison.

At the end of the article, we discuss the limitations of our method. The information about the genetic recombination is composed of the reversal, translocation, and transposition. Our local distance measure is based on the common words of two sequences, but if one sequence contains a reversal gene segment of the other sequence, then the segment is hardly a common word between the two sequences. As a result, information about the reversal cannot be detected by our method. Part of our future work is to explore the utilization of the reversal information on suitability for the large local analysis problem.

Acknowledgment

This work is supported by the National Natural Science Foundation of China (Grant No.10871219).

Disclosure Statement

The authors declare that no competing financial interests exist.