The synthesis-diffusion-degradation model explains Bicoid gradient formation in unfertilized eggs

Abstract

Precise formation of morphogen gradients is essential to the establishment of reproducible pattern in development. Mechanisms proposed for obtaining the requisite precision range from simple models with few parameters to more complex models involving many regulated quantities. The synthesis-diffusion-degradation (SDD) model is a relatively simple model explaining the formation of the Bicoid gradient in Drosophila melanogaster, in which the steady-state characteristic length of the gradient is determined solely by the rates of diffusion and degradation of the morphogen. In this work, we test the SDD model in unfertilized D. melanogaster eggs, which contain a single female pronucleus and lack the nuclear division cycles and other zygotic regulatory processes seen in fertilized eggs. Using two-photon live imaging as well as a novel method for quantitative imaging based on decorrelation of photoswitching waveforms, we find that the Bicoid gradient is longer and shallower in unfertilized eggs as compared to the gradient at the same time points in fertilized eggs. Using a means of measuring the Bicoid lifetime by conjugation to a photoconvertible fluorophore, we find that the lifetime is correspondingly longer in unfertilized eggs, providing qualitative and quantitative agreement with the predictions of the SDD model.

Introduction

Fate specification in multicellular organisms is accomplished by the establishment of concentration gradients of chemical substances called morphogens [1, 2]. Cells measure the concentration of a given morphogen in their local area, and express various combinations of downstream genes at appropriate concentration thresholds [3]. The physical mechanisms that underlie gradient formation and read-out are of special interest, as their precision directly affects the reproducibility of the patterning process [4, 5].

One of the best-studied examples of a morphogen gradient is generated by the maternal effect gene bicoid in Drosophila melanogaster [6, 7]. Bicoid is a transcription factor that drives the expression of genes controlling anterior development, and forms a graded distribution along the anterior-posterior axis of the embryo in the interval between egg deposition and cellularization [8, 9, 10]. The mechanism responsible for Bicoid gradient formation, however, remains unclear. The synthesis-diffusion-degradation (SDD) model, named by Gregor et. al. in 2007 [11], but described in essence by Driever and Nusslein-Volhard in 1988 [9], is a relatively simple model proposed to explain this phenomenon. In the SDD model, bicoid mRNA is localized to a small region at the anterior of the embryo [12, 13, 14], and translation of the protein occurs at a constant rate following egg deposition. Bicoid then diffuses throughout the embryo with a diffusion coefficient D and undergoes ubiquitous first-order degradation at a rate k, leading to an exponential profile in steady state with length constant $\lambda =\sqrt{D∕k}$. It has been suggested that small deviations from this prediction may be observed due to pre-steady-state effects, either because of an insufficiently short protein lifetime compared to the available developmental time, or because of changing rates of synthesis [15]. However, others have suggested that the deficiency of the SDD model is even more fundamental, in particular because it neglects sequestration effects introduced by nuclei [16, 17], or simply because morphogen diffusion may not be accurately described by Fick's law [18]. While the measurements of Grimm and Wieschaus suggest that the specific effect of nuclear import on Bicoid gradient shape is small [19], the more general claim that other uniquely zygotic regulatory processes do not affect Bicoid gradient formation has not been demonstrated.

In this work, we treat the subject of gradient formation in unfertilized eggs, which undergo no nuclear cleavage divisions or zygotic regulation, bcd mRNA is nevertheless localized and protein is translated beginning at oviposition; the event of fertilization is known to not be necessary for bcd translation to occur [9]. However, only limited mention of the shape of the unfertilized gradient exists in the published literature. Imaging of unfertilized eggs, fluorescence imaging in particular, presents special challenges due to the lack of a region of transparent cortical cytoplasm that forms with the syncytial blastoderm in fertilized eggs. Two studies examine the unfertilized case in some detail. Driever and Nusslein-Volhard quantified immunostaining intensities from unfertilized eggs of various ages, reporting that the development of the gradient proceeds normally until 2–4 hours after egg deposition, at which point levels of total Bcd protein in unfertilized eggs begin to exceed those in fertilized eggs [9]. More recently, Gregor et al. measured the ratio of eGFP-Bcd fluorescence intensity at the anterior as compared to the posterior of fertilized and unfertilized eggs and found a smaller value in the unfertilized case, reflecting a putatively shallower gradient in the unfertilized egg [11]. Together, these observations are consistent with a gradient formation process similar to that envisioned by the SDD model, incorporating a smaller time-averaged protein degradation rate in the unfertilized case.

Nevertheless, traditional views on the Bcd gradient formation process make somewhat vague and inconsistent predictions about the properties of the unfertilized Bcd distribution. A number of potentially significant differences exist between fertilized and unfertilized eggs: among them, differences in cytoskeleton architecture, and regulation of RNA and protein degradation. On the one hand, one might expect the unfertilized gradient to be longer and shallower, reflecting the presumed greater stability of Bcd protein. On the other, one might expect a shorter, steeper gradient, reflecting the absence of cytoplasmic contractions coincident with nuclear cleavage divisions, which are only present in fertilized eggs and which have been conjectured to augment Bcd diffusivity [9].

In this work, we first obtained time series data of the unfertilized gradient formation process using eggs expressing eGFP-bcd imaged under two-photon laser scanning microscopy, which is notable for its capacity to acquire fluorescence images deeper in living tissue than confocal microscopy [20]. We developed a technique to compute the gradient at equal optical depth at all points along the anterior-posterior (A–P) axis, to minimize the potentially severe effect of visible-light scattering in unfertilized eggs. Next, we developed a novel method to obtain quantitative concentration measurements from repeatedly photoswitched images of photoconvertible fluorophores, and applied this technique to eggs expressing both dronpa-bcd and h2a-rfp, to again compare the Bcd gradient in fixed populations of fertilized and unfertilized eggs. From both of these experiments, we noted several significant differences in the unfertilized as compared to the fertilized case, such as monotonically increasing Bcd levels and the accretion of Bcd at the posterior end of the egg. One potential explanation for these observations, according to the SDD model, is a longer Bcd protein lifetime in unfertilized eggs. We then applied the optical technique for measuring protein lifetime described in Ref. [21] to unfertilized eggs expressing dronpa-bcd alone, providing a direct test of the assumption that the protein is more stable in unfertilized eggs. We show that, taken together, these measurements suggest that the SDD model describes equally well the unfertilized case using the longer Bcd lifetime we observe.

Finally, we calibrated fluorescence intensities from the live imaging data to absolute protein concentrations, and compared the results to previously published estimates of Bcd copy number at relevant developmental timepoints. Because the effect of protein degradation is small in the unfertilized case, it presents an especially good opportunity to calculate the Bcd protein synthesis rate, and we have estimated this value over the entire embryo as well as on a per-RNP-granule basis.

Materials and Methods

Preparation of samples

Sterile XO males were generated as in Ref. [11] and crossed to females from the fluorescent bcd transgene stocks to produce unfertilized eggs. We used a combined dronpa-bcd/h2a-rfp transgene provided by O. Grimm for comparison of the fertilized and unfertilized gradients in fixed tissue. For live imaging, we used an eGFP-bcd transgene in a bcd⁻ background, provided by T. Gregor [11].

For the fixed samples, flies were kept at 22°C and their eggs collected on plates of apple juice and agar mixture for 60 minutes. Plates removed at the end of this interval were aged for two additional hours. Eggs were dechorionated for 90 seconds in bleach and fixed in a solution of 20% paraformaldehyde and 1× PBS for 45 minutes. The eggs were then devitellinized by hand and mounted according to the procedure of Ref. [22].

For the live samples, eggs were collected similarly, with 60–80 minute intervals between plate changes. As the agar was generally free of eggs up to 40 minutes following a plate change, we estimate the mean egg age at collection to be 15 minutes after oviposition. Eggs were dechorionated for 1 minute in bleach, washed in dH₂O, arranged on a piece of agar, and glued to a glass slide with adhesive derived from scotch tape and heptane. Eggs were allowed to dry briefly and then immersed in halocarbon oil (Sigma-Aldrich). No coverslip was used.

Two-photon laser scanning microscopy of live samples

The microscope apparatus was modeled on that described in Ref. [23]. A Coherent Verdi V10 diode-pumped laser was fed into a mode-locked Coherent Mira 900 Ti-sapphire oscillator, generating 80 fs pulses at 918 nm with a repetition rate of 80 MHz. Intensity was modulated with a Pockels cell (Conoptics, model 350–50). The beam was fed through a shutter (UniBlitz) and scanned via a pair of galvo driven mirrors. We used a 20× infinity-corrected 0.75 NA multi-immersion objective (Nikon, CFI Plan Fluor 20× MI). Light emitted from the specimen was reflected by a dichroic beamsplitter into a two-channel photomultiplier system, with a HQ610/75 two-photon 18° emission filter (Chroma) in the first bay and a BG39 filter in the second. Laser scan generation and PMT signal acquisition were controlled using MATLAB and the ScanImage software suite [24]. Laser power was measured to be 85 mW at the sample. The point spread function of this apparatus was determined by imaging a set of four 100 nm diameter fluorescent microspheres (Polysciences). We recovered an approximately Gaussian relationship (data not shown).

Two-photon image analysis and gradient computation

We developed a method for measuring gradients in live embryos by acquiring z-stacks under two-photon illumination and measuring the specific signal at various A-P positions and depths within the embryo. The primary objective was to minimize the effects of unequal optical depth, which can distort gradient measurements based on a single z-slice in highly-scattering samples such as unfixed unfertilized eggs.

Spatial inhomogeneities in beam intensity across the field of view were mitigated by flat-fielding all images, normalizing each by a smoothed image of uniform concentration of 100 μM fluorescein. Autofluorescence was then minimized and specific eGFP signal maximized by creating a compound image whose intensity at each pixel represented a linear combination of measured intensity in both PMT channels:

$$I_{eGFP}(\overrightarrow{x},t)=I_{BG39}(\overrightarrow{x},t)-A{I}_{610}+(\overrightarrow{x},t)+B$$ (1)

Coefficients were determined by acquiring images in wild-type embryos lacking fluorescent markers. The method was based on the observation that the autofluorescent signal in the red channel correlated strongly with that in the green channel, and that eGFP bleed through into the red channel was a small effect that could be corrected for (~ 4%, see Calibration section). The coefficient A was chosen to minimize the variance $<I_{eGFP}^2>-{<I_{eGFP}>}^2$ inside the egg, and B was chosen such that < I_eGFP >= 0. The ensemble average was taken over the length of the egg and the developmental time range of interest (1–3 hours after oviposition).

Gradient computation in unfertilized eggs requires a more robust technique than that typically used in fertilized eggs, as late syncytial embryos have a layer of cortical cytoplasm 25 μm thick [25] which is transparent to visible light. In unfertilized eggs, by contrast, the cortex and core are equally opaque, and yolk granules extend nearly to the surface of the egg. To obtain an accurate reading of the Bed gradient it was necessary to compute the fluorescence intensity at equal optical depth along the length of the egg. A stack of 30 images, each averaged over two complete scans, with stepping 4 μm in the z-direction, was acquired beginning at the mid-sagittal plane of the embryo and proceeding upward. The anterior-posterior (A-P) axis was chosen manually and spanned with 200 equally-spaced points. An example of the A-P axis selection is shown in Fig. 1a. A MATLAB routine calculated the mean intensity in an 8 μm × 8 μm box centered at each AP axis point, and for each of the 30 z-stacked images. The vitelline membrane height S_vit(x, t) at each point was located by plotting I₆₁₀(x, z, t), applying a smoothing spline in the z coordinate, and finding the first zero of the first derivative approaching the egg from above. This calculation is illustrated in Fig. 1b. Statistical outliers in the vitelline membrane location, due to occasional debris adhering to the membrane surface, were replaced by a moving mean. The Bed gradient G_Bcd was computed by summing

$$G_{Bcd}(x,t)=\sum _{i=1}^{d_{\max ∕\Delta z}}\frac{I_{eGFP}(x,z=S_{vit}(x,t)+i\Delta z,t)}{d_{\max ∕\Delta z}}$$ (2)

This assumes that observed intensities at various depths, after background subtraction (see Fig. 1c), are linearly proportional to each other with a single value along the entire A-P axis of the embryo. We chose the maximum depth d_max to be 40 μm and the z stepping Δz to be 5 μm. To reduce noise, this calculation was repeated, beginning with the vitelline membrane computation, for two different axes parallel to the A-P axis and separated by 16 μm on each side.

Figure 1. Illustration of vitelline membrane identification and gradient calculation in two-photon live imaging.

a) Composite BG39 image of a fertilized eGFP – bcd expressing egg in early mitotic cycle 14. A–P axis is indicated by dashed line b) Fluorescence intensity in the 610 nm channel for a z-stack centered at x = 150 μm along the A–P axis of the embryo, at different time points indicated by color from blue to red. The vitelline membrane location is taken as the peak in the fluorescence intensity, and is indicated by an asterisk for each respective time point. Region over which the specific intensity I_eGFP is summed to calculate eGFP-Bcd concentration is indicated by gray shading, c) Fluorescence intensity in the BG39 channel (I_BG39) for a z-stack centered at x = 150 μm along the A–P axis at time t = 3 h after oviposition (red line). Dashed line indicates background autofluorescence to be subtracted (AI₆₁₀ = B). Region of integration is again indicated by gray shading.

G_Bcd was converted to an absolute concentration of eGFP-Bcd $(C_{Bcd}^{obs}=\left[\mathrm{e}\mathrm{GFP}-B\mathrm{cd}\right])$, using the scale factor obtained by calibration and adjusting for the loss of specific eGFP intensity removed during the background subtraction process due to bleed-through (see Calibration section).

Total quantity of mature eGFP-Bcd Q_mat was determined by the integration

$$Q_{\mathrm{mat}}\left(t\right)={\int }_0^L\Gamma \left(t\right)C_{Bcd}^{obs}(x,t)\pi R^2\left(x\right)dx$$ (3)

where $R=b\sqrt{1-x^2∕a^2}$, which assumes the embryo is a prolate spheroid with major axis a = 250 μm and minor axis b = 90 μm. The integral was computed by Riemann sum using 200 equipartitioned boxes along the A-P axis. Lacking data at the poles of the embryo (x < 0.1L, x > 0.9L), we used the nearest value of $C_{Bcd}^{obs}$ at these locations; however, due to the prolate spheroidal geometry these make only a small contribution (~ 5%) to the embryo volume. The scale factor Γ(t) was set to unity in the unfertilized case. In the fertilized case, Γ was fixed at unity at the first time point, t = 87 min. post-oviposition, and subsequently computed by fitting to simulation according to Eq. 10.

Imaging of Dronpa-Bcd in fixed tissue by photoswitching decorrelation

The advent of photoswitchable fluorescent proteins has led to new methods for measuring specific fluorescent signals in cells [26]. We developed and used a method better suited for quantitative measurement of fluorophore concentrations in fixed tissue. Each fixed Dronpa-Bcd/H2A-RFP-expressing embryo was imaged in a repetitive sequence with 6–8 images at 496 nm excitation followed by a single image at 405 nm excitation. These wavelengths correspond to the conversion and activation wavelengths of Dronpa [27], and served to switch the fluorophore population between bright and dark states. This procedure was repeated through 10–30 cycles. Additionally, during each cycle, we acquired a single image at 561 nm to measure H2A-RFP fluorescence. The strategy we developed to quantitatively measure Dronpa concentration exploits the changes in the state distribution of the fluorophore effected by each of these different wavelength pulses in sequence.

The means of obtaining the specific Dronpa-Bcd signal intensity is as follows. We subdivide the A–P axis of the embryo into 200 boxes and find the mean green and red channel intensity in each box: I_green(x,t) and I_res(x,t). We then normalize by the mean red channel intensity in each box to correct for small inhomogeneities due to variance in DNA content as represented by Histone-RFP, such as differing numbers of nuclei in a given slice of the image; this results in a significant smoothing of the calculated gradients. The derived quantity, y(x,t), can be written as:

$$y(x,y)=\frac{I_{\text{green}}(x,t)}{{<I_{\text{red}}(x,t)>}_t}=F\left(x\right)s_1\left(t\right)+G\left(x\right)s_2\left(t\right)+\xi (x,t)+\sigma n(x,t)$$ (4)

where F(x) and G(x) vary only in space, s₁ and s₂ are zero-mean unit-norm processes, ξ(x, t) is a general function of time in each box, σis the noise level, and n(x, t) is a Gaussian random variable. Because the embryos were fixed, there is a general loss of fluorescence from photobleaching that we seek to capture in the quantity ξ(x, i); we define it by filtering the measured signal by moving mean:

$$\xi (x,t)=\frac{1}{2T}{\int }_{-T}^{T}y(x,t)dt$$ (5)

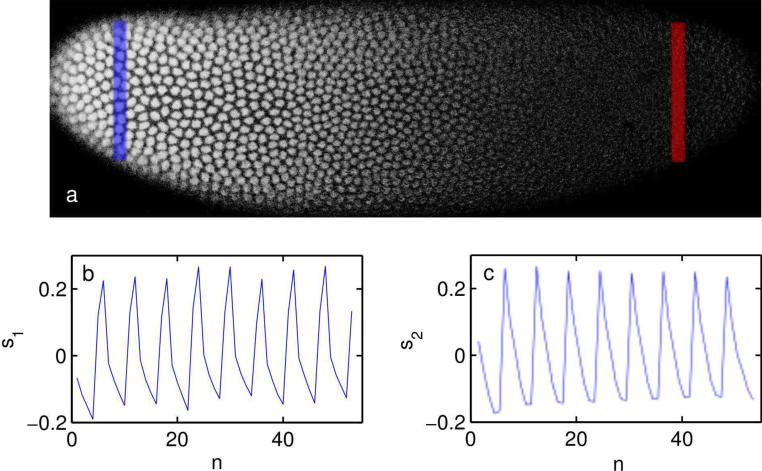
where Tis the period of the conversion-reactivation cycle. The detrended intensity signal y(x, t) − ξ(x, t) then takes the form of the two-user synchronous channel defined in Ref. [28]. Our problem is to determine the received amplitude G(x) = G_Bcd(x), representing Dronpa-Bcd concentration along the anterior-posterior axis of the embryo. As all GFP-like fluorophores have some photoactivation cross-section [29], there is also some residual oscillation due to H2A-RFP. We let s₁ represent the signature waveform of H2A-RFP emission; s₁ is found by imaging embryos containing H2A without Dronpa-Bcd and choosing G(x) = 0. The characteristic waveform of Dronpa-Bcd emission s₂ is found by subtracting the posterior intensity signal y(0.9L, t) from the anterior signal y(0.1L, t) (see Fig. 2). Provided beam intensity is uniform across the sample, the difference between the signals is due to Dronpa-Bcd alone.

Figure 2. Detection of Dronpa-Bcd and Histone-RFP signature waveforms.

a) Green channel fluorescence intensity of Dronpa-Bcd in a Dronpa-Bcd/Histone-RFP expressing embryo at mid-cycle 14. The blue bar indicates region of integration for anterior signal y(0.1L, t) and the red bar indicates region of integration for posterior signal y(0.9L, t). b) Signature waveform of RFP emission s₁, determined by averaging signal from an ensemble of embryos expressing Histone-RFP alone, c) Signature waveform of Dronpa emission S₂, determined by the difference of signals from blue and red regions in a set of dronpa – bcd/h2a – RFP expressing embryos similar to the one shown in (a).

The maximum likelihood estimator for G(x) is given by the decorrelating detector c₂ [28, 30]:

$$c_2=\frac{s_2-{\rho }_{12}{s}_1}{1-{\rho }_{12}}$$ (6)

where ρ₂ is the cross-correlation between the Dronpa-Bcd and H2A-RFP waveforms:

$${\rho }_{12}={\int }_0^{mT}{s}_1{s}_{2}dt$$ (7)

and m is the total number of cycles. G is determined at each point by the inner product $G\left(x\right)={\int }_0^{mT}{c}_2\left(t\right)(y(x,t)-\xi (x,t))dt$

Numerical simulation methods

Simulated Bed gradients were calculated by numerical integration. We used the one-dimensional diffusion equation with uniform degradation:

$$\frac{\partial c(x,t)}{\partial t}=s(x,t)+D{\nabla }^{2}c(x,t)-k_{deg}\left(t\right)c(x,t)$$ (8)

This equation was integrated using a forward-time centered-space finite difference scheme, imposing the Neumann condition $\partial c∕\partial x=0$ at the anterior and posterior boundaries of the embryo, x = 0 and x = L = 500 μm, respectively. We used a mesh size of 5μm and a time step of 2 s. Neither the source function, s(x, t), nor the degradation rate, k_deg(t), was assumed to be constant. In the fertilized case, k_deg was taken from Ref. [21], extended backwards in time on the assumption that k_deg(0 < t < 105min.) = 0.020 min⁻¹. In the unfertilized case, we assumed a constant protein degradation rate of 0.009 min.⁻¹ (see Results and Discussion). In all cases we took the diffusion coefficient D to be 4μm²/s, consistent with Ref. [21]. We further separated the source function into time-varying and space-varying components:

$$s(x,t)=p\left(t\right)\stackrel{‒}{s}\left(x\right)$$ (9)

where p(t) is the production function and $\stackrel{‒}{s}\left(x\right)$ is the normalized source distribution, such that ${\int }_0^L\stackrel{‒}{s}\left(x\right)dx=1$. The spatial distribution of $\stackrel{‒}{s}\left(x\right)$ was given by the early (pre-cycle-11) mRNA distribution as reported in Ref. [22].

Calibration of two-photon fluorescence intensity to absolute eGFP concentration

Following the method of Gregor et al. [11], we converted fluorescence intensities to absolute eGFP concentrations by imaging a sample of purified eGFP. We obtained a set of four samples of purified eGFP from L. Schepis, and measured the absorption in a spectrophotometer (Biorad SmartSpec Plus). Using the molar extinction coefficient of eGFP [31], we determined that the samples were of concentration 2.8 μM, 3.8 μM, 4.4 μM, and 7.5 μM. Dilution of each sample 100-fold produced a fluorescence intensity under two-photon microscopy within the dynamic range of the settings used for embryo imaging. We filled a square glass capillary of width 100 μm with the diluted eGFP solution and acquired a z-stack of fluorescence images through the sample. Importantly, an intensity plateau was reached, indicating that the axial point spread function was contained entirely within the solution at the maximum intensity value. As the PMT attached to the BG39 filter on our imaging system had a negative offset, we used the intensity in the 610/75 channel to determine the location of the half-maximum of the plateau, and found the total fluorescence intensity in the green channel by doubling the difference between the plateau and the half-maximum. The plateau in the red channel additionally allowed for the calculation of the bleed-through of eGFP fluorescence into the 610/75 filter, relative to the BG39, which we found to be 4% for our system.

Results and Discussion

Two-photon imaging shows time evolution of unfertilized Bed gradient

Given the high photostability and quantum yield of eGFP under two-photon illumination, we first acquired images of the time evolution of the Bcd gradient in unfixed, unfertilized eggs by laser scanning two-photon microscopy. The time evolution of the unfertilized gradient is of particular interest because it lacks the interference of nuclei, which amplify the observed intensity of the gradient by shifting the total distribution of Bcd towards the cortex of the embryo. Nuclei have also been conjectured on theoretical grounds to modify the length of the gradient [11, 16, 17, 32], though experimental evidence suggests otherwise [19].

In Fig. 3, we show the mean eGFP-Bcd concentration gradients we observed in sets of unfertilized (Fig. 3a,c) and fertilized (Fig. 3b,d) eggs under two-photon microscopy. As mentioned previously, multiphoton microscopy is noted for its ability to penetrate more deeply in tissue than single-photon fluorescence microscopy, and we in fact observed greatly improved signal-to-noise and signal-to-background ratios compared to in vivo measurements using a confocal system (data not shown).

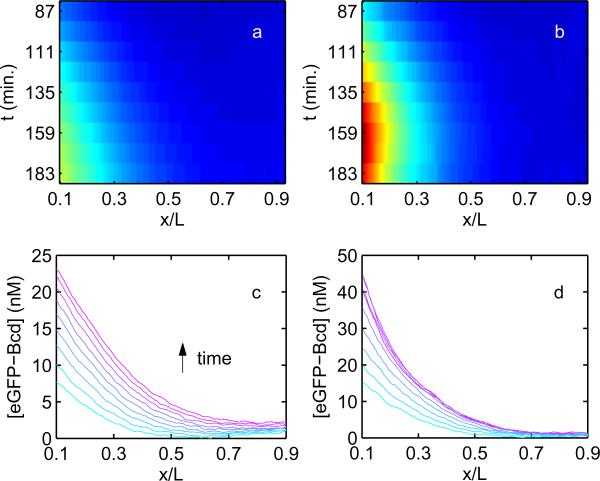
Figure 3. Evolution of unfertilized and fertilized Bcd gradients in time.

a) Mean eGFP-Bcd concentration gradient observed in eGFP-bcd unfertilized eggs, with concentration indicated as a heat map spanning 0 to 50 nM. Mean is taken over a population of 12 eggs. Time in minutes since egg deposition is indicated on the vertical axis. Horizontal axis indicates normalized position along the A-P axis, b) Identical to (a), for a population of 6 fertilized embryos, c) Mean unfertilized gradients from (a) displayed with concentration on the y-axis, after background subtraction and normalization to absolute eGFP concentrations (see Materials and Methods). Time is indicated by color, from cyan to magenta, and the increasing intensity at the egg posterior is clearly seen. Error bars overlap, obscuring consecutive gradients, and are omitted, d) Identical to (c), calculated from 6 fertilized eGFP-bcd embryos.

Several differences between the fertilized and unfertilized cases become apparent with this data set. First, the fertilized gradient is noticeably steeper and shorter than the unfertilized gradient. This is most obvious in considering the ratio of the posterior (0.9L) eGFP-Bcd concentration to the anterior (0.1L) eGFP-Bcd concentration. In the unfertilized case, this ratio is 0.10 ± 0.03 three hours after egg deposition, more than three fold larger than in the fertilized case, where the value is 0.03 ± 0.02. As an aside, we note that while the intensity of the fertilized gradient decreases nearly to background at the egg posterior, the deviation from zero is significant, which is consistent with the in vivo measurements in Ref. [21], as well as computational studies of the gradient, which suggest that it should extend to the posterior of the embryo [33].

Second, the unfertilized gradient rises steadily throughout the entire period of observation, rising monotonically in each segment of the egg. The fertilized gradient, by contrast, plateaus at approximately 2.5 hours after oviposition, equivalent to 15 minutes after the beginning of interphase 14, and subsequently regresses slightly at the anterior end of the embryo. This is qualitatively consistent with previously published measurements of upregulated Bcd degradation in fertilized eggs [21], and the absence of this upregulation in unfertilized eggs.

High-contrast imaging confirms greater spatial extent of unfertilized Bcd gradient

While the yolky nature of the unfertilized egg makes it impossible to image live under confocal microscopy, the optical clearing effect of fixation makes confocal imaging of the gradient feasible. Measurements of the unfertilized eGFP-Bcd gradient have in fact been made in fixed tissue [34]; these suggested the existence of a shallower unfertilized gradient based on different posterior-to-anterior intensity ratios, but precision remained limited by high background fluorescence levels.

To extend our confidence in the gradients obtained via live imaging of eGFP–Bcd expressing eggs, we used a different fluorescent Bcd fusion protein, Dronpa-Bcd, to make measurements of the gradient in fixed eggs. Additionally, to improve upon the signal-to-noise ratio of simple intensity measurements, we developed a high-contrast imaging method based on decorrelation of photoswitching waveforms (see Materials and Methods) to obtain quantitative estimates of the gradient shapes.

The Bcd gradients in both the fertilized (blue curve) and unfertilized (green curve) cases, after 3 hours of developmental time, are shown in Fig. 4a and b, respectively. The background intensity value for each case is given by the red curve, representing fertilized (Fig. 4a) and unfertilized (Fig. 4b) Histone-RFP expressing eggs. Because the specific signal is identified by a decorrelation procedure using the fertilized Histone-RFP as a control, the fertilized background intensity has a zero mean value. The ratio of Dronpa-Bcd concentration at 0.9L to that at 0.1L in the fertilized case is .036 ± .017, consistent with our in vivo measurements in the previous section. As shown in Fig. 4c, the unfertilized gradient is shallower, and, correspondingly, shows a larger posterior-to-anterior ratio than the fertilized gradient: $C_{Dronapa-Bcd}^u(3h,0.9L)∕C_{Dronapa-Bcd}^u(3h,0.1L)=0.14\pm 0.07$. We conclude that the observation that unfertilized Bcd gradients are longer and shallower than their fertilized counterparts is again verified with high precision techniques in fixed tissue.

Figure 4. Measurement of Bcd gradient in fertilized and unfertilized eggs by decorrelation of photoswitching waveforms.

a) Fertilized eggs: G represents decorrelated Dronpa-Bcd signal, after prior division by red channel intensity to normalize for Histone-RFP signal (see Materials and Methods). Blue curve indicates the mean signal extracted from 27 fixed, fertilized dronpa – bcd/h2a–rfp expressing embryos, of age 3±0.3 hours at the beginning of fixation. Shaded region indicates standard deviation. Red curve is the decorrelation transform applied to 16 fixed, fertilized h2a – rfp expressing embryos of the same age. b) Unfertilized eggs: Green curve indicates the mean decorrelated Dronpa-Bcd signal from 19 fixed, unfertilized dronpa – bcd/h2a – rfp expressing eggs of the same age as in (a), with shading indicating standard deviation. Red curve is the same calculation applied to 5 fixed, unfertilized h2a – rfp expressing eggs, c) Blue and green curves indicate the A-P axis Dronpa-Bcd concentration gradients in fixed fertilized and unfertilized eggs, as in (a) and (b), here plotted on semi-log axes. Shading indicates standard error. d,e) Composite heat map images of C_Dronpa–_Bcd fertilized (d) and unfertilized eggs (e). Anterior is at left and dorsal edge is at the top. Gradients in (c) represent the mean concentration values projected onto the A-P axis.

Bcd protein lifetime in unfertilized eggs is longer than that in fertilized eggs

One possible explanation for the shallower unfertilized gradient is a longer protein lifetime in the unfertilized case. Liu and Ma demonstrated the existence of a similar effect on gradient shape in mutant fertilized eggs with impaired Bcd degradation [35]. To test this hypothesis, the technique of measuring Bcd lifetime by means of timed photoconversions of Dronpa-Bcd, described in Ref. [21], can be extended to unfertilized eggs with relatively minor modifications, and we used this technique to make a direct measurement of the unfertilized protein lifetime. Two principal challenges needed to be overcome. First, the signal-to-background ratio of the green channel fluorescence intensity of Dronpa-Bcd is significantly lower in unfertilized eggs, due both to the contamination of the cortical cytoplasm with yolk granules and to the lack of accretion of Bcd at the embryo surface. This challenge is substantially identical to that encountered in fertilized eggs prior to the clearing of the cortical cytoplasm in mitotic cycle 14. However, a second complication exists in the unfertilized case. In the fertilized case, nuclei are visible at the embryo surface beginning at cycle 10, and can be counted to make a precise determination of embryo age. This method was used to establish the existence of and average out cyclic Bcd flux in Ref. [21]. In the unfertilized case, no morphological cues give evidence of the developmental age of the egg, and the time since oviposition must be used instead.

To obtain a sufficiently strong Dronpa-Bcd fluorescence signal in the unfertilized eggs, we waited a longer time post-oviposition (~ 4 hrs.) before imaging and performing the photoconversion experiment on the eggs. As a result, the distribution of egg ages was larger and not directly comparable to the fertilized case. However, it was noted in fertilized eggs that the Bcd lifetime is downregulated to a value of approximately 15 min. within three hours after egg deposition [21], and this provided a baseline for comparison. In Fig. 5 the fraction of Dronpa-Bcd recovered from the dark state following an 8 minute delay interval is plotted. The recovery is initially low (<90%), and subsequently relaxes to an approximately constant value that is greater than 90% after 45 minutes of imaging. This trend was observed in all eggs, even though they were of different ages. This suggests that the initial slow recovery is artifactual, possibly due to depletion of photoswitchable background fluorescence. After this time, $k_{deg}^u$ takes an approximately constant value of 0.009±0.006min.⁻¹, which corresponds to a lifetime range of 70 to 300 minutes, confirming the conjecture of Driever and Nusslein-Volhard that Bcd protein is significantly more stable in unfertilized eggs [9].

Figure 5. Measurement of Bcd lifetime in unfertilized eggs.

Fraction of Dronpa-Bcd recovered from the dark state Q_df (t₀+T)/Q_df (t₀) in a population of 8 unfertilized eggs for a series of photoconversion experiments with delay T = 8 min. Solid line represents smoothing spline fit to all data smoothed by a Savitzky-Golay filter [42] of span 6. Time is expressed in minutes since the start of imaging, which occurs at approximately 4 ± 1 hours post-oviposition for the unfertilized eggs. Initial lower recovery appears to be a transient principally attributable to build-up of endogenous autofluorescence in the unfertilized eggs, as it is correlated much more strongly with total image count than would be reasonable if it were a function of developmental age alone. Recovery after transient corresponds to an unfertilized Bcd degradation rate of $k_{deg}^u=0.009\pm 0.006{\min }^{-1}$.

Simulation of unfertilized gradient dynamics

The longer Bcd protein lifetime in unfertilized eggs presents an opportunity to quantitatively test the prediction of the SDD model regarding the relationship between morphogen lifetime and gradient length. To determine the extent to which the unfertilized gradient is quantitatively consistent with this prediction, we performed a coarse-grained, one-dimensional simulation of Bcd gradient evolution, incorporating a realistic source distribution derived from recent measurements of bed mRNA [22]. We also assumed a fluorophore maturation lifetime of 30 minutes.

In Fig. 6a we show the experimentally observed time series of eGFP-Bcd unfertilized gradients, and in Fig. 6b, the corresponding simulated time series using a diffusion coefficient of 4 μm²/s (as in Ref. [21]) and a constant protein degradation rate of 0.009 min.⁻¹. Only the mature component of the simulated Bcd distribution is displayed. We converted to absolute concentration values by setting the anterior value (0.1L) of the final simulated profile equal to that of its experimentally observed counterpart. By this method, the simulation predicted well the final concentration at the far posterior (0.9L) of the unfertilized egg three hours after egg deposition, giving a value of 2.4 nM, as compared to an observed value of 2.3 ± 0.9 nM^‡. The evolution in time of the concentration at the anterior end (0.1L) was also captured fairly well by the simulation, predicting a mean concentration increase of 0.13 nM · min⁻¹, as compared to an observed value of 0.16 ± .02 nM · min⁻¹.

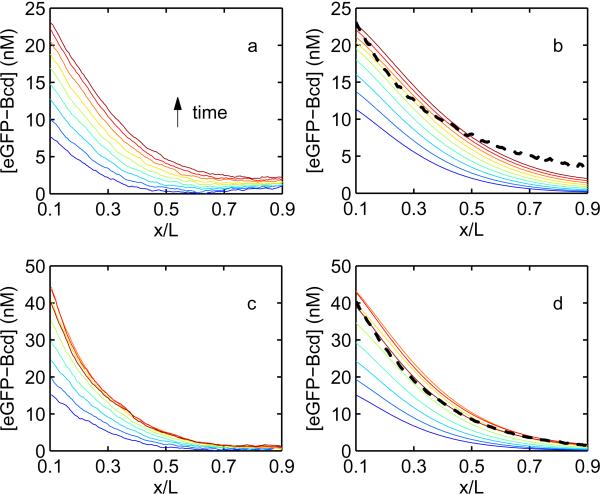
Figure 6. Comparison of fertilized and unfertilized Bcd gradients with simulation.

a) Mean eGFP-Bcd gradients in unfertilized eggs from 87 to 183 minutes after egg deposition, as shown in Fig. 3c, with time indicated by color proceeding from blue to red. 12 minutes elapse between successive gradients. b) eGFP-Bcd gradients obtained from a one-dimensional finite-difference simulation of gradient dynamics assuming a realistic source distribution [22], a 30 minute eGFP maturation lifetime, and a 110 minute Bcd lifetime. The absolute concentration is obtained by normalizing the anterior value of simulated gradient to the observed value at the last time point only. Dashed line: Unfertilized gradient at 3 hours developmental time as measured by photoswitching decorrelation in fixed tissue (Fig. 4(c), green curve), normalizing the anterior (0.1L) concentration value to the two-photon data, c) Identical to (a), showing the observed fertilized eGFP-Bcd gradients d) Simulated gradients in the fertilized case, obtained as in (b) but assuming a protein lifetime as determined in Ref. [21], and normalizing the anterior (0.1L) value to the observed concentration at each time point. Dashed line: Fertilized gradient at 3 hours developmental time as measured by photoswitching decorrelation in fixed tissue (Fig. 4(c), blue curve), normalizing the anterior concentration value to the two-photon data.

The same procedure applied to the fertilized gradient time series (Fig. 6c) did not reproduce the observed data. This is because the one-dimensional simulation predicts only a single concentration over the entire radial cross-section at each A-P axis position. This assumption appears to be satisfied in the unfertilized case, as shown in Ref. [11]. In the fertilized case, however, the distribution of Bcd between core and cortex is highly inhomogeneous and, importantly, changes in time [21]. To correct for this we introduce an additional parameter, Γ(t), to convert simulated Bcd concentrations to cortical values. We define Γ by the following:

$$C_{Bcd}^{sim-cort}=\Gamma \left(t\right)C_{Bcd}^{sim}(x,t)=\frac{C_{Bcd}^{ods}(0.1L,t)}{C_{Bcd}^{sim}(0.1L,t)}{C}_{Bcd}^{sim}(x,t)$$ (10)

where $C_{Bcd}^{sim}$ and $C_{Bcd}^{ods}$ are simulated and observed Bcd concentrations, respectively, and $C_{Bcd}^{sim-cort}$ is the simulation value rescaled to predict cortical concentration in the embryo. We plot $C_{Bcd}^{sim-cort}$ in Fig. 6d. The predicted mean value at the posterior (0.9L) over the entire experiment time is 1.2 nM, as compared to an observed value of 0.8 ± 0.8 nM.

Though we take the predicted behavior of posterior intensity levels as evidence that the unfertilized gradient length can be explained by the SDD model in a broad sense, the full shape of the gradient along the A-P axis, as measured by two-photon live imaging, is not well captured by the above simulation in either the unfertilized or the fertilized case. The observed gradients are steeper and more concave than the simulated gradients; this effect may be due to an overcorrection in the flat-fielding procedure used to correct for inhomogeneities in beam intensity and collection efficiency over the field of view. When the fertilized gradient at 3 hours as measured by photoswitching decorrelation in fixed tissue is plotted (Fig. 6d, dashed line), the simulation reproduced the gradient almost perfectly. While the fit is not as good in the unfertilized case (Fig. 6b, dashed line), we speculate this may in part be due to the slightly higher autofluorescence correlation bleed-through observed in the unfertilized case distorting the true shape of the gradient (Fig. 4b, red curve). Another plausible explanation is a difference in the source distribution in the unfertilized relative to the fertilized case, as the message gradient has not been quantified in unfertilized eggs. However, both the fixed and live unfertilized gradients are shallower than the fertilized gradient, as predicted by the lifetime measurement, and the agreement with the anterior-posterior ratio shift observed in the live imaging data is quantitatively very good.

One possible explanation for the discrepancies between the simulated and observed gradients is the use of a one-dimensional gradient formation model. Recent work has suggested that the dorsal-ventral (D-V) asymmetry of Bcd (see Fig. 4d) is important for regulation of genes downstream from bcd [36]. We have repeated the simulations of Fig. 6b,d in three-space according to the method described in Ref. [22], using the embryonic geometry of Ref. [37]. While the 3-D simulation reproduces the observed D-V asymmetry of the Bcd distribution (data not shown), we find that the evolution of the A-P gradient is described similarly well by the 1-D simulation. The greater spatial extent of the unfertilized gradient, upon lengthening the protein lifetime consistent with measured values, is also observed in the 3-D case.

Measurement of total Bcd quantity in fertilized and unfertilized eggs

Knowledge of absolute concentrations of signaling molecules is of special biophysical importance because it allows for the determination of physical limits on the precision of the signaling process [4, 38]. We calibrated the intensities obtained from the two-photon imaging data (as shown in Fig. 3c,d) to absolute eGFP concentrations using purified eGFP (see Materials and Methods). Unlike the measurements of Gregor et al. [4], the concentrations we report are not exclusively nuclear concentrations; rather they are averages over larger regions containing both nuclei and cytoplasm in the fertilized case, and cytoplasm alone in the unfertilized case. However, because Bcd is believed to be distributed uniformly between cortex and core in unfertilized eggs [11], the measurement of cortical unfertilized eGFP-Bcd concentrations offers an especially good way to determine the absolute number of Bcd molecules in the entire egg.

One major limitation of calibrating absolute intensities by using a reference solution is the problem of fluorophore maturation, and our direct measurements are limited to mature fluorophore only. In Fig. 7a, we show the total quantity of mature eGFP-Bcd in fertilized and unfertilized eggs, computed by integrating the measured concentration at each point along the A-P axis over the volume it represents (see Materials and Methods). The unfertilized quantity increases steadily, as observed previously [9, 34], and the fertilized quantity peaks shortly after the onset of cycle 14, consistent with the upregulation of degradation and decline of synthesis described in Ref. [21]. The fertilized and unfertilized quantities are not identical prior to this time; this is perhaps due to the fact that we fix Γ to unity at the beginning of data acquisition. This is equivalent to the assumption that the core eGFP-Bcd concentration is equal to the cortical concentration at t = 87 minutes. If we relax this assumption, then it is possible that unfertilized and fertilized concentrations follow equivalent trajectories prior to cycle 14.

Figure 7. Calculation of total number of Bcd molecules in embryos and unfertilized eggs.

a) Total number of mature eGFP-Bcd molecules in fertilized (red) and unfertilized (blue) eggs, computed from the gradients in Fig. 3. Time indicates minutes since egg deposition, b) Total number of Bcd molecules, in eGFP-bcd/bcd⁻ embryos, calculated by determining the fraction of mature fluorophore to total fluorophore at each point and time in the fertilized (red) and unfertilized (blue) egg by simulation.

To compensate for the omission of immature fluorophore, we found the ratio of mature eGFP-Bcd to total eGFP-Bcd, both mature and immature, at all points and times in our simulation, assuming an eGFP maturation time of 30 minutes. We used this matrix to rescale the measured concentrations of mature fluorophore to total fluorophore, and the integrated result is shown in Fig. 7b. The shapes of each curve are qualitatively similar, though we obtain a peak total eGFP-Bcd quantity nearly double that of the mature component alone. This value is 4.5±0.6×10⁷ molecules of Bcd at time t = 124 min., which corresponds to mid-cycle-13, and is roughly consistent with the peak of Bcd expression reported by Little et al. [22]. The error reported here and in the figure consists of uncertainty introduced by the fluorescence measurement and inter-embryo expression differences alone; it does not include error introduced from the calibration process, which is substantial. Including uncertainty from all sources, the measurement of peak eGFP-Bcd quantity is 4.5 ± 1.2 × 10⁷ molecules.

The low rate of protein degradation and quasi-linear increase in Bcd quantity in the unfertilized egg presents a good opportunity to measure the rate of Bcd translation. After accounting for maturation, we calculated a Bcd protein synthesis rate of 4.2 ± 0.4 × 10⁵ molecules per minute over the entire embryo. Using the number of 70,000 Bcd RNP granules observed in early embryos in Ref. [22], this equates to 6 Bcd protein molecules being produced by each RNP granule each minute. Other published studies have found that translation in eukaryotes occurs at a rate of approximately 6 amino acid residues per mRNA per second [39, 40]. As Bcd contains 494 amino acids, the measured rate of translation can be explained if each granule contains approximately 8 mRNA molecules. Alternatively, each granule could consist of a single mRNA bound by 8 ribosomes translating simultaneously. Further single molecule studies will be necessary to determine which hypothesis, or combination of them, is true.

We note that these estimates of absolute Bed quantities are still only within a factor of approximately 3 of the value of 1.5±0.2×10⁸ total Bed molecules reported in Ref. [21]. Clearly there is some source of systematic error which remains unaccounted for in one or both of these measurements. Potential candidates for this source of error are pH imbalances affecting fluorescence intensities, opacity of the vitelline membrane, scattering of visible light within the embryo, and mistaken assumptions regarding core-to-cortex concentration ratios. In particular, small pH differences at values near neutral can causes several-fold intensity variations in eGFP [41]. Further quantitative controls are needed in both cases to arrive at better estimates of absolute protein concentration values.

Conclusion

We have presented results suggesting that the formation of the Bcd gradient in unfertilized eggs is well explained by the SDD model. We performed two-photon live imaging of unfertilized eggs, and additionally developed a new method for quantitatively measuring the Bed gradient in fixed tissue by decorrelation of photoswitching waveforms. These measurements of the unfertilized gradient show a longer characteristic length, and are qualitatively and quantitatively consistent with our measurement of a longer protein lifetime in the unfertilized case and the predictions of the SDD model. We find that the lower protein degradation rate in unfertilized eggs offers an especially good opportunity to measure the Bed translation rate, and expect this measurement to stimulate future interest in single molecule studies designed to test this number.