Abstract
Recently, Block and coworkers [Visscher, K., Schnitzer, M. J., & Block, S. M. (1999) Nature (London) 400, 184–189 and Schnitzer, M. J., Visscher, K. & Block, S. M. (2000) Nat. Cell Biol. 2, 718–723] have reported extensive observations of individual kinesin molecules moving along microtubules in vitro under controlled loads, F = 1 to 8 pN, with [ATP] = 1 μM to 2 mM. Their measurements of velocity, V, randomness, r, stalling force, and mean run length, L, reveal a need for improved theoretical understanding. We show, presenting explicit formulae that provide a quantitative basis for comparing distinct molecular motors, that their data are satisfactorily described by simple, discrete-state, sequential stochastic models. The simplest (N = 2)-state model with fixed load-distribution factors and kinetic rate constants concordant with stopped-flow experiments, accounts for the global (V, F, L, [ATP]) interdependence and, further, matches relative acceleration observed under assisting loads. The randomness, r(F,[ATP]), is accounted for by a waiting-time distribution, ψ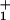 (t), [for the transition(s) following ATP binding] with a width parameter ν ≡ 〈t〉2/〈(Δt)2〉≃2.5, indicative of a dispersive stroke of mechanicity ≃0.6 or of a few (≳ν − 1) further, kinetically coupled states: indeed, N = 4 (but not N = 3) models do well. The analysis reveals: (i) a substep of d0 = 1.8–2.1 nm on ATP binding (consistent with structurally based suggestions); (ii) comparable load dependence for ATP binding and unbinding; (iii) a strong load dependence for reverse hydrolysis and subsequent reverse rates; and (iv) a large (≳50-fold) increase in detachment rate, with a marked load dependence, following ATP binding.
(t), [for the transition(s) following ATP binding] with a width parameter ν ≡ 〈t〉2/〈(Δt)2〉≃2.5, indicative of a dispersive stroke of mechanicity ≃0.6 or of a few (≳ν − 1) further, kinetically coupled states: indeed, N = 4 (but not N = 3) models do well. The analysis reveals: (i) a substep of d0 = 1.8–2.1 nm on ATP binding (consistent with structurally based suggestions); (ii) comparable load dependence for ATP binding and unbinding; (iii) a strong load dependence for reverse hydrolysis and subsequent reverse rates; and (iv) a large (≳50-fold) increase in detachment rate, with a marked load dependence, following ATP binding.
Kinesins are motor proteins that play an important role in cellular transport (1). They use the energy of hydrolysis of ATP molecules for moving vesicles and organelles along microtubules (MTs). Understanding the mechanism of motor protein motion is a serious challenge of modern biology.
Experimental investigation of motor proteins includes the determination of biochemical cycles (1), the measurement of rate constants by standard chemical kinetic methods (2), and the elucidation of molecular structure by x-ray crystallography, etc. (1, 3, 4). Also important are measurements of mechanical properties by laser-based optical trap spectrometry or by the use of microneedles (5–10).
Theoretical modeling of the motion of motor proteins has involved mainly two approaches. The first is based on thermal ratchet models in which a motor is viewed as a Brownian particle moving in two (or more) periodic but spatially asymmetric stochastically switched potentials (11). A different approach uses a multistate chemical kinetic description and postulates that the motor protein molecule steps through a sequence of discrete chemical states, possibly with branches, etc., linked by rate constants (12–16).
Recently, precise and extensive observations of the mechanical behavior of individual kinesin molecules moving in vitro under controlled external loads have been reported by Visscher, Schnitzer, and Block (9). In their unique experiments the tail or tether of a (squid axon) kinesin molecule was bound chemically to a silica bead while the head moved along an immobilized MT. An optical force clamp, using a feedback-driven optical trap, monitored the displacement, x(t), of a single kinesin molecule while keeping the load on the motor close to a fixed value, F. The principal findings of Block and colleagues were: (i) the stalling force, FS, which brings the mean velocity V to zero, depends on the concentration of ATP; (ii) under increasing external loads the maximum velocity of the motor protein decreases while the effective Michaelis–Menten constant increases; (iii) the force-velocity plots exhibit different shapes depending on [ATP]; and (iv) the randomness parameter, r, which is a dimensionless measure of the dispersion of the motion along the track (5, 13, 14), as a function of external load at saturating [ATP] is almost constant at low and intermediate loads but increases rapidly near the stalling force. Block and coworkers concluded that their experimental data necessitated revisions to the theoretical understanding of kinesin motor function. Subsequently, they published (10) processivity data over similar force and [ATP] ranges, specifically, mean run-lengths, L (along the MT, before individual kinesin motors irreversibly detach). They also proposed various theoretical/mathematical descriptions of varying degrees of elaboration. However, their analysis did not address the previous observations of randomness or describe stall forces.
Our aim here is to show that these striking observations (9, 10) can be described well qualitatively and with reasonable quantitative precision by using simple sequential stochastic models, which have been extended recently and analyzed critically (12–16). We fit all of the experimental data of Block and colleagues and show that our analysis is consistent with other experiments (7) in which kinesin molecules move on MTs under negative (F < 0) or assisting external loads (for which the analysis of ref. 10 fails).
Summary of Theoretical Approach
Following refs. 12–16, we suppose that a motor protein molecule steps a distance d (equal to 8.2 nm for kinesins on MTs) between consecutive binding sites located at positions x = ld (l = 0, ±1, ±2, …) on a linear track (the MT) by passing through a sequence of N intermediate biochemical states, j = 0, 1, … , N − 1. The motor in state jl (at site l) can jump forward to state (j + 1)l at a rate uj and can move backward to state (j − 1)l at a rate wj as described by the stochastic reaction scheme
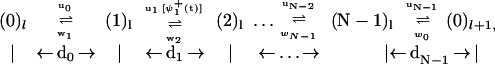 |
1 |
where the significance of the waiting-time distribution function, ψ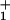 (t), which extends the scheme, is explained below. The dj represent substep lengths for the center of force of the motor as projected onto the mean direction of motion along the track: they are defined more explicitly below. As expected, the total step length is d = Σ
(t), which extends the scheme, is explained below. The dj represent substep lengths for the center of force of the motor as projected onto the mean direction of motion along the track: they are defined more explicitly below. As expected, the total step length is d = Σ dj.
dj.
Note that we always suppose that the state (0)l represents the motor clamped on the track in the absence of a necessary fuel molecule. For kinesins, which consume one ATP molecule per step, the known chemical details of the hydrolysis of ATP in the presence of MTs (see, e.g., ref. 2) suggest that the discrete motor states in an N = 4 reaction scheme can be explicitly identified as
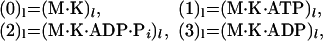 |
2 |
where (M ⋅ K)l stands for an MT-kinesin complex at site l while Pi and ADP are the successive products of the hydrolysis.
As our previous analysis demonstrated (13, 14), the effect of an external load F opposing forward motion should be taken into account by modifying the transition rates according to
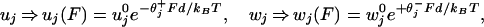 |
3 |
where θ and θ
and θ are load distribution factors that reflect how the external force affects the individual rates. [See also, in the context of ion channels, chapter 14 of Hille (16). Note that we may assume Σ
are load distribution factors that reflect how the external force affects the individual rates. [See also, in the context of ion channels, chapter 14 of Hille (16). Note that we may assume Σ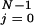 (θ
(θ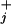 + θ
+ θ ) = 1 (13, 14).]
) = 1 (13, 14).]
These factors embody important and, indeed, inescapable mechanistic details of the motor protein action. Together they constitute a load-distribution pattern, as illustrated for kinesin in Fig. 1 (in terms of the fits described below). In a simple peaks and valleys picture of the (effective) free energy along a reaction coordinate (projected on to the MT axis) the valleys represent the intermediate chemical states at spacings
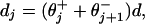 |
4 |
while the peaks are located in between at relative distances θ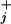 /(θ
/(θ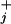 + θ
+ θ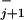 ) (17).
) (17).
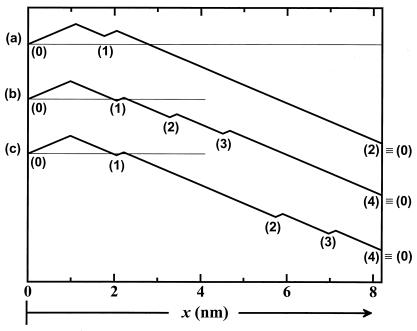
Figure 1.
Load distribution patterns for kinesin (a) for our (N = 2)-state model and (b and c) for two (N = 4)-state models. The projected lengths, Δxi, of successive segments are θ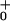 d, θ
d, θ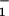 d, θ
d, θ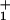 d, … ; the slopes are of arbitrary, fixed magnitude but positive/negative for forward/reverse transitions. Thus the minima locate intermediate chemical states (0), (1), … , (N) ≡ (0) separated by substeps d0 = (θ
d, … ; the slopes are of arbitrary, fixed magnitude but positive/negative for forward/reverse transitions. Thus the minima locate intermediate chemical states (0), (1), … , (N) ≡ (0) separated by substeps d0 = (θ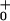 + θ
+ θ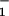 )d ≃ 2.0 nm, d1 = … .
)d ≃ 2.0 nm, d1 = … .
One may read off from Fig. 1 that all backwards rates (long downward slopes) are strongly load-dependent whereas only the first forward rate, u0 (for ATP binding), is significantly load-dependent. Likewise, the ATP-binding substep, d0, lies between 1.8 and 2.1 nm (with the higher range near 2.0 nm preferred because the N = 4 fits are better: see the figures and discussion below). This value appears to correlate with recent conformational suggestions based on structural studies of kinesin on MTs (3, 4). It may be anticipated that corresponding load-distribution patterns for other members of the kinesin family, for ncd, etc. (4), will reveal instructive similarities and differences.
Given a set of N rate constants, the previous mathematical analysis (13, 14) provides exact, relatively simple closed-form expressions for the mean velocity, V, for the dispersion, D [proportional to 〈[Δx(t)]2〉, where Δx = x(t) − 〈x(t)〉], and thence for the randomness, r = 2D/dV (5, 13, 14). Indeed, for an N = 2 model one simply has
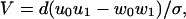 |
5 |
where σ = u0 + u1 +w0 +w1. The expression for general N leads to the stall force relation (13, 14)
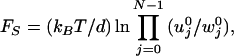 |
6 |
defined by V(F → FS) → 0.
If irreversible detachment (or “death”) rates δj, from states j, are included in Eq. 1, the corresponding N = 2 expressions for V and D are given in equations 31–35 of ref. 15. The merit of such easily programmable expressions is that the full parameter space of the model can be readily explored when searching for fits to extensive data such as provided by Block and coworkers (9).
More generally, one may extend the standard chemical kinetic models (with a simple Poissonian or exponential waiting time in each state j) by introducing arbitrary, waiting-time distribution functions, ψ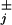 (t), which specify the probability densities for the corresponding forward or reverse transitions at a time t after the system arrives in state j. Such a description is potentially more economical in describing motor dynamics (as will be seen); it escapes a stringent lower bound on the randomness, namely, r ≥ 1/N (13, 14); and it may, for example, be used to summarize diffusive motion on a ratchet potential (11) in lieu of integrating the Fokker–Planck equations.
(t), which specify the probability densities for the corresponding forward or reverse transitions at a time t after the system arrives in state j. Such a description is potentially more economical in describing motor dynamics (as will be seen); it escapes a stringent lower bound on the randomness, namely, r ≥ 1/N (13, 14); and it may, for example, be used to summarize diffusive motion on a ratchet potential (11) in lieu of integrating the Fokker–Planck equations.
The analysis presented in ref. 16 shows that when effective transition rates, uj and wj, are defined appropriately in terms of the ψ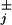 (t), the expressions for the velocity, V, do not change. However, the dispersions change dramatically. To be concrete, for the N = 2 model described in Eq. 1 with only a single nonexponential waiting-time distribution, for example of the form,
(t), the expressions for the velocity, V, do not change. However, the dispersions change dramatically. To be concrete, for the N = 2 model described in Eq. 1 with only a single nonexponential waiting-time distribution, for example of the form,
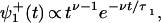 |
7 |
where τ1 = 1/(u1 + w1) is a mean dwell time, the dispersion, D, is the sum of the terms (16)
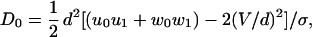 |
8 |
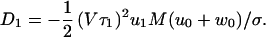 |
9 |
Here the parameter M represents the mechanicity, which is usefully introduced to quantify generally the deviation from an exponential waiting-time distribution function (see ref. 16). Thus the degree of mechanicity ranges from 0 for a chemical kinetic process (with ν = 1 in Eq. 7) to 1 for a purely mechanical, “clockwork” transition (ν → ∞) (16). Indeed, when Eq. 7 holds, one has M = 1 − ν−1, and ν = 〈t〉2/〈(Δt)2〉 measures the waiting time sharpness; by the convolution theorem this process (neglecting reverse transitions) also can be mimicked by a sequence of ≥ν simple Poisson processes.
Analysis of Kinesin Data
To analyze the data of Block and coworkers (9) note, first, that the forward transition from (0)l, which represents ATP binding, should have a rate u0 = k0[ATP], whereas the subsequent reverse and forward rates, w1 and u1, should not depend on [ATP]. Stopped-flow chemical experiments (using Drosophila kinesins) (2) indicate
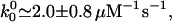 |
10 |
 |
(where the superscripts denote zero load, F ≡ 0).
The final reverse reaction rate, w0 (see Eq. 1), is undetectably small chemically (2) but, in principle, might be expected to vary as k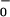 [ADP][Pi]. However, we cannot use this because current experiments employ an ATP regeneration system (5, 9) in which [ADP] and [Pi] are not separately monitored.§ Accordingly, we adopt the phenomenological form
[ADP][Pi]. However, we cannot use this because current experiments employ an ATP regeneration system (5, 9) in which [ADP] and [Pi] are not separately monitored.§ Accordingly, we adopt the phenomenological form
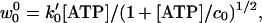 |
11 |
where, in effect, the concentration c0 describes the ATP regeneration process. The proportionality to [ATP] at low concentrations is plausible; but no special significance attaches to the exponent 1/2, which comes into play near saturation [ATP] and serves, via Eq. 6, to represent the observed increase of the stall force, FS, with [ATP] (see Fig. 2). Beyond this, the specific form (Eq. 11) plays only a small role in fitting the data of Block and coworkers (9) and Coppin et al. (7).
Figure 2.
Observations of stall force, FS, at specified ATP concentration by Block and colleagues (9), ▴ (joined by dotted lines) using a position clamp and ● using a fixed trap; and derived from Coppin et al. (7), ○. The solid, dashed, and dot-dashed curves are theoretical fits (see text).
Two-State Models
Consider, initially, the simplest N = 2 kinetic model. By systematic exploration using Eq. 10 for initial guesses and matching limiting behavior under large and small ATP concentrations and loads, we find that V(F,[ATP]) and FS([ATP]) can be fairly well described by
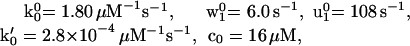 |
12 |
and (see the load distribution pattern in Fig. 1a)
 |
13 |
The (somewhat correlated) fitting uncertainties here amount to 1–4 digits in the last decimal places quoted.
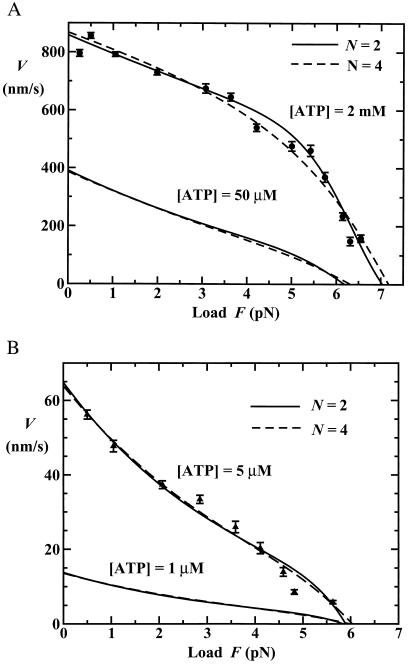
The quality of these N = 2 fits for V can be judged from Figs. 3 and 4 (solid lines). In fact, the Michaelis–Menten forms seen in Fig. 3 do not represent a particularly sensitive test; but Vmax decreases with load while the effective Michaelis–Menten constant, KM, increases, as observed by Block and coworkers (9). On the other hand, the changes of shape with [ATP] of the velocity-load plots in Fig. 4 are striking and well represented. (The plots for [ATP] = 1 μM and 50 μM represent predictions.)
Figure 3.
Kinesin velocity as a function of [ATP] under external loads, F, fixed by a force clamp. The plots, from the top down, are for F = 0, 1.05, 3.59, 4.60, and 5.63 pN, respectively. Data from Block and colleagues (9): solid curves, N = 2 fits; dashed curves, N = 2 predictions (see text).
Figure 4.
Fits to the data of Block and colleagues (9) (and predictions) for velocity as a function of load for fixed concentrations of ATP. Note the inflection points at low [ATP] and convex profile at saturating [ATP].
The fitted values of w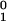 and u
and u in Eq. 12 differ noticeably from those recorded in Eq. 10. Although the different kinesin types involved may play a role, we believe that the larger overall turnover rates typically observed in optical trap experiments probably arise because single, active motor proteins are examined whereas in chemical measurements the properties of many molecules with different levels of activity are averaged together.
in Eq. 12 differ noticeably from those recorded in Eq. 10. Although the different kinesin types involved may play a role, we believe that the larger overall turnover rates typically observed in optical trap experiments probably arise because single, active motor proteins are examined whereas in chemical measurements the properties of many molecules with different levels of activity are averaged together.
Randomness Data
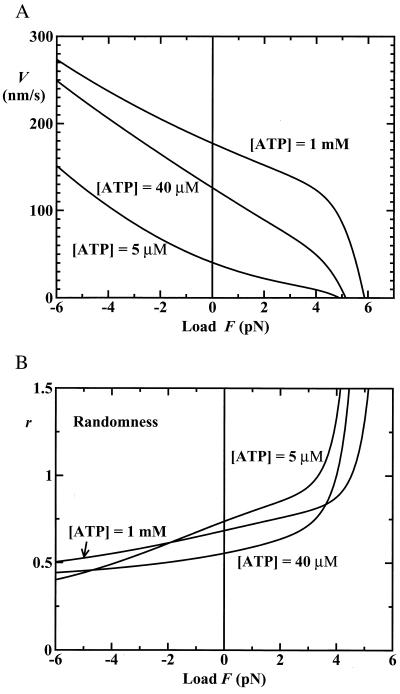
Despite our success in describing the data of Block and colleagues (9) relating V, F, and [ATP], no set of (N = 2)-state rate parameters and load distribution factors can fit the randomness observations (see Fig. 5). This is because the randomness falls below the N = 2 bound, r = ½ (5, 13, 14), for a wide range of loads (up to ≃4.5 pN) and ATP concentrations (exceeding ≃100 μM). The simplest, and most economical route to circumvent this difficulty is to introduce into the (N = 2)-state model a single, nonexponential waiting-time distribution, ψ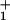 (t) (see Eqs. 1 and 7–9 and the previous discussion). On doing this, we find that a mechanicity M1 ≃ 0.6—or, equivalently, an exponent ν ≃ 2.5 in Eq. 7—provides reasonable fits for [ATP] ≳ 300 μM (see Fig. 5).
(t) (see Eqs. 1 and 7–9 and the previous discussion). On doing this, we find that a mechanicity M1 ≃ 0.6—or, equivalently, an exponent ν ≃ 2.5 in Eq. 7—provides reasonable fits for [ATP] ≳ 300 μM (see Fig. 5).
Figure 5.
Randomness data from Block and colleagues (9) and theoretical fits (A) as a function of external load, F, at fixed [ATP] (note that the two data points at F≃5.7 pN and [ATP] = 2 mM appear separately in Block and coworkers: see figure 4 a and b of ref. 9, respectively) and (B) as a function of [ATP] at fixed loads of, from top down, F = 5.69 pN (○), 5.35 and 4.60 pN (dashed-line predictions), 3.59 pN (●), and 1.05 pN (▴).
At low ATP concentration, however, our present treatment seems to underestimate r. This could mean that parallel biochemical pathways (e.g., detachment followed by diffusive reattachment) and/or the existence of branches off the main processive path play a role. But, at the cost of introducing further rate constants, etc., these possibilities are also susceptible to closed-form analysis (see ref. 15).
An alternative approach to the randomness data is to use only a pure kinetic description. In this case the simplest acceptable model must have N = 4, because Block and coworkers (9) observed r ≃ 0.39 at saturating [ATP], which implies that at least three other [ATP]-independent transitions are needed to describe the motor. Indeed, we find that all of the experimental observations of Block and coworkers can be fitted with the N = 4 parameters:
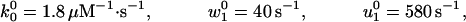 |
 |
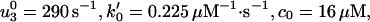 |
14 |
and, see the loading pattern in Fig. 1b,
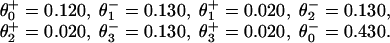 |
15 |
Note the (θ + θ
+ θ ) implies an ATP-binding substep d0 ≃ 2.05 nm in encouraging agreement with 1.76 nm from Eq. 13. Furthermore, the quality of these fits, as may be assessed from the dashed lines in Figs. 2, 4, and 5, appears somewhat better than those for N = 2. (Essentially no differences appear in Fig. 3.)
) implies an ATP-binding substep d0 ≃ 2.05 nm in encouraging agreement with 1.76 nm from Eq. 13. Furthermore, the quality of these fits, as may be assessed from the dashed lines in Figs. 2, 4, and 5, appears somewhat better than those for N = 2. (Essentially no differences appear in Fig. 3.)
However, the fitted values of θ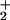 to θ
to θ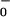 are now significantly underdetermined by the available data. In particular, if one interchanges the values of θ
are now significantly underdetermined by the available data. In particular, if one interchanges the values of θ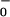 and θ
and θ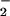 , the fits are sensibly unchanged. Nevertheless, as evident from Fig. 1c, the overall aspect of the load distribution pattern remains quite similar, suggesting that it is a robust feature of the kinesin motor.
, the fits are sensibly unchanged. Nevertheless, as evident from Fig. 1c, the overall aspect of the load distribution pattern remains quite similar, suggesting that it is a robust feature of the kinesin motor.
Assisting Loads
A further check on the N = 2 models is provided by observations of Coppin et al. (7) of kinesin moving under assisting or negative loads (F < 0), which they felt could not be explained by existing models. Specifically, their data yield the acceleration ratios V(F=−5 pN)/V(F=0) = 2.9 ± 0.3, 2.15 ± 0.15, and 1.48 ± 0.06 for [ATP] = 5 μM, 40 μM, and 1 mM, respectively. If one merely adopts the values in Eqs. 12 and 13 and uses Eqs. 3 and 5, these ratios are well reproduced. However, better fits to the actual (fairly noisy) V vs. F data (7) are obtained by replacing the rates w1 and u1 in Eq. 12 by 9.0 s−1 and 22 s−1, respectively [these lower rates seem to result from the sampling and averaging methods used (7) relative to Block and coworkers (9)] (see Figs. 2 and 6A). The corresponding acceleration ratios are then 3.13, 1.80 and 1.44, respectively, in good agreement with the observations.
Figure 6.
(A) Force-velocity plots for assisting and resisting loads (F ≶ 0) according to the N = 2 model adapted to the data of Coppin et al. (7). (B) The corresponding predicted load dependence of the randomness.
Furthermore, Fig. 6B provides predictions for the variation of the randomness under assisting (and resisting) loads at fixed [ATP], based on the same N = 2 model with a processive step of mechanicity M1 = 0.6 (as above). Corresponding measurements would provide an interesting check on the theory (although for F ≤ −5 pN evidence of a new process affecting the velocity is seen (7) and, as remarked above, other pathways may play a role at low [ATP]).
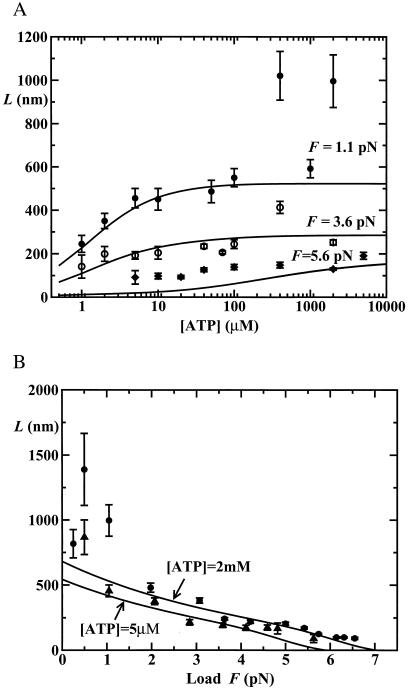
Processivity
The mean run lengths, L(F,[ATP]), exhibited by single kinesin molecules proceeding along an MT up to detachment, recently have been reported by Block and coworkers (10) on the basis of direct observations of runs up to x = 300 nm supplemented by estimates of the contributions from longer runs. The data points in Fig. 7 represent the conclusions (10). To analyze these results, we follow ref. 15, and, as mentioned above, introduce detachment or dissociation rates, δj(F). For the force dependence we adopt δj(F) = δ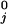 exp(θ
exp(θ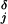 Fd/kBT). Precise expressions for L when all runs are fully observed require further computation. However, recognizing the high processivity of kinesins we may, in leading approximation, neglect changes in the velocity, V, resulting from δj ≠ 0 [which has been checked by using the explicit results for V(δ0, δ1) in ref. 15] and examine the results of Block and coworkers (10) within the previous N = 2 model (Eqs. 11–13) by using the mean run length estimate
Fd/kBT). Precise expressions for L when all runs are fully observed require further computation. However, recognizing the high processivity of kinesins we may, in leading approximation, neglect changes in the velocity, V, resulting from δj ≠ 0 [which has been checked by using the explicit results for V(δ0, δ1) in ref. 15] and examine the results of Block and coworkers (10) within the previous N = 2 model (Eqs. 11–13) by using the mean run length estimate
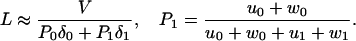 |
16 |
Here P1 = 1 − P0 is the (steady-state) probability that the motor is in a state processing ATP (i.e., j = 1).
Figure 7.
Results for mean run lengths, L, obtained by Block and colleagues (10) (A) as a function of [ATP] for fixed loads F = 1.1 pN (●), 3.6 pN (○), and 5.6 pN (⧫), and (B) as a function of load for [ATP] = 2 mM (●) and 5 μM (▴). The solid lines are corresponding fits (see text).
Reasonable fits to the run length results are then provided by the detachment parameters.
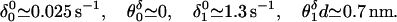 |
17 |
See Fig. 7, but note that the relatively poor fits for high loads (≳5 pN) and low [ATP] (≲100 μM) may result from undercounting of nonprocessing motors that are close to stall and move little. In words, our fits indicate: (i) no detectable load dependence of the low detachment rate in the bound (ATP-free) state, j = 0; but (ii) a roughly 50-fold rate increase when the motor is stepping (j = 1) even under zero load, and (iii) a further marked rate increase under load.
Summary
We have applied previously developed explicit theoretical expressions for the velocity, V, and dispersion, D, predicted for molecular motors by various discrete-state, sequential stochastic models (13–16) to analyze extensive experimental observations by Block and coworkers (9, 10) of the mechanical properties of single kinesin molecules moving in vitro on MTs. The data relating velocity, V, load, F, and ATP concentration, are well described by the simplest (N = 2)-state model with appropriate rate constants (allowing for ATP regeneration) and load distribution factors, θ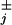 (see Figs. 2–4).
(see Figs. 2–4).
The load distribution pattern specified by the θ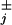 may be conveniently summarized graphically (see Fig. 1). Its overall form seems fairly robust because (N = 4)-state fits provide a similar pattern. In particular, a mechanical substep of magnitude d0 ≃ 2.0 nm is associated with ATP binding, and this transition and its reverse are about equally sensitive to the imposed load, F. Nevertheless, about 70% of the overall load dependence is carried by the reverse hydrolysis steps.
may be conveniently summarized graphically (see Fig. 1). Its overall form seems fairly robust because (N = 4)-state fits provide a similar pattern. In particular, a mechanical substep of magnitude d0 ≃ 2.0 nm is associated with ATP binding, and this transition and its reverse are about equally sensitive to the imposed load, F. Nevertheless, about 70% of the overall load dependence is carried by the reverse hydrolysis steps.
On the other hand, to describe the data for the randomness, r = 2D/dV, (d = 8.2 nm being the motor step length per consumed ATP molecule) it proves necessary, within an N = 2 model, to introduce a waiting time distribution, ψ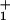 (t) (16), into the stochastic scheme (see Eq. 1). A mechanicity [characterizing the sharpness of ψ
(t) (16), into the stochastic scheme (see Eq. 1). A mechanicity [characterizing the sharpness of ψ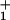 (t)] M1 ≃ 0.6 for the ATP hydrolysis reactions after ATP binding then provides an effective and economical fit (see Fig. 5). Alternatively, purely kinetic (N = 4)-state models suffice (see Figs. 2–5), although the load distributions for the hydrolysis steps are not uniquely determined by the data (see Fig. 1).
(t)] M1 ≃ 0.6 for the ATP hydrolysis reactions after ATP binding then provides an effective and economical fit (see Fig. 5). Alternatively, purely kinetic (N = 4)-state models suffice (see Figs. 2–5), although the load distributions for the hydrolysis steps are not uniquely determined by the data (see Fig. 1).
The (N = 2)-state models also describe kinesin dynamics under assisting loads (7) (see Fig. 6) and, with the introduction of detachment rates, etc., account for mean run-length studies (10) (see Fig. 7). The latter reveal a large increase in detachment rate while the motor turns over ATP.
In conclusion, relatively simple mechanochemical models account well for the dynamical observations of kinesins. Although the theory provides some structural pointers, establishing more elaborate and microscopic pictures requires further experimentation.
Acknowledgments
Interactions with Steven M. Block, Joe Howard, George Oster, Hong Qian, Ronald A. Vale, and Koen Visscher have been appreciated. The support of the National Science Foundation (Grant CHE 99–81772) is gratefully acknowledged. A.B.K. also acknowledges the financial support of the Camille and Henry Dreyfus New Faculty Awards Program (Grant NF-00–056).
Abbreviation
- MT
microtubule
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
We remark that backward steps of kinesin on MTs are seen near stall conditions (7, 8). These may be envisaged as resulting from ADP and Pi associated with kinesins and the MT in a successor complex for which the overall solution concentrations, [ADP] and [Pi], may have relatively little direct relevance.
References
- 1.Vale R D, Fletterick R J. Annu Rev Cell Dev Biol. 1997;13:745–777. doi: 10.1146/annurev.cellbio.13.1.745. [DOI] [PubMed] [Google Scholar]
- 2.Moyer M L, Gilbert S P, Johnson K A. Biochemistry. 1998;37:800–813. doi: 10.1021/bi9711184. [DOI] [PubMed] [Google Scholar]
- 3.Rice S, Lin A W, Safer D, Hart C L, Naber N, Carragher B O, Cain S M, Pechatnikova E, Wilson-Kubalek E M, Whittaker M, et al. Nature (London) 1999;402:778–784. doi: 10.1038/45483. [DOI] [PubMed] [Google Scholar]
- 4.Cross R A, Creval I, Carter N J, Alonso M C, Hirose K, Amos L A. Philos Trans R Soc London B. 2000;355:459–464. doi: 10.1098/rstb.2000.0587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Svoboda K, Mitra P P, Block S M. Proc Natl Acad Sci USA. 1994;91:11782–11786. doi: 10.1073/pnas.91.25.11782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Meyhöfer E, Howard J. Proc Natl Acad Sci USA. 1995;92:574–578. doi: 10.1073/pnas.92.2.574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Coppin C M, Pierce D W, Hsu L, Vale R D. Proc Natl Acad Sci USA. 1997;94:8539–8544. doi: 10.1073/pnas.94.16.8539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Kojima H, Muto E, Higuchi H, Yanagida T. Biophys J. 1997;73:2012–2022. doi: 10.1016/S0006-3495(97)78231-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Visscher K, Schnitzer M J, Block S M. Nature (London) 1999;400:184–189. doi: 10.1038/22146. [DOI] [PubMed] [Google Scholar]
- 10.Schnitzer M J, Visscher K, Block S M. Nat Cell Biol. 2000;2:718–723. doi: 10.1038/35036345. [DOI] [PubMed] [Google Scholar]
- 11.Jülicher F, Ajdari A, Prost J. Rev Mod Phys. 1997;69:1269–1281. [Google Scholar]
- 12.Kolomeisky A B, Widom B. J Stat Phys. 1998;93:633–645. [Google Scholar]
- 13.Fisher M E, Kolomeisky A B. Proc Natl Acad Sci USA. 1999;96:6597–6602. doi: 10.1073/pnas.96.12.6597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Fisher M E, Kolomeisky A B. Physica A. 1999;274:241–266. [Google Scholar]
- 15.Kolomeisky A B, Fisher M E. Physica A. 2000;279:1–20. [Google Scholar]
- 16.Kolomeisky A B, Fisher M E. J Chem Phys. 2000;113:10867–10877. [Google Scholar]
- 17.Hille B. Ionic Channels of Excitable Membranes. 2nd Ed. Sunderland, MA: Sinauer; 1992. [Google Scholar]