Mechanisms of cytoskeleton-mediated mechanical signal transmission in cells

Abstract

Recent experiments have demonstrated very rapid long-distance transmission of mechanical forces within cells. Because the speed of this transmission greatly exceeds that of reaction-diffusion signaling, it has been conjectured that it occurs via the propagation of elastic waves through the actin stress fiber network. To explore the plausibility of this conjecture, we recently developed a model of small amplitude stress fiber deformations in prestressed viscoelastic stress fibers subjected to external forces. The model results demonstrated that rapid mechanical signal transmission is only possible when the external force is applied orthogonal to the stress fiber axis and that the dynamics of this transmission are governed by a balance between the prestress in the stress fiber and the stress fiber's material viscosity. The present study, which is a follow-up on our previous model, uses dimensional analysis to: (1) further evaluate the plausibility of the elastic wave conjecture and (2) obtain insight into mechanical signal transmission dynamics in simple stress fiber networks. We show that the elastic wave scenario is likely not the mechanism of rapid mechanical signal transmission in actin stress fibers due to the highly viscoelastic character of these fibers. Our analysis also demonstrates that the time constant characterizing mechanical stimulus transmission is strongly dependent on the topology of the stress fiber network, implying that network organization plays an important role in determining the dynamics of cellular responsiveness to mechanical stimulation.

Introduction

Mechanical stimulation regulates growth, differentiation, motility, and apoptosis in many cell types. Therefore, understanding the mechanisms by which mechanical stimuli are transmitted within cells and are subsequently transduced into biochemical signals is a critical issue in cellular and tissue engineering. Mechanical forces applied to cell surfaces activate a variety of mechanotransducers including mechanosensitive ion channels,^1,2 cell-cell adhesion complexes,³ G-protein-coupled receptors,⁴ focal adhesion sites,⁵ and the nucleus.⁶ Stimulation of these structures elicits the activation of downstream signaling pathways⁷ that ultimately regulate gene expression and protein synthesis and hence modulate cellular phenotype.

An important feature of cellular mechanotransduction is that mechanical signals can be transmitted very rapidly to intracellular sites far away from the location of force application.⁶ For example, recent experiments on vascular smooth muscle cells have demonstrated mechanical activation of the tyrosine kinase Src more than 50 μm away from the point of force application in less than 300 msec.⁸ This time constant of mechanical signal transmission is orders of magnitude faster than that associated with reaction-diffusion signaling cascades which typically require more than 10 sec to travel the same distance.^6,8 It has been suggested that rapid long-distance mechanical signal transmission occurs via the cytoskeleton, most notably the actin stress fiber network. In support of this notion, both pharmacological disruption of actin filaments and dissipation of stress fiber prestress (i.e., pre-existing tension provided by the actomyosin machinery) appear to impair rapid long-distance mechanochemical conversion in smooth muscle cells.^8-10

Despite the experimental evidence implicating actin stress fibers in rapid long-distance mechanical signal transmission, how this transmission occurs remains unknown. It has been conjectured that mechanical forces applied to cell surfaces generate elastic stress waves which rapidly propagate through actin stress fibers, thus transferring the mechanical stimulus.^6,8 In order to evaluate the plausibility of this conjecture, we recently developed a mathematical model for mechanical stimulus transmission through an actin stress fiber.¹¹ This model accounts for the various physical factors that govern stress fiber displacement in response to an applied force including fiber inertia, prestress generated by myosin motor activity, fiber viscoelasticity, and cytosolic damping. As described in more detail in the next section, the predictions of this model raise doubts about the validity of the elastic stress wave conjecture.

The editors of Communicative and Integrative Biology invited us to submit a brief follow-up to our earlier modeling study.¹¹ Thus, in the present paper we use dimensional analysis to: 1) further evaluate the plausibility of the elastic stress wave conjecture, and 2) qualitatively describe expected mechanical signal transmission dynamics in simple stress fiber networks.

Results and Discussion

Plausibility of elastic stress wave conjecture

Stress fibers are viscoelastic structures that are surrounded by cytosolic fluid. If the internal (material) viscosity of stress fibers and the viscosity of the surrounding cytosol were both negligible, then the elastic stress wave speed within a stress fiber would be predicted to be 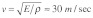[where and 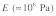are the density and elastic modulus of the stress fiber, respectively]. At this speed, the time scale for a mechanical stimulus to travel a typical intracellular distance of 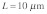would be:

(1)

At first glance, this time scale appears to be consistent with the experimental findings on the dynamics of Src activation described above.⁸ However, recent experiments on the dynamics of stress fiber retraction following laser severing suggest prominent viscoelastic behavior with large values of stress fiber internal (or material) viscosity [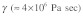].¹² This finding raises questions about the validity of treating stress fibers as elastic structures. A simple dimensional analysis in the case of a viscoelastic stress fiber leads to the following time scale for mechanical stimulus transmission:

(2)

This time scale is very much larger than the time scale for rapid mechanotransduction.^6,8 An additional issue is that in both the time scales given by Eqs. (1) and (2), the influence of stress fiber prestress does not appear, even though a number of experimental studies have reported that prestress plays a crucial role in rapid cytoskeleton-mediated mechanical stimulus transmission.^6,9,10 Therefore, the following question naturally arises: what is the fundamental mechanism that governs rapid mechanical stimulus transmission through actin stress fibers?

In our recently published modeling study,¹¹ we considered mechanical signal transmission through an actin stress fiber. The model accounted for stress fiber inertia, prestress generated by myosin motor activity, fiber viscoelasticity (elasticity, bending rigidity and material viscosity implemented using the Kelvin-Voigt model following recent measurements¹¹), and cytosolic damping (an external damping force based on the assumption of Stokes flow¹²). Thus, two types of system damping were considered: internal (material) damping due to the viscous portion of the viscoelastic mechanical behavior and external damping due to cytosolic drag resulting from stress fiber displacement. The model equations for small amplitude stress fiber displacement were solved in response to forces applied either orthogonal to or in the direction of the stress fiber axis as depicted in Figure 1. The results demonstrated that when the force is applied in the transverse direction (Fig. 1A), prestress in the stress fiber acts as the primary restoring (spring-like) force and dominates the effect of bending rigidity. This restoring force is balanced virtually entirely by the stress fiber's material viscosity, whereas the roles of both stress fiber inertia and cytosolic damping are negligible. A dimensional analysis of this force balance leads to the following time scale for mechanical stimulus transmission for a force applied in the transverse direction:

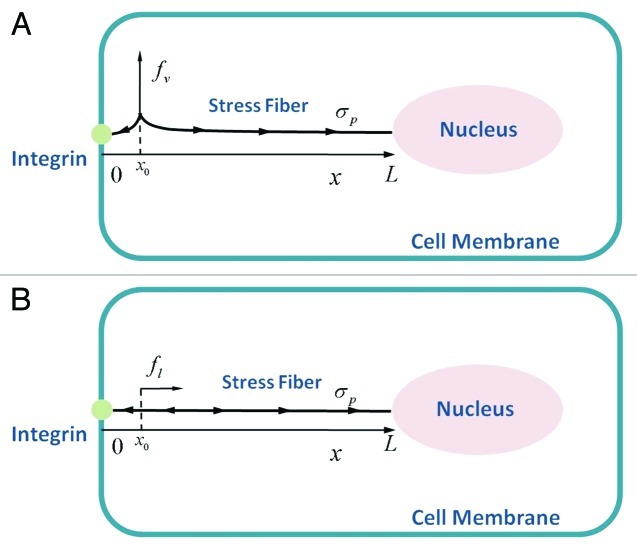
Figure 1. Schematic diagram of the model for mechanical stimulus transmission through an actin stress fiber in Hwang and Barakat.¹¹ The integrin is positioned at 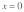and the nuclear edge at 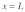. An actin stress fiber of length 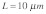directly links the integrin to the nucleus. A prestress 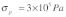is generated due to myosin motor activity and is assumed to be uniformly distributed throughout the stress fiber. Forces are applied to the stress fiber at a location close to the integrin (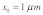) in the direction (A) orthogonal to the stress fiber axis and (B) along the stress fiber axis.

(3a)

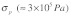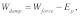where and are the prestress level and the radius of the stress fiber, respectively. In contrast, when the force is applied in the axial direction (Fig. 1B), prestress plays no role contrary to the transverse case. Therefore, elasticity acts as the only restoring force and is balanced primarily by the damping force due to material (internal) viscosity. As in the case of transverse motion, the effects of both inertia and cytosolic damping are found to be negligible. Therefore, using dimensional analysis, the time scale for mechanical stimulus transmission for a force applied along the stress fiber axis is found to be:

(3b)

The dimensional scaling above implies that mechanical signal transmission via deformation of actin stress fibers is anisotropic with very different dynamics depending on the direction of force application. In practice, forces applied to the surface of a cell within which stress fibers are randomly oriented would be expected to lead to both transverse and axial loading on the stress fibers; thus, both time scales derived in Eq. (3) above would be observed simultaneously.

The time scale for transverse motion in Eq. (3a) is consistent with the experimental observations of long-distance and rapid stress fiber-mediated Src activation.⁸ In contrast, the time scale for axial motion in Eq. (3b), which corresponds well to the viscoelastic time scale provided by Eq. (2) as well as the experimental measurements on the dynamics of stress fiber retraction following severing,¹² is found to be much larger than the time scale for transverse motion. These results suggest that rapid mechanical stimulus transmission in cells is only enabled via transverse stress fiber motion. Importantly, these dynamics are not mediated by the elasticity of the stress fiber but rather by its prestress, consistent with experiments showing that dissipation of prestress inhibits rapid mechanical stimulus transmission.^6,9,10 These results lead us to conclude that the elastic stress wave conjecture proposed in previous studies^6,8 and whose dynamics scale according to Eq. (1) is likely not the mechanism by which mechanical stimuli are rapidly transmitted via actin stress fibers. Rather, stress fiber deformation whose dynamics are governed by the balance between prestress and material viscosity constitutes the likely mechanism for this transmission.

Simple stress fiber networks

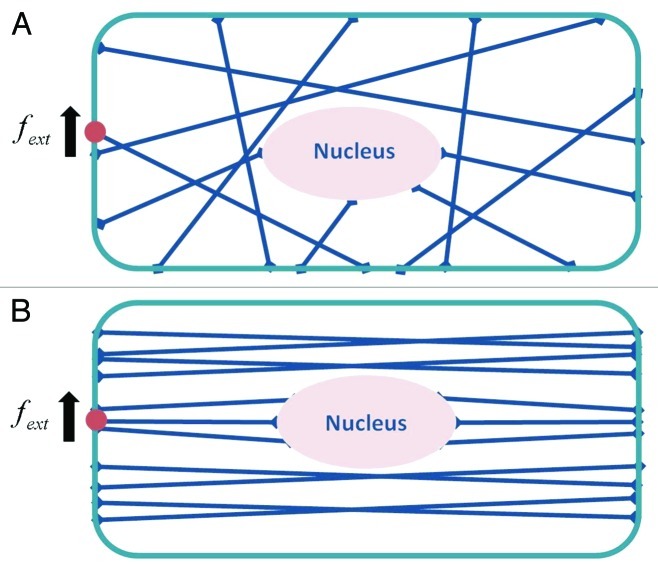
The discussion thus far has been confined to mechanical signal transmission dynamics in a single actin stress fiber. The cytoskeleton, of course, is a complex network of tightly linked filaments, and network topology is expected to modulate the dynamics of mechanical stimulus transmission. In order to probe this issue in a qualitative manner, we will use dimensional analysis to investigate the two representative networks shown in Figure 2. Figure 2A represents a network where stress fibers are randomly linked to one another, whereas Figure 2B depicts a network of highly organized and aligned stress fibers. For both networks, we consider that a mechanical force is applied to a particular location on the cell surface. In the case of the network in Figure 2A, we expect the resulting steady-state longitudinal and transverse deformations for each stress fiber to be approximately equal due to the links among the stress fibers: i.e., 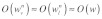, where 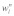and 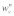are the longitudinal and transverse deformations of the 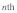stress fiber. The longitudinal and transverse forces along the 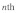stress fiber can then be approximated as 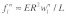and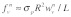, respectively. Therefore, the work done on the stress fiber network by the mechanical force applied at the cell surface can be written as:

Figure 2. Schematic diagram of two representative stress fiber networks: (A) randomly oriented case; (B) case where stress fibers are aligned nearly parallel to one another. A force 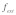is applied to an integrin on the cell surface to which an actin stress fiber is linked as shown.

(4a)

while the potential energy stored in the stress fiber network can be approximated as

(4b)

Here, note that 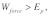implying that some of the work done by the applied force is lost due to the material (internal) viscous damping force which acts as frictional work within the network. The lost work done due to the material damping force scales as:

(4c)

where 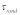is the time scale for which the damping force is active. Here, it should be pointed out that the lost work done related to the vertical motion is proportional to 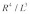because the vertical damping force of the 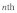fiber is given as 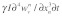(where 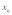is the axial direction of the fiber). Using Eqs. (4a)-(4c), the energy balance, 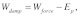yields the following :

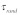(5)

This result implies that the mechanical stimulus applied to the cell surface for the network in Figure 2A would be transmitted to other subcellular sites with a time scale of O(1) sec.

In contrast, if the stress fiber network is highly organized as in Figure 2B, the time scale for mechanical stimulus transmission, similar to the case of a single stress fiber, would be determined by the direction of the applied force relative to the orientation of the organized network. In this case, the fastest time scale of mechanical stimulus transmission would be obtained by setting 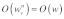and 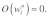Applying a similar scaling as that given in Eq. (4) to the aligned stress fiber network depicted in Figure 2B yields the time scale given in Eq. (3a).

The dimensional analysis based on energy balance outlined above for idealized and simple networks suggests that the topology of the cytoskeletal network plays a critical role in determining the dynamics of mechanical stimulus transmission. Importantly, this conclusion remains robust over a wide range of stress fiber dimensions and mechanical properties. This is important in light of the large variations in these properties reported in the literature for different cell types, measurement techniques, and experimental conditions. Examples of these variations include stress fiber elastic modulus in the range of 10⁴ - 10⁶ Pa,^13-16 stress fiber prestress in the range of 10⁵ - 10⁶ Pa,¹⁴ and stress fiber radius in the range of 0.1 - 0.4 μm.¹²

The finding that the topology of stress fiber networks plays an important role in regulating how rapidly forces applied to cell surfaces are transmitted within the intracellular space may have a number of important physiological implications. A concrete example can be found in the field of vascular biology. The two different network topologies analyzed in this study are broadly representative of distinct phenotypes of vascular endothelial cells.^7,13 The network with randomly oriented stress fibers is characteristic of cuboidal (or round) endothelial cells found in arterial regions prone to the development of early atherosclerotic lesions. Within these regions, endothelial cells exhibit a pro-inflammatory and dysfunctional phenotype. In contrast, the network with highly aligned stress fibers is representative of elongated endothelial cells within arterial zones that are largely protected from the disease and within which endothelial cells exhibit an anti-inflammatory phenotype. In light of the role of blood flow-derived mechanical forces in the development of atherosclerosis,^7,13 a particularly intriguing notion that merits experimental investigation is whether or not the endothelial dysfunction observed in atherosclerosis-prone endothelial cells is related to those cells' inability to transmit force and hence initiate particular intracellular signaling cascades sufficiently rapidly.

It is of course recognized that the conclusions made in the present work are based on approximate scaling arguments and on highly simplified stress fiber network topologies. In cells, stress fiber networks are three-dimensional and are expected to exhibit considerably more complicated topologies. Furthermore, other components of the cellular cytoskeleton, most notably microtubules and intermediate filaments, probably interact with stress fibers and influence the dynamics of mechanical signal transmission; however, the nature of these interactions remains poorly understood. Therefore, a more complete understanding of how stress fiber network topology modulates the dynamics of mechanical stimulus transmission awaits extending the current dimensional analysis to a quantitative study of mechanical signal transmission in realistic stress fiber networks that also account at some level for interactions with microtubules and intermediate filaments. Such an analysis promises to significantly enhance our understanding of cellular mechanotransduction and its implications for health and disease.