Mechanical behavior in living cells consistent with the tensegrity model

Abstract

Alternative models of cell mechanics depict the living cell as a simple mechanical continuum, porous filament gel, tensed cortical membrane, or tensegrity network that maintains a stabilizing prestress through incorporation of discrete structural elements that bear compression. Real-time microscopic analysis of cells containing GFP-labeled microtubules and associated mitochondria revealed that living cells behave like discrete structures composed of an interconnected network of actin microfilaments and microtubules when mechanical stresses are applied to cell surface integrin receptors. Quantitation of cell tractional forces and cellular prestress by using traction force microscopy confirmed that microtubules bear compression and are responsible for a significant portion of the cytoskeletal prestress that determines cell shape stability under conditions in which myosin light chain phosphorylation and intracellular calcium remained unchanged. Quantitative measurements of both static and dynamic mechanical behaviors in cells also were consistent with specific a priori predictions of the tensegrity model. These findings suggest that tensegrity represents a unified model of cell mechanics that may help to explain how mechanical behaviors emerge through collective interactions among different cytoskeletal filaments and extracellular adhesions in living cells.

Mechanical stress-induced alterations in cell shape and structure are critical for control of many cell functions, including growth, motility, contraction, and mechanotransduction (1). These functional alterations are mediated through changes in the internal cytoskeleton (CSK), which is composed of an interconnected network of microfilaments, microtubules, and intermediate filaments that links the nucleus to surface adhesion receptors. Advances in cell biology have resulted in better understanding of the polymerization behavior and physical properties of individual CSK filaments as well as of gels composed of combinations of filaments. Yet, the material properties measured in vitro neither explain nor predict complex mechanical behaviors that are observed in living cells (2, 3). At the same time, engineers have approached the problem of how cells stabilize their shape by developing mechanical models, without considering molecular specificity. For example, the living cell is often modeled as a continuum that contains an elastic cortex that surrounds a viscous (4) or viscoelastic (5) fluid; a more complex variation includes an elastic nucleus within a viscous cytoplasm (6). These models provide reasonable empirical fits to measured elastic moduli and viscosity in cells under specific experimental conditions (4–6), but they cannot predict from mechanistic principles how these properties alter under different challenges to the cell. Continuum models also assume that the load-bearing elements are infinitesimally small relative to the size of the cell and thus, they do not provide insight into how distinct molecular structures, such as CSK filaments, contribute to cell mechanics. This is a critical limitation because it is not possible to explain how mechanical forces regulate cell function without linking mechanics to microstructure and molecular biochemistry.

We previously proposed an alternative microstructural model of cell mechanics that depicts the cell as a prestressed tensegrity structure (7–9). This class of structures maintains shape stability within a continuous, tensed network of structural members by incorporating other isolated support elements that resist compression (10). The deformability of these structures depends on the level of prestress (preexisting tension) in the structure before application of an external load. In the simplest embodiment of the cellular tensegrity model (8, 9), this stabilizing prestress is generated actively by the cell's actomyosin-based contractile apparatus and passively by distension through the cell's adhesions to extracellular matrix (ECM). The model assumes that the prestress is carried primarily by tensile microfilaments and intermediate filaments. This prestress is balanced by interconnected structural elements that resist being compressed, including internal microtubules, and by traction on the ECM. Thus, this model differs from the established continuum models in that it leads to predictions relating to the mechanical role of distinct molecular elements and it suggests a central unifying role for prestress.

A growing body of evidence indicates that the tensegrity model can account for many features of living cells (reviewed in refs. 1, 7, and 11). A theoretical formulation of the model developed starting from first principles also has shown qualitative and quantitative consistencies with experimental results in various cell types and has led to several a priori predictions (8, 9). Nevertheless, tensegrity remains controversial because key pieces of evidence that are essential for its validation are missing (11). These critical experiments include unequivocal demonstration that the CSK behaves as a discrete network composed of different types of CSK filaments; direct evidence that microtubules function as compression struts and contribute significantly to cell mechanics; quantitative measurements demonstrating that CSK prestress is a major determinant of cell deformability; and experimental confirmation of a priori predictions of the theoretical tensegrity model. Providing this evidence is the focus of this study.

Materials and Methods

Experimental System.

Methods for coating microbeads (4.5 μm diameter; Dynal, Great Neck, NY) with RGD-peptide (Peptite 2000; Integra, San Diego) and acetylated low-density lipoprotein (AcLDL; Biomedical Technology, Stoughton, MA) (12, 13), micromanipulation (13), immunofluorescence staining (14), cell culture (12–15), and oscillatory magnetic twisting cytometry (16) have been published. A traction force microscopy technique (17) was adapted to create thin (50–70 μm), flexible (Young's modulus ≈1,300 Pa; Poisson's ratio = 0.48) sheets of polyacrylamide gel (2% acrylamide/0.25% bis-acrylamide) containing 0.2 μm fluorescent beads (FluoSpheres; Molecular Probes) and coated with type I collagen (0.2 mg/ml; Collagen Biomedical Products, Bedford, MA). Bead displacements were analyzed in the horizontal plane (vertical motions were <10% of horizontal displacements). Traction at the cell–gel interface was obtained from the displacement field by solving the problem of Boussinesq (boundary conditions: measured displacements at the cell–gel interface and zero tractions outside the cell), using a Fourier transform (J. P. Buttler, I.M.T.M., and J.J.F., unpublished results); similar results also were obtained by using a finite element method. The mean traction (τ) for a given cell section was obtained as a mean value integral of the component of the traction field perpendicular to the cell cross-section over the corresponding interfacial area (A_τ). The mean prestress (σ) was then obtained from the force balance of a section of the cell: σ = τA_τ/A_σ, where A_σ was the cross-sectional area of the cell. In total, displacement of ≈1,000 beads was analyzed per cell and seven cells were analyzed for each experimental condition.

Microscopy.

For traction analysis, phase and fluorescent images were recorded simultaneously by using a cooled charge-coupled device (CCD) camera on a Zeiss microscope and processed for background subtraction. Fusion constructs containing genes for enhanced yellow fluorescent protein (EYFP) and the mitochondrial targeting sequence from human cytochrome C oxidase (pEYFP-Mito; CLONTECH) and for a red-shifted GFP with human α-tubulin (pEGFP-Tub; CLONTECH) were transfected into endothelial cells by using the Effectene (Qiagen, Chatsworth, CA) technique. Fluorescently labeled proteins were visualized and recorded by using a Sensys KAF 1400 (Photometrics, Tucson, AZ) camera on a Nikon Diaphot 300 microscope equipped with image analysis software (SCANOLYTICS, Fairfax, VA). Similar results were observed in at least four different cells for each experimental condition.

Analysis of Myosin Light Chain (MLC) Phosphorylation and Intracellular Calcium.

MLC phosphorylation was analyzed in sparsely plated cells cultured on collagen-coated (1 μg/cm²) dishes by using a published technique (19). MLC bands were detected by immunoblotting with an anti-MLC monoclonal antibody (MY-21; Sigma). The stoichiometry of MLC phosphorylation (moles phosphate/mole MLC) was determined by densitometry of the unphosphorylated (0P), singly phosphorylated (1P), and doubly phosphorylated (2P) MLC bands, using NIH-IMAGE software, and calculated by using the formula (1P + 2 × 2P)/(0P + 1P + 2P). Microfluorimetric quantitation of intracellular calcium levels was carried out by using Fura-2 in conjunction with ratio imaging.

Results and Discussion

Internal Cell Deformation Depends on Molecular Connectivity.

Established engineering (4–6) and biological (20) models of cell mechanics assume that the dense cortical microfilament network that lies directly beneath the cell membrane is the primary load-bearing element in the cell. In contrast, the cellular tensegrity model predicts that mechanical loads are borne by discrete molecular networks composed of interconnected actin microfilaments, microtubules, and intermediate filaments that extend through the cytoplasm and link to adhesion receptors, such as integrins, that span the cell surface (7–9, 12, 13). We therefore examined whether externally applied stresses are borne exclusively by the cell cortex in cultured endothelial cells. Mechanical stresses were applied directly to integrins by using micropipettes to pull on membrane-bound microbeads that were coated with a synthetic RGD-containing peptide from fibronectin (12, 13). Binding of these beads induces mechanical coupling to the internal CSK, as indicated by local recruitment of focal adhesion proteins (e.g., vinculin, talin) as well as F-actin to the site of bead binding (14), and by a large measurable increase in cell stiffness in response to stress, which can be partially inhibited by disrupting either microfilaments, microtubules, or intermediate filaments (12, 13). Mitochondria that were fluorescently labeled by transfecting cells with EYFP-cytochrome C oxidase were used as fiducial markers to measure changes in internal cell structure that result from stress transmitted from integrins. Confocal microscopy confirmed that mitochondria associate directly with microtubules and distribute throughout the entire cytoplasm, while being relatively excluded from the actin-rich cortex.

Real-time fluorescence microscopic analysis of living endothelial cells revealed coordinated movement and alignment of mitochondria throughout the depth of the cell when a mechanical pulling stress was applied to integrins; even movement of mitochondria near the surface of the nucleus was observed (Fig. 1A). Neighboring mitochondria also sometimes exhibited distinct and even movements opposite to the direction of the applied stress field (Fig. 1 A and B). In contrast, over the 2 to 3 seconds of stress application, endogenous movement of mitochondria was not observed in control cells. Quantitative analysis of the experimental data obtained by using RGD-beads confirmed that local stresses applied at the membrane induced displacement of mitochondria up to 20 μm away in the depth of the cytoplasm (Fig. 1C). These results demonstrate that a distinct cytoplasmic strain field can be visualized in living cells and show that stresses transferred across integrins to microfilaments are passed via load-bearing interconnections to microtubules on which the mitochondria anchor. Importantly, these data are not consistent with cell models that only incorporate an elastic membrane surrounding a viscous cytosol (4, 6, 20).

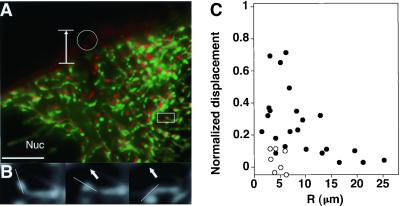
Figure 1.

Analysis of mechanical connectivity in living cells. (A) An endothelial cell containing EYFP-labeled mitochondria that was stressed by pulling on a surface-bound RGD-microbead by using a micromanipulator. Vertical arrow, direction and extent of bead displacement; white circle, position of bead after stress application; green, position of mitochondria before stress application; red, their position ≈3 s after stress was applied; Nuc, nucleus of the cell (scale bar = 10 μm). (B) A magnified view of the region outlined by a rectangle in A before stress application (Left) and after increasing levels of distortion were induced (Center and Right). White line indicates orientation of the main axis of the portion of a mitochondrion that moved in a direction opposite to that of the applied stress (arrows). (C) Quantitation of data obtained by pulling on surface-bound beads showing mitochondrial displacement normalized for microbead displacement as a function of the distance, R, from the site of stress application. Each point indicates an individual mitochondrion. Closed circles, RGD-beads; open circles, AcLDL-beads.

In contrast to integrins, there was almost no displacement of mitochondria when cells were probed with beads bound to transmembrane acetylated low-density lipoprotein (AcLDL) scavenger receptors using similar magnitudes of deformation (Fig. 1C). The cellular response to stress therefore appears to depend on the connectivity within discrete molecular networks that span the cell surface and extend through the cytoplasm as well as on cooperative interactions between the different CSK filament systems. These findings also clarify that the cell may appear to behave like an elastic cortex surrounding a viscous cytosol, if the submembranous actin network is probed independently of the internal CSK (microfilament–microtubule–intermediate filament lattice), as done here by using AcLDL receptors. Importantly, integrin receptors that provide deeper linkages appear to be more critical for adhesion, cell shape control, and cellular mechanotransduction (1, 12, 13, 21, 22).

Microtubules Bear Compression in Living Cells.

Direct visualization of microtubule dynamics in cells transfected with GFP-tubulin confirmed that some polymerizing microtubules buckled locally when they extended and impinged end-on on other structures in the cell cortex (Fig. 2A), as previously observed in other cells (23). Buckling observed in an end-on loading configuration is indicative of compressive loading; however, some investigators have suggested that this form of microtubule buckling could result from fluid flow in the surrounding cytosol (24). To directly determine the relative importance of fluid flow for structural reorganization in the cytosol, displacements of EYFP-mitochondria and GFP-microtubules were analyzed in live endothelial cells adherent to deformable polyacrylamide gels (17). Cells were mechanically distorted by impaling the flexible ECM-coated gel with a glass micropipette ≈5 μm from the cell periphery and applying force by using a micromanipulator. When a single cell containing EYFP-mitochondria was repeatedly pulled and pushed through its physiological adhesions to the ECM substrate, the mitochondria extended along the direction of the pull and then returned to their preexisting location and pattern after force was released (Fig. 2B). Repeated deformation resulted in similar displacements and nearly identical results were obtained with cells expressing GFP-tubulin; microtubules immediately returned to their preexisting shape and position even after the extended cell was held in place for more than 2 min (data not shown). Curved microtubules also immediately straightened along almost the entire length of the cell when cells were uniaxially stretched by 20% using a flexible, ECM-coated, silicone culture membrane driven by a motor-controlled device (Fig. 2C). Taken together, these results indicate that: (i) microtubules do not “float” free in the cytosol, (ii) changes in microtubule curvature do not result from cytoplasmic flow, and (iii) microtubules can bear mechanical loads that are transmitted over long distances inside the cytoplasm.

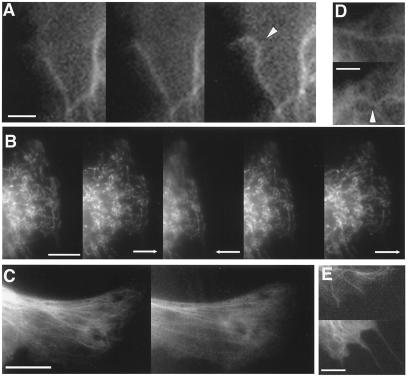
Figure 2.

Fluorescence video microscopy images of cells cultured on flexible polyacrylamide gels (A, B, D, and E) or a silicone rubber (C) substrate. (A) Three images of the same cell expressing GFP-tubulin showing buckling of a microtubule (arrowhead) as it polymerizes and impinges end-on on the cell cortex. (B) A cell containing EYFP-labeled mitochondria at rest (Left) and after the flexible substrate was pulled to the right (Left Center), pushed to the left (Center), released (Center Right), or pulled again with a micropipette (Right) over a period of 15 s. Arrow indicates direction of force application. Note that the spatial relationships between neighboring mitochondria remains constant throughout these deformations and that the mitochondria returned to their preexisting position when the stress was released. (C) A cell expressing GFP-tubulin before (Left) or ≈4 s after (Right) the substrate was stretched by 20% in the horizontal direction by using a motor-controlled device (18). (D) Local buckling of a GFP-labeled microtubule (arrowhead) after tension was increased in the CSK by addition of thrombin (Upper vs. Lower; 3 min after addition of drug). (E) GFP-labeled microtubules in a cell before (Upper) or after (Lower) disruption of the tensile actin network, using cytochalasin D (1 μg/ml for 30 min). Note the two microtubules that push outward past the original membrane boundary toward the bottom right corner of the Lower and form microspike-like extensions after release of tensile restrictions. (Scale bars: 2 μm in A and D; 10 μm in B and C; and 5 μm in E.)

The possibility that microtubules bear compression in cells was further supported by the finding that microtubule buckling increased when CSK contraction was stimulated by addition of thrombin to cells cultured on flexible gels (Fig. 2D). Conversely, microtubules straightened and pushed outward through the cell surface when the restraining, tensile actin network was disrupted by using cytochalasin D (Fig. 2E). Curved microtubules also straighten when CSK tension is chemically dissipated without altering CSK integrity (25). More importantly, if microtubules are internal compression elements that maintain cell shape stability by supporting a substantial part of the cellular prestress, then their disruption should cause part of this prestress to be transferred to their external adhesions, thereby increasing the traction at the cell–ECM interface. In contrast, if microtubules carried tension, their removal would lead to a decrease in traction, as observed when microfilaments are disrupted using cytochalasin D (26) or when intermediate filaments are knocked out genetically (27). In fact, many cells increase ECM traction when treated with microtubule disrupting agents (26, 28, 29); however, this effect has been attributed to increases in MLC phosphorylation due to release of tubulin monomers (29) or to changes in intracellular calcium (30), which regulate microfilament contractility, rather than to a tensegrity-based force balance.

To explore this idea in greater detail, microtubules were disrupted with colchicine in human airway smooth muscle cells that were already activated with a dose of histamine (10 μM) that induces optimal contraction. Interfacial traction on the adhesive substrate and cellular prestress were quantitated by using traction force microscopy (17) in which cells are cultured on flexible, ECM-coated, polyacrylamide gels that contain small fluorescent beads as fiducial markers. Importantly, the addition of 1 μM colchicine increased the mean traction (obtained as a root-mean-square over the cell projected area) by about 13%, ranging from 2–22% in histamine-treated cells (n = 7; P < 0.008; paired t test). Moreover, Western blot analysis revealed that although treatment of unstimulated cells with colchicine did induce a small increase in MLC phosphorylation, microtubule depolymerization (and tubulin monomer release) did not produce any further increase in MLC phosphorylation above the saturating levels induced by histamine (Fig. 3). Microfluorimetric analysis using cells loaded with Fura-2 also confirmed that calcium levels did not change significantly when colchicine was added to histamine-treated cells (105 ± 12 nM vs. 122 ± 12 nM before addition; n = 4). Similar results on MLC phosphorylation were obtained in vascular smooth muscle cells stimulated with endothelin-1 and treated with nocodazole (data not shown). Other groups also have failed to observe a change in intracellular calcium in response to microtubule disruption (31).

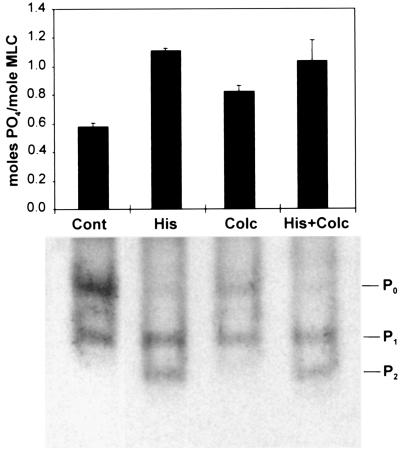
Figure 3.

Analysis of MLC phosphorylation. Bar graph (Upper) indicating stoichiometry of MLC phosphorylation as determined from densitometric analysis of MLC bands within immunoblots from two separate experiments (error bars, SD; P₀ = unphosphorylated, P₁ = singly phosphorylated, and P₂ = doubly phosphorylated MLC). (Lower) A representative blot. Smooth muscle cells were treated with PBS alone (Cont), 10 μM histamine for 10 min (His), 1 μM colchicine for 8 min (Colc), or histamine for 2 min followed by histamine and colchicine for 8 min (His + Colc), as used in the tractional analysis shown in Fig. 5.

Taken together, these data demonstrate that microtubules bear compressive forces in living cells, that these compressive forces can be transferred between microtubules and the ECM, and that together these support elements balance tensile forces generated within the contractile actin CSK. This demonstration of a three-way force balance between microtubules, microfilaments, and ECM, which is consistent with the tensegrity model and with experimental findings obtained in many cell types (26–29), cannot be explained by other existing models of cell mechanics. Interestingly, these findings also suggest that the forces that are transferred from microtubules upon their disruption to the ECM and remaining CSK via a tensegrity force balance (Fig. 5) may be translated in some way into biochemical signals that elevate MLC phosphorylation in unstimulated cells, as observed in our smooth muscle cells without histamine (Fig. 3) or in fibroblasts without serum (29).

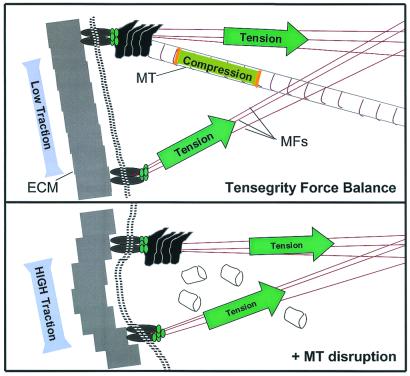
Figure 5.

A schematic diagram of the complementary force balance between tensed microfilaments (MFs), compressed microtubules (MT), and the ECM in a region of a cellular tensegrity array. Compressive forces borne by microtubules (Upper) are transferred to ECM adhesions when microtubules are disrupted (Lower), thereby increasing substrate traction, as observed in experiments described in Fig. 4A.

Quantitative Measurements Support the Tensegrity Model.

A key quantitative a priori prediction that has arisen from the theoretical formulation of the tensegrity model of cell mechanics is that the shear modulus (stiffness) of the cell should increase approximately linearly with the prestress in the CSK (9). In fact, previous qualitative studies have demonstrated that altering CSK prestress by modulating actomyosin-based contractility, using drugs (15), by transfecting cells with constitutively active MLC kinase (32), by varying transmembrane osmotic forces (32), or by quickly distending a flexible ECM substrate results in immediate changes in cell stiffness (33). However, it has not been possible to quantitatively measure prestress in individual living cells and thus, to test this a priori prediction of the tensegrity model. To accomplish this, we adapted the traction force microscopy technique (17) to calculate the average prestress within individual smooth muscle cells under different experimental conditions by quantitating fluorescent bead displacement relative to the rest (traction-free) state of the gel after the cells were released from their adhesions by using trypsin.

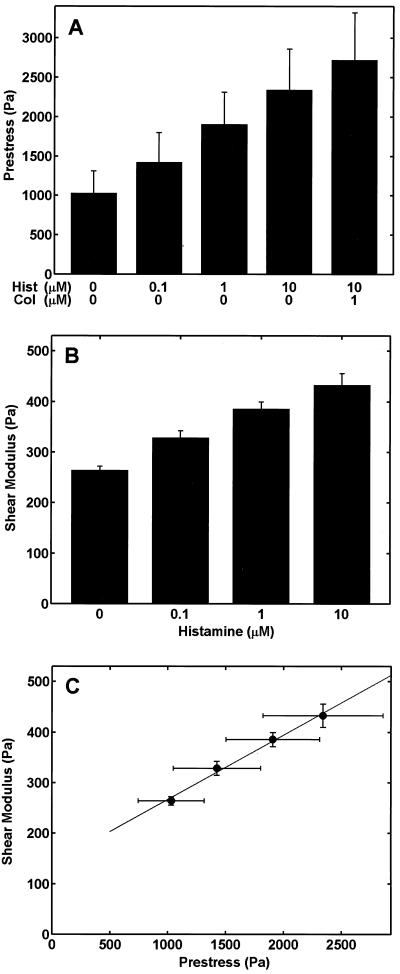
These experiments produced the first quantitative experimental measurements of average prestress within individual cultured cells and revealed that both prestress (Fig. 4A) and the shear modulus (measured with oscillatory magnetic twisting cytometry; ref. 16; Fig. 4B) increased as the concentration of histamine, and thus the level of tension in the actin CSK, was raised. Most importantly, the shear modulus versus prestress relationship obtained in this study (Fig. 4C) and the relationship predicted a priori from a tensegrity model (9) were remarkably consistent: the shear modulus increased linearly with increasing prestress as predicted. The values of the prestress were of the order of 10²–10³ Pa, whereas the shear modulus was of the order of 10² Pa. Taken together, these data suggest that in a relatively low range of applied stress (10¹ Pa), the cell's elastic response is primarily determined by prestress, and not by bending of the actin filaments, as predicted by an alternative “porous cellular solid” model of the cell (34); if the latter mechanism applied, then the shear modulus would have been much larger (10⁴ Pa). The total cellular prestress [the sum of the prestress balanced by the ECM before microtubule disruption (≈2,341 Pa) plus the stress transferred from the depolymerized microtubules to the ECM (384 Pa)] was determined to be ≈2,725 Pa from the traction measurements (Fig. 4A). Thus, microtubules counterbalanced about 14% (ranging from 4–29%) of the prestress within an individual histamine-treated cell cultured on the flexible gel before colchicine treatment. Pharmacological disruption of microtubules also reduces cell stiffness (shear modulus) in various cell types (12, 13). Thus, these results confirm that the ability of microtubules to bear compression contributes significantly to cellular prestress and that prestress, in turn, is critical for maintenance of cell shape stability.

Figure 4.

Relation between prestress and shear modulus in smooth muscle cells. (A) Prestress calculated from traction in the gel and presented as a function of histamine (0–10 μM) and colchicine (1 μM) treatment (P < 0.02 for all comparisons except between 0 vs. 0.1 μM histamine; paired t test, n = 7 cells per condition). (B) Shear modulus measured in cells adherent to ECM-coated rigid dishes presented as a function of increasing histamine concentration (0–10 μM) (P < 0.04 for all comparisons; n = 8 wells with 2 × 10⁴ cells per well). (C) Plot of the shear modulus as function of prestress demonstrating a linear relationship, as predicted by a theoretical tensegrity model (9).

The mathematical formulation of the tensegrity model also leads to other a priori predictions. For example, the general expression for the relationship between the shear modulus and the microstructural properties of these structures predicts that the cell's dynamic shear modulus can be decomposed into the product of a prestress-dependent component and a frequency-dependent component (see Appendix). Specifically, tensegrity predicts that at a given frequency, both the storage and loss moduli should increase with increasing prestress, whereas the hysteresivity coefficient (the fraction of the frictional energy loss relative to the elastic energy storage) should be independent of prestress. Importantly, this a priori prediction of the model is consistent with results of a recent experimental study in which the dynamic behavior of the same smooth muscle cells as used here were analyzed in response to a physiological range of frequencies (0.05 to 0.20 Hz) and forcing amplitude of ≈8 Pa, before and after addition of 10 μM histamine (16). As predicted by the tensegrity model, both the storage and loss moduli increased (by roughly 70%), whereas the hysteresivity coefficient remained constant when contractility (prestress) was increased by histamine treatment. Although other cell structures (e.g., microtubules, intermediate filaments, viscous cytoplasm) may also affect the cell's dynamic response, the results suggest that prestress and tensegrity have a unifying role in terms of explaining both the static and dynamic mechanical behaviors of living cells.

An Improved Model of Cell Structure and Mechanics.

To understand the relation between cell mechanics, molecular structure, and biochemical function, it is critical that a physical and mathematical framework be developed to explain the mechanical behavior of cells and tissues. In this study, we demonstrated that the cellular response to mechanical stress applied to the cell surface depends on molecular connectivity to the internal CSK lattice, that microtubules bear compression in cells and contribute significantly to cellular mechanics under physiological conditions, and that prestress in the CSK is critical for cell shape stability. These are all key features of the tensegrity model. In addition, we carried out quantitative measurements that generated results that are consistent with specific a priori predictions of this model. Clearly, the living cell is a dynamic structure that continually changes under the influence of thermal motions, CSK filament polymerization dynamics, and viscous forces that retard these motions. The current formulation of the tensegrity model does not include these features. Nevertheless, it apparently does incorporate the subset of features that are sufficient to predict many complex mechanical behaviors of living cells.

Importantly, there may be alternative explanations or models for any single result presented in this study. For example, other tensile models of the cell, including the cortical membrane model, the rubber ball model, and the liquid drop model (refs. 4 and 20, reviewed in ref. 11) may exhibit a similar linear dependence of stiffness on prestress when analyzed under similar loading conditions (35). However, unlike tensegrity, these models are not consistent with the discrete network behavior that we observed in the cytoplasm of living cells (Figs. 1 and 2). The observation that certain mitochondria move in a direction opposite to the applied force (Fig. 1) also could be explained by a liquid crystal model of the cytoplasm (36); however, this model is not consistent with the immediate restoration of mitochondrial position upon force removal (Fig. 2B). Other mechanical models based on porous cellular solids (34), filament dynamics (thermal fluctuations; ref. 37), and percolation theory (38) take into account that the CSK is organized as a porous network composed of discrete structural elements, as does tensegrity. But, these models do not incorporate prestress that we find to be critical for control of cell mechanics, nor do they or the cable net model (9) predict that intracellular compression-bearing structures (e.g., MTs) would balance CSK prestress. Furthermore, none of these other models incorporate features that can explain the increased transfer of traction to the substrate when microtubules are disrupted (Fig. 5), nor are they consistent with the highly organized microarchitecture that can be observed within the cytoskeleton of living cells (e.g., actin-based geodesic domes).

Only the tensegrity model is compatible with all of these findings, in addition to providing a priori predictions of cell mechanical behaviors that match closely with experimental results. Furthermore, the cellular tensegrity theory also can incorporate increasing levels of complexity, including multimodularity and the existence of structural hierarchies (7, 11, 39), which have not yet been incorporated into the theoretical model. These features of tensegrity may help to explain how molecular structures in specialized regions of the cell (filopodia, microvilli), organelles (mitotic spindle, transport vesicles), viruses, and enzyme complexes are independently stabilized on progressively smaller size scales while, at the same time, displaying integrated mechanical behavior as part of the whole cell. Interestingly, even the highly elastic, submembranous actin–spectrin lattice appears to require prestress to provide its characteristic mechanical functions (40). Tensegrity therefore may be the most unified model of cell mechanics at the present time.

Abbreviations

CSK

cytoskeleton

ECM

extracellular matrix

EYFP

enhanced yellow fluorescent protein

MLC

myosin light chain

Theoretical Implications for Dynamic Behavior.

Given the nearly linear relationship between shear modulus (G) and prestress (σ) (Fig. 4C) and assuming that for uniformly distributed tensile filaments of the CSK, σ = E_TFϕɛ/3, where E_TF, ϕ, and ɛ are static Young's modulus, volumetric fraction, and initial distending strain of tensile filaments, respectively (9), it follows that:

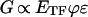1

Through use of the correspondence principle (41) and assuming that inertial effects are negligible, in the dynamic frequency (f) domain, Eq. 1 becomes.

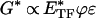2

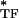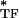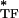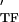where G* is cell dynamic shear modulus and E is the dynamic modulus of an individual tensile filament that is f-dependent. For a given ɛ (i.e., for a given prestress), E can be decomposed into elastic and dissipative components as E = E + iE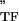, where 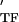E and E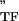 are the storage and loss moduli of a tensile filament, respectively, and i is the imaginary unit that indicates the out-of-phase behavior. Taking this and Eq. 2 into account, G* was decomposed into G′ ∝ E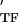ϕɛ, G" ∝ E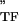ϕɛ and the hysteresivity coefficient (η) was obtained as follows:

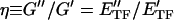3

Eq. 3 shows that η depends only on rheological properties of tensile filaments and not on their volume fraction or on the prestress (i.e., ɛ).