Effects of Sample Delivery on Analyte Capture in Porous Bead Sensors

Abstract

Sample delivery is a crucial aspect of point-of-care applications where sample volumes need to be low and assay times need to be short, while providing high analytical and clinical sensitivity. In this paper, we explore the influence of the factors surrounding sample delivery on analyte capture in an immunoassay-based sensor array manifold of porous beads resting in individual wells. We model using computational fluid dynamics and a flow-through device containing beads sensitized specifically to C-reactive protein (CRP) to explore the effects of volume of sample, rate of sample delivery, and use of recirculation vs. unilateral delivery on the effectiveness of the capture of CRP on and within the porous bead sensor. Rate of sample delivery lends to the development of a time-dependent, shrinking depletion region around the bead exterior. Our findings reveal that at significantly high rates of delivery, unique to porous bead substrates, capture at the rim of the bead is reaction-limited, while capture in the interior of the bead is transport-limited. While the fluorescence signal results from the aggregate of captured material throughout the bead, multiple kinetic regimes exist within the bead. Further, under constant pressure conditions dictated by the array architecture, we reveal the existence of an optimal flow rate that generates the highest signal, under point-of-care constraints of limited-volume and limited-time. When high sensitivity is needed, recirculation can be implemented to overcome the analyte capture limitations due to volume and time constraints. Computational simulations agree with experimental results performed under similar conditions.

Introduction

The fields of oligonucleotide profiling, sequencing and detection have grown tremendously with the creation of new tools including high sequencing instruments and DNA microarrays.^{1, 2} These tools have led to explosive growth of the genomics disciplines.³ The related field of high throughput protein detection has been pushed forward somewhat through the availability of mass spectrophotometers, but precious few of these discovered protein fingerprints have moved into clinical practice.^{4, 5} While protein arrays are available as a potential tool to move past the mass-spectrometry-derived discovery phase, non-specific reactivity, high background responses, lack of quality standards, and overall poor quality control plague their usefulness.^5–8 More typically, the highly manual and time consuming completion of an ELISA test has been used to secure the validation data.⁹ The requirement of the adaptation to yet another instrumentation platform in the final clinical implementation has led to the crippling influence on proteomics translational efforts.¹⁰

The development of microfluidic based tools for the completion of clinical measurements on protein samples offers new hope for this area. Microfluidic lab-on-a-chip (LOC) devices have emerged in the past two decades as detection systems for clinical, military, and environmental applications.^11–15 Some of these devices offer point-of-care (POC) capabilities and can provide rapid turnaround results while maintaining or even surpassing the advanced analytical performance of their laboratory confined counterparts.^16–18 Further, in addition to their cost effectiveness, they often feature multiplexing capabilities, which capitalize on the simultaneous detection of a variety of analytes using low sample volumes. In this space, however, there are significant challenges yet to be overcome related to device integration and scalability as well as defining optimal strategies for analyte capture on time frames consistent with point-of-care measurements.^{19, 20} The preponderance of laminar flow in such systems creates a potential barrier for efficient capture of analytes within typical microfluidic structures.²¹ The small dimensions here employed along with laminar flow make it challenging to capture sufficient quantities of analyte that can be measured with the simple detection modality that is desired for cost effective point-of-care instrumentation.^{20, 22}

Recently, porous beads supported in microfluidic-based sensor systems have garnered major support for their use in detection of a wide range of analyte classes. These microbead sensors offer several advantages over the traditional ELISA gold standard or reference method, with benefits stemming from their high surface to volume ratios, high binding densities, and the ability for internal transport of analytes.^23–27 Medical microdevices based on porous bead sensors, used for the detection of DNA oligonucleotides, human immunoglobulin A, and biotinylated quantum dots,^{23, 28, 29} offer high analytical performance characteristics for various essential point-of-care applications.^{30, 31}

For these detection ensembles an understanding of the effects of sample delivery conditions is crucial for optimal capture and detection of analytes. Factors pertaining to such conditions include the rate of sample delivery to the bead sensing elements, size of the sample volume, total time for analyte incubation, and mode of delivery, specifically unilateral delivery or use of recirculation to recycle the sample. Consideration of these factors provides guidance during the developmental stage of the point-of-care device to deliver fluids quickly and inexpensively without exploiting excess amounts of reagents while developing strong detection signals.

Some initial important studies have been completed in this area. Studies by Parsa et al. revealed, under volume- and time-based constraints, an additional reagent-limited regime in addition to the classical transport- and reaction-limited regimes.³² This surface binding study revealed benefits of using short, concentrated delivery of fluids and critical flow rate for optimal assay performance. Hu and Vijayendran examined the capture of delivered analytes by antibodies immobilized on patches of binding surfaces in a microfluidic channel.^{33, 34} These studies provided an understanding of reaction kinetics as well as guidance for development of microfluidic immunoassays. Similarly, Fu et al. developed a computational model for competitive, heterogeneous immunoassays.³⁵ Their model provides guidance on assay performance for assay parameters, including flow rate and binding density, and reveals details on the operating range of these parameters to improve assay sensitivity.

Recently, we developed a computational tool to predict the spatial and temporal binding of analytes delivered to porous bead sensors.³⁶ Similarly, Bau and co-workers modelled analyte capture on both porous and nonporous beads trapped in microfluidic wells.^{23, 37} In spite of these efforts there remains little information related to an understanding of the influence of the effects of sample delivery on the binding of analytes using porous bead sensor systems. In this paper, we examine the effects of the sample volume, rate of sample delivery, and analyte incubation time, under either unilateral delivery or recirculation of the sample, on the capture of the C-reactive protein (CRP), an inflammation and cardiac risk biomarker. We examine these factors using a 2-site immunometric immunoassay with AlexaFluor®488 labelled antigen using porous, agarose beads sensors in a flow-through, pressure driven system. Further, we attempt to validate our experimental findings with computational simulations to model the capture of analytes under such conditions.

Experimental

Reagents and bead sensors

Cross-linked and glyoxylated 280µm diameter, 2% agarose beads were prepared from previously developed methods.³⁸ Briefly, heated agarose was stirred in a beaker of suspending solution consisting of Span-85 and heptane. Specific bead sizes were filtered using selective sieves. Detecting and capturing antibodies specific to CRP were purchased from Fitzgerald (Concord, MA). Agarose beads were conjugated overnight with 4mg/mL anti-CRP capturing antibodies per 500µL of beads using previously developed methods.³⁹ Detecting anti-CRP antibodies, diluted 1:250 in phosphate buffered saline (PBS), were conjugated to Alexa-Fluor®488 (Invitrogen, Carlsbad, CA). Stock purified, native human CRP antigen was diluted to 50ng/mL in PBS. The CRP antigen was co-incubated and labelled with detecting anti-CRP antibodies. Calibration and negative control beads were conjugated overnight with 0.02mg/mL Alexa-Fluor®488 bound donkey anti-sheep IgG (Invitrogen, Carlsband, CA) and 4mg/mL anti-TNF-α antibody (Cell Sciences, Canton, MA), respectively.

Device construction

Agarose beads were manually loaded using precision forceps onto an anisotropically etched silicon chip containing an array of inverted, pyramidal-pit-shaped, through-hole micro-containers. Dimensions of each well were 500µm×500µm for the top opening and 100µm×100µm for the bottom of the well. Corner wells contained two diagonally positioned calibration beads and two negative control beads. These beads were strategically placed for automatic bead position detection for data analysis using custom-built image analysis in ImageJ.⁴⁰ The chip was sandwiched between two acrylic inserts with micro-milled inlet and outlet channels of diameter 1mm. The top insert contains one inlet that overlays over a 60µm-thick vinyl flow chamber positioned over the bead array. A bubble trap, at the end of the chamber, served to flush out dead volume air. The bottom insert contained a 60µm vinyl drain layer and channel connected to waste. The three-piece fluidic device was housed in a stainless steel chassis and tightened with a circular screw top. Tubing from a peristaltic pump (FiaLAB, Bellevue, WA) was connected to the device using PEEK connectors. For recirculation, the drain tubing was placed back into a 5mL tube containing 1mL of sample.

Data acquisition

Images with TIFF format and 8-bit depth were acquired using a DVC camera connected to an Olympus BX-2 microscope (Center Valley, PA) with 4× objectives. Each image was an aggregation of signal from a single 50µm focal plane. Images were saved with 500ms, 1000ms, and 2000ms exposure times. The beads were located using a custom written ImageJ macro that automatically located the bead positions based on pixel positions of corner calibration beads. The intensities of the beads were extracted from the image using the average of the maxima of a series of line profile scans down the bead. A dose response was plotted from the imported fluorescent averages using SigmaPlot 10 (Systat Software Inc., San Jose, CA).

Computational Modelling

Computational simulations were modelled with COMSOL 3.5a (Burlington, MA) using the Chemical Engineering module. Based on previous work that compared computational simulations with analytical solutions, a 2D system, with the Incompressible Navier-Stokes and Convection-Diffusion add-on's, was sufficient to accurately predict the transport and binding of analytes on a bead substrate.²⁴ Briefly, a 280µm bead was positioned inside a 250µm thick inverted pyramidal shaped well with walls with 54.7° inclines. The pore size of the bead was set to 400nm, based on microscopy calculations for a 2% agarose bead.²⁴ The inlet was set to volumetric flow rates ranging from 6.25µL/min to 1600µL/min. Assuming uniform flow through each well in a 3×4 array, the exiting flow rate at the top of the modelled well was set to 75% of the entrance flow rate. The pressure at the drain below the bead was set to atmospheric pressure. Internal flow through the porous bead was modelled using Brinkman's Equation. Based on binding rates for CRP, published previously, the binding association rate was 10⁵L/(mol·s) and dissociation rate was 10⁻⁵ 1/s.³⁶ To reduce the time to convergence, the time independent Navier-Stokes equation was solved prior to the transient convection-diffusion equation and reaction equations. The mesh was continuously refined until computational solutions did not change with a final mesh size of 37600 elements.

Results and Discussion

Theory

The unique bead-based microfluidic system involves multiple chemical and physical equations that govern fluidic flow, transport and capture of analytes.³⁶ Navier-Stokes (equation 1), with stress expanded into pressure and viscous terms, governs fluidic flow through the microfluidic channels. Brinkman's equation (equation 2), an extension of Navier-Stokes, defines flow through the porous bead medium.^{36, 41} Here, ρ is the fluid density (kg·m⁻³); u is the flow velocity (L/min); P is the pressure (Pa); η is the dynamic viscosity (kg/(m·s); k is the permeability (m²); and ε_ρ is the dimensionless porosity.

$$\rho (\frac{\partial u}{\partial t}+u·\nabla u)+\nabla P-\eta {\nabla }^{2}u=0$$ (1)

$$\nabla P=-\frac{\eta }{k}u+\frac{\eta }{{\epsilon }_p}{\nabla }^{2}u$$ (2)

The convection and diffusion (equation 3) equation models the time-dependent concentration of species in the bulk solution and porous bead. Here C (mol/L) is the concentration of the analyte and D is the diffusion coefficient of the species (m²/s). In the immunoformat system, C designates the concentrations cAb, cAg, and cAbAg. cAg (mol/L) is the concentration of antigen, cAb (mol/L) is the concentration of loaded antibodies immobilized on the beads, and cAbAg is the bound complex (mol/L).

$$\frac{\partial C}{\partial t}+u·\nabla C=D{\nabla }^{2}C$$ (3)

$$\mathit{\text{cAb}}+\mathit{\text{cAg}}\stackrel{k_{\mathit{\text{on}}},k_{\mathit{\text{off}}}}{\iff }\mathit{\text{cAbAg}}$$ (4)

The binding kinetics equation (equation 4) is described with the reaction rate law. Kinetic rates for association and dissociation are given by the association and dissociation rates, k_on (L/(mol·s)) and k_off (1/s). The unknown flow rate, u, is calculated using finite elements and the defined pressure, density, and viscosity terms, and permeability terms. This calculated flow rate and pre-defined binding kinetics is then used to calculate the time-dependent concentrations of the analyte and antibody species.

Rate of sample delivery

As with nearly all microfluidic systems, flow rate is one of the major factors affecting analyte capture. In this case the capture location involves the use of a porous bead. The rate of sample delivery directly affects the rate of replenishment of antigen to the bead sensor through modulation of the internal pressure inside the system. Figure 1B shows a time-course delivery of analyte to a single bead. On the 100ms time frame, the antigen completely surrounds the bead, as shown by the antigen concentration, [Ag], normalized to the antigen concentration in the bulk solution.

Figure 1.

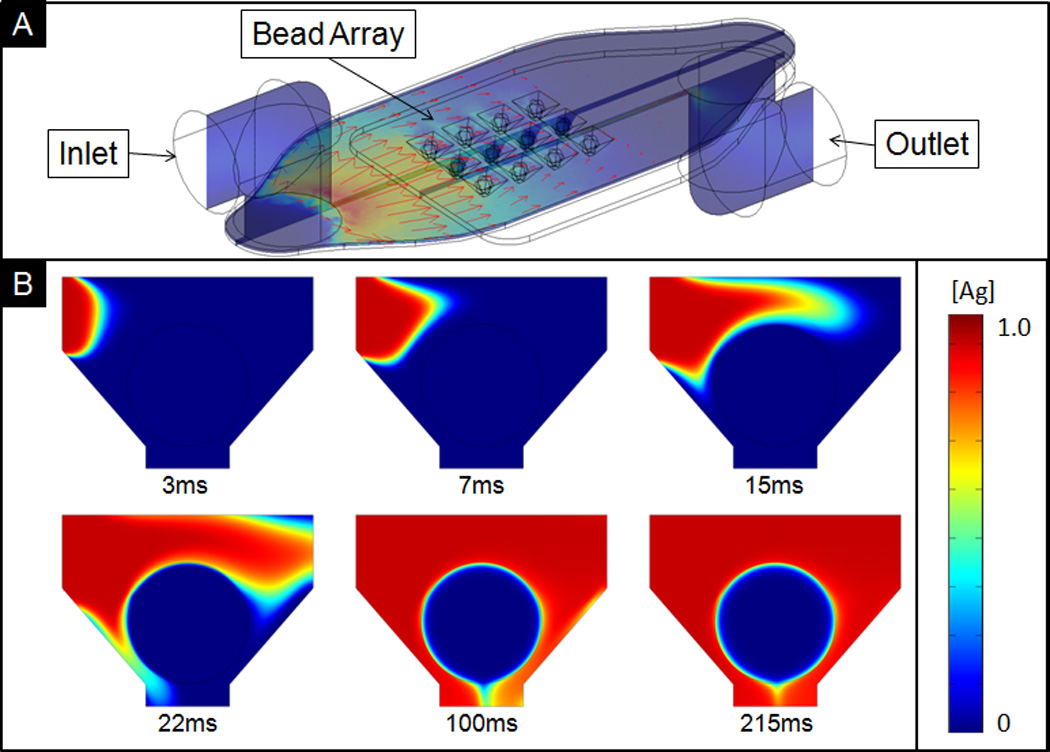
A) Isometric, cross-section views of the bead array showing flow profile in red arrows, with maximum flow rate of 3.26µL/min. Under recirculation, unspent reagents from tubing connected to outlet are continuously recycled back into the inlet. B) Cross-sectional view showing delivered sample containing CRP to a single bead with diameter of 290µm.

While labelled antigen completely surrounds the bead in less than 100ms, the antigen concentration local to the bead surface is much lower than that of the bulk solution. This local region, described here as the depletion layer, is a result of the relative ratio of the low rate of replenishment to the rate of depletion as the antigen binds to the bead. When the flow rate increases, this depletion layer size is reduced as delivered sample replenishes the local region. For the purposes of this manuscript, we define the depletion layer as the region around the bead such that the antigen concentration is 95% that of the bulk solution. As such, two regimes exist: a transport-limited regime and a reaction-limited regime. In the former, the flow rate is not sufficiently high enough to replenish the antigen concentration that is depleting as the antigen reacts with unbound sites on the bead.

Here, total analyte capture is limited by the flow, or transport, of analytes to the beads. In the latter reaction-limited regime, no depletion layer exists outside the bead. Here, total analyte capture is limited by the rate of capture or the inherent association constant, k_on. Figure 2 compares this depletion layer under low and high flow rates. At the low end of 100µL/min (Figure 2A), soon after the sample reaches the bead (top, 2s), a depletion layer forms at the exterior of the bead. This asymmetric shape of the depletion layer is due to the direction of flow and geometry of the bead holder. On the side of the bead opposite to the direction of flow, the wrapped around fluid is already slightly depleted as it reacts with the top of the bead. At the base of the bead, due to the drain-bound trajectory of the fluid, not much antigen is being replenished.

Figure 2.

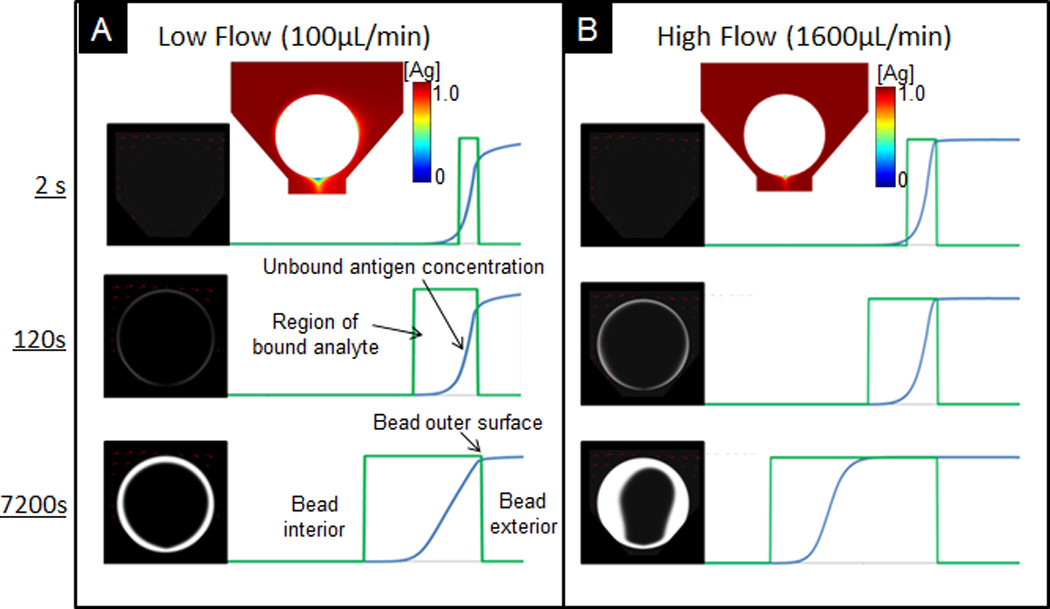
Comparison of spatial and temporal distribution of captured analytes under low (A) and high (B) flow rate. To the right, region of bound analyte and distribution of unbound analytes. Boxed regions (green) depict the width of the reaction front and the blue curves show the distributions of unbound antigen in bead. Cross sectional plots above figures show distribution of free antigen at the exterior of the bead.

As the unbound sites near the bead surface become saturated, as observed at 7200s, the depletion layer and rate of depletion are reduced. While there are plenty of remaining unbound sites inside the bead, the rate of reaction is limited due to the need for the analyte to be transported to the internal binding sites via convection and diffusion. Because the bead internal is more transport-limited, most of the fluorescent signal quickly develops at the outer rim of the bead. The maximum attainable fluorescent signal depends on the concentration of capturing antibody, which can be up to several thousand times that of the concentration of delivered analyte.

For a higher flow rate, as shown for 1600µL/min in Figure 2B, no depletion layer forms. This lack of a depletion layer enables maximum capture where the capture rate is limited by binding kinetics. After 7200s, the depletion layer, consisting of unbound antigen, transitions into the bead interior. Unlike most lateral flow 2D systems, in which unbound antigen binds to antibodies immobilized on a solid surface, the unbound analytes in this bead-based format can bind to the binding sites inside the fibrous network. In other words, when the outer surface of the bead saturates with bound antigen, unbound antigen, which cannot bind to any unbound sites near the rim of the bead, can be transported further into the bead before capture. This porous medium enables an extended signal development, in which final signal is an aggregation of the total fluorescence on multiple focal planes across the semi-transparent, agarose bead.

Influence of porous bead interior on capture

Porous microbeads offer the advantage for delivery of analytes into the interior core, provided that the labelled analyte complex is much smaller than the pore size of the fibrous network. Under high rates of delivery, fluorescent signal develop further inside the bead, as shown with simulated data in Figure 3A–B after 2600s. This higher penetration, due to the minimal external depletion layer, as well as a higher convection driven internal flow, previously found to be proportional to the external delivery rate,³⁶ ultimately leads to a higher fluorescent signal. After initially binding to the outer surface of the bead, the amount of penetration from bound CRP increases over time. Typically, free analytes only penetrate 25% into the bead, with the core of the bead unused for binding. This effect is due to the rapid binding of analytes to available capture probes at the exterior of the site. Figure 3D contrasts the fluorescent intensity on the bead under various delivery rates from 59µL/min to 700µL/min taken after 10min.

Figure 3.

A) Profile of captured CRP antigen cross medial slice of bead derived from computational simulations for different flow rates. B) Progression of penetration depth of bound analytes under different flow rates based on models. C) Calculated depletion width outside the bead at different simulated times for various flow rates. Negative values signify the interior of the bead. D) Experimental data showing different signals at a low, medium, and high flow rate after 10min delivery. E) Experimental data showing signal development over time at 100µL/min flow rate and 100ng/mL concentration. F) Comparison of cell Péclet number for various flow rates. G) Cross sectional xz-view of bead showing distribution of Péclet number on the bead.

The CFD modelling of antigen penetration reveals that the amount of penetration into the bead is non-linear with respect to the rate of sample delivery (Figure 3B). This nonlinearity, in part due to reaction kinetics, is also a result of the slower transport of antigen inside the bead. Thus, while the signal development is reaction-limited at the rim of the bead under high flow rates of delivery, the signal at the bead interior is transport-limited. This trend is in agreement with previous studies that have revealed that the small pore sizes of the agarose fibrous network hinders the transport of analytes further into the bead.²⁴ The occurrence of two distinct transport regions involving both interior and exterior regions allows for some interesting options to expand the dynamic range of the bead sensor ensembles as will be described in more detail below.

While the total amount of fluorescent signal increases over time, as shown in Figure 3E for a flow rate of 1300µL/min, for a delivery flow rate of 700µL/min, there is a decrease in the depletion width over time, as revealed in Figure 3C. At low flow rates, the system is transport-limited with a large depletion width. As the sites of the outer surface of the bead become saturated, the depletion width reduces due to the limited remaining amounts of unbound sites at the rim of the bead. After these sites become bound in less than 2min, there is a quick drop in the rate of binding on the bead, as implied by the sudden drop in depletion width for flow rates of 25 and 100µL/min. The initial steep drop in the depletion rate is not shown for 6µL/min because the analyte concentration at 20s never reached 95% of the bulk solution in the region near the well. A negative depletion width, represents the cutoff inside the bead where the analyte concentration is 95% that of the bulk solution. This internal unbound antigen concentration is also observed in Figure 2B at 7200s. The unbound, internal antigen concentration drops as the antigen reaches the open sites inside the bead.

It should be noted that in POC devices, the analyte of interest is typically not labelled. Rather, a labelled detecting antibody would allow the quantification and detection of the analytes. Further, the complete removal of unbound labelled antibodies from the interior of the bead is important. As such, the final wash step is required to facilitate the removal of unbound detection antibodies from the interior of the bead.

As shown in Figure 3F, computational modelling shows a linear increase in average ratio of convection to diffusion, or cell Péclet number, as flow rate increases. This linear trend suggests a proportional increase in internal convection as external delivery rate increases. In Figure 3G, the cell Péclet number at the outer rim of the bead is significantly higher than at the inside of the bead. This 55× increase in Péclet number at the outer rim of the bead is a result of steric hindrance of convective flow inside the bead due to both the small porous agarose nanonets and the high association of free analytes onto immobilized binding sites.

The ability to control system parameters allows for the expansion of the dynamic range of the assay and high fidelity sensing. Higher flow rates allow for faster capture at the surface of the bead and penetration into its interior. Higher sample volumes allow longer durations for capture. Further, as previously reported, the ratio of internal to external convection is 1:170 to 1:3100 for beads ranging from 0.5% to 8% agarose.³⁶ The ability to tailor porous beads as well as controlling delivery rates allow for the expansion of the assay dynamic range for the detection of larger ranges of analyte concentrations. These findings provide a better understanding of capture under a range of transport conditions as well as guidance in making better engineering and assay decisions for rapid time frames for detection.

Maintaining high flow rates under point-of-care constraints

Small sample volumes and short assay times are attributes that dominate the stringent requirements for operation of point-of-care devices and that often result in limitations in term of detection sensitivity. As such, evaluation of the total amount of analyte captured under various volumes of the sample and incubation times must be examined.

In the case where sample volume is not a concern, the time of incubation of the antigen, often specified to be short for point-of-care assays, can be extended to improve the sensitivities of the assay. As shown in Figure 4B from computational modelling of total antigen capture for various delivery flow rates over incubation time lengths from 5min to 30min, an increase in the time of incubation provides diminishing returns in additional antigen capture. This lower incremental increase is due to the reduction in unbound capture sites at the rim of the bead over the time of incubation.

Figure 4.

CFD trials and experimental results exploring the total capture of CRP under conditions of limited sample volume and/or incubation time. A) Comparison of simulation derived capture changes under various flow rates for different volumes of sample with no time constraint. B) Comparison of simulated capture under various flow rates for different assay times under no volume constraint. C) Comparison of capture under both time and volume constraints. D) Comparison of experimental data showing effects of a time constraint on sensor response. E) From simulations, comparison of normalized analyte concentration at bead surface as a function of flow rate. F) Cut-off flow rates between reaction limited and transport limited regimes over duration of the assay.

While a large sample size is required in the case above, which results in a higher fluorescent signal as flow rate increases, the volume of acquired sample is typically limited in point-of-care settings. Under limited volume constraints where the time of incubation can be extended until the sample depletes, the total capture of antigen drops significantly at high flow rates. This inverse trend, as shown in Figure 4A, results from the significant increase in time of incubation at slower flow rates. Similarly, Figure 4D (v – limited) reveals that experimental assay runs using CRP, with a volume constraint of 1mL, show agreement with computational modelling, with a drop in signal for higher flow rates. At the slower flow rates, the longer residency time of the analyte overcomes drawbacks of slower capture of antigen due to the smaller depletion layer. The incubation time scales with the sample volume, while the increase in sample volume provides diminishing returns in fluorescence signal, as shown for sample volumes of 0.5 to 2.0mL. In the first case, which revealed a higher fluorescent signal as flow rate increases, a large sample size is required in order to achieve such high signals. However, under point-of-care conditions, at high flow rates, the entire sample would be depleted before the duration of the incubation time, curtailing further antigen incubation. In this situation, termed by Parsa as reagent-limited regime, the assay depletes the sample too quickly and, thus, reduces the final signal.³² As such, under constraints on both incubation time and volume of sample, maximum capture at the end of the assay occurs at the flow rate that depletes the volume at the specified incubation time. As shown in Figure 4C with CFD modelling of the flow-through bead system, for 1mL of sample volume and 10min of incubation time, the optimal flow rate occurs at 100µL/min. This maximum signal was also observed experimentally (Figure 4D – v, t limited), in which the time of incubation of CRP was restricted to 10min.

With a constraint only on the time of incubation (Figure 4D – v limited), the signal is reduced 5-fold at the low flow rate of 6.25µL/min. However, with a sample volume size of 1mL, this 5-fold reduction in signal is equivalent to ~94% reduction in the total time to complete the assay, from 160min to 10min. Similarly, with a constraint only on the volume of sample, extending the total sample volume 4-fold, from 0.5mL to 2.0mL leads to a 4× increase in completion time with diminishing gains in signal. Figure 4C reveals that the maximum increase of antigen capture occurs at 100µL/min. Lower flow rates provide limited return due to complete saturation of the binding sites at the rim of the bead where the bead signal is acquired. Alternatively, at higher flow rates, the rate of sample delivery is much greater than the rate of capture, leading to lower total capture than that achieved at 100µL/min.

Because sample volume is often constrained, defined both by patient needs and metered devices, the total time of incubation is typically the only factor that can be extended. As revealed by the slopes of signal changes in Figure 4C, signal increase is much higher for an incremental decrease in flow rate above 100uL/min or by lengthening the assay time as in the sample constrained case (4A) than for the same incremental increase in flow rate below 100uL/min as in the time constrained case (4B). In other words, a sacrifice in assay time by slowing down the delivery rate of the sample, would allow for more analyte capture. This increase is more beneficial than the increase in sample volume with respect to the total capture of analytes. Additionally, while being in a reaction-limited regime does provide benefits of higher antigen concentration local to the bead, we find that at the optimal flow rate for an assay constrained by both time of incubation and sample volume, the assay is actually transport-limited. Figure 4E shows the antigen concentration, normalized to that of the bulk solution, at the bead boundary approaches 1.0 as the flow rate increases for an assay constrained by both time of incubation and sample volume. At a cAg = 0.95 cutoff, corresponding to 417uL/min, the assay transitions from transport-limited to reaction-limited regime.

Figure 4F, reveals the dynamic transport and kinetic regimes within the bead over the course of the assay. A decrease in the cutoff flow rate at which the assay transitions from a transport-limited regime to a reaction-limited regime occurs as the assay progresses. As the duration of the assay is extended, transport-limited capture at the bead surface eventually transitions into reaction-limited capture. The dynamic transport and binding duo within the bead gives rise to a moving boundary of captured analytes, directed radially towards the internal core of the bead.

Unilateral vs. recirculation

Due to unilateral sample delivery in many microfluidic systems, a high flow rate would lead to an inefficient capture delivery as most of the sample is sent to a waste reservoir. To alleviate such limitations, a sample can be delivered using recirculation where the drain-bound sample is recycled back into the inlet. Under recirculation conditions, the amount of unbound analytes depletes at a rate dependent on the capturing efficiency. Figure 5 shows a comparison between assays in which CRP sample is delivered either unilaterally, in which fluid is continuously delivered without volume constraints, or under recirculation conditions with a total sample volume of 1mL. Use of recirculation of a 1mL sample volume of CRP reduces labelled antigen capture over time because the CRP concentration in the recycled sample diminishes as unbound CRP is captured (Figure 5A). Computational modelling suggests that each subsequent cycle has an antigen concentration of 98.5% of that from the previous cycle. While unilateral signal development under volume constraints is still higher than recirculated signal under lower volumes, limitations in sample volume at the point-of-care can be alleviated with use of recirculation. This trend of higher signal by recycling the antigen, as opposed to that of unilateral delivery under the same volume constraints (Figure 4D), can be observed for flow rates 59, 150, 300, 500, and 700µL/min. The use of recirculation is particularly beneficial at higher flow rates, as the sample does not deplete before the end of a single incubation cycle (Figure 5C). As higher flow rates are used to deliver the sample, there is a larger reduction in sample volume. For example, for 700µL/min, recirculation uses 85% less sample volume at a reduced signal cost of 26%.

Figure 5.

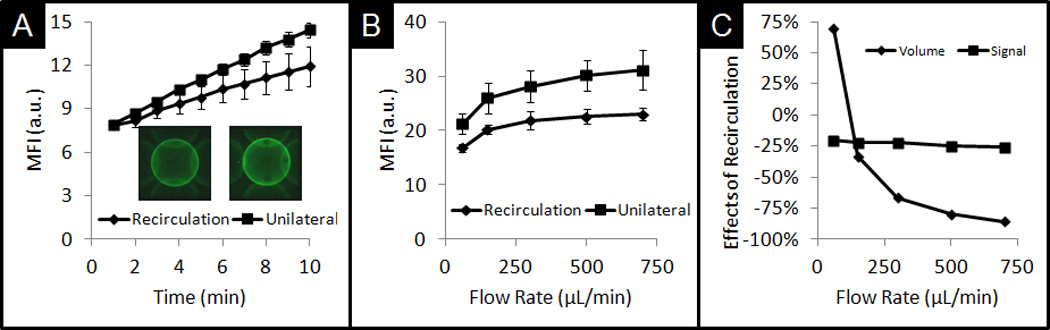
A) Comparison of signal development on bead under recirculation and unilateral conditions with no constraints on volume. B) Comparison of final signal observed after 10min for various flow rates. C) Comparison of signal drop with the use of recirculation and reduced volume needs for various flow rates.

For 700µL/min, only 1mL of sample is needed for recirculation, while 7mL of sample is needed for unilateral delivery. Higher flow rates equate to more capture under both delivery modes. However, as flow rate increases, the differences in signal capture between these two modes increase. While higher flow rates equate to more cycles, under recirculation, the total CRP concentration in the sample decreases, leading to diminishing gains in antigen capture.

Conclusion

Whereas ELISA can take between 2 to 12hr for incubation, microfluidics offers benefits of shorter assay times with smaller sample volumes. With more efforts directed towards point-of-care diagnostics, an understanding of the response of sensing elements under low volume and time constraints is crucial to improve the development of assays. Yet, inefficiencies of capture and diffusive transport occur at the depletion zone in such laminar flow-dominated microfluidic systems. The use of porous beads in the flow-through, bead based system reported here, can alleviate transport inefficiencies at the depletion zone to complete assays within minutes. Further, the positioning of porous beads in individual flow-through containers enables the use of image-based approach of regional pixel analysis of the interrogation zones to allow for multiple biomarker recognition.

A thorough understanding of assay conditions for the optimization of porous bead-based point-of-care devices is needed in order to fully take advantage of these benefits. Here, experimental immunoassay findings using AlexaFluor®488 labelled CRP antigen, in conjunction with computational fluid dynamics, reveal both external and internal saturation regimes with variations in their apparent binding kinetics. Further, the resultant temporal and spatial distribution of capture of analytes is a function of delivery rates. We found that under unilateral flow with constrained sample volume and assay time, an optimal flow rate exists for optimal signal development, such that the entire sample is depleted in the allotted time. Since higher internal flow and capture exists for higher delivery rates, recirculation can be implemented in the system to increase analyte capture. Recirculation offers benefits over unilateral delivery with slightly reduced total capture at significantly reduced sample volumes. While the fluids described here were delivered externally, for the POC device, we envision on-card storage of buffers and reagents and manual insertion of the sample into the device. Pressure-driven motors will deliver the fluids to the bead array.