Abstract
The Dirichlet process is used to model probability distributions that are mixtures of an unknown number of components. Amino acid frequencies at homologous positions within related proteins have been fruitfully modeled by Dirichlet mixtures, and we use the Dirichlet process to derive such mixtures with an unbounded number of components. This application of the method requires several technical innovations to sample an unbounded number of Dirichlet-mixture components. The resulting Dirichlet mixtures model multiple-alignment data substantially better than do previously derived ones. They consist of over 500 components, in contrast to fewer than 40 previously, and provide a novel perspective on the structure of proteins. Individual protein positions should be seen not as falling into one of several categories, but rather as arrayed near probability ridges winding through amino acid multinomial space.
Key words: alignment, computational molecular biology, dynamic programming, multiple alignment, sequence analysis
1. Introduction
Given a multiple alignment of sequences from a particular protein family, how may one estimate the amino acid frequencies found in related sequences at a specific alignment position, and thereby construct scores for adding a new sequence to the alignment? An elegant Bayesian approach to this problem was proposed in the 1990s by researchers at University of California at Santa Cruz (UCSC) (Brown et al., 1993; Sjölander et al., 1996). In brief, one may model a particular position in a particular protein family by an unknown set of 20 amino acid probabilities, a point in the multinomial space Ω20. Given a prior probability density P over Ω20, Bayes' theorem implies a posterior density P′ after the observation of several amino acids at the position in question. An estimate 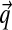 for the amino acid frequencies of the protein family at this position may then be derived by integrating P′ over Ω20. Although the prior density P may be of arbitrary form, it is mathematically convenient if P is assumed to be a Dirichlet distribution or a mixture of M Dirichlet distributions.
for the amino acid frequencies of the protein family at this position may then be derived by integrating P′ over Ω20. Although the prior density P may be of arbitrary form, it is mathematically convenient if P is assumed to be a Dirichlet distribution or a mixture of M Dirichlet distributions.
As the number of observed amino acids at a position grows, 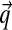 converges to the observed frequencies, no matter what the prior P is. However, given a small number of observations,
converges to the observed frequencies, no matter what the prior P is. However, given a small number of observations, 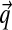 will in general be a better estimate of the actual probabilities at the protein position if the prior P accurately describes the density over Ω20 characteristic of real protein families. Discovering such a P given data is a problem of posterior inference. One starts with a large “gold standard” dataset S of protein multiple alignments, which are assumed to be accurate. Each “column” from these multiple alignments represents a particular position within a particular protein family, and it is really these columns that may be considered as constituting the dataset. One then seeks the maximum-likelihood Dirichlet mixture (DM).
will in general be a better estimate of the actual probabilities at the protein position if the prior P accurately describes the density over Ω20 characteristic of real protein families. Discovering such a P given data is a problem of posterior inference. One starts with a large “gold standard” dataset S of protein multiple alignments, which are assumed to be accurate. Each “column” from these multiple alignments represents a particular position within a particular protein family, and it is really these columns that may be considered as constituting the dataset. One then seeks the maximum-likelihood Dirichlet mixture (DM).
One immediate problem arises. The likelihood of S may in general be improved by increasing the number of components of a DM until it roughly equals the number of columns in S. Doing so, however, leads to the classic problem of overfitting the data, which causes degraded predictions on new data. One solution is to apply the Minimum Description Length principle (Grünwald, 2007), and seek instead to minimize the “total description length” COMP( ) + DL(S|θ) (Ye et al., 2011b).a The first term of this expression is the “complexity” of the model
) + DL(S|θ) (Ye et al., 2011b).a The first term of this expression is the “complexity” of the model 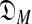 consisting of all M-component DMs; this can be understood as the log of the effective number of independent theories
consisting of all M-component DMs; this can be understood as the log of the effective number of independent theories 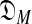 contains (Grünwald, 2007). The second term is the negative log likelihood of S implied by the maximum-likelihood θ drawn from
contains (Grünwald, 2007). The second term is the negative log likelihood of S implied by the maximum-likelihood θ drawn from 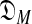 . Although no feasible algorithm for minimizing DL(S|θ) is known, approximations may be found using approaches based on expectation maximization (Brown et al., 1993; Sjölander et al., 1996) or Gibbs sampling (Ye et al., 2011b).
. Although no feasible algorithm for minimizing DL(S|θ) is known, approximations may be found using approaches based on expectation maximization (Brown et al., 1993; Sjölander et al., 1996) or Gibbs sampling (Ye et al., 2011b).
An alternative approach that never fixes M, but treats the number of components as unknown, is possible using nonparametric Bayesian models. One such model is the Dirichlet process (DP), which we apply to multiple-alignment data. In brief, the DP allows us to create a generalized prior probability density over the space of DMs with an unlimited number of components. Posterior inference using a Gibbs sampling algorithm moves naturally among mixture models with varying numbers of components. The DP and its generalization, the Pitman-Yor distribution (Pitman and Yor, 1997), have been applied previously to Gaussian mixtures (Antoniak, 1974), mixtures of multinomials (Hardisty et al., 2010), admixtures of multinomials (Teh et al., 2006), time-dependent mixtures of multinomials (Beal et al., 2002), and mixtures of linear models (Hannah et al., 2011), but not to Dirichlet mixtures. In describing probability densities over ΩL, Dirichlet mixtures have much greater flexibility than do multinomial mixtures. An individual multinomial component can model only probability concentrated at a specific location in ΩL, whereas a single Dirichlet component can model densities that are arbitrarily concentrated around such a location, and even densities with most of their mass near the boundaries of ΩL. The components of a Dirichlet mixture may have probability densities of variable concentration. Thus, for example, one component can favor positions with a fairly precise amino acid probability signature, whereas another can favor positions that contain hydrophobic amino acids, but only one or a small subset of them.
When used to analyze the same dataset for which a previous study (Ye et al., 2011b) yielded a 35-component DM, our DP-based Gibbs sampling algorithm yields substantially improved solutions with over 500 components. Such large DMs may be cumbersome for practical algorithms, but a specified trade-off between component number and total description length can be used to select a DM with fewer components.
Of perhaps greater interest is the perspective on the structure of protein space provided by DMs with many components. The DM formalism suggests, at first, the metaphor of a small number of probability hills in Ω20, corresponding to different types of protein positions—hydrophobic, aromatic, charged, etc. However, the density implied by the many-component DMs we derive is dominated by a continuous probability ridge winding through Ω20. This may provide a new perspective on how selective pressures are felt at individual protein positions.
2. Methods
Here we describe the mathematical underpinnings of our approach, providing a brief review of standard material and devoting more detailed discussion to less familiar or novel methods.
2.1. Multinomial space
A multinomial probability distribution on an alphabet with L letters is a vector with L positive components that sum to 1, and the space of all possible multinomials is the simplex ΩL. Due to the constraints on the vector components, ΩL is finite and has (L−1) degrees of freedom. For example, Ω3 is the two-dimensional equilateral triangle, embedded in Euclidean three-space, with vertices (1,0,0), (0,1,0), and (0,0,1). We will be interested primarily in the standard amino acid alphabet, and therefore in the 19-dimensional space Ω20.
2.2. The Dirichlet distribution
For an alphabet of L letters, a Dirichlet distribution D is a probability density over ΩL, parameterized by an L-dimensional vector 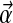 of positive real numbers; it is convenient to define α as
of positive real numbers; it is convenient to define α as 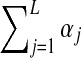 . The density of D at
. The density of D at 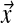 is given by
is given by
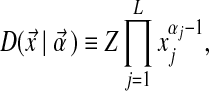 |
(1) |
where the normalizing scalar 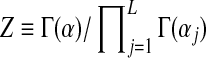 is chosen so that integrating D over ΩL yields 1. The expectation or mean of
is chosen so that integrating D over ΩL yields 1. The expectation or mean of 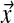 under the density of Equation (1) is the multinomial distribution parameterized by
under the density of Equation (1) is the multinomial distribution parameterized by 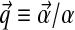 . It is frequently useful to write D's parameters in the form
. It is frequently useful to write D's parameters in the form 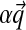 , with
, with 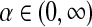 and
and 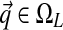 . When we use this alternative parametrization for D, we write it as
. When we use this alternative parametrization for D, we write it as  . Intuitively, one may visualize a Dirichlet distribution as a probability hill in ΩL, centered at
. Intuitively, one may visualize a Dirichlet distribution as a probability hill in ΩL, centered at  , and with greater α corresponding to greater concentration of probability mass near
, and with greater α corresponding to greater concentration of probability mass near  . For α near 0, the “hill” in fact becomes a trough, with most probability concentrated near the boundaries of ΩL. Thus, such Dirichlet distributions favor sparse multinomials, where only a few letters have non-negligible probability (Fig. 1).
. For α near 0, the “hill” in fact becomes a trough, with most probability concentrated near the boundaries of ΩL. Thus, such Dirichlet distributions favor sparse multinomials, where only a few letters have non-negligible probability (Fig. 1).
FIG. 1.
Density plots for four Dirichlet distributions. The densities are over the triangular simplex that represents multinomial distributions over three letters, and demonstrate how different Dirichlet components can accommodate variable concentrations. Darker coloring denotes higher probability density. (a) Dirichlet parameters that are all 1.0 yield a uniform density over multinomial distributions. (b) Dirichlet parameters that are all greater than 1.0 yield a density concentrated near the mean  , in this case (0.6250, 0.0625, 0.3125). (c and d) Dirichlet parameters that are all less than 1.0 yield a density concentrated near the edges and corners of the simplex. Such a density favors sparse multinomials, in which only a subset of letters has appreciable probability. Symmetric (c) and asymmetric (d) cases are shown.
, in this case (0.6250, 0.0625, 0.3125). (c and d) Dirichlet parameters that are all less than 1.0 yield a density concentrated near the edges and corners of the simplex. Such a density favors sparse multinomials, in which only a subset of letters has appreciable probability. Symmetric (c) and asymmetric (d) cases are shown.
2.3. Mixture models
Given a proposed set of observations, a theory may be thought of as assigning probabilities to all possible datasets or outcomes. If a theory has a particular set of adjustable parameters, we call the set of all such theories a model. More generally, we may wish to consider multiple models, usually nested, or characterized by different numbers or sets of parameters.
Mixture models are a formalism frequently used to discover clustering patterns in data. In a mixture model, all observations are associated with clusters, each of which has a corresponding probabilistic mixture “component” that explains its data. For example, multinomial mixture models are frequently used in text analysis (Lewis, 1998).
Multinomial mixtures have difficulty modeling many probability densities over ΩL, because the L – 1 free parameters of an individual multinomial component can only describe probability concentrated at a specific location 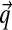 . In contrast, with the addition of the single extra parameter α, a Dirichlet component can describe probability densities of arbitrary concentration around
. In contrast, with the addition of the single extra parameter α, a Dirichlet component can describe probability densities of arbitrary concentration around 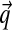 , including, when α is small, densities that favor sparse multinomials (Fig. 1). This greatly enhanced flexibility allows a Dirichlet mixture to model most real-world probability densities over ΩL much better than a multinomial mixture with many times as many components.
, including, when α is small, densities that favor sparse multinomials (Fig. 1). This greatly enhanced flexibility allows a Dirichlet mixture to model most real-world probability densities over ΩL much better than a multinomial mixture with many times as many components.
An M-component DM is a probability density over ΩL, defined as the weighted sum of M Dirichlet distributions, called Dirichlet components. Such a mixture has ML + M – 1 free parameters. Each of the M Dirichlet components contributes L “Dirichlet parameters.” In addition, the weights 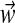 or “mixture parameters” are M positive real numbers that sum to 1, only M – 1 of which are independent. A DM may be thought of as a superposition of M probability hills in ΩL, each with its particular volume, center of mass, and concentration.
or “mixture parameters” are M positive real numbers that sum to 1, only M – 1 of which are independent. A DM may be thought of as a superposition of M probability hills in ΩL, each with its particular volume, center of mass, and concentration.
2.4. The Dirichlet process
When seeking a theory for a set of data, a difficulty is that theories with more parameters generally can explain the data better, but overfitting can result in poor predictions on future data. One approach to this problem is the Minimum Description Length principle (Grünwald, 2007), which explicitly favors theories drawn from mixture models with fewer components (Ye et al., 2011b). An alternative approach is provided by the Dirichlet process (DP), which effectively subsumes in a single formalism mixture models with an arbitrary number of components. A mathematically detailed description of the Dirichlet process (DP) can be found elsewhere (Antoniak, 1974; Pitman and Yor, 1997; Müller and Quintana, 2004); here we will review only its essentials.
The DP generally is applied to problems where data are postulated to be well-modeled as generated by a mixture of multiple instances (often called “atoms” but here called “components”) of an underlying distribution of known parametric form. In the DP formalism, every mixture consists of a countably infinite number of components, each with its own weight and set of component parameters. In essence, a DP defines a generalized probability distribution over this infinite-dimensional space of mixtures.
Two elements completely specify a DP:
1. A “base” probability distribution H over the space of component parameters. For example, if the components are Gaussians on
 with unit variance, H is a specified distribution for their means.
with unit variance, H is a specified distribution for their means.2. A positive real parameter, which implicity defines a probability distribution on component weights. This parameter is usually called α, but we will call it γ here to avoid the potential confusion arising from the multiple distinct uses we make of Dirichlet distributions. As we will see, the smaller γ, the greater the implied concentration of weight in a few components.
Analysis using the DP is Bayesian. A DP is used to define a prior over mixture distributions which, when combined with observed data, implies a posterior for the weights and component parameters of these mixtures. A special feature of this inference is that, although all mixtures are assumed to have a countably infinite number of components, only a finite number can ever explain a given set of data. The posterior distribution thus differs from the prior only for finitely many components. Bayesian analysis allows one to estimate the number of these components, as well as their associated weights and component parameters.
2.5. The Chinese restaurant process
The “Chinese restaurant process” (CRP) (Ferguson, 1973) is closely related to the Dirichlet process and is useful for understanding the properties of the DP, as well as for posterior inference. The metaphor in the name refers to a restaurant with an unbounded number of tables.
The Chinese restaurant is patronized by customers. Each customer represents an i.i.d. draw from a distribution G drawn from a Dirichlet process DP(γ,H).b Each customer sits at one of the tables, and when customers sit at the same table it means they are associated with the same component, drawn from the base distribution H. In our application, a customer represents a multiple-alignment column, and a table represents a DM component,  .
.
Draws from the Dirichlet process are exchangeable (Aldous, 1985), so each customer can be viewed as the “last” customer to enter the restaurant. When customers enter, they choose to sit either at a new table or at one that is already occupied. This choice is made randomly, but with each occupied table selected with probability proportional to the number of people already seated there and a new table selected with probability proportional to the parameter γ. It is evident that smaller values for γ imply a greater concentration of customers at a small number of tables.
The exchangeability of the Dirichlet process is important for Gibbs sampling inference, because it allows us to condition one column's component assignment on the other columns' assignments.
2.6. A base distribution for Dirichlet-component parameters
Specifying a DP for Dirichlet mixtures requires specifying a base distribution H over the space of Dirichlet parameters. Rather than defining H on the standard Dirichlet parameters 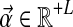 , we find it more natural to define it on the alternative parameters
, we find it more natural to define it on the alternative parameters 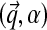 . Specifically, we propose H ≡ (H1, H2), where H1 and H2 are independent distributions for
. Specifically, we propose H ≡ (H1, H2), where H1 and H2 are independent distributions for 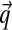 and α.
and α.
Because 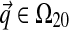 , a natural base distribution H1 for
, a natural base distribution H1 for 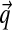 is itself Dirichlet. Furthermore, because we seek a DM that describes protein columns, it is appropriate to choose H1's center of mass to be
is itself Dirichlet. Furthermore, because we seek a DM that describes protein columns, it is appropriate to choose H1's center of mass to be 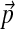 , the “background” amino acid frequencies typical for proteins. This leaves only the single concentration parameter, which we will call β. In short, we propose choosing H1 to be the Dirichlet distribution with parameters (
, the “background” amino acid frequencies typical for proteins. This leaves only the single concentration parameter, which we will call β. In short, we propose choosing H1 to be the Dirichlet distribution with parameters (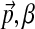 ).
).
When specifying H2, the base distribution for 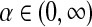 , we will see that it is convenient if we require H2 to have a long, uninformative tail. An exponential function of the form H2 ≡ λe−λα, with λ small, serves the purpose, and the precise value of λ will be irrelevant.
, we will see that it is convenient if we require H2 to have a long, uninformative tail. An exponential function of the form H2 ≡ λe−λα, with λ small, serves the purpose, and the precise value of λ will be irrelevant.
By choosing 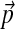 as the center of mass for H1, and requiring H2 to have a long tail, the base distribution H ≡ (H1, H2) we propose for Dirichlet-component parameters has, in effect, only the one free parameter β, as results are insensitive to the choice of λ. This, in conjunction with the parameter γ, completes our specification of a DP for Dirichlet mixtures. We will discuss in the Results section the effects of different choices for β and γ.
as the center of mass for H1, and requiring H2 to have a long tail, the base distribution H ≡ (H1, H2) we propose for Dirichlet-component parameters has, in effect, only the one free parameter β, as results are insensitive to the choice of λ. This, in conjunction with the parameter γ, completes our specification of a DP for Dirichlet mixtures. We will discuss in the Results section the effects of different choices for β and γ.
2.7. Model
To review, we posit the following generative process for observed data:
• We draw component
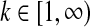 of the Dirichlet process from the base distribution; this draw has two parts:
of the Dirichlet process from the base distribution; this draw has two parts:– the component's mean
 is sampled from Dirichlet(
is sampled from Dirichlet(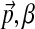 );
);– the component's concentration αk is sampled from Exponential(λ), which is equivalent to a gamma distribution with shape = 1 and rate = λ.
• We draw weights
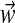 for all of the Dirichlet process components from GEM(γ).c
for all of the Dirichlet process components from GEM(γ).c• For each column
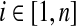 :
:– We draw a component assignment zi from the distribution
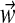 ;
;– We draw a multinomial distribution
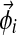 over letters from Dirichlet(
over letters from Dirichlet(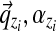 );
);– We draw the letters of column i from Multinomial(
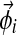 ), resulting in the observation vector
), resulting in the observation vector 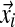 , with associated letter count vector
, with associated letter count vector 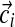 .
.
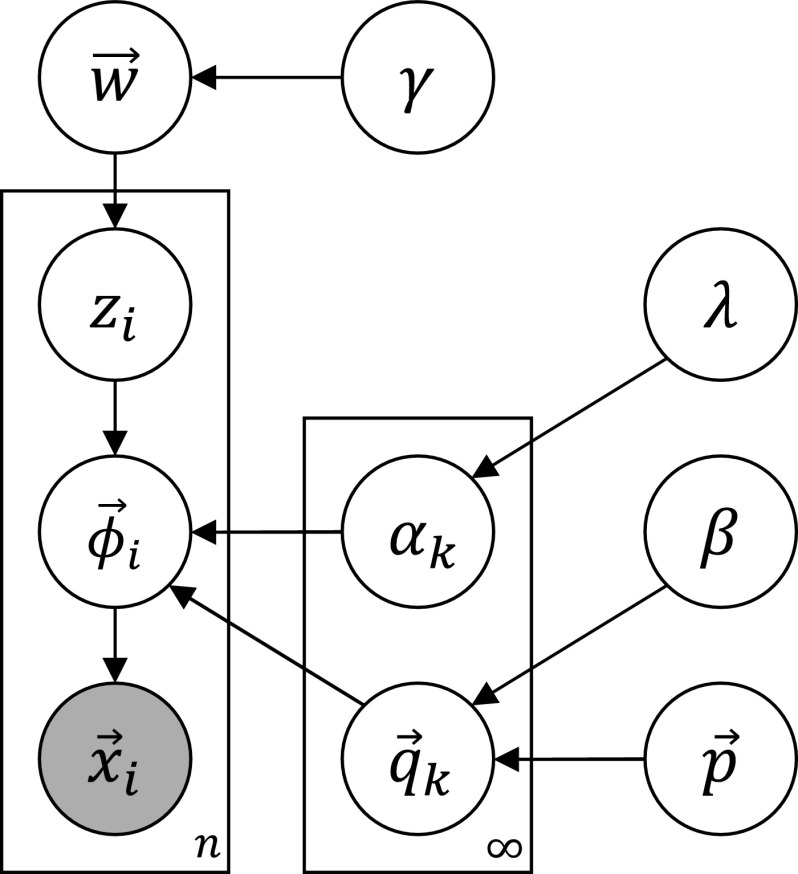
We assume that this process created the observed columns and uses posterior inference, described in the rest of the section, to uncover the latent variables that best explain the observed data. The generative process may be expressed using the graphical model in Figure 2.
FIG. 2.
Graphical model representing the Dirichlet process Dirichlet mixture model proposed in this article. Nodes represent variables, shaded nodes are observed, edges show probabilistic dependencies, and plates denote replication.
At this point, we pause to recognize that our terminology has potential confusions. Our model has three different uses of the word “Dirichlet.” One is a Dirichlet process, and two are ordinary Dirichlet distributions:
• At the top level, a Dirichlet process gives us a countably infinite number of components. This is a nonparametric Bayesian distribution over distributions.
• Each component k of the Dirichlet process is itself a Dirichlet distribution, parameterized by (
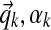 ). This is a finite distribution over Ω20. Columns are generated from a multinomial drawn from this distribution.
). This is a finite distribution over Ω20. Columns are generated from a multinomial drawn from this distribution.• The mean of each component's Dirichlet distribution is itself drawn from a Dirichlet distribution parameterized by (
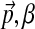 ).
).
2.8. MCMC inference for Dirichlet process Dirichlet mixtures
The Gibbs sampling algorithm for DMs described in Ye et al. (2011b) assumed a fixed number of components M. The algorithm alternated between a first stage, in which the component assignments zi for columns were chosen by Gibbs sampling, conditioned on the complete set of component parameters, and a second stage, in which each component's parameters were updated using maximum-likelihood estimates based on the columns associated with that component. Our approach here, although similar in many ways, has a few key differences.
Like the previous approach, our Gibbs sampler forms a Markov chain over assignments to components 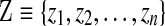 and component parameters
and component parameters 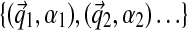 . However, unlike the previous approach, the number of components is not fixed. Components can be both lost and created, but only finitely many components are ever used to describe a given dataset. Specifically, before being assigned stochastically to a new component, by means of the latent variable zi, a column i is first removed from an existing one, and if this component is left with no associated columns, it is abolished. Then, for the column's new assignment, it may choose among the existing components, but it may also start a new one. Unlike in Ye et al. (2011b), this sampling is conditioned on the current component assignments of all other columns rather than on those assignments only from the previous round. During the algorithm's second stage, we sample component parameters rather than update them by maximum-likelihood estimation. There are various ways in which one may initialize the algorithm, but the simple expedient of assigning all columns to a single component at the start does not appear to cause any difficulties. We describe in greater detail below various technical aspects of these modifications to the algorithm of Ye et al. (2011b).
. However, unlike the previous approach, the number of components is not fixed. Components can be both lost and created, but only finitely many components are ever used to describe a given dataset. Specifically, before being assigned stochastically to a new component, by means of the latent variable zi, a column i is first removed from an existing one, and if this component is left with no associated columns, it is abolished. Then, for the column's new assignment, it may choose among the existing components, but it may also start a new one. Unlike in Ye et al. (2011b), this sampling is conditioned on the current component assignments of all other columns rather than on those assignments only from the previous round. During the algorithm's second stage, we sample component parameters rather than update them by maximum-likelihood estimation. There are various ways in which one may initialize the algorithm, but the simple expedient of assigning all columns to a single component at the start does not appear to cause any difficulties. We describe in greater detail below various technical aspects of these modifications to the algorithm of Ye et al. (2011b).
2.9. Sampling an existing or new component for a column
Our DP-sampling algorithm creates a Markov chain of component assignments and component parameters. While sampling component assignments, we assume that the Dirichlet parameters 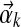 associated with an existing component k remain fixed. However, the number of columns nk associated with component k may change.
associated with an existing component k remain fixed. However, the number of columns nk associated with component k may change.
Gibbs sampling conditions a column's assignment zi on the other columns' assignments and the component parameters. This is where the exchangeability of the Chinese restaurant process (Section 2.5) is advantageous. Computing the conditional distribution is equivalent to removing column i from its current component and then assigning it to an existing component or a completely new one. Assuming the observations 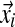 of column i contain ci total amino acids, with the amino acid counts given by the vector
of column i contain ci total amino acids, with the amino acid counts given by the vector 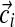 , the likelihood for an existing component k is proportional to
, the likelihood for an existing component k is proportional to
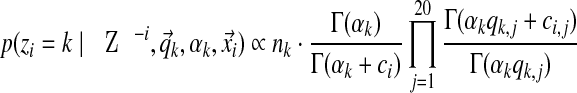 |
(2) |
(Brown et al., 1993; Sjölander et al., 1996; Altschul et al., 2010; Ye et al., 2011b). Here, Z−i denotes the set of component assignments for all columns except column i. In the Chinese restaurant metaphor, this corresponds to sitting at an existing table.
In addition to being associated with an existing table, there is also a probability of sitting at a new table; this happens with probability proportional to γ. Because this is a new table, the component parameters are unknown; however, we still must calculate the probability of the column's observations  . The proper Bayesian approach is to integrate this likelihood over all possible Dirichlet distributions
. The proper Bayesian approach is to integrate this likelihood over all possible Dirichlet distributions  , given the base distribution H ≡ (H1, H2), so that
, given the base distribution H ≡ (H1, H2), so that
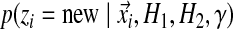 |
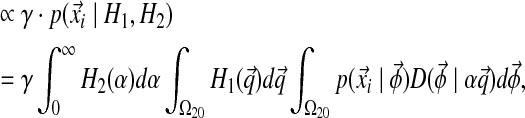 |
(3) |
where p( ) is the probability of observing column i given the multinomial distribution
) is the probability of observing column i given the multinomial distribution  .
.
This is where our choice of H2 is first advantageous. Because H2 is a function that decays very slowly in α, almost all of the mass of such a density is contributed by large α, for which the corresponding Dirichlet distributions can be considered delta functions at 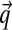 . This reduces the right side of Equation (3) to
. This reduces the right side of Equation (3) to
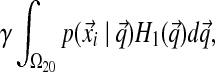 |
(4) |
which, analogously to before (Brown et al., 1993; Sjölander et al., 1996; Altschul et al., 2010; Ye et al., 2011b), is just the probability of observing the amino acid vector  given the Dirichlet distribution (
given the Dirichlet distribution (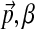 ) over multinomials. Thus,
) over multinomials. Thus,
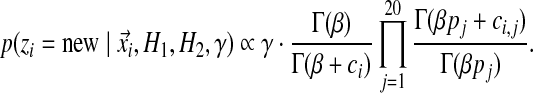 |
(5) |
Given Equation 2 and Equation 5, we may now sample column i into an existing or a new component. If a new component is selected, our final problem is how to assign it a set of Dirichlet parameters. Here, we simply use the sampling method described in the next section but applied to a component with only a single associated column.
2.10. Sampling Dirichlet component parameters
In addition to sampling column assignments, we must also sample the Dirichlet component parameters 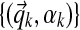 . As in prior work (Ye et al., 2011b), we take a coordinate-wise approach for sampling these parameters: for each component k, first sampling
. As in prior work (Ye et al., 2011b), we take a coordinate-wise approach for sampling these parameters: for each component k, first sampling 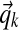 and then sampling αk.
and then sampling αk.
We sample 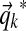 from a Dirichlet distribution with parameters
from a Dirichlet distribution with parameters 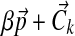 , where
, where 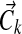 is the aggregate observation vector, summing over all columns associated with component k. This approximates the true posterior of
is the aggregate observation vector, summing over all columns associated with component k. This approximates the true posterior of  under the maximal path assumption (Wallach, 2008).
under the maximal path assumption (Wallach, 2008).
Given our sampled 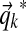 , the column data yields an analytic formula for the log-likelihood function
, the column data yields an analytic formula for the log-likelihood function 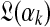 as a function of αk, as well as for its first and second derivatives (Minka, 2000; Ye et al., 2011b). If, as suggested above, the prior on αk takes the form λe−λαk then the posterior log-likelihood is, up to a constant,
as a function of αk, as well as for its first and second derivatives (Minka, 2000; Ye et al., 2011b). If, as suggested above, the prior on αk takes the form λe−λαk then the posterior log-likelihood is, up to a constant,  . Assuming λ is small permits us to ignore the second term and to sample
. Assuming λ is small permits us to ignore the second term and to sample 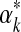 with reference only to
with reference only to 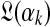 . For certain special cases,
. For certain special cases, 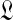 has a supremum at 0 or ∞, and in these instances one may set
has a supremum at 0 or ∞, and in these instances one may set 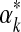 respectively to a fixed small or large number. (In either case, the likelihood subsequently implied for amino acid count vectors is insensitive to the precise value chosen for
respectively to a fixed small or large number. (In either case, the likelihood subsequently implied for amino acid count vectors is insensitive to the precise value chosen for 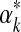 .) Otherwise, it has been postulated but not proven (Ye et al., 2011b) that
.) Otherwise, it has been postulated but not proven (Ye et al., 2011b) that 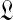 has a unique maximum at
has a unique maximum at 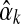 , which it is easy to locate using Newton's method. If
, which it is easy to locate using Newton's method. If 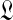 's second derivative at
's second derivative at 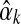 is –X, we can use the Laplace approximation to sample
is –X, we can use the Laplace approximation to sample 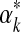 from a normal distribution with mean
from a normal distribution with mean 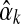 and variance 1/X.
and variance 1/X.
2.11. Refinements to inference
While the above methods were used to generate the results reported in Section 3 up to Section 3.3, we describe here alternative methods for those interested in more refined inference techniques that allow a joint search over more of the model's parameters.
In Section 3, we employ a grid search to determine the Dirichlet process parameter γ that optimizes the Minimum Description Length (MDL), an objective function previously proposed for Dirichlet mixture models used in computational biology (Ye et al., 2011b). Alternative objective functions could be classification performance, interpretability, or biological plausibility.
The objective function of likelihood can be optimized with approximate inference or, more specifically, using slice sampling (Neal, 2003). Slice sampling is a general MCMC algorithm to draw random samples from an unknown probabilistic distribution by sampling uniformly from the region under the variable's density function. In our case, we would like to sample the hyperparameter γ from p(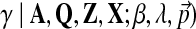 .d This density is proportional to the data likelihood p
.d This density is proportional to the data likelihood p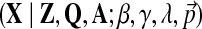 , where
, where
• X =
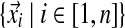 denotes all observed amino acid columns.
denotes all observed amino acid columns.• Z =
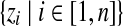 denotes the component assignments for all columns.
denotes the component assignments for all columns.• Q =
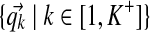 denotes the centers of mass for all components.
denotes the centers of mass for all components.• A =
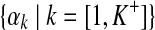 denotes the concentration parameters for all components.
denotes the concentration parameters for all components.
Here, K+ is the current number of components.e This density can be rewritten as:
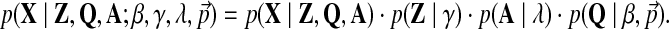 |
(6) |
The right-hand side of Equation 6 consists of the following factors:
• The likelihood of tables' parameters given the observed columns:
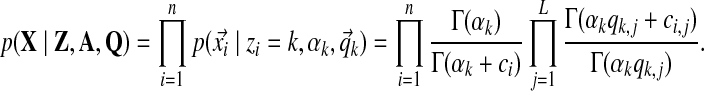 |
(7) |
• The joint distribution of table assignments:f
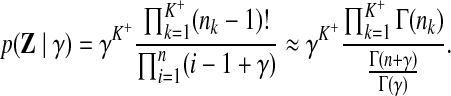 |
(8) |
Note that nk is the number of columns currently assigned to table k, and n is the total number of columns. The expression in Equation 8 is exact when γ is an integer.
• The likelihood of λ given the current values of concentration parameters A:
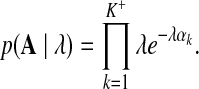 |
(9) |
• The likelihood of β given the current values of centers of mass Q:
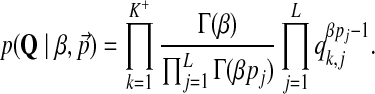 |
(10) |
The detailed pseudo-code of the slice sampling used is shown in Algorithm 1 (Wallach, 2008). The algorithm requires two inputs: (1) R is the number of iterations and is typically set to 10, and (2) σ is the step size and set to one tenth the current value of γ. For notational convenience, we use (γleft, γright) to denote the range around γ we sample from, and use f (γ) to denote p(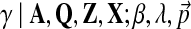 ).
).
| Algorithm 1: Pseudo-code for slice-sampling algorithm used. |
|---|
| Input: R: number of iterations. σ: step size. |
| Initialize γ |
foreach do do
|
| Draw u∼ Uniform(0, f (γ)); |
| Draw v ∼ Uniform(0, 1) |
| γleft ← γ−vσ |
| γright ← γleft + σ |
| while true do |
| Draw γ′∼ Uniform(γleft, γright) |
| iff (γ′) > uthen |
| break; |
| else |
| ifγ′ < γthen |
| γleft ← γ′ |
| else |
| γright ← γ′ |
3. Results
The research group at UCSC that first proposed Dirichlet mixtures for protein analysis currently makes a number of multiple-alignment datasets available on their web site, http://compbio.soe.ucsc.edu/dirichlets/index.html. We consider their dataset “diverse-1216-uw,” called SUCSC here, which was studied also in Ye et al. (2011b). SUCSC consists of 23,903,805 amino acids arranged into 314,585 columns, and thus containing a mean of approximately 76.0 amino acids per column.
3.1. The quality of Dirichlet mixtures
It is useful to have an objective measure for the quality of a DM, and for this purpose we turn to the MDL principle (Grünwald, 2007), whose essentials we review here.
One may define the description length of a dataset S, given a theory θ, as DL(S|θ) ≡−log2
Pθ(S), i.e., the negative log of the probability for the dataset implied by the theory. Because the logarithm is to the base 2, DL is said to be expressed in bits. This definition may be extended to a model  by defining
by defining 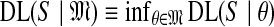 .
.
If one wishes to find the model that best describes a set of data, using DL alone as a criterion is problematic because, for nested models, increasing the number of parameters can only decrease DL. Accordingly, MDL theory introduces the formal concept of the complexity of a model COMP( ) (Grünwald, 2007), which may be thought of, intuitively, as the log of the effective number of independent theories the model contains. The MDL principle then asserts that the model best justified by a set of data is that which minimizes COMP(
) (Grünwald, 2007), which may be thought of, intuitively, as the log of the effective number of independent theories the model contains. The MDL principle then asserts that the model best justified by a set of data is that which minimizes COMP( )+DL(
)+DL(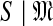 ). In essence, the principle supports a theory drawn from a model of greater complexity only when this increased complexity is offset by a sufficient decrease in data description length.
). In essence, the principle supports a theory drawn from a model of greater complexity only when this increased complexity is offset by a sufficient decrease in data description length.
To select among Dirichlet mixture models 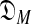 with a variable number M of components using the MDL principle, one must be able to at least approximate both COMP(
with a variable number M of components using the MDL principle, one must be able to at least approximate both COMP(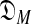 ) and DL(
) and DL(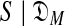 ). Heuristic arguments (Ye et al., 2011b) have extended to COMP(
). Heuristic arguments (Ye et al., 2011b) have extended to COMP(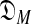 ) an analytic formula for the complexity of a single-component Dirichlet model (Yu and Altschul, 2011). Calculating DL(
) an analytic formula for the complexity of a single-component Dirichlet model (Yu and Altschul, 2011). Calculating DL(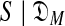 ) entails finding the maximum-likelihood M-component DM. This is an instance of the classic hard problem of optimization within a rough but correlated high-dimensional space, and approximation algorithms have been based on expectation maximization (EM) (Brown et al., 1993) and Gibbs sampling (Ye et al., 2011b).
) entails finding the maximum-likelihood M-component DM. This is an instance of the classic hard problem of optimization within a rough but correlated high-dimensional space, and approximation algorithms have been based on expectation maximization (EM) (Brown et al., 1993) and Gibbs sampling (Ye et al., 2011b).
For the sake of analysis, we may treat our DP-sampler as simply an improved algorithm for finding DMs that minimize total description length. To evaluate a particular DM, we compare it to the baseline multinomial model in which all amino acids are drawn randomly according to background probabilities 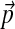 inferred from the data. For this model, the description length of SUCSC is 99,604,971 bits, and the complexity of the model is 206 bits (Ye et al., 2011b), so the total description length can be expressed as 4.1669 bits/amino acid (a.a.). We assess a DM by the decrease Δ (bits/a.a.) in total description length it implies with respect to this baseline, and use Δ as an objective function of mixture quality.
inferred from the data. For this model, the description length of SUCSC is 99,604,971 bits, and the complexity of the model is 206 bits (Ye et al., 2011b), so the total description length can be expressed as 4.1669 bits/amino acid (a.a.). We assess a DM by the decrease Δ (bits/a.a.) in total description length it implies with respect to this baseline, and use Δ as an objective function of mixture quality.
3.2. The optimal number of Dirichlet components
Our DP-sampling procedure does not converge on a unique DM, and selecting different parameters β and γ of course yields different results. However, given a set of real protein multiple-alignment data, the results produced by the procedure after several hundred iterations share various broad qualitative and quantitative features, which we describe here.
At a given iteration, the current DM generated by the DP-sampler typically contains many components to which only a small number of columns are assigned. These components are particularly unstable, and with further iterations tend either to evaporate or to grow in the number of associated columns. In general, they are unsupported by the MDL principle when seeking a DM that maximizes Δ. Thus, after any given iteration, we first arrange the sampler-generated Dirichlet components in decreasing order of their number of associated columns, and then calculate the Δ implied by the DMs consisting of increasing numbers of these components. Although this greedy method does not necessarily identify the optimal subset, it provides a reasonable approximation. Typically, the MDL principle excludes sets of components to which, in aggregate, less than 2% of the columns are associated, with no single excluded component representing more than 0.05% of the columns.
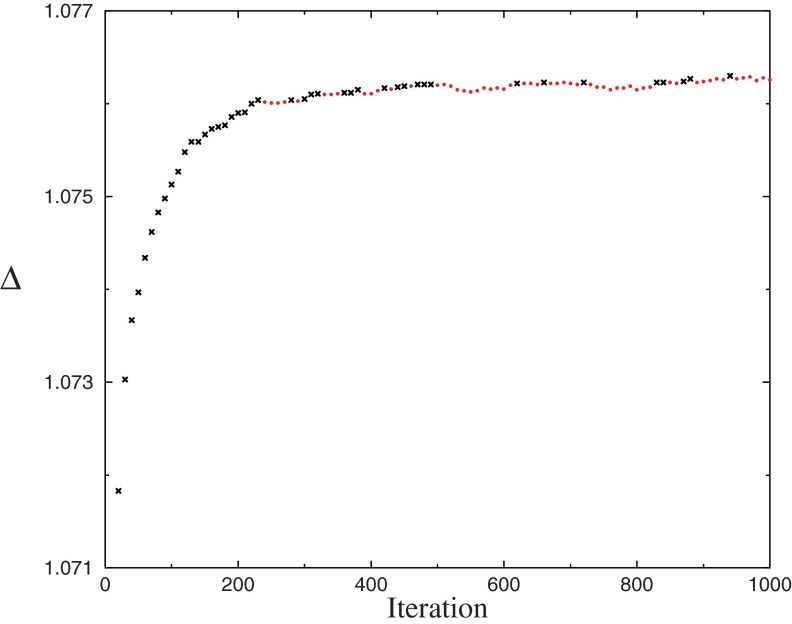
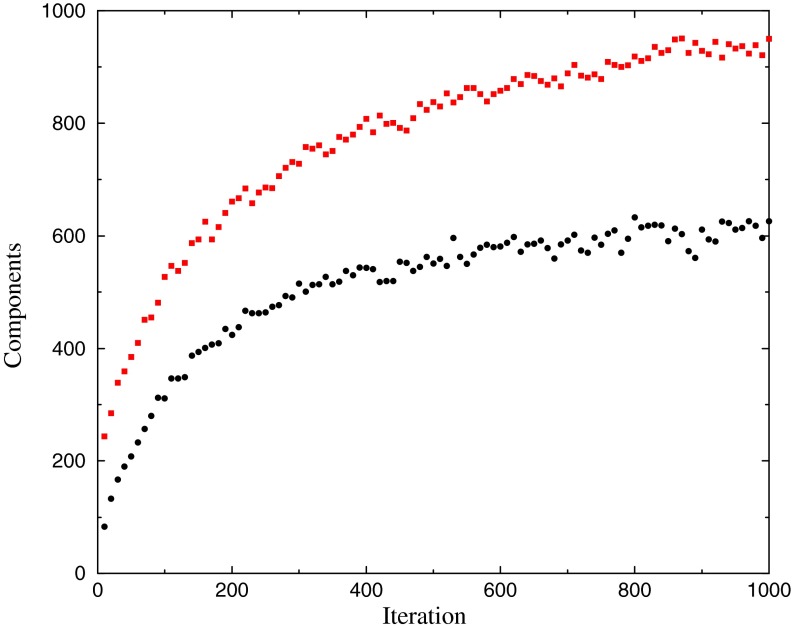
Using a range of settings for the DP parameters β and γ described in the next section, we ran the DP-sampler on SUCSC for 1000 iterations and estimated an optimal Δ after every 10th iteration. Although the best Δ frequently continued to improve past the 900th iteration, its rate of improvement always flattened out much earlier. For example, using parameters β = 400 and γ = 100, we graph in Figure 3 the best Δ found at each iteration, and in Figure 4 the number of components in the associated DM, as well as the total number of components returned. The optimal Δ of 1.0763 bits/a.a., for a 623-component DM found at iteration 940, substantially exceeds the 1.0654 bits/a.a of a 35-component DM achieved by Ye et al. (2011b), as well as the 1.0594 bits/a.a. of the 20-component DM “dist.20comp,” derived from SUCSC, that is reported on the UCSC web site. We will consider below why the DP-sampler returns DMs with so many more components than those found by earlier methods, as well as what the sizes of these DMs imply about the structure of protein space.
FIG. 3.
Δs for Dirichlet mixtures found by the DP-sampler. Using parameters β = 400 and γ = 100, the DP-sampler was run on SUCSC for 1000 iterations. After every 10th iteration, the MDL principle was applied to the components returned, to find a DM with optimal Δ. Black crosses indicate Δs that are greater than those for all previous iterations; red circles, others. For iteration 10, Δ = 1.0666 is off the scale. DP, Dirichlet process; DM, Dirichlet mixture; MDL, minimum description length.
FIG. 4.
Number of Dirichlet mixture components returned. The DP-sampler was run as described in the caption to Figure 3. Red squares show the number of components returned by the DP-sampler after every 10th iteration. Black circles show the number of components in DMs supported by the MDL principle; their corresponding Δs are shown in Figure 3.
3.3. Dependence on Dirichlet-process parameters
The results we obtain depend on the Dirichlet-process parameters β and γ, but their most important qualitative and quantitative features are not very sensitive to these parameters. The Dirichlet process is a Bayesian prior and its particular parameters should thus be outweighed by sufficient data. Nevertheless, it is instructive to consider the practical effects of these parameters.
We ran the DP-sampler as described above using values for β ranging from 100 to 1000, and for γ from 5 to 100, with the results summarized in Table 1. We obtained almost equally high Δs for β from 200 to 800, with γ ≥ 60.
Table 1.
Effect of Dirichlet Process Parameters
| β | γ | Best Δ (bits/a.a.) | Number of components | Iteration found | β | γ | Best Δ (bits/a.a.) | Number of components | Iteration found |
|---|---|---|---|---|---|---|---|---|---|
| 100 | 5 | 1.0756 | 470 | 950 | 600 | 5 | 1.0757 | 361 | 980 |
| 10 | 1.0758 | 520 | 860 | 10 | 1.0760 | 406 | 960 | ||
| 20 | 1.0759 | 644 | 980 | 20 | 1.0762 | 471 | 930 | ||
| 40 | 1.0760 | 689 | 980 | 40 | 1.0762 | 481 | 980 | ||
| 60 | 1.0760 | 720 | 800 | 60 | 1.0763 | 533 | 910 | ||
| 80 | 1.0760 | 717 | 630 | 80 | 1.0762 | 526 | 900 | ||
| 100 | 1.0760 | 808 | 1000 | 100 | 1.0762 | 541 | 780 | ||
| 200 | 5 | 1.0757 | 449 | 1000 | 800 | 5 | 1.0757 | 341 | 1000 |
| 10 | 1.0759 | 498 | 840 | 10 | 1.0759 | 378 | 1000 | ||
| 20 | 1.0761 | 586 | 960 | 20 | 1.0761 | 431 | 960 | ||
| 40 | 1.0761 | 597 | 600 | 40 | 1.0761 | 466 | 830 | ||
| 60 | 1.0762 | 665 | 750 | 60 | 1.0762 | 472 | 830 | ||
| 80 | 1.0762 | 709 | 870 | 80 | 1.0762 | 471 | 730 | ||
| 100 | 1.0762 | 679 | 590 | 100 | 1.0762 | 499 | 760 | ||
| 400 | 5 | 1.0757 | 400 | 980 | 1000 | 5 | 1.0755 | 314 | 1000 |
| 10 | 1.0760 | 452 | 910 | 10 | 1.0758 | 350 | 1000 | ||
| 20 | 1.0762 | 505 | 960 | 20 | 1.0759 | 375 | 990 | ||
| 40 | 1.0763 | 562 | 860 | 40 | 1.0760 | 429 | 860 | ||
| 60 | 1.0763 | 588 | 1000 | 60 | 1.0761 | 433 | 910 | ||
| 80 | 1.0763 | 603 | 990 | 80 | 1.0761 | 447 | 910 | ||
| 100 | 1.0763 | 623 | 940 | 100 | 1.0761 | 444 | 990 |
a.a., amino acids.
The β parameter specifies the concentration of the prior for the 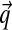 parameters corresponding to each Dirichlet component. When inferring
parameters corresponding to each Dirichlet component. When inferring 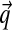 for a particular component, the aggregate amino acid counts from its associated columns are added to β pseudocounts. The columns in SUCSC have a mean of 76 amino acids, so the seemingly large value of β = 400 in fact corresponds to only about five average-composition columns. This is not a very great number when, on average, >500 columns from SUCSC are assigned to each component. Because larger values for β render components with few associated columns less distinctive, they favor mixtures with fewer components, as seen in Table 1.
for a particular component, the aggregate amino acid counts from its associated columns are added to β pseudocounts. The columns in SUCSC have a mean of 76 amino acids, so the seemingly large value of β = 400 in fact corresponds to only about five average-composition columns. This is not a very great number when, on average, >500 columns from SUCSC are assigned to each component. Because larger values for β render components with few associated columns less distinctive, they favor mixtures with fewer components, as seen in Table 1.
For all the β we tested, the best Δ found initially grew with increasing γ, but plateaued by γ = 60. Although larger values for γ favor DMs with more components, the number of components comprising the optimal results found was not very sensitive to the choice of γ. As discussed in the next section, one may avoid specifying a particular γ.
One may prefer DMs with fewer components for algorithmic reasons. In this case, it may be advantageous to use both large β and small γ; this tends to favor DMs with fewer components and thus improve their corresponding Δs. We consider below the tradeoff of Dirichlet mixture size and accuracy.
3.4. Slice sampling γ
To avoid the arbitrariness of specifying a particular value for a DP parameter, or the time involved in testing multiple values, we may use the slice-sampling procedure described above. In brief, after a given iteration of the DP-sampling algorithm, we sample a new value γ′ within a range centered on the current value γ. We then compute the likelihood of the current mixture model with this new γ′. If this likelihood is greater than the likelihood with the current γ, there is a high probability that we will accept this new γ′ and use it in the next iteration.
We implemented this sampling procedure for the DP parameter γ, using an initial value of γ = 50 and a “burn-in” period of 25 iterations before γ is allowed to vary. For β ranging from 200 to 1000, we ran this refined algorithm for 1000 iterations; for β = 100, the program terminated after 323 iterations because the number of components it generated exceeded a limit imposed by memory constraints. In Table 2, we report for each β the mean and standard deviation for γ during the program's last 100 iterations. We also report the optimal Δ found, its corresponding number of components, the iteration yielding this Δ, and the value of γ during this iteration.
Table 2.
The DP-Sampler, with Slice Sampling for γ
| β | Mean and standard deviation of γ | Best Δ (bits/a.a.) | Number of components | Iteration found | γ |
|---|---|---|---|---|---|
| 100 | 199.7 ± 13.0 | 1.0760 | 767 | 280 | 200 |
| 200 | 183.9 ± 6.8 | 1.0762 | 721 | 580 | 166 |
| 400 | 129.6 ± 4.3 | 1.0763 | 608 | 790 | 128 |
| 600 | 95.5 ± 3.9 | 1.0762 | 537 | 930 | 94 |
| 800 | 82.2 ± 3.5 | 1.0762 | 482 | 990 | 83 |
| 1000 | 66.8 ± 2.8 | 1.0760 | 442 | 940 | 69 |
DP, Dirichlet process.
As can be seen, slice sampling converges on a relatively small range of values for γ, and the best Δ found is always within 0.0001 bits/a.a. of the best yielded by the multiple searches shown in Table 1, which employ fixed, specified γ. As before, β≈400 appears optimal, but this conclusion is now reached by a one-parameter rather than a two-parameter search.
One may employ slice sampling to determine β as well as γ, but doing so is problematic. Although we have being using Δ as an objective function for Dirichlet mixtures, the DP-sampler is ignorant of this function, instead sampling mixtures according their posterior likelihood, given the prior imposed by the Dirichlet process. Indeed, the DP-sampler returns mixtures with many more components than supported by the MDL principle, as seen in Figure 4. We have been able to elide this inconsistency because, for fixed β, greater posterior likelihoods for the larger mixtures correlate well with greater values for Δ. This correlation is broken, however, once β may vary. The generalized DP-sampler then prefers small β, yielding mixtures with many components, which are penalized by the model-complexity term of the MDL principle.
3.5. Tradeoff of Δ and the number of Dirichlet components
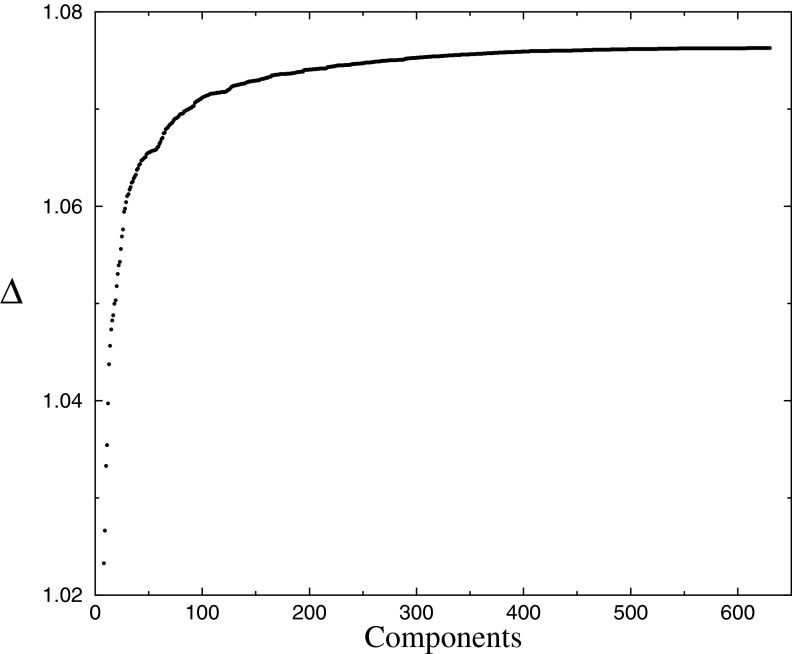
So far we have been concerned only with maximizing Δ. However, DMs are derived for use in profile-sequence, profile-profile, or multiple-alignment programs (Brown et al., 1993; Edgar and Sjölander, 2004; Altschul et al., 2010; Ye et al., 2011a), and in these applications DMs with fewer components have a speed advantage. As seen in Figures 3 and 4, DMs with only slightly suboptimal Δ can have significantly fewer components, and such DMs may well be preferred in certain circumstances.
To study this tradeoff explicitly, we recorded over all iterations of the run described in Figures 3 and 4, as well as the greedy DM-construction procedure described above, the greatest Δ found for DMs with varying numbers of components; the results are shown in Figure 5. A particular application, implementation, and preference for speed versus DM accuracy (i.e., Δ) can be used with such a curve to derive an optimal DM size from a software engineering perspective.
FIG. 5.
Best Δ for a specified number of mixture components. The DP-sampler was run as described in the caption to Figure 3. Shown are the best Δs found, during any iteration, for DMs with a given number of components.
3.6. The topography of protein space
What do the hundreds of Dirichlet components returned by the DP-sampler imply about proteins? To study this question, it is useful to develop a representation of DMs that is easier to comprehend than would be a mere tabulation of thousands of parameters. The approach we take is to represent each component of a DM by a single line of text. On this line, we focus primarily on the component's center-of-mass vector 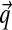 , which we represent by a string
, which we represent by a string 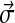 of twenty symbols, although we also report the component's mixture parameter w and concentration parameter α numerically.
of twenty symbols, although we also report the component's mixture parameter w and concentration parameter α numerically.
In constructing the 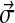 to represent a Dirichlet component, it is useful first to order the amino acids in a manner that corresponds to their mutual similarities, even though any linear arrangement must elide some of these multidimensional relationships. Various orders have previously been proposed (Swanson, 1984; Brown et al., 1993), but our data suggest the order “RKQEDNHWYFMLIVCTSAGP,” using the one-letter amino acid code.
to represent a Dirichlet component, it is useful first to order the amino acids in a manner that corresponds to their mutual similarities, even though any linear arrangement must elide some of these multidimensional relationships. Various orders have previously been proposed (Swanson, 1984; Brown et al., 1993), but our data suggest the order “RKQEDNHWYFMLIVCTSAGP,” using the one-letter amino acid code.
Because within proteins the amino acids occur with widely differing background frequencies pj, it is fruitful to represent a Dirichlet component's mean “target frequencies” qj in relation to the corresponding pj. Accordingly, we base the symbol σj on the implied “log-odds score” sj = log2(qj/pj) according to the following system:
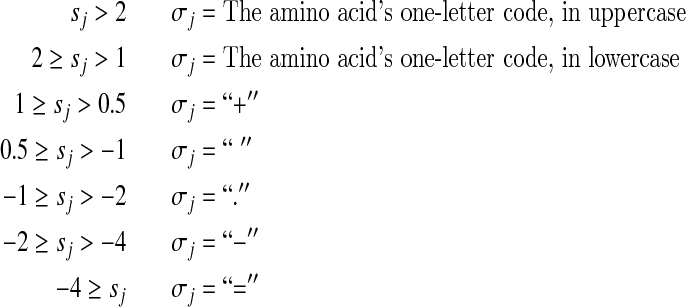 |
In other words, for a particular component, an uppercase letter implies that the frequency of the corresponding amino acid is enriched vis-a-vis background by a factor greater than 4.0, while the symbol “=” means it is decreased by a factor of at least 16. We choose such a positive/negative asymmetry among the categories for defining the σj because 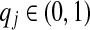 implies an upper bound on sj, but no lower bound.
implies an upper bound on sj, but no lower bound.
As seen in Table 1, the DMs with greatest Δ can have over 600 components. Although we could analyze mixtures of this size, most of their important qualitative features are apparent in mixtures with many fewer components, so we will consider such a smaller DM here. As discussed above, Δ for DMs with fewer components tends to be optimized using relatively large β and small γ. Choosing β = 1000 and γ = 10, and requiring an improvement of at least 4 × 10−5 bits/a.a. in Δ for each additional component, our best result was a 134-component DM with Δ = 1.0732 bits/a.a, which we call θ134. The parameters associated with all components of θ134 are presented in Tables 3–5.
Table 3.
Parameters of θ134: Group A
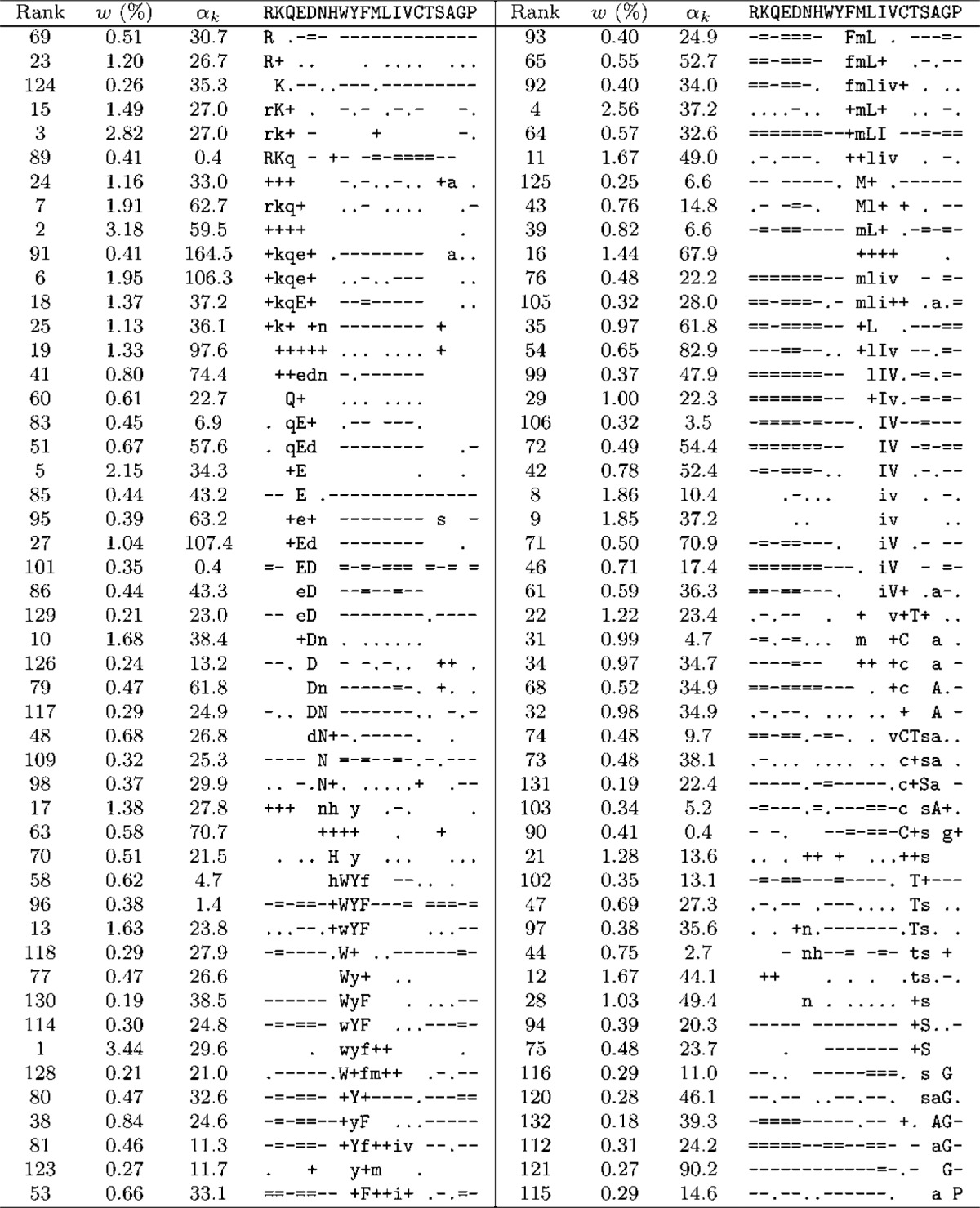 |
Table 5.
Parameters of θ134: Group C
 |
A DM's components may be listed in arbitrary order. One reasonable choice is by decreasing order of mixture parameter w, and in Tables 3–5, we give the rank for each component that such an ordering would yield. However, we have found it instructive to divide θ134's components into three groups and to manually reorder the components of each group in order to elucidate several prominent features of the probability landscape the DM represents. It may be possible to automate such a grouping and ordering using distance measures between Dirichlet distributions (Rauber et al., 2008). Developing such a method would be of interest, but for our present purposes it would provide only a distraction.
Perhaps the most important feature of θ134 is represented by the 98 components of Group A (Table 3). As one moves from one component to the next within this group, the center of mass usually changes only slightly and in a relatively continuous manner. The superposition of the probability hills represented by individual components can thus be visualized as a probability ridge threading its way through Ω20, with several minor spurs.
The second feature of θ134 is represented by the 17 components of Group B (Table 4), which share two main properties: a preference for the amino acids glycine (G) and/or proline (P), and an aversion to hydrophobic amino acids. This group of components can be seen as a secondary ridge, separated from the first.
Table 4.
Parameters of θ134: Group B
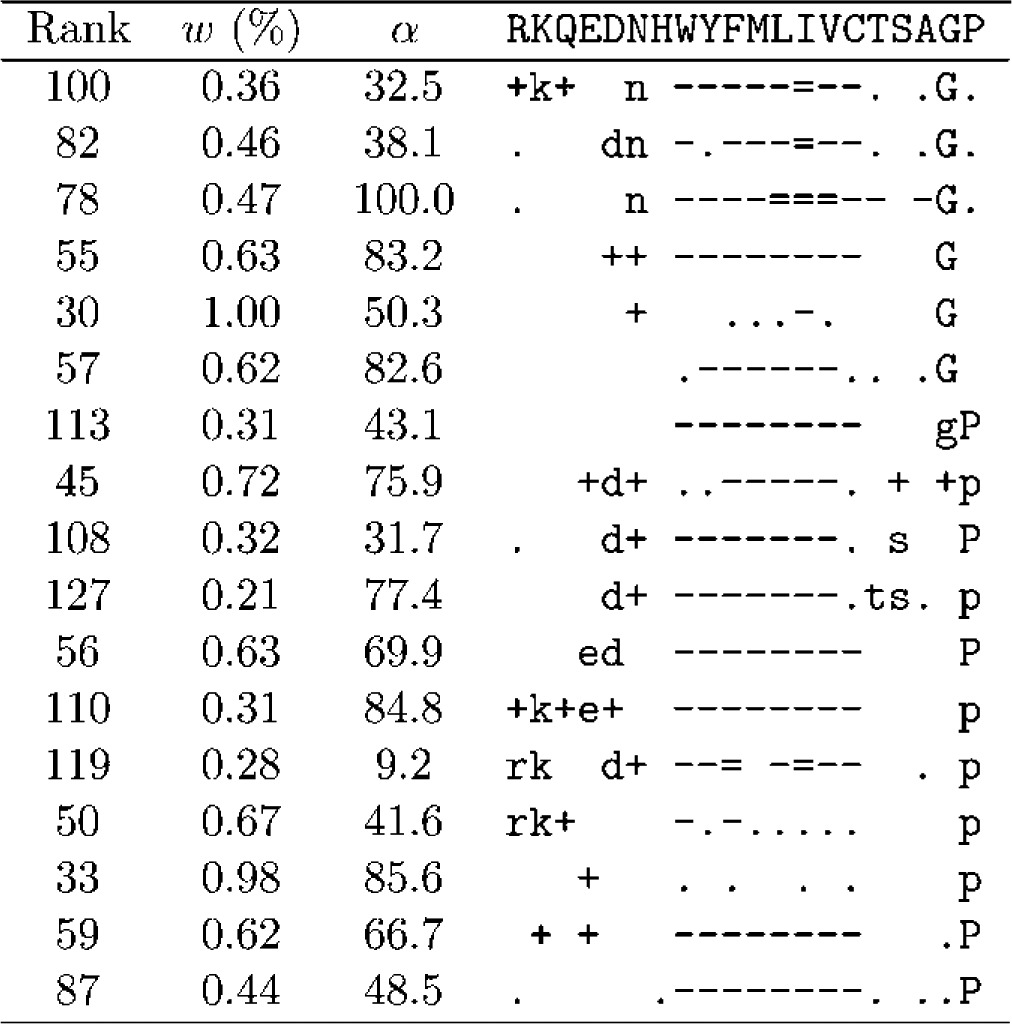 |
A third feature is represented by the 19 components of Group C (Table 5). These components strongly favor a single amino acid, without clear secondary preferences that would attach them to the major ridge of Group A. Of note is the last component in this group, whose concentration parameter α is very close to 0. This implies a probability density concentrated almost completely near the vertices of Ω20. It is a peculiarity of DMs that such densities can be approximated either by a single component with small α and probability mass dominated by several letters, or by the superposition of multiple components each with large α and probability mass dominated by a single letter. Thus this last component can be seen, in essence, as a formal alternative to the type of probability density represented by the other components of Group C.
In general, it may seem surprising that the data will support the identification of the 134 Dirichlet components shown in Tables 3–5, not to mention the >600 components of many DMs with greater Δ. However, the >300,000 columns in SUCSC can associate on average >500 columns to each of 600 components, and this much data is able to support relatively fine distinctions between similar probability densities.
When one compares different mixtures returned by the DP-sampler, the overall shape of the probability densities they describe can be recognized as remarkably similar. In contrast, the parameters of the individual components that go into approximating this shape have no particular stability. For example, a point that is halfway between the crests of two components in one mixture may very well be at the crest of an individual component in another.
4. Conclusion
When a set of data is believed to be well described by a mixture distribution, but with an unknown number of components, the Dirichlet process may be applied to infer the mixture (Blei and Jordan, 2005). Because homologous positions within protein families have been fruitfully described by Dirichlet mixtures (Brown et al., 1993; Sjölander et al., 1996; Altschul et al., 2010), we have sought here to infer such mixtures from multiple-alignment data using a Gibbs sampling algorithm based upon the Dirichlet process. This required us to develop several technical innovations, because the Dirichlet process has not previously been applied to DMs.
In contrast to previous approaches (Brown et al., 1993; Sjölander et al., 1996; Ye et al., 2011b), our DP-sampler yields many hundreds of Dirichlet components when applied to real multiple-alignment data. To understand these results, one should recognize that DMs are employed to model proteins primarily for mathematical as opposed to biological reasons: With Bayesian analysis, the posterior of a DM prior is still a DM (Brown et al., 1993; Sjölander et al., 1996; Altschul et al., 2010). The DM formalism suggests the metaphor of discrete probability hills in Ω20, each representing a category for classifying protein positions. However, the actual probability topography in Ω20 that describes proteins appears to be qualitatively different, having, for example, long probability ridges. To model such features well using Dirichlet components requires a large number of them, with closely spaced centers of mass. Our analysis suggests there is no “correct” number of components or categories for describing the probability distribution over Ω20 implied by proteins. Instead, when the MDL principle is applied, steadily increasing amounts of data should support steadily increasing numbers of components. However, as the number of components grows, there is also steadily diminishing improvement, as measured by Δ, in modeling the underlying probability distribution.
The DP-sampler is able to find DMs that model multiple-alignment data better than do those mixtures found by previously proposed methods. A key to its relative success is its ability to seed new components with columns that are not modeled well by any existing components, but to abandon components that do not then attract other columns. This fosters a much more efficient search of the very high-dimensional Dirichlet-mixture space than does seeding the space with random starting positions.
Although existing multiple-alignment datasets may support DMs with over 500 components, speed considerations may favor smaller mixtures for use in practical sequence comparison algorithms. The DP-sampler can generate mixtures of many different sizes to facilitate such a tradeoff.
At a deeper level, the DP-sampler provides a new perspective on the topography of protein space. This perspective suggests that the amino acid preferences at individual protein positions should, in general, be thought of not as falling into one of several categories, but rather as arrayed along a continuum. These preferences, represented by points in Ω20, fall mainly near a long, almost one-dimensional probability ridge winding through the space. This perspective may suggest interesting questions for further investigation. For example, multiple alignment columns that imply similar high likelihoods for components situated far from one another along the ridge might imply either misalignment or the presence of distinct protein subfamilies within the alignment.
Footnotes
Other validation approaches that are robust to overfitting include held-out perplexity (Blei et al., 2003) or extrinsic evaluation.
Note that the Chinese restaurant does not model a specific measure G; it only models draws from G and integrates over all possible G. However, this representation is sufficient for our purposes. For a constructive definition of the Dirichlet process, see Sethuraman (1994).
The vector 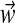 is a point on the infinite simplex (Sethuraman, 1994), and GEM stands for Griffiths (Griffiths, 1980), Engen (Engen, 1975), and McCloskey (McCloskey, 1965). This, along with the separate component draws, form a constructive “stick breaking” definition of the Dirichlet process.
is a point on the infinite simplex (Sethuraman, 1994), and GEM stands for Griffiths (Griffiths, 1980), Engen (Engen, 1975), and McCloskey (McCloskey, 1965). This, along with the separate component draws, form a constructive “stick breaking” definition of the Dirichlet process.
Slice sampling can be applied to more general parameters. A more general alternative would be to slice sample a vector v ≡ (β,γ,λ) (Wallach, 2008).
The superscript + is to denote that the number of components is unbounded and varies during our sampling process.
For detailed derivation of Equation 8, refer to Gershman and Blei (2012).
Acknowledgments
Jordan Boyd-Graber is supported by National Science Foundation grant #1018625. Stephen Altschul is supported by the Intramural Research Program of the National Library of Medicine at the National Institutes of Health.
Disclosure Statement
The authors declare that no competing financial interests exist.
References
- Aldous D. Ecole d'Ete de Probabilities de Saint-Flour XIII 1983. Springer; New York: 1985. Exchangeability and related topics; pp. 1–198. [Google Scholar]
- Altschul S.F. Wootton J.C. Zaslavsky E., et al. The construction and use of log-odds substitution scores for multiple sequence alignment. PLoS Comp. Biol. 2010;6:e1000852. doi: 10.1371/journal.pcbi.1000852. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Antoniak C.E. Mixtures of Dirichlet processes with applications to Bayesian nonparametric problems. Ann. Stat. 1974;2:1152–1174. [Google Scholar]
- Beal M.J. Ghahramani Z. Rasmussen C.E. Adv. Neural Inf. Process. Syst. MIT Press; Cambridge, Massachusetts: 2002. The infinite hidden Markov model. [Google Scholar]
- Blei D.M. Jordan M.I. Variational inference for Dirichlet process mixtures. J. Bayesian Anal. 2005;1:121–144. [Google Scholar]
- Blei D.M. Ng A. Jordan M. Latent Dirichlet allocation. J. Mach. Learn. Res. 2003;3:993–1022. [Google Scholar]
- Brown M. Hughey R. Krogh A., et al. Using Dirichlet mixture priors to derive hidden Markov models for protein families. Proc. First International Conf. on Intell. Syst. for Mol. Biol.; AAAI Press; Palo Alto, CA. 1993. pp. 47–55. [PubMed] [Google Scholar]
- Edgar R.C. Sjölander K. A comparison of scoring functions for protein sequence profile alignment. Bioinformatics. 2004;20:1301–1308. doi: 10.1093/bioinformatics/bth090. [DOI] [PubMed] [Google Scholar]
- Engen S. A note on the geometric series as a species frequency model. Biometrika. 1975;62:697–699. [Google Scholar]
- Ferguson T.S. A Bayesian analysis of some nonparametric problems. Ann. Stat. 1973;1:209–230. [Google Scholar]
- Gershman S.J. Blei D.M. A tutorial on Bayesian nonparametric models. J. Math. Psych. 2012;56:1–12. [Google Scholar]
- Griffiths R. Lines of descent in the diffusion approximation of neutral Wright-Fisher models. Theoretical Population Biol. 1980;17:37–50. doi: 10.1016/0040-5809(80)90013-1. [DOI] [PubMed] [Google Scholar]
- Grünwald P.D. The Minimum Description Length Principle. Vol. 1. The MIT Press; Cambridge, Massachusetts: 2007. MIT Press Books. [Google Scholar]
- Hannah L. Blei D.M. Powell W.B. Dirichlet process mixtures of generalized linear models. J. Mach. Learn. Res. 2011;12:1923–1953. [Google Scholar]
- Hardisty E. Boyd-Graber J. Resnik P. Modeling perspective using adaptor grammars; Proc. Conf. Empirical Methods in Natural Language Processing.2010. [Google Scholar]
- Lewis D.D. Naive (Bayes) at forty: The independence assumption in information retrieval. European Conf. on Mach. Learn.; 1998. pp. 4–15. [Google Scholar]
- McCloskey J. A Model for the Distribution of Individuals by Species in an Environment [Ph.D. thesis] Department of Statistics, Michigan State University; Lansing, MI: 1965. [Google Scholar]
- Minka T.P. Estimating a Dirichlet distribution. Technical report, Microsoft, Redmond; Washington: 2000. [Google Scholar]
- Müller P. Quintana F.A. Nonparametric Bayesian data analysis. Statist. Sci. 2004;19:95–110. [Google Scholar]
- Neal R.M. Slice sampling. Ann. Stat. 2003;31:705–767. [Google Scholar]
- Pitman J. Yor M. The two-parameter Poisson-Dirichlet distribution derived from a stable subordinator. Ann. Probab. 1997;25:855–900. [Google Scholar]
- Rauber T.W. Braun T. Berns K. Probabilistic distance measures of the Dirichlet and Beta distributions. Pattern Recogn. 2008;41:637–645. [Google Scholar]
- Sethuraman J. A constructive definition of Dirichlet priors. Statistica Sinica. 1994;4:639–650. [Google Scholar]
- Sjölander K. Karplus K. Brown M., et al. Dirichlet mixtures: a method for improved detection of weak but significant protein sequence homology. Comput. Appl. Biosci. 1996;12:327–345. doi: 10.1093/bioinformatics/12.4.327. [DOI] [PubMed] [Google Scholar]
- Swanson R. A vector representation for amino acid sequences. Bull. Math. Biol. 1984;46:623–639. doi: 10.1007/BF02460068. [DOI] [PubMed] [Google Scholar]
- Teh Y.W. Jordan M.I. Beal M.J., et al. Hierarchical Dirichlet processes. J. Amer. Statist. Assoc. 2006;101:1566–1581. [Google Scholar]
- Wallach H.M. Structured Topic Models for Language [Ph.D. thesis] University of Cambridge; Cambridge, United Kingdom: 2008. [Google Scholar]
- Ye X. Wang G. Altschul S.F. An assessment of substitution scores for protein profile-profile comparison. Bioinformatics. 2011a;27:3356–3363. doi: 10.1093/bioinformatics/btr565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ye X. Yu Y.-K. Altschul S.F. On the inference of Dirichlet mixture priors for protein sequence comparison. J. Comput. Biol. 2011b;18:941–954. doi: 10.1089/cmb.2011.0040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu Y.-K. Altschul S.F. The complexity of the Dirichlet model for multiple alignment data. J. Comput. Biol. 2011;18:925–939. doi: 10.1089/cmb.2011.0039. [DOI] [PMC free article] [PubMed] [Google Scholar]