BirdcageBuilder: Design of Specified-Geometry Birdcage Coils with Desired Current Pattern and Resonant Frequency

Abstract

A simple method for birdcage coil design (high pass, low pass, and band pass) is presented. Rather than iteratively approaching the Larmor resonant frequency with known capacitances and calculated inductances, a more versatile approach to birdcage coil design is developed and validated, in which the necessary capacitances are calculated using a desired current pattern, a calculated inductance, and a predetermined resonant frequency. In order to expedite coil design for experienced and novice coil builders, a computer program (BirdcageBuilder) is also implemented based on this method. Experimental results show that the calculated capacitances and actual capacitances for several existing birdcage coils are in good agreement.

INTRODUCTION

Birdcage coils (1, 2) have been utilized to generate homogeneous B₁ fields, large imaging volumes, and good signal to noise ratios. Birdcage coils typically include two conducting loops, referred to as end rings (ERs), connected by a number of conducting rungs, referred to as legs. Legs are often distributed equidistantly around the perimeter of the ERs; thus, the ERs are divided into ER segments by the adjacent legs. Capacitors are inserted into these conducting paths (legs or ERs) to achieve resonant modes. A high-pass (HP) coil has distributed capacitors situated on ER segments, while a low-pass (LP) coil has capacitors placed on the legs. A band-pass (BP) coil has capacitors at both locations.

Although birdcage coils are typically constructed by iteratively adjusting capacitances to achieve a desired resonant frequency experimentally, several the-oretical descriptions have been formulated. Joseph presented a mesh eigenvalue method to solve for the resonant frequencies of a double-tuned HP birdcage coil by exploiting a lumped element circuit model (3), and an open coil design was implemented with similar treatment (4). Using transmission line theory, Pascone et al. illustrated a general analysis to accurately predict resonant frequencies for HP and LP birdcage coil designs (5). In another work by Vullo et al., a non-cylindrical birdcage coil design was also demonstrated (6). Recently, treating the coil as a periodic structure, Leifer performed the resonant frequency calculation using discrete Fourier transform of the coupling vectors (7). These previous studies focus on predicting resonant frequencies and corresponding current patterns from known capacitances and calculated inductances. Although this approach demonstrated the accuracy of resonant frequency prediction, it is not efficient because the birdcage coil’s Larmor precession frequency should be a specification in coil design rather than the predicted result; thus, this method requires iteration for coil design. Because the desired current pattern and resonant frequency are known ahead of time and the coil inductances are determined by coil geometry and current pattern, the capacitor values should be the result of the calculation. It is of the utmost importance that choosing the capacitor values as the calculation result allows the user great flexibility in defining the desired current pattern and resonant frequency.

Here a simple and versatile method is presented to calculate the necessary capacitances to achieve the desired field distribution and resonant frequency in birdcage coils. We describe the method for calculating capacitor values for placement in ER segments (8); introduce extensions for calculating capacitor values for placement on legs; and discuss applications for HP, LP, and BP coils. In contrast to methods used in previous studies, with this approach the focus is on capacitance calculations, rather than on prediction of resonant frequencies. A computer program, BirdcageBuilder, was written to implement the method for certain cases and distributed as freeware to benefit NMR practitioners. A comparison of calculated capacitances to capacitor values in existing coils is also presented along with discussion of the accuracy and limitations of the method in its current form.

MATERIALS AND METHODS

Current Pattern and Effective Inductance Calculation

Two key components of our method are the birdcage coil’s desired current pattern and the effective inductance calculations of the coil’s legs and ER segments. The desired current pattern should generate a desired B₁ field distribution inside the birdcage coil. For example, to create a homogeneous B₁ field inside cylindrical birdcage coils, the current pattern on a conducting surface (or discrete legs) should have a sinusoidal dependence on the azimuthal angle of the leg location. Optimal current patterns can also be defined to produce, for example, a homogeneous field in an unshielded elliptical birdcage coil (8) or to create an RF gradient (9) in a birdcage coil with a circular cross section.

Calculations of the effective inductance for conducting elements are vital in the implementation of our circuit analysis. The effective inductance of a conductor includes the self-inductance of the conductor and the mutual inductance between conductors. This method was utilized in our previous work (8, 9), and the essential details are given below. The effective inductance of the conductor was defined by the ratio of the total flux linkage of this conductor divided by its current intensity. For the simple case of two conductors in the same plane with current intensities I₁ and I₂, the effective inductance for conductor one (L₁) can be defined as

$$L_1=\frac{{\mathrm{\Phi }}_1}{I_1}=\frac{L_1^{\text{self}}{I}_1+\mathrm{\delta }{M}_{12}{I}_2}{I_1}=L_1^{\text{self}}+\mathrm{\delta }{M}_{12}\frac{I_2}{I_1}$$ [1]

where Φ₁ is the total flux linkage of conductor one, $L_1^{\text{self}}$ is the self-inductance of conductor one, and M₁₂ is the mutual inductance between conductors one and two. The value of δ is determined by the angle θ between the directions of the currents in two conductors; and δ is equal to −1 for cos(θ) <0, 1 for cos(θ) > 0, and 0 for cos(θ) = 0. Consequently, for k conducting elements, the effective inductance of the nth conductor can be obtained by using the expression

$$L_n=L_n^{\text{self}}+{\displaystyle \sum _{m=1,m\ne n}^k}{\mathrm{\delta }}_{\mathit{\text{nm}}}\left|\frac{I_m}{I_n}{M}_{\mathit{\text{nm}}}\right|$$ [2]

where the subscript n = 1, 2, …, k, the index for each of the k conductors; subscript m = 1, 2, … , k; and M_nm is the mutual inductance between conductors. Experimentally, legs and ERs are often constructed with copper tape, copper tubes, or circuit board; therefore, they are treated as either rectangular or tubular conducting elements in inductance calculations. The self-inductance values of the leg and ER segments can be calculated based on the inductance calculation formulas for tubular or rectangular elements (10).

The mutual inductance calculations of legs and ERs are handled differently. Legs are treated as parallel conductors along the longitudinal direction of coils, and ERs are treated as segments on the transverse plane at the ends of the coil. In this manner mutual inductance between legs can be calculated using a formula for mutual inductance between parallel conducting elements (10). In the presence of a radio frequency (RF) shield, the shield was replaced with mirror images of the legs (3) and subsequently included in the calculations. For ER segments, in order to apply Eq. [2], the current intensity in each segment was first calculated with the given current pattern in the legs using Kirchhoff’s current law. Then the mutual inductance between ER segments can be calculated using mutual inductance formulas for parallel and nonparallel conducting elements (10).

For a shielded birdcage coil with N legs, the effective inductance of the nth leg can be calculated using Eq. [2]. The first term will be obtained from a self-inductance calculation, the second term will involve the mutual inductance calculation between the nth leg and the other N − 1 legs and N leg mirror images, so k in Eq. [2] will be equal to 2N − 1 for calculation of the leg effective inductances. The effective inductance calculation of ER segments was carried out considering only self-inductance and mutual inductance between the N − 1 ER segments on the same ER plane. The mutual inductance between the ER segment and segments on the other ER plane and the mutual inductance between the ER segments and the shield were neglected, so k in Eq. [2] will be equal to N − 1 for calculation of the ER effective inductances. The details of the formulas to perform mutual inductance calculations for the ER segments are found in previous works (8, 10, 11).

Capacitance Calculations

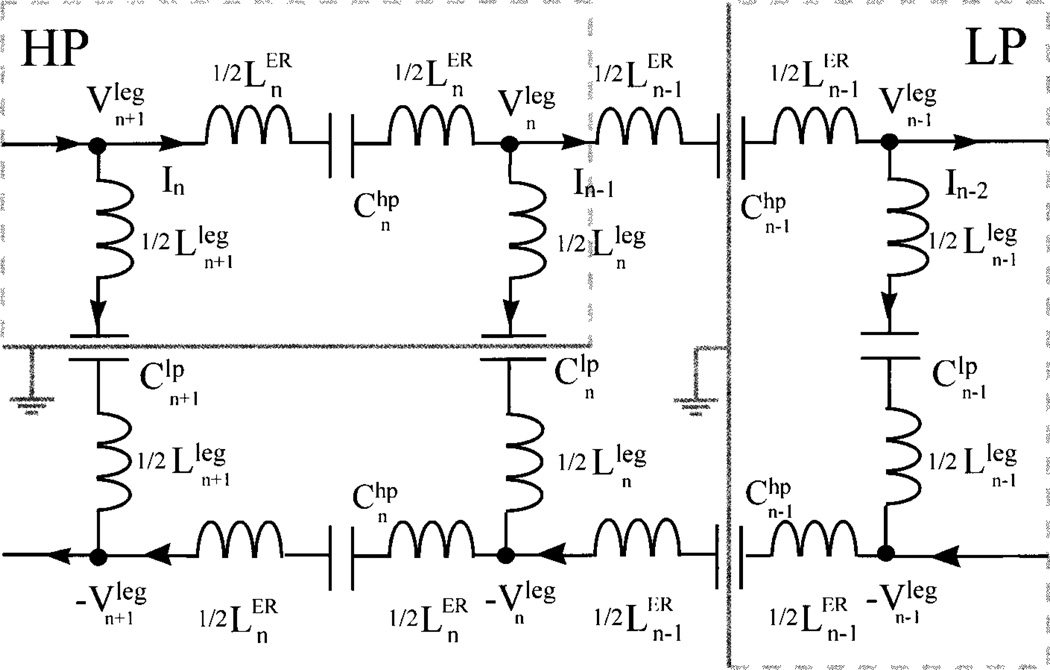
With a desired current pattern in the coil, the calculated effective inductance of the legs and ER segments, and the desired resonant frequency, the necessary capacitances can be calculated by performing lumped circuit analysis using virtual ground assumptions. A lumped circuit model to represent the BP birdcage coil is shown in Figure 1. Using Ohm’s law, the voltage difference across the end points of the nth ER segment ($\mathrm{\Delta }{V}_n^{\text{ER}}$) can be expressed as

$$\mathrm{\Delta }{V}_n^{\text{ER}}=I_n[j\mathrm{\omega }{L}_n^{\text{ER}}+{(j\mathrm{\omega }{C}_n^{\mathit{\text{hp}}})}^{-1}]$$ [3]

where ω is the predetermined resonant angular frequency, $L_n^{\text{ER}}$ is the effective inductance of the nth ER segment, I_n is the nth mesh current, and $C_n^{\mathit{\text{hp}}}$ is the capacitance located on the nth ER segment. The voltage difference across the (n − 1)th leg $(\mathrm{\Delta }{V}_{n-1}^{\text{leg}})$ can be expressed as

$$\mathrm{\Delta }{V}_{n-1}^{\text{leg}}=(I_{n-1}-I_{n-2})[j\mathrm{\omega }{L}_{n-1}^{\text{leg}}+{(j\mathrm{\omega }{C}_{n-1}^{\mathit{\text{lp}}})}^{-1}]$$ [4]

where $L_{n-1}^{\text{leg}}$ is the effective inductance of the (n − 1)th leg and $C_{n-1}^{\mathit{\text{lp}}}$ is the capacitance inserted on the (n − 1)th leg. In the capacitance calculation for a BP birdcage coil, either the capacitances on the legs $(C_n^{\mathit{\text{lp}}})$ or on the ER segments $(C_n^{\mathit{\text{hp}}})$ must be given. Our objective is to calculate the one that is unknown. For an HP coil the C^lp is known to be infinite and for a LP coil the C^hp is known to be infinite.

Figure 1.

A circuit model for a band-pass birdcage coil design. The L_n and $L_n^{\text{ER}}$ are the effective inductances of the nth leg and ER segment, respectively; $C_n^{\mathit{\text{lp}}}$ and $C_n^{\mathit{\text{hp}}}$ are the capacitances on the nth leg and ER segment, respectively; and I_n is the current intensity in the nth loop. The voltage at the end point of the nth leg is $V_n^{\text{leg}}$. When $C_n^{\mathit{\text{lp}}}$ is given, the virtual ground is assumed at the middle of the legs (see the left box labeled HP); if $C_n^{\mathit{\text{hp}}}$ is known, a virtual ground is inserted at the middle of the (n − 1)th ER segments on both ER planes (see the right box labeled LP).

Calculation of ER Capacitors

In the case when the capacitances on the legs $(C_n^{\mathit{\text{lp}}})$ are known, the capacitances on the ER segments $(C_n^{\mathit{\text{hp}}})$ can be calculated (8). To further simplify our circuit analysis, a virtual ground is assumed to be at the middle of all legs. Therefore, the voltage value at the top end point of the nth leg is equal to half of $\mathrm{\Delta }{V}_n^{\text{leg}}$ (see the box labeled HP in Fig. 1).

$$V_n^{\text{leg}}=1/2·(\mathrm{\Delta }{V}_n^{\text{leg}})=1/2·(I_n-I_{n-1})[j\mathrm{\omega }{L}_n^{\text{leg}}+{(j\mathrm{\omega }{C}_n^{\mathit{\text{lp}}})}^{-1}]$$ [5]

By using Eq. [5], the voltage drop across the nth ER segment can be calculated as the voltage difference between end points of the (n + 1)th leg and nth leg, and this result should be equal to the expression in Eq. [3].

$$V_{n+1}^{\text{leg}}-V_n^{\text{leg}}=\mathrm{\Delta }{V}_n^{\text{ER}}=I_n[j\mathrm{\omega }{L}_n^{\text{ER}}+{(j\mathrm{\omega }{C}_n^{\mathit{\text{hp}}})}^{-1}]$$ [6]

Finally, the capacitance on the nth ER segment can be calculated.

$$C_n^{\mathit{\text{hp}}}={[j\mathrm{\omega }/I_n·(V_{n+1}^{\text{leg}}-V_n^{\text{leg}})+{\mathrm{\omega }}^2{L}_n^{\text{ER}}]}^{-1}$$ [7]

Calculation of Leg Capacitances

With a similar approach the capacitances on the legs $(C_n^{\mathit{\text{lp}}})$ can be calculated when the capacitances on the ER segments $(C_n^{\mathit{\text{hp}}})$ are known. Now a virtual ground is assumed at the middle of the (n − 1)th ER segments on both ER planes. Due to symmetry, the voltage values at the end points of the (n − 1)th leg are equal to half of $\mathrm{\Delta }{V}_n^{\text{ER}}$ (see the box labeled LP in Fig. 1).

$$V_{n-1}^{\text{leg}}=-1/2·(\mathrm{\Delta }{V}_{n-1}^{\text{ER}})=-1/2·I_n[j\mathrm{\omega }{L}_{n-1}^{\text{ER}}+{(j\mathrm{\omega }{C}_{n-1}^{\mathit{\text{hp}}})}^{-1}]$$ [8]

Subsequently, the voltage difference across the (n − 1)th leg can be calculated using Eq. [8] and its value should be the same as the expression in Eq. [4].

$$V_{n-1}^{\text{leg}}-(-V_{n-1}^{\text{leg}})=\mathrm{\Delta }{V}_{n-1}^{\text{leg}}=(I_{n-1}-I_{n-2})\times [j\mathrm{\omega }{L}_{n-1}^{\text{leg}}+{(j\mathrm{\omega }{C}_{n-1}^{\mathit{\text{lp}}})}^{-1}]$$ [9]

Then the capacitance on the (n − 1)th leg can be calculated.

$$C_{n-1}^{\mathit{\text{lp}}}={[j\mathrm{\omega }/(I_{n-1}-I_{n-2})·2V_{n-1}^{\text{leg}}+{\mathrm{\omega }}^2{L}_{n-1}^{\text{leg}}]}^{-1}$$ [10]

For the cylindrical birdcage coil with equal-value capacitors the virtual ground should be halfway between the legs having equal and opposite current magnitudes. In general, the virtual ground must be placed at a location where it is possible for the points of intersection to have the same electrical potential.

Software Development and Coil Construction

The computer program BirdcageBuilder was developed to facilitate birdcage coil design for NMR practitioners (12). The BirdcageBuilder program can be downloaded from http://nmrr.hmc.psu.edu. This program encapsulates the details of effective inductance and capacitance calculations with a user-friendly interface and provides a simple and efficient solution for birdcage coil design. The computer program was written in MS Visual Basic 5.0 (Microsoft, Redmond, WA), and calculations are carried out using the following steps: retrieval of information about the coil configuration (HP, LP, or BP; number of legs; radii of the coil and RF shield; dimensions of legs and ER segments; and the desired resonant frequency), calculation of the values of the current intensity in the legs and ER segments following the desired current pattern (sinusoidal for coils with circular cross section, as described previously (8) for coils with elliptical cross section), calculation of the effective inductance of the legs, calculation of the effective inductance of the ER segments, and calculation of the necessary capacitances based on the above formulas and display of the results.

The calculated capacitances from BirdcageBuilder for configurations of existing coils at several laboratories are presented in Table 1, along with the actual capacitor values used in the coils.

Table 1.

Experimental Data of 10 Constructed Birdcage Coils and Their Calculated Capacitances

Coil	Type/ #Legs	Freq. (MHz)	Coil/Shield Radius (cm)	Leg Size (cm)	ER Segment Sizea (cm)	Calcd Cap. (pF)	Exptl Cap. (pF)
A	LP/12	21.25	3.8/100	10/0.6a	1.98/0.6	269.54	270
B	LP/12	63	4.45/0.0	8.9/0.6a	2.33/0.6	29.56	30.0
C	LP/8	127.8	6.35/8.95	12.6/1.27a	4.98/1.27	9.76	9.8
D	LP/8	400.1	1.25/1.87	2.4/0.1a	0.98/0.1	3.38	3.3
E	HP/16	106	9.52/35.5	22.2/0.4/0.3b	3.72/1.3	47.47	47.0
F	HP/12	200.1	9.7/12.8	20/0.65/0.40b	5.08/1.4	11.62	12.0
G	HP/8	200.5	1.9/50	7.3/0.6a	1.49/0.6	25.58	26.7
H	BP/12	125.2	9.5/0.0	20/1.25a	4.97/1.25	15.04 (33)c	15.0 (33)
I	BP/12	170	9.5/0.0	17.2/0.6a	4.97/0.5	14.26 (11.7)d	13.8 (11.7)
J	BP/12	173	8.4/0.0	22.5/0.6a	4.4/0.6	11.62 (47)d	11.0 (47)

^aLength/width.

^bLength/outer diameter/inner diameter.

^cThe given capacitance on the ER segment.

^dThe given capacitance on the leg.

RESULTS AND DISCUSSION

Program Interface

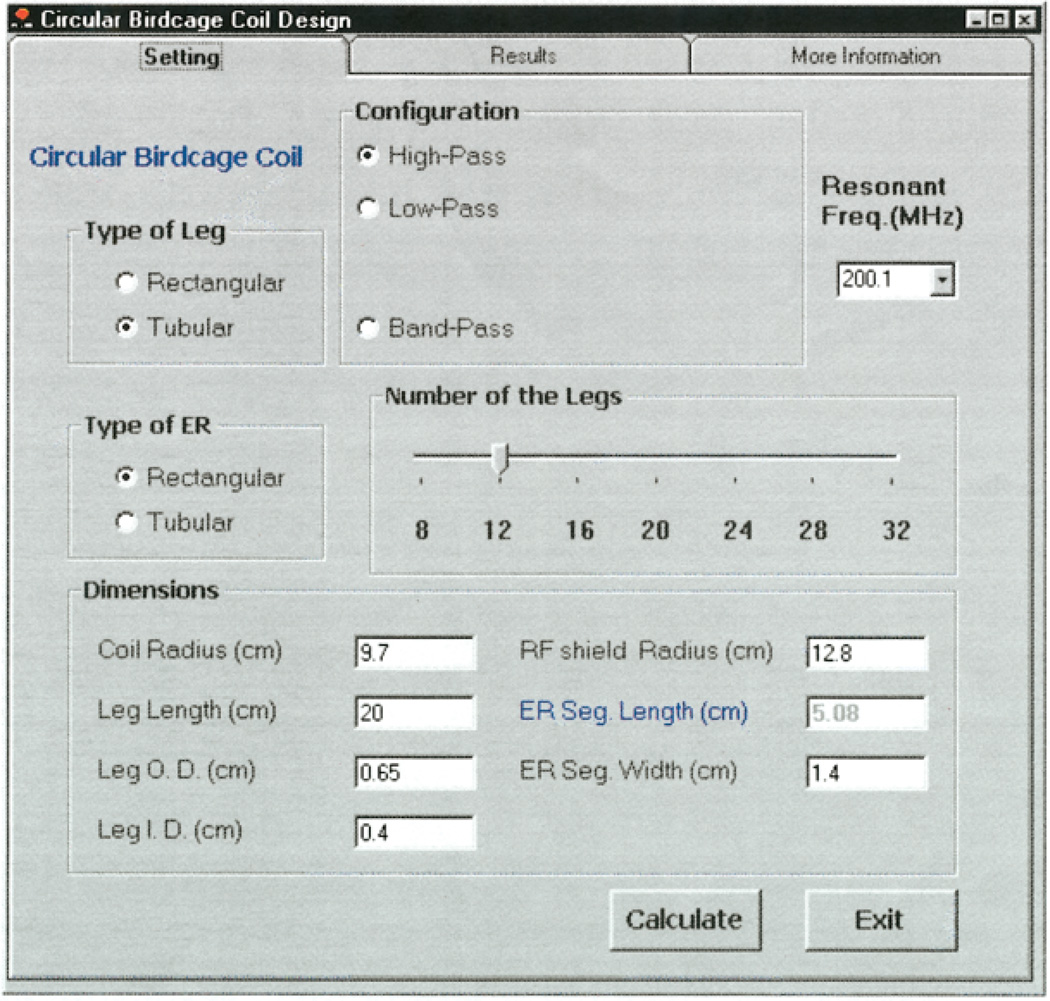
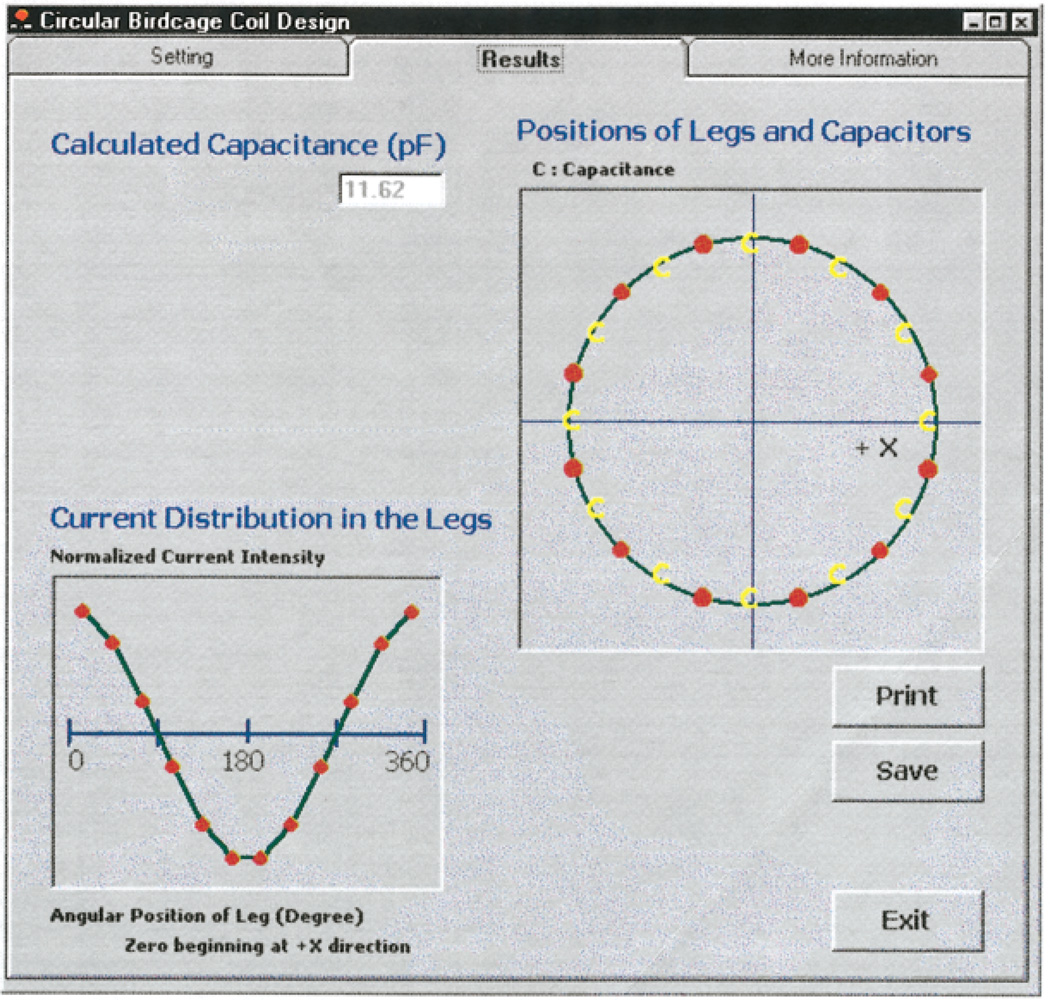
An example of a capacitance calculation for a HP coil design is demonstrated here. Calculations for LP and BP coils can be performed using similar procedures. In the Setting Menu (Fig. 2) users are requested to enter the radii of the coil and RF shield, the number of legs, and the desired resonant frequency. The length of the leg entered by the user should be the distance between the centers of the opposite ER segments. Users should enter the outer diameter and inner diameter for tubular legs or the length and width for rectangular legs. The lengths of the ER segments are automatically calculated as the distance between adjacent legs, and users are asked to describe their cross-sectional geometry as they did for the legs. In the Results Menu (Fig. 3) the calculated capacitance, the current distribution in the legs, and the positions of legs and capacitors are presented. Only one calculated capacitance is shown for a cylindrical birdcage coil design. Multiple capacitance values will be displayed for an elliptical coil calculation (12). All the necessary information for the coil construction can be saved in a file or printed out. The More Information Menu shows the results of the calculated effective inductance of legs and ER segments, which have a profound impact on the accuracy of the capacitance calculations (11). In summary, BirdcageBuilder is easy to use and its versatility allows rapid coil construction for both the novice and experienced coil builder.

Figure 2.

The BirdcageBuilder program interface for the Setting Menu. Users input all the necessary information in the Setting Menu and then click the Calculate Button. The program will automatically display the calculated capacitance. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Figure 3.

The BirdcageBuilder program interface for the Results Menu. The positions of the legs and capacitors, the calculated capacitance, and the current distribution are shown in the Results Menu. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]

Calculated Capacitance and Measured Resonant Frequency

The calculated and experimental capacitances for 10 constructed coils are shown in Table 1. The results indicate our method can be used to correctly calculate the necessary capacitances to generate a homogenous B₁ field at a desired resonant frequency. The deviations between the desired and measured resonant frequencies are either negligible or within a tunable range when coils are attached with experimental capacitance values (Table 1). There are some limitations in our method resulting from simplifying the coil model employed in the calculations. The program assumes that the size of the gaps for capacitor placement is negligible in comparison to the lengths of the legs and the ER segments. Because the mirror images of the legs are calculated assuming an infinitely long shield, an error in the calculated capacitances will increase if the experimental shield is not longer than the coil. Because the mirror images of the ERs are not considered, an error in the calculated capacitances will increase as the shield diameter approaches the coil diameter. Because the coupling between opposite ERs is not considered, the error in the calculated capacitances will increase if the coil length is shorter than its diameter. Because ER segment lengths are calculated as straight lines that connect legs (rather than curves), errors will increase for cases with coils built having only a few legs. Finally, because quasistatic assumptions are made in all inductance and capacitance calculations, errors will increase as the desired resonant frequency increases to a point at which the wavelengths are on the order of the coil dimensions (13).

Arbitrary Coil Geometry and Field Profile

The novel feature of a cylindrical birdcage coil is that the fundamental resonant mode that generates a homogenous B₁ field can be easily achieved by placing equal-value capacitors in the coil. By iteratively soldering known capacitances, it is not too difficult to reach a desired resonant frequency experimentally. However, once the coil geometry or field profile deviates from a cylindrical shape, the capacitances required to produce a homogeneous field are not necessarily all equal; therefore, the trial and error approach becomes impossible.

Our method has been utilized to design and build birdcage coils with noncylindrical cross sections (8) and with a nonhomogeneous B₁ field distribution (9). Conceptually, once the desired current pattern (which must at least satisfy Kirchoff’s current law) is determined, our method can create the corresponding B₁ field at the desired resonant frequency. Consequently, this method could potentially be used to design bird-cage coils having arbitrary geometries or B₁ field distributions. Future applications of this method, including applicability to quadrature coils not having geometric and electrical symmetry about the longitudinal axis, remain to be explored.

Similar design difficulty is often encountered in the building of the BP birdcage coil. Because capacitors are placed on both the leg and ER segments, an infinite number of capacitor combinations are possible for coil tuning. BirdcageBuilder is designed such that either the leg or ER capacitance can be provided as an initial guess, then the remaining capacitance value is calculated. This procedure allows for the custom selection of the capacitor magnitude at the tuning site to be similar or smaller than the value of the adjustable tuning capacitor, providing the largest tunable range for the coil. The procedure significantly simplifies the design of such coils.

CONCLUSIONS

We presented a general method for birdcage coil design (HP, LP, and BP). Rather than predict resonant frequencies with calculated inductance and known capacitances, this method calculates the necessary capacitances from a given current pattern, a desired resonant frequency, and calculated inductances. The computer program BirdcageBuilder was implemented based on this method to facilitate birdcage coil design. Strong agreement between experimental and calculated capacitances for the constructed coils provides validation of the accuracy of our straightforward method. Although the BirdcageBuilder program has a limited number of current patterns and coil geometries from which to choose, the method that it uses (described in this work) could in theory be implemented for an infinite number of current patterns and coil geometries.