Computational model for autophagic vesicle dynamics in single cells

Abstract

Macroautophagy (autophagy) is a cellular recycling program essential for homeostasis and survival during cytotoxic stress. This process, which has an emerging role in disease etiology and treatment, is executed in four stages through the coordinated action of more than 30 proteins. An effective strategy for studying complicated cellular processes, such as autophagy, involves the construction and analysis of mathematical or computational models. When developed and refined from experimental knowledge, these models can be used to interrogate signaling pathways, formulate novel hypotheses about systems, and make predictions about cell signaling changes induced by specific interventions. Here, we present the development of a computational model describing autophagic vesicle dynamics in a mammalian system. We used time-resolved, live-cell microscopy to measure the synthesis and turnover of autophagic vesicles in single cells. The stochastically simulated model was consistent with data acquired during conditions of both basal and chemically-induced autophagy. The model was tested by genetic modulation of autophagic machinery and found to accurately predict vesicle dynamics observed experimentally. Furthermore, the model generated an unforeseen prediction about vesicle size that is consistent with both published findings and our experimental observations. Taken together, this model is accurate and useful and can serve as the foundation for future efforts aimed at quantitative characterization of autophagy.

Introduction

Autophagy is an evolutionarily conserved cellular digestive process whereby cytosolic contents are sequestered in double-membrane vesicles and delivered to the lysosome for degradation.¹ The breakdown of autophagic cargo generates basic biochemical building blocks, such as fatty acids and amino acids, which can be exported back to the cytosol for reuse. This process is used by the cell to rid itself of long-lived or damaged proteins and organelles in an effort to maintain homeostasis. In addition, autophagy is dramatically upregulated during bouts of stress or starvation, which generates an internal nutrient pool in a more energetically favorable way than de novo synthesis.¹

We conceptualize autophagy as a process consisting of four stages: initiation, nucleation, maturation and cargo delivery/degradation. Nutrient-activated TORC1 (mechanistic target of rapamycin complex 1) controls autophagy initiation by inhibiting the ULK1-ATG13-RB1CC1 complex.^2-4 When TORC1 activity is low (i.e., during nutrient deprivation), ULK1 is functional and permits the nucleation of a phagophore (PG). The synthesis of this cup-shaped, double-membrane structure is promoted in large part by the class III phosphatidylinositol 3-kinase, PtdIns3KC3, which generates phosphatidylinositol 3-phosphate (PtdIns3P) on autophagic membranes and ATG9, a transmembrane protein and putative lipid-carrier involved in membrane growth.^5,6 Expansion of the PG and eventual closure into a mature autophagosome (i.e., maturation) is controlled by two ubiquitin-like conjugation systems involving ATG12–ATG5-ATG16L1 and LC3 (Atg8 in yeast).⁷ The last stage of autophagy involves fusion of an autophagosome with a lysosome (or endocytic compartment destined for the lysosome) and degradation of sequestered material.^1,8,9

Despite its initial discovery over 50 years ago, essential questions about autophagy remain unanswered.¹⁰ Elegant studies in yeast and mammalian systems have identified more than 30 proteins required for autophagy; however, their mechanisms of action and regulation are incompletely understood. Furthermore, autophagy contributes to cell fate in a complicated manner that is only beginning to be elucidated. Although autophagy functions as a survival mechanism to delay or prevent apoptosis during periods of stress, it may also participate in cell death when activated in excess or for prolonged periods.¹¹ Along these same lines, dysregulated autophagy has been found to contribute to the pathology of several diseases, including cancer and neurodegeneration.^12,13 Thus, a greater knowledge of the regulation, molecular underpinnings, and cellular consequences of autophagy is critical not only for understanding normal physiology, but also for comprehending disease etiology and rationally designing therapies.

Complex cellular processes can be described and studied with computational or mathematical models.^14,15 When these models are driven by biological data, they provide reliable platforms for interrogating cell systems in silico. Models have proven useful in characterizing signaling pathways and generating predictions of specific interventions (e.g., genetic changes).^16-21 Here, we report the generation of a computational model that characterizes autophagic vesicle (AV) dynamics in single mammalian cells. Live-cell fluorescent microscopy was used to measure the synthesis and lysosomal turnover of LC3-positive AVs. These biological data, collected during both basal and induced autophagy, were used to build and refine a model that accurately predicted vesicle dynamics observed in cells over a range of conditions. Taken together, this computational model provides a framework from which more comprehensive autophagy models can be built.

Results

Single cell autophagy analysis

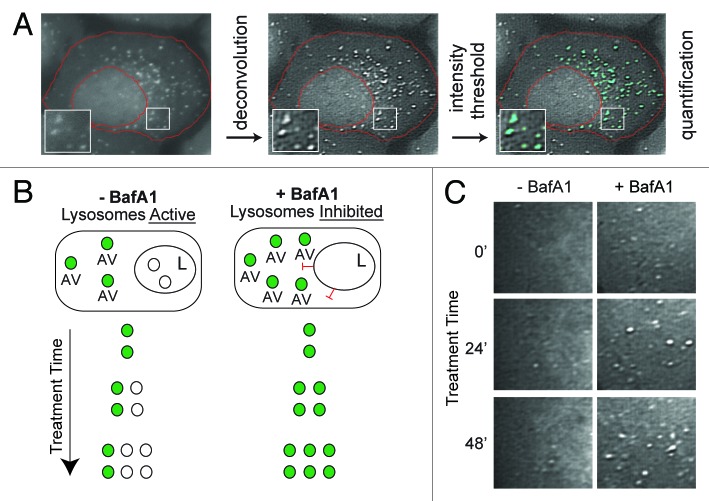
We developed a cell system that allowed us to monitor both the synthesis and turnover of AVs. We generated a monoclonal U2OS cell line stably expressing LC3 fused to a fluorescent tag, EGFP, similar to the line previously used in our laboratory.^22,23 We confirmed that the relative production and turnover of LC3-II in this cell line was similar to that observed endogenously in nontransfected U2OS cells, despite the increase in total LC3 protein abundance (Fig. S1). EGFP-LC3 puncta could be detected by fluorescent microscopy and provided an accurate marker of LC3-positive AVs. We designed an image processing protocol that allowed for the accurate quantification of AVs from single cells using fluorescent images (Fig. 1A).

Figure 1. Experimental design for measuring autophagic vesicle dynamics using EGFP-LC3. (A) EGFP-LC3 vesicles were imaged in U2OS cells by fluorescent microscopy and subjected to an image processing protocol including deconvolution, intensity thresholding and object quantification (see Materials and Methods for details). Example cell shown was cropped from a 60×-captured image. The red boundary defines the cellular region-of-interest. EGFP-positive puncta above the intensity threshold are highlighted in cyan. Insets are 2× magnifications of boxed regions. (B) Simplified model of lysosomal inhibition. Cells treated with vehicle control (−BafA1) have active lysosomes and EGFP-LC3 vesicles are continually synthesized and cleared by lysosomal fusion (fluorescence quenched). Bafilomycin A₁ (BafA1) treatment inhibits lysosome function (indicated with red inhibitory symbols) and thereby causes accumulation of EGFP-LC3 vesicles, which are protected from lysosome-mediated fluorescent quenching. Green-filled circles represent EGFP-LC3-positive AVs, whereas white-filled circles represent AVs that have fused with a lysosome (L). (C) Snapshots from areas imaged within single cells treated with vehicle (left panels; −BafA1) or BafA1 (right panels; +BafA1) for 0 min, 24 min or 48 min. Images are from deconvolved 60×-captured images.

EGFP-LC3 has several properties that we exploited for measurement of vesicle synthesis and degradation rates. LC3 incorporated on the outer membrane of AVs is recycled back to the cytosol, but LC3 embedded on the inner membrane is carried into the lysosome and degraded along with vesicle cargo.^24,25 Thus, LC3 turnover is a measure of autophagic flux.²⁴ In other words, the rate at which LC3 accumulates in response to lysosome inhibition, measured at either the level of protein or vesicle abundance, correlates with the rate of autophagy. Furthermore, the EGFP moiety of the EGFP-LC3 fusion is pH-sensitive and quenched by the acidity of the lysosome. Thus, EGFP-LC3 selectively labels PGs and autophagosomes, but not autolysosomes.²³

We used this knowledge to construct a system for determining rates of AV synthesis (the appearance of new EGFP-LC3 puncta) and turnover (the deposition of EGFP-LC3 puncta into the lysosome). In cells with active lysosomes, EGFP-LC3-positive puncta represent AVs at discrete stages of maturation between production and degradation (PGs or autophagosomes). In many cell types, this number is low and stable in the absence of cellular stress or nutrient starvation, presumably representing the steady-state of basal autophagy. Cellular stress or starvation would be predicted to destabilize this basal steady condition by inducing vesicle production. When lysosomal fusion is blocked by treatment with bafilomycin A₁ (BafA1), a lysosomal proton pump inhibitor, turnover of vesicles in the lysosome is inhibited. In this context, if AV synthesis continues unimpeded, vesicles will accumulate at a rate that corresponds to the rate of their production. By quantifying EGFP-LC3 vesicle abundance in cells cultured in both the presence and absence of BafA1, we reasoned that we could determine the rate at which vesicles were synthesized or degraded over an interval of time (Fig. 1B and C).

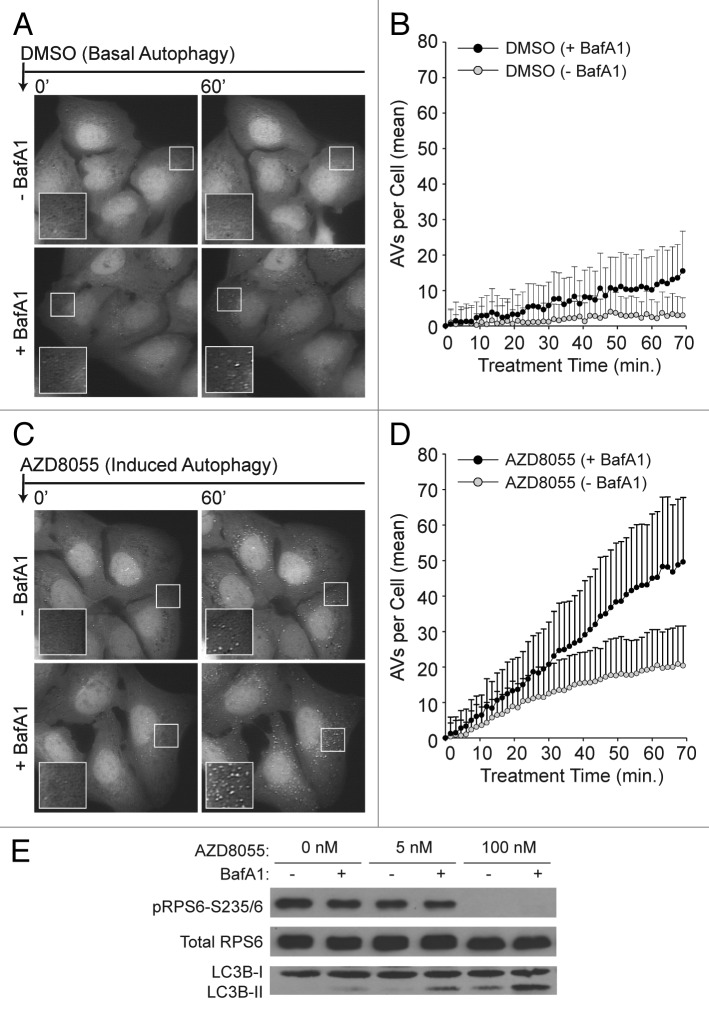
To characterize basal autophagy in U2OS cells, we imaged and quantified AV dynamics in single cells cultured in full-nutrient media with or without BafA1. Following a short pretreatment period with either vehicle (–BafA1) or BafA1 (+BafA1), medium was supplemented with DMSO (to control for subsequent compound treatments) and cells were then imaged once every 1.5 min for 70 min. Representative images are shown in Figure 2A. Regardless of cotreatment condition (–BafA1 or +BafA1), vesicle counts were initially low and then increased with time (Fig. 2B). The rate of increase was significantly higher in cells treated with BafA1. Without BafA1 treatment, vesicle counts remained low over the entire time period and reached an apparent steady-state around 40 min after DMSO addition. The accumulation of LC3-positive puncta upon BafA1-mediated inhibition of lysosomal activity suggested that the basal steady condition does not reflect a static “off” state of the autophagic machinery, but rather a balance of continual synthesis and turnover. This observation is in agreement with observations reported for most cell types.^24,26

Figure 2. Single-cell counts of EGFP-positive puncta under conditions of basal and induced autophagy. (A) Basal autophagy reflected EGFP-LC3 vesicle dynamics in full nutrient medium. Following a 21 min pre-incubation period with vehicle (−BafA1; top panels) or BafA1 (+BafA1; bottom panels), U2OS-EGFP-LC3 cells were treated with DMSO control at time t = 0 and 46 images were captured at 1.5 min intervals. Along with addition of DMSO, media was replaced with fresh media containing or lacking BafA1 at time t = 0. Images of several cells are shown at time t = 0 min and at time t = 60 min. Insets are 2× magnifications of boxed regions. (B) Population-averaged basal AV dynamics. The number of EGFP-LC3 vesicles that accumulated in the presence (black circles) or absence (gray circles) of BafA1 was plotted from time t = 0 through t = 70 min. Values on the vertical axis represent mean numbers of vesicles with adjustment such that the value at t = 0 is 0. Means were adjusted by subtracting the mean number of vesicles at t = 0. Means were calculated on the basis of measurements from all cells across three independent experiments (−BafA1: n = 51 cells at each time point; +BafA1: n = 44 cells at each time point). Bars represent standard deviations. (C) Induced autophagy reflected EGFP-LC3 vesicle dynamics in full nutrient medium supplemented with 100 nM AZD8055 at time t = 0. Cells were pretreated with vehicle or BafA1 as described above. (D) Population-averaged induced AV dynamics. The experiments and quantitative measurements of (A and B) were repeated but with the addition of 100 nM AZD8055 at time t = 0. Mean values were determined using measurements from all cells imaged across three independent experiments (–BafA1: n = 70 cells at each time point; +BafA1: n = 51 cells at each time point). As in (B), the mean AV count per cell at t = 0 was subtracted from the mean determined at each time point. (E) U2OS cells were treated with AZD8055 (5 nM and 100 nM) or vehicle (DMSO) control for 1 h in the presence (+) or absence (−) of BafA1 (following a 30 min pretreatment with or without BafA1) and whole cell lysates probed by immunoblotting for total RPS6, phospho-RPS6 (S235/6) and LC3B.

Next, we compared basal and induced autophagy. To do so, we removed the inhibition of autophagy conferred by active TORC1 by treating cells with an ATP-competitive catalytic MTOR inhibitor, AZD8055 (Fig. 2C and D). We verified that AZD8055 effectively reduced TORC1 activity and stimulated autophagy by observing both reduced phosphorylation of RPS6, a substrate downstream of TORC1, and increased levels of endogenous autophagic LC3 (LC3-II) (Fig. 2E). To quantify vesicle dynamics under these conditions, we pretreated cells with either vehicle or BafA1, then supplemented media with AZD8055 and imaged once every 1.5 min for 70 min. AZD8055 treatment increased the number of AVs in cells cotreated with BafA1, consistent with an increase in the rate of AV synthesis (Fig. 2D). The number of AVs in cells treated with AZD8055 plus vehicle (i.e., no BafA1) also increased, but at a slower rate, and began to plateau at later time points (Fig. 2D). This latter observation suggested that vesicle turnover gradually approached a new steady-state wherein vesicle turnover matches increased vesicle synthesis.

Model-based analysis of population-averaged AV dynamics

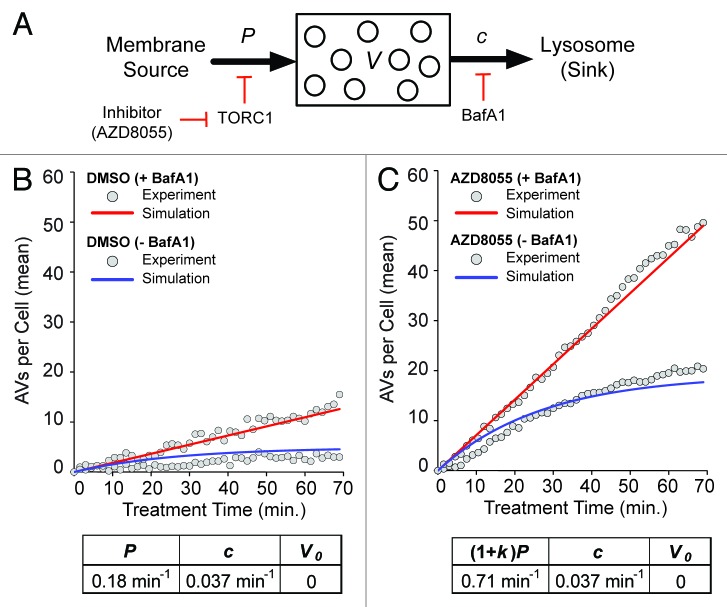
To estimate key kinetic parameters of autophagy, we formulated a deterministic mathematical model for AV dynamics that accounted for the processes and perturbations illustrated in Figure 3A. According to this model, there are three key parameters, P, c and k, defined as follows. AVs are produced at a constant rate P in a basal steady-state and AVs are cleared at a rate proportional to the number of AVs at time t, denoted by V(t), with rate constant c. BafA1 treatment is modeled by setting to c to zero (c = 0). AZD8055 treatment is modeled by setting the rate of vesicle production to (1 + k)P, where k > 0 is a parameter that characterizes the increased rate of synthesis of AVs caused by inhibition of MTOR activity. The model can be written as the following ordinary differential equation (ODE):

Figure 3. Model-based analysis of basal and induced autophagy dynamics. (A) A population dynamics model was formulated that captures the processes illustrated here: production of AVs (from membrane sources) at a constant rate P, increased production at a constant rate (1 + k)P in the presence of an MTOR (and thereby, TORC1) inhibitor, clearance of AVs (into a pool of lysosomes, the sink, where they fuse and deliver cargo) in a first-order process with rate constant c, and complete inhibition of clearance in the presence of BafA1. Presence (absence) of an MTOR inhibitor (e.g., AZD8055) is signified by δ_a = 1 (0). Likewise, presence (absence) of BafA1 is signified by δ_b = 1(0). Analytical expressions for V(t), which represents the average number of AVs per cell as a function of time t, are given in Materials and Methods. (B and C) Values of model parameters (P, c and k) and the initial condition V(0) = V₀ were estimated through nonlinear least squares fitting; the goodness of fit is illustrated in these panels. Fits are based on the data of Figure 2. The gray circles in (B and C) represent the adjusted mean AV counts reported earlier in Figure 2B (basal autophagy, δ_a = 0) and Figure 2D (AZD8055-induced autophagy, δ_a = 1). In (B and C), time courses produced by the model with best-fit parameter values (p = 0.18 min⁻¹, c = 0.037 min⁻¹ and k = 2.9) and V₀ = 0, the best-fit initial condition, are shown for δ_b = 1 (+BafA1; red curves) and δ_b = 0 (−BafA1; blue curves).

where the overall rate of change of V(t), dV/dt, is given by the expression on the right-hand side. In this expression, the term (1 + δ_αk)P represents the rate of AV production and the term (1 − δ_b)cV represents the rate of AV degradation. The binary variable δ_a takes the value 0 to indicate the absence of AZD8055 and 1 to indicate the presence of AZD8055. Similarly, δ_b takes the value 0 to indicate the absence of BafA1 and 1 to indicate the presence of BafA1. Analytical expressions for V(t) are given in Materials and Methods. Simulation of the model required specification of an initial condition, V₀ = V(0). We took time t = 0 to be the time at which DMSO or AZD8055 was added.

We estimated values of the model parameters P, c and k and the initial condition V₀ through nonlinear least squares fitting (see Materials and Methods). In the fitting procedure, we considered the averaged kinetic data collected for t = 0 through 70 min, with each data point transformed by subtraction of the mean AV count at t = 0, for each of the following conditions (Fig. 2B and D): (1) basal autophagy without BafA1 (δ_a = 0, δ_b = 0), (2) basal autophagy with BafA1 (δ_a = 0, δ_b = 1), (3) AZD8055-induced autophagy without BafA1 (δ_a = 1, δ_b = 0), and (4) AZD8055-induced autophagy with BafA1 (δ_a = 1, δ_b = 1). Averages were computed over all cells imaged at each time point and the quality of fit illustrated (Fig. 3B and C). Best-fit parameter values were as follows: p = 0.18 min⁻¹, c = 0.037 min⁻¹, k = 2.9 and V₀ = 0. This indicated that the basal rate of AV synthesis was 0.18 min⁻¹ and AZD8055 treatment increased this rate approximately 4-fold to 0.71 min⁻¹. The mean lifetime of n EGFP-LC3 AV, which was the expected time between production and quenching of EGFP (i.e., entry to the lysosome), was 1/c (because for first-order decay, the mean lifetime equals the inverse of the rate constant for decay). During both basal and AZD8055-induced autophagy, the AV lifetime was approximately 27 min in our cell system. This lifetime was consistent with previous estimates based on both endogenous and fluorescently labeled LC3, measured basally and in response to MTOR inhibition.^27,28 Importantly, one of these studies concludes that the half-life of autophagic vesicles is the same both basally and in cells treated with rapamycin, again consistent with our findings.²⁸ It should be noted that the best-fit initial condition was 0 (i.e., V₀ = 0) in large part because fitting was based on adjusted mean AV counts. Each adjusted mean AV count was the number of AVs per cell averaged over all cells imaged minus the average count at t = 0. Thus, a value of V = 0 in the model corresponded to a baseline adjusted mean number of AVs rather than an absence of AVs. The baseline mean number of AVs varied from cell to cell and from condition to condition with a mean count of 9 AVs per cell at t = 0.

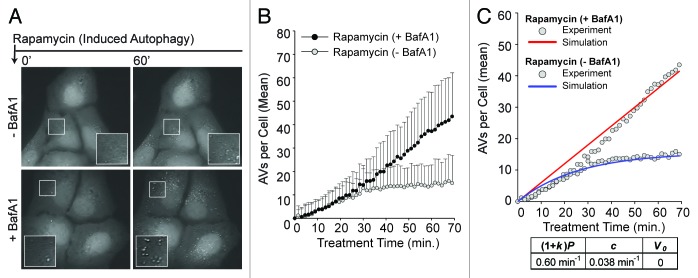
To determine if AZD8055 treatment elicited AV dynamics that can be considered typical of induced autophagy, we repeated the experiments in which autophagy was induced using rapamycin, an allosteric inhibitor of TORC1 (Fig. 4A–C). Parameter estimates specific for rapamycin were then determined through model-based analysis as follows. We set V₀ and P to the values determined above for basal autophagy (0 and 0.18 min⁻¹, respectively), reasoning that these parameters should be independent of the small-molecule inhibitors used to induce autophagy. We then measured AVs per cell over the same time course (Fig. 4B) to estimate k and c through fitting. We obtained fits of good quality (Fig. 4C) and parameter estimates similar to those based on experiments with AZD8055 (k = 2.3 and c = 0.038 min⁻¹). The turnover rate constant, c, was nearly identical in DMSO, AZD8055 and rapamycin-treated cells, suggesting that AV degradation was unperturbed by AZD8055 or rapamycin treatment. Furthermore, consistent with a similar mechanism of action, rapamycin treatment induced an elevated rate of AV synthesis (0.60 min⁻¹, k = 2.8), although slightly lower than that observed with AZD8055 (compare Fig. 3C and Fig. 4C). From this data, we concluded that in our cellular system, AZD8055 and rapamycin had similar effects on AV dynamics although AZD8055 induced autophagy more robustly, consistent with previous studies comparing catalytic and allosteric MTOR inhibitors.^29-31

Figure 4. Induced autophagy dynamics are similar for different MTOR inhibitors. (A) Following a 21 min pre-incubation period with vehicle (−BafA1; top panels) or BafA1 (+BafA1; bottom panels), U2OS-EGFP-LC3 cells were treated with 100 nM rapamycin and 46 images were captured at 1.5 min intervals in media containing or lacking BafA1. Images of several cells are shown at time t = 0 min and at time t = 60 min. Insets are 2× magnifications of boxed regions. (B) The number of EGFP-LC3 vesicles in the presence (black circles) or absence (gray circles) of BafA1 was plotted as a function of time after rapamycin treatment. Rapamycin was added at t = 0. Values represent the mean number of vesicles minus the mean number of vesicles at time t = 0, with averages taken over all cells imaged at each time point across three independent experiments (−BafA1: n = 52 cells at each time point; +BafA1: n = 69 cells at each time point). Bars indicate standard deviations. (C) The population dynamics model reproduced the rapamycin data. Red and blue curves represent model-derived time courses for conditions with and without BafA1, respectively. Gray circles represent the adjusted experimental averages shown in (B). Best-fit values of (1 + k)P, c, V₀ are as indicated.

Mechanistic stochastic model for autophagy in a single cell

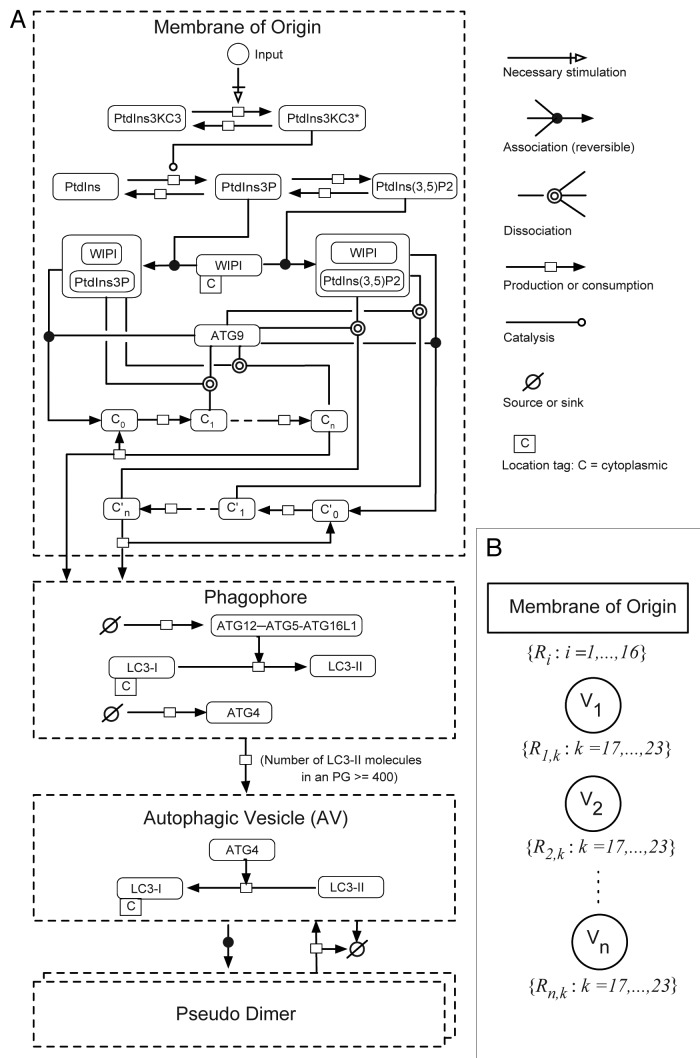
We constructed a computational model intended to capture known mechanisms of autophagy regulation and observed AV dynamics from synthesis to turnover in single cells. The model was also formulated with the intention of reproducing and explaining the observed cell-to-cell variability. The model incorporated a series of biochemical and physiological steps in the autophagic pathway from PtdIns3KC3 activation through LC3 conjugation comprising PG nucleation, vesicle maturation and lysosomal degradation (Fig. 5A). The processes included in the model are discussed below and formally described in Materials and Methods.

Figure 5. Overview of key molecules included in the mechanistic stochastic model of autophagic vesicle dynamics. (A) Molecules and reactions included in this model are illustrated using the conventions of Systems Biology Graphical Notation (SBGN). Compartments are indicated by dashed lines. Chemical species are represented by rounded rectangles. Arrows represent interactions as indicated in the legend on the right. Reactions considered in the model are listed in Equations 1–23. (B) Reaction nomenclature. For our model, the reactions that take place in a given cell at a given time t are partitioned into n(t) + 1 sets, where n(t) is the number of PGs and mature AVs present in the cell at time t. Recall that we consider 23 different reactions (Eqns. 1–23). Sixteen of these reactions involve chemical species in the membrane-of-origin compartment (Eqns. 1–16), i.e., the compartment from which all PGs and mature AVs emerge. The other seven reactions (Eqns. 17–23) are associated with specific PGs or AVs, and as a result, there are n(t) instances of each reaction described by Equations 17–23. For example, in our model, each PG is allowed to mature into an AV (Eqn. 20), and each mature AV is allowed to fuse with a lysosome (Eqn. 23). Thus, the total number of reactions in a cell at time t, including multiple instances of reactions, is 16 + 7n(t). We label all n(t) maturing and mature vesicles present in a cell at time t as follows: V₁, V₂…, V_n. The reactions specific to vesicle k are labeled R_k,17, R_k,18, R_k,19, R_k,20, R_k,21, R_k,22 and R_k,23. The reactions involving chemical species in the membrane-of-origin are labeled R₁, R₂,…, R₁₆.

In the model, an input I, representing an autophagic stimulus (for example, AZD8055), activates autophagic PtdIns3KC3. Activated PtdIns3KC3 catalyzes conversion of phosphatidylinositol (PtdIns) into PtdIns3P. PtdIns3P is converted into PtdIns(3,5)P₂ via phosphorylation (mediated by PIKFYVE) and PtdIns(3,5)P₂ can be converted back to PtdIns3P via a dephosphorylation reaction.^32,33 Both PtdIns3P and PtdIns(3,5)P₂ serve as second messengers that recruit lipid-binding proteins to specific subcellular compartments, in this case the membranes from which PGs originate. WIPI (represented by two genetic isoforms in mammals, WIPI1 and WIPI2) is capable of binding both PtdIns3P and PtdIns(3,5)P₂ and serves as an effector for both of these lipids in the model.^34,35

ATG9 has been shown to cycle from peripheral locations to the PG assembly site, where it is important for membrane growth at this stage of autophagy.⁶ Although the mechanism is unknown, it has been shown that in mammals, ATG9 cycling is dependent upon PtdIns3KC3 activity, and in yeast, ATG9 function requires ATG18, a PtdIins3P-binding protein.^5,36 Furthermore, ATG5 fails to be recruited to PGs in yeast lacking ATG9.³⁷ Accordingly, we placed ATG9 downstream of PtdIns3P and PtdIns(3,5)P₂ formation and took ATG9 association with WIPI1/2-bound PtdIns3P or PtdIns(3,5)P₂ to be a prerequisite for PG synthesis. ATG9 has been shown to self-oligomerize and was also detected in an asymmetric distribution on autophagic membranes.^38,39 Therefore, we included a process wherein PtdIns3P- or PtdIns(3,5)P₂-bound WIPI1/2 engages ATG9 to form a complex [ATG9-WIPI1/2-PtdIns3P or ATG9-WIPI1/2-PtdIns(3,5)P₂] and then, ATG9 within this complex is activated through multiple steps. The fully active form of ATG9 catalyzes the nucleation of a PG. Although the precise interactions and activation requirements for WIPI1/2 and ATG9 have not yet been characterized, the steps outlined in this model represent a plausible hypothesis that can be tested and refined.

A PG, once nucleated, acquires its own set of reactions, which contribute to its growth and maturation. In the model, an enzyme X, representing the ATG12–ATG5-ATG16L1 complex, is recruited to a PG at a constant rate. The PG-associated pool of X in turn recruits Y, which represents cytosolic LC3-I. In the model, it is assumed that the maturation of a PG depends on a reaction wherein X catalyzes conversion of Y to Z (representing lipid-conjugated LC3-II). This step captures the E3-like enzymatic activity of ATG12–ATG5-ATG16L1 that controls LC3-II lipidation to autophagic membranes.⁴⁰ As long as Z is present below a threshold number, Z_th, a PG is considered immature and not allowed to form a closed vesicle, in our model. When Z ≥ Z_th, a PG can form a closed vesicle through a process with first-order kinetics. ATG4, the protease that initially generates LC3-I, has been shown to delipidate LC3-II from the outer membrane of the autophagic vesicle near or at the point of lysosomal fusion.²³ Therefore, in the model, ATG4 is allowed to be recruited to mature PGs with ATG4 mediating the release of Z and generation of soluble Y. Once a PG matures into a closed vesicle, further vesicle-specific reactions, except for the ATG4-mediated release of Z, are prohibited and the vesicle is considered susceptible to degradation. Degradation of vesicles takes place in a first-order process. Any Z associated with a degraded AV is removed from the system.

In the model, the input I is assigned a nominal value to represent the basal autophagic condition, which is characterized by a relatively small number of vesicles at steady-state (based on Fig. 2B). Other conditions in the model are represented as follows: addition of AZD8055, which induces autophagy, is represented by a step increase in the input; addition of BafA1, which inhibits vesicle degradation, is represented by a zero rate of vesicle degradation; knockdown of ATG9 is represented by setting ATG9 concentration to 20% of its nominal value (Table 1).

Table 1. Mechanistic model parameter values for a cell volume assumed to be 3 × 10⁻¹² L.

Parameter	Value	Description
I	4.48 × 10−6 (1 + 2.62 × δazd)	Input function; the binary variable δazd takes a value of 1 to indicate the presence of AZD8055 and a value of 0 to indicate the absence of AZD8055
PtdIns3KC3	105/cell	Concentration of PtdIns3KC3
PtdIns	106/cell	Concentration of PtdIns that are substrates of PtdIns3KC3
WIPI	105/cell	Concentration of WIPI1/2
ATG9	105/cell	Concentration of ATG9
LC3-I	105/cell	Concentration of LC3
kdea	0.1 sec−1	PtdIns3KC3 deactivation
k+1	10−6 (molecule/cell)−1sec−1	Rate constant for association of activated PtdIns3KC3 and PtdIns
k-1	0.1 sec−1	Rate constant for dissociation of activated PtdIns3KC3 and PtdIns in complex
kcat	1 sec−1	Rate constant for catalytic conversion of PtdIns to PtdIns3P
kase	1 sec−1	Pseudo first-order rate constant for dephosphorylation of PItdIns3P, which generates PtdIns
kpip2	1 sec−1	Rate constant for catalytic conversion of PtdIns3P to PtdIns(3,5)P2
kdpip2	1 sec−1	Pseudo first-order rate constant for dephosphorylation of PtdIns(3,5)P2, which generates PtdIns3P
kcap	10−6 (molecule/cell) −1sec−1	Rate constant for association of WIPI and PtdIns3P or PtdIns(3,5)P2
krel1	0.1 sec−1	Rate constant for dissociation of WIPI and PtdIns3P in complex
krel2	1 sec−1	Rate constant for dissociation of WIPI and PtdIns(3,5)P2 in complex
keng	10−6 (molecule/cell) −1sec−1	Rate constant for association of ATG9 and WIPI.PtdIns3P or WIPI.PtdIns(3,5)P2
kdis	0.1 sec−1	Rate constant for dissociation of ATG9 from a ternary complex of ATG9.WIPI.PtdIns3P or ATG9.WIPI.PtdIns(3,5)P2
kfor	0.1 sec−1	Rate constant for an ATG9 activation step
knu	0.01 sec−1	Rate constant for nucleation of an phagophore, which requires fully activated ATG9
kflux	0.1 sec−1	Rate at which X is added to a growing IM
kfluxATG4	0.1 sec−1	Rate at which ATG4 is added to a growing IM
kp	10−6 (molecule/cell) −1sec−1	Rate constant for association of X and Y
km	0.1 sec−1	Rate constant for dissociation of X and Y in complex
kmat	1 sec−1	Rate constant for catalytic conversion of Y to Z
krela	10−6 sec−1	Effective rate constant for ATG4-mediated release of Z from a closed vesicle
kves	0.05 sec−1	Rate constant for vesicle formation, which requires a suprathreshold number of Z present in the precursor IM
kagg	5 × 10−4 (number/cell) −1sec−1	Rate constant for generation of a pseudo dimer
ksplit	0.15 sec−1	Rate constant for breakup of a pseudo dimer
kdeg	4.5 × 10−4 sec−1	Rate constant for vesicle degradation

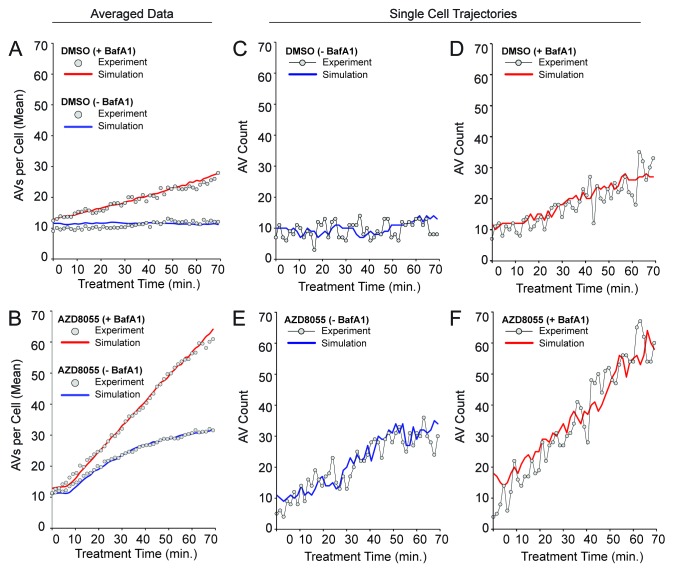
The above model provided a stochastic characterization of autophagy in a single cell, and was simulated using a modified form of Gillespie’s method.⁴¹ Details of the simulation algorithm are provided in Materials and Methods. Estimates of the parameters used in the mechanistic model are summarized in Table 1 and described in Materials and Methods. Parameters were either assigned values deemed reasonable or determined through a fitting procedure using the experimental time courses of Figure 2. The agreement between simulation results, averages of 100 individual stochastic simulations, and data are illustrated in Figure 6A and B. The basal value of I and the step change in I upon AZD8055 treatment were consistent with vesicle synthesis rates of ~0.18 AV min⁻¹ basally and ~0.71 min⁻¹ under AZD8055 treatment (Fig. 6A and B).

Figure 6. The stochastic mechanistic model is consistent with population-averaged AV counts as well as single-cell trajectories. As discussed in the text, the values of selected parameters were varied systematically to find values that allow the model to reproduce the population-averaged data of Figure 2 (gray circles in Fig. 2A and B). Other parameter values were estimated as described in Model Parameters. The quality of fit obtained is illustrated in (A and B) for basal autophagy dynamics and AZD8055-induced autophagy dynamics, respectively. In these panels, solid curves are based on averages from 100 stochastic simulation runs. Red and blue curves correspond to +BafA1 and −BafA1 conditions, in these panels as well as in (C–F). For details about the simulation method, see Materials and Methods. For standard deviations of averaged simulation results, see Figure S4. In (C–F), it can be seen that single stochastic traces produced by simulation of the model (solid curves) resemble experimentally determined time courses (circles). An experimental time course and a corresponding simulation are shown for each of the following conditions: (C) DMSO (basal autophagy) −BafA1, (D) DMSO (basal autophagy) +BafA1, (E) AZD8055 (induced autophagy) −BafA1 and (F) AZD8055 (induced autophagy) +BafA1. To allow comparison of the simulated and experimental curves despite minor variations in initial vesicle counts observed experimentally, we adjusted experimental values using the following offsets (values were added to the experimental counts): 4.25 (DMSO – BafA1), 3.5 (DMSO + BafA1), 1.0 (AZD8055 – BafA1), 1.0 (AZD8055 + BafA1). The experimental and simulation results shown in (C–F) were chosen to demonstrate that single simulation runs (solid curves) resemble data from time-lapse microscopy experiments (gray circles).

It is worth noting that this model recapitulated a minor lag in vesicle formation at early timepoints of treatment. This lag represented the time required to produce AVs in response to treatment initiation. To identify the parameters with most influence on this lag, we performed a sensitivity analysis and found that k_flux, the rate constant for ATG12─ATG5-ATG16L1 recruitment to the phagophore, had the strongest influence on lag time (Table S1). The total initial concentration of LC3-I as well as k_p, the rate constant for LC3-I recruitment to the ATG12–ATG5-ATG16L1-positive membrane, also had relatively strong influences on lag time.

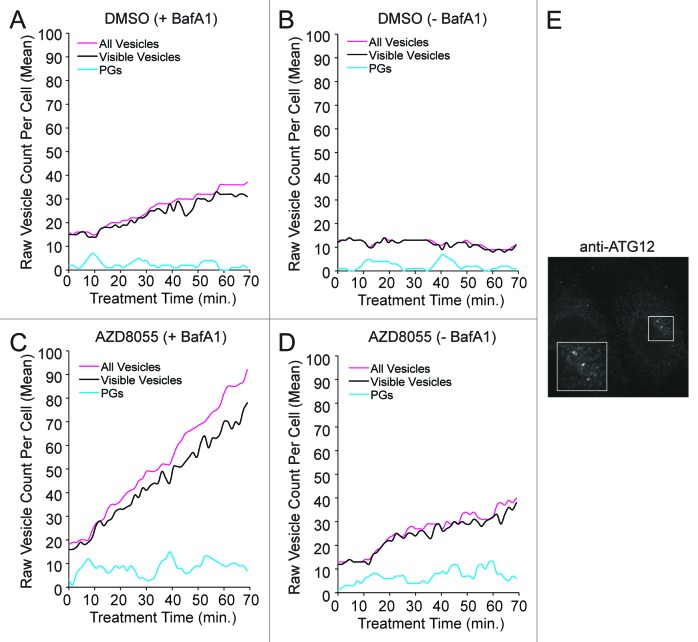
The model exhibited stochastic variations (fluctuations in vesicle counts) similar to the variations seen in single-cell trajectories for both basal and AZD8055-induced autophagy (Fig. 6C–F). We initially hypothesized that fluctuations in the number of AVs might be explained by intrinsic noise in AV dynamics (e.g., by a small population of ATG9 poised to initiate PG formation leading to stochastic nucleation of PGs and bursts of AV production). As suggested by the simulations of Figure 7A–D, which showed fluctuations in the number of PGs, AV dynamics may indeed be intrinsically noisy. However, we were unable to find parameter values consistent with this intrinsic noise being the source of the observed fluctuations in AV number. The reason may be that AVs were more abundant than PGs, which we determined through ATG12 immunostaining (Fig. 7E). This finding, which is consistent with observations of others, suggested that LC3-positive puncta largely reflect mature AVs.^27,42 Accumulation of AVs in excess of PGs was consistent with our estimates of a fairly long mean AV lifetime of ~26 to 27 min (Fig. 3 and Fig. 4). Thus, to explain fluctuations in AV number, our mechanistic model included an extrinsic source of noise, namely pseudo dimerization. We defined pseudo dimers as pairs of vesicles that were detected as a single punctum because of the resolution of our imaging and image analysis. Although U2OS cells are very thin, it is possible for a vesicle to be hidden from view during image capture (e.g., in the perinuclear region where the cell is slightly thicker) then reappear in a later image at a new visible cellular location. Behavior consistent with this view could be observed in Movie S1. We set the rate constants for formation and break up of pseudo dimers, k_agg = 900 μM⁻¹sec⁻¹ [or 5 × 10⁻⁴ (number/cell) ⁻¹sec⁻¹] and k_split = 0.15 sec⁻¹ (Table 1), such that predicted fluctuations in the number of visible vesicles, V + (V.V), recapitulated the observed fluctuations in single-cell trajectories (Fig. 6C–F). Using the model, we could relate actual vesicle counts (those visible vesicles captured by microscopy) to true vesicle counts (of all vesicles, visible and hidden) (Fig. 7A–D). In most cases, according to the model, actual counts reflected true counts, although combined AZD8055 and BafA1 treatment can lead to a significant divergence (Fig. 7C).

Figure 7. The mechanistic model is consistent with a greater abundance of closed vesicles than phagophores. (A–D) Trajectories generated from the tuned model are depicted for treatment periods with DMSO control (A and B; basal autophagy) or AZD8055 (C and D; induced autophagy) in the presence (+BafA1; A and C) or absence (−BafA1; B and D) of BafA1. In plots (A–D), vesicle counts per cell were not adjusted to 0 at t = 0, as in Figure 6, to accommodate visualization of the low PG counts. Fluctuations were observed in the experimental data and this presumed extrinsic noise was accounted for by including pseudo dimers in the model (see Eqn. 22). Inclusion of pseudo dimers in the model was intended to account for vesicle aggregates being miscounted as a single vesicle or vesicles disappearing from the focal plane. Predicted true total vesicle counts are indicated by magenta curves (“All Vesicles”) and predicted visible vesicle counts are indicated by black curves. Cyan curves represent predicted counts of phagophores (PGs). (E) Wild-type U2OS cells were immunostained for endogenous ATG12, a marker of PGs. Immunostaining indicates that PGs were less abundant than free AVs. AF488-conjugated secondary antibodies were used to detect primary ATG12 staining and image captured at 100×. Inset represents a 2× magnification of the boxed region.

Predictions and tests of the mechanistic model

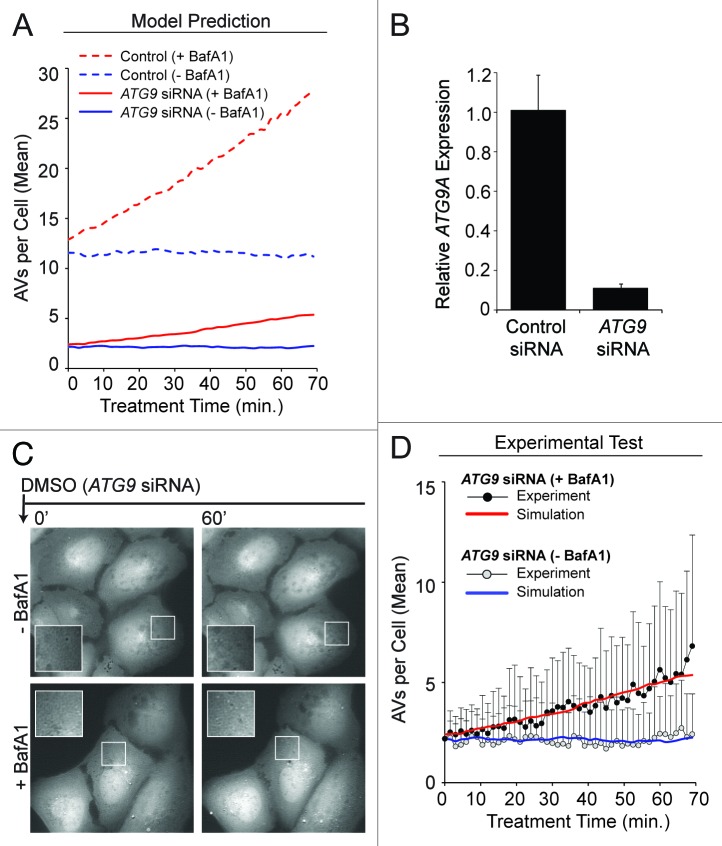
We tested one of the assumptions of the model, a requirement for ATG9 in nucleation of PGs. The role of ATG9 in autophagy, especially in our cellular system, is unclear. Our model predicted that an 80% reduction in ATG9 content would cause a proportional reduction in vesicle synthesis rate, from 0.18 min⁻¹ in the basal steady-state to 0.04 min⁻¹ (Fig. 8A). To test this prediction, we transfected cells with siRNAs targeting ATG9 prior to analysis and live-cell imaging. We determined that depletion of ATG9 (by 89%, as measured by mRNA transcript abundance; Fig. 8B) reduced vesicle synthesis rate substantially (Fig. 8C and D). The data revealed a vesicle synthesis rate estimated to be 0.04 min⁻¹ for the case of BafA1 treatment under the constraint that k = V₀ = c = 0. Thus, the predicted effect of ATG9 knockdown was qualitatively and quantitatively consistent with our mechanistic model (Fig. 8D). These findings support a critical role for ATG9 in autophagy.

Figure 8. Experimental data supported the predicted effects of ATG9 depletion. (A) Model-predicted effects of 80% ATG9 depletion (solid curves) under DMSO conditions +BafA1 (red curve) or −BafA1 (blue curve). Basal autophagy control simulations (averaged results from 100 single stochastic simulations) are shown as broken curves, +BafA1 (red curve) or −BafA1 (blue curve), for comparison. (B and C) Approximately 40 h prior to imaging and quantification, U2OS-EGFP-LC3 cells were transfected with siRNAs targeting ATG9. (B) Relative ATG9A expression (mRNA) was measured by qRT-PCR (relative to GAPDH; normalized to control siRNA). Bars represent standard deviations. (C) Following a 21 min preincubation period with media containing (bottom panels) or lacking (top panels) BafA1, cells were imaged 46 times at 1.5 min intervals in full-nutrient media in the presence or absence of BafA1. Images of several cells at each 0 min and 60 min are shown. Insets are 2× magnifications of boxed regions. (D) Total EGFP-LC3 vesicles accumulating during ATG9 knockdown +BafA1 (black circles) or −BafA1 (gray circles) are plotted across time. Values represent the mean vesicles accumulating (normalized to 0 at time 0 min) from all cells measured across 3 independent experiments (−BafA1: n = 36 cells per time point; +BafA1: n = 34 cells per time point). Bars represent standard deviations. The red and blue curves represent the mechanistic model simulations from (A) for ATG9 knockdown with and without BafA1, respectively. To allow comparison of the simulated and experimental curves despite minor variations in initial vesicle counts observed experimentally, we adjusted experimental values using the following offsets (values were added to the experimental counts): 0.75 (ATG9 siRNA – BafA1), 1.25 (ATG9 siRNA +BafA1).

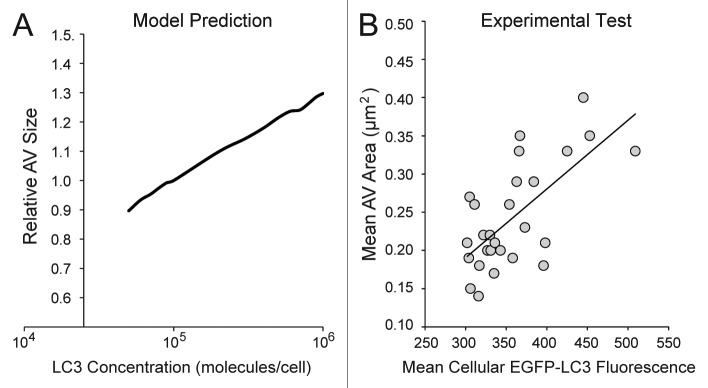
Another assumption of the model was that LC3-II lipidation plays a role in terminating growth of a PG. According to the model, maturation of a growing PG requires incorporation of a suprathreshold number of LC3 molecules. Unexpectedly, the model predicted a positive correlation between LC3 copy number and mean AV size (Fig. 9A). To test this prediction, we took advantage of natural cell-to-cell variability in LC3 copy number across a polyclonal population of EGFP-LC3 cells. We measured the following single-cell properties: relative LC3 expression levels (indicated by the intensity of cellular EGFP-LC3 fluorescence) and average area of EGFP-LC3 puncta. AV area was correlated positively with fluorescence intensity (Fig. 9B), which was consistent with the model prediction and the postulated role of LC3 in AV size control.

Figure 9. The model predicted a positive correlation between cellular LC3 concentration and autophagic vesicle size. (A) The model was used to generate predictions for a range of relative LC3 concentrations (normalized to the value used in the model, 100,000 molecules/cell) and resulting outputs of relative autophagic vesicle size. In this analysis, we assumed that the size of a vesicle was proportional to X. Simulation results were reported after 90 min treatment with DMSO + BafA1 (matching the time of pre-treatment and treatment in previous experiments). (B) A polyclonal population of U2OS-EGFP-LC3 cells was treated with full-nutrient media and BafA1 for 90 min (matching the time of preincubation and treatment for previous experiments) and imaged. The mean fluorescent intensity of the green channel (an indicator of relative EGFP-LC3 levels) and mean area of AVs (in µm²) was plotted for individual cells (n = 27). The solid trendline indicates a positive correlation, which is consistent with the model prediction in (A).

Discussion

In summary, we have developed a deterministic population dynamics model that accurately reproduced observed population-averaged autophagic vesicle dynamics under conditions of basal and AZD8055-induced autophagy. We have also developed a more mechanistic model that utilized stochastic simulation to reproduce observed autophagic vesicle dynamics at the single-cell level and in addition, predicted the effects of ATG9 depletion and variation in LC3 copy number.

To evaluate and compare the deterministic and stochastic models, we calculated the Akaike information criterion (AIC) for each (Table S2).⁴³ The AIC is a sum of two quantities that can be viewed as a penalty for discrepancies between data and model predictions and a penalty for the number of parameters in a model. Consistent with intuition, a “good” model is one for which the AIC is small (i.e., one that reasonably reproduces the available data with a minimal number of adjustable parameters). According to AIC, the deterministic model had a better fitting function than the stochastic model (Table S2), largely because it has fewer parameters. Nevertheless, the stochastic model, which captured mechanistic understanding not considered in the deterministic model, has many more valuable features. First, the mechanistic model better accounted for the minor lag in vesicle production observed at the onset of MTOR inhibition. Second, this model reflected the stochastic variability across the cell population. Finally, the mechanistic model permits the interrogation of individual parameters and autophagy components, and accordingly, renders it the superior tool for generating new hypotheses. In fact, the value of a mechanistic model should be judged by its ability to generate non-obvious testable predictions and to serve as a vehicle of understanding. By this measure, we demonstrated that the mechanistic model has considerable value.

Intriguingly, measurements from our cell system suggested that vesicle turnover occurs at a rate proportional to the number of vesicles in a cell (i.e., AV degradation occurs by a first-order process). Notably, when MTOR activity was chemically inhibited, not only was the rate of autophagic vesicle synthesis increased (as predicted by an increase in initiation), but vesicle turnover was as well. This finding suggested that, at least in our system, cells responded to an increase in AV abundance by increasing the rate of lysosomal turnover. The constants of proportionality governing this degradation reaction in our models are c (in the deterministic model) or k_deg (in the stochastic model). Assuming lysosomes (or endosomes destined to lysosomes) are not limiting, then the rate law cV or k_degV (in the deterministic or mechanistic models, respectively) follows from the law of mass action. Intuitively, if the number of AVs in a cell increases, so will the number of encounters with lysosome (or endosomes), and accordingly, the rate of degradation will increase. Our observation that MTOR inhibition effectively increased autophagic flux, not only the number of vesicles that are initiated, was consistent with reports that rapamycin treatment in neurons increased autophagic maturation and degradation, in addition to increasing vesicle synthesis.⁴⁴ Moreover, the therapeutic benefit conferred by MTOR inhibition in models of neurodegeneration support the notion that MTOR inhibitors are efficient inducers of the complete autophagic process.^44-46

Our mechanistic model for AV dynamics is a stochastic model, which we formulated in an attempt to understand the fluctuations and considerable dynamic range of behavior observed in single-cell experiments. Stochastic models are an ideal choice when randomness, or noise, is present in a system.^47-49 In addition to fluctuations detected in vesicle dynamics within single cells over time, we also observed a wide range of raw vesicle counts and dynamic rates of synthesis and turnover across the population of cells studied. Note the standard deviations in Figure 2B, D and Figure 4B. This variability may have a number of underlying explanations, including variations in cell-cycle status (our cell populations were asynchronous), genetic makeup, protein concentrations or drug sensitivity (in conditions of drug treatment).^50,51 Regardless of the source, this dynamic variability may be a physiologically important feature of autophagy signaling within a larger network (e.g., a population of cells). In the absence of single-cell measurements, this heterogeneity would not have been observed, and thus, our results contribute to accumulating evidence that resolution at the level of single cells is critical for a complete understanding of cellular processes.^50,52,53

Not only did the mechanistic model make accurate predictions about the requirement of a key autophagic machinery component (ATG9), it also generated an unforeseen hypothesis about LC3 concentration and vesicle size. When input parameters were modulated to incrementally increase the concentration of LC3, the model predicted a concurrent increase in mean vesicle size. In agreement with the model, we discovered a positive correlation between LC3 level and AV size across single cells. Importantly, published reports from both yeast and mammalian systems have supported such a positive correlation.^54,55 Notably, mutant yeast strains engineered for reduced LC3 expression accumulate autophagosomes smaller than wild-type yeast in response to starvation.³⁵ Within the mutant strains, the more substantial the LC3 reduction, the smaller the size of resulting autophagosomes.³⁵ These studies, and now our model, are consistent with a proposed function for LC3 in phagophore elongation.

The models presented here were consistent with a variety of experimental data. However, even the mechanistic model contains only minimal molecular details (i.e., key proteins from PtdIns3K through LC3). To comprehensively model autophagy, an expansion of this framework is required. Models that incorporate multiple inputs to autophagy, including contributions that feed through TORC1 and also inducers that function independently of MTOR [e.g., IP₃ depletion], or oncogenic stress will be important.⁵⁶ Additionally, models that capture processes happening on a slow time scale (i.e., hours to days) will be valuable for generating and testing predictions relevant to the global consequences of autophagy, especially in disease. Finally, we expect that an extended model, built on the foundation of the formal framework presented here, could be developed that includes much of the known molecular machinery involved in vesicle dynamics. The increased complexity of such a model may necessitate the use of the rule-based modeling approach, which is designed for reaction networks with large numbers of proteins with complicated interactions, activities and post-translational modifications.⁵⁷ A rule-based model, parameterized through the measurement of several key readouts in the autophagy pathway, will be an additional focus of future efforts.

Arguably the most important feature of a computational model is that it generates novel hypotheses that can be tested experimentally. The mechanistic model for autophagic vesicle dynamics presented here reproduced empirical data and proved to be predictive through experimental tests. Its accuracy demonstrated that it can serve as a solid foundation for an even more comprehensive model of autophagy in the future.

Materials and Methods

Live-cell microscopy

A monoclonal U2OS cell line was generated which displayed moderate fluorescent intensity (easily detected fluorescent puncta without saturation of signal) of ptfLC3B plasmid (Addgene plasmid 21074) (Fig. S1).²³ Although this construct expresses both an mRFP and EGFP tag fused to LC3, we only measured EGFP-LC3 dynamics (to exclude RFP-positive autolysosomes) and thus, for simplicity, we refer to EGFP-LC3 and U2OS-EGFP-LC3 cells within the text.

U2OS-EGFP-LC3 cells were seeded at a density of 1.25 × 10⁵ cells on 35 mm dishes with a number 1.5 uncoated coverglass bottom (MatTek, P35G-1.5-10-C) in 2 ml normal cell maintenance media [McCoy’s 5A (Invitrogen, 16600-082] supplemented with 10% fetal bovine serum [FBS, CellGro, 35-101-CV)]. Approximately 48 h later, cells were switched to 1.6 ml fresh insulin-containing media [McCoy’s 5A supplemented with 20 mM HEPES (Invitrogen, 15630-080) to buffer the pH and 100 nM insulin (Sigma, I1882)] for 1 h prior to treatment and imaging (this full nutrient media is henceforth called “control media”). Insulin activates PI3K-MTOR signaling; therefore, we confirmed that insulin did not reduce the ability of rapamycin to inhibit MTOR signaling (and thereby induce autophagy) by measuring MTOR-mediated RPS6KB1 phosphorylation (Fig. S2). The use of insulin as a growth factor supply in our assay permits future investigation of the contribution growth factors to autophagy.

Cells were then placed on the stage of a Nikon Ti Eclipse fluorescent microscope within an environmental chamber which maintained a humid environment at 37°C and 5% CO₂. Ten fields of view were chosen and NIS Elements software (Nikon) was set to automatically image each position every 1.5 min using a Perfect Focus System (PFS) to maintain the desired focal plane. Pretreatment was initiated by adding 0.4 ml of a 5× solution of bafilomycin A₁ (BafA1; A.G. Scientific, B-1183) or DMSO (−BafA1) to a final concentration of 125 nM BafA1 or 0.1% DMSO. Cells were imaged 15 times at 1.5 min intervals (see below for acquisition details). Following compound treatment (0.5 ml of a 5× solution), imaging resumed at 1.5 min intervals for 46 additional frames. Treatments included DMSO (0.1% final concentration), 100 nM AZD8055 (Selleck Chemicals, S1555) and 100 nM rapamycin (Calbiochem, 553210). All treatments were performed in control media (supplemented with 0.1%DMSO or BafA1). For each condition, three independent experiments were performed (biological replicates), yielding approximately 50 cells each (see figure legends for exact cell counts).

EGFP-LC3 was imaged in the FITC channel (12% lamp power; ND4 neutral density filter; 200 ms exposure) using a 60× oil objective and a Nikon Ti Eclipse fluorescent microscope. The third replicate of each condition studied was completed with a new fluorescent bulb and the exposure adjusted down to 100 ms to compensate. All representative images are of the FITC channel displayed in black-and-white for easier visualization of puncta.

Image processing and vesicle quantification

Image processing and quantification was completed with NIS Elements (Nikon). To quantify, images were deconvolved using a 2D fast deconvolution function with settings of thick (cell thickness), noisy (image noise level) and strong (contrast enhancement). Following, regions of interest were drawn around the cytosol of each cell, excluding the nucleus (because it generally stained brightly for EGFP-LC3) (Fig. S3). Intensity thresholds were set to include all pixels equal to and greater than 1.45× the mean background fluorescence from the cell (to control for background fluorescence and minor variation in fluorescent expression level). For cells transfected with ATG9 siRNAs, the threshold was adjusted to include objects greater than 1.7× the mean background fluorescence (to accommodate increased overall intensity). Objects were quantified using an automated object count function from this thresholded region and exported to Excel (Microsoft). For this model, vesicle count was the most utilized parameter although other parameters (size and intensity) were collected.

ATG12 immunofluorescence

ATG12 immunofluorescence was performed as described previously.²² Briefly, U2OS cells were immunostained with ATG12 antibodies (Cell Signaling Technologies, 2010) and anti-rabbit-AF488 secondary antibodies (Invitrogen, A11008) and imaged with a 100× oil objective on a Nikon Eclipse Ti microscope (25% FITC lamp power, 300 ms exposure).

ATG9 knockdown

U2OS-EGFP-LC3 cells were seeded at a density of 65,000 cells on 35 mm dishes with a number 1.5 coverglass bottom in 2 ml normal cell maintenance media (McCoy’s 5A with 10% FBS). The next day, cells were transfected with either control (nontargeting) siRNAs or a pool of four siRNAs targeting ATG9 (ATG9A: Qiagen SI04364675, SI04162781; ATG9B: Qiagen SI04364535, SI04309389) at a final concentration of 50 nM (total siRNA) using 2 µl oligofectamine (Invitrogen, 12252-011) in 0.2 ml Optimem (Invitrogen, 31985-062) and 0.8 ml normal cell maintenance media. Image capture and quantification was completed approximately 40 h post-transfection. Knockdown was measured by qRT-PCR using ATG9A-specific primers and an endogenous GAPDH control. ATG9B levels were too low for detection and knockdown was not determined. Delta delta Ct method was used to determine relative copy numbers from control and ATG9 siRNA samples.

Immunoblotting

U2OS cells were lysed [in 10 mM KPO₄, 1 mM EDTA, 10 mM MgCl₂, 5 mM EGTA, 50 mM bis-glycerophosphate, 0.5% NP40, 0.1% Brij35, 0.1% sodium deoxycholate, 1 mM NaVO₄, 5 mM NaF, 2 mM DTT, and complete protease inhibitors (Sigma-Aldrich, P8340)] and proteins resolved by SDS-PAGE. Proteins were transferred to nitrocellulose membranes and probed with primary antibodies (total RPS6: Cell Signaling Technologies, 2217; phospho-RPS6-S235/236: Cell Signaling Technologies, 2211; LC3B: Sigma-Aldrich, L7543; phospho-RPS6KB1-T389: Cell Signaling Technologies, 9234; α-tubulin: Sigma-Aldrich, T6199) overnight at 4°C followed by secondary antibodies (HRP-linked rabbit- or mouse-IgG, GE Healthcare, NA931 and NA934) for 1 h at room temperature. Proteins were detected by enhanced chemiluminescence.

Analytical expressions for V(t) in the deterministic population dynamics model

The simple model for AV dynamics (Fig. 3A) is written as a single ODE:

where P is the vesicle synthesis rate in the basal steady-state, c is the rate constant for vesicle degradation; k is a parameter that characterizes the effect of MTOR inhibition, δ_a is a binary variable that takes a value of 0 to indicate the absence of an MTOR inhibitor and 1 to indicate the presence of an MTOR inhibitor, and δ_b is a binary variable that takes a value of 0 to indicate the absence of BafA1 and 1 to indicate the presence of BafA1. From the ODE above, it is straightforward to find the following analytical expressions for V(t), the number of AVs per cell as a function of time t:

(Eqn. a) Basal condition (δ_a = 0; δ_b = 0):

(Eqn. b) +BafA1 (δ_a = 0; δ_b = 1):

V = V₀ + Pt

(Eqn. c) +AZD8055 or rapamycin (δ_a = 1; δ_b = 0):

(Eqn. d) +BafA1 and +AZD8055 or rapamycin (δ_a = 1; δ_b = 1):

V = V₀ + (1 + k)Pt

In these expressions, the quantity V₀ is V(0), the number of vesicles per cell when DMSO or an MTOR inhibitor is added in an experiment (at time t = 0). This number was always close to 0 because we adjusted all measured counts by subtracting the mean vesicle count at time t = 0 and considered the adjusted measurements in fitting. We used the above expressions (Eqns. a–d) in nonlinear least squares fitting to determine best-fit parameter values, i.e., the values of the model parameters (P, k and c) and initial condition (V₀) that allow the model to most closely reproduce a given set of measured time courses.⁵⁸ Additional details about fitting are provided in the main text.

Reactions comprising the mechanistic stochastic model

The model accounts for the reactions listed below. The reactions are illustrated schematically in Figure 5A. The source code used to simulate the model is provided as Supplementary Material.

(Eqn. 1) Input-controlled activation of PtdIns3KC3:

where PtdIns3KC3 is the inactive form, PtdIns3KC3* is the active form, I = I₀(1 + kδ_azd) and, I₀ is the basal level of stimulation, k is a constant, and δ_azd is a binary variable that takes a value of 1 if stimulation is present and 0 if stimulation is absent.

(Eqn. 2) Spontaneous deactivation of PtdIns3KC3 in a first-order process:

where k_dea is a rate constant.

(Eqn. 3) PtdIns3KC3-catalyzed conversion of PtdIns to PtdIns3P via a Michaelis-Menten mechanism:

where k₊, k₋ and k_cat are rate constants.

(Eqn. 4) Reversion of PtdIns3P to PtdIns catalyzed by a phosphatase assumed to be available in excess:^34,35

where k_ase is a pseudo first-order rate constant that incorporates the phosphatase level.

(Eqn. 5) Reversible recruitment of WIPI1/2 (for simplicity, referred to as “WIPI” in all equations) to PtdIns3P:

where k_cap and k_rel1 are rate constants.

(Eqn. 6) Binding of PtdIns3P-bound WIPI1/2 to free inactive ATG9:

where k_eng is a rate constant and C₀ represents the ternary complex of ATG9, WIPI1/2 and PtdIns3P.

(Eqn. 7) Activation of WIPI1/2-bound ATG9 through a series of n modifications:

where k_for is a rate constant and C_i represents a ternary complex of ATG9, WIPI1/2 and PtdIns3P modified i times. We set n = 3. The activation cascade is disrupted if ATG9 dissociates. For simplicity, in our model, WIPI1/2 and PtdIns3P are not allowed to dissociate from a ternary complex of ATG9, WIPI1/2 and PtdIns3P.

(Eqn. 8) Dissociation of ATG9 from a ternary complex of ATG9, WIPI1/2 and PtdIns3P:

for i = 0,…n and where k_dis is a rate constant.

(Eqn. 9) PG nucleation by fully active ATG9 with concomitant inactivation of ATG9:

,

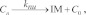where k_nu is a rate constant.

(Eqn. 10) Conversion of PtdIns3P into PtdIns(3,5)P₂:

where k_pip2 is a rate constant.

(Eqn. 11) Conversion of PtdIns(3,5)P₂ into PtdIns3P:

where k_dpip2 is a rate constant.

(Eqn. 12) Reversible recruitment of WIPI1/2 to PtdIns(3,5)P₂:

where k_cap and k_rel2 is rate constants.

(Eqn. 13) Binding of PtdIns(3,5)P₂-bound WIPI1/2 to free inactive ATG9:

where k_eng is a rate constant and C^ʹ_i represents a ternary complex of ATG9, WIPI1/2 and PtdIns(3,5)P₂.

(Eqn. 14) Activation of WIPI1/2-bound ATG9 through a series of n modifications:

where k_for is the same rate constant that appears in Reaction 7 and C^ʹ_i represents a ternary complex of ATG9, WIPI1/2 and PtdIns(3,5)P₂ modified i times. As before, we set n = 3 and only allow ATG9 to dissociate from a ternary complex of ATG9, WIPI1/2 and PtdIns(3,5)P₂. The activation cascade is disrupted if ATG9 dissociates.

(Eqn. 15) Dissociation of ATG9-WIPI1/2-PtdIns(3,5)P₂:

for I = 0,…,n and where k_dis is the same rate constant in Reaction 8.

(Eqn. 16) PG nucleation by fully active ATG9 with concomitant inactivation of ATG9:

,

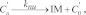where k_nu is the same rate constant in Reaction 9.

(Eqn. 17) Recruitment of enzyme X into a PG in a zero-order (saturated) process:

where k_flux is the constant rate of recruitment. The quantity X represents the level of a ternary complex of ATG12, ATG5 and ATG16 (ATG12–ATG5-ATG16L1).

(Eqn. 18) Recruitment of ATG4 into a PG in a zero-order (saturated) process:

where k_fluxATG4 is the constant rate of recruitment.

(Eqn. 19) Recruitment of Y (LC3-I) by PG-associated X, and conversion of Y into Z (LC3-II) through a Michaelis-Menten mechanism:

where k_p, k_m and k_mat are rate constants.

(Eqn. 20) Formation of a closed vesicle through a first-order process after a threshold level of Z has accumulated in a PG:

where k_ves is a rate constant and Z_th is the threshold number of Z molecules that must be exceeded for PG maturation. The number of molecules of Z is taken to be a measure of PG maturation in the model. We set Z_th = 400.

(Eqn. 21) ATG4-mediated conversion of Z on a closed vesicle into Y and release of Y from the closed vesicle:

where k_rela is an effective second-order rate constant. Representation of ATG4 activity in this way assumes that ATG4 is a Michaelis-Menten enzyme operating in the regime of substrate limitation.

(Eqn. 22) Vesicle pseudo dimerization and splitting:

where k_agg and k_split are rate constants. It is assumed that when two vesicles are sufficiently close in a cell, they appear to be one single vesicle, i.e., a pseudo dimer. It is assumed that the two vesicles in a pseudo dimer do not fuse. Thus, there is no mixing of the contents of the vesicles in a pseudo dimer.

(Eqn. 23) Degradation of vesicles:

where k_deg is a rate constant. Note that any Z associated with a degraded AV is also removed from the system in the degradation step.

Mechanistic model parameters

Parameter values in Table 1 are given in the unit system recommended by Faeder et al.,⁵⁹ whereas parameter values given below are in customary units. All proteins (PtdIns3KC3, WIPI1/2, ATG9 and LC3) were considered to be expressed at the same level, 10⁵ molecules per cell. This copy number corresponds to a concentration of 0.06 μM for a cytoplasmic volume of 3 × 10⁻¹² L.⁶⁰ The assumption that all proteins are equally expressed is consistent with gene expression analysis from U2OS cells (data not shown). We considered PtdIns to be present at a level of 10⁶ molecules per cell (~0.6 μM).

Selected parameters (I, k, k_dea and k_deg) were determined through fitting. The fitting procedure used was simple grid search, i.e., we systematically calculated goodness of fit at each point of a lattice in parameter space. Goodness of fit was measured by the residual sum of squares. The input variable/and PtdIns3K deactivation parameter k_dea determine the amount of active PtdIns3K in the model. The basal input value of the model (I) was chosen such that V₀ = 10 vesicles, roughly the average number present in cells measured at time t = 0 in the absence of BafA1. A step increase in I from a basal value, from I to (1 + k)I, is used to characterize the addition of an MTOR inhibitor (e.g., AZD8055) and consequent induction of vesicle synthesis. The rate constant k_deg characterizes vesicle turnover (degradation). The basal value of I and its step change under AZD8055 treatment (1 + k), the PtdIns3K deactivation parameter k_dea, and the vesicle degradation parameter k_deg = 4.5 × 10⁻⁴sec⁻¹ were estimated by simultaneously fitting the model to the experimental time courses of Figure 2. The quality of fit is illustrated in Figure 6A and B.

The various other parameter values listed in Table 1 were set as follows. For all bimolecular protein-protein and protein-lipid interactions, we assigned association rate constants a typical value, 1.8 μM⁻¹sec⁻¹, which corresponds to approximately 10⁻⁶ (molecules/cell)⁻¹sec⁻¹. For all protein-protein interactions, we assigned dissociation rate constants a typical value, 0.1 sec⁻¹. For these choices of association and dissociation rate constants, the equilibrium dissociation constant K_D for a protein-protein interaction in the model is ~0.05 μΜ.⁶¹ For WIPI1/2 binding to PtdIns3P, we set the dissociation rate constant to 0.1 sec⁻¹, whereas for WIPI1/2 binding with PtdIns(3,5)P₂, we set the dissociation rate constant to 1 sec⁻¹. These choices are consistent with the affinity of WIPI1/2 for PtdIns(3,5)P₂ being less than that for PtdIns3P.^34,62 We assumed that interconversion between PtdIns3P and PtdIns(3,5)P₂ is governed by first-order processes that each have a rate constant of 1 sec⁻¹. We assumed activation of ATG9 in the PtdIns3P-WIPI1/2-ATG9 or PtdIns(3,5)P₂-WIPI1/2-ATG9 ternary complex is completed in three successive steps (i.e., we set n = 3). We took each of these steps to be characterized by the same rate constant k_for = 0.1 sec⁻¹. We took nucleation of a PG to be a first-order process with rate constant k_nu = 0.01 sec⁻¹ that depends on activation of ATG9. We took accumulation of protein X (ATG12–ATG5-ATG16L1) and ATG4 in a PG to each occur at a constant rate of 0.1 sec⁻¹. We assumed formation of a closed vesicle (i.e., maturation of a PG) to take place in a first-order process with rate constant k_ves = 0.05 sec⁻¹ once a threshold level of LC3 has been incorporated into a growing PG. We assumed ATG4-mediated LC3-II release from a closed vesicle to be a one-step process with rate constant k_rela = 10⁻⁶ sec⁻¹. The rate constants for processes that affect PG nucleation and termination of PG growth, k_for, k_nu, k_flux, k_ves and k_rela, are set such that the model predicts a small number of PGs relative to the number of closed vesicles (Fig. 7A–D). A relatively low abundance of PGs is consistent with ATG12 immunostaining (Fig. 7E).⁴²

Simulation of the mechanistic stochastic model

To simulate this model, we used a modified version of Gillespie’s method⁴¹ that allows for dynamic compartments. The 23 different reactions in our model (Eqns. 1–23) take place in different compartments, each of which is assumed to be well mixed. We considered a cytoplasmic compartment, in which WIPI1/2, LC3-I and mature AVs are found, and a membrane-of-origin compartment, from which all PGs emerge. In addition, each PG or mature AV is a separate compartment. Because PGs are produced and converted to mature AVs and because mature AVs are lost through fusion with lysosomes, the number of reaction compartments present in a cell is not static, but rather a function of time t.

Because the numbers of AVs in single cells can be small, we reasoned that a stochastic model is appropriate. Thus, we used a stochastic simulation algorithm to characterize the chemical kinetics of the reactions in the model (Eqns. 1–23). To present the algorithm, which is a simple variation of Gillespie’s method,⁴¹ we must be able to refer to the reactions being considered concisely and precisely. The nomenclature that we used for this purpose is defined in Figure 5B and was used to describe the stochastic simulation algorithm used in this study as follows:

(1) We specified the initial condition to be the steady-state basal condition (I = 4.48 × 10⁻⁶, Table 1). This condition represented the control medium in the absence of AZD8055 or BafA1. In the model, we specified the numbers of PtdIns3KC3, PtdIns, WIPI1/2, ATG9 and Y(LC3-I) (Table 1), and simulated the model to steady-state for a long time period (> 10,000 sec) at I = 4.48 × 10⁻⁶. This initial steady-state condition represented a relatively small number of AVs (n ~11), as observed in experiments (Fig. 6A).

(2) We computed the instaneous overall rate of reaction a₀, i.e., the sum of the rates of all possible reactions at the current time t: 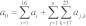, where a_i was the rate of reaction R_i and a_j,k was the rate of reaction R_j,k.

(3) We selected a random number ρ₁ from the uniform distribution U(0,1).

(4) If 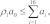we selected a reaction from among the set {R₁,R₂,…,R₁₆}. The index of the selected reaction is the least value of i for which 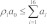holds true. The transformation of the selected reaction was applied (i.e., the selected reaction was fired), and counts of reactant and product species were updated. Rates of reactions were updated as needed. If the selected reaction is R₉ or R₁₆, a new PG was created, which introduced a new reaction compartment and a set of associated reactions and reaction rates.

(5) On the other hand, if 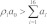, we selected a reaction R_j′,k′ from among the sets {R_1,17, R_1,18,…, X_1,23}, {R_2,17, R_2,18,…, X_2,23}, …,{R_n,17, R_n,18,…, X_n,23}. The indices of the selected reaction, j′ and k′, were such that 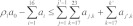holds true and 7(j′ – 1) + k′ was minimal. The selected reaction was fired, and counts of reactant and product species were updated. Rates of reactions were updated as needed. If the selected reaction had index k = 20, a mature AV was formed and a PG was lost in the process (Eqn. 20). The rates of the reactions that were affected by this transformation were updated. Reactions 17–20 were relevant for a PG, whereas Reactions 21–23 were relevant for a mature AV. Reactions were made active or inactive by assigning positive or zero rates, respectively. If the selected reaction had index k = 22, the list of visible and hidden AVs was updated. A visible AV was lost in the forward transformation in the reaction to produce a hidden AV, whereas a hidden AV was lost in the reverse transformation to produce a visible AV (Eqn. 22). If the selected reaction had index k = 23, a mature AV was lost through fusion with a lysosome, which removed a reaction compartment from the system and the set of associated reactions and reaction rates.

(6) We selected a random number ρ₂ from the uniform distribution U(0,1) and increment time by –ln(ρ₂)/a₀.

(7) We returned to Step 1. The procedure was iterated until a specified stopping criterion was satisfied.

For the individual simulation trajectories shown in Figure 6C–F, it should be noted that the model did not predict the outcome of any given experiment and that there was high variability from simulation run to simulation run as well as from experiment to experiment.

Glossary

Abbreviations:

TORC1

mechanistic target of rapamycin complex 1

ULK1

unc-51-like kinase 1 (C. elegans)

ATG13

autophagy-related 13 homolog (S. cerevisiae)

RB1CC1

RB1-inducible coiled-coil 1

PG

phagophore

PtdIns3KC3

class III phosphatidylinositol 3-kinase

ATG12

autophagy-related 12 homolog (S. cerevisiae)

ATG5

autophagy-related 5 homolog (S. cerevisiae)

ATG16L1

ATG16 autophagy-related 16-like 1 (S. cerevisiae)

LC3

microtubule-associated protein 1 light chain 3

Atg8

autophagy-related protein 8

AV

autophagic vesicle

EGFP

enhanced green fluorescent protein

BafA1

bafilomycin A₁

AZD8055

ATP-competitive inhibitor of MTOR

RPS6

ribosomal protein S6

DMSO

dimethylsulfoxide

PIKFYVE

phosphoinositide kinase, FYVE finger containing

WIPI1

WD repeat domain, phosphoinositide interacting 1

WIPI2

WD repeat domain, phosphoinositide interacting 2

ATG9

ATG9 autophagy-related 9 homolog (S. cerevisiae)

ATG4

ATG4 autophagy-related 4 homolog (S. cerevisiae)

AIC

Akaike information criterion

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Supplemental Materials

Supplemental materials may be found here:www.landesbioscience.com/journals/autophagy/article/22532