Abstract
Much of current understanding of cell motility arose from studying steady treadmilling of actin arrays. Recently, there have been a growing number of observations of a more complex, non-steady, actin behavior, including self-organized waves. It is becoming clear that these waves result from activation and inhibition feedbacks in actin dynamics acting on different scales, but the exact molecular nature of these feedbacks and respective roles of biomechanics and biochemistry are still unclear. Here, we review recent advances achieved in experimental and theoretical studies of actin waves and discuss mechanisms and physiological significance of wavy protrusions.
Introduction
Actin polymerization endows eukaryotic cells with, among other things, the ability to migrate and modulate cell shape [1]. Usually, cell migration is dissected into discrete steps: (i) protrusion based on actin growth and polymerization force, (ii) adhesion at the front, (iii) actin-myosin-powered contraction of the cytoplasm, (iv) release of adhesions at the rear, and (v) forward translocation of the cell body and recycling of the motility machinery [2]. Yet, much of our understanding of cell motility stems from studies of steadily and continuously treadmilling dendritic actin arrays in flat lamellipodia, in which nascent actin filaments are branched by Arp2/3 complex from the sides of existing elongating filaments pushing the leading edge forward until capped, while across the lamellipodium the capped filaments are disassembled by cofilin [3,4]. However, more often than not, cells in physiological circumstances move unsteadily, and so actin also exhibits a range of non-steady behavior including spatiotemporal patterns [5] for which our understanding is just beginning. A beautiful and paradigmatic example of such behavior comes from recent reports of actin traveling waves (t-waves).
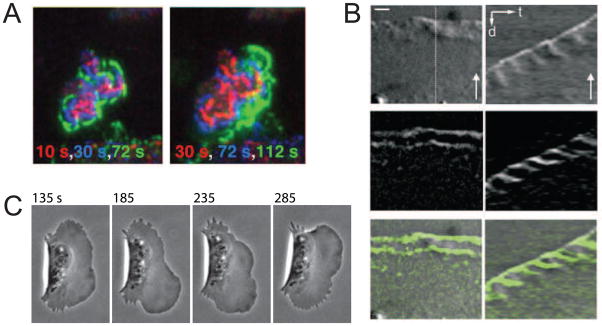
Early reports of actin t-waves traveling around the perimeter of human keratinocytes [6] and other cells types [7] preceded a recent windfall of reported t-waves [8–14]. Remarkably, one of the early reports posited that nonlinear mechanics of actin-myosin gels is responsible for the waves [6], while another proposed an underlying biochemical reaction-diffusion system [7]. The recent boom of actin t-waves studies was arguably triggered by reports that the Arp2/3 activator Hem-1 is not distributed uniformly on the ventral surface of neutrophils but rather exhibits irregular, F-actin-dependent t-waves that move towards the cell periphery [9] (Fig. 1A). In fibroblasts, local oscillations of protrusion and retraction at the edge are associated with waves of actin, myosin light chain kinase and alpha-actinin [14,15] that travel both rearward and laterally along the cell perimeter (Fig. 1B). Fish epithelial keratocytes exhibit robust t-waves of F-actin density and protrusion that travel along the leading edge [10] (Fig. 1C). When Dictyostelium cells are held away from a substrate, either electrostatically or by extending off a cliff, they exhibit rearward waves of curvature and protrusion [12].
Figure 1. Experimental observations of actin traveling waves.
(A) Waves of YFP-Hem1 on the ventral surface of neutrophils (reproduced from [9] under the CCA License). Time is indicated by color as the wave spreads outward. (B) Rearward waves of alpha-actinin in fibroblasts shown in micrograph (left) and kymograph (right) (reproduced from [14] with permission). Scale bars 2 microns, 30 sec. (C) Wave of protrusion across the keratocyte’s leading edge (provided by E. Barnhart).
T-waves extend across subcellular domains (Table 1) that may be the 1d cell edge [8,16]; 2d ventral [9,17,18] or dorsal [7] surfaces, or even 3d bulk of the cytoplasm [11]. Wave-like patterns are reported in a variety of cell types, some spreading [19], migrating [10] or stationary [8], and classifying these patterns and identifying common mechanisms is a daunting task. Major questions about the actin t-wave dynamics include: What combination of positive and negative feedbacks gives rise to t-waves? Do both mechanical and chemical pathways participate in t-waves? Given the diversity of cells exhibiting t-waves, do these patterns play a functional role? We complement a number of recent reviews, (see especially [5]), by outlining conceptual wave-generating mechanisms and the evidence for each in various cell types. We demonstrate that though actin t-waves appear to be highly cell-dependent, recent quantitative modeling, spawned by the need to augment qualitative arguments [20], demonstrates how this diversity is reconciled by the concept of excitability.
Table 1. Traveling waves in observation and theory.
We attempt to classify experimentally observed actin and protrusion t-waves by the wave propagation mechanism. Theoretical models are classified by the dominant spatial coupling that gives rise to spatial propagation. Note that we classify papers containing both theoretical models and experimental results under “experimental”.
| Spatial propagation | 1D domain | 2D or 3D domain | |
|---|---|---|---|
| Diffusion | exp | ||
| theory | |||
| Polymerization | exp | ||
| theory | |||
| Experimental, Yet to be classified | |||
| Stress (all 1D so far) | exp | ||
| theory | |||
| Pacemaker (all 2D so far) | exp | ||
| theory |
|
||
Diversity of mechanisms leading to traveling waves
Waving behavior is ubiquitous from population dynamics [21] to chemical reactions [22] to excitable waves in electrophysiology [23]. The concept of excitability (see Box) has provided valuable insight into actin t-waves. Evidence that a diversity of actin waves are well-described as excitable systems comes from, among other things, observations that they annihilate upon collision [9,11,24], which is a signature of the excitation waves. One way of obtaining excitability is by combining fast positive feedback coupled with slow negative feedback.
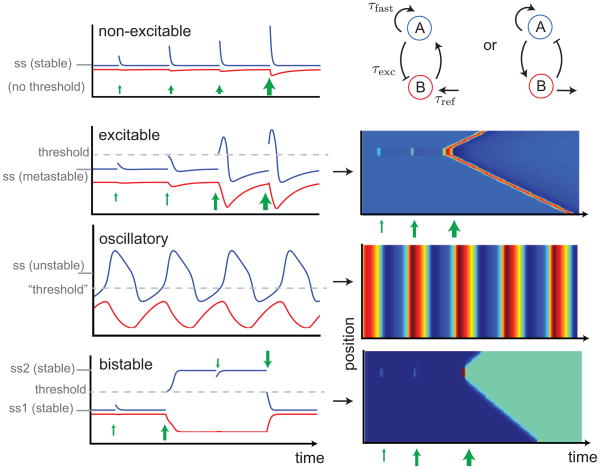
Box. Excitable dynamics.
Fast positive feedback combined with slow negative feedback is a motif that recurs in many biological systems. An example is a fast component A being local actin barbed-end density, and a slow component B being local density of an F-actin promoting factor or density of F-actin itself [8,9]. For some parameters, such a system has a unique stable steady state in which a stimulus in A, regardless of size, decays without significantly affecting B. By varying parameters, for example increasing the replenishment rate of B, the steady state of A is made less trivial and can give rise to a range of dynamics including excitability, oscillation and bistability (Box Figure).
Excitability arises from a steady state in which small perturbations decay, but perturbations larger than a threshold result in a large excursion that eventually, albeit indirectly, returns to the original steady state. The time taken to recover is known as the refractory period. Increasing the replenishment rate of B further effectively increases the steady state of A above the threshold; large excursions occur spontaneously and the system is intrinsically oscillatory. Bistability is when there are two stable steady states; perturbations larger than a threshold send the system into a different state.
When local dynamics are spatially coupled between neighboring areas, excitability allows for traveling waves pulses, while bistability allows for traveling wave fronts (Box Figure). In both cases, threshold perturbations are required somewhere in the domain to initiate the excitation, which spreads in all directions if prior conditions are spatially homogenous. Two colliding excitable waves annihilate, since each wave is trailed by a refractory region, making these distinct from, e.g., pressure waves. A wave train is a sequence of wave pulses; under certain conditions, oscillatory dynamics with spatial coupling give rise to wave trains [36], however these trains are not robust and often transition to synchronized oscillations [54].
Cellular wave-generating systems have more than two participants and multiple spatial couplings, but the above simple cases provide a framework for understanding more complex systems, e.g., which include long-range dynamics mediated by fast-diffusing regulators [27] or membrane tension [26] and which display exotic behaviors including “bipedal” oscillations in which two domains oscillate out of phase evocative of recent observations in cells [55], wave fronts that become “pinned” inside the domain [56,57], reflecting waves [27], periodic wave trains [28] and t-waves with dead zones [16].
Triggering each wave
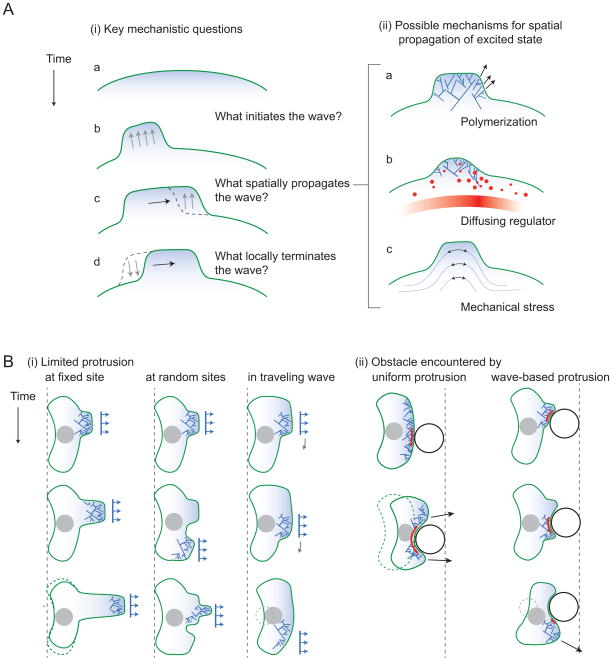
Once a system is capable of supporting excitation waves, in general each wave requires a perturbation to “kick-start” it (Box, Fig 2Ai), which must be greater than a threshold. A cell may transition into waving by upstream signaling events, such as activation of adhesions and consequent triggering of biochemical pathways. However, the simplest hypothesis for the source of this perturbation is a random fluctuation [8,25] in F-actin densities or concentrations of factors, possibly arising from inhomogeneities in the environment or thermal fluctuations. There is a narrow window for which random fluctuations are consistent with observed t-waves though: Too little, and fluctuations above the threshold will be rare; too large, and threshold fluctuations will effectively send the system into an oscillatory state in which t-waves are replaced by spatially-synchronized oscillations.
Figure 2. Major questions.
(A) Mechanisms of waving: (i) T-waves arising from excitability require an initial trigger, typically above a threshold, to initiate a wave (a–b). Once one subcellular region is excited, neighboring regions must be coupled for the wave to propagate (b–c). Many cells exhibit transient wave pulses, after which the region returns to its initial state (c–d). This return is posited to arise because of the depletion of a promoter or replenishment of an inhibitor. (ii) Three possible spatial couplings. (a) Polymerization of actin with a lateral component could transports the excited state. (b) Diffusion of a regulator. (c) Transmission of stress to neighboring regions. The stress could be mediated by the membrane or actin(-myosin) gel. (B) Possible functional roles of waving. (i) Migration in the face of limited resources. Unable to protrude uniformly along the entire leading edge, cells may focus their protrusive machinery to a limited region. If this region is stationary (a), protrusion may result in fingering and translocation of the cell body will not occur. (An alternative is narrowing of the migrating cell.) If the protruding region moves randomly (b), cell coherence could be jeopardized. A sequence of traveling waves (c) results in smooth translocation of the cell body, without affecting cell width. (ii) Avoidance of obstacles. A uniformly protruding leading edge could become stuck upon encountering an obstacle (black circle) if the stalled region (red) has no effective means of communicating with nearby regions of the edge. Waves of protrusion may circumvent this problem since the direction of cell migration is defined locally.
An alternative, more robust, kick-starter is a global negative feedback, which may be provided by membrane tension [26] or fast-diffusing inhibitors [27]. Under appropriate circumstances, localized excitations of F-actin occur spontaneously (for example, if the system is in an oscillatory regime). This could activate global negative feedback, transforming the localized activity into the seed of a t-wave. Recent observations of t-waves in keratocytes [28] demonstrate sequential waves, in which the subsequent wave appears shortly after the previous wave extinguishes. Global negative feedback is necessary for cells to have this apparent ability to limit themselves to one concurrent wave.
Spatial coupling
Regardless of the triggering mechanism, a t-wave requires a connection between neighboring subcellular regions. What mediates this spatial coupling? Three possibilities are summarized in Fig. 2Aii. The most widely hypothesized spatial coupling is the diffusion of an actin regulator molecule (see Table; Fig. 2Aii b) that either promotes or inhibits F-actin polymerization or branching. Such t-waves fall into the class of reaction-diffusion systems and their propagation velocity is proportional to the square root of the regulator’s diffusion coefficient [29], and also depends on the timescale of the regulator’s turnover, which could vary spatially and thus give rise to a spatially-dependent wave velocity as observed by Weiner et al [9]. Evidence for the identity of this regulator in various cells include various actin nucleating factors such as Hem1 [9].
An alternative possible spatial coupling arises from F-actin polymerization itself (Fig. 2Aii a). For example, Arp2/3-mediated branching of filaments occurs at +/− 35 degrees relative to the direction of actin network growth, so the protrusion is accompanied by the lateral propagation of the barbed end along the leading edge, allowing the possibility of propagating a t-wave. Coupling by polymerization predicts a wave propagation velocity that is proportional not to the square root of the diffusion coefficient of a chemical, but to the protrusion velocity, which has been confirmed in high-adhesion keratocyte waves [28].
A third possibility is that neighboring regions are mechanically coupled, and F-actin affects a regional increase in stress (Fig. 1Aii c). Several possibilities exist for what mediates the stress. One is the actin gel itself [30 – 31]). Another possibility involves membrane advancement or retraction, either in combination with membrane proteins that prefer membrane curvature [25] or simply by itself, which exerts additional stresses on nearby filaments by compression or stretching, if they are membrane-anchored [32]. Each of these has been theoretically shown to allow for t-waves. A recent study [33] reconstituted actin and myosin in an in vitro assays with profilin, Arp2/3 and its activator and observed t-waves of contraction and depolymerization in which myosin was an essential player. In stress-mediated t-waves, the wave propagation velocity would be proportional neither to the square root of the diffusion coefficient of a chemical, nor to the actin polymerization rate, but to some function of the mechanical moduli of the cytoskeleton. Using this distinction for experimental testing of the t-wave mechanisms may be complicated, as cell interiors are connected by a combination of all spatial couplings discussed above, each of which may generate a t-wave with a distinct propagation velocity. Theoretically speaking, the coupling that is fastest and capable of supporting excitable t-waves should be the one observed in a given cell. Note also that in contrast to well-studied examples of excitable media, actin polymerization phenomena are coupled to a phase transition, i.e. drastic changes in the transport and mechanical properties of the actin network. How this coupling affects the actin wave dynamics is an open question.
Terminating the excitation behind the wave
Once the wave has passed a subcellular domain, the region has to return to a steady state in which it can support future excitation. A favored mechanism to explain termination behind the wave is depletion (or accumulation) of an F-actin promoter (inhibitor) on a slower timescale, giving rise to a refractory period after excitation during which the promoter (inhibitor) replenishes (depletes). Without this, t-waves would manifest as t-wave fronts (Box) permanently invading the domain and remaining in the excited state. Progress has been made in identifying these “refractory” factors: In high-adhesion keratocyte t-waves [10], recent evidence suggests that it is a depletion of VASP and subsequent decrease of an anti-capping activity that extinguishes the actin protrusion [28]. Some models [8,9] hypothesize that the accumulation of the F-actin down-regulates a barbed-end nucleation factor, identified as Hem1 [9]. Machacek et al [13] suggest the depletion of G-actin or Arp2/3 as the effective inhibitor.
Traveling waves from non-excitable sources
One alternative to excitability for inducing t-waves is to use local oscillations as pacemakers [15]. Examples of pacemaker waves in other areas of biology include segmentation clocks in development [34] and rippling in bacterial colonies [35]. In such systems, a region (e.g., the leading edge) undergoes periodic, intrinsic oscillations, and these oscillations are transmitted by advection to neighboring regions (e.g., by retrograde flow) [15]. In this case, the t-wave velocity is the velocity of advection. Evidence for similar pacemaker waves in actin are reported in epithelial cells [15], where these waves originate from cycles of protrusion and retraction at the leading edge and travel rearward at the velocity of retrograde flow. We note that in order for pacemakers to result in robust t-waves, regions away from the pacemaker must not be intrinsically oscillatory, otherwise the domain will gradually settle into a synchronized oscillation (Box). (Under narrow circumstances, intrinsic oscillations can avoid synchronization and exhibit t-waves [36].)
A dramatic example of t-waves occurs in some blebbing cells [37]. Blebs are regions of the plasma membrane that have become transiently detached from the underlying actin cortex and bulge outward under cell pressure. Occasionally, a bleb migrates around the periphery of a cell in what is termed bleb circus movement [37]. These can be thought of as anti-actin t-waves, since the excited state is one in which actin is absent from the plasma membrane. Evidence suggests that spatial propagation is via pressure in the cytosolic fluid and refraction occurs when enough cortical actin and myosin have accumulated to retract the trailing edge of the bleb. These blebs appear to play a role in several instances of cell migration [38].
Functional role and physiological implications of actin traveling waves
Motility when protrusive machinery is scarce
If t-waves arise from such a diversity of mechanisms in a diversity of cell types, do they play a functional role that confers evolutionary fitness? One speculative idea concerns how cells respond when they do not have sufficient material to form a protrusion along their entire leading edge. This limiting material may include total actin, ingredients for focal adhesions, or actin-regulating proteins such as VASP. If an environmental or intracellular perturbation depletes this material, for example by moving to a higher adhesion surface [28], there are two possible cellular responses: If slight decreases in material result in a slightly hampered protrusion (i.e., the protrusive material is linear), then the cell can uniformly distribute the limited supply and suffer a slightly hampered migration. If, however, the protrusive machinery is highly nonlinear and there is a threshold below which the protrusion is entirely inhibited, migration requires the cell to concentrate its limited supply, resulting in a small region of protrusion (Fig 2Bi). Assuming that overall cell geometry is preserved, moving the protrusion by employing a t-wave would result in successful, albeit slow, translocation of the cell body. In comparison, protrusion at a fixed site would result in a finger-like protrusion without cell body translocation, and protrusion at random sites may jeopardize cell coherence. The question of how cells respond to a shortage of protrusive machinery is intimately linked to the mechanism determining cell width [39]. Indeed, in some circumstances cells may respond to limited protrusive machinery by becoming skinny (Fig. 2Bi left row), obfuscating this hypothesized need for protrusive t-waves.
Obstacle avoidance
An attractive hypothesis put forward by Weiner et al [9] is that, in the presence of obstacles, cell migration is favored by a wave-based form of protrusion rather than a uniform protrusion (Fig. 2Bii). The in situ environment of many cells is indeed crowded. The conceptual idea is that, in the case of uniform protrusion, a barrier that stalls a region of the cell’s leading edge may stall the entire cell or threaten cell coherence. Alternatively, if protrusions arise from waves with some degree of randomness, the leading edge will explore alternative routes around the obstacle. Indeed Bretschneider et al. [11] describe ventral waves as a “free-running actin assembly in search of a leading edge”. Cell strategies for avoidance were addressed in a recent theoretical study [40], where the authors simulated a cell that secretes a repellant to accelerate obstacle-avoidance. Similar simulations with wave-based protrusion will help to resolve whether t-waves play a role in obstacle avoidance, which for now remains a thought experiment.
‘Chimneying’ through 3D ECM
Another possibility is that protrusion waves at the cell sides act as paddles allowing cells to swim through viscous media [12]. This could be especially important for cells crawling through the 3D extracellular matrix (ECM): even though the ECM is not viscous, but rather elastic or viscoelastic, the t-waves at the cell sides could press on the ECM fibers and help the cell to ‘chimney’ through ECM pores, for example if adhesion to ECM is insufficient [41]. Actin t-waves could also aid in the search for larger ECM pores for protrusion. Other oscillatory mechanical strategies in 3d motility have recently been considered [42].
A side-effect of local excitability
It is possible that t-waves do no directly confer evolutionary advantage, but rather are a side-effect of local excitable dynamics which, when combined with the unavoidable spatial coupling, naturally give rise to t-waves (Box). The concept is similar to oscillations during the polarization of budding yeast [43], in which negative feedback confers robustness to the polarity cue, and the observed oscillations are a natural side-effect of negative feedback. What could be the role of excitability? If F-actin’s effects are highly nonlinear, then rapid, localized spikes in local F-actin density may be favored over a lower uniform density. Recent work [44] demonstrates that mechanisms for directional sensing leading to polarity in migration, such as local-excitation global-inhibition, can be made more responsive when coupled with local excitable dynamics, and that explains observed alternating “zig-zag” protrusion patterns.
Other possible functional roles include (i) possibility that actin waves scan a surface for particles that might be engulfed during phagocytosis [45], based on the observation that the phosphoinositide content of actin waves resembles the interior of phagocytic cups; (ii) effective closure of cell wounds by a centripetal wave of F-actin, Cdc42 and Rho recently shown to occur in the absence of contractility [46].
Open questions and future directions
Actin t-waves are observed in vitro [33,47], and one of the open questions is about the connection between these in vitro waves and those in the motile cells. If there is such connection, in vitro reconstitution will help understanding the minimal ingredients required for generating t-wave behavior. More generally, the molecular pathways underlying non-steady actin dynamics will have to be elucidated. These include the recently discovered ‘rocket launcher’ mechanism which involves a delicate balance of interactions between actin filaments, formins on growing barbed ends and the tumor suppressor adenomatous polyposis coli that jump-starts actin growth [48], as well as the complex interactions of actin dynamics, contractility and adhesion, which generate oscillatory behavior on many scales, from filopodia [49], to leading edges of flat protrusions [14,50–52], to whole-cell traction forces [53]. Of particular importance will be to analyze actin t-wave in 3d and to test their functional roles. Last but not least, quantitative understanding will require continuing collaboration between experimentalists and modelers, which proved to be crucial in the initial surge of the actin t-wave studies of the past decade.
Box figure.
Biochemical networks (top right) comprised of fast positive and slow negative feedbacks can exhibit qualitatively different behavior (time series, left) depending on parameters, on several timescales. Blue and red curves show behavior of molecular species A and B respectively. Steady state values of A marked by ss. Green arrows are external stimuli which instantaneously increases A and, if above a threshold (dashed lines), may relax to the only steady state, induce transient excitations in excitable systems, switch to a new steady state in bistable systems, or start fluctuating in oscillatory systems. In a region of space where each location exhibits the local dynamics shown on the left, as well as a spatial coupling to neighboring locations, spatiotemporal patterns of pulse wave, spatially uniform periodic oscillations, or wave of invasion emerge (kymographs, right).
A growing number of studies report observations of self-organized actin waves
A majority (not all) of actin waves occur in excitable cytoskeleton
Mechanochemical feedbacks cause wave triggering, termination and spatial coupling
Actin waves can help cell movement in crowded space or when protrusion is limited
Acknowledgments
This work was supported by NIH grant 2R01GM068952 and NSF grant DMS-1118206 to A.M and by an NSERC fellowship to J.A.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References and recommended reading
Papers of particular interest have been highlighted as:
• of special interest
•• of outstanding interest
- 1.Bray D. Cell Movements. Garland Science; 2001. [Google Scholar]
- 2.Sheetz MP, Felsenfeld D, Galbraith CG, Choquet D. Cell migration as a five-step cycle. Biochem Soc Symp. 1999;65:233–243. [PubMed] [Google Scholar]
- 3.Borisy GG, Svitkina TM. Actin machinery: pushing the envelope. Curr Opin Cell Biol. 2000;12:104–112. doi: 10.1016/s0955-0674(99)00063-0. [DOI] [PubMed] [Google Scholar]
- 4••.Carlsson AE. Dendritic Actin Filament Nucleation Causes Traveling Waves and Patches. Phys Rev Lett. 2010;104:228102. doi: 10.1103/PhysRevLett.104.228102. Anders Carlsson uses his pioneering stochastic simulation method to demonstrate computationally that actin growth via branching at a cell membrane containing nucleation-promoting factors transitions from patches of actin to waves at high actin concentration. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Ryan GL, Watanabe N, Vavylonis D. A review of models of fluctuating protrusion and retraction patterns at the leading edge of motile cells. Cytoskeleton. 2012 doi: 10.1002/cm.21017. [DOI] [PubMed] [Google Scholar]
- 6.Alt W, Brosteanu O, Hinz B, Kaiser HW. Patterns of spontaneous motility in videomicrographs of human epidermal keratinocytes (HEK) Biochem Cell Biol. 1995;73:441–459. doi: 10.1139/o95-051. [DOI] [PubMed] [Google Scholar]
- 7.Vicker MG. Eukaryotic cell locomotion depends on the propagation of self-organized reaction-diffusion waves and oscillations of actin filament assembly. Exp Cell Res. 2002;275:54–66. doi: 10.1006/excr.2001.5466. [DOI] [PubMed] [Google Scholar]
- 8••.Ryan GL, Petroccia HM, Watanabe N, Vavylonis D. Excitable Actin Dynamics in Lamellipodial Protrusion and Retraction. Biophysical Journal. 2012;102:1493–1502. doi: 10.1016/j.bpj.2012.03.005. After observing waves of protrusion at the lamellipodial leading edge and finding that they are driven by fluctuations of the actin polymerization rate, rather than by the retrograde flow, the authors propose a model of these actin dynamics as an excitable system in which a diffusive, autocatalytic activator causes actin polymerization. As Arp2/3-complex concentrations spiked several seconds before rise of F-actin concentration, the authors suggest that the Arp2/3 complex participates in an activation mechanism that includes additional diffuse components, while F-actin accumulation inhibits further activator accumulation. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9•.Weiner OD, Marganski WA, Wu LF, Altschuler SJ, Kirschner MW. An Actin-Based Wave Generator Organizes Cell Motility. PLoS Biol. 2007;5:e221. doi: 10.1371/journal.pbio.0050221. In this seminal paper that started the current actin waves’ boom, advanced light microscopy was used to follow the distribution of Hem-1, which is WAVE complex that activates Arp2/3 in neutrophils. The authors found that Hem-1 does not moves laterally, but exhibits complex cycles of activation and inhibition to generate waves of propagating Hem-1 and actin assembly. F-actin dynamics was essential for the waves, which annihilated upon collisions and showed zones of inhibition between consequitive waves. Based on analogy with previously studied waves in excitable systems, the authors suggested that mechanisms similar to those generating the action potentials in neuronal signaling are responsible for the actin waves that potentially explain the ability of cells to flow around barriers. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10••.Barnhart EL, Lee K-C, Keren K, Mogilner A, Theriot JA. An Adhesion-Dependent Switch between Mechanisms That Determine Motile Cell Shape. PLoS Biol. 2011;9:e1001059. doi: 10.1371/journal.pbio.1001059. Fish keratocytes that for decades were renown for their fast and steady protrusions exhibited traveling waves of protrusions when crawling on highly adhesive surfaces. The waves usually started at one side of the cell, propagated in 100–400 sec to another side and extinguished, after which another wave started. Interestingly, the wave lateral propagation speed was similar to the actin polymerization speed hinting that it is skewed growth of actin filaments rather than a biochemical oscillator coupled with diffusion that underlies the waves. The authors propose that a competition of the actin protrusion machinery with mature adhesion complexes for an unidentified molecular regulator is necessary for these protrusion waves. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11••.Bretschneider T, Anderson K, Ecke M, Muller-Taubenberger A, Schroth-Diez B, Ishikawa-Ankerhold HC, Gerisch G. The Three-Dimensional Dynamics of Actin Waves, a Model of Cytoskeletal Self-Organization. Biophysical Journal. 2009;96:2888–2900. doi: 10.1016/j.bpj.2008.12.3942. Three proteins are shown to form distinct three-dimensional patterns in the actin waves: Myosin-IB is enriched at the wave front and close to the plasma membrane, the Arp2/3 complex is distributed throughout the waves, and coronin forms a sloping layer on top of them. The authors suggest that propagation of the waves is based on an actin treadmilling mechanism, indicating a program, autonomous from signaling molecules, that couples actin polymerization to depolymerization and molecular motors in a three-dimensional pattern. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12••.Driscoll MK, McCann C, Kopace R, Homan T, Fourkas JT, Parent C, Losert W. Cell Shape Dynamics: From Waves to Migration. PLoS Comput Biol. 2012;8:e1002392. doi: 10.1371/journal.pcbi.1002392. Quantitative experiment demonstrates that cell shape of motile amoeba Dictyostelium discoideum, either adherent to the surface or not, changes in a wave-like manner, and that at the leading edge of adherent cells, curvature waves are associated with protrusive activity. The authors propose that the wave-like character of protrusions provides a plausible mechanism for the ability of cells both to swim in viscous fluids and to navigate complex three dimensional topography. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13•.Machacek M, Danuser G. Morphodynamic Profiling of Protrusion Phenotypes. Biophysical Journal. 2006;90:1439–1452. doi: 10.1529/biophysj.105.070383. Using advanced computational framework for tracking arbitrary complex cell boundary movements, the authors quantify the subtle process of bursts of protrusion initiating waves propagating transversally. Cells switch between bursts and waves dependent on the Rac1 activation level. The data support a model where activation of Rac1 mediates the propagation of protrusion waves, whose persistence depends on the relative abundance of activated Arp2/3 and polymerizable G-actin. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14•.Giannone G, Dubin-Thaler BJ, Rossier O, Cai Y, Chaga O, Jiang G, Beaver W, Döbereiner H-G, Freund Y, Borisy G, et al. Lamellipodial actin mechanically links myosin activity with adhesion-site formation. Cell. 2007;128:561–575. doi: 10.1016/j.cell.2006.12.039. The authors find that myosin pulls the rear of the lamellipodial actin network (which appears to sit above the lamellum), causing upward bending and edge retraction. The network then separates from the edge and condenses. Protrusion resumes as lamellipodial actin regenerates from the front and extends rearward until it reaches newly assembled myosin, initiating the next cycle. Thus, actin polymerization periodically builds the lamellipodium, connecting myosin motors with the initiation of adhesion sites, suggesting that the actin oscillator and retrograde waves are mechanical in nature. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Giannone G, Dubin-Thaler BJ, Döbereiner H-G, Kieffer N, Bresnick AR, Sheetz MP. Periodic lamellipodial contractions correlate with rearward actin waves. Cell. 2004;116:431–443. doi: 10.1016/s0092-8674(04)00058-3. [DOI] [PubMed] [Google Scholar]
- 16.Meinhardt H. Orientation of chemotactic cells and growth cones: models and mechanisms. Journal of Cell Science. 1999;112 ( Pt 17):2867–2874. doi: 10.1242/jcs.112.17.2867. [DOI] [PubMed] [Google Scholar]
- 17.Bretschneider T, Diez S, Anderson K, Heuser J, Clarke M, Müller-Taubenberger A, Köhler J, Gerisch G. Dynamic actin patterns and Arp2/3 assembly at the substrate-attached surface of motile cells. Curr Biol. 2004;14:1–10. doi: 10.1016/j.cub.2003.12.005. [DOI] [PubMed] [Google Scholar]
- 18.Case LB, Waterman CM. Adhesive F-actin Waves: A Novel Integrin-Mediated Adhesion Complex Coupled to Ventral Actin Polymerization. PLoS ONE. 2011;6:e26631. doi: 10.1371/journal.pone.0026631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dubin-Thaler BJ, Hofman JM, Cai Y, Xenias H, Spielman I, Shneidman AV, David LA, Döbereiner H-G, Wiggins CH, Sheetz MP. Quantification of Cell Edge Velocities and Traction Forces Reveals Distinct Motility Modules during Cell Spreading. PLoS ONE. 2008;3:e3735. doi: 10.1371/journal.pone.0003735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Mogilner A, Allard J, Wollman R. Cell polarity: quantitative modeling as a tool in cell biology. Science. 2012;336:175–179. doi: 10.1126/science.1216380. [DOI] [PubMed] [Google Scholar]
- 21.Fisher RA. The wave of advance of advantageous genes. Annals of Human Genetics. 1937;7:355–369. [Google Scholar]
- 22.Zaikin AN, Zhabotinsky AM. Concentration wave propagation in two-dimensional liquid-phase self-oscillating system. Nature. 1970;225:535–537. doi: 10.1038/225535b0. [DOI] [PubMed] [Google Scholar]
- 23.Hodgkin AL, Huxley AF. A quantitative description of membrane current and its application to conduction and excitation in nerve. J Physiol (Lond) 1952;117:500–544. doi: 10.1113/jphysiol.1952.sp004764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Döbereiner H-G, Dubin-Thaler BJ, Hofman JM, Xenias HS, Sims TN, Giannone G, Dustin ML, Wiggins CH, Sheetz MP. Lateral Membrane Waves Constitute a Universal Dynamic Pattern of Motile Cells. Phys Rev Lett. 2006;97:038102. doi: 10.1103/PhysRevLett.97.038102. [DOI] [PubMed] [Google Scholar]
- 25.Shlomovitz R, Gov N. Membrane Waves Driven by Actin and Myosin. Phys Rev Lett. 2007;98:168103. doi: 10.1103/PhysRevLett.98.168103. [DOI] [PubMed] [Google Scholar]
- 26.Houk AR, Jilkine A, Mejean CO, Boltyanskiy R, Dufresne ER, Angenent SB, Altschuler SJ, Wu LF, Weiner OD. Membrane Tension Maintains Cell Polarity by Confining Signals to the Leading Edge during Neutrophil Migration. Cell. 2012;148:175–188. doi: 10.1016/j.cell.2011.10.050. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Holmes WR, Carlsson AE, Edelstein-Keshet L. Regimes of wave type patterning driven by refractory actin feedback: transition from static polarization to dynamic wave behaviour. Phys Biol. 2012;9:046005. doi: 10.1088/1478-3975/9/4/046005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Barnhart EL, Allard J, Boehm H, Spatz JP, Mogilner A, Theriot JA. Traveling waves in crawling cells. (in preparation) [Google Scholar]
- 29.Edelstein-Keshet L. Mathematical models in biology. SIAM; 2005. [Google Scholar]
- 30.Stephanou A, Chaplain MAJ, Tracqui P. A mathematical model for the dynamics of large membrane deformations of isolated fibroblasts. Bull Math Biol. 2004;66:1119–1154. doi: 10.1016/j.bulm.2003.11.004. [DOI] [PubMed] [Google Scholar]
- 31.Alt W, Dembo M. Cytoplasm dynamics and cell motion: two-phase flow models. Math Biosci. 1999;156:207–228. doi: 10.1016/s0025-5564(98)10067-6. [DOI] [PubMed] [Google Scholar]
- 32.Enculescu M, Sabouri-Ghomi M, Danuser G, Falcke M. Modeling of Protrusion Phenotypes Driven by the Actin-Membrane Interaction. Biophysical Journal. 2010;98:1571–1581. doi: 10.1016/j.bpj.2009.12.4311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33••.Reymann A-C, Boujemaa-Paterski R, Martiel J-L, Guérin C, Cao W, Chin HF, La Cruz De EM, Théry M, Blanchoin L. Actin network architecture can determine myosin motor activity. Science. 2012;336:1310–1314. doi: 10.1126/science.1221708. Beautiful in vitro study one of which findings is that myosins selectively contract and disassemble antiparallel actin structures, while parallel actin bundles remain unaffected. This leads to traveling actin-myosin wave coupled with actin disassembly. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Baker RE, Schnell S, Maini PK. Waves and patterning in developmental biology: vertebrate segmentation and feather bud formation as case studies. Int J Dev Biol. 2009;53:783–794. doi: 10.1387/ijdb.072493rb. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Igoshin OA, Mogilner A, Welch RD, Kaiser D, Oster G. Pattern formation and traveling waves in myxobacteria: theory and modeling. P Natl Acad Sci Usa. 2001;98:14913–14918. doi: 10.1073/pnas.221579598. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Murray J. Mathematical Biology. Springer-Verlag; 2007. [Google Scholar]
- 37.Charras GT, Coughlin M, Mitchison TJ, Mahadevan L. Life and times of a cellular bleb. Biophysical Journal. 2008;94:1836–1853. doi: 10.1529/biophysj.107.113605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Charras G, Paluch E. Blebs lead the way: how to migrate without lamellipodia. Nat Rev Mol Cell Biol. 2008;9:730–736. doi: 10.1038/nrm2453. [DOI] [PubMed] [Google Scholar]
- 39.Mogilner A, Keren K. The Shape of Motile Cells. Current Biology. 2009;19:R762–R771. doi: 10.1016/j.cub.2009.06.053. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Hecht I, Levine H, Rappel W-J, Ben-Jacob E. “Self-Assisted” Amoeboid Navigation in Complex Environments. PLoS ONE. 2011;6:e21955. doi: 10.1371/journal.pone.0021955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Lämmermann T, Sixt M. Mechanical modes of “amoeboid” cell migration. Curr Opin Cell Biol. 2009;21:636–644. doi: 10.1016/j.ceb.2009.05.003. [DOI] [PubMed] [Google Scholar]
- 42.Allena R, Aubry D. ‘Run-and-tumble’ or ‘look-and-run’? A mechanical model to explore the behavior of a migrating amoeboid cell. J Theor Biol. 2012;306:15–31. doi: 10.1016/j.jtbi.2012.03.041. [DOI] [PubMed] [Google Scholar]
- 43.Howell AS, Jin M, Wu C-F, Zyla TR, Elston TC, Lew DJ. Negative Feedback Enhances Robustness in the Yeast Polarity Establishment Circuit. Cell. 2012;149:322–333. doi: 10.1016/j.cell.2012.03.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Xiong Y, Huang C-H, Iglesias PA, Devreotes PN. Cells navigate with a local-excitation, global-inhibition-biased excitable network. P Natl Acad Sci Usa. 2010;107:17079–17086. doi: 10.1073/pnas.1011271107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gerisch G, Ecke M, Schroth-Diez B, Gerwig S, Engel U, Maddera L, Clarke M. Self-organizing actin waves as planar phagocytic cup structures. Cell Adh Migr. 2009;3:373–382. doi: 10.4161/cam.3.4.9708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Burkel B, Benink H, Vaughan E, von Dassow G, Bement W. SA Rho GTPase Signal Treadmill Backs a Contractile Array. Dev Cell. 2012;23:384–396. doi: 10.1016/j.devcel.2012.05.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Schaller V, Weber C, Semmrich C, Frey E, Bausch AR. Polar patterns of driven filaments. Nature. 2010;467:73–77. doi: 10.1038/nature09312. [DOI] [PubMed] [Google Scholar]
- 48.Breitsprecher D, Jaiswal R, Bombardier JP, Gould CJ, Gelles J, Goode BL. Rocket launcher mechanism of collaborative actin assembly defined by single-molecule imaging. Science. 2012;336:1164–1168. doi: 10.1126/science.1218062. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Chan CE, Odde DJ. Traction dynamics of filopodia on compliant substrates. Science. 2008;322:1687–1691. doi: 10.1126/science.1163595. [DOI] [PubMed] [Google Scholar]
- 50.Machacek M, Hodgson L, Welch C, Elliott H, Pertz O, Nalbant P, Abell A, Johnson GL, Hahn KM, Danuser G. Coordination of Rho GTPase activities during cell protrusion. Nature. 2009;461:99–103. doi: 10.1038/nature08242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Shemesh T, Verkhovsky AB, Svitkina TM, Bershadsky AD, Kozlov MM. Role of Focal Adhesions and Mechanical Stresses in the Formation and Progression of the Lamellum Interface. Biophysical Journal. 2009;97:1254–1264. doi: 10.1016/j.bpj.2009.05.065. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Burnette DT, Manley S, Sengupta P, Sougrat R, Davidson MW, Kachar B, Lippincott-Schwartz J. A role for actin arcs in the leading-edge advance of migrating cells. Nat Cell Biol. 2011;13:371–382. doi: 10.1038/ncb2205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Bastounis E, Meili R, Alonso-Latorre B, del Álamo JC, Lasheras JC, Firtel RA. The SCAR/WAVE complex is necessary for proper regulation of traction stresses during amoeboid motility. Mol Biol Cell. 2011;22:3995–4003. doi: 10.1091/mbc.E11-03-0278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Fall C, Marland E, Wagner J, Tyson J. Computational Cell Biology. Springer; 2010. [Google Scholar]
- 55.Barnhart EL, Allen GM, Julicher F, Theriot JA. Bipedal Locomotion in Crawling Cells. Biophysical Journal. 2011;98:933–942. doi: 10.1016/j.bpj.2009.10.058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Mori Y, Jilkine A, Edelstein-Keshet L. Wave-pinning and cell polarity from a bistable reaction-diffusion system. Biophysical Journal. 2008;94:3684–3697. doi: 10.1529/biophysj.107.120824. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Jilkine A, Edelstein-Keshet L. A Comparison of Mathematical Models for Polarization of Single Eukaryotic Cells in Response to Guided Cues. PLoS Comput Biol. 2011;7:e1001121. doi: 10.1371/journal.pcbi.1001121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Zeng Y, Lai T, Koh CG, Leduc PR, Chiam K-H. Investigating Circular Dorsal Ruffles through Varying Substrate Stiffness and Mathematical Modeling. Biophysical Journal. 2011;101:2122–2130. doi: 10.1016/j.bpj.2011.09.047. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59••.Tkachenko E, Sabouri-Ghomi M, Pertz O, Kim C, Gutierrez E, Machacek M, Groisman A, Danuser G, Ginsberg MH. Protein kinase A governs a RhoA-RhoGDI protrusion-retraction pacemaker in migrating cells. Nat Cell Biol. 2011 doi: 10.1038/ncb2231. The authors use live-cell imaging of biosensors and correlative image analysis to examine the role of cyclic-AMP-activated protein kinase A (PKA) in protrusion regulation. PKA activity at the leading edge is synchronized with rapid protrusion and with the activity of RhoA. Ensuing PKA phosphorylation of RhoA and the resulting increased interaction between RhoA and RhoGDI (Rho GDP-dissociation inhibitor) establish a negative feedback mechanism. Cooperation between PKA, RhoA and RhoGDI forms a pacemaker that governs the waves of protrusion. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Killich T, Plath PJ, Ha EC, Xiang W, Bultmann H, Rensing L, Vicker MG. Cell movement and shape are non-random and determined by intracellular, oscillatory rotating waves in Dictyostelium amoebae. Biosystems. 1994;33:75–87. doi: 10.1016/0303-2647(94)90048-5. [DOI] [PubMed] [Google Scholar]
- 61.Vicker MG, Grutsch JF. Dual chemotaxis signalling regulates Dictyostelium development: Intercellular cyclic AMP pulses and intracellular F-actin disassembly waves induce each other. European Journal of Cell Biology. 2008;87:845–861. doi: 10.1016/j.ejcb.2008.03.010. [DOI] [PubMed] [Google Scholar]
- 62.Vicker MG. F-actin assembly in Dictyostelium cell locomotion and shape oscillations propagates as a self-organized reaction-diffusion wave. Febs Lett. 2002;510:5–9. doi: 10.1016/s0014-5793(01)03207-0. [DOI] [PubMed] [Google Scholar]
- 63.Cirit M, Krajcovic M, Choi CK, Welf ES, Horwitz AF, Haugh JM. Stochastic Model of Integrin-Mediated Signaling and Adhesion Dynamics at the Leading Edges of Migrating Cells. PLoS Comput Biol. 2010;6:e1000688. doi: 10.1371/journal.pcbi.1000688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Nishimura SI, Ueda M, Sasai M. Cortical Factor Feedback Model for Cellular Locomotion and Cytofission. PLoS Comput Biol. 2009;5:e1000310. doi: 10.1371/journal.pcbi.1000310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Whitelam S, Bretschneider T, Burroughs N. Transformation from Spots to Waves in a Model of Actin Pattern Formation. Phys Rev Lett. 2009;102:198103. doi: 10.1103/PhysRevLett.102.198103. [DOI] [PubMed] [Google Scholar]
- 66.Gerisch G, Bretschneider T, Müller-Taubenberger A, Simmeth E, Ecke M, Diez S, Anderson K. Mobile actin clusters and traveling waves in cells recovering from actin depolymerization. Biophysical Journal. 2004;87:3493–3503. doi: 10.1529/biophysj.104.047589. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Schroth-Diez B, Gerwig S, Ecke M, Hegerl R, Diez S, Gerisch G. Propagating waves separate two states of actin organization in living cells. HFSP Journal. 2009;3:412–427. doi: 10.2976/1.3239407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Doubrovinski K, Kruse K. Cytoskeletal waves in the absence of molecular motors. European Physics Letters. 2008;83:18003. [Google Scholar]
- 69.Gov NS, Gopinathan A. Dynamics of Membranes Driven by Actin Polymerization. Biophysical Journal. 2006;90:454–469. doi: 10.1529/biophysj.105.062224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Veksler A, Gov NS. Calcium-actin waves and oscillations of cellular membranes. Biophysical Journal. 2009;97:1558–1568. doi: 10.1016/j.bpj.2009.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Enculescu M, Falcke M. Actin-based propulsion of spatially extended objects. New J Phys. 2011;13:053040. [Google Scholar]
- 72.Enculescu M, Gholami A, Falcke M. Dynamic regimes and bifurcations in a model of actin-based motility. Phys Rev E. 2008;78:031915. doi: 10.1103/PhysRevE.78.031915. [DOI] [PubMed] [Google Scholar]