Abstract
Circadian (∼24 h) timekeeping is essential for the lives of many organisms. To understand the biochemical mechanisms of this timekeeping, we have developed a detailed mathematical model of the mammalian circadian clock. Our model can accurately predict diverse experimental data including the phenotypes of mutations or knockdown of clock genes as well as the time courses and relative expression of clock transcripts and proteins. Using this model, we show how a universal motif of circadian timekeeping, where repressors tightly bind activators rather than directly binding to DNA, can generate oscillations when activators and repressors are in stoichiometric balance. Furthermore, we find that an additional slow negative feedback loop preserves this stoichiometric balance and maintains timekeeping with a fixed period. The role of this mechanism in generating robust rhythms is validated by analysis of a simple and general model and a previous model of the Drosophila circadian clock. We propose a double-negative feedback loop design for biological clocks whose period needs to be tightly regulated even with large changes in gene dosage.
Keywords: biological clocks, circadian rhythms, gene regulatory networks, mathematical model, robustness
Introduction
Circadian (∼24 h) clocks time many physiological and metabolic processes. When these clocks were first discovered, three basic properties were identified (Dunlap et al, 2004). (1) Rhythms need to be autonomous. (2) Rhythms need to be capable of adjusting in response to external signals. (3) Rhythms need to persist over a wide range of temperatures. More recently, the biochemical mechanisms of circadian timekeeping have been identified (Ko and Takahashi, 2006). In particular, interlocked transcription–translation feedback loops (TTFLs) have been discovered as the basic mechanism of rhythm generation in many organisms (Novak and Tyson, 2008). With this discovery, recent experimentation has identified another property of circadian rhythms in higher organisms. Circadian rhythms persist with a 24-h period even in the presence of large changes in the expression of the components of these TTFLs (Ko and Takahashi, 2006; Dibner et al, 2009). While mechanisms for rhythm generation with a flexible period have been identified (Stricker et al, 2008; Tsai et al, 2008; Tigges et al, 2009), mechanisms for this robustness of period to gene dosage remain unexplained, even by mathematical models (Dibner et al, 2009).
Two interlocked negative feedback loops have been identified in the TTFL networks generating circadian rhythms in higher organisms (Figure 1) (Blau and Young, 1999; Glossop et al, 1999; Benito et al, 2007; Liu et al, 2008). A ‘core’ negative feedback loop consists of repressors (PERIOD and TIMELESS in Drosophila or PERIOD1–3 and CRYPTOCHROME1–2 in mammals), which inactivate activators (CYCLE and CLOCK in Drosophila and BMAL1–2 and CLOCK in mammals) of their own transcription. An additional negative feedback loop controls the expression of the activators, which inactivate their own transcription through Vrille (Drosophila) or the Rev-erbs genes (Mammals) (Blau and Young, 1999; Preitner et al, 2002). While other feedback loops have also been identified, these two negative feedback loops seem to predominate (Blau and Young, 1999; Glossop et al, 1999; Benito et al, 2007; Liu et al, 2008; Bugge et al, 2012; Cho et al, 2012).
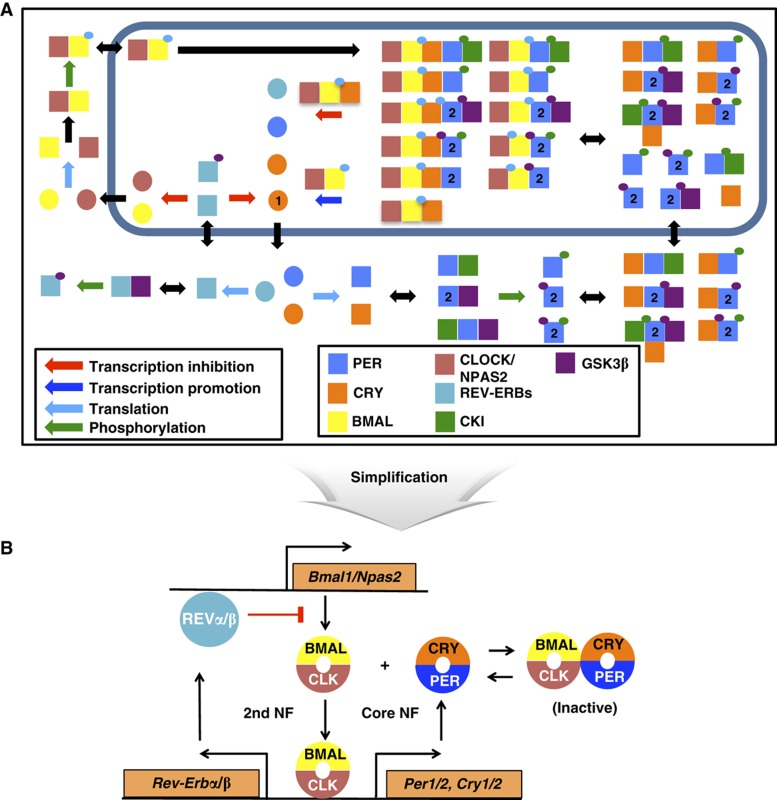
Figure 1.
Schematic of the detailed mammalian circadian clock model. (A) Only some of the relevant species are shown. Circles refer to transcripts and squares are proteins, possibly in complex. Small circles refer to phosphorylation states that are color coded by the kinases that perform the phosphorylation. See section ‘Description of the detailed model’ in Supplementary information for details. (B) The detailed model consists of a core negative feedback loop and an additional negative feedback loop (the NNF structure). The repressors (PER1–2 and CRY1–2) inactivate the activators (BMALs and CLOCK/NPAS2) of their own transcription expression through the core negative feedback loop. The activators inactivate their own transcription expression by inducing the Rev-erbs through the secondary negative feedback loop.
Near 24-h oscillations persist even when the components of the TTFLs of the circadian clock are over or under expressed. Heterozygous mutations of clock genes never abolish rhythmicity, and their period phenotypes are either indistinguishable from the wild-type (WT) phenotypes or much smaller than mutations that affect post-translational modifications (Baggs et al, 2009; Etchegaray et al, 2009; Lee et al, 2009). Abolishing rhythmicity through single gene knockout is surprisingly difficult (Baggs et al, 2009; Ko et al, 2010). Moreover, the mammalian circadian clock is also resistant to global changes in transcription rates (Dibner et al, 2009). These results all suggest that gene dosage may not be important for circadian timekeeping in higher organisms.
Gene dosage, however, is not completely unimportant for timekeeping. Knockdown of clock genes causes increased expression in similar components through paralog compensation, which may help restore gene dosage and indicates that gene dosage needs to be tightly regulated (Baggs et al, 2009). Population rhythmicity in mouse embryonic fibroblasts shows much lower amplitude than in liver, which might be due to the fact that the ratio of repressors to activators is significantly lower in fibroblasts than that found in liver (Lee et al, 2001, 2011). A 1–1 stoichiometric binding occurs between the activators and repressors driving rhythms in Drosophila (Menet et al, 2010), although not in Neurospora (He et al, 2005; Huang et al, 2007).
Here, we propose a mechanistic explanation for the robustness to gene dosage in the circadian clock of higher organisms through mathematical modeling. We develop the most detailed mathematical model of the mammalian circadian clock available, which should be useful in many future studies. Our model reproduces a surprising amount of experimental data on the mammalian circadian clock including the time courses and relative concentrations of key transcripts and proteins, the effects of mutations of key clock genes, and the effects of changes in gene dosage. With this model, we show that proper stoichiometric balance between activators (BMAL–CLOCK/NPAS2) and repressors (PER1–2/CRY1–2) is key to sustained oscillations. Furthermore, we find that an additional slow negative feedback loop, in which activators indirectly inactivate themselves, improves the regulation of the stoichiometric balance and sustains oscillations with a nearly constant period over a large change in gene expression level. Tight binding between activators and repressors is also predicted to be crucial for rhythm generation. These mechanisms are also validated by mathematical analysis of a simplified mathematical model of the mammalian circadian clock, and simulations of a previously published Drosophila model. We here propose a novel design for biological oscillators where maintaining period is crucial: a core negative feedback loop with repression by protein sequestration, with an additional negative feedback loop, which controls a relatively stable activator.
Results
Mathematical modeling of the mammalian circadian clock
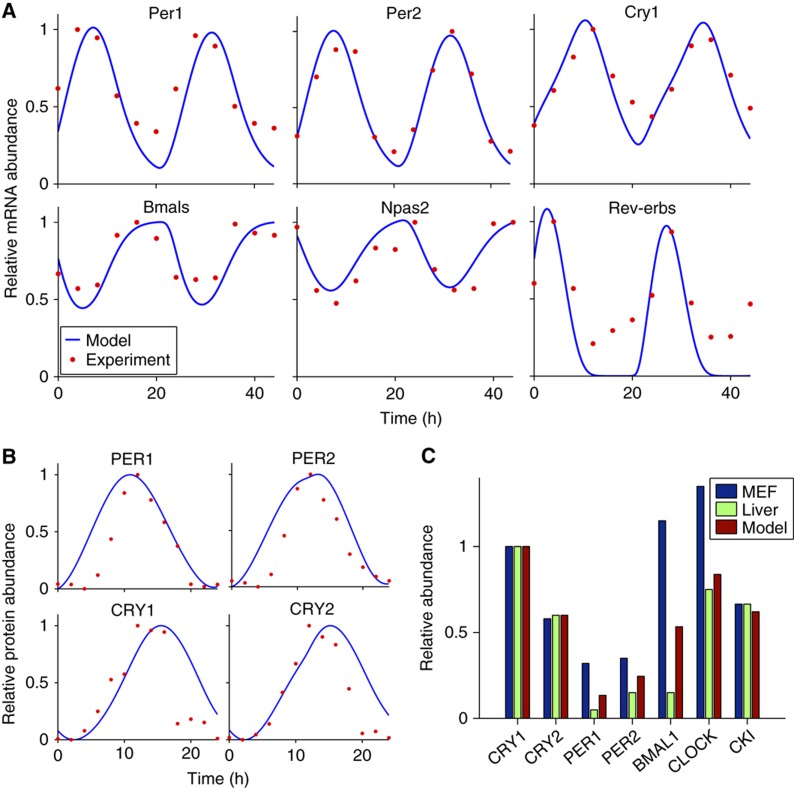
We develop a new mathematical model of the intracellular mammalian circadian clock. This model contains key genes, mRNAs and proteins (PER1, PER2, CRY1, CRY2, BMAL1/2, NPAS2, CLOCK, CKIε/δ, GSK3β, Rev-erbα/β) that have been found to be central to mammalian circadian timekeeping (Figure 1A). While greatly expanded, the model is largely based on our previous model, which has made surprising predictions about mammalian timekeeping that have been subsequently verified experimentally (Forger and Peskin, 2003; Gallego et al, 2006; Ko et al, 2010; Yamada and Forger, 2010). Modifications and extensions of the model are described in the Materials and methods, Supplementary information and Supplementary Tables 1 and 2. The parameters of the model are estimated using experimental data and a simulated annealing method (a global stochastic parameter searcher) (Gonzalez et al, 2007) (see Materials and methods, Supplementary information and Supplementary Table 3 for details). In particular, we incorporated experimentally determined rate constants (Supplementary Table 3) (Kwon et al, 2006; Siepka et al, 2007; Chen et al, 2009; Suter et al, 2011), fit the time courses of both mRNA and proteins (Figure 2A and B) (Lee et al, 2001; Reppert and Weaver, 2001; Ueda et al, 2005) and fit the relative abundance of proteins (Figure 2C) (Lee et al, 2001).
Figure 2.
Validation of the detailed model. (A) Predicted mRNAs time courses in SCN (Ueda et al, 2005). Time courses were normalized so that the peak value is 1, matching experimental data. (B) Predicted protein time courses in SCN (Reppert and Weaver, 2001). As had been done previously, we normalize the protein time courses so that the maximum is 1 and the minimum is 0. (C) Model comparison of the relative abundance of proteins in liver and fibroblast (Lee et al, 2001, 2009, 2011). All of the values were normalized so that the maximum abundance of the CRY1 protein is 1. For the CKIε/δ, CKIε maximal expression is ∼22.5% of the maximum abundance of CRY1 in the liver (Lee et al, 2001) and CKIδ is two times more abundant than CKIε in the fibroblast (Lee et al, 2009). From this, we assumed that total CKIε/δ would be ∼67.5% of the maximum value of CRY1 in mice liver and fibroblast.
Our model accurately predicts the phenotype of known mutations of genes in the central circadian clock (suprachiasmatic nuclei, SCN) (Yoo et al, 2005; Baggs et al, 2009; Ko et al, 2010), which other models do not predict (Table I) (Forger and Peskin, 2003; Leloup and Goldbeter, 2003; Mirsky et al, 2009; Relógio et al, 2011). Interestingly, our model shows opposite phenotypes for Cry1−/− and Cry2−/− matching experimental data (Liu et al, 2007). There are two differences between CRY1 and CRY2 in our model. First, Cry1 transcription is delayed through repression by Rev-erbα and Rev-erbβ (Preitner et al, 2002; Liu et al, 2008; Ukai-Tadenuma et al, 2011). Additionally, Cry1 mRNA is more stable than Cry2 mRNA and CRY1 protein is more stable than CRY2 protein (Busino et al, 2007; Siepka et al, 2007; Chen et al, 2009). Since a longer half-life causes rhythms to be delayed, and delayed rhythms cause a longer period (Forger, 2011; Ukai-Tadenuma et al, 2011), removing CRY1 shortens the period and removing CRY2 lengthens the period. The opposite phenotypes of Clock−/− (null mutation) and ClockΔ19/+ (dominant-negative mutation) are also correctly simulated in the model for the first time (Vitaterna et al, 1994; Herzog et al, 1998; Debruyne et al, 2006). Moreover, our model also predicts the mutant phenotypes of isolated SCN neurons, which are different from the SCN slices (Liu et al, 2007). We note that SCN slices have significantly higher gene expression of per1 and per2 through CREB/CRE pathway than isolated SCN neurons (Yamaguchi et al, 2003). Interestingly, when we reduced per1 and per2 expression about 60% in our model, our model was able to accurately reproduce the phenotypes of isolated SCN neurons (Table II).
Table 1. Comparison of model predictions with experimental data and previous model predictions on the phenotypes of circadian mutations.
| Gene | SCN | Animal | New model | Relógio et al (2011) | Mirsky et al (2009) | Leloup and Goldbeter (2003) | Forger and Peskin (2003) |
|---|---|---|---|---|---|---|---|
| Cry1 −/− | Short | Short | −1 | Long | AR | Short | WT |
| Cry2 −/− | Long | Long | +1.6 | Long | Long | Short | Long |
| Per1 −/− | WT | AR | AR | Short | Long | ||
| Per1 ldc | WT | Short/AR | |||||
| Per2 −/− | AR | AR | AR | Short | Short | ||
| Per2 ldc | Short/AR | ||||||
| Bmal1 −/− | SR** | AR | AR | AR | AR | AR | |
| Bmal1 −/+ | WT* | +0.1 | AR | NA | AR | Long | |
| Clock −/− | WT | Short | −0.2 | Long | AR | AR | AR |
| Clock Δ19/Δ19 | AR* | Long | AR | Long | NA | NA | NA |
| Clock Δ19/+ | Long* | +1.1 | Long | NA | NA | NA | |
| Npas2 −/− | WT | Short | WT | NA | NA | NA | NA |
| Rev-erbα−/− | Short | −0.2 | AR | Short | NA | WT | |
| CK1εtau/tau | Short | Short | −3 | NA | NA | Short | Short |
Here we indicate whether the phenotype predicted by our model, or seen in experimental data is WT, stochastically rhythmic (SR), arrhythmic (AR) or shows a change in period in hours. Experimental data can be found in Baggs et al (2009) as well as references cited therein, except those marked with * which can be found in Yoo et al (2005) and ** which can be found in Ko et al (2010). See Materials and methods for details. Bold represents different phenotype prediction of previous models from the new model. NA represents not available. For the Leloup–Goldbeter model, first parameter set of the model is used.
Table 2. Comparison of modified model predictions with experimental data of single SCN neurons on the phenotypes of circadian mutations.
| Gene | dSCN | Model |
|---|---|---|
| Cry1 −/− | AR | AR |
| Cry2 −/− | Long | +2.3 |
| Per1 −/− | AR | |
| Per1 ldc | AR | |
| Bmal1 −/− | AR* | AR |
Here, we indicate whether the phenotype predicted by our model, or seen in experimental data is arrhythmic (AR) or shows a change in period in hours. Experimental data can be found in Liu et al (2007), except those marked with * which can be found in Ko et al (2010). See Materials and methods for details.
We also conducted a sensitivity analysis to look at what parameters determine the period of our model. Four of the top five high parameters, in our sensitivity analysis, were also in the top five found in a previous sensitivity analysis with the original Forger and Peskin model and which was used to conclude that PER2 plays a dominant role in period determination (Wilkins et al, 2007) (see Supplementary Figure 1).
Proper stoichiometric balance between activators and repressors is crucial to sustained rhythms
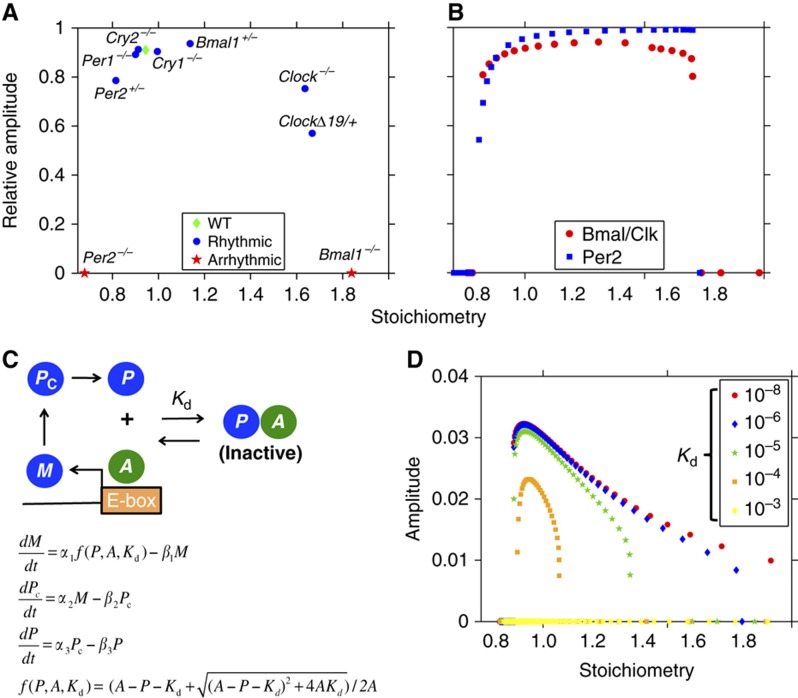
Since our mathematical model can accurately predict the phenotype of known mutations of the mammalian circadian clock, we next looked for a mechanism that could explain why some phenotypes were rhythmic, while others were not. We found that stoichiometry plays a key role in determining which mutations showed rhythmic phenotypes. Here, we define stoichiometry as the average ratio between the concentration of repressors (all forms of PER and CRY in the nucleus) to that of activators (all forms of BMAL–CLOCK/NPAS2 in the nucleus) over a period. Moreover, we specifically refer to repressors and activators of E/E’-boxes when discussing stoichiometry. We found that mutations that caused the stoichiometry to be too high or too low, yielded arrhythmic phenotypes (Figure 3A). So long as the mutations allowed the stoichiometry to be around a 1–1 ratio, relatively high amplitude oscillations were seen. Thus, we predict that stoichiometry provides a unifying principle to determine the rhythmicity of mutations of the mammalian circadian clock. To further test this principle, we constitutively expressed either the Per2 gene (the dominant repressor gene) or the Bmal and Clock genes (the dominant activator genes) at different levels. Interestingly, within a range centered near a 1–1 stoichiometry, the model shows sustained oscillations with high amplitude (Figure 3B). However, if the stoichiometry was too high or too low, rhythms are dampened or completely absent (Figure 3B). This matches a recent experimental study showing that the amplitude and sustainability of population rhythms increase when the level of PER–CRY is increased closer to that of BMAL1–CLOCK in mouse fibroblasts (Lee et al, 2011).
Figure 3.
Proper stoichiometry between activators and repressors is the key to sustained oscillations. (A) Our detailed mathematical model accurately predicts the phenotype of the known mutations in circadian genes (Table I). We plot the stoichiometry predicted by our model in these mutants with the relative amplitude of Per1 mRNA rhythms (or Per2 mRNA when considering the Per1−/−). Here, an amplitude of zero means rhythms are not sustained. These results indicate that the phenotype of the mutants can be predicted by their effects on stoichiometry. (B) The stoichiometry between repressors and activators is changed by constitutively expressing either the Per2 gene or the Bmals and Clock genes at different levels. Note that the model is rhythmic only when the stoichiometry is near 1–1. The relative amplitude of the Per1 mRNA is measured. (C) Schematic of a simplified model based on the Goodwin oscillator. Instead of a Hill-type equation, the sequestration of the activator (A) by the repressor (P) is used to describe repression of the gene. (D) Oscillations are seen around a 1–1 stoichiometry as the level of activator is changed. The range of the stoichiometry widens as the dissociation constant (Kd) decreases or the binding between the activator and the repressor tightens.
We defined the stoichiometry as the average ratio between the total concentrations of repressors to that of activators over a period. However, recent work has shown that CRY1 has stronger repressor activity than CRY2. The underlying biochemical mechanisms for this result have not been fully identified (Khan et al, 2012). If the difference is due to a different post-translational mechanism (e.g., binding between PER and CRY, which could affect the repressor concentration in the nucleus), the current definition of stoichiometry can be kept. Otherwise, a more sophisticated definition of stoichiometry may be needed (e.g., one that gives more weight to concentration of CRY1 than that of CRY2).
How stoichiometry generates rhythms
To test the role of stoichiometry in sustaining oscillations, we developed a simple model by modifying the well-studied Goodwin model (Goodwin, 1965) to include an activator (A), which becomes inactive when bound by a repressor (P) (Figure 3C). Transcription is proportional to the fraction of free activator that is not bound by the repressor, f(P, A, Kd) (Buchler and Cross, 2009), matching experimental data from the mammalian circadian clock (Supplementary Figure 2) (Froy et al, 2002). mRNA (M) is translated to a repressor protein (Pc). The protein enters the nucleus (P) and binds and inhibits the activator (A). This generates a single-negative feedback loop (SNF) since the activator is constitutively expressed. The model is similar to a previously published mathematical model (Francois and Hakim, 2005); however, we allow for both association and dissociation of the activator and repressor (through a defined Kd), which turns out to be crucial for understanding the effects of stoichiometry. By nondimensionalization and setting the clearance rates of all species to be equal (to increase the chance of oscillations, see Forger, 2011), only two parameters remain: the activator concentration (A) and the dissociation constant (Kd) (see Supplementary information).
When we changed the activator concentration, which changed the stoichiometry (average ratio between the level of repressor (P) to the level of activator (A)), sustained oscillations were only seen at around a 1–1 stoichiometry similar to our detailed model (Figure 3D). As the other parameter (Kd) decreased (indicating tight binding), the range of stoichiometry that permitted oscillation increased (Figure 3D). Interestingly, if the binding was too weak, the rhythms did not occur. The tight binding between activators and repressors is also found in the detailed model, and in the mammalian circadian clock (Lee et al, 2001; Froy et al, 2002; Sato et al, 2006). This indicates that the sustained rhythms require tight binding as well as balanced stoichiometry in the circadian clock.
Many previous studies have argued that ultrasensitive responses (e.g., a large change in transcription rate for a small change in repressor or activator concentration) can cause oscillations in feedback loops (Kim and Ferrell, 2007; Buchler and Louis, 2008; Novak and Tyson, 2008; Forger, 2011). A previous study showed that an ultrasensitive response can be generated by tight binding of activators and repressors in a synthetic system (Buchler and Cross, 2009). Taken together, this provides a potential mechanism of rhythm generation. That is, when the total concentration of repressor is higher than that of activators, the repressor sequesters and buffers activator and inhibits transcription completely (Buchler and Louis, 2008). As the repressor is depleted, the excess free activators are no longer sequestered by repressors and are free to turn on the transcription. At this threshold, transcription of repressor shows an ultrasensitive response to the concentration of repressor or activator. Ultrasensitive responses amplify rhythms and prevent rhythms from dampening (Forger, 2011). In both our simple and our detailed model, we found ultrasensitive responses around a 1–1 stoichiometry (Supplementary Figure 3A). When the stoichiometry was not around 1–1, an ultrasensitive response was not seen, and both models did not show sustained rhythms.
Over the course of a day, as levels of repressor and activator change, the stoichiometry and also sensitivity change as well. We found that the 1–1 average stoichiometry is required to generate the ultrasensitive response, which causes rhythms through mathematical analysis, confirming our simulation results (Figure 3D). That is, via both local and global stability analysis, we derived an approximate range of the stoichiometries (〈S〉) that permit oscillations
 |
(see Supplementary information). In agreement with our simulations shown in Figure 3D, this mathematical analysis also suggests that (1) oscillations are seen around a 1–1 stoichiometry; (2) the stoichiometry needs to be >8/9 for sustained rhythmicity; (3) as the binding between activators and repressors becomes tighter, the upper bound on stoichiometry increases; (4) if the binding is too weak (e.g., Kd=10−3), sustained oscillations do not occur.
An additional negative feedback loop improves the regulation of stoichiometric balance
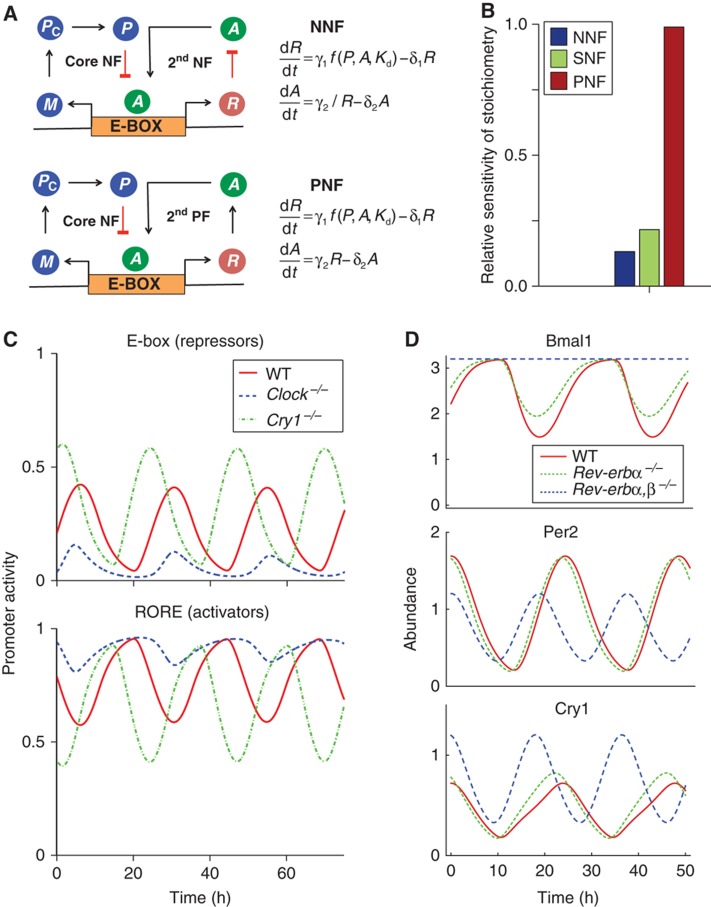
If stoichiometry is key to sustained oscillation, are there mechanisms within circadian clocks that keep the stoichiometry of components balanced? Does the additional negative feedback loop of the negative–negative feedback loop (NNF) structure, found in circadian clocks, help balance stoichiometry? To test this structure, we added an additional negative feedback loop into our simple model (Figure 4A). Previously, other studies suggested that an additional positive, rather than negative, feedback loop could sustain intracellular clocks (Barkai and Leibler, 2000; Stricker et al, 2008; Tsai et al, 2008; Tigges et al, 2009). We tested these structures by including an additional protein R (Rev-ERBs or RORs in the mammalian circadian clocks) that is transcribed in a similar way to P. R then represses (as in the Rev-erbs) or promotes (as in the Rors) the production of A in the negative–negative feedback loop (NNF) or the positive–negative feedback loop (PNF) structure, respectively (Figure 4A).
Figure 4.
The NNF structure maintains stoichiometry in balance by active compensation of both repressors and activators. (A) A negative or positive feedback controlling the activator is added to the original negative feedback controlling the repressor. (B) The relative sensitivity (% change in mean level of stoichiometry per % change in transcription rate of repressor) in the simple models with SNF, NNF and PNF structure were measured over a range of the transcription rates of repressor (see Supplementary Figure 4A). Then, we calculated the average of relative sensitivity over the range of parameters. On average, the relative sensitivity of the NNF model is about two-fold less sensitive than that of the SNF model, but that of the PNF model is about four-fold more sensitive than that of the SNF model (see Supplementary information and Supplementary Figure 4A–C for details). (C) The detailed model matches data from Gene Dose Network Analysis experiments (Baggs et al, 2009). After the knockout of a repressor gene (here, Cry1), the activity of the repressor promoters, controlled by an E-box, increases. This increases the expression of Rev-Erbs and reduces the activity of the activator promoter, controlled by a RORE. An opposite phenotype is seen when an activator (here, Clock) is knocked out. The activity of E-box decreases. This decreases the expression of Rev-Erbs and increases the activity of RORE. This active compensation through the NNF structure allows the stoichiometry to be balanced after the repressors or activators knockout. (D) The detailed model matches data from Rev-erbs−/− (Liu et al, 2008; Bugge et al, 2012; Cho et al, 2012). Rev-erbα−/− (50% reduction of transcription rate of the Rev-erbs due to the presence of Rev-erbβ) slightly shortens the period and has little effect on the expression level of Per2, Cry1 and Bmal1. Double knockout of the Rev-erbα and Rev-erbβ (100% reduction of transcription rate of the Rev-erbs) increases the expression level of Bmal1 and Cry1, but decreases that of Per2. All the values were normalized by the average of Per2 expression level in WT.
We studied how the SNF, NNF and PNF structures effectively maintain the stoichiometric balance when model parameters (e.g., transcription rate) are changed. With both simulation and steady-state analysis, we found that the NNF structure is best at keeping stoichiometry balanced while the PNF structure is worst at keeping stoichiometry balanced, regardless which parameters are perturbed (see Supplementary information, Figure 4B and Supplementary Figure 4A–C). Moreover, our detailed model, which also follows the NNF structure, also carefully balanced the stoichiometry by controlling the expression of repressors and activators. Knockdown of the repressor Cry1 leads to higher expression of the repressors, which are controlled by E-boxes, and lower expression of the activators, which are controlled by a ROREs (Figure 4C). Opposite effects are seen when the activator CLOCK is removed (Figure 4C). This active control of repressors and/or activators via the NNF structure regulates the stoichiometric balance tightly (Supplementary Figure 4D) and matches experimental data on gene dosage (Baggs et al, 2009). Moreover, the detailed model (with the NNF structure) also correctly predicts the change of clock gene expression after the removal of the additional negative feedback loop (Rev-erbα,β−/−) (Figure 4D) (Liu et al, 2008; Bugge et al, 2012; Cho et al, 2012). In particular, knockout of the Rev-erbα,β decreases PER expression, but increase CRY1 expression. For our nominal set of parameters, oscillations are still possible when this additional negative feedback is removed. However, for other sets of parameters, where stoichiometry is not as well balanced, removal of this additional negative feedback stops rhythmicity (see below). This could explain the phenotype of the Rev-erbα,β−/−, which show some indications of rhythmicity (Bugge et al, 2012; Cho et al, 2012). Our model predicts that rhythm generation remains in cell types that have a near balanced stoichiometry, and a lack of rhythms in cell types without a balanced stoichiometry.
A slow additional negative feedback loop improves the robustness of rhythms
Our central hypothesis is that, as stoichiometry is more tightly regulated, oscillations will occur over a wider range of parameters. To confirm this, we varied the transcription rate of the activator (or activator concentration in the SNF) and the transcription rate of the repressor to determine which sets of parameters yielded oscillations. While the SNF, NNF and PNF structures have almost the same behavior with their nominal parameters (mean stoichiometry, amplitude and period, see Supplementary Figure 5A), the NNF structure oscillated over the widest range of parameters and the PNF oscillated over the narrowest range of parameters in the simple model (Figure 5A; Supplementary Figure 5C). Interestingly, as the activator becomes more stable (i.e., the additional negative feedback becomes slower), the NNF structure allows sustained oscillations over a wider range of parameters (Supplementary Figure 5D). Indeed, the clearance rate of the activators is significantly slower than other circadian clock components (Supplementary Table 4) (Kwon et al, 2006).
Figure 5.
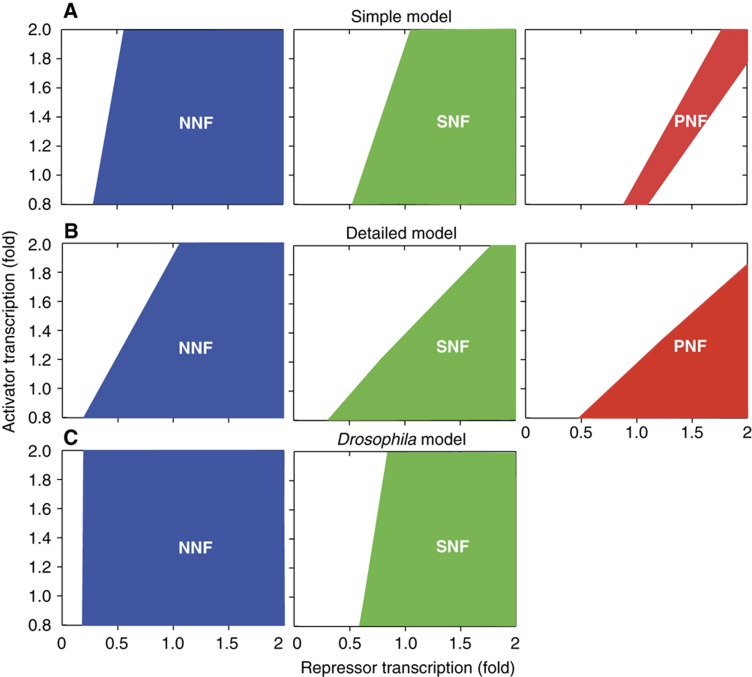
The NNF structure oscillates over the widest range of parameters. (A) The transcription rate of the repressor and the activator are changed from their initial value, and the range of parameters where the rhythms persist is shown. Here, dissociation constant, Kd=10−5 and clearance rate of activator, δ=0.2. When Kd is varied, the NNF model still has the widest range of parameters (Supplementary Figure 5C). When δ increases, the range of parameters that generate the sustained rhythms decreases (Supplementary Figure 5D). (B) Repeats the tests with the detailed mammalian model and (C) uses a Drosophila model. Details about these plots, as well as our methods for generating them are described in Supplementary Figure 5A–C.
We also checked the role of the NNF structure in our detailed mammalian clock model. We modified the NNF structure of the detailed model to that of an SNF by fixing the activator (BMAL, CLOCK and NPAS2) concentration to the average value found in their WT simulations. We also constructed the PNF structure by converting the repressor (REV-ERBs) to an activator (e.g., the RORs) in the NNF structure. This did not significantly change the rhythms in the core feedback loop (Supplementary Figure 5B), matching previous studies that showed that the loss or change in rhythms in the activators had little effect on the circadian rhythms (Liu et al, 2008). It is tempting to conclude that the additional feedback loops controlling activators are not important in the circadian clocks. However, when we changed the transcription rate of the repressor (Per) and activator (Bmal, Clock and Npas2), the original model (with an NNF structure) had the widest range of parameters where oscillations occur while the PNF structure had the narrowest range of parameters (Figure 5B). Interestingly, experiments have shown that REV-ERBs play a more dominant role than the RORs, indicating that our proposed mechanism may play an important role in in vivo timekeeping (Liu et al, 2008). Thus, the choice of the additional feedback greatly affected the range of parameters where oscillations are seen.
We also examined the role of the additional negative feedback loop in a mathematical model of the Drosophila circadian clock (Smolen et al, 2002). The original study that developed the model concluded that the NNF and SNF structures were equally likely to show oscillations. However, their study only changed transcription rates by 20%. With a larger perturbation of parameters, we found that the additional negative feedback loop significantly extends the range of parameters that yield oscillations (Figure 5C).
A network design for cellular timekeeping where maintaining a fixed period is crucial
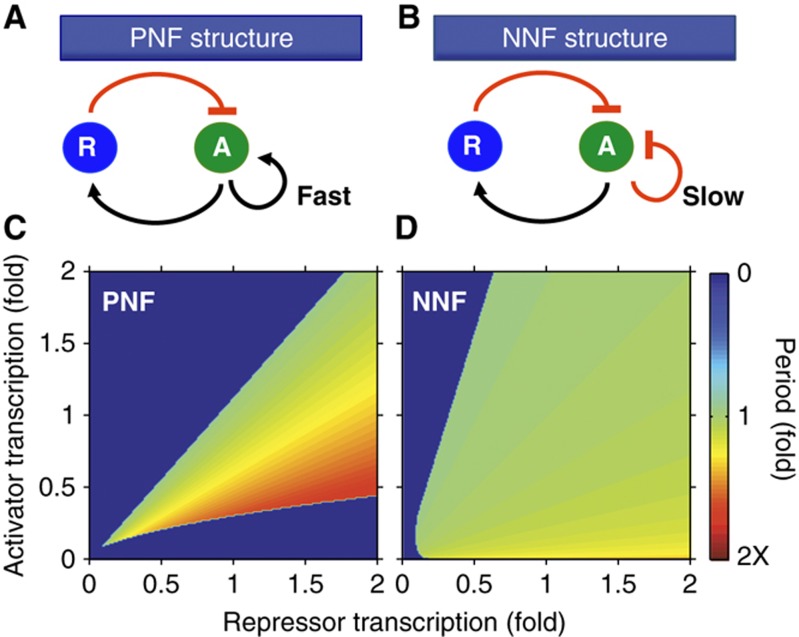
The PNF structure can create a robust biological oscillator that has a tunable period when the additional positive feedback loop is fast (i.e., the activator degrades quickly) (Stricker et al, 2008; Tsai et al, 2008; Tigges et al, 2009) (Figure 6A). Consistent with these findings, our simple model with the PNF structure has a tunable period for changes in gene expression levels (Figure 6C). However, the simple model with the NNF structure has a nearly constant period in the presence of large changes in gene expression levels (Figure 6B and D). Furthermore, this NNF structure becomes more robust as the additional negative feedback loop slows (i.e., the activator degrades more slowly) (Supplementary Figure 5D) in contrast to the fast positive feedback of the tunable clocks (Stricker et al, 2008; Tsai et al, 2008; Tigges et al, 2009). Consequently, our results propose two different designs for robust biological oscillators. The NNF structure (Figure 6B) is suitable for biological clocks in which the maintenance of a fixed period is crucial (e.g., circadian clocks). The PNF structure (Figure 6A) is suitable for the biological oscillators that need to tune their period (e.g., cell cycle or pacemaker in the sino-atrial node) (Tsai et al, 2008). This is also supported by mathematical analysis of the simple model (for more details, see Supplementary information).
Figure 6.
A design suitable for the cellular clocks with a fixed period. (A) A single-negative feedback loop with an additional fast positive feedback loop, with which activator (A) activates itself and degrades quickly. This structure has been identified in various biological oscillators like the cell cycle and pacemaker in the sino-atrial node (Tsai et al, 2008). (B) A single-negative feedback loop with an additional slow negative feedback loop, with which activator (A) represses itself and degrades slowly. Circadian clocks in mammals or Drosophila have been shown to have this structure (Supplementary Table 4) (Blau and Young, 1999; Benito et al, 2007; Liu et al, 2008). (C, D) The period of the NNF is nearly constant for the perturbations in transcription rates while the period of the PNF changes about two-fold. Parameters used are as in Supplementary Figure 5C. The period is plotted as a color where green refers to the period with the unperturbed parameters.
Discussion
Our work identifies several key mechanisms that allow 24-h rhythms in the circadian clocks of higher organisms: (1) Proper stoichiometric balance between the activators and the repressors, (2) tight binding between activators and repressors, (3) the NNF structure and (4) longer half-life of activators than repressors. These mechanisms synergistically generate rhythms with periods robust to gene dosages (Figure 6D). The range of the stoichiometry where the rhythms occur widens as binding between activators and repressors tightens (Figure 3D). Moreover, the NNF structure regulates the expression of activators as well as repressors to balance stoichiometry (Figure 4B and C). For instance, increased stoichiometry (elevated repressor concentrations) strengthens the repression in the core negative feedback loop and reduces the expression of the repressors (e.g., Pers and Crys) and Rev-erbs. The decreased expression of Rev-erbs weakens the additional negative feedback and increases the expression of activators (Bmal1 and Npas2), which lowers the stoichiometry (Supplementary Figure 4D). When this is done on a slower timescale, so that the basics of the 24-h timekeeping are unaffected, the robustness of the rhythms is enhanced (Supplementary Figure 5D).
Relation to previous experimental data
Many experimental observations could be interpreted as mechanisms by which the mammalian circadian clock balances stoichiometry. When the repressor (CRY) is overexpressed or the repressor (PER) is removed, the activator (BMAL1) concentration is found to increase or decrease, respectively (Shearman et al, 2000; Fan et al, 2007). When a repressor’s expression is reduced, the expression of other repressors is increased and the expression of activators is decreased (Baggs et al, 2009). Knockdown of activators yields opposite effects (Baggs et al, 2009). Both our detailed and simplified NNF models confirm these results (Figure 4B and C; Supplementary Figure 4D). Additionally, the rhythms of the mammalian circadian clock persist even after the transcription of all clock genes are reduced significantly (Dibner et al, 2009). In agreement with these data, both the detailed and the simple model oscillate after significant reduction of the transcription rates of both activators and repressors because their stoichiometry is maintained (Supplementary Figure 5E). Our study also suggests an underlying mechanism (ultrasensitive response) for a previous experimental observation showing that the robustness of circadian rhythms is enhanced by making the level of PER–CRY closer to that of CLOCK–BMAL1 in mouse fibroblasts (Supplementary information; Supplementary Figure 3A) (Lee et al, 2011).
Experimental data also support the role of the slow additional negative feedback loop in regulating circadian timekeeping in higher organisms. The time course of the activator (BMAL1 in mammal or CLK in Drosophila) seems to be controlled mainly by the additional negative feedback loop (Rev-Erbs or Vrille) (Blau and Young, 1999; Benito et al, 2007; Liu et al, 2008). The elimination of additional positive feedback loop has little effect on circadian clocks in contrast to other cellular clocks based on the PNF structure (Benito et al, 2007; Kim and Ferrell, 2007; Liu et al, 2008; Tsai et al, 2008). Furthermore, a key step, the clearance rate of the activators, which governs the timescale of the additional feedback loop, is significantly slower than other circadian clock components (Supplementary Table 4) (Kwon et al, 2006). Removing the slow additional negative feedback loops in the mammalian clock (Rev-erbα−/−) yields timekeeping where the period is not as well-maintained (Preitner et al, 2002). Moreover, recent studies have confirmed a pivotal role for the additional negative feedback loop for regulating the circadian rhythms via double knockout of Rev-erbα and Rev-erbβ (Bugge et al, 2012; Cho et al, 2012). Thus, our proposed mechanism of robust circadian timekeeping matches known data on the mammalian circadian clock. Further comparison with known experimental data is shown in Supplementary Figure 7.
Relation to previous modeling work
Our study is the first circadian modeling study that shows the importance of a balanced stoichiometry in rhythm generation. Our results for the SNF structure match a previous model based on the protein sequestration (Francois and Hakim, 2005), which focuses on other mechanisms, for example, slow RNA dynamics, that do not play a role in circadian clocks. We have identified a basic mechanism of tight binding and protein sequestration for generating high sensitivity, similar to what has been proposed in the cell cycle and synthetic studies (Buchler and Cross, 2009), as the key rhythm generating mechanism in our model. Previous circadian clock models do not use this mechanism, and a careful justification, based on experimental data from higher organisms, of the mechanisms for generating high sensitivity and, consequently, oscillations, in these models has yet to be performed (Yoo et al, 2005). In fact, several of these mechanisms have been called into question (Forger and Peskin, 2003).
Previous models have used different mechanisms for rhythm generation (e.g., high-Hill coefficients) and have proposed different roles for the additional negative feedback loop. They have proposed that the additional negative feedback loop is capable of independent oscillations, even when the core negative feedback loop was removed (Leloup and Goldbeter, 2004; Relógio et al, 2011). However, despite much experimental study, no oscillations have yet been found from this additional feedback loop in isolation (Sato et al, 2006) and the known phenotypes of knockout of genes in this additional feedback loop had not been correctly predicted (Preitner et al, 2002; Relógio et al, 2011). Moreover, other previous studies argued that the additional negative feedback loop is not important (Becker-Weimann et al, 2004), which does not match with recent experimental data on the mammalian circadian clock (Bugge et al, 2012; Cho et al, 2012). We claim that the additional negative feedback loop is not an independent oscillator, nor ancillary, but acts to regulate stoichiometry.
Interestingly, the predictions of previous modeling studies (Griffith, 1968; Becker-Weimann et al, 2004) match experimental data from the Neurospora circadian clock, in which a 1–1 stoichiometry is not important and the additional negative feedback loop seems to not play an important role (Baker et al, 2012). Our predictions match experimental data from circadian clocks in higher organisms (Supplementary Figures 7 and 8).
Proposed experiments based on model predictions
Our most important prediction may be the following: when the stoichiometry between activators and repressors is within a fixed range, oscillations are sustained, and outside this range oscillations are damped (Figure 3). This can be tested by measuring the relative concentration of activators and repressors in many tissues and in the presence of several possible mutations that lead to damped or sustained rhythms. This has been done in WT fibroblasts and liver (Lee et al, 2001, 2011), but has not been done in other tissues or mutants. Moreover, we note that these previous experiments were done in population cell assays, whereas single-cell measurements may be needed to determine whether damped oscillations are the result of damped rhythms in single cell, or greater population desynchrony (Welsh et al, 2004; Leise et al, 2012).
The behavior of isolated SCN neurons is similar to fibroblasts in that mutations of circadian genes can easily lead to arrhythmicity (Liu et al, 2007). We note that intercellular coupling in the SCN not only synchronizes SCN neurons, but also increases transcription of per1 and per2 (Yamaguchi et al, 2003), which may balance stoichiometry and help sustain rhythms when repressors are effectively removed (Tables I and II). Thus, we predict that increasing transcription of per1 and/or per2 could enhance rhythmicity in isolated SCN neurons similar to what is seen in fibroblasts (Lee et al, 2001). Moreover, our model predicts that cells with low stoichiometry (e.g., isolated SCN neurons) shows larger phase shifts in response to light than cells with 1–1 stoichiometry (e.g., SCN slices) (data not shown). It would be interesting future work to see whether different cell types have different PRCs depending on their stoichiometry.
We also predict that tight binding between activators and repressors is required for rhythmicity (Figure 3D). Several studies have identified binding sites for PER and CRY on BMAL1 and CLOCK (Sato et al, 2006; Langmesser et al, 2008; Ye et al, 2011). Point mutations in binding sites can generate different binding affinities between PER–CRY and BMAL1–CLOCK. Comparing the experimentally measured binding affinities of these mutants, with the resultant rhythms, or lack thereof, would directly test this prediction.
Loss of the additional negative feedback loop (e.g., in the Rev-erbs−/−, constitutive expression of Rev-erbs or constitutive expression of BMAL) is predicted to cause the intracellular circadian clock to oscillate over a much narrower range of conditions (Figure 5). It would be interesting to test whether these cells would have less temperature compensation or would lose rhythms more easily when other genes are knocked out (e.g., Cry2−/−, Per1−/−). Moreover, we predict that in the Rev-erbs−/−, rhythms persist in cell types with a balanced stoichiometry, but not in poorly balanced cells (Figure 5). It would be interesting future work to investigate whether SCN and peripheral clocks have different phenotypes of Rev-erbs−/− depending on their stoichiometry. We also predict that Rev-erbs−/− cells show a wider period distribution than WT (Figure 6).
Our modeling and analysis also predict that relatively stable activators (e.g., BMAL1 and CLOCK) in the additional negative feedback loop allow rhythmicity over a wide range of conditions (Supplementary Figure 5D). These activators can be destabilized with point mutations (Sahar et al, 2010). Simply destabilizing the activators might lead to lower activator concentrations and unbalance stoichiometry, which is also predicted to reduce rhythmicity. However, we predict a loss of rhythmicity when these activators are destabilized, even when the overall activator concentrations are controlled for.
Perhaps the most direct way to test our model is to build the clock described in our simple NNF model using the tools of synthetic biology. Other synthetic clocks have been built, and the design we propose is not more complex than what has been previously built (Stricker et al, 2008; Tsai et al, 2008; Tigges et al, 2009). Validation could first be done in an analog electric circuit, even though this might be much less convincing. Building a synthetic clock would be of particular importance since it would be the first synthetic clock predicted to have a tightly regulated period.
Future work
Further work should explore the role of the NNF structure in the presence of molecular noise (Forger and Peskin, 2005; Li and Li, 2008). Here, we studied the role of an additional negative feedback loop controlling the activators of the circadian clocks of higher organisms. Future work could consider the functions of the additional negative feedback loops in other organisms. In particular, the plant circadian clock has a different feedback loop structure than the mammalian or Drosophila circadian clocks (Pokhilko et al, 2012). It would be interesting to see if our ideas carry over to other organisms and other cellular clocks. Furthermore, other types of feedback loops in the circadian clocks of higher organisms could be explored. Here, we found that balancing stoichiometry properly might be a universal principle of biological timekeeping. This finding not only is in agreement with experiment data from the circadian clocks in higher organisms, but even in agreement with the circadian clock in cyanobacteria as well (Rust et al, 2007). It would be interesting to test the role of stoichiometry in other cellular clocks, such as developmental clocks.
Materials and methods
Modifications and extensions of the detailed model
The modifications and extensions of the detailed model from the original model (Forger and Peskin, 2003) are listed. See Supplementary information and Supplementary Tables 1 and 2 for details.
Detailed modeling of additional feedback loops: The new model includes the secondary feedback loops, which regulate transcription of genes with a RORE in their promoters, including Bmals, Npas2 and Cry1 (Preitner et al, 2002; Debruyne et al, 2006; Liu et al, 2008).
Updated mechanisms of BMAL–CLOCK/NPAS2 repression: Matching recent findings, we updated the mechanisms by which the repressor (PER/CRY) inhibits the activator (BMAL–CLOCK/NPAS2) (Kondratov et al, 2006; Dardente et al, 2007; Chen et al, 2009; Ye et al, 2011).
Accounting for the heterogeneity of different genes with E-boxes: We introduced three different types of E-boxes for Per1/Per2/Cry1, Cry2 and Rev-erbs, matching experimental data (Ueda et al, 2005; Lee et al, 2011).
Inclusion of kinase GSK3β: The new model includes another important kinase GSK3β for post-translational modification of the circadian clock as well as CKIε/δ (Iitaka et al, 2005; Yin et al, 2006).
Improved description of the effect of light on the circadian clock: We included a previous model of the effect of light on the circadian clock (Kronauer et al, 1999).
Variables and equations of the detailed model
The monomer proteins considered in our model are PER1, PER2, CRY1, CRY2, BMALs, CLOCK/NPAS2, REV-ERBs, CKI and GSK3β. Although only 10 monomers are considered in the model, they can produce many complexes depending on the state of binding, phosphorylation and subcellular locations. To describe these all complexes, 181 variables are needed (Supplementary Tables 1 and 2): 159 variables are for protein complexes, 12 variables are for mRNAs, 8 variables are indicator of the promoter activity and 2 variables are for light effect and GSK3β activity. The reactions between these variables are described by ODE systems using explicit mass kinetics as in the original model (Forger and Peskin, 2003). More details of the detailed equations are provided in the Supplementary information.
Parameter estimation of the detailed model
While the original model used 36 parameters, the new model has the 75 parameters due to the extensions and modifications of the model. Despite the increased number of parameters, we could get tighter restriction on the range of parameters with newly published data (listed below). Over these ranges, parameters are estimated by fitting to more various types of data: time courses of gene expressions and proteins, abundance of proteins and mutation phenotypes.
We choose 14 parameters (degradation rate of mRNAs and proteins) matching published experimental data. These parameter values were allowed to vary up to 50% from the experimentally determined values to account for experimental error and cellular heterogeneity.
PER1’s phosphorylation rate is set lower than that of PER2 (Lee et al, 2001). Light induced-Per1 transcription is set lower than light induced-Per2 transcription (Challet et al, 2003).
The dissociation constant between BMALs–CLOCK and CRY is set greater than that between BMALs–CLOCK and PER (Chen et al, 2009).
The ratio between cytoplasm and nucleus volume are limited to between 1 and 3.5 (Miller et al, 1989).
The other parameters are also restricted into a biologically reasonable range (see Supplementary Table S3).
Within these restrictions, a simulated annealing method (SA, a global stochastic parameter searcher) (Gonzalez et al, 2007) was used to estimate the parameters in two steps. First, we found parameters that provides a good fit with mRNA and protein time profiles measured in mouse SCN (Reppert and Weaver, 2001; Ueda et al, 2005) and relative abundance of clock proteins measured in mouse liver (Lee et al, 2001) and fibroblast (Lee et al, 2009, 2011) (Figure 2A–C). In this fitting, we used a similar cost function to that used in estimating the parameters of the original model (Forger and Peskin, 2003)
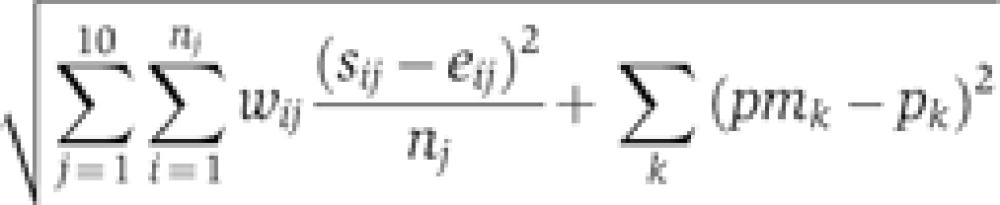 |
Here, j runs through 6 mRNAs and 4 proteins. nj is the number of data points (12 for mRNA and 13 for protein). sij and eij are simulated time courses and experimentally measured time courses, respectively. sij are normalized, in the same way as was done in the experimental data (see Figure 2 for details). wij=5 when eij=1 and wij=1 otherwise, so that the cost function has more weight at the peak time than other times. pmk and pk are maximum value of protein abundance, respectively. pmk and pk are normalized, so that the maximum abundance of the CRY1 protein is 1.
After the first round of SA, we found several parameter sets qualitatively matching with experimental data on phenotypes of mutations of mice (WT, short, long and AR) (Table I). Then we used these parameter sets as initial parameter sets for another round of SA to get the final parameter set, which shows a quantitatively good fit with knockout mutation phenotype as well as time profiles (Supplementary Table 3). The cost function used for the second round is followed.
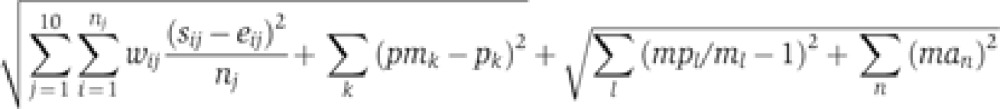 |
mpl and ml are simulated period and experimentally measured period of rhythmic phenotypes of mutations, respectively. man are simulated relative amplitude of arrhythmic phenotypes of mutation (e.g., Per2−/− or Bmal1−/−).’
Validation of the detailed model with experimental data
Time profile of mRNA and proteins
As previously mentioned, we fit the model simulations with time profiles of clock mRNA and proteins in SCN to estimate the unknown parameters. We followed the same experimental procedures used to measure time profiles. The model was entrained under 12 h–12 h light/dark cycle with 500 lux light strength for 20 days. Then, the concentrations of mRNAs were measured during the following 48 h in darkness and measured time courses were compared with experimental data (Ueda et al, 2005) (Figure 2A). In the same way, the simulated protein time profiles are also fit with the data (Reppert and Weaver, 2001) (Figure 2B).
Relative abundance of proteins
Relative abundance among core clock proteins were compared with liver (Lee et al, 2001) and fibroblast data (Lee et al, 2011) because SCN data has not yet been reported (Figure 2C).
Knockout mutation phenotype
We also tested whether our model could predict the phenotype of mutations of clock genes (Table I). Overall, the model simulation well matches with SCN or behavioral phenotype. Homozygous and heterozygous knockouts were simulated by reducing transcription rates by 100% and 50%, respectively. To simulate the Rev-erbα−/−, we also reduced the transcription rate of the Rev-Erbs by 50%, which represented both Rev-erbα and Rev-erbβ in our model. To model the Bmal1−/−, we reduced transcriptional rate of Bmals by 95%, which accounts for the low levels of Bmal2 when compared with Bmal1 (Ko et al, 2010). For the ClockΔ19/+, the half of WT CLOCK proteins were mutated to be transcriptionally inactive, yet still competed with the remaining WT CLOCK proteins. For the CK1εtau/tau, we increase the CK1 phosphorylation rate for PER1 and PER2 by four times.
Simulation of the detailed model
All the simulations and parameter search were done with 150 × 8 Ghz CPU using MATHEMATICA 8.0 (Wolfram Research).
Model description and analysis of the simple model
The simple model is available in SBML, Mathematica, Matlab, C++ and XPPAUT format from the ModelDB (Access code: 145800) (Hines et al, 2004; Mendes et al, 2009). The detailed model is available in Mathematica, Matlab and XPPAUT format from the ModelDB (Access code: 145801). (Schmidt and Jirstrand, 2006). See Supplementary information.
Supplementary Material
Supplementary Figures S1–8, Supplementary Tables S1–4
Acknowledgments
We thank Choogon Lee, John Hogenesch, Saad Kahn, Jihwan Myung and Justin Blau for comments on this manuscript; and Justin Dunmyre for help on XPP-AUTO program. This work was supported by NSF DMS-1026317 for computing resources and by AFOSR Grant FA 9550-11-1-0165.
Author contributions: JK and DF designed the research; JK performed the experiments; JK and DF analyzed the data; JK and DF did mathematical analysis and JK and DF wrote the paper.
Footnotes
The authors declare that they have no conflict of interest.
References
- Baggs JE, Price TS, DiTacchio L, Panda S, Fitzgerald GA, Hogenesch JB (2009) Network features of the mammalian circadian clock. PLoS Biol 7: e52. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker CL, Loros JJ, Dunlap JC (2012) The circadian clock of Neurospora crassa. FEMS Microbiol Rev 36: 95–110 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barkai N, Leibler S (2000) Circadian clocks limited by noise. Nature 403: 267–268 [DOI] [PubMed] [Google Scholar]
- Becker-Weimann S, Wolf J, Herzel H, Kramer A (2004) Modeling feedback loops of the Mammalian circadian oscillator. Biophys J 87: 3023–3034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Benito J, Zheng H, Hardin PE (2007) PDP1epsilon functions downstream of the circadian oscillator to mediate behavioral rhythms. J Neurosci 27: 2539–2547 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blau J, Young MW (1999) Cycling vrille expression is required for a functional Drosophila clock. Cell 99: 661–671 [DOI] [PubMed] [Google Scholar]
- Buchler NE, Cross FR (2009) Protein sequestration generates a flexible ultrasensitive response in a genetic network. Mol Syst Biol 5: 272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buchler NE, Louis M (2008) Molecular titration and ultrasensitivity in regulatory networks. J Mol Biol 384: 1106–1119 [DOI] [PubMed] [Google Scholar]
- Bugge A, Feng D, Everett LJ, Briggs ER, Mullican SE, Wang F, Jager J, Lazar MA (2012) Rev-erbalpha and Rev-erbbeta coordinately protect the circadian clock and normal metabolic function. Genes Dev 26: 657–667 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Busino L, Bassermann F, Maiolica A, Lee C, Nolan PM, Godinho SI, Draetta GF, Pagano M (2007) SCFFbxl3 controls the oscillation of the circadian clock by directing the degradation of cryptochrome proteins. Science 316: 900–904 [DOI] [PubMed] [Google Scholar]
- Challet E, Poirel VJ, Malan A, Pevet P (2003) Light exposure during daytime modulates expression of Per1 and Per2 clock genes in the suprachiasmatic nuclei of mice. J Neurosci Res 72: 629–637 [DOI] [PubMed] [Google Scholar]
- Chen R, Schirmer A, Lee Y, Lee H, Kumar V, Yoo SH, Takahashi JS, Lee C (2009) Rhythmic PER abundance defines a critical nodal point for negative feedback within the circadian clock mechanism. Mol Cell 36: 417–430 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cho H, Zhao X, Hatori M, Yu RT, Barish GD, Lam MT, Chong LW, DiTacchio L, Atkins AR, Glass CK, Liddle C, Auwerx J, Downes M, Panda S, Evans RM (2012) Regulation of circadian behaviour and metabolism by REV-ERB-alpha and REV-ERB-beta. Nature 485: 123–127 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dardente H, Fortier EE, Martineau V, Cermakian N (2007) Cryptochromes impair phosphorylation of transcriptional activators in the clock: a general mechanism for circadian repression. Biochem J 402: 525–536 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debruyne JP, Noton E, Lambert CM, Maywood ES, Weaver DR, Reppert SM (2006) A clock shock: mouse CLOCK is not required for circadian oscillator function. Neuron 50: 465–477 [DOI] [PubMed] [Google Scholar]
- Dibner C, Sage D, Unser M, Bauer C, d'Eysmond T, Naef F, Schibler U (2009) Circadian gene expression is resilient to large fluctuations in overall transcription rates. EMBO J 28: 123–134 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunlap JC, Loros JJ, DeCoursey PJ (2004) Chronobiology: Biological Timekeeping Sunderland, MA: Sinauer Associates, [Google Scholar]
- Etchegaray JP, Machida KK, Noton E, Constance CM, Dallmann R, Di Napoli MN, DeBruyne JP, Lambert CM, Yu EA, Reppert SM, Weaver DR (2009) Casein kinase 1 delta regulates the pace of the mammalian circadian clock. Mol Cell Biol 29: 3853–3866 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fan Y, Hida A, Anderson DA, Izumo M, Johnson CH (2007) Cycling of CRYPTOCHROME proteins is not necessary for circadian-clock function in mammalian fibroblasts. Curr Biol 17: 1091–1100 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forger DB (2011) Signal processing in cellular clocks. Proc Natl Acad Sci USA 108: 4281–4285 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forger DB, Peskin CS (2003) A detailed predictive model of the mammalian circadian clock. Proc Natl Acad Sci USA 100: 14806–14811 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forger DB, Peskin CS (2005) Stochastic simulation of the mammalian circadian clock. Proc Natl Acad Sci USA 102: 321–324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Francois P, Hakim V (2005) Core genetic module: the mixed feedback loop. Phys Rev E Stat Nonlin Soft Matter Phys 72: 031908. [DOI] [PubMed] [Google Scholar]
- Froy O, Chang DC, Reppert SM (2002) Redox potential: differential roles in dCRY and mCRY1 functions. Curr Biol 12: 147–152 [DOI] [PubMed] [Google Scholar]
- Gallego M, Eide EJ, Woolf MF, Virshup DM, Forger DB (2006) An opposite role for tau in circadian rhythms revealed by mathematical modeling. Proc Natl Acad Sci USA 103: 10618–10623 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glossop NR, Lyons LC, Hardin PE (1999) Interlocked feedback loops within the Drosophila circadian oscillator. Science 286: 766–768 [DOI] [PubMed] [Google Scholar]
- Gonzalez OR, Kuper C, Jung K, Naval PC Jr, Mendoza E (2007) Parameter estimation using simulated annealing for S-system models of biochemical networks. Bioinformatics 23: 480–486 [DOI] [PubMed] [Google Scholar]
- Goodwin BC (1965) Oscillatory behavior in enzymatic control processes. Adv Enzyme Regul 3: 425–438 [DOI] [PubMed] [Google Scholar]
- Griffith JS (1968) Mathematics of cellular control processes. I. Negative feedback to one gene. J Theor Biol 20: 202–208 [DOI] [PubMed] [Google Scholar]
- He Q, Shu H, Cheng P, Chen S, Wang L, Liu Y (2005) Light-independent phosphorylation of WHITE COLLAR-1 regulates its function in the Neurospora circadian negative feedback loop. J Biol Chem 280: 17526–17532 [DOI] [PubMed] [Google Scholar]
- Herzog ED, Takahashi JS, Block GD (1998) Clock controls circadian period in isolated suprachiasmatic nucleus neurons. Nat Neurosci 1: 708–713 [DOI] [PubMed] [Google Scholar]
- Hines ML, Morse T, Migliore M, Carnevale NT, Shepherd GM (2004) ModelDB: a database to support computational neuroscience. J Comput Neurosci 17: 7–11 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang G, Chen S, Li S, Cha J, Long C, Li L, He Q, Liu Y (2007) Protein kinase A and casein kinases mediate sequential phosphorylation events in the circadian negative feedback loop. Genes Dev 21: 3283–3295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iitaka C, Miyazaki K, Akaike T, Ishida N (2005) A role for glycogen synthase kinase-3β in the mammalian circadian clock. J Biol Chem 280: 29397–29402 [DOI] [PubMed] [Google Scholar]
- Khan SK, Xu H, Ukai-Tadenuma M, Burton B, Wang Y, Ueda HR, Liu AC (2012) Identification of a novel cryptochrome differentiating domain required for feedback repression in circadian clock function. J Biol Chem 287: 25917–25926 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim SY, Ferrell JE Jr (2007) Substrate competition as a source of ultrasensitivity in the inactivation of Wee1. Cell 128: 1133–1145 [DOI] [PubMed] [Google Scholar]
- Ko CH, Takahashi JS (2006) Molecular components of the mammalian circadian clock. Hum Mol Genet 15(Spec No 2): R271–R277 [DOI] [PubMed] [Google Scholar]
- Ko CH, Yamada YR, Welsh DK, Buhr ED, Liu AC, Zhang EE, Ralph MR, Kay SA, Forger DB, Takahashi JS (2010) Emergence of noise-induced oscillations in the central circadian pacemaker. PLoS Biol 8: e1000513. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kondratov RV, Kondratova AA, Lee C, Gorbacheva VY, Chernov MV, Antoch MP (2006) Post-translational regulation of circadian transcriptional CLOCK(NPAS2)/BMAL1 complex by CRYPTOCHROMES. Cell Cycle 5: 890–895 [DOI] [PubMed] [Google Scholar]
- Kronauer RE, Forger DB, Jewett ME (1999) Quantifying human circadian pacemaker response to brief, extended, and repeated light stimuli over the phototopic range. J Biol Rhythms 14: 500–515 [DOI] [PubMed] [Google Scholar]
- Kwon I, Lee J, Chang SH, Jung NC, Lee BJ, Son GH, Kim K, Lee KH (2006) BMAL1 shuttling controls transactivation and degradation of the CLOCK/BMAL1 heterodimer. Mol Cell Biol 26: 7318–7330 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmesser S, Tallone T, Bordon A, Rusconi S, Albrecht U (2008) Interaction of circadian clock proteins PER2 and CRY with BMAL1 and CLOCK. BMC Mol Biol 9: 41. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee C, Etchegaray JP, Cagampang FR, Loudon AS, Reppert SM (2001) Posttranslational mechanisms regulate the mammalian circadian clock. Cell 107: 855–867 [DOI] [PubMed] [Google Scholar]
- Lee H, Chen R, Lee Y, Yoo S, Lee C (2009) Essential roles of CKIdelta and CKIepsilon in the mammalian circadian clock. Proc Natl Acad Sci USA 106: 21359–21364 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee Y, Chen R, Lee HM, Lee C (2011) Stoichiometric relationship among clock proteins determines robustness of circadian rhythms. J Biol Chem 286: 7033–7042 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leise TL, Wang CW, Gitis PJ, Welsh DK (2012) Persistent cell-autonomous circadian oscillations in fibroblasts revealed by six-week single-cell imaging of PER2:LUC bioluminescence. PLoS One 7: e33334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leloup JC, Goldbeter A (2003) Toward a detailed computational model for the mammalian circadian clock. Proc Natl Acad Sci USA 100: 7051–7056 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leloup JC, Goldbeter A (2004) Modeling the mammalian circadian clock: sensitivity analysis and multiplicity of oscillatory mechanisms. J Theor Biol 230: 541–562 [DOI] [PubMed] [Google Scholar]
- Li D, Li C (2008) Noise-induced dynamics in the mixed-feedback-loop network motif. Phys Rev E Stat Nonlin Soft Matter Phys 77: 011903. [DOI] [PubMed] [Google Scholar]
- Liu AC, Tran HG, Zhang EE, Priest AA, Welsh DK, Kay SA (2008) Redundant function of REV-ERBalpha and beta and non-essential role for Bmal1 cycling in transcriptional regulation of intracellular circadian rhythms. PLoS Genet 4: e1000023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu AC, Welsh DK, Ko CH, Tran HG, Zhang EE, Priest AA, Buhr ED, Singer O, Meeker K, Verma IM, Doyle FJ III, Takahashi JS, Kay SA (2007) Intercellular coupling confers robustness against mutations in the SCN circadian clock network. Cell 129: 605–616 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mendes P, Hoops S, Sahle S, Gauges R, Dada J, Kummer U (2009) Computational modeling of biochemical networks using COPASI. Methods Mol Biol 500: 17–59 [DOI] [PubMed] [Google Scholar]
- Menet JS, Abruzzi KC, Desrochers J, Rodriguez J, Rosbash M (2010) Dynamic PER repression mechanisms in the Drosophila circadian clock: from on-DNA to off-DNA. Genes Dev 24: 358–367 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller MM, Gould BE, Nelson JF (1989) Aging and long-term ovariectomy alter the cytoarchitecture of the hypothalamic-preoptic area of the C57BL/6J mouse. Neurobiol Aging 10: 683–690 [DOI] [PubMed] [Google Scholar]
- Mirsky HP, Liu AC, Welsh DK, Kay SA, Doyle FJ III (2009) A model of the cell-autonomous mammalian circadian clock. Proc Natl Acad Sci USA 106: 11107–11112 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novak B, Tyson JJ (2008) Design principles of biochemical oscillators. Nat Rev Mol Cell Biol 9: 981–991 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pokhilko A, Fernandez AP, Edwards KD, Southern MM, Halliday KJ, Millar AJ (2012) The clock gene circuit in Arabidopsis includes a repressilator with additional feedback loops. Mol Syst Biol 8: 574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Preitner N, Damiola F, Lopez-Molina L, Zakany J, Duboule D, Albrecht U, Schibler U (2002) The orphan nuclear receptor REV-ERBalpha controls circadian transcription within the positive limb of the mammalian circadian oscillator. Cell 110: 251–260 [DOI] [PubMed] [Google Scholar]
- Relógio A, Westermark PO, Wallach T, Schellenberg K, Kramer A, Herzel H (2011) Tuning the mammalian circadian clock: robust synergy of two loops. Plos Comput Biol 7: e1002309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reppert SM, Weaver DR (2001) Molecular analysis of mammalian circadian rhythms. Annu Rev Physiol 63: 647–676 [DOI] [PubMed] [Google Scholar]
- Rust MJ, Markson JS, Lane WS, Fisher DS, O'Shea EK (2007) Ordered phosphorylation governs oscillation of a three-protein circadian clock. Science 318: 809–812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sahar S, Zocchi L, Kinoshita C, Borrelli E, Sassone-Corsi P (2010) Regulation of BMAL1 protein stability and circadian function by GSKβ-mediated phosphorylation. PLoS ONE 5: e8561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sato TK, Yamada RG, Ukai H, Baggs JE, Miraglia LJ, Kobayashi TJ, Welsh DK, Kay SA, Ueda HR, Hogenesch JB (2006) Feedback repression is required for mammalian circadian clock function. Nat Genet 38: 312–319 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schmidt H, Jirstrand M (2006) Systems Biology Toolbox for MATLAB: a computational platform for research in systems biology. Bioinformatics 22: 514–515 [DOI] [PubMed] [Google Scholar]
- Shearman LP, Sriram S, Weaver DR, Maywood ES, Chaves I, Zheng B, Kume K, Lee CC, van der Horst GT, Hastings MH, Reppert SM (2000) Interacting molecular loops in the mammalian circadian clock. Science 288: 1013–1019 [DOI] [PubMed] [Google Scholar]
- Siepka SM, Yoo SH, Park J, Song W, Kumar V, Hu Y, Lee C, Takahashi JS (2007) Circadian mutant overtime reveals F-box protein FBXL3 regulation of cryptochrome and period gene expression. Cell 129: 1011–1023 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smolen P, Baxter DA, Byrne JH (2002) A reduced model clarifies the role of feedback loops and time delays in the Drosophila circadian oscillator. Biophys J 83: 2349–2359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stricker J, Cookson S, Bennett MR, Mather WH, Tsimring LS, Hasty J (2008) A fast, robust and tunable synthetic gene oscillator. Nature 456: 516–519 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Suter DM, Molina N, Gatfield D, Schneider K, Schibler U, Naef F (2011) Mammalian genes are transcribed with widely different bursting kinetics. Science 332: 472–474 [DOI] [PubMed] [Google Scholar]
- Tigges M, Marquez-Lago TT, Stelling J, Fussenegger M (2009) A tunable synthetic mammalian oscillator. Nature 457: 309–312 [DOI] [PubMed] [Google Scholar]
- Tsai TY, Choi YS, Ma W, Pomerening JR, Tang C, Ferrell JE Jr (2008) Robust, tunable biological oscillations from interlinked positive and negative feedback loops. Science 321: 126–129 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ueda HR, Hayashi S, Chen W, Sano M, Machida M, Shigeyoshi Y, Iino M, Hashimoto S (2005) System-level identification of transcriptional circuits underlying mammalian circadian clocks. Nat Genet 37: 187–192 [DOI] [PubMed] [Google Scholar]
- Ukai-Tadenuma M, Yamada RG, Xu H, Ripperger JA, Liu AC, Ueda HR (2011) Delay in feedback repression by cryptochrome 1 is required for circadian clock function. Cell 144: 268–281 [DOI] [PubMed] [Google Scholar]
- Vitaterna MH, King DP, Chang AM, Kornhauser JM, Lowrey PL, McDonald JD, Dove WF, Pinto LH, Turek FW, Takahashi JS (1994) Mutagenesis and mapping of a mouse gene, Clock, essential for circadian behavior. Science 264: 719–725 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Welsh DK, Yoo SH, Liu AC, Takahashi JS, Kay SA (2004) Bioluminescence imaging of individual fibroblasts reveals persistent, independently phased circadian rhythms of clock gene expression. Curr Biol 14: 2289–2295 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilkins AK, Barton PI, Tidor B (2007) The Per2 negative feedback loop sets the period in the mammalian circadian clock mechanism. Plos Comput Biol 3: e242. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamada Y, Forger D (2010) Multiscale complexity in the mammalian circadian clock. Curr Opin Genet Dev 20: 626–633 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamaguchi S, Isejima H, Matsuo T, Okura R, Yagita K, Kobayashi M, Okamura H (2003) Synchronization of cellular clocks in the suprachiasmatic nucleus. Science 302: 1408–1412 [DOI] [PubMed] [Google Scholar]
- Ye R, Selby CP, Ozturk N, Annayev Y, Sancar A (2011) Biochemical analysis of the canonical model for the mammalian circadian clock. J Biol Chem 286: 25891–25902 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yin L, Wang J, Klein PS, Lazar MA (2006) Nuclear receptor Rev-erbalpha is a critical lithium-sensitive component of the circadian clock. Science 311: 1002–1005 [DOI] [PubMed] [Google Scholar]
- Yoo SH, Ko CH, Lowrey PL, Buhr ED, Song EJ, Chang S, Yoo OJ, Yamazaki S, Lee C, Takahashi JS (2005) A noncanonical E-box enhancer drives mouse Period2 circadian oscillations in vivo. Proc Natl Acad Sci USA 102: 2608–2613 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Figures S1–8, Supplementary Tables S1–4