Spectrotemporal Contrast Kernels for Neurons in Primary Auditory Cortex

Abstract

Auditory neurons are often described in terms of their spectrotemporal receptive fields (STRFs). These map the relationship between features of the sound spectrogram and firing rates of neurons. Recently, we showed that neurons in the primary fields of the ferret auditory cortex are also subject to gain control: when sounds undergo smaller fluctuations in their level over time, the neurons become more sensitive to small-level changes (Rabinowitz et al., 2011). Just as STRFs measure the spectrotemporal features of a sound that lead to changes in the firing rates of neurons, in this study, we sought to estimate the spectrotemporal regions in which sound statistics lead to changes in the gain of neurons. We designed a set of stimuli with complex contrast profiles to characterize these regions. This allowed us to estimate the STRFs of cortical neurons alongside a set of spectrotemporal contrast kernels. We find that these two sets of integration windows match up: the extent to which a stimulus feature causes the firing rate of a neuron to change is strongly correlated with the extent to which the contrast of that feature modulates the gain of the neuron. Adding contrast kernels to STRF models also yields considerable improvements in the ability to capture and predict how auditory cortical neurons respond to statistically complex sounds.

Introduction

One of the central questions that we ask about sensory neurons is what stimulus features they encode in their spike trains. When characterizing neurons throughout the auditory pathway, modelers and electrophysiologists have long used the spectrotemporal receptive field (STRF) to answer this question (Aertsen et al., 1980; Aertsen and Johannesma, 1981; deCharms et al., 1998; Klein et al., 2000; Theunissen et al., 2000; Escabi and Schreiner, 2002; Miller et al., 2002; Fritz et al., 2003; Linden et al., 2003; Gill et al., 2006; Christianson et al., 2008; Gourévitch et al., 2009; David et al., 2009). The success of STRFs at this task, however, has been somewhat limited (Sahani and Linden, 2003; Machens et al., 2004), necessitating the development of nonlinear extensions, such as adding input nonlinearities (Ahrens et al., 2008b), output nonlinearities (Atencio et al., 2008; Rabinowitz et al., 2011), feedback kernels (Calabrese et al., 2011), simplified second-order interaction terms (Ahrens et al., 2008a), and multiple feature dimensions (Atencio et al., 2008).

One reason for the limited predictive power of the STRF is that the encoding of stimulus features by auditory neurons is modulated by stimulus context (Blake and Merzenich, 2002; Valentine and Eggermont, 2004; Ahrens et al., 2008a; Gourévitch et al., 2009). For neurons in the mammalian primary auditory cortex (A1), the statistics of recent stimulation are a major modulatory influence on the encoding of sound. We recently described a gain control process that is in place by this stage of the auditory pathway (Rabinowitz et al., 2011): neurons in ferret auditory cortex adjust their gain according to the contrast of sound stimulation. When sounds, on average, only change in level by a small amount over time, the neurons scale up their sensitivity to the small fluctuations in sound level. Other authors have observed similar compensatory effects when changing stimulus statistics, from the auditory periphery (Joris and Yin, 1992) to the midbrain (Rees and Møller, 1983; Kvale and Schreiner, 2004; Dean et al., 2005; Nelson and Carney, 2007; Dahmen et al., 2010) and the higher auditory pathway (Nagel and Doupe, 2006; Malone et al., 2010).

Just as STRFs estimate which features of a spectrotemporally complex stimulus drive a neuron to spike, we might ask a similar question of gain changes. What features of a spectrotemporally complex stimulus drive a neuron to change its gain? Our previous work demonstrated, at a coarse, population level, that gain changes are predominantly driven by contrast in sound frequency bands that are local to the best frequencies (BFs) of cortical neurons. However, we do not know how this dependency operates on a neuron-by-neuron basis or what its relationship is to the STRFs of individual neurons.

To answer these questions, we recorded from neurons in the primary auditory fields of the anesthetized ferret, while presenting a set of stimuli with complex patterns of contrast. For each neuron, we determined the spectrotemporal window within which sound contrast informs the gain of that neuron. We did this by extending the notion of the STRF and estimating a set of “gain receptive fields,” i.e., spectrotemporal kernels for stimulus contrast. This class of contrast kernel models extends the linear–nonlinear (LN) framework of models by capturing the modulation of the input/output functions of neurons by patterns of stimulus statistics.

Several possibilities could have arisen. The gain of neurons may be a function of the sound statistics in a broad or a narrow set of frequency bands and may depend only on the statistics within the short time windows of STRF or on those over longer periods. Our results reveal the relationship between the range of stimulus features that auditory cortical neurons encode and the range of stimulus statistics that modulate this encoding.

Materials and Methods

Animals.

All animal procedures were approved by the local ethical review committee and performed under license from the United Kingdom Home Office. Full surgical procedures are provided by Bizley et al. (2010). Briefly, three female adult pigmented ferrets were chosen for electrophysiological recordings under ketamine (5 mg · kg⁻¹ · h⁻¹) and medetomidine (0.022 mg · kg⁻¹ · h⁻¹) anesthesia. Bilateral extracellular recordings were made in the two auditory cortices using silicon probe electrodes (Neuronexus Technologies) with 16 sites on a single probe, vertically spaced at 50 μm. Spikes were sorted offline using spikemonger, an in-house software package. Stimuli were presented via earphones, as described by Rabinowitz et al. (2011).

Stimuli.

The main stimulus used was a variant of the dynamic random chord (DRC) stimuli presented by Rabinowitz et al. (2011), which we define here as random contrast DRCs (RC-DRCs). As with ordinary DRCs, RC-DRCs comprise a sequence of chords, composed of tones whose levels were drawn from particular distributions. For these RC-DRCs, we used N_F = 23 pure tones, with frequencies log-spaced between f_low = 500 Hz and f_high = 22.6 kHz at ¼ octave intervals. The levels of the tones were changed every 25 ms, with 5 ms linear ramps between chords. As in the study by Rabinowitz et al. (2011), the amplitude of each tone was always non-zero.

The major distinguishing feature of RC-DRCs is the organization of these chords into segments of several seconds duration. In each segment, the distribution of levels for each of the N_F bands had different parameters. A random subset of N_high of the N_F tones had their levels drawn from a high-contrast (half-width w_L = 15 dB; SD σ_L = 8.7 dB; contrast c = 92%) uniform level distribution, whereas the remaining N_low = N_F − N_high tones had their levels drawn from a low-contrast (w_L = 5 dB; σ_L = 2.9 dB; c = 33%) uniform level distribution. Both tone distributions had mean level μ_L = 40 dB SPL; these are shown in Figure 1C. By virtue of the 3 s duration, each segment consisted of a sequence of 120 chords, sufficient for a rough approximation of the output nonlinearity during that contrast condition (as explained below).

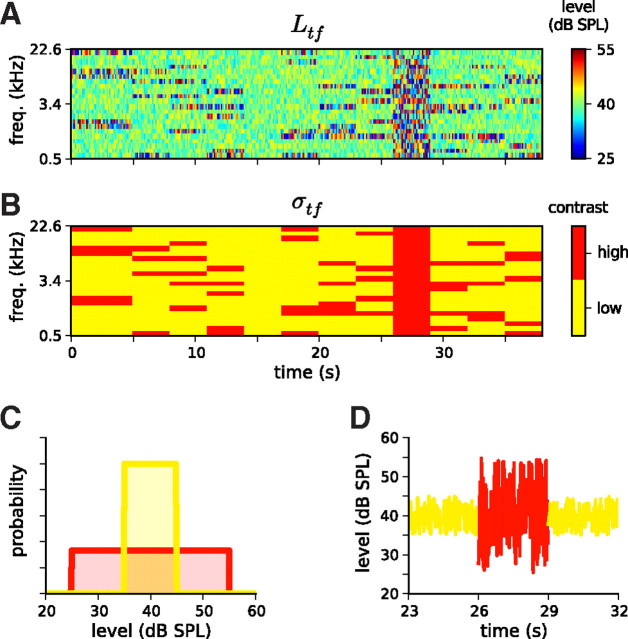
Figure 1.

Stimuli used to estimate contrast kernels and their statistics. A, Schematic of an RC-DRC stimulus. The stimulus comprises a sequence of chords, which change every 25 ms. The elements of the chords are pure tones, whose levels are drawn from one of the distributions shown in C. The color grid shows the sound level (L_tf) of a particular tone frequency at a particular time. B, The 38 s DRC stimulus shown in A comprises 12 segments in which the contrast in different frequency bins, σ_tf, is either high (red) or low (yellow). C, Tone level distributions for low (yellow) and high (red) contrast segments. D, Level as a function of time for the 2.4 kHz tone over a 9 s period, i.e., a cross-section of A. This shows the transition from a segment in which the level distribution of this tone was low contrast (yellow), to a segment in which it was high contrast (red), to a third segment in which it was low contrast again (yellow).

To explore as large a region of contrast space as possible, between N_S = 80 and N_S = 120 segments were presented at each electrode penetration. Two types of segment were necessary to establish baselines for gain measurements: one in which all tone distributions were low contrast, and one in which all were high. Given the importance of these two baseline conditions, nine of the N_S segments were reserved for each. The remaining segments all had a randomized partition of tones into N_high = 5 high-contrast bands and N_low = 18 low-contrast bands, as described above. Thus, the set of segments provided an ensemble of contrast conditions in an analogous way to how an ordinary DRC would provide an ensemble of tone level conditions.

The segments were packaged into individual RC-DRC sequences, each consisting of 12 segments. The first segment of each sequence was 5 s in duration, so that the first 2 s of each stimulus presentation could be discarded. This was necessary because units often showed transient responses to the onset of each DRC sequence that depended on the duration of silence since the end of the last sequence presentation (typically 1–2 s). From each 3 s segment, the first 0.5 s of data was set aside for the analysis of temporal contrast kernels (TCKs), with the remaining 2.5 s of data used to fit spectral contrast kernels (SCKs). The 38 s sequences were presented 10 times each, randomly interleaved.

Unit selection criteria.

Only units that modulated their firing rate in response to the RC-DRCs in a reliable, repeatable manner were included for analysis. This was measured via the noise ratio (NR; Sahani and Linden, 2003; Rabinowitz et al., 2011) for the peristimulus time histogram (PSTH) of each unit:

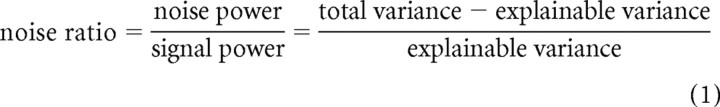The PSTH was binned at 25 ms, with bins offset by between 0 and 25 ms to allow for response latency. The offset was chosen on a unit-by-unit basis to minimize the NR. This same offset was used to bin all PSTHs throughout the study; fixing offsets at 10 ms produced similar results. The maximum admitted NR was 40 (estimated across the whole ensemble of stimuli); units with NR > 40, i.e., whose explainable variance was less than ∼2.5% of the total variance, were excluded from analysis. Models were evaluated while taking NR into consideration (see below).

Notation.

We use the following notation throughout this paper. Each DRC stimulus grid is uniquely identified by a matrix (i.e., two-tensor), L_tf, in which each component of the matrix describes the sound pressure level (in dB SPL) of a tone with frequency f at time t. To simplify the notation used for fitting STRFs below, we define the three-tensor L_tfh as a time-lagged version of L_tf, where h is a history index, and the elements of L_tfh are defined as the elements of L_tf from h time bins in the past, i.e., L_{(t − h),f}. The (trial-averaged) response is denoted as y_t, and any model predictions of this response are denoted ŷ_t. Once the STRF was fitted, it was fixed; the output of the STRF model for a given unit is denoted x_t throughout.

As with the tone levels, the contrast profile of the stimulus is denoted by σ_tf; this matrix (or two-tensor) defines the contrast of the level distribution for the tone at frequency f and time t. Because only two distributions were presented, we define σ = 0 for the low-contrast distribution (Fig. 1B–D, yellow) and σ = 1 for the high-contrast distribution (Fig. 1B–D, red). Similarly, the recent history of contrast is denoted by σ_tfh, whose elements are defined by the time-lagged contrast profile, as σ_tfh = σ_{(t − h),f}.

Model structure: STRFs and the LN model.

The models developed in this study begin with STRFs. These were estimated by correlating the stimulus history, L_tfh, with the spike PSTH, y_t, at a 25 ms resolution. This involved fitting the general model:

STRFs that are separable in frequency, f, and time history, h, often provide better fits than fully inseparable STRFs (Linden et al., 2003; Simon et al., 2007; Ahrens et al., 2008a; Rabinowitz et al., 2011). This was generally the case for this dataset as well. Thus, we assume k_fh = k_f ⊗ k_h, where ⊗ is the outer product. This is illustrated in Figure 2B.

Figure 2.

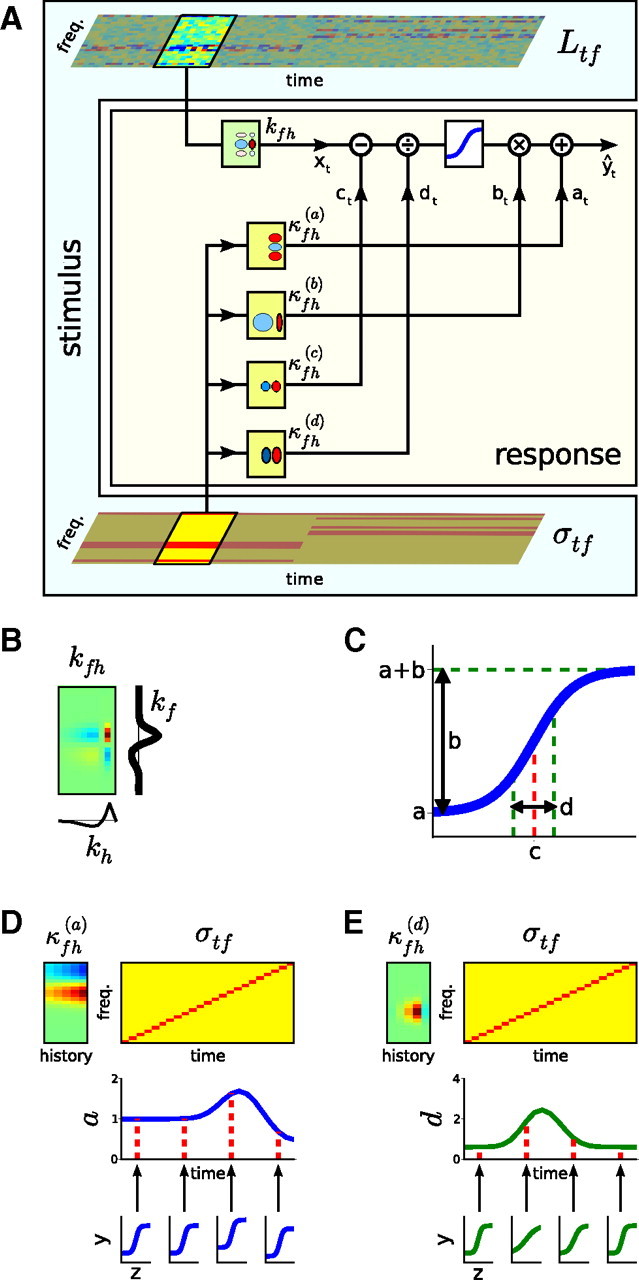
Schematic of the contrast kernel model. A, The relationship between stimulus and neuronal response. The sound input is represented by its spectrogram, L_tf (top), and by its contrast profile, σ_tf (bottom). As in a standard LN model, the neural response is determined by convolving the spectrogram with a linear spectrotemporal kernel (k_fh) and passing the output of this operation (x_t) through a static output nonlinearity (here, a 4-parameter sigmoid, denoted by the blue curve) to produce the predicted spike rate (ŷ_t). The model developed here extends this by allowing each of the four parameters of the output nonlinearity (a–d, as shown in C) to change over time, depending on the statistics of recent stimulation. The evolution of each parameter θ ϵ {a, b, c, d} over time is determined by convolving the contrast profile of the sound, σ_tf, with a linear contrast kernel, κ_fh^(θ). The effects of this on the shape of the output nonlinearity are illustrated in D and E. B, All STRFs and contrast kernels are assumed to be separable in frequency and time, such that k_fh = k_f ⊗ k_h, and κ_fh^(θ) = κ_f^(θ) ⊗ κ_h^(θ). This allows contrast kernels to be fitted in two stages: (1) the spectral component (SCKs) in Figures 3–6 and (2) the temporal component (TCKs) in Figure 7. C, The parameters of a sigmoidal static nonlinearity: a, the minimum firing rate; b, the output dynamic range; c, the stimulus inflection point; d, the (inverse) gain. D, An illustration of the effect of a contrast kernel for the nonlinearity parameter a, which sets the minimum firing rate of the output nonlinearity. Top left, A contrast kernel κ_fh^(a) is shown. Top right, The contrast profile of an example stimulus. Middle right, As a result of changing contrast, the parameter a changes with time. Bottom right, The effective shape of the output nonlinearities at different times attributable to the changing value of a. These shifts would be combined with the contrast-dependent changes to the other nonlinearity parameters, b, c, and d, such as shown in E. E, Effect of a contrast kernel for the nonlinearity parameter d, which sets the (inverse) gain of the output nonlinearity. This neuron decreases its gain when there is high contrast anywhere within a relatively broad region demarcated by κ_fh^(d).

We also fitted the majority of the models presented here using inseparable kernels as the first stage of the LN and contrast kernel models. Prediction scores for these models (evaluated using Eq. 23 below) were typically 2–5 percentage points lower than the corresponding models fitted using separable kernels. Nevertheless, the general trends as presented in this study were the same (data not shown).

For comparison with the contrast kernel models developed below, the linear STRF was refined by fitting a static LN model to the responses of the units (Chichilnisky, 2001; Simoncelli et al., 2004). This involved passing the output of the linear model, x_t, through a static (i.e., memory-less), nonlinear function F, such that ŷ_t = F[x_t]. As per Rabinowitz et al. (2011), a logistic curve (sigmoid) was fitted to the data via gradient descent:

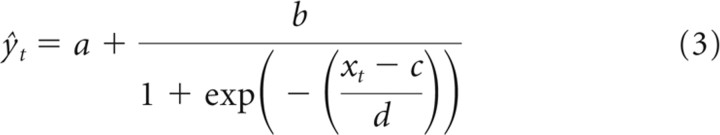The parameters a through d are illustrated in Figure 2C. They can be interpreted as follows: a, as the minimum firing rate; b, as the output dynamic range; c, as the stimulus inflection point; and d, as the (inverse) gain.

Model structure: contrast kernels.

To consider how the ongoing contrast profile of the stimulus affects the coding of a cortical neuron, we extended the static LN model above by rendering each of the four parameters, a–d, depending on the recent history of contrast:

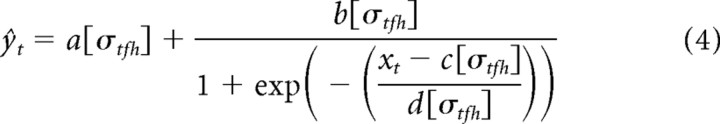There is considerable freedom in Equation 4 to specify the form of the functions a[σ_tfh] through d[σ_tfh]. The simplest assumption, which we consider here, is that these are linear functions of σ_tfh. This is motivated by three factors: (1) symmetry with the STRF; (2) a linearization of the results of Rabinowitz et al. (2011); and (3) simplicity. The full model takes the following form:

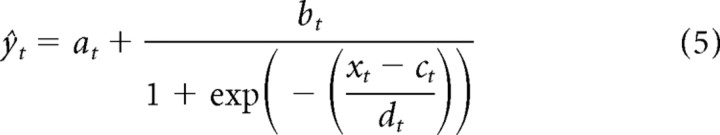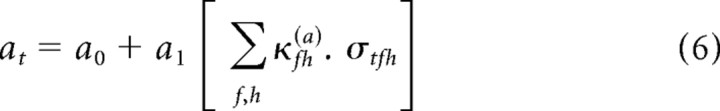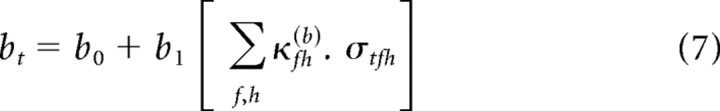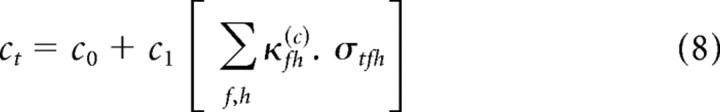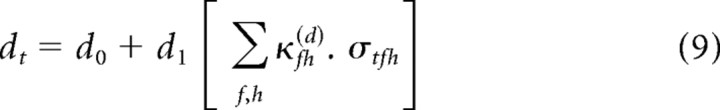For brevity of notation, we use the generic parameter θ to denote each of the four nonlinearity parameters, a–d. Thus, Equations 6–9 can be written as follows:

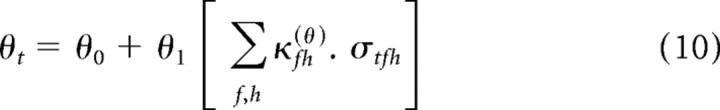Because the profile of recent contrast, σ_tfh, varies with time, so each parameter θ ϵ {a, b, c, d} of the output nonlinearity varies with time. These changes are mediated via a weighted sum of the contrasts in different frequency bands, provided by the term κ_fh^(θ), which we refer to as the spectrotemporal contrast kernel (STCK) for the parameter θ. The form of this model is illustrated in Figure 2A.

As with the STRF, the number of parameters of the contrast kernels can be dramatically reduced by assuming that they are separable in frequency and time history. Thus, we constrained κ_fh^(θ) = κ_f^(θ) ⊗ κ_h^(θ), such that the STCK could be decomposed into the outer product of a SCK and a TCK. We took further advantage of this property by fitting the SCK and TCK separately.

The full model of Equations 5–9 has a large number of parameters, numbering 4 × (N_F + N_H + 1) parameters (there being redundancy between κ_fh^(θ) and θ₁, as discussed below), in addition to the N_F + N_H parameters of the separable STRF. We made several assumptions to reduce the number of parameters. First, not all of the nonlinearity parameters {a, b, c, d} need to be contrast dependent. For such parameters θ, we set θ₁ = 0, such that θ_t = θ₀. Next, it is possible that changes to some of these parameters are the result of the same physiological process. This would allow us to assume a shared contrast kernel between pairs of parameters θ and θ′, with κ_fh^(θθ′) ≡ κ_fh^(θ) = κ_fh^(θ′).

For brevity, we assign the following notation to individual models. The full model, wherein all nonlinearity parameters have separate contrast kernels, is denoted as the a/b/c/d model. When a nonlinearity parameter is assumed to be contrast independent, we omit the corresponding letter from the name. Thus, b does not change with contrast in the a/c/d model. Finally, we concatenate letters when they share the same contrast kernel. Thus, in the a/cd model, κ_fh^(a) ≠ κ_fh^(c) = κ_fh^(d) ≡ κ_fh^(cd).

One special case is worth particular mention. The results of Rabinowitz et al. (2011) demonstrate that the primary effects of changing contrast lie in changes to the gain, via the parameter d, with some correlated changes in threshold, via the parameter c. These effects can be most simply captured by the cd model, wherein the nonlinearity parameters a and b are contrast independent, whereas c and d share a single contrast kernel. The cd model thus takes the following form:

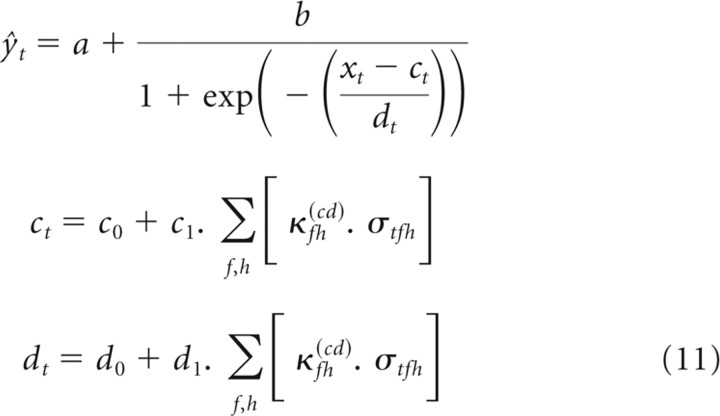Fitting procedures.

With the assumption that contrast kernels could be separated into spectral (SCK) and temporal (TCK) components, we first fitted SCKs. We limited the TCKs to cover 500 ms of history; as a consequence of both this and the segmented structure of the RC-DRCs, the values of the parameters a_t through d_t would be constant from 500 ms after each segment transition until the next segment transition. We thus fitted SCKs by using only the last 2.5 s of data from each segment and the following set of equations:

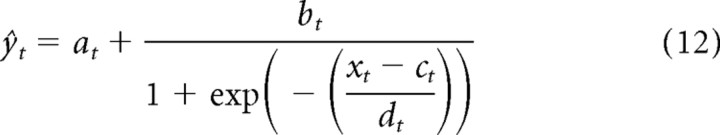To reduce the time taken to fit models, we took further advantage of the segmented nature of the RC-DRCs. Because σ_tf does not change with time within a segment k, the set of contrast values can be summarized as a matrix s_kf, capturing the contrast in segment k of frequency band f. Rather than fitting the parameters directly to the entire, trial-averaged training dataset (with N_T ≈ 8000), the set of (STRF-weighted) stimulus/response pairs (x_t, y_t) within each segment was divided equally into 20 bins along the x-axis (Chichilnisky, 2001; Simoncelli et al., 2004). This reduced the size of the dataset fivefold and enabled us to confirm that the sigmoid parameterization was appropriate (see Fig. 5, middle column). For bin j in segment k, we denote the bin center as x̄_jk and the mean firing rate ȳ_jk. This resultant model was considerably more efficient to fit:

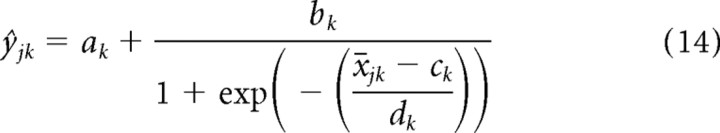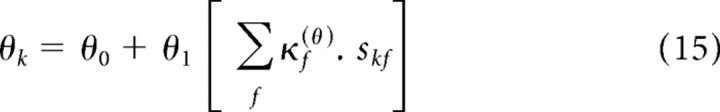This reduction in the size of the dataset was necessary for the bootstrapping and Markov Chain Monte Carlo (MCMC) analyses (explained below). On a subset of units, we confirmed the validity of this approximation by comparison with fits to Equations 12 and 13. These produced near identical results.

Figure 5.

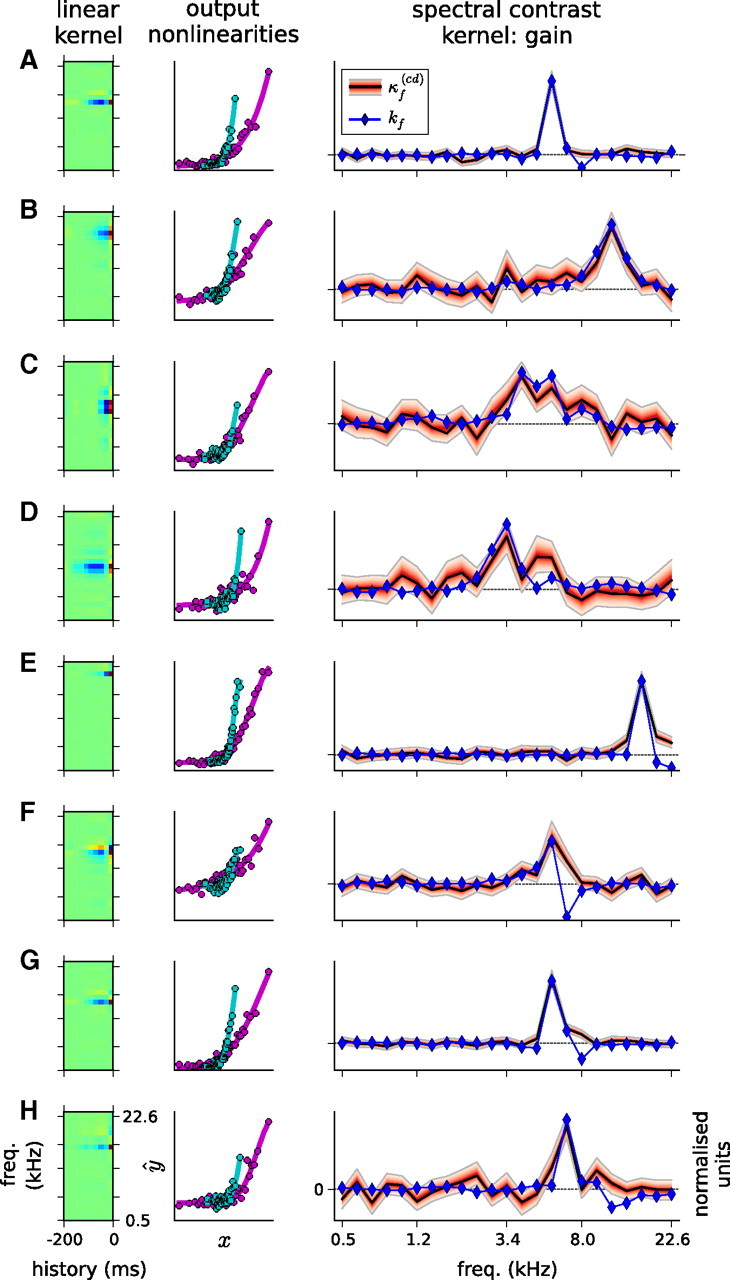
Gain SCKs, for eight example units. These are fits of the cd model, with contrast-independent a and b, and a shared, real-valued SCK, κ_f^(cd), for c and d. Left, STRF for each unit. Middle, Static output nonlinearities for each unit, when estimated under the all-high-contrast condition (magenta) and the all-low-contrast condition (cyan), showing the gain change between the two conditions. Right, SCK for each unit. The black line shows the MAP estimate for κ_f^(cd); the red filled region, bounded by the gray lines, shows a 95% credible interval for the posterior distribution over these coefficients. The red shading increases in darkness with probability. The blue line and blue diamonds show the frequency component of the linear, separable STRF, k_f. Both k_f and κ_f^(cd) have been normalized by the respective SDs to facilitate visual comparison. A–D exemplify how k_f and κ_f^(cd) align in BF and bandwidth. E–G (but not H) show examples in which κ_f^(cd) covers the inhibitory sidebands of the receptive field.

Equations 13 and 15 each contain a redundancy between θ₁ and κ_h^(θ). We therefore constrained each SCK to sum to unity, i.e., Σ_f κ_f^(θ) = 1. For the purposes of including priors (see below), we defined λ_f^(θ) as the unnormalized SCK for θ, such that

To fit TCKs for each unit, we returned to the first 0.5 s of data that followed each segment transition. We fixed the values of θ₀ and θ₁ for each θ, together with the SCKs, κ_f^(θ), that had already been fitted for each unit. To ensure consistency with Equation 13, we also constrained each TCK to sum to unity, i.e., Σ_hκ_h^(θ) = 1, by defining λ_h^(θ) as the unnormalized TCK for θ, via

Because TCKs could only be fitted to the periods immediately after each segment transition, there were limited data available to fit the TCK parameters. One consequence of this was that allowing the coefficients of κ_h^(θ) to take on any value (subject to a Gaussian prior) resulted in considerable overfitting (see the ℜ performance in Fig. 7G). Thus, TCKs were fitted with the constraint that all coefficients be positive.

Figure 7.

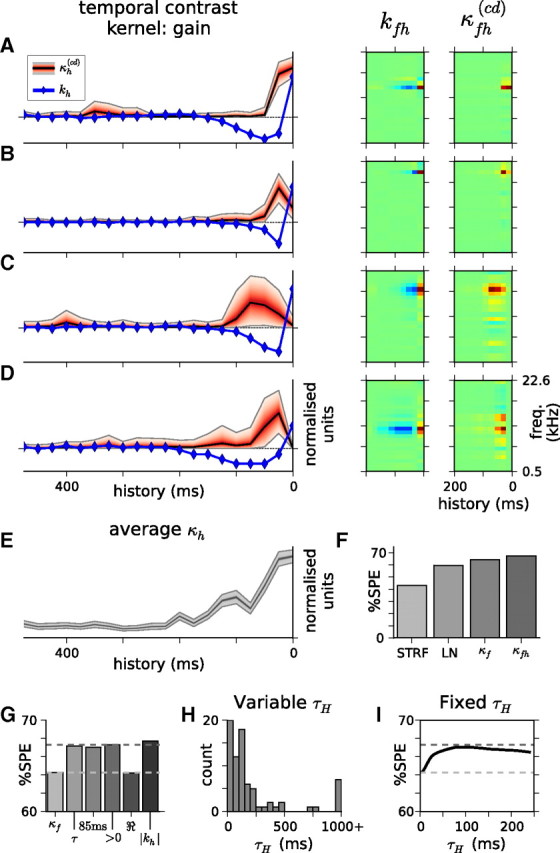
TCKs. A–D, Left panels show the TCKs for four example units. As in Figures 5 and 6, red area shows the gain TCK, κ_h^(cd), whereas blue line and diamonds show the temporal component of the STRF, k_h. Right panels compare the STRF, k_fh, with the full STCKs, κ_fh^(cd), as per Figure 2. E, Mean of the contrast time kernels from the 77 cortical units, ¯κ_h^(cd). This shows the approximately exponential shape of the time kernels. The mean contrast kernel had a fitted time constant of 86 ms. F, Model predictive power. Including a history component to the contrast kernels (κ_fh) improves the performance of the model compared with the assumption that only the current contrast matters (κ_f). Prediction scores for the simple STRF model and the LN model are shown for comparison. Note that this is fitted over a different dataset from that used in Figures 3–6, so the values of %SPE in this figure do not match those presented previously. G, Model predictive powers for a range of TCK models. In order, from left to right, these models are the following: (κ_f), no history dependence, i.e., κ_h = δ_h0; (τ), exponential model with time constant τ_H fitted (see H); (85 ms), exponential model with τ_H fixed at 85 ms (see I); (>0), κ_h constrained to be positive; (ℜ), κ_h allowed to take on any real value; (|k_h|), κ_h approximated as the absolute value of the STRF time kernel. Dashed horizontal lines show the model predictive power for the κ_f and the >0 models. Note that allowing the coefficients of the TCK to be real-valued (the ℜ model) led to considerable overfitting; the >0 model is thus the STCK model considered in Materials and Methods. H, Fits of the time constant τ_H for the exponential model for all 77 units. The median time constant was 117 ms. I, Model predictive power for the exponential model when τ_H was fixed rather than fitted. Abscissa denotes the fixed value of τ_H, ordinate as in G. The horizontal dashed lines are as in G. The most predictive model had τ_H = 85 ms. Thus, three different measures of the time course of gain changes (in E, H, and I) give approximately consistent answers.

The dataset for each unit was subdivided randomly into training (90%) and prediction (10%) subsets. All parameter fitting took place on the training dataset. Separable STRF models were first fitted to the whole training dataset using maximum likelihood, ignoring the segmented structure of the RC-DRCs. STRFs were fixed thereafter. Next, maximum a posteriori (MAP) estimates of the nonlinearity and contrast kernels were estimated all together, using gradient descent. For each model, the log posterior probability was calculated, as well as its derivatives with respect to all the parameters. Minimization of the negative log posterior was performed using the Limited-memory Broyden-Fletcher-Goldfarb-Shanno (L-BFGS-B) algorithm (Zhu et al., 1997), via SciPy (http://www.scipy.org/). This assumed that x_t, i.e., the output of the linear STRF model, was observed. The log likelihoods (and the log posteriors) were only convex with respect to some parameters; the gradient descent algorithm thus needed to be initialized at a number of different initial conditions to reduce the chances of settling in local minima. Forty different starting locations were chosen by random draws from the prior distributions over the parameters, with an additional initialization condition at the mean of the priors (see below). Generally, at least half of these repeats converged to the same (best) fixed point.

In principle, we could have merged the STRF fitting with the nonlinearity/contrast kernel fitting and minimized a single objective function. However, optimizing all parameters proved computationally impractical. Alternatively, we could have iterated between optimizing the nonlinearity/contrast kernel parameters (with the STRF fixed) and optimizing the STRF (with the other parameters fixed). However, we observed that this iterative procedure typically made little to no difference to prediction scores, and STRFs did not noticeably change over successive iterations. Because the focus here is not on the STRF but on the contrast-dependent changes in output nonlinearities, no successive refinements to STRFs were pursued beyond the initial fit.

A major goal of this work was to characterize the contrast kernels for cortical neurons. This involves estimating not only the best parameter values for κ_f^(θ) but also their error bounds. In addition to the MAP estimates, which pinpoint the mode of the posterior parameter distributions, we approximated the shape of these posterior distributions by sampling from them using MCMC methods. MCMC models were constructed in Python, using the PyMC package (Patil et al., 2010). Chains were initialized at the MAP parameter values and advanced using a Metropolis–Hastings step method. A barrage of diagnostics, including trace plots, Geweke's diagnostic (Geweke, 1992), and autocorrelation analyses, was used to assess convergence and mixing. From these diagnostics, we found that minimum chain lengths of 120,000 samples, with a 20,000-sample burn-in and 20× thinning, were sufficient for a reasonable characterization of the posteriors. As always for MCMC methods, longer and parallel chains would improve the representation of the posteriors; nevertheless, the observed results satisfied the above diagnostics and are therefore used here to provide an approximate measure of the error bounds on the contrast kernels. When illustrated in figures, and for computing statistics, these error bounds are summarized in terms of credible intervals, a Bayesian analog of confidence intervals (Carlin and Louis, 2009).

Priors on nonlinearity parameters.

Priors were chosen for simplicity of form rather than analytic tractability. From Equations 6–9, we see that each parameter θ ϵ {a, b, c, d} is the sum of a contrast-independent term, θ₀, and a contrast-dependent term, weighted by θ₁. Rather than placing priors directly on these terms, it was more convenient to reparameterize the model as follows.

The contrast in segment k and frequency f, s_kf, could only take on binary values. In the all-low-contrast segment, when s_kf = 0 ∀ f, it follows from Equation 15 that θ_k = θ₀. In the all-high-contrast segment, when s_kf = 1 ∀ f, we use the fact that the contrast kernel, κ_f^(θ), is normalized (from Eq. 16) to find that θ_k = θ₀ + θ₁. Defining these two values as θ_low and θ_high, respectively, we can rewrite Equation 15 as follows:

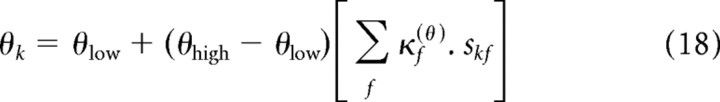Thus, the parameters {a_low, b_low, c_low, d_low} describe the output nonlinearity in the all-low-contrast segment, and the parameters {a_high, b_high, c_high, d_high} describe the output nonlinearity in the all-high-contrast segment. In each segment, the value of θ_k typically lies between θ_low and θ_high, depending on the projection of s_kf onto κ_f^(θ) (although θ_k can take on more extreme values when some of the coefficients of κ_f^(θ) are negative).

For each θ, identical priors were placed on each of θ_low and θ_high. The respective priors were primarily chosen to satisfy three purposes: (1) to enforce a set of hard constraints, namely that a, b, and d all be positive; (2) to apply some regularization, i.e., to ensure that b, c, and/or d did not grow excessively large; and (3) to provide a suitable set of initial conditions for MAP fitting. As a result, the priors were relatively broad, with data-driven hyperparameters.

For each unit, we defined a set of intermediate statistics on the binned stimulus–response data (x̄_jk, ȳ_jk):

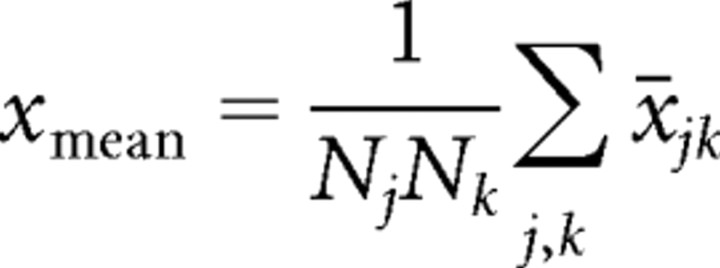where N_j is the number of bins (here, 20), and N_k = N_S, the number of segments.

In turn, the priors P(θ_low) = P(θ_high) were defined via

where exponential distributions are given in terms of their scale parameters, β.

The L-BFGS-B algorithm used to minimize the negative log posterior allows the explicit specification of parameter boundary values; for the exponentially distributed variables, a lower bound of 1 × 10⁻¹⁵ was provided.

Finally, for those models in which only a subset of the nonlinearity parameters were contrast dependent, θ₁ = 0 was enforced, such that θ_high = θ_low.

Priors on contrast kernels.

As discussed in Results, three different approaches to the values of SCKs were taken: (1) in the first approach, the kernels were allowed to take any real value; (2) in the second approach, they were constrained to be positive; and (3) in the third approach, they were fixed at particular values.

Priors were placed on the coefficients of the unnormalized contrast kernels, λ_f^(θ). Because these were normalized via Equation 16 to give κ_f^(θ), the scale of the respective priors was not important.

When real-valued kernels were used, the prior on λ^(θ) was chosen to be a spherical Gaussian, with λ_f^(θ) ∼ Normal(0, 0.1²). When positive-valued kernels were used, the prior on each coefficient was chosen as λ_f^(θ) ∼ Exp(0.1). In this latter situation, as for the positive nonlinearity parameters, the L-BFGS-B algorithm bounded each coefficient below at a value of 1 × 10⁻¹⁵.

When real-valued contrast kernels were used, it was possible for the denominator of Equation 16 to approach zero, giving untenable values of κ_f^(θ). As a result, the minimization algorithm occasionally yielded zero-division errors. When this occurred, the algorithm was reset with a new initial value. This discontinuity also meant that the algorithm was more likely to get stuck in local minima of the negative log posterior, requiring a larger number of repeated fittings from random initial conditions.

Model success.

To compare different models for the firing rate behavior of auditory cortical neurons, we made use of the strategy developed by Sahani and Linden (2003). For each unit, the amount of its total response variance that can be explained is bounded by the signal power (SP). Model success should therefore be measured as the percentage of signal power explained (%SPE). This is the percentage reduction in the SP from fitting the model and is equivalent to the following:

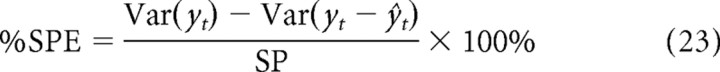By subdividing the data for each unit into a training and prediction dataset, one can obtain two values for %SPE for that unit. The %SPE from the training data is inflated as a result of overfitting to the noise in the training data. Thus, %SPE_training provides an upper bound for the model performance. The %SPE from the prediction data is expected to be lower, because it tests the generalizability of the model to new data. Thus, %SPE_prediction provides a lower bound for the model performance.

Because these two measures diverge as a function of NR, a suitable method for measuring the predictive power of the model from the population data is to extrapolate from the two sets of estimates of model success above to those for a hypothetical zero-noise neuron (Sahani and Linden, 2003; Ahrens et al., 2008a). The resultant upper and lower estimates bound the true predictive power of the model, i.e., that which would be obtained in the limit of zero noise. Bounds of model prediction power reported here come from linear extrapolations to the zero case. When only a single value is cited (as in the figures), this is the lower bound.

To correct against sampling biases, we cross-validated the results across 10 different partitions of the data. The %SPE values reported here are medians across these 10 partitions. The same set of partitions were used for fitting all models to the same unit.

Results

Our primary objective was to determine the spectrotemporal window within which changes in stimulus contrast inform changes in neuronal gain. To do so, we designed a set of stimuli, known as RC-DRC sequences (Fig. 1). This provided an ensemble of stimulation conditions, each with a different profile of contrast statistics.

We recorded from 168 units in the A1 and anterior auditory field (AAF) of three anesthetized ferrets, while presenting RC-DRCs. These areas were identified on the basis of their location on the middle ectosylvian gyrus and the tonotopic organization, which is organized approximately dorsoventrally across the gyrus (Nelken et al., 2004; Bizley et al., 2005). Among this set of units, we identified 77 units that responded reliably to the RC-DRCs, as measured via a maximum noise level criterion (see Materials and Methods).

Spectral contrast kernels

We constructed a class of models to analyze the responses of the units to the RC-DRCs (Eqs. 5–9; Fig. 2). These build on LN models, which have been used previously to characterize the relationship between stimuli and neuronal responses (Chichilnisky, 2001; Simoncelli et al., 2004). As in a standard LN approach, we modeled the responses of units as a two-stage process: (1) a reduction of the dimensionality of stimulus space, by filtering the ongoing (log) spectrogram through an STRF; and (2) a nonlinear transformation stage, by passing the filtered stimulus through a static output nonlinearity. Our models expanded on this schema by allowing the parameters of the output nonlinearity—and therefore its shape—to change over time. In particular, we enabled these parameters to change as a function of stimulus statistics. Because the RC-DRC stimuli were constructed by defining a matrix of contrast statistics, which varied over frequency and time, we modeled the changes to the nonlinearity parameters via a set of spectrotemporal contrast kernels (STCKs). Each STCK filters the ongoing contrast profile of the sound, σ_tf, in the same way that the STRF filters the ongoing spectrogram, L_tf.

The most general model of this scheme has a large of number of parameters. We therefore began by making a few key simplifications. First, we assumed that STCKs could be separated into a spectral component and a temporal component, in the same way that it is often reasonable to make separable approximations to cortical STRFs (see above). Thus, we first fitted spectral contrast kernels (SCKs) and later temporal contrast kernels (TCKs).

Our second simplification was to consider, for each parameter of the output nonlinearity, whether that parameter showed evidence of being dependent on stimulus contrast. This was motivated by our previous results (Rabinowitz et al., 2011) that showed that changing the global stimulus contrast primarily produced changes in gain (here, the d parameter of the nonlinearity) and the stimulus inflection point (here, the c parameter). Finally, additional reductions in the parameter load could be made by sharing contrast kernels between multiple parameters.

To assess the validity and utility of such simplifications, we fitted a range of SCK models to the responses of the cortical units. For each model and unit, we measured the fit quality, together with its ability to predict responses outside of the training dataset. These were quantified as the percentage of stimulus-locked response variance that the model explained in each of the two datasets (Eq. 23). Previous authors have demonstrated that the measured values of such quantities depend on the trial-to-trial reliability of the stimulus-evoked spiking patterns of the units: for less reliable (i.e., noisier) units, fitted models are more likely to capture noise in the training dataset and therefore make poorer predictions (Sahani and Linden, 2003). We thus followed Sahani and Linden's lead and assessed model performance across the population of cortical units by extrapolating from the set of scores to an idealized, zero-noise unit. This produced two estimates of the predictive power of the model: (1) an upper bound, from the fit quality of the model on the training sets; and (2) a lower bound, from the ability of the model to predict outside the training sets (Ahrens et al., 2008a). This process is illustrated in Figure 3A for the lower bounds.

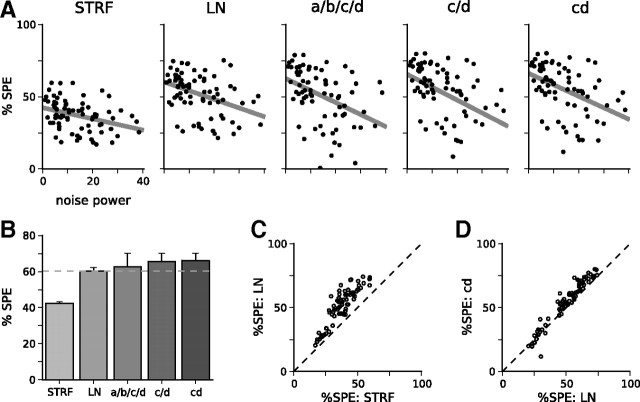
Figure 3.

Including SCKs in models of neural responses improves their predictive power over the LN model; this is further improved by simplifying the model. A, Model predictive power, as measured by Sahani and Linden (2003). Model names are defined in Materials and Methods. For each model, scatter plots show the cross-validated prediction scores across all 77 units. These are calculated as the percentage of the signal power (%SPE) of the unit captured by the model on the prediction dataset and shown as a function of the normalized noise power in the responses of the unit. Gray line shows the extrapolation of prediction scores to an idealized zero-noise unit, producing a lower bound on the overall predictive power of the model over the population of auditory cortical units. The upper bound on predictive power has been omitted for clarity. B, Summary of predictive powers for the models in A. Solid bars show the lower bound (as plotted in A) from cross-validation; error bars show the upper bound from the training dataset. Although adding a full set of contrast kernels (a/b/c/d) leads to a modest improvement in prediction scores over the LN model, the large number of parameters in the full model leads to overfitting. Rendering a and b contrast independent reduces overfitting and improves prediction scores (the c/d model). The best-performing model is the cd model, with a shared contrast kernel between c and d. C, Comparison between prediction scores for the LN model and for the STRF model, on a unit-by-unit basis. D, Comparison between the LN model and cd model on a unit-by-unit basis.

As a baseline, we fitted simple (separable) STRF and LN models to each unit. These models were fitted to data that were pooled across all segments of the RC-DRCs and therefore did not take into account changes in contrast from segment to segment. The predictive power of the STRF model was 42.4–43.4%, whereas the predictive power of the LN model was 60.2–62.2%. Adding an output nonlinearity considerably improves model performance.

Including a full set of independent SCKs for each nonlinearity parameter also improved model predictions (Fig. 3). This a/b/c/d model (for naming conventions, see Materials and Methods) had a prediction score of 62.7–70.1%. However, we found that we could substantially further improve the predictive performance of the models by adding constraints to reduce the degree of overfitting. First, we found that the parameters a and b did not generally change with contrast. Fixing these to be contrast independent (i.e., fitting the c/d model) yielded better prediction performance of 65.6–70.1%. In turn, the SCK for the c parameter, κ_f^(c), and the SCK for the d parameter, κ_f^(d), were generally highly correlated with each other (median correlation coefficient of r(κ_f^(c), κ_f^(d) = 0.89). We therefore constrained these two contrast kernels to be identical (the cd model). This outperformed the other SCK models, with a prediction score of 66.2–70.1%. On a unit-by-unit basis, the cd model outperformed the standard LN model for 62 of 77 units; this improvement was significant for 48 of these units (Wilcoxon's signed-rank test on N = 40 cross-validated scores, p < 0.01).

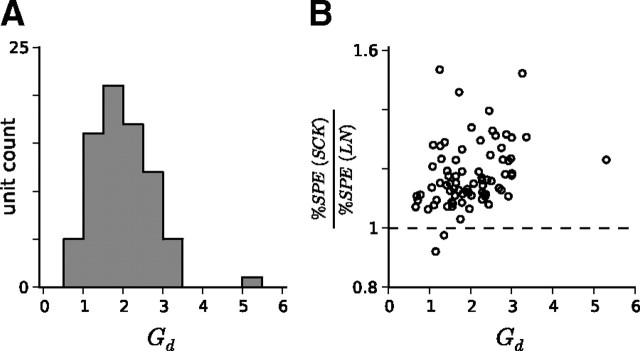
According to the cd model, 72 of 77 units decreased their gain as contrast increased. The extent of gain changes can be quantified as the ratio G_d = d_high/d_low (see Eq. 18), which measures the proportional dilation of the output nonlinearity along the x-axis as a result of switching from the all-high-contrast condition to the all-low-contrast condition. A histogram of G_d values for the population of units is shown in Figure 4A. The median G_d was 1.92, which is in good agreement with our previous observations (Rabinowitz et al., 2011). As expected, units with larger G_d tended to experience the greatest improvements in model prediction by including the SCK (Fig. 4B; Spearman's correlation of 0.40; p < 0.001).

Figure 4.

Gain model: contrast-dependent gain changes across the population of A1/AAF units. A, The majority of units decreased their gain as contrast was increased, as expected. This is measured here by the radio G_d = d_high/d_low. B, The larger the contrast-dependent gain of a unit changes, the greater the improvement in model predictive power over the standard LN model. The (nonparametric) Spearman's correlation coefficient between G_d and model improvement was 0.40 (p < 0.001).

In summary, the most parsimonious model for capturing contrast-dependent changes to the firing behavior of the units is the cd model of Equation 11. As contrast is varied, the output nonlinearities of auditory cortical neurons undergo a slope change and a horizontal shift. These changes can be described as a linear function of the spectral profile of contrast. In the sections that follow, we concentrate exclusively on the cd model.

The shape of SCKs

We next asked what the SCKs looked like. Examples of SCKs fitted to the responses of the cortical units are shown in Figure 5. The most striking aspect of the SCKs is their similarity in shape to the STRF frequency kernels, k_f. For the frequencies in the excitatory component of the receptive field of these units, the weights of the SCK, κ_f^(cd), match almost precisely the weights of k_f. As the BF and bandwidth of k_f change across these units, so the BF and bandwidth of κ_f^(cd) change, too.

There was generally a good correlation between the gain SCKs of the units, κ_f^(cd), and the frequency component of their linear STRF kernels, k_f; across units, the median correlation coefficient was r(κ_f^(cd), k_f) = 0.69.

These kernels thus reveal an important aspect of contrast gain control: the same frequency channels whose level changes additively contribute to the firing rate of a cortical unit also divisively contribute to its gain. In these bands, an increase in tone level increases the firing rate of the unit, whereas an increase in the contrast of the tone level distribution of these bands decreases the gain of the unit. In turn, the relative size of the gain change produced by varying the contrast in a particular band is approximately proportional to the size of the change in firing rate produced by increasing the level of the band.

Contrary to this pattern, we found that, when units had strong inhibitory sidebands in their STRF—i.e., when there were coefficients of k_f, nearby to the BF, which were negative—the SCKs often had positive, rather than negative, coefficients for these same frequencies (Fig. 5E–G). In these bands, an increase in tone level decreases the firing rate of the neuron; however, an increase in the contrast of the tone level distribution of these bands also decreases the gain of the neuron.

These qualitative observations capture the major trends we observed. Among those units that deviated somewhat from this pattern, some had slightly wider SCKs and others slightly narrower than the excitatory band of the STRF. In addition, not all of the units with inhibitory sidebands produced significantly non-zero κ_f^(cd) coefficients at the sidebands (Fig. 5H). Finally, ∼20% of units (17 of 77) produced noisy, random-shaped contrast kernels. Among this last group, the SCK models still produced reasonable prediction scores; the results for these units are discussed in more detail below.

Simplifying SCKs

It is clear from the examples of Figure 5 that the most salient features of the gain SCKs are their large, positive coefficients in a localized region of frequency space. As mentioned above, these coefficients are often also positive in the inhibitory sidebands. Increasing the contrast of any of these bands thus yields a decrease in neuronal gain. However, very few κ_f^(cd) coefficients across the set of models appeared to be genuinely negative, such that high contrast in these bands would lead to an increase in neuronal gain.

Although 45% of all κ_f^(cd) coefficients were fitted to negative values, these values were typically small in magnitude. They were also generally not significant: the marginal posteriors on these coefficients rarely had all their weight below zero. In total, according to a 95% credible interval criterion, 7% of κ_f^(cd) coefficients across all units were significantly negative; according to a 99% credible interval criterion, only 3% of κ_f coefficients were significantly negative. These values compare with 19 and 13% for significantly positive κ_f coefficients.

Thus, the coefficients of SCKs were rarely negative and were generally larger in magnitude when the STRF frequency kernel was larger in magnitude. As a result, rather than describing a correlation between the coefficients of κ_f^(cd) of the units and their k_f (as above), there was actually a better correlation between κ_f^(cd) and the absolute value of the STRF frequency kernel, |k_f| for each unit, with a median correlation coefficient of r(κ_f^(cd), |k_f|) = 0.80.

There is reason to suspect that none of the coefficients of the gain contrast kernel should be negative. In principle, negative κ_f^(cd) values indicate frequency bands for which high contrast would cause an increase in neuronal gain. This may not be possible under certain mechanistic implementations of contrast gain control. To test this possibility, we enforced the constraint that coefficients of κ_f^(cd) must be positive. Examples of the resulting kernels are shown in Figure 6A–H. This model provided even better predictions than using real-valued (i.e., unconstrained) κ_f^(cd), with a prediction score of 67.1–69.9% (Fig. 6I). The constrained-positive cd model was, in total, the best predicting SCK model, and outperformed the standard LN model for 68 of 77 units. This improvement was significant for 52 of these units (p < 0.01). Thus, it is likely that negative values in the unconstrained contrast kernels reflect an overfitting of the parameter values to the small sample of conditions presented.

Figure 6.

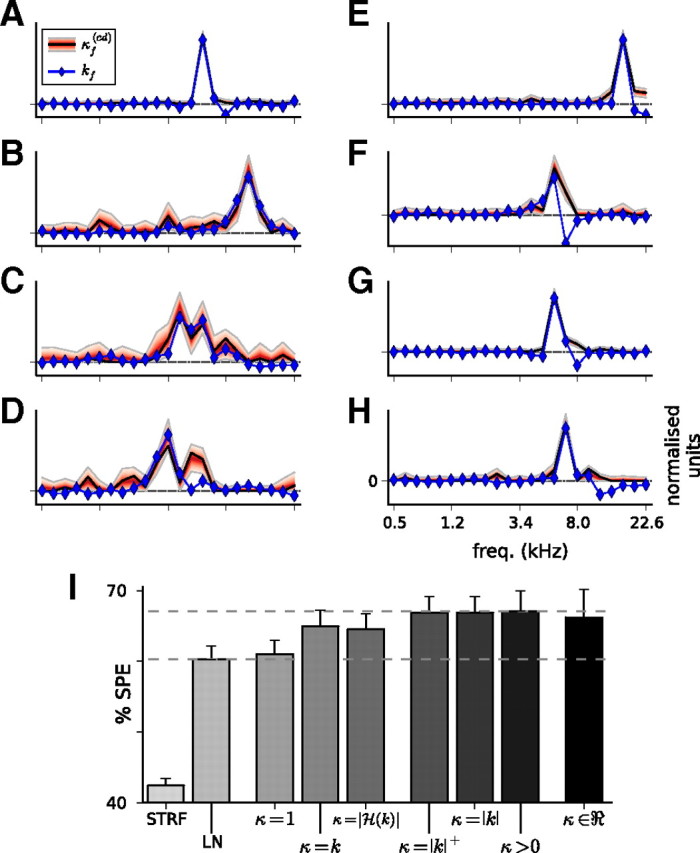
Approximations to the cd model. A–H, Gain SCKs when coefficients were constrained to be positive. This shows the same eight units as shown in Figure 5. Again, the frequency component of the STRF, k_f (blue), approximately matches the gain SCK, κ_f^(cd) (black line and red area). I, Model predictive power for the cd model with constrained coefficients; as in Figure 3B, solid bars show prediction scores, and error bars show training scores. When the contrast kernel coefficients are unconstrained (κ ϵ ℜ; right), the model performance is better than the linear (STRF) and LN models (left). Restricting the coefficients of the SCK to be positive (κ > 0) reduces overfitting and improves prediction scores. Excellent approximations are provided by fixing the SCKs as either the absolute value of the STRF frequency kernel (κ = |k|) or the rectified value (κ = |k|⁺). Models that do not perform as well include fixing the contrast kernel as the STRF frequency kernel (κ = k), fixing it as the magnitude of the Hilbert transform of the STRF frequency kernel (κ = |H(k)|), or assuming that it is constant with respect to frequency (κ = 1). These still outperform the simple LN model. Dashed lines are shown at the model performance values for the LN model and the constrained-positive cd model.

As mentioned above, the gain contrast kernels of a number of units were noisy, with little observable structure when κ_f^(cd) was unconstrained. For all but five of these units, constraining κ_f^(cd) > 0 yielded contrast kernels that more closely resembled the respective STRF frequency kernels of the units. Constraining the coefficients of the gain kernels to be positive therefore reveals an underlying structure to the kernels of noisier units.

A striking feature of the constrained-positive kernels is that, across all units that gave reliable responses to RC-DRCs, the correlations between the coefficients of κ_f^(cd) and |k_f| are even stronger than for the unconstrained models, with a median r(κ_f^(cd), |k_f|) = 0.93. This suggests that one may be able to approximate the gain contrast kernels simply as κ_f^(cd) = |k_f|. We implemented this as an additional set of models. These showed that, when the SCK was fixed in this manner rather than fitted, the model performance was only slightly impaired relative to fitting an SCK, as shown in Figure 6I. Almost identical prediction scores were obtained when we fixed κ_f^(cd) to be a rectified version of k_f, indicating that the contribution from the inhibitory sidebands to the model success was small. Finally, as a control, we also tested three alternative models: (1) one with κ_f = k_f, i.e., without the absolute value; (2) a second where κ_f = |H(k_f)|, i.e., as the magnitude of the Hilbert transform of k_f (which produced wider bandwidth SCKs); and (3) a third in which we ignored all spectral information and assumed a constant SCK (κ_f = 1/N_F). In all three cases, the model performed substantially worse. These data are summarized in Figure 6I.

The usefulness of the approximation κ_f^(cd) ≈ |k_f| is important. As this experiment demonstrates, the number of conditions needed to estimate gain contrast kernels is large, making it a time-consuming process. Conversely, including gain changes leads to substantial increases in model performance. When using the approximation, only two additional variables beyond the standard output nonlinearity need to be estimated (c₁ and d₁), which can be done quickly using only two contrast conditions. Thus, greatly improved models of the responses of auditory cortical neurons can be readily implemented using this approach.

Temporal contrast kernels

Just as the SCKs reveal how units integrate the spectral pattern of stimulus contrast to determine their gain, TCKs reveal how units integrate the recent history of stimulus contrast to the same effect. To map the TCKs of the cortical units, we fixed their SCKs and fitted models to the neuronal responses immediately after each segment transition.

Examples of TCKs, κ_h^(cd), are shown in Figure 7A–D. As for the temporal component of the STRFs of these units, the units were most sensitive to the contrast in the most recent 50–100 ms of stimulation and retained a weak dependence on the contrast statistics further back in history.

Including the TCK for gain changes led to an overall improvement in the model predictive power. For the responses during these transition periods, the prediction scores were 43.1% for the STRF model, 59.7% for the LN model, 64.3% when only the SCK was considered, and 67.3% when the full STCK was implemented (Fig. 7F). The STCK outperformed the LN model for 72 of 77 units, of which 54 were significant (Wilcoxon's signed-rank test on N = 100 cross-validated scores; p < 0.01).

Simplifying TCKs

A secondary goal of this work is to develop simple approximations to contrast kernels that can be applied without requiring the time-consuming exploration of stimulus space attempted here. We therefore considered a number of simplifications to the TCK model. The success of each of these simplifications is summarized in Figure 7G.

We noted that the population mean of the TCKs, shown in Figure 7E, followed an approximately exponential decay, with a time constant of τ = 86 ms. We therefore fitted a simplified, single-parameter TCK model to each unit, κ_h^(cd) ∝ exp(−h/τ_H), where τ_H is the time constant (Fig. 7H). The median time constant fitted to the 77 units was τ_H = 117 ms. The model performed well compared with fitting a full TCK, with a score of 67.2%. We also considered whether, for the purposes of parsimony, a single time constant could be used for all units within the population. By fixing τ_H at different values, we found that the most predictive model had τ_H = 85 ms, with a prediction score of 67.1%. There was, however, a reasonably broad range of τ_H values between 80 and 120 ms that gave similarly respectable scores (Fig. 7I).

Finally, in the same way that the SCKs could be approximated, up to a normalization constant, as the absolute value of the frequency component of the STRF, so too the TCKs could be approximated as the absolute value of the temporal component of the STRF. This produced a prediction score of 67.2%. Thus, the absolute value of the STRF provides an excellent approximation for the STCK of a cortical neuron.

Discussion

The goal of this study was to determine the spectrotemporal windows within which stimulus contrast modulates the gain of auditory cortical neurons. We therefore constructed a stimulus set that provided an ensemble of different contrast conditions (Fig. 1) and investigated how the response properties of cortical units changed under these conditions (Fig. 2). We were able to estimate the relative contributions of the contrast in different frequency bands and different time bins to the gain of individual units, via their STCKs.

We found that the spectral components of these kernels (the SCKs) typically place their weight on the same frequency bands that contribute to the STRF of a neuron (Fig. 5). Thus, when the firing rate of a neuron is linearly sensitive to the level variations in a particular band, then it is also divisively sensitive to changes in the contrast of that band. Not only are SCKs coextensive with the frequency component of the STRF, but they are also matched in magnitude: the extent to which the contrast of a band contributes to the gain of a neuron is approximately proportional to the extent to which the level of that band contributes to the firing rate of the neuron (Fig. 6I). Neurons with narrow tuning curves are sensitive to contrast in a narrow frequency window, whereas the gain of neurons with broad tuning curves can be influenced by contrast over a similarly broad frequency range. Curiously, the spectral region whose statistics determine gain includes the inhibitory sidebands of a neuron: high contrast in the sidebands also reduces neural gain.

The temporal component of these kernels (the TCKs) could be fitted reasonably well by an exponential curve, with a time constant of ∼85 ms. Similar to the SCKs, the TCKs could also be approximated well as the absolute value of the time component of the corresponding STRF (Fig. 7). Thus, a simple approximation of the gain contrast kernel is κ_fh^(cd) ≈ |k_fh|. In summary, cortical neurons integrate stimulus contrast and level fluctuations over a similar spectrotemporal window, albeit to different effects. This is summarized in Figure 8.

Figure 8.

Summary of results. We find that the gain changes undergone by cortical neurons in response to complex patterns of stimulus contrast can be captured by this simplified contrast kernel model. The neural response is determined by convolving the spectrogram with a linear spectrotemporal kernel (k_fh) and passing the output of this operation (x_t) through a static output nonlinearity to produce the predicted spike rate (ŷ_t). The minimum and maximum firing rate of the output nonlinearity are fixed, but the stimulus inflection point (c) and the (inverse) gain (d) change over time, depending on the statistics of recent stimulation. The evolution of c and d over time is determined by convolving the contrast profile of the sound, σ_tf, with a single contrast kernel, κ_fh^(cd), as in Equation 11. Finally, the contrast kernel can be approximated as κ_fh^(cd) ≈ |k_fh|. This model captures 20–25% of the residual variance not explained by the LN model by adding only an additional two parameters.

Little contribution to the gain from remote spectral and temporal regions

This study considerably extends a preliminary estimation of contrast kernels presented by Rabinowitz et al. (2011). There, we attempted a coarse, population-level characterization of the SCKs of auditory cortical neurons and found that the gain of neurons depended predominantly on the contrast in spectral regions local to the BFs of the units. This is confirmed by the results presented here.

Although our previous study ruled out strong contributions to the gain from frequency bands outside the STRFs of neurons, we did find evidence for weak contributions from these bands, suggesting that gain control in the auditory cortex is, to some extent, dependent on global statistics. In the present study, however, we found that the gain kernels were primarily restricted to the frequency bands present in the STRF.

Stimulus design may explain this discrepancy. In the study by Rabinowitz et al. (2011), we categorically divided frequency bands into local and remote groups, in a way that may have underestimated the range of frequency bands that additively contributed to the STRF. Our approach here circumvented this problem by being noncategorical. Conversely, the subset of contrast space explored here may have been insufficient to reveal the contributions from remote bands, which could be weak (or superadditive) and only detectable as a compound effect. These results therefore bound the magnitude of extra-classical receptive field contributions to neuronal gain.

The match between the domains of SCKs and linear STRFs is consistent with previous findings on forward suppression: in general, the more a sound matches the preferred stimulus of a neuron, the more it suppresses subsequent responses (Calford and Semple, 1995; Brosch and Schreiner, 1997; Reale and Brugge, 2000; Zhang et al., 2005; Scholl et al., 2008). The match between TCKs and STRFs, however, initially seems at odds with the long timescales of adaptation reported previously in the auditory cortex (Ulanovsky et al., 2004; Wehr and Zador, 2005; Asari and Zador, 2009). The contrast kernel models therefore capture only a fast component of this adaptation, much like the rapid luminance and contrast gain control identified in the retina (Enroth-Cugell and Shapley, 1973; Baccus and Meister, 2002). It is possible that we did not see slower adaptation components because our DRCs switched contrast rapidly: in the retina, the timescale and parameters of stimulus dynamics directly impact on the timescale of slow contrast adaptation (Wark et al., 2009).

The similarity between the domains of STCKs and STRFs suggest that both phenomena share some common source. However, our results can only partially constrain this mechanism. The shape of STRFs depends on complex interactions between excitation and inhibition (Wallace et al., 1991; Budinger et al., 2000; Winer et al., 2005; Liu et al., 2007; Wu et al., 2008; Moeller et al., 2010). Gain control could therefore be explained by a combination of excitatory and/or inhibitory inputs (Chance et al., 2002; Murphy and Miller, 2003; Katzner et al., 2011), the action of intrinsic currents (Abolafia et al., 2011), or the activation of local layer six neurons with similar tuning, as observed recently in primary visual cortex (V1) (Olsen et al., 2012). Given the rapidity of the TCKs, our results are unlikely to be fully described by cortical synaptic depression, which appears to operate at longer timescales (Wehr and Zador, 2005). Gain control may have subcortical origins (Anderson et al., 2009; Malmierca et al., 2009), provided these combine in a similar manner to the way they produce cortical STRFs. It may be possible to evaluate the relative likelihood of these mechanisms by comparing STRFs and STCKs under different stimulation conditions because STRFs are known to change under different stimulus contexts (Theunissen et al., 2000; Blake and Merzenich, 2002; Valentine and Eggermont, 2004; Woolley et al., 2005; David et al., 2009; Schneider and Woolley, 2011).

Implications for modeling

The contrast kernel models advanced in this work provide considerably better predictions of the responses of neurons compared with STRF and LN models. They capture ∼20% of the residual variance not explained by the LN model. Because STCKs can be approximated well from the absolute value of the STRF, this model requires only two additional parameters beyond the LN model (and hence six parameters beyond the STRF). The model presented in Figure 8 thus provides a simple and powerful way of extending existing models for the responses of auditory cortical neurons, capturing the sensitivity of these neurons to patterns of stimulus contrast.

The gold standard for models such as these is to be able to predict responses of auditory neurons to natural stimuli (Wu et al., 2006). Studies that have estimated receptive field models using synthetic stimuli have repeatedly found that the models do not generalize well to natural sounds (Theunissen et al., 2000; Rotman et al., 2001; Machens et al., 2004; David et al., 2009). One compelling reason for this is that natural sounds likely engage nonlinear coding mechanisms, which may not be activated within the spaces of synthetic stimuli, such as DRCs or ripples (Theunissen et al., 2000; Woolley et al., 2006; David et al., 2009). Furthermore, the linear approximations made during model construction are sensitive to the statistics of the subspace of stimuli explored (Christianson et al., 2008). Because natural scenes vary in their statistics over time, it is likely that including time-varying gain control will improve the predictions of STRF-based models.

One particular difficulty in extending these models to other domains is knowing how to measure stimulus contrast. For the synthetic stimuli we used here, the contrast was specified by design; we therefore used the stimulus parameters as input into the models. For arbitrary sounds, an algorithm for estimating σ_tfh would need to be specified; provided this algorithm makes broadly consistent measurements of the stimulus parameters that we used here, we anticipate that the benefits of including gain control will be considerable.

Gain control and divisive normalization

One form in which gain control is often cast is that of divisive normalization. In the abstract, this is a gain standardization process by which an initial set of responses—usually the result of information fed forward from earlier brain areas—is rescaled. The scaling factor takes the form of a local response normalizer: the activity of each neuron is divided by the pooled activity over other neurons in a local neighborhood (Heeger, 1992; Carandini et al., 1997). There is considerable evidence for normalization in a large number of systems, including V1 (Heeger, 1992; Carandini et al., 1997; Rust et al., 2005), extrastriate visual cortex (Miller et al., 1993; Missal et al., 1997; Recanzone et al., 1997; Simoncelli and Heeger, 1998; Britten and Heuer, 1999; Heuer and Britten, 2002; Zoccolan et al., 2005), superior colliculus (Basso and Wurtz, 1997), and the Drosophila antennal lobe, which mediates olfaction (Olsen et al., 2010), as well as in multisensory integration (Ohshiro et al., 2011).

There remains considerable debate as to what combination of cellular and circuit mechanisms actually mediates divisive normalization in the visual system (Carandini and Heeger, 2012). Nevertheless, it has proved to be a powerful idea for advancing our understanding of the computations actually being performed by a given system. Normalization promotes efficient coding, not only by shifting stimulus representations to use more of the dynamic range of neurons but also by encouraging decorrelated, higher-entropy representations of natural signals (Ruderman and Bialek, 1994; Olshausen and Field, 1996; Brady and Field, 2000; Fairhall et al., 2001; Schwartz and Simoncelli, 2001). Theoretical work has also argued for a role for normalization in other computations, such as decoding (Deneve et al., 1999; Ringach, 2010) and marginalization (Beck et al., 2011).

If we consider a network implementation of gain control, our result that κ ≈ |k| demonstrates that auditory cortical neurons have gain pools that share similar spectrotemporal sensitivity profiles. Thus, just as many systems appear to construct representations that are invariant to the normalized statistic, including visual representations in V1 that are contrast invariant (Albrecht and Hamilton, 1982; Heeger, 1992; Busse et al., 2009; Ringach, 2010), velocity representations in MT that are spatial-pattern-invariant (Heeger et al., 1996; Simoncelli and Heeger, 1998), and odor representations in the antennal lobe that are concentration invariant (Luo et al., 2010; Olsen et al., 2010), so it appears that the auditory cortex builds representations of sounds that are partially invariant to their spectrotemporally local contrast.