MRI and quantitative autoradiographic studies following bolus injections of unlabeled and ¹⁴C-labeled gadolinium-diethylenetriamine-pentaacetic acid in a rat model of stroke yield similar distribution volumes and blood-to-brain influx rate constants

Abstract

In previous studies on a rat model of transient cerebral ischemia, the blood and brain concentrations of gadolinium-diethylenetriaminepentaacetic acid (Gd-DTPA) following intravenous bolus injection were repeatedly assessed by dynamic contrast-enhanced (DCE)-MRI, and blood-to-brain influx rate constants (K_i) were calculated from Patlak plots of the data in areas with blood–brain barrier (BBB) opening. For concurrent validation of these findings, after completing the DCE-MRI study, radiolabeled sucrose or α-aminoisobutyric acid was injected intravenously, and the brain disposition and K_i values were calculated by quantitative autoradiography (QAR) assay employing the single-time equation. To overcome two of the shortcomings of this comparison, the present experiments were carried out with a radiotracer virtually identical to Gd-DTPA, Gd-[¹⁴C]DTPA, and K_i was calculated from both sets of data by the single-time equation. The protocol included 3 h of middle cerebral artery occlusion and 2.5 h of reperfusion in male Wistar rats (n = 15) preceding the DCE-MRI Gd-DTPA and QAR Gd-[¹⁴C]DTPA measurements. In addition to K_i, the tissue-to-blood concentration ratios, or volumes of distribution (V_R), were calculated. The regions of BBB opening were similar on the MRI maps and autoradiograms. Within them, V_R was nearly identical for Gd-DTPA and Gd-[¹⁴C]DTPA, and K_i was slightly, but not significantly, higher for Gd-DTPA than for Gd-[¹⁴C]DTPA. The K_i values were well correlated (r = 0.67; p = 0.001). When the arterial concentration–time curve of Gd-DTPA was adjusted to match that of Gd-[¹⁴C]DTPA, the two sets of K_i values were equal and statistically comparable with those obtained previously by Patlak plots (the preferred, less model-dependent, approach) of the same data (p = 0.2–0.5). These findings demonstrate that this DCE-MRI technique accurately measures the Gd-DTPA concentration in blood and brain, and that K_i estimates based on such data are good quantitative indicators of BBB injury.

INTRODUCTION

The blood–brain barrier (BBB) is a major part of the neurovascular unit, and is often breached following brain injuries, such as stroke (1). It is therefore important to image and evaluate BBB function following brain injury and to repeat such measurements to not only stage the lesion but also to evaluate the efficacy of treatment (2,3). Dynamic contrast-enhanced (DCE) imaging of the blood–brain distribution of magnetic resonance contrast agents (MRCAs) that do not permeate the normal BBB has the potential to do this, and has the advantage of being minimally invasive (4–7). This raises the question of the accuracy of MRI estimates of MRCA concentration in blood and brain (8) and of the pathophysiological parameters that can be derived from them, e.g. the blood-to-brain influx rate constant (K_i) (9,10) and the volume of circulating blood in the microvasculature.

In previous studies with rat brain tumor (11) and a suture model of reversible cerebral ischemia (10,12), gadolinium-diethylenetriaminepentaacetic acid (Gd-DTPA) was injected by intravenous (iv) bolus for DCE-MRI. In the latter studies, the pre- to post-injection difference in the longitudinal relaxation rate ΔR₁ (R₁ = 1/T₁), assumed to approximate the MRCA concentration, was repeatedly measured in blood and brain over time (13). The resulting plasma and tissue ΔR₁ data were used to prepare Patlak plots and to estimate K_i. After the DCE-MRI measurements, either [¹⁴C]-sucrose or [¹⁴C]-α-aminoisobutyric acid (AIB) was injected by an iv bolus, a series of carefully timed blood samples was taken over the next 20 min and, immediately thereafter, the brain was rapidly removed and processed for quantitative autoradiography (QAR). Subsequently, K_i was calculated from the blood and tissue radioactivity concentrations and the single-time equation (StEq) (14). The results indicated that the MRI-Patlak plot estimates of K_i of Gd-DTPA were well correlated with the radiotracer-QAR-StEq-assessed K_i values of [¹⁴C]-AIB in rat brain tumor (11) and stroke (12) models and of [¹⁴C]-sucrose in the same stroke model (10).

One study reported agreement between MRI- and QAR-derived tissue-to-blood concentration ratios, or volumes of distribution (V_R), and K_i values employing essentially identical preparations of MRCA and radiotracer with an iv step-down infusion in a rat model of cerebral ischemia (15). Almost all DCE-MRI studies, however, administer MRCA as a bolus that yields a rapid rise and fall in blood concentration during the initial minute. A recent report, in which Gd-DTPA and, somewhat later, Gd-[¹⁴C]DTPA were injected by iv bolus suggested that the Look–Locker (L–L) sequence underestimates the rapid rise and fall phase of the Gd-DTPA concentration–time course and produces an arterial input function (AIF) for a 20-min experiment that is low by 10–15% (16). This finding raised the possibility that the time course of MRCA concentration in tissue estimated by the L–L sequence might also be in error with iv bolus injections.

To address this possibility and to test further the accuracy of MRI estimates of Gd-DTPA concentration and K_i, the present experiments were performed with the same rat model of ischemia and nearly identical markers, Gd-DTPA and Gd-[¹⁴C]DTPA. In contrast with previous studies, the K_i values of both Gd-DTPA and Gd-[¹⁴C]DTPA were estimated using StEq. Testing involved comparisons of the spatial distribution of the tracers and the V_R and K_i values; positive outcomes would strongly imply that DCE-MRI accurately measures Gd-DTPA concentrations in brain following iv bolus injection and could be used to localize and quantify BBB opening.

MATERIALS AND METHODS

Preparation of unlabeled and radiolabeled Gd-DTPA

Custom-synthesized, ¹⁴C-labeled DTPA (specific activity, 30.69 mCi/mmol) was purchased from New England Nuclear (Perkin-Elmer, Wellesley, MA, USA), and all other reagents were purchased from Sigma-Aldrich (St. Louis, MO, USA) and were used as received. Unlabeled Gd-DTPA and radiolabeled Gd-[¹⁴C]DTPA were prepared and characterized using the methods of Strich et al. (17) and Nagaraja et al. (16).

Animal model

Fifteen male Wistar rats, weighing about 300 g (Charles River Laboratories, Wilmington, MA, USA), were used. All animal handling and surgical procedures were performed using a protocol approved by the Institutional Animal Care and Use Committee. All animals were anesthetized with 4% halothane and then spontaneously respired with 1% halothane in a 2 : 1 mixture of N₂O–O₂. The middle cerebral artery (MCA) was occluded for 3 h using a 4.0 nylon suture with a heat-blunted tip inserted through the external carotid artery and guided into the internal carotid and Circle of Willis (18–20). A femoral artery and vein were cannulated with PE-50 catheters for continuous blood pressure monitoring, blood sampling and MRCA administration during imaging. After this, the rats were placed in a supine position in an acrylic holder equipped with a nose cone for the administration of anesthetic gases, and positioned inside the magnet. Blood pressure, blood gases and pH (Chiron Diagnostics, Halstead, Essex, UK), blood glucose (Beckman Instruments Inc., Brea, CA, USA), osmolality (Wescor, Logan, UT, USA) and hematocrit (Hct) were measured.

MRI system and protocol

All studies were carried out using a 7-T, 20-cm horizontal bore, superconducting Magnex magnet (Magnex Scientific Inc., Abingdon, Oxfordshire, UK) interfaced to a Bruker console (Bruker Biospin MRI, Inc., Billerica, MA, USA) and equipped with a 12-cm, self-shielded, gradient set capable of producing gradients of 25 Gauss/cm with rise times of 100 ms. Estimates of cerebral blood flow (CBF), T₁, T_1sat, apparent diffusion coefficient of water (ADC) and T₂-weighted images were acquired 45–120 min after MCA occlusion, as described previously (10,20–22). After 3 h of occlusion, the rat was removed from the magnet, and the occluding suture was withdrawn to begin reperfusion. The rat, still in the holder, was returned to the magnet immediately afterwards. Another identical set of MRI data was acquired 30–120 min thereafter. At approximately 2.5 h after reperfusion, Gd-DTPA-based contrast-enhanced MRI was carried out to visualize blood-to-brain leakage and to quantify the blood-to-brain transfer rate constants.

CBF measurements

The CBF estimates were acquired using an arterial spin labeling technique (23). This technique is based on the selective inversion of inflowing blood water protons at the level of the carotid arteries prior to ¹H MRI measurement in the brain. The inversion labeling pulse was applied for 1 s at a B₁ amplitude of 0.3 kHz, and had a frequency offset of ± 8.5 kHz. Inversion tagging was followed by a spin-echo (SE) sequence with TR/TE = 1060 ms/20 ms. Four averages of the image were acquired with the gradient polarities, and the radiofrequency (RF) pulse frequency offsets were reversed to remove any gradient asymmetries in the axial direction. The labeled slice was located approximately 2 cm distal to the imaging slice. The 1-mm-thick image slice was acquired using a 64 × 64 matrix with a 32-mm field of view. The total scan time was approximately 18 min.

T₂ measurements

The proton spin–spin relaxation time (T₂) was measured using a standard Carr–Purcell–Meiboom–Gill two-dimensional Fourier transform multi-slice (13 slices, each with a thickness of 1 mm), multi-echo (six echoes) MRI sequence. The TE values were 20, 40, 60, 80, 100 and 120 ms, and TR was 8.0 s. Images were produced using a 128 × 64 matrix. The total time for the entire sequence was approximately 8.5 min.

T₁ and T_1sat measurements

Estimates of T₁ were acquired using an imaging variant of the ‘T-one by multiple readout pulses’ sequence (24,25). Measurements of T₁ in the presence of off-resonance saturation of the bound proton signal (T_1sat) were also generated using this method. This was performed by inserting two continuous-wave RF saturation pulses into the L–L sequence: the first (duration, 4.5 s) immediately before the inversion pulse and the second (duration, 40 ms) after the signal acquisition. The offset frequency of the saturation pulses was 8 kHz, and the rotational frequency of the B₁ field was 0.5 kHz. Initially, the longitudinal magnetization was inverted using an 8-ms nonselective adiabatic hyperbolic secant pulse. One phase encode line of 32 small-tip-angle gradient-echo images (TE = 7.0 ms) was acquired at 80-ms intervals after each inversion. With this sequence, a single slice T_1sat map was obtained in approximately 12 min (TR = 11 s; 128 × 64 matrix; slice thickness, 2 mm). Similarly, a T₁ map was obtained following the same procedures as used for the T_1sat map, but without saturation pulses.

ADC measurements

ADC was based on diffusion-weighted imaging and was measured using a two-dimensional Fourier transform multi-slice SE sequence (13 slices, each with a thickness of 1 mm; 128 × 64 matrix; TR/TE = 1500 ms/40 ms) with two 10-ms diffusion-weighted gradient pulses, one on either side of the refocusing 180° RF pulse, as described by Le Bihan et al. (26). A series of images was obtained with gradient b values of 0, 600 and 1200s/mm² in each of the three orthogonal diffusion sensitizing directions. The total time for the entire series was approximately 15 min (about 5 min for each direction).

Measurement of Gd-DTPA concentration

For this measurement, an L–L sequence (TR/TE = 80 ms/4 ms; 128 × 64 matrix; 24 echoes; five 1.8-mm-thick slices) was run to produce T₁ estimates at approximately 2.5-min intervals. Baseline, pre-contrast SE T₁-weighted images (TR = 500 ms; TE = 7 ms; field of view, 32 mm; 128 × 64 matrix; 13 slices, each with a thickness of 1 mm) and L–L T₁ measurements were acquired to establish pre-contrast T₁ signal intensity and values. Immediately after this, Gd-DTPA (80 µmol/kg body weight) was injected as an iv bolus and a series of 10 L–L T₁ measurements was acquired sequentially; this was followed by a post-contrast SE T₁-weighted imaging sequence. The pre- and post-Gd-DTPA SE T₁-weighted images were subtracted as a fast method to assess the leakage of contrast agent. From the L–L maps, the time course of R₁ was determined to compute ΔR₁ for each of the 10 post-Gd-DTPA intervals of L–L measurement. From these maps, the time course of ΔR₁ within the superior sagittal sinus was determined, and assumed to approximate the Gd-DTPA concentration in cerebral arterial blood over the duration of the experiment, or the AIF (10,16).

Selection of regions of interest (ROIs)

All MRI data analysis was performed offline on a SUN workstation (SUN Microsystems, Inc., Santa Clara, CA, USA). The tissue readings were always taken from the ‘central slice’, which was 2.0 mm thick and extended from − 1.85 mm to + 0.15 mm relative to the bregma. A semi-automated segmentation algorithm was employed to minimize user bias in circumscribing the brain areas with Gd-DTPA enhancement and leakage: the ROI.

Assuming that the relaxivity of Gd-DTPA for the water protons of plasma and tissue is approximately the same, the concentrations of Gd-DTPA in plasma (C_pa) and tissue (C_tis) were calculated using the following relationships:

$$C_{\text{pa}}(t_n)\propto \frac{\mathrm{\Delta }{R}_{1\mathrm{a}}(t_n)}{(1-\text{Hct})}$$ [1a]

$$C_{\text{tis}}(t_n)\propto \mathrm{\Delta }{R}_{1\text{tis}}(t_n)$$ [1b]

where Hct refers to the arterial Hct, which was measured to be 0.45; ΔR_1tis(t_n) and ΔR_1a(t_n) are the differences in R₁ values measured at time t = t_n relative to time t = 0 in the tissue and venous blood within the superior sagittal sinus, respectively. These concentrations were used for several calculations indicated below.

The values of ΔR₁ vs time were obtained using in-house software, and F-test maps for a Patlak plot were then produced for each pixel (27). The threshold F-value for the acceptance of significant leakage in a voxel was set at p = 0.01. The K_i values produced from these Patlak plots have been published (16), and are used in the present instance to demarcate the regions of significant Gd-DTPA leakage.

QAR with Gd-[¹⁴C]DTPA

QAR assessment of the Gd-[¹⁴C]DTPA concentration in brain tissue was begun 20–30 min after the L–L MRI study. After removal from the magnet, the rat was placed on a water-heated mat and kept anesthetized using the halothane–N₂O–O₂ gas mixture. After collection of an arterial blood sample for physiological measurements, an intravenous bolus injection of Gd-[¹⁴C]DTPA (approximately 80 µCi in 0.5 mL) was made, and blood samples (approximately 50 µL per sample) were taken at 16 prescribed times: 0, 5, 10, 15, 25, 35, 45, 60, 90 and 120 s plus 3, 5, 7.5, 10, 15 and 20 min. The rats were decapitated after the last sampling period and the heads were immediately frozen in 2-methylbutane cooled to − 45°C with dry ice.

The frozen brains with attached meninges and pial vasculature were removed by careful dissection in a freezer chest and processed for QAR (12,28). Sets of five frozen 20-µm-thick brain sections were generated at 400-µm intervals along the rostrocaudal axis. The first and last sections were placed on serially numbered slides and Nissl stained. The middle three sections from each set were placed on numbered, individual coverslips that were affixed in numerical order to a cardboard sheet. Such sheets were placed in an X-ray cassette, together with ¹⁴C calibration standards, and exposed to Kodak MR2000 autoradiography film (Eastman Kodak Co., Rochester, NY, USA). After about 25 days, the films were developed to produce autoradiograms (ARGs) of the brain sections and standards.

Radioactivity was quantified from the ARGs by a computerized image analysis system (Model AIS, Imaging Research, St. Catharines, ON, Canada). To do this, the optical density was determined and converted to radioactivity using a curve generated from the ¹⁴C standard data. The ROIs identified on the F-test maps were outlined on the ARGs, and the radioactivity was determined within each of them and for topographically matching areas on the contralateral side. The radioactivity in the ipsilateral and contralateral ROIs was assessed on the five sets of ARGs that fell within the 2-mm-thick central slice of the L–L T₁-weighted imaging MR maps. The results were averaged across this group of ARGs to give a single value per ROI for the subsequent calculation of K_i.

Terminal tissue-to-plasma ratio (V_R)

Among the differences in the MRCA-MRI and radiotracer-QAR techniques in these experiments is the signal being detected. For the MRI method, ΔR₁, the change in the relaxation rate of mobile protons caused by Gd-DTPA, is assessed; for the radiotracer-QAR technique, the radiation emitted by the ¹⁴C incorporated into the Gd-DTPA moiety is determined. The latter approach is extremely accurate over a broad range of radioactivity, has excellent spatial resolution (29) and thus demarcates the Gd-[¹⁴C]DTPA distribution very accurately.

As a test of the validity and accuracy of MRI for the measurement of concentration vis-á-vis the QAR method, an identical, model-independent calculation was made with MRCA and radiotracer data. It is known that there is a linear relationship between the concentration of MRCA and the relaxation rate, R₁(t) = r₁C + R₁(t = 0), where R₁(t = 0) and R₁(t) are the longitudinal relaxation rates just before MRCA administration and at time t after the beginning of administration, respectively, r₁ is the relaxivity and C is the MRCA concentration. Therefore, ΔR_1pa = r₁C_pa and ΔR_1tis = r₁C_tis, where C_pa and C_tis are the arterial plasma and tissue concentrations of MRCA, ΔR_1pa and ΔR_1tis are the changes in the relaxation rates of arterial plasma and tissue, respectively, after MRCA administration, and r₁ is the constant of proportionality between the change in the relaxation rate and the MRCA concentration.

As the terminal tissue-to-plasma distribution ratio (V_R) for Gd-[¹⁴C]DTPA in the QAR experiment is given by:

$$V_{\mathrm{R}}=\frac{C_{\text{tis}}(t_{\mathrm{f}})}{C_{\text{pa}}(t_{\mathrm{f}})}$$ [2]

V_R for Gd-DTPA in MRI can be obtained using the relation:

$$V_{\mathrm{R}}=\frac{(1-\text{Hct})\mathrm{\Delta }{\mathrm{R}}_{1\text{tis}}(t_{\mathrm{f}})}{\mathrm{\Delta }{R}_{1\mathrm{a}}(t_{\mathrm{f}})}$$ [3]

where t_f is the final time point of observation and ΔR_1a = ΔR_1pa(1 – Hct) is ΔR₁ within the superior sagittal sinus.

Specifically, the 20-min tissue MRCA concentration within each ROI, which included the signals from both the intravascular and extravascular compartments, was divided by the 20-min plasma MRCA concentration. In the parlance of these two methods, this terminal tissue-to-plasma ratio V_R is a volume fraction for MRI-Gd-DTPA (e.g. mL/mL) and a volume of distribution for Gd-[¹⁴C]DTPA (e.g. mL/g). As the specific gravity is 1.045 for normal brain and approaches 1.03 for edematous brain tissue (30,31), these are essentially equal units and measures.

StEq calculation of K_i

StEq is generally used to calculate the influx rate constant of radiotracers, such as [¹⁴C]-AIB and [¹⁴C]-sucrose (10,12), and assumes that the backflux of radiotracer across BBB is negligible relative to the influx. The equation requires a correction of the tissue radioactivity for that contained in blood within the ROI; this is a weakness of the StEq approach. As often performed in stroke studies, the average ¹⁴C radioactivity in the contralateral tissue in an area comparable with the ROI is assumed to approximate this correction (10,12). With this assumption, StEq is written as:

$$K_{\mathrm{i}}=\frac{C_{\text{tis}\_\mathrm{i}}(t_{\mathrm{f}})-C_{\text{tis}\_\mathrm{c}}(t_{\mathrm{f}})}{{\int }_0^{t_{\mathrm{f}}}{C}_{\text{pa}}(t)\mathrm{d}t}$$ [4]

where t_f is the time at which the animal was decapitated and the experiment was stopped (20 min in these experiments), C_{tis_i} and C_{tis_c} are the concentrations of radioactivity per gram of ispilateral and contralateral brain tissue, respectively, at 20 min, and ${\int }_0^{t_{\mathrm{f}}}{C}_{\text{pa}}(t)\mathrm{d}t$ is the Gd-[¹⁴C]DTPA radioactivity/mL of plasma integrated over the sampling period: 0–t_f. This concentration–time integral was referred to as AIF^* in a previous study (16), and is similarly denoted herein.

StEq is also used in the present work to estimate K_i from the MRCA-MRI data with the same assumption for the intravascular correction. That is [using the same symbols and eqn (1b)], C_{tis_c} is subtracted from C_{tis_i} to obtain the numerator in eqn (4). The denominator is the original concentration–time integral for the 20-min period from MRI [eqn (1a)], previously denoted as AIF-I (16). In addition, a hypothetical Gd-DTPA concentration–time integral, designated as AIF-II, that is identical in shape to AIF^* (16), is also used in eqn (4) for an alternative estimate of K_i. This was performed because previous findings have suggested that AIF-I underestimates this integral, leading to a small error in the K_i calculation (16). As a test of the validity of the K_i values calculated using StEq, those calculated with AIF-I and AIF-II were compared with those published previously using the same Gd-DTPA data, but analyzed by Patlak plots, which test for uptake linearity and negligible backflux and do not require a blood correction. The Patlak plot is therefore model independent and more rigorous than StEq.

Lesion volumes

The Nissl-stained brain sections obtained for each level were used to measure the volumes of the ipsilateral and contralateral hemispheres and striatum (Str). These sections spanned the entire forebrain (approximately 10 mm and 25 sets of sections) and not just the ROIs. On the better of the two sections per set, the areas of each of the listed structures or regions were traced with the image analysis system and multiplied by the distance between sets, 0.4 mm, yielding a per slice volume (mm³) that was summed across the entire brain to obtain the total volume (20). The differences between the ipsilateral and contralateral volumes of the forebrain and Str are the indices of tissue swelling or edema.

In a similar manner, the volume of the ischemic lesion was quantified by measurement of the area of tissue pallor (i.e. little or no staining) on the individual histological images by a blinded analyst, conversion to volumes and addition of the results. The volume of tissue with leaky microvessels was determined from the ARGs. The area of all tissue loci with an optical density greater than the mean normal optical density plus three standard deviations (SDs) was measured on the best ARG in each set, multiplied by the distance between sets and the resulting volumes were summed (20).

Statistics

All data are given as the mean ± SD. Differences between the MRI and QAR estimates of V_R and K_i were compared using two-tailed, paired t-tests. Scatter plots with linear regressions were used to test the correlation between the MRI K_i estimates and MRI CBF during the period of occlusion and after reperfusion. Significance was inferred at p ≤ 0.05.

RESULTS

General observations

The home-prepared Gd-DTPA was paramagnetically and physically comparable with a commercially available MRCA (16). In the custom-synthesized [¹⁴C]DTPA preparation, the carbon moiety of the ‘carbonyl’ (C=O) group in the DTPA molecule is ¹⁴C labeled; there are only five such groups in DTPA and substituting ‘C’ with ‘¹⁴C’ does not lead to structural changes (Y. Lin, Perkin-Elmer, personal communication). The formula weights of DTPA and [¹⁴C]DTPA are identical, i.e. 393.35 Da. The function of the DTPA molecule is to chelate Gd and render the latter nontoxic. This chelation does not affect either the paramagnetic properties of Gd or the radioactive decay of ¹⁴C.

The measured physiological parameters of all the rats were within normal ranges for halothane-anesthetized rats, albeit with some hypercapnia [pCO₂ = 53 mmHg (16)].

During the MCA occlusion period, the CBF values in the regions of BBB opening (ROIs) within the preoptic area (PoA), Str and parietal cortex (PCx) were less than 35% of the corresponding regions on the contralateral side (Table 1; Fig. 1A). After the initiation of reperfusion, the CBF values increased somewhat in the ipsilateral ROIs, but remained 40–65% below the contralateral flow rates. The CBF maps indicated that the changes were not uniform within these ROIs and that the flow patterns were variable after reperfusion (Fig. 1B). In many cases, the CBF values in the contralateral Str and PoA were unusually high, both during occlusion and after reperfusion. For instance, the CBF value in Str for more than 50% of the contralateral side measurements was greater than 1.85 mL/g/min (i.e. at least 20% higher than the mean for anesthetized controls, which was 1.55 mL/g/min; n = 6; Knight RA, Karki K, Nagaraja TN, unpublished data), both during and after occlusion. Accordingly, the low CBF ratios for Str and PoA at both times (Table 1) are the result of not only a fall in flow on the ipsilateral side, but also a rise on the contralateral side, in many, if not all, of the animals.

Table 1.

Ipsi- to contralateral ratios of some measured MR parameters in the 13 rats showing blood–brain barrier (BBB) damage

	PoA (13)		Str (10)		PCx (2)
	Occlusiona	Reperfusionb	Occlusiona	Reperfusionb	Occlusiona	Reperfusionb
CBF	0.30 ± 0.17	0.43 ± 0.16c	0.23 ± 0.07	0.39 ± 0.19	0.32 ± 0.09	0.63 ± 0.24
ADC	0.74 ± 0.16	0.75 ± 0.10	0.70 ± 0.07	0.70 ± 0.12	0.72 ± 0.05	0.75 ± 0.11
T2	1.12 ± 0.11	1.20 ± 0.15	1.13 ± 0.03	1.32 ± 0.14d	1.11 ± 0.05	1.24 ± 0.09
T1	1.11 ± 0.04	1.20 ± 0.08d	1.10 ± 0.04	1.20 ± 0.07e	1.20 ± 0.02	1.20 ± 0.06
T1sat	1.07 ± 0.06	1.20 ± 0.15c	1.07 ± 0.03	1.25 ± 0.09f	1.07 ± 0.04	1.15 ± 0.05

ADC, apparent diffusion coefficient of water; CBF, cerebral blood flow.

The regions of interest in the preoptic area (PoA), striatum (Str) and parietal cortex (PCx) were segmented with Patlak plot F-test maps that demarcated areas with significant BBB damage. Sample sizes are given in parentheses next to the region of interest. All values are given as the mean ±standard deviation.

^aDuring middle cerebral artery occlusion.

^bAfter reperfusion.

Paired t-tests:

^cp = 0.007;

^dp = 0.001;

^ep = 0.002;

^fp = 0.0001. Significances were not calculated for PCx because of the very small sample size.

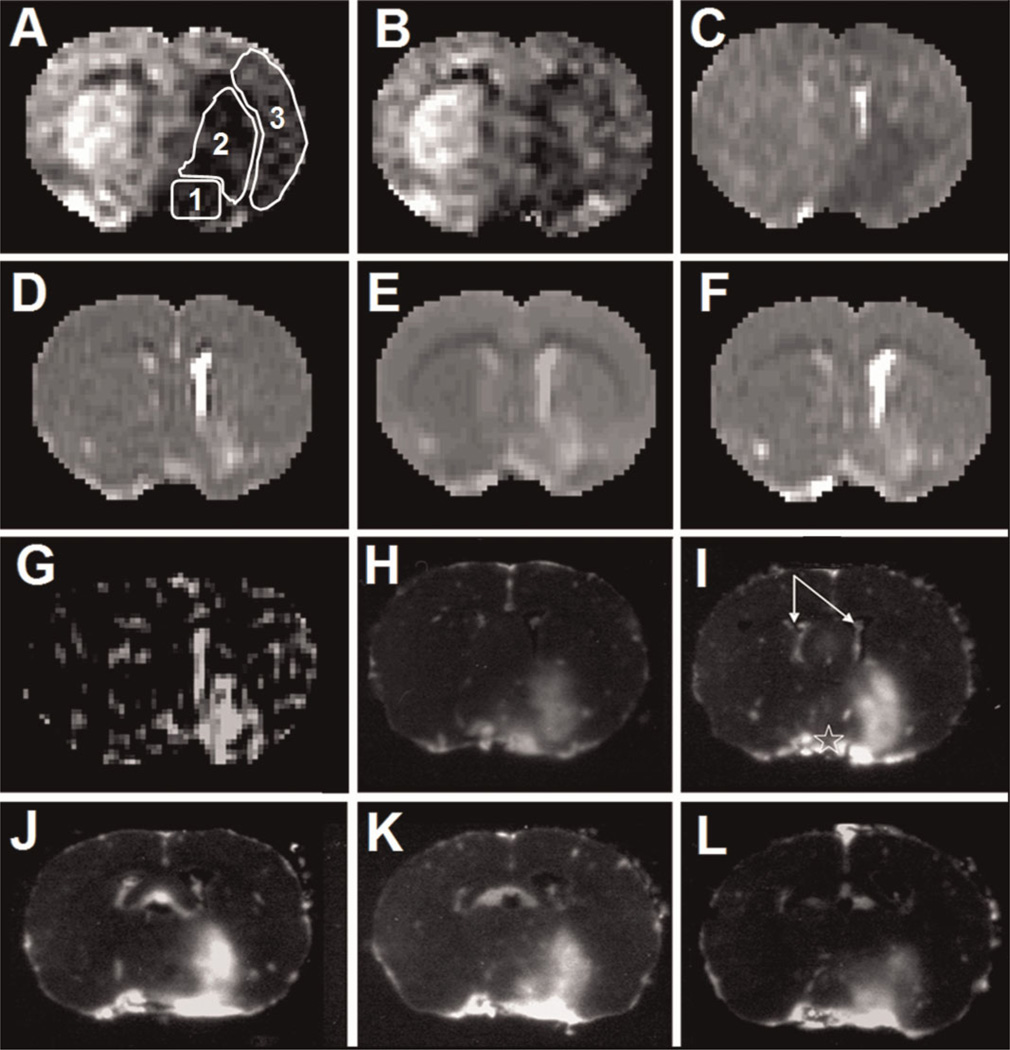
Figure 1.

Representative MR maps and their corresponding autoradiograms (ARGs) from quantitative autoradiography (QAR) generated as part of a single dataset from one experiment. The maps are the cerebral blood flow (CBF) during middle cerebral artery (MCA) occlusion (A) and after reperfusion (B), apparent diffusion coefficient of water (ADC; C), T₂ (D), T₁ (E), T_1sat (F) and Patlak plot influx rate constant (K_i; G). The white outlines in (A) show the three regions of interest: 1, preoptic area; 2, striatum; 3, parietal and insular cortex. The series of ARGs obtained within the 2.0-mm-thick central slice of the MRI technique are shown in (H) to (L). Each of these images is from a 20-µm-thick frozen brain section, and the distance between adjacent images is 400 µm. This set of five images exhibits the intraslice variations in blood–brain barrier (BBB) damage within the central MRI slice after about 2.5 h of reperfusion following 3 h of MCA occlusion. The ARGs are inverted to photonegatives so that the normally darker parts with radiotracer leakage visually match the hyperintense areas seen on the K_i map (G). In this rat, the regions of gadolinium-diethylenetriaminepentaacetic acid (Gd-DTPA) enhancement and leakage are in the preoptic area and striatum. The five QAR images (H–L) represent the rostral–caudal distribution of this lesion. The spatial variations in the BBB lesion seen in these five images are significantly reduced in (G) because of partial volume averaging by MRI. The two lateral ventricle choroid plexuses are marked by the arrows in (I). They are highly vascular and the large accumulation of radiotracer therein is normal and can also be seen in (G). Of note, ADC (C), T₂ (D), T₁ (E) and T_1sat (F) maps show prominent abnormalities in these MR parameters for the ipsilateral choroid plexus and surrounding cerebrospinal fluid and periventricular tissues. The bright rim around the brain is a result of tracer within the pial blood vessels. The brightness on the contralateral side at the base of the brain (star in I) arises from the large blood vessels around the optic chiasm and possibly from some spread of radiotracer from the ipsilateral preoptic area. The ‘blackness’ in the parenchyma of the contralateral hemisphere indicates no radiotracer leakage.

The ipsi-/contralateral ADC ratios were around 0.70–0.75 during occlusion for the ROIs within PoA, Str and PCx, and did not change with reperfusion (Table 1; Fig. 1C). T₂, T₁ and T_1sat were greater than unity during occlusion for PoA, Str and PCx, and appeared to rise further after reperfusion (Table 1; Fig. 1D–F). This increase with reperfusion was significant for T₂ within Str and for T₁ and T_1sat within both PoA and Str.

Terminal tissue-to-plasma ratio, or distribution volume (V_R)

To test the reliability of the L–L T₁-weighted measurements, the terminal tissue concentration of Gd-DTPA within the identified ROI – which included both intravascular and extravascular contrast agent – was divided by the terminal plasma concentration. This ratio, V_R, was then compared with that from the radiotracer-QAR data measured some 30 min later in the same animal. The mean V_R ± SD values for Gd-DTPA were 0.142 ± 0.050 mL/mL for PoA (n = 13) and 0.117 ± 0.050 mL/mL for Str (n = 10) and, for Gd-[¹⁴C]DTPA, were 0.135 ± 0.048 mL/g for PoA and 0.126 ± 0.066 mL/g for Str. As 1 g of brain essentially equals 1 mL of tissue, direct comparison of these two sets of V_R data is permissible. As can be surmised by inspection, the slight differences in the measured concentration ratios between these two forms of Gd-DTPA were not statistically significant for either ROI. Accordingly, ΔR₁ appears to reflect the Gd-DTPA concentration in brain tissue with considerable accuracy in these experiments.

Variations in BBB opening and K_i

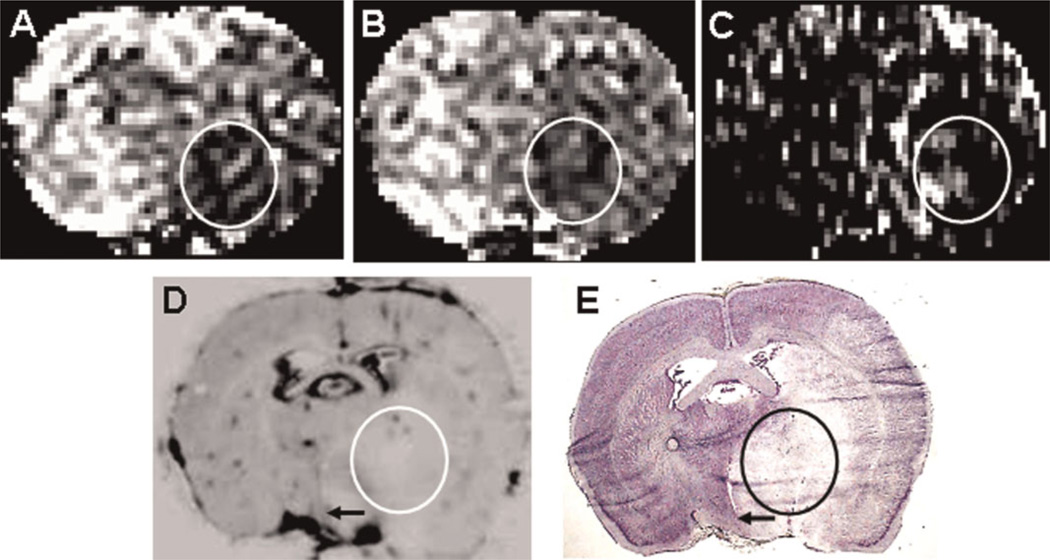
Appreciable MRCA or radiotracer leakage during reperfusion was not observed in two of the 15 rats. In one animal, there was adequate blood flow during the reperfusion period and discernible tissue injury by the end of that period, but no leakage of MRCA or radiotracer. In the other (Fig. 2), the rate of blood flow was decreased significantly throughout the ischemic hemisphere during the occlusion period (Fig. 2A). On withdrawal of the occluding suture, CBF increased slightly in much of the ischemic hemisphere, but a somewhat oblong patch of very poorly perfused tissue was evident within Str (Fig. 2B). There were a few contiguous spots of somewhat higher perfusion within this low-flow patch and around its edges. The Gd-DTPA K_i map (Fig. 2C) indicated some leakage along the ventromedial edge of this patch and one small area of leakage within it. On the more sensitive ARGs of Gd-[¹⁴C]DTPA distribution (Fig. 2D is one example of the central slice set), the optical density of this oblong patch was lower than on the contralateral side and the ipsilateral cortex with the exception of three small spots within it. The latter suggests some points of leakage (and sufficient blood flow) within this part of Str. A similar, but not identical, pattern of patches and spots was seen on the other four ARGs of the central slice series from this experiment, accounting for the difference between Fig. 2C and 2D. These observations suggest that the near or complete absence of blood flow within this patch during the reperfusion period greatly limits the delivery of MRCA and radiotracer to much of Str. Moreover, the Nissl-stained brain section (Fig. 2E) corresponding to Fig. 2D confirms a similar extent of ischemic injury, with a normal and hypostaining pattern that roughly follows the leakage pattern in Fig. 2D. As a result, leakage and BBB permeability could not be assessed in this tissue, and the results of this experiment were dropped.

Figure 2.

A rare observation of blood flow-limited delivery of radiotracer. In this rat, cerebral blood flow (CBF) was reduced in an oblong area of the striatum (circled) during both occlusion (A) and after reperfusion (B). A few spots of better perfused tissue are visible in both (A) and (B). A somewhat similar pattern of spots within this oblong area is seen in the K_i map (C) and quantitative autoradiography (QAR) image (D), which shows slivers of tissue within the oval in the corresponding Nissl-stained section (E). Based on the CBF pattern in (B), the absence of ¹⁴C-labeled gadolinium-diethylenetriaminepentaacetic acid (Gd-[¹⁴C]DTPA) in the tissue around these spots appears to be the result of severely reduced post-reperfusion CBF and not of the absence of blood–brain barrier (BBB) damage in this instance. The arrows in (D) and (E) indicate the shifting of the midline as a result of edema in the ipsilateral hemisphere.

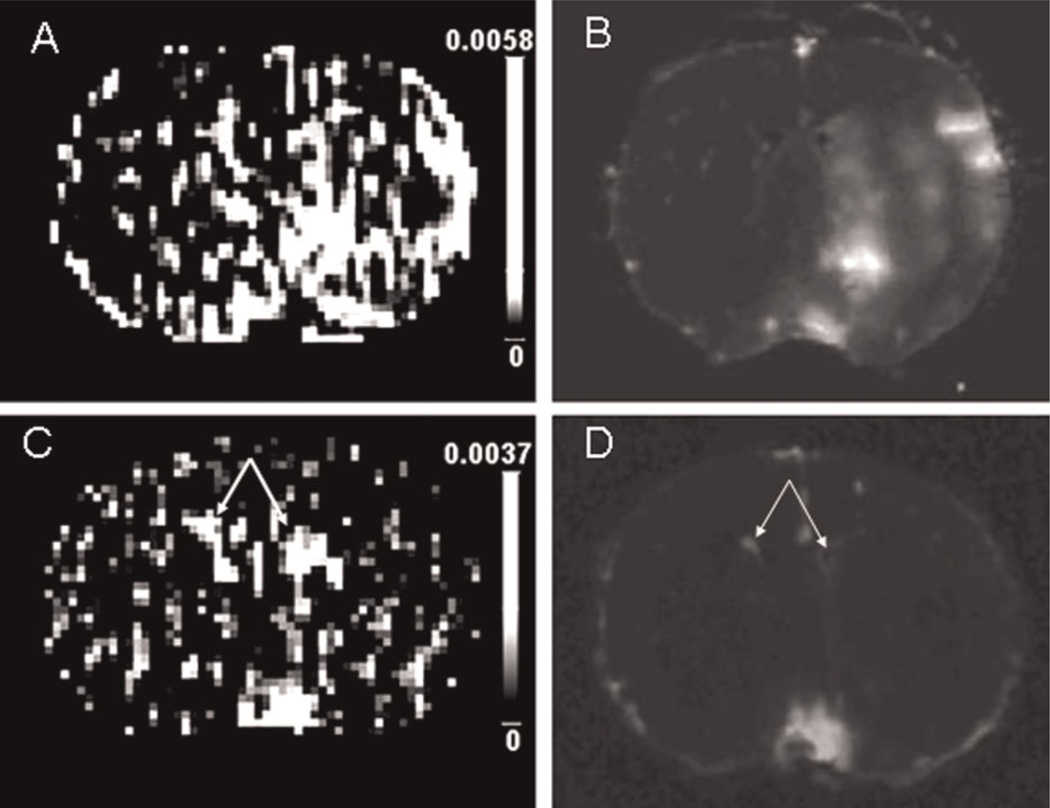
In the remaining 13 rats, only two showed appreciable leakage of Gd-DTPA and Gd-[¹⁴C]DTPA in all three areas, i.e. PoA, Str and PCx, 10 in both PoA and Str, and all 13 in PoA. Thus, of the three affected brain regions in this model, PoA, Str and PCx, in that order, were decreasingly susceptible to injury. An example of BBB opening in both PoA and Str is presented in Fig. 1. The set of five central slice ARGs showed a rather variable pattern of brightness (density inverted in Fig. 1H–L); collectively, this ‘brightness’ resembles that of ‘enhancement’ seen on the companion MR image obtained some 30 min earlier (Fig. 1G). The intraslice variations evident on the sets of five QAR images were, of course, lost in the MRI ΔR₁ map, which was also rather noisy. To illustrate the other two patterns of leakage, Fig. 3 shows four nearly contiguous, but distinct, ROIs of varying size and intensity within PoA, Str and PCx (Fig. 3A, B), whereas, in a different rat, a small area of Gd-DTPA enhancement (Fig. 3C) and high Gd-[¹⁴C]DTPA leakage (Fig. 3D) are seen in PoA only. These three representative DCE-MRI maps and their corresponding ARGs demonstrate the variations in acute BBB damage in this model, as well as the relative sensitivity of the two techniques. Moreover, the findings of BBB damage within PCx in only two of the 15 rats are consistent with previous reports of a lower susceptibility of the neocortical microcirculation to ischemic injury in this model (32).

Figure 3.

Pairs of MRI K_i maps and quantitative autoradiography (QAR) images from two different rats showing various patterns of blood–brain barrier (BBB) opening. The MRI K_i map (A) and QAR image (B) show a large BBB lesion involving all three regions of interest, namely the preoptic area, striatum and parietal-insular cortex, in one rat. In a different rat, the MRI K_i map (C) and QAR image (D) indicate a small region of gadolinium-diethylenetriaminepentaacetic acid (Gd-DTPA) and Gd-[¹⁴C]DTPA leakage within the preoptic area only. The patterns of demonstrable Gd-DTPA influx in (A) and (C) are almost completely mimicked by those of Gd-[¹⁴C]DTPA leakage in (B) and (D). The scale bars in (A) and (C) indicate the range of blood-to-brain influx rates (K_i). In (C), the two bright patches in the middle of the K_i map to the left and right of the midline mark the lateral ventricle choroid plexuses (arrows in C and D). As mentioned in the legend of Fig. 1, the plexuses are highly vascular, have very permeable capillaries in both normal and stroke animals, and are obviously filled with magnetic resonance contrast agent.

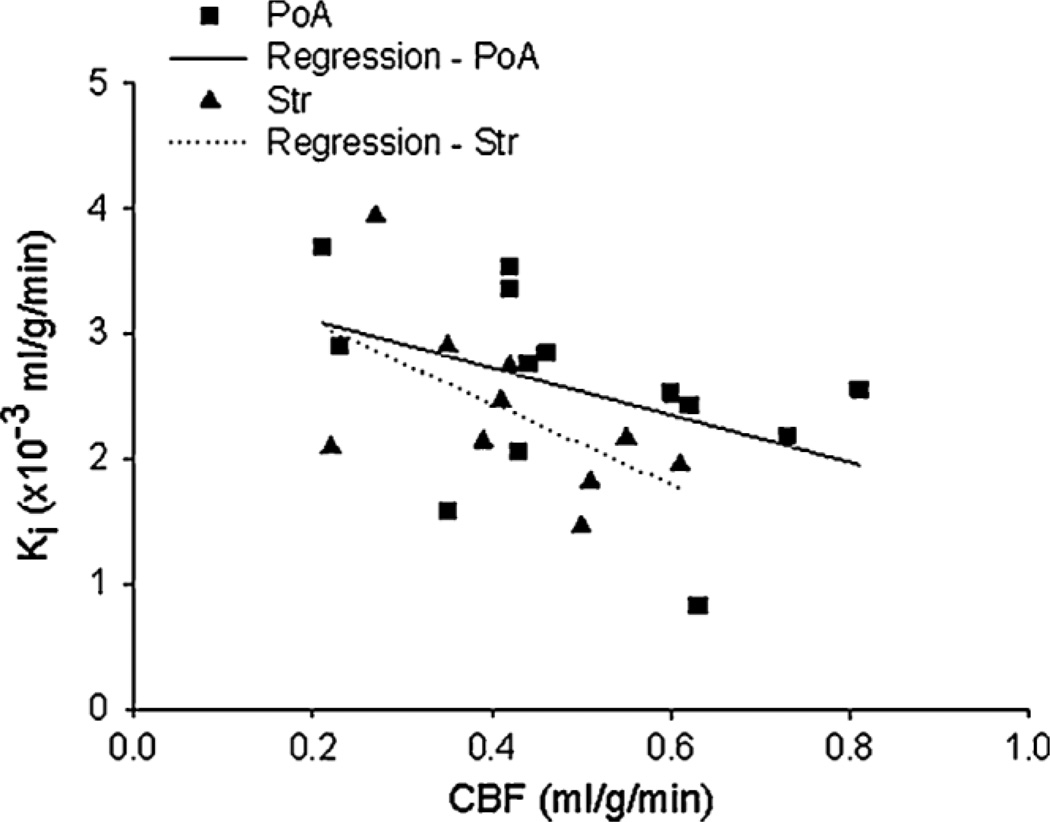
As for the group results, the influx rate constants determined by StEq were slightly, but not significantly, higher when calculated with the tissue ΔR₁ data and the plasma ΔR₁–time courses (AIF-I) than with the QAR data and the plasma radioactivity–time courses (AIF^*) (Table 2). A possible explanation for this small discrepancy is that AIF-I was underestimated because of the initial rapid rise and fall in plasma concentration following a bolus injection, as reported recently (16). To investigate this possibility, a ‘corrected’ AIF for Gd-DTPA was obtained by converting AIF^* to a ΔR₁–time curve, as outlined in the ‘Materials and methods’ section and denoted as AIF-II. The resulting AIF-IIs were slightly larger than AIF-I (16). Accordingly, for Gd-DTPA, the K_i values obtained with AIF-I were larger than those calculated with AIF-II, but the differences were not significant. When AIF-II was used in StEq, the resulting K_i estimates for Gd-DTPA were remarkably similar to those determined with Gd-[¹⁴C]DTPA-QAR data and AIF^* (PoA and Str values in Table 2). As for regional variations, the K_i values obtained with both MRI and QAR data were slightly, but not significantly, higher for PoA than for Str. A scatter plot of K_i and CBF findings for PoA and Str suggested that Gd-DTPA influx after 3 h of reperfusion was greater in ROIs in which blood flow was lower during the occlusion period (Pearson correlation coefficient r = − 0.43 for PoA and r = − 0.57 for Str; Fig. 4). Further analyses indicated, however, that this relationship between CBF and K_i was not statistically significant (p = 0.14 for PoA and p = 0.08 for Str). A scatter plot of K_i and CBF after the initiation of reperfusion was essentially flat (plot not shown), and statistical analysis indicated no correlation between these two variables (r = 0.19, p = 0.53 for PoA; r = 0.04, p = 0.92 for Str). These observations, nonetheless, raise the possibility that reperfusion in this model of reversible ischemia does little to alleviate BBB injury, and that the severity of the BBB lesion is mainly set by the drop in blood flow during the period of occlusion. Given the variation in these data, a larger sample size is necessary to establish unequivocally this suggested relationship between CBF during the occlusion period and K_i.

Table 2.

Mean (± standard deviation) blood-to-brain influx constant (K_i; × 10⁻³ mL/g/min) of areas with blood–brain barrier opening as determined by two different methods of calculation and sources of data, MRI and radiotracer-quantitative auto-radiography (QAR), from the same experiment

Method of calculation	Source of data	Arterial input function (AIF)	Ki per brain structure (n)
			PoA (13)	Str (10)	PCx (2)
Single-time equation	MRI	AIF-I	3.5 ± 0.6	2.9 ± 0.9	4.4 ± 3.1
	MRI	AIF-II	3.2 ± 1.0	2.6 ± 1.0	3.9 ± 3.7
	QAR	AIF*	3.0 ± 1.0	2.7 ± 1.0	4.2 ± 1.7
Patlak plot	MRI	AIF-I	2.9 ± 0.6	2.6 ± 0.9	3.7 ± 3.1
	MRI	AIF-II	2.6 ± 0.7	2.4 ± 0.7	3.2 ± 2.0

n, sample size; PCx, parietal cortex; PoA, preoptic area of anterior hypothalamus; Str, striatum.

The sample size is given in parentheses. The differences between the K_i values of the two methods were not significant for PoA and Str (two-tailed, paired t-test). Calculations showed that K_i values approximated the permeability–surface area product in these experiments, and therefore the latter are not reported separately.

Figure 4.

A scatter plot of the influx rate constants (K_i) vs cerebral blood flow (CBF) measured during the period of middle cerebral artery (MCA) occlusion for 23 regions of interest within the preoptic area (PoA) and striatum (Str). Separate regression lines are drawn for the PoA and Str data. An apparent inverse relationship was observed between the two measurements, suggesting that the extent of CBF reduction during occlusion may be a factor contributing to later blood–brain barrier (BBB) damage. That is, BBB opening tended to be highest in regions of interest with the lowest rates of flow during occlusion and lowest in those with the highest rates. Statistical analysis, however, did not support this suggestion.

Lesion volumes

The contralateral hemisphere had a volume of 638 ± 26 mm³ and the ipsilateral hemisphere had a volume of 694 ± 47 mm³, indicating an 8% increase in volume (p < 0.05; paired t-test) or significant brain swelling. The contralateral Str had a volume of 59 ± 5 mm³ and the ipsilateral Str had a volume of 69 ± 11 mm³, i.e. an increase of about 16% (p < 0.05; paired t-test). These data implied considerable edema formation – presumably from leaky microvessels – and fluid retention. Such swelling is classically referred to as vasogenic edema, and its overall significant magnitude in this model at this time is shown by the obvious midline shifts seen on the ARGs and histologies (arrows in Fig. 2D, E).

Tissue pallor (little or no staining) is seen on histological sections in which nuclear material has broken down and no longer binds dye, and in which edema fluid swells the cells (especially the neuronal and glial processes that form the neuropil). The latter process appears to be one of the causes of the drop in ADC that occurs during the occlusion period and persists after reperfusion (Table 1). Tissue pallor defined an ischemic lesion of considerable size after 3 h of reperfusion, namely 122 ± 73 mm³, which is about 20% of the volume of the contralateral hemisphere.

The volume of tissue with microvascular damage, as indicated by radiotracer leakage on the ARGs, was 81 ± 54 mm³ (approximately 30% smaller than that of the ischemic lesion or pallor). This suggests that the core of the area of ischemic injury is characterized, at least in part, by BBB opening, whereas the penumbra is not, and that the tightness of the BBB may be what saves the penumbra from irreversible damage at this stage.

Of relevance to these two volume measurements was the fact that the BBB lesion was estimated from the ARGs, whereas the ischemic lesion was calculated from the histologies. Although, in many cases, a comparison of volumes derived from these two different preparations is not warranted, in the current experiments, tissue handling (from freezing the brain in situ through to the virtually instantaneous fixation of brain sections by heat drying) was identical, and a comparison of the volumes calculated by each approach seems to be acceptable and valid.

DISCUSSION

By employing virtually identical tracers in the same animal, consecutive times of measurement and the same formulae for the calculation of distribution parameters, a direct comparison of MRI-derived estimates of V_R and K_i could be made with those obtained from QAR data. If there is good agreement between the two techniques for both V_R and K_i, it is highly likely that ΔR₁ accurately assesses Gd-DTPA concentration in brain tissue. Such agreement was, indeed, found. Two incidental observations support this conclusion. First, the spatial distribution of the two tracers showed nearly identical patterns. Second, little or no tracer leakage was seen in two rats with both procedures.

Tissue handling may have contributed to such excellent agreement. The MRI and QAR procedures followed each other in quick succession to minimize the elapsed time between the periods of measurement. To further reduce technical differences, the method of tissue preparation employed, namely freezing of the whole head at the conclusion of Gd-[¹⁴C]DTPA circulation, maintained the contours of the brain, minimized shrinkage and preserved the pre-mortem shape and size and all the vital intracranial contents, such as blood and cerebrospinal fluid. It also minimized any post-mortem loss and/or movement of the radioactivity (28,33), and gave an excellent image of pre-mortem tracer distribution in the brain. Therefore, this technique almost completely preserved the in vivo distribution of brain fluid compartments and facilitated direct comparisons of MR and QAR data.

A few attempts have been made to correlate BBB permeability changes observed on MRI with those from conventional tracer techniques to confirm the MR observations. In the first attempt of this kind, Kenney et al. (11) used MRI data from a 36B-10 rat glioma model and Patlak plots to generate K_i values for Gd-DTPA at three times after tumor implantation. The K_i values determined in rats, 13–18 days after implantation, were compared with those reported previously for AIB obtained by QAR in different animals at 15 days after implantation (34). Supporting the accuracy of their MRI data and the use of the Patlak plot, the two sets of K_i data were reasonably similar. Preston and Foster (35) employed K_i estimates to quantify the leakage of radiolabeled Gd-DTPA and shift reagents by MRI after cerebral ischemia, and found that their estimates for Gd-DTPA were reasonable for a damaged BBB when compared with the K_i values reported for [⁵⁷Co]-DTPA in normal rats by Blasberg et al. (36). In other studies, K_i values for Gd-DTPA determined by MRI and Patlak plots have been found to correlate well with those measured minutes later in the same experiment with QAR, the radiotracers [¹⁴C]-sucrose and [¹⁴C]-AIB, and StEq (10,12).

In the present work, the DCE-MRCA values were entered into StEq – and not the Patlak plot – to calculate K_i. This eliminated the differences in the distribution models and modes of calculation of this parameter between the two techniques. The present findings indicate that the tissue concentration is accurately measured by the L–L MRI procedure when Gd-DTPA is injected as a bolus. Support for this comes from the identity of the K_i values when AIF^* for the radiotracer and its equivalent for Gd-DTPA, AIF-II, are inserted into the StEq calculations (Table 2). Despite this agreement, better K_i estimates are found when the Patlak plot and model are chosen. This is because: (i) there are fewer assumptions involved and the results are less model dependent; (ii) the period of unidirectional influx (i.e. little or no backflux) is determined; and (iii) all of the tissue time–concentration data are employed in the plot (9,37,38).

In addition to this advantage, another physiological parameter of importance is determined with the Patlak plot, i.e. the distribution volume at time zero of the protons with magnetization affected by intravascular Gd-DTPA (V_p + V_o). When determined in tissue devoid of large vessels, V_p + V_o is thought to approximate the volume of water within the perfused micro-vessels of the imaged tissue, and includes both plasma water (V_p) and water associated with red blood cell and other blood compartments (V_o) (10). Until further experimentation is performed, this definition of V_p + V_o will suffice.

Both intravascular and extravascular tracer, be it protons with magnetization affected by Gd-DTPA, as with MRI, or Gd-[¹⁴C]DTPA, as with QAR, are included in the numerator of V_R. For both, the mean V_R value was around 0.12–0.15 mL/mL or mL/g for PoA and Str. The meaning of V_R is unequivocal for Gd-[¹⁴C]DTPA: it is the distribution volume or space (mL/g) of the radiotracer, often expressed as a volume percent in physiology. The volume percent of microvascular plasma water is less than 1% in normal brain and is probably around that in ischemic brain areas during the acute phase of reperfusion, where local blood flow is about 70–75% of the contralateral CBF (Table 1). This consideration indicates that, after 3 h of reperfusion: (i) most of the Gd-[¹⁴C]DTPA is in the extracellular space (ECS); (ii) the major contributor to V_R is the volume of extracellular fluid; and (iii) ECS in these areas is greater than 13%. The interstitium or ECS in normal brain is about 20% (39,40). Almost certainly, ECS of at least 13% in the ischemia-injured brain is sufficiently large for radiotracer movement within the tissue by diffusion and, if a pressure gradient is present, by bulk or convective flow (i.e. by solvent drag).

The volume of tissue pallor after 3 h of reperfusion was sizable in the present investigation (subsection ‘Lesion volumes’ in ‘Results’ section). One of the major contributors to tissue pallor is the swelling of brain cells and their processes, often referred to as cytotoxic edema. Such cellular swelling may be a partial cause of the increase in hemispheric and striatal volume determined at the end of the experiment. In addition, cytotoxic edema is likely to encroach on the ECS and diminish it, but, as indicated by the preceding V_R discussion, the volume of Gd-[¹⁴C]DTPA distribution, an approximation of ECS, was sizable. This, together with the ipsilateral/contralateral ADC ratio of 0.70–0.75 in the areas of BBB opening (Table 1), suggests that the movement of water by diffusion and, if it occurs, by convection was not greatly restricted by cytotoxic edema and its impingement on the interstitium.

Patlak plots of the multiple-time tissue ΔR₁ data from the current study have been published (16), and have shown that K_i is slightly lower when determined with the concentration-corrected AIF-II than with AIF-I (PoA and Str results in Table 2). For these same regions, the K_i values estimated by Patlak plots using either AIF-I or AIF-II tended to be smaller than those calculated with StEq, but the differences were not significant (Table 2). These observations indicate that, for this model of reversible MCA occlusion and these experimental conditions: (i) StEq approximates K_i fairly well; (ii) the backflux of Gd-DTPA is negligible during the time of measurement; and (iii) the assumption of the contralateral tissue concentration as the correction for the distribution of the protons affected by intravascular Gd-DTPA in ROI leads to, at worst, a slight overestimation of K_i.

Despite these conclusions, the Patlak plot should be used whenever the MRI data permits because of its fewer assumptions, the inclusion of all of the tissue ΔR₁ data – not just the terminal sample – in the estimation of K_i, and its inherent simplicity. Several experimental and human MRI studies performed using the Patlak plot technique for cerebrovascular evaluations lend additional support to this suggestion. For instance, the K_i values calculated by the Patlak plot have been used to quantify BBB opening in stroke (3,41–44) and brain tumors (27,45), and to evaluate therapeutic efficacy in brain tumor models (46). As for other applications, K_i, when elevated, has also been assumed to reflect newly formed, leaky microvessels, and has been employed to assess angiogenesis in recovering post-stroke brain (47). Patlak plots of MRCA data are highly applicable for studies of brain diseases in humans, as each case is unique and the plotting routine corrects the uptake data for the amount of MRCA in blood, determines the period in which influx dominates and calculates the influx rate constant K_i. The advantage of determining K_i in this rigorous manner is that it can be converted to a permeability–surface area (PS) product, the physiological measure of capillary permeability, when the rate of blood flow is known. Apropos of this point, CBF can be readily measured in the same individual by MRI during the same imaging session, and the PS product can be calculated. Plot modeling can also be modified to address the pathology in question, e.g. tumor vasculature (27), to accommodate a scenario of relatively leaky microvasculature and the presence of a sizable backflux of MRCA; an extended version of the Patlak plot can be employed for such calculations and a set of three blood–brain transfer constants, including K_I, can be estimated (9,37,38). Moreover, sagittal sinus imaging of venous blood as a surrogate for arterial blood sampling and AIF evaluation (10) is also being employed in human MRI (48).

As the L–L T₁-based estimates of Gd-DTPA concentrations in brain tissue after a bolus iv injection appear to be quite accurate, the K_i values reported herein, especially those obtained by Patlak plot, are reliable measures of the influx rate and can be used to calculate the PS product of Gd-DTPA in the system. The blood flow rates in PoA and Str were in the range 0.4–0.5 mL/g/min, whereas the Patlak plot K_i values obtained with AIF-II were less than 1.0% of that rate (Table 2). Taken together, and assuming the Krogh cylinder model of the capillary and the Renkin–Crone equation (49), these values indicate that the rate of blood-to-brain influx in ROIs with leaky microvessels is not limited by blood flow, and that K_i approximates the PS product of Gd-DTPA. A possible exception to this, the case of influx being mostly limited by flow, was mentioned in the results for one rat. As to which component of the PS product, P or S, is affected, the still low blood flow during reperfusion and the spotty pattern of flow (Fig. 2) suggest that the surface area of the perfused microvessels has, if anything, decreased, and that the permeability has increased more than is suggested by the change in the PS product.

The PS product of [⁵⁷Co]-DTPA for normal rat brain micro-vascular systems is around 2 × 10⁻⁵ mL/g/min, as determined by Patlak plots of serial QAR data (29). The K_i and PS products found for the areas of Gd-DTPA leakage are therefore more than 100-fold higher than normal, and yet are still PS product limited at this stage of occlusion–reperfusion. Other findings indicate that BBB opening occurs at a few spots in the microvascular system – perhaps only at some post-capillary venules – and not among all the microvessels (32). At such points, the opening may be very wide and permit the ready flow of water and solutes, including proteins, by both diffusion and convection–filtration.

The tissue volume data show that considerable swelling of the ipsilateral hemisphere occurred after 3 h of reperfusion. As mentioned previously, cytotoxic edema may be part of this gross swelling, but fluid must also have been taken up from the blood, and contributed to this increase in brain volume. This vasogenic edema fluid would distribute initially into the perivascular space around the leaky microvessels and, subsequently, into the adjacent interstitium; some of it would subsequently be taken up by brain cells and their processes, most notably the astrocytic foot processes. The remainder of this fluid, driven by the local hydrostatic pressure gradient and following the pathway of least resistance, would move further through the interstitium into the surrounding gray and white matter and add to the tissue volume.

Although not statistically significant, our findings suggest that the leakiness of BBB was greatest in ROIs with the lowest rate of blood flow during the 3-h occlusion period (Fig. 4) and was independent of CBF during reperfusion. This implies that the initial ischemic damage to the tight junctions of BBB or some other component of the neurovascular unit begins during the 3-h occlusion period, and that reperfusion 3 h after occlusion does not completely reverse it. If this observation is corroborated by further studies, the need for rapid recanalization and restitution of CBF after embolic stroke is obvious, supporting the expression: ‘time is brain’ (50).

CONCLUSION

The high degree of correlation between the blood-to-brain transfer constants, V_R and K_i, and the good spatial agreement between the MRI and QAR images observed in this study indicate collectively that, despite some spatial resolution limitations (15), this minimally invasive DCE-MRI-based quantitative technique is useful for the assessment of ischemic BBB damage. It may also aid in the evaluation of putative vasoprotective therapies in stroke and in other cerebrovascular diseases.

Abbreviations used

ADC

apparent diffusion coefficient of water

AIB

α-aminoisobutyric acid

AIF

arterial input function

ARG

autoradiogram

BBB

blood–brain barrier

CBF

cerebral blood flow

DCE-MRI

dynamic contrast-enhanced-MRI

ECS

extracellular space

Gd-DTPA

gadolinium-diethylenetriaminepentaacetic acid

Hct

hematocrit

iv

intravenous

K_i

blood-to-brain influx rate constant

L–L

Look–Locker

MRCA

magnetic resonance contrast agent

PCx

parietal cortex

PoA

preoptic area

PS product

permeability–surface area product

QAR

quantitative autoradiography

RF

radiofrequency

ROI

region of interest

SD

standard deviation

SE

spin-echo

StEq

single-time equation

Str

striatum

V_R

terminal tissue-to-blood concentration ratio or volume of distribution.