MRI estimation of gadolinium and albumin effects on water proton

Abstract

The longitudinal relaxivity on the protons of water of a Gd–chelate–albumin compound was measured at 7 T as a function of the macromolecular content of a cross-linked matrix. In agreement with previous works, the results demonstrate that the effect of gadolinium on water proton relaxivity is not constant, rising moderately with increase in the concentration of bovine serum albumin (BSA). About 35% variation in relaxivity was observed over a 0%–25% range of BSA concentrations (ℜ = 3.893 + 0.0502 × BSA [%], SE = 0.0119 and 0.1740, t = 4.215 and 22.383, p<0.014 and 0.001).

Introduction

Contrast agents (CAs) are widely used to evaluate cerebral perfusion and blood–brain barrier (BBB) permeability by MR imaging in animal models of cerebral tumor (Ewing et al., 2008; Ewing et al., 2006) and stroke (Knight et al., 2005; Nagaraja et al., 2005), as well as in human cerebral pathologies (Tofts et al., 1995). The most common MR CAs in current use are paramagnetic-labeled gadolinium chelates —e.g., Gd-DTPA (~600Da). CAs generate tissue contrast by affecting the water proton longitudinal relaxation time T₁ (T₁ = 1/R₁) via a dipolar mechanism, and the transverse dephasing times T₂ (T₂ = 1/R₂) and $T_2^{*}\mathit{(}{\mathrm{T}}_2^{*}=1/R_2^{*})$, of nearby aqueous hydrogen nuclei in biological systems. The dipolar effect is a function of Gd concentration ([Gd]) and is effective only at short range (nanometers). CA does not generally cross the blood–brain barrier (BBB) in healthy brain, and when CA leaks into the interstitial space, due to a disrupted BBB, it is an indication of pathology. Thus, accurate measurement of [Gd] in biological fluids is of considerable importance to dynamic contrast-enhanced (DCE) and dynamic susceptibility contrast (DSC) MRI studies (Bashir et al., 1999).

The theory of nuclear spin relaxation in paramagnetic systems is based on the Solomon–Bloembergen–Morgan theory of paramagnetic relaxivity (Bloembergen et al., 1948). The CA acts as a catalyst to relax the water protons in tissue; a CA's effect on the water protons' relaxation time is typically characterized by the constant relaxivity, defined as the change in T₁ relaxation rate induced by the contrast agent, per unit concentration of the contrast agent (mM) (Caravan et al., 2009). Under fast exchange conditions, there is a linear relationship between the reciprocal of the T₁ relaxation rate constant and [Gd] concentration. Under this assumption, the observed T₁ relaxation rate in the presence of Gd can be formulated as (Strich et al., 1985):

$$\frac{1}{T_1}=\frac{1}{T_{10}}+\Re [\text{Gd}]$$ (1)

where T₁ (s) and T₁₀ (s) are the tissue relaxation times with and without Gd, respectively. The slope of 1/T₁ as a function of [Gd] is the longitudinal relaxivity ℜ [mM⁻¹ s⁻¹] of a [Gd].

In general, the relaxivity of a CA such as Gd-DTPA is not constant but may depend on parameters such as the strength of the main field, the electronic properties of the gadolinium, water exchange, rotational diffusion, the ion-to-water proton distance, temperature, and also on the pH of the solution (Caravan et al., 2009; Stanisz and Henkelman, 2000; Wang et al., 2010). At ambient temperatures, proton relaxivity is constant at a given magnetic field strength but is dependent on the type of tissue (Bashir et al., 1999; Stanisz and Henkelman, 2000). In tissue, the relationship between longitudinal relaxation time T₁ and NMR frequency has been determined empirically in data collected from the literature at frequencies between 1 and 100 MHz using the formula: T₁ = kf^α, where k and α are constants depending on the tissue type and f is the Larmor frequency in hertz (Bottomley et al., 1984) and are validated at different field strengths (Rooney et al., 2007).

The present study is performed at field of 7 T (300 MHz) MR system. High-field MRI provides a good signal-to-noise ratio and resolution for structural and microvascular imaging in small animals (Vaughan et al., 2006). At these higher fields, magnetic resonance spectroscopy (MRS) provides better sensitivity and nonproton techniques (i.e.,²³Na, and ³¹P) become more useful clinical tools (Moser, 2010). The extent to which a metal complex influences tissue relaxation rates depends on three factors: the chemical environment encountered by the metal complex, compartmentalization of the contrast agent in tissue, and the magnetic susceptibility of the contrast agent.

The hypothesis that the Gd relaxivity at different field strengths (1.5 and 3 T) depends on macromolecular content (agar, solid skim milk powder in solution, egg white, etc.) has been tested in the past studies (Bashir et al., 1999; Caravan et al., 2009; Stanisz and Henkelman, 2000; Wang et al., 2010). This study will test a similar hypothesis that water proton relaxation rate in gel phantoms at 7 T depends on the concentrations of Gd and BSA.

Materials and methods

Extrapure reagents were obtained (Sigma Chemical Co., St. Louis, MO) and used as received. Forty-two phantom tubes with diameter of 0.5 cm of varying combinations and concentrations of Gd-DTPA at 400 mM (Strich et al., 1985) and BSA in gel were prepared. In the phantom preparation, a few milliliters of double-distilled water was boiled and allowed to return to room temperature to remove air bubbles. A typical concentration of BSA stock was diluted in a tube. After adding Gd-DTPA chelate in solution, the liquid was well mixed, and then heated at 90 °C and cooled to room temperature. The Gd concentrations in these gel solutions were 0.4, 0.2, 0.1, 0.05, 0.025, 0.0125, and 0 mM. Six aliquots were taken of each, and BSA was added to yield percentages of either 0%, 2.5%, 5%, 15%, 20%, or 25% among the six gels with identical [Gd]. Table 1 shows a diagram of the arrangement of seven gel phantom tubes and the Gd/BSA combinations for the seven phantom tubes. The gel tubes were placed in a 7-T MRI system (Magnex Scientific, Abingdon, UK, and Bruker Scientific, Billerica, MA). To reduce the magnetic field inhomogeneity and phase effects, all tubes were put in a polyethylene box subsequently filled with paraffin. Previously established procedures (Bagher-Ebadian et al., 2007; Ewing et al., 2006) were used to acquire a set of 24 sampling intervals of 50 ms in duration (total time = 1200 ms) by T1 One by Multiple Read Out Pulses (TOMROP) (Brix et al., 1990), an imaging version of Look–Locker sequence (Look and Locker, 1970). Matrix size was 128 × 64, FOV was 32 × 32 cm², 3 slices (2 mm thickness with 2 mm gap), and total imaging time was 145 sec. Signal to-noise ratio (SNR) for all measured samples was about 25. Amplitudes of 24 reconstructed images for 7 individual ROIs corresponding to 7 different concentrations in each experiment were used to calculate relaxivity. Three 2-mm-thick slices were selected for each tube, and its T₁ map was constructed from the 24 images acquired along the relaxation curve using the Simplex fitting method (Gelman et al., 2001). In each tube, T₁ maps of three slices were averaged to calculate the T₁ map of the tube. For different BSA levels, the average of ΔR₁ was calculated for each gel tube. The relaxivity ℜ at each level of BSA was then calculated from the slope of a linear regression of R₁ (= 1/T₁) against the Gd concentration. Finally, the slopes of the fitted lines were plotted at different BSA levels to demonstrate the dependency of proton relaxivity on this protein. As an alternative model, the quadratic behavior of R₁ versus Gd concentration was tested using quadratic fittings.

Table 1.

A schematic diagram of the arrangement of seven gel phantom tubes (left) and the Gd/albumin combinations for the seven phantom tubes (right).

Results

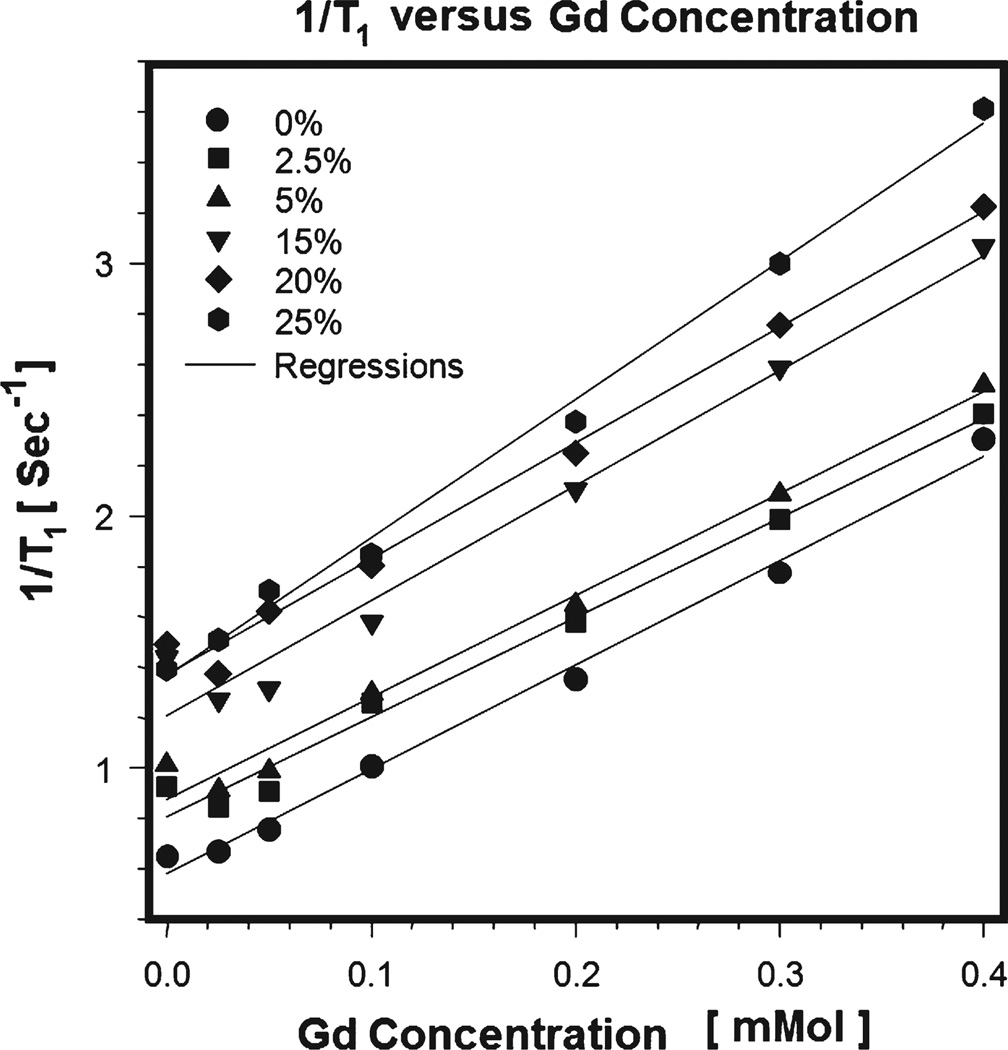
Fig. 1 demonstrates the variation in relaxation rates, R₁ of each sample against the concentration of [Gd] for different BSA. As expected, in this figure, R₁ rose linearly as [Gd] increased. This figure illustrates a family of the curves in which appear to differ mostly due to the variation of macromolecular BSA concentration. The slopes of linear fits to data at zero concentration of BSA gave MR relaxivity of Gd ℜ = 4.2 ± 0.83 mM⁻¹ s⁻¹ at 7 T. When the R₁ versus [Gd] linearity condition was tested with quadratic fittings, for this data set, the quadratic fits were not significant (p>0.2). Table 2 shows Gd concentrations for the seven phantoms and the measured fitted longitudinal relaxation rate at the typical value of 0% of BSA at 7 T.

Fig. 1.

Family curves for R₁ change versus [Gd] for different bovine serum albumin (BSA) concentrations measured at 7 T along with linear regression fits to the data. Error bars represent the standard deviation on the R₁ vs. [Gd] fit.

Table 2.

Gadolinium concentrations for the seven phantom tubes and the measured fitted longitudinal relaxation rate at 0% of BSA at 7 T.

Phantom no.	Gd (mmol)	R1 (s−1)—measurement	R1 (s−1)—fitting
1	0	0.62	0.57
2	0.025	0.68	0.68
3	0.050	0.72	0.78
4	0.100	1.00	1.00
5	0.200	1.40	1.42
6	0.300	1.76	1.85
7	0.400	2.30	2.27

R₁ = 0.574 + 4.14 × Gd (mmol).

Standard error (slope) = 0.15, p<0.001.

In Fig. 2, Gd relaxivities (line slope) calculated by linear fitting versus the concentration of macromolecular compound BSA is plotted. This plot indicates that the water protons' relaxivity is dependent on the concentration of the Gd-based macromolecular content of the system, showing a 35% relaxivity change in 0%–25% of BSA (ℜ = 3.893 + 0.0502 × BSA%), SE = 0.0119 and 0.1740, t = 4.215 and 22.383, p<0.014 and 0.001). Table 3 shows BSA concentrations for different aliquots and the measured and fitted longitudinal relaxivity at 7 T. It was also shown that, for both data sets (relaxivity and relaxation), an alternative fit to quadratic curves was not significant (p>0.12).

Fig. 2.

Gd longitudinal relaxivity as a function of the different BSA concentrations in the gel phantoms measured at 7 T. A solid line is a linear regression fit to the data. Error bars represent the standard deviation on the R₁ vs. [Gd] fit.

Table 3.

Bovine serum albumin concentrations for different aliquots and the measured and fitted longitudinal relaxivity at 7 T.

Aliquot no.	BSA%	ℜ [mM−1 s−1]—measurement	ℜ (mM−1 s−1)—fitting
1	0	4.2	3.89
2	2.5	3.92	4.11
3	5.0	4.10	4.24
4	15	4.60	4.76
5	20	4.62	5.02
6	25	5.51	5.28

ℜ = 3.893 + 0.0502 × BSA (%).

Standard error (slope) = 0.0119, p<0.014.

Discussion

The data demonstrate that the slopes of the relaxivities in all samples are dependent on macromolecular content. Thus, the in vitro longitudinal relaxivity differs moderately with the concentration of the Gd-based macromolecular content. The longitudinal relaxivity of the CA complex describes the efficiency of magnetic dipolar coupling occurring between the solvent nuclei and the paramagnetic [Gd]. Note that longitudinal relaxivity of a CA depends on the solvent and the distribution space. This statement has two aspects. One aspect is associated with the contribution of the inner and outer sphere mechanisms, while other is the compartmentalization of biological tissue. The inner sphere proton relaxation mechanism depends on the number of co-ordinate water molecules, their mean residence lifetime, the distance between the water protons and the metal center, r, the electronic relaxation time of the gadolinium ion, and the reorientational correlation time of the whole complex (Bloembergen et al., 1948). The outer sphere relaxivity depends on the relative diffusion coefficient of solute and solvent, and the distance of minimum approach between the metal ion and the protons of the diffusing water molecules (Bloembergen et al., 1948). It is possible that other chemical species may compete with water and inhibit the interaction with the paramagnetic chelate. These effects may reduce relaxation effects in the presence of macromolecules. However, the BSA works in the other direction: It enhances longitudinal relaxivity.

The Gd ion increases the longitudinal and transverse relaxation rates of water protons as water molecules diffuse in its vicinity (Bloembergen et al., 1948), but increasing protein concentration may reduce the mobility of both Gd ions and water protons, i.e., may yield slower tumbling. Protein changes the correlation time (the average time between the mean free path of the molecules in a given environment), and higher albumin concentration increases relaxivity. As noted, the degree of relaxivity increase will depend on the extent of protein binding (Wang et al., 2010). Relaxivity also depends on the water residency time, the inverse of exchange rate. Obviously, if residence time becomes too long, there is little or no exchange of the relaxed water with the lattice and relaxivity will be limited. This study demonstrates results that imply that environment affects MR estimates of Gd-induced changes in proton relaxivity in vitro and suggests that something similar would occur in normal and abnormal tissue. These findings are in agreement with the results of similar experiments done by other researchers (Bashir et al., 1999; Stanisz and Henkelman, 2000; Wang et al., 2010) at lower field strengths.

As noted, relaxivity is dependent on CA, macromolecular content, and applied field. In DCE MRI studies, to relate MR signal to CA concentration, it is necessary to measure CA relaxivity under the similar conditions (temperature, field). Since tissue is highly compartmentalized because the transport of CA is strictly restricted to the water-filled cellular compartments (Buckely et al., 2008; Landis et al., 1999, 2000). Note that water comprises about 80% of most soft tissues. As a result, the observed tissue relaxivity of CA will change; depending upon the rate of water exchange between cellular- and CA-occupied compartments (Paudyal et al., 2009).

Taken together, these results imply that the effects of Gd on proton relaxivity may not be the same among tissues of differing protein composition. With the phantom studies presented here, we believe that the relaxivities measured can be used for the compartmental relaxivity in the DCE model, which is typically utilized for unbiased estimation of the vascular physiological parameters.