Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2013 Dec 7.
Published in final edited form as: Phys Med Biol. 2012 Nov 8;57(23):N457–N467. doi: 10.1088/0031-9155/57/23/N457

Experimental demonstration of benchtop x-ray fluorescence computed tomography (XFCT) of gold nanoparticle-loaded objects using lead- and tin-filtered polychromatic cone-beams

Bernard L Jones 1,1, Nivedh Manohar 1, Francisco Reynoso 1, Andrew Karellas 1,2, Sang Hyun Cho 1,*
PMCID: PMC3543152  NIHMSID: NIHMS420952  PMID: 23135315

Abstract

This report presents the first experimental demonstration, to our knowledge, of benchtop polychromatic cone-beam x-ray fluorescence computed tomography (XFCT) for a simultaneous determination of the spatial distribution and amount of gold nanoparticles (GNPs) within small-animal-sized objects. The current benchtop experimental setup successfully produced XFCT images accurately showing the regions containing small amount of GNPs (on the order of 0.1 mg) within a 3-cm diameter plastic phantom. In particular, the performance of the current XFCT setup was improved remarkably (e.g., at least a factor of 3 reduction in XFCT scan time) using a tin-filtered polychromatic beam in comparison with a lead-filtered beam. The results of this study strongly suggest the current benchtop XFCT configuration can be made practical with a few modifications such as the deployment of array detectors, while meeting realistic constraints on x-ray dose, scan time, and image resolution for routine pre-clinical in-vivo imaging with GNPs.

1. Introduction

Some notable applications with gold nanoparticles (GNPs) have emerged for cancer imaging (Sokolov et al., 2003; Hainfeld et al., 2006; Qian et al., 2008; Li et al., 2010), radiation therapy (Hainfeld et al., 2004; Cho, 2005; Cho et al., 2009; Jones et al., 2010; Hainfeld et al., 2008; Hainfeld et al., 2010), and thermal therapy (Hirsch et al., 2003; Diagaradjane et al., 2008; von Maltzahn et al., 2009; Krishnan et al., 2010). Many of these approaches are currently undergoing pre-clinical testing using small animal models. One of the key tasks during pre-clinical studies is to determine the biodistribution of GNPs, and this task is typically handled by somewhat cumbersome and time-consuming ex-vivo analysis after sacrificing animals. Ideally, it is desirable to determine the biodistribution of GNPs in vivo using a tool capable of identifying both the spatial distribution and amount of GNPs simultaneously. This will also enable GNP-based pre-clinical molecular imaging of cancer and other diseases, especially with bioconjugated GNPs.

In principle, x-ray fluorescence computed tomography (XFCT) can be a powerful quantitative imaging tool for small samples containing high atomic number (Z) materials such as iodine, gadolinium, and gold. Especially in the case of gold, the relatively low attenuation of K-shell x-ray fluorescence photons (~69 and 78 keV) in soft tissue may enable XFCT of small animals. Therefore, XFCT appears to be particularly well suited for the determination of GNP biodistribution in vivo. Monochromatic x-ray sources are highly desirable for XFCT because their energy can easily be tuned to maximize the fluorescence-to-background ratio for the interrogated material (Boisseau, 1986; Cesareo and Mascarenhas, 1989; Hogan et al., 1991; La Rivière, 2004; La Riviere et al., 2009; Schroer, 2001; Simionovici et al., 2000; Yuasa et al., 1997). Synchrotron x-ray sources are excellent for this purpose but they are clearly impractical for most biomedical research laboratories.

For routine benchtop applications, an implementation of XFCT using a conventional polychromatic source is much more realistic but far more challenging than that using a monochromatic source primarily due to the polychromatic nature of x-ray source resulting in less efficient fluorescence x-ray production/detection (e.g., leading to much lower fluorescence-to-background ratio). These challenges often resulted in a pessimistic outlook about a benchtop XFCT system for in-vivo imaging (von Busch et al., 2005). Recently, however, we showed the possibility for simultaneously determining GNP location and concentration using a benchtop XFCT setup with a polychromatic x-ray source (i.e., 110 kVp) under the pencil-beam geometry (Cheong et al., 2010). We also demonstrated in a more recent Monte Carlo (MC) study that the inherent limitations of the pencil-beam geometry, such as long scan time and excessive x-ray dose, can be overcome using a fan/cone-beam geometry (Jones and Cho, 2011). Nevertheless, the approaches and results from this MC study need to be validated by an experimental study in order to fully establish the feasibility of a polychromatic cone-beam XFCT setup.

Therefore, the primary goals of the current experimental study were to build a benchtop polychromatic cone-beam XFCT system as proposed in our previous MC study and to assess its performance via phantom studies in view of realistic constraints on x-ray dose, scan time, and image resolution for XFCT of small animals injected with GNPs. After the initial construction and testing, we also investigated the possibility to further enhance the performance of our benchtop XFCT system by a simple modification adopting a tin-filtered polychromatic x-ray spectrum instead of a lead-filtered one. Overall, the results and findings from this experimental study provide much more realistic insight, compared to our previous pencil beam and MC studies, about the challenges and promises for building a practical and useful benchtop XFCT device for in-vivo imaging with GNPs.

2. Methods and Materials

2.1. Imaging Phantoms

Samples were prepared based on realistic tumor/blood gold concentrations achievable in vivo (Chang et al., 2008; Hainfeld et al., 2004): namely, 0.5, 1.0, and 2.0% gold by weight (wt.), mimicking a practical small-animal XFCT scenario. Roughly cylindrical tubes (6 mm in diameter) were filled with saline solution, and commercially available 1.9 nm diameter GNPs (Aurovist™, Nanoprobes Inc) were added. The GNP-loaded tubes were then inserted into a small-animal-sized polymethyl methacrylate (PMMA) cylindrical phantom 3 cm in diameter and 5 cm in height. The GNP-loaded tubes contained 1.6–6.5 mg of GNPs (corresponding to 0.5 to 2.0 wt. % of GNP concentrations within the entire tubes).

2.2. Benchtop XFCT Setup

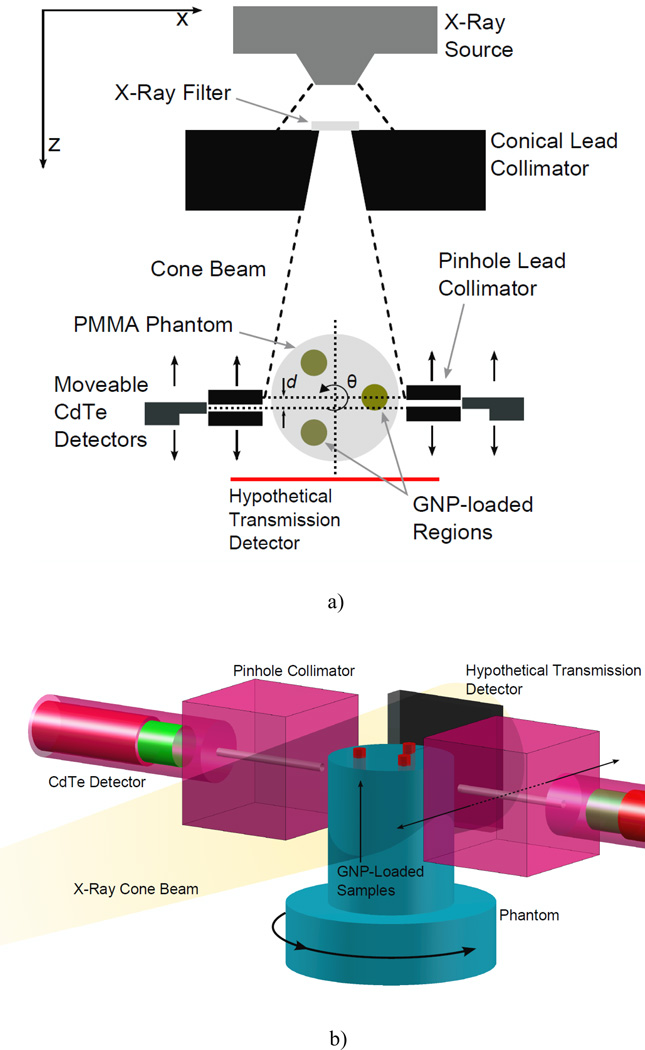
To acquire images showing the GNP-loaded regions with associated gold concentrations, each phantom was irradiated with a microfocus x-ray source (L9631, Hamamatsu Photonics, Inc) operating at tube potential of 105 kVp and tube current of 400 µA. The source had a nominal focal spot size less than 100 µm and an emission angle of 62°. As shown in Fig. 1, the beam was collimated by a conical hole through a 5 cm-thick lead block. The angle of the conical hole was 11.4°, with front and back hole diameters of 1 and 2 cm, respectively. The center of the phantom was roughly 8 cm from the collimator surface (14.5 cm from exit window of source), yielding a beam with a diameter just exceeding the 3-cm phantom diameter.

Figure 1.

Figure 1

Open in a new tab

Experimental setup for benchtop XFCT. (a) Cross-sectional view in the imaging plane. The angle of the conical collimator was 11.4°, with front and back opening diameters of 1 and 2 cm, respectively. The center of the phantom was roughly 8 cm from the collimator surface (14.5 cm from exit window of source). Each detector was positioned behind a 2.5 mm-diameter lead pinhole collimator that was placed 0.75 cm away from the phantom surface. (b) 3-D view of the detector and imaging phantom setup. A 3-cm-diameter polymethyl methacrylate phantom containing three GNP-loaded regions is irradiated by a cone beam of filtered x-rays. The gold Kα fluorescence and Compton-scattered photons are detected by two CdTe detectors placed at 90° relative to the beam central axis. The imaging sinogram S(q, d) is assembled via successive rotations of the phantom and translations of the fluorescence detectors. Although not used in this study, the geometry is compatible with standard transmission imaging, allowing simultaneous acquisition of a transmission CT image.

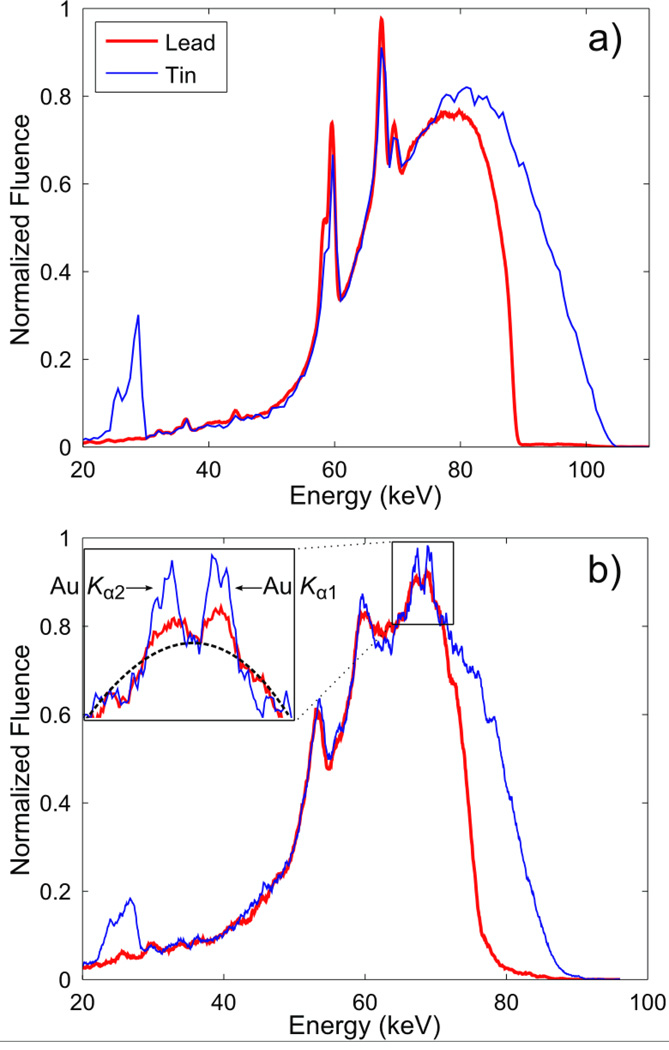
As shown previously (Cheong et al., 2010; Jones and Cho, 2011), significant hardening or quasi-monochromatization of polychromatic x-ray spectrum was necessary to implement XFCT with an ordinary x-ray source. By adopting x-ray filters made of lead (Pb: 1.0 mm) and tin (Sn: 0.9 mm), therefore, we achieved a reasonable suppression of those x-ray photons below the K-absorption edge of gold (80.7 keV) that would not produce gold K-shell fluorescence photons (Fig. 2a). Lead has been used in our previous benchtop XFCT studies; however, we have also used tin as a filter material in the current study because tin has much lower absorption above 80 keV (where lead K-shell absorption is peaked) than lead, yielding a higher number of gold Kα fluorescence per primary photon. In fact, the performance of our benchtop XFCT setup has improved remarkably with the filter made of tin, as shown later in this report.

Figure 2.

Figure 2

Open in a new tab

(a) Measured energy spectra of 105 kVp x-rays filtered by 1 mm of lead and 0.9 mm of tin. The x-ray beams with these spectra were incident onto the imaging phantom for XFCT. Spectra are normalized to have the same maximum value. The relative amount of photons above the K-edge of gold is greater with the tin filter. (b) Typical photon spectra emitted from the imaging phantom showing the Compton scatter background and gold fluorescence peaks (GNP concentration at 2 wt. %). Spectra were measured by a CdTe detector at a 90° angle to the central axis of lead-/tin-filtered incident beams. The inset shows more detail around the gold K-shell fluorescence peaks. The dotted line is an example fit to the scatter background. It can be seen that the fluorescence photons constitute a small fraction of the overall signal.

Gold K-shell fluorescence photons were detected by two identical thermoelectrically cooled cadmium telluride (CdTe) detectors (XR-100T-CdTe, Amptek Inc) (see Fig. 1). A digital pulse processor and multichannel analyzer (PX4, Amptek Inc) interfaced between the detectors and a personal computer, which collected, stored, and analyzed the results. Measured photon spectra were corrected for the energy-dependent efficiency of the current CdTe detector. Since the measured spectrum of photons emitted from the phantom was overwhelmingly dominated by Compton scatter as shown in Fig. 2(b), the detectors were placed behind lead pinhole collimators. Each detector was positioned behind a 4 cm-thick lead pinhole collimator with an aperture diameter of 2.5 mm, which was placed 0.75 cm away from the phantom surface. Note the detector collimation is referred to as “pinhole” collimation here for convenience despite its relatively larger aperture size. Only a fraction of the GNP-loaded tubes was ever in view of the detector, since the height of the tubes (>2 cm) is much larger than the pinhole diameter (2.5 mm). For the 0.5 wt. % GNP tube, this translated into less than 0.5 mg of GNPs visible in the best-case scenario.

2.3. Data Acquisition and Image Reconstruction

As shown in Fig. 1, the view of each detector was along the x-axis, at a 90° angle to the central axis of the beam (i.e., z-axis). The system remained stationary for the acquisition of each projection, and then the phantom was rotated about its central axis by 6° (along the angular direction θ as shown in Fig. 1). This process was repeated for 60 projections, corresponding to 360° coverage of the phantom. In order to simulate an 11-pixel serial detector, each CdTe detector was translated along the z-axis (e.g., to position d as shown in Fig. 1) in equal intervals (3 mm) after the completion of a full 360° rotation. In order to increase the data collection rate, as well as the spatial resolution, the two detectors were slightly offset (1.5 mm) along the z-axis.

Data were acquired as a series of at least three sets of 60 projections, allowing the reconstruction of images corresponding to three different levels of x-ray exposure per projection (e.g., 1, 2, and 3 minute exposure per projection). For each sinogram element S(θ, d), the gold fluorescence peak height was extracted from the Compton scatter background by fitting a 3rd degree polynomial to the measured data points on either side of the gold Kα channels, and subtracting out the interpolated values for the scatter background. These signals were assembled to form a sinogram of gold fluorescence signal with respect to position and angle. More details about this procedure can be found elsewhere (Cheong et al., 2010). Using the sinograms created during the data acquisition, an image of the GNP distribution inside the phantom was reconstructed by applying an approach developed in our previous Monte Carlo study (Jones and Cho, 2011) following the Maximum Likelihood Expectation Maximization (ML-EM) iterative reconstruction algorithm (Shepp and Vardi, 2007; Lange and Carson, 1984; Cherry et al., 2003), taking into account various factors affecting the fluorescence photon emission and detection probability. A measured attenuation map of the phantom was unavailable from the current experimental setup due to the absence of a transmission detector. As a result, attenuation coefficients for gold and PMMA were taken as priori knowledge.

2.4. X-ray Dose Measurements

In order to measure the x-ray dose delivered during XFCT scanning, ion chamber measurements were performed using a standard Farmer-type ionization chamber (PTW N30013, PTW Freiburg GmbH) and an electrometer (Max 4000), Standard Imaging, Inc). The dose measurement geometry was identical to the irradiation geometry for the phantom used for XFCT scanning via the utilization of a PMMA phantom constructed to hold the ion chamber. The x-ray beam matched the beam used in the corresponding imaging scenario in terms of power/filtration used. The AAPM TG-61 protocol (Coffey et al., 2001) was applied to determine the x-ray dose rates from ionization chamber measurements.

3. Results

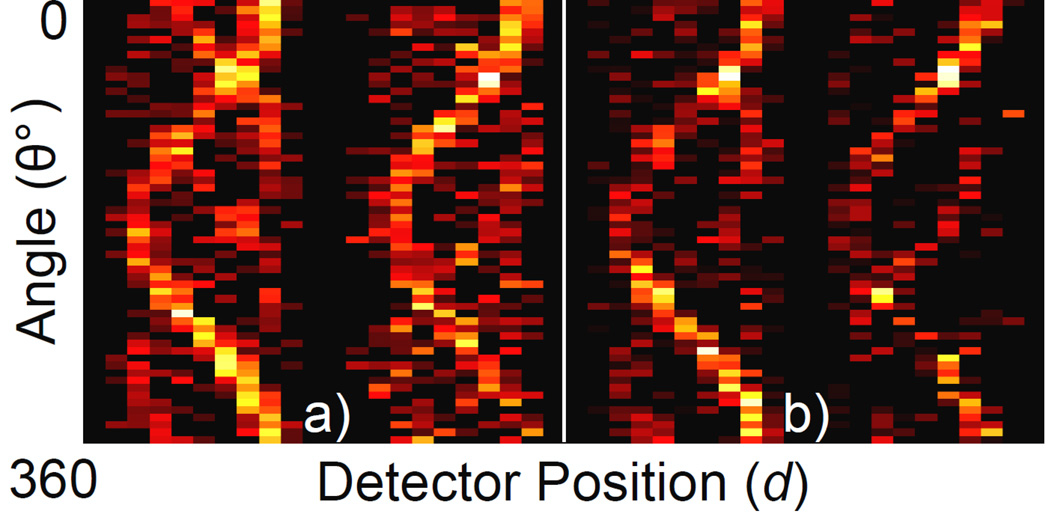
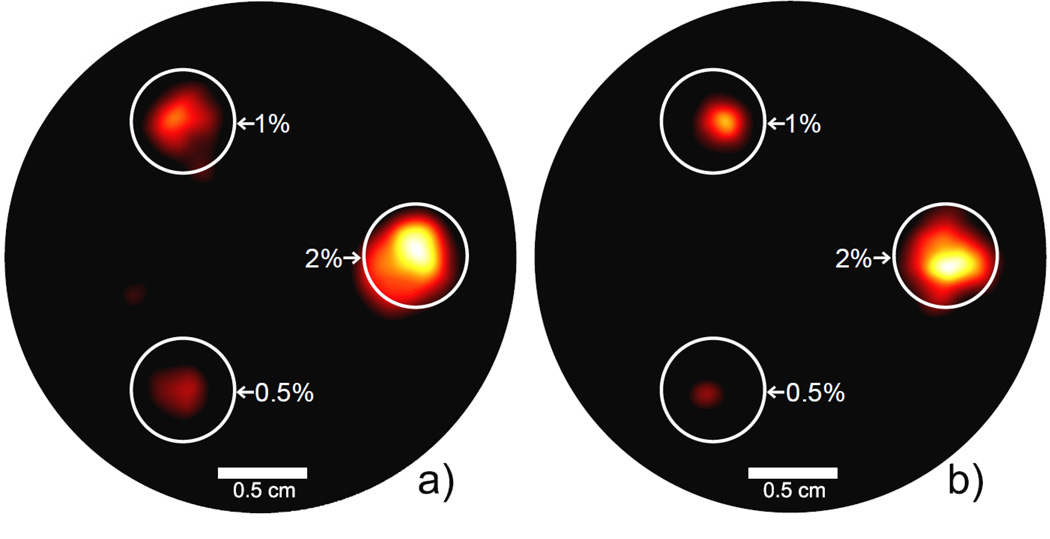
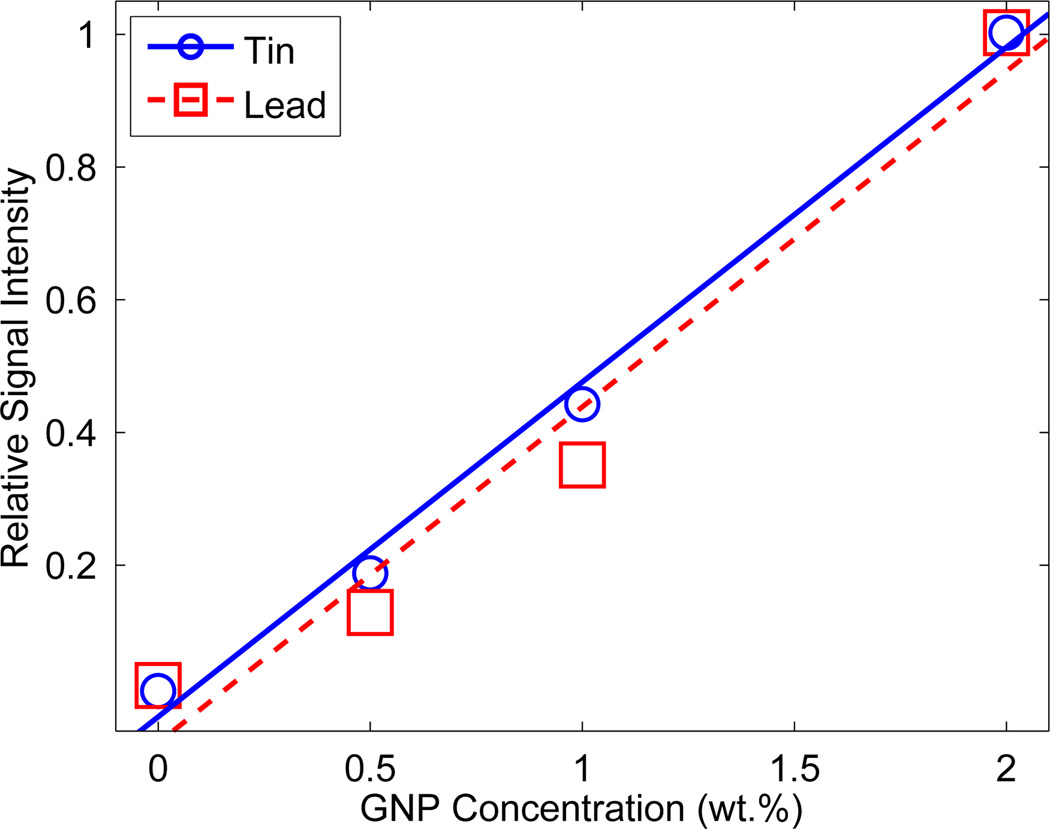
The measured sinograms for the two most representative cases are shown in Fig. 3. Using these data, the images of GNP location and concentration were reconstructed (Fig. 4). As shown, using the Sn-filter, one minute of exposure at each projection was sufficient to produce an XFCT image significantly better than that reconstructed using the data acquired from three minute exposure time per projection with the Pb-filter. In terms of scan time alone, this means the Sn-filter yielded at least a factor of 3 reduction over the Pb-filter. All three GNP-loaded columns were well defined in each image (with some regions of low-intensity noise). Fig. 5 shows the relationship between signal intensity and GNP concentration in each image. Each data point represents the mean intensity in each region of the image in Fig. 4 (i.e., regions denoted as 0.5%, 1%, and 2 %). The relative concentration of GNPs was accurately determined in both images, showing a good linear relationship between gold concentration and signal intensity.

Figure 3.

Figure 3

Open in a new tab

Measured sinograms for the 3 cm-diameter phantom. (a) tin-filtered polychromatic beam, 1 minute exposure per projection. (b) lead-filtered polychromatic beam, 3 minute exposure per projection. Since detectors were placed on both sides of the phantom, the full sinogram dataset contains data from both sides (i.e., left and right sinograms in each panel of this figure).

Figure 4.

Figure 4

Open in a new tab

Reconstructed XFCT images for the 3 cm-diameter phantom. (a) tin-filtered polychromatic beam, 1 minute exposure per projection. (b) lead-filtered polychromatic beam, 3 minute exposure per projection. Each phantom is labeled with the GNP concentration (by weight) of each GNP-loaded column included. The GNP-loaded regions are well delineated, and the tin-filtered beam was able to reconstruct an image using much less scan time and dose. The display window in both figures is 10%–100% of the maximum intensity value.

Figure 5.

Figure 5

Open in a new tab

Measurement of relative GNP concentration. A linear curve was fit to the integrated signal in each region of Fig. 4. The XFCT images are able to accurately reproduce the relative GNP concentration in each GNP-loaded tube.

The measured dose rates at the center of the phantom were 1.7 mGy/min for the Pb-filtered beam and 3.4 mGy/min for the Sn-filtered beam. The Sn-filtered beam delivers twice the dose rate of the Pb-filtered beam, but acquires a better image in 1/3 of the time, making the tin filter at least 50% more effective for XFCT imaging per unit dose.

4. Discussion

With a proper choice of x-ray filter (i.e., tin), the current XFCT setup appears to require no more than 1 minute of data acquisition time at each projection angle in order to produce reconstructed XFCT images showing all three GNP-loaded tubes within a small-animal-sized PMMA phantom. This means, with the deployment of two 11-pixel CdTe array detectors to the current XFCT setup, the total scan time would be just about an hour, presumably acceptable for unconventional in-vivo imaging tasks such as the determination of GNP biodistribution. Thus, it is foreseeable to perform a practical benchtop XFCT scanning of small animals, at least those animals comparable in their sizes to the current imaging phantom (e.g., transgenic nude mice). A similar argument can also be made for x-ray dose. Specifically, the use of 11-pixel CdTe detectors would reduce the total x-ray dose by a factor of 11, resulting in the total x-ray dose required for XFCT imaging using the current methodology to be roughly 20 cGy. This is clearly much less than the general LD50 (50% Lethal Dose) for mice of about 7 Gy (Hall and Giaccia, 2006), and possibly less than typical ranges of x-ray doses delivered during micro-CT scanning of small animals (Boone et al., 2004; Obenaus and Smith, 2004).

A few more modifications of the current XFCT setup and approaches can be made for further improvement in image quality, detection limit, and scan time (or x-ray dose). The use of a two-dimensional (2-D) array detector (Schlomka et al., 2008) with more pixel elements than the currently simulated 11 pixels in 2-D space would significantly improve the resolution of XFCT images at the same x-ray dose. The scan time can be easily reduced further because it is not essential to perform a full 360° scanning in order to reconstruct XFCT images (Jones and Cho, 2011; La Riviere et al., 2007; Jones, 2011). Moreover, it is possible that the amount of data required to reconstruct an acceptable image could be further reduced by using a more sophisticated gold fluorescence peak extraction algorithm, or by using a detector with a higher energy resolution at the energies considered (65–70 keV). Besides, the current experimental setup, especially the source and detector collimators, may also be further optimized to improve the detection of fluorescence photons while reducing the production of unwanted scattered photons.

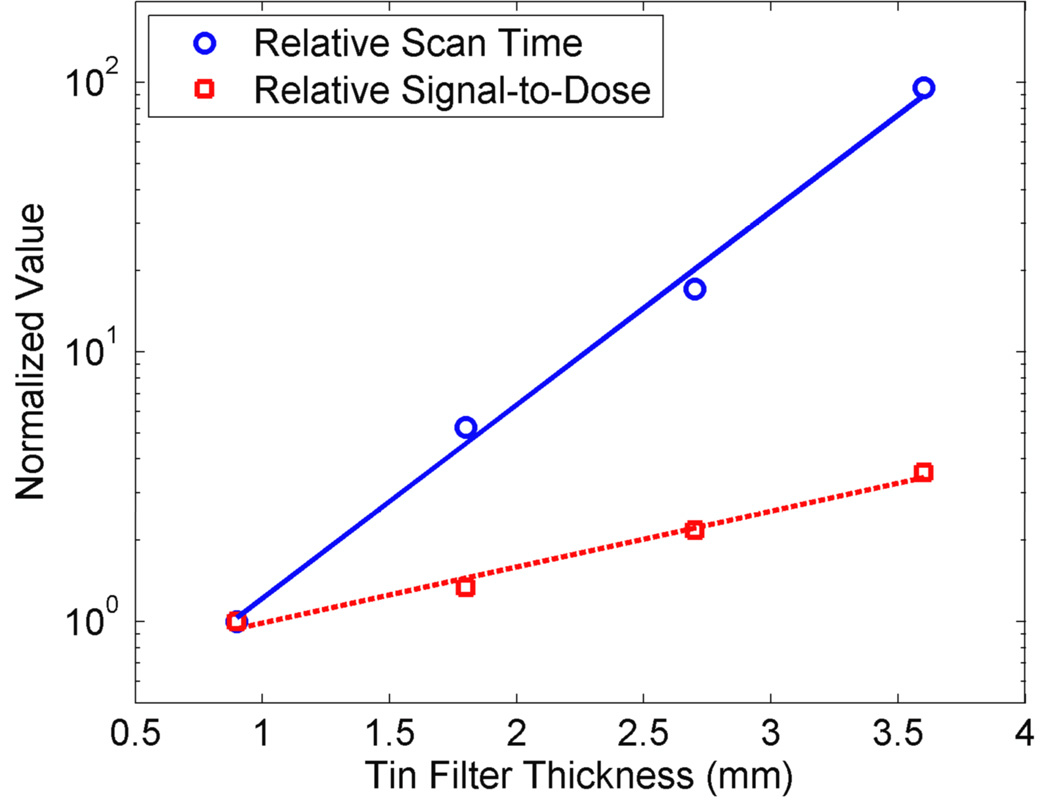
Additionally, the scan time and detection limit could be further reduced by optimizing the incident x-ray spectrum using higher x-ray tube potentials/currents and/or beam filtration techniques that improve the ratio of photons above/below the K-absorption edge of gold (80.7 keV). To illustrate this possibility in a more quantitative fashion, an extra set of fluorescence and dose measurements was also made in this investigation using the same beam geometry and phantoms as described earlier. As shown in Fig. 6, the ratio of gold fluorescence signal to delivered dose increases exponentially with tin filter thickness (i.e., hardness of the incident photon spectrum). However, the scan time to produce the same magnitude of gold fluorescence signal (from the 2 wt. % GNP region) also increases with tin filter thickness, at a much higher rate, under the current x-ray tube power setting (i.e., 105 kVp and 400 µA). Thus, it is imperative to use a higher power x-ray tube for XFCT scanning in order to fully take advantage of an increased fluorescence signal-to-dose ratio from the use of thicker filters. The current results will be useful for the determination of an optimum combination of filter thickness and x-ray power setting. In summary, with the implementation of all or part of the aforementioned modifications for the current XFCT setup, benchtop XFCT will ultimately be available for routine in-vivo imaging, offering a new and unique option for pre-clinical multimodal molecular imaging of various diseases in conjunction with bioconjugated GNPs and simultaneous micro-CT in the same platform.

Figure 6.

Figure 6

Open in a new tab

Results from measurements of gold fluorescence signal and dose with varying thickness of tin filters. During these measurements, x-ray power setting was kept constant at 105 kVp and 400 µA. Measurements were taken under the same geometry as that resulted in Fig. 2(b). Experimental errors were smaller than the size of symbols. As the thickness of the tin filter increases from 0.9 mm to 3.6 mm, the ratio of gold fluorescence signal (for GNP concentration at 2 wt. %) to delivered dose increases exponentially. However, the scan time to produce the same magnitude of gold fluorescence signal (for GNP concentration at 2 wt. %) also increases with tin filter thickness, at a much higher rate, under the current x-ray tube power setting. Thus, it is imperative to use a higher power x-ray tube in order to fully take advantage of an increased fluorescence signal-to-dose ratio from the use of thicker filters.

5. Conclusions

In the current experimental investigation, we demonstrated the feasibility to image low local concentrations of GNPs (e.g., 0.5 mg within the region seen by a 2.5 mm-diameter pin-hole collimator) in small-animal-sized objects (e.g., 3 cm in diameter and 5 cm in height) by a benchtop XFCT setup utilizing a polychromatic cone-beam x-ray source in the diagnostic energy range. The use of Sn-filtered polychromatic beam, in comparison with the Pb-filtered beam, improved the performance of the current experimental XFCT setup remarkably (e.g., at least a factor of 3 reduction in XFCT scan time), strongly suggesting the feasibility to build a practical benchtop XFCT device based on the current setup with a few modifications. Considering the results shown in this study, it can be projected without loss of generality that, using array detectors, the current experimental setup would be capable of producing useful XFCT images of small animals injected with GNPs with a total scan time (< 1 hour) and a tissue dose (~ 20 cGy) acceptable for routine pre-clinical in-vivo imaging.

Acknowledgments

This investigation was supported by Georgia Research Alliance and Georgia Institute of Technology faculty startup funds and in part by NIH/NCI grant R01CA155446. Dr. Karellas was supported in part by NIH/NCI grant R21CA134128. The contents are solely the responsibility of the authors and do not represent the official views of the NCI or NIH. The authors acknowledge Dr. Chris Wang at Georgia Tech for helpful discussion and kindly sharing an electrometer during the current investigation. The authors are also grateful to Dr. John Oshinski and Dr. Eric Elder at Emory University for constructive criticisms on the current investigation.

References

  1. Boisseau P. Determination of three dimensional trace element distributions by the use of monochromatic x-ray microbeams. Ph.D. Thesis. Massachusetts Institute of Technology; 1986. [Google Scholar]
  2. Boone JM, Velazquez O, Cherry SR. Small-animal X-ray dose from micro-CT. Mol Imag. 2004;3:149–158. doi: 10.1162/15353500200404118. [DOI] [PubMed] [Google Scholar]
  3. Cesareo R, Mascarenhas S. A new tomographic device based on the detection of fluorescent x-rays. Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment. 1989;277:669–672. [Google Scholar]
  4. Chang M-Y, Shiau A-L, Chen Y-H, Chang C-J, Chen HHW, Wu C-L. Increased apoptotic potential and dose-enhancing effect of gold nanoparticles in combination with single-dose clinical electron beams on tumor-bearing mice. Cancer Science. 2008;99:1479–1484. doi: 10.1111/j.1349-7006.2008.00827.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Cheong SK, Jones BL, Siddiqi AK, Liu F, Manohar N, Cho SH. X-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects using 110 kVp x-rays. Physics in Medicine and Biology. 2010;55:647–662. doi: 10.1088/0031-9155/55/3/007. [DOI] [PubMed] [Google Scholar]
  6. Cherry S, Sorenson J, Phelps M. Physics in Nuclear Medicine. 3rd edn. Philadelphia, PA: Saunders; 2003. [Google Scholar]
  7. Cho SH. Estimation of tumour dose enhancement due to gold nanoparticles during typical radiation treatments: a preliminary Monte Carlo study. Phys Med Biol. 2005;50:N163–N173. doi: 10.1088/0031-9155/50/15/N01. [DOI] [PubMed] [Google Scholar]
  8. Cho SH, Jones BL, Krishnan S. The dosimetric feasibility of gold nanoparticle-aided radiation therapy (GNRT) via brachytherapy using low-energy gamma-/x-ray sources. Phys Med Biol. 2009;54:4889–4905. doi: 10.1088/0031-9155/54/16/004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Coffey C, DeWerd L, Liu C, Nath R, Seltzer S, Seuntjens J. AAPM protocol for 40–300 kV x-ray beam dosimetry in radiotherapy and radiobiology. Medical Physics. 2001;28:868. doi: 10.1118/1.1374247. [DOI] [PubMed] [Google Scholar]
  10. Diagaradjane P, Shetty A, Wang JC, Elliott AM, Schwartz J, Shentu S, Park HC, Deorukhkar A, Stafford RJ, Cho SH, Tunnell JW, Hazle JD, Krishnan S. Modulation of in vivo tumor radiation response via gold nanoshellmediated vascular-focused hyperthermia: characterizing an integrated antihypoxic and localized vascular disrupting targeting strategy. Nano Lett. 2008;8:1492–1500. doi: 10.1021/nl080496z. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Hainfeld J, Dilmanian F, Zhong Z, Slatkin D, Kalef-Ezra J, Smilowitz H. Gold nanoparticles enhance the radiation therapy of a murine squamous cell carcinoma. Physics in Medicine and Biology. 2010;55:3045. doi: 10.1088/0031-9155/55/11/004. [DOI] [PubMed] [Google Scholar]
  12. Hainfeld J, Slatkin D, Focella T, Smilowitz H. Gold nanoparticles: a new X-ray contrast agent. British Journal of Radiology. 2006;79:248. doi: 10.1259/bjr/13169882. [DOI] [PubMed] [Google Scholar]
  13. Hainfeld JF, Dilmanian FA, Slatkin DN, Smilowitz HM. Radiotherapy enhancement with gold nanoparticles. J Pharm Pharmacol. 2008;60:977–985. doi: 10.1211/jpp.60.8.0005. [DOI] [PubMed] [Google Scholar]
  14. Hainfeld JF, Slatkin DN, Smilowitz HM. The use of gold nanoparticles to enhance radiotherapy in mice. Phys Med Biol. 2004;49:N309–N315. doi: 10.1088/0031-9155/49/18/n03. [DOI] [PubMed] [Google Scholar]
  15. Hall EJ, Giaccia AJ. Radiobiology for the Radiologist. Philadelphia, PA: Lippincott Williams & Wilkins; 2006. [Google Scholar]
  16. Hirsch LR, Stafford RJ, Bankson JA, Sershen SR, Rivera B, Price RE, Hazle JD, Halas NJ, West JL. Nanoshell-mediated near-infrared thermal therapy of tumors under magnetic resonance guidance. Proc Natl Acad Sci U S A. 2003;100:13549–13554. doi: 10.1073/pnas.2232479100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Hogan JP, Gonsalves RA, Krieger AS. Fluorescent computer tomography: a model for correction of X-ray absorption. IEEE Transactions on Nuclear Science. 1991;38:1721–1727. [Google Scholar]
  18. Jones BL. Development of dosimetry and imaging techniques for pre-clinical studies of gold nanoparticle-aided radiation therapy. Ph.D. Thesis. Georgia Institute of Technology; 2011. [Google Scholar]
  19. Jones BL, Cho SH. The feasibility of polychromatic cone-beam x-ray fluorescence computed tomography (XFCT) imaging of gold nanoparticle-loaded objects: a Monte Carlo study. Phys Med Biol. 2011;56:3719–3730. doi: 10.1088/0031-9155/56/12/017. [DOI] [PubMed] [Google Scholar]
  20. Jones BL, Krishnan S, Cho SH. Estimation of microscopic dose enhancement factor around gold nanoparticles by Monte Carlo calculations. Med Phys. 2010;37:3809–3816. doi: 10.1118/1.3455703. [DOI] [PubMed] [Google Scholar]
  21. Krishnan S, Diagaradjane P, Cho SH. Nanoparticle-mediated thermal therapy: Evolving strategies for prostate cancer therapy. International Journal of Hyperthermia. 2010:1–15. doi: 10.3109/02656736.2010.485593. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. La Rivière P. Approximate analytic reconstruction in x-ray fluorescence computed tomography. Physics in Medicine and Biology. 2004;49:2391. doi: 10.1088/0031-9155/49/11/019. [DOI] [PubMed] [Google Scholar]
  23. La Riviere PJ, Vargas P, Fu G, Meng LJ. Accelerating X-ray fluorescence computed tomography. Conf. Proc. IEEE Eng. Med. Biol. Soc. 2009:1000–1003. doi: 10.1109/IEMBS.2009.5333568. [DOI] [PubMed] [Google Scholar]
  24. La Riviere PJ, Vargas P, Newville M, Sutton SR. Reduced-Scan Schemes for X-Ray Fluorescence Computed Tomography. Nuclear Science, IEEE Transactions on. 2007;54:1535–1542. [Google Scholar]
  25. Lange K, Carson R. Em Reconstruction Algorithms for Emission and Transmission Tomography. Journal Of Computer Assisted Tomography. 1984;8:306–316. [PubMed] [Google Scholar]
  26. Li J, Chaudhary A, Chmura SJ, Pelizzari C, Rajh T, Wietholt C, Kurtoglu M and Aydogan B. A novel functional CT contrast agent for molecular imaging of cancer. Physics in Medicine and Biology. 2010;55:4389–4397. doi: 10.1088/0031-9155/55/15/013. [DOI] [PubMed] [Google Scholar]
  27. Obenaus A, Smith A. Radiation dose in rodent tissues during micro-CT imaging. Journal of X-Ray Science and Technology. 2004;12:241–249. [Google Scholar]
  28. Qian X, Peng XH, Ansari DO, Yin-Goen Q, Chen GZ, Shin DM, Yang L, Young AN, Wang MD, Nie S. In vivo tumor targeting and spectroscopic detection with surface-enhanced Raman nanoparticle tags. Nat Biotechnol. 2008;26:83–90. doi: 10.1038/nbt1377. [DOI] [PubMed] [Google Scholar]
  29. Schlomka JP, Roessl E, Dorscheid R, Dill S, Martens G, Istel T, Bäumer C, Herrmann C, Steadman R, Zeitler G. Experimental feasibility of multi-energy photon-counting K-edge imaging in pre-clinical computed tomography. Physics in Medicine and Biology. 2008;53:4031. doi: 10.1088/0031-9155/53/15/002. [DOI] [PubMed] [Google Scholar]
  30. Schroer C. Reconstructing x-ray fluorescence microtomograms. Applied Physics Letters. 2001;79:1912–1914. [Google Scholar]
  31. Shepp L, Vardi Y. Maximum likelihood reconstruction for emission tomography. IEEE Transactions on Medical Imaging. 2007;1:113–122. doi: 10.1109/TMI.1982.4307558. [DOI] [PubMed] [Google Scholar]
  32. Simionovici A, Chukalina M, Schroer C, Drakopoulos M, Snigirev A, Snigireva I, Lengeler B, Janssens K, Adams F. High-resolution X-ray fluorescence microtomography of homogeneous samples. Nuclear Science, IEEE Transactions on. 2000;47:2736–2740. [Google Scholar]
  33. Sokolov K, Follen M, Aaron J, Pavlova I, Malpica A, Lotan R, Richards-Kortum R. Real-time vital optical imaging of precancer using anti-epidermal growth factor receptor antibodies conjugated to gold nanoparticles. Cancer research. 2003;63:1999. [PubMed] [Google Scholar]
  34. von Busch H, Harding G, Martens G, Schlomka JP, Schweizer B. Investigation of externally activated x-ray fluorescence tomography for use in medical diagnostics. Medical Imaging 2005: Physics of Medical Imaging. 2005;5745:90–101. [Google Scholar]
  35. von Maltzahn G, Park J, Agrawal A, Bandaru N, Das S, Sailor M, Bhatia S. Computationally guided photothermal tumor therapy using long-circulating gold nanorod antennas. Cancer research. 2009;69:3892. doi: 10.1158/0008-5472.CAN-08-4242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Yuasa T, Akiba M, Takeda T, Kazama M, Hoshino A, Watanabe Y, Hyodo K, Dilmanian FA, Akatsuka T, Itai Y. Reconstruction method for fluorescent X-ray computed tomography by least-squares method using singular value decomposition. Nuclear Science, IEEE Transactions on. 1997;44:54–62. [Google Scholar]

RESOURCES