Local variation of fragility and glass transition temperature of ultra-thin supported polymer films

Abstract

Despite extensive efforts, a definitive picture of the glass transition of ultra-thin polymer films has yet to emerge. The effect of film thickness h on the glass transition temperature T_g has been widely examined, but this characterization does not account for the fragility of glass-formation, which quantifies how rapidly relaxation times vary with temperature T. Accordingly, we simulate supported polymer films of a bead-spring model and determine both T_g and fragility, both as a function of h and film depth. We contrast changes in the relaxation dynamics with density ρ and demonstrate the limitations of the commonly invoked free-volume layer model. As opposed to bulk polymer materials, we find that the fragility and T_g do not generally vary proportionately. Consequently, the determination of the fragility profile—both locally and for the film as a whole—is essential for the characterization of changes in film dynamics with confinement.

INTRODUCTION

Ultra-thin polymer films have ubiquitous technological applications, ranging from the electronic devices to artificial tissues. There has been extensive experimental^{1, 2, 3, 4, 5, 6, 7, 8, 9} and computational^{10, 11, 12, 13, 14, 15} studies of polymer films aimed at trying to understand the large property changes that are frequently observed under nanoconfinement in relation to bulk materials. Changes in mechanical properties and the dynamical properties of amorphous polymer films have particular importance for applications, and much of the effort in characterizing thin polymer films has centered on measurements related to the stiffness of these films^{16, 17} and changes of molecular mobility as quantified by the glass-transition temperature T_g.^{6, 18}

From prior studies on the effects of confinement on polymer dynamics and T_g in ultra-thin films (<100 nm), it is appreciated that attractive interfacial interactions typically slow polymer dynamics near the surface and increase T_g.^{2, 4, 5, 6, 7, 8, 10, 12, 15, 19, 20, 21} However, simulations of a smooth attractive substrate show that mobility near the surface can be enhanced,^{3, 5, 8, 10, 22} demonstrating that surface roughness also affects interfacial mobility change significantly. Neutral or repulsive interfacial interactions—such as near a free surface—consistently lead to enhanced polymer dynamics¹⁴ and normally decrease T_g. For supported films with a free surface,^{2, 5, 14, 15, 19, 20, 21, 23} these effects can compete, resulting in T_g changes (or a lack thereof) that can be difficult to rationalize without a molecular scale understanding of the local dynamical changes within the film. Various probe methods have been used to infer the variability of the mobility within the film by reporting T_g near the surface,^{1, 2, 3, 5, 23, 24} or as function of distance z from the film boundaries.⁸ Many phenomenological trends are clear from this wealth of data, but the understanding of the changes in the glass transition with confinement remains qualitative.

The molecular picture often invoked to explain T_g changes in thin films envisions that the film can be split up into the contributions of independent polymer “layers,” so that the effect of film thickness is understood as a consequence of perturbing the polymer layers near the film interfaces. Free volume ideas have been very influential in this thinking.^{6, 25, 26} In this scenario, one imagines that, when the attractive boundary interactions of the substrate are large, the density is increased there (and thus free volume is reduced) leading to sluggish interfacial dynamics. In contrast, the relatively diffuse nature of the polymer-air interface (increased free volume) is expected to lead to a relatively high molecular mobility, reflected in reduced values of the local T_g. Away from these perturbing interfaces within the film, the dynamics are presumed to be bulk-like. From this perspective, the change in dynamics is “local,” reflecting changes in density within the film, so that changes in the film dynamics can be engineered through control of boundary interaction and geometry.

A significant drawback to characterizing dynamical changes by a local T_g in the layer picture is that it does not account for possible variations in the T dependence of dynamics—commonly referred to as the fragility of glass formation. Changes in the fragility of glass formation can significantly alter the properties of the film both above and below T_g. Consequently, T_g alone provides a limited metric to describe confinement and surface induced changes the dynamics in polymer films.

Seeking a more complete description of glass formation and a clearer understanding of how confinement perturbs the film dynamics, we use molecular dynamics computer simulations of supported polymer films to systematically characterize the effects on T_g and fragility, both for the entire film and locally; we find that there is a substantial and non-monotonic variation of T_g, both for the film as a whole, as well as locally; T_g alone evidently provides an incomplete picture of the effects of film confinement. We further examine to what degree a free-volume layer (FVL) picture can be applied. Partitioning the film into layers using the local density or relaxation time also yields qualitatively inconsistent definitions of the free-surface layer scale, indicating the limitations of a free-volume based layer model. Moreover, the dynamics of the middle layer can differ dramatically from the bulk, even though the density is bulk-like. We conclude that there are clearly non-local effects of confinement on dynamics, so the film cannot be treated as a slice of the bulk with only local surface effects. Evidently, the FVL model must be modified to incorporate both fragility variations and non-local changes to the film relaxation dynamics.

MODELING AND SIMULATIONS

The films we model consist of dense, unentangled polymer on a smooth, impenetrable attractive surface, and a free surface (corresponding to zero external pressure). We also simulate a bulk polymer system for comparison purposes. Our results are based on equilibrium molecular dynamics simulations of a well-studied bead-spring model,²⁷ which models polymers as chains of monomers. The model has been extensively studied in the literature, so we briefly summarize the salient features. All monomers interact via the Lennard-Jones (LJ) potential V_LJ, and bonded monomers along a chain are connected via a finite extensible nonlinear elastic (FENE) spring potential with spring constant k = 30ε/σ² and maximum extension R₀ = 1.5σ, as commonly chosen in the literature;²⁷ ε is the LJ energy parameter and σ is the diameter of the monomer. LJ interactions are truncated and shifted at a cutoff distance r_c = 2.5σ as described in Ref. 28. This value of r_c includes attractive interactions, which are necessary for film stability.

The interactions of monomer with the substrate is given by

$$V_{\mathrm{wall}}=\epsilon \left[\frac{2}{15}{\left(\frac{\sigma }{z}\right)}^9-{\left(\frac{\sigma }{z}\right)}^3\right],$$ (1)

where z is the distance of a monomer from the wall. This potential is also force-shifted like the LJ potential with the same cutoff distance. A similar model has been extensively studied by Baschnagel and co-workers.^{14, 22} The potential arises from an analytical approximation to a semi-infinite slab of LJ particles of uniform density, yielding the non-intuitive factor of prefactor of 2/15²⁹ on the repulsive r⁻⁹ term.

To address the effect of varying the scale of confinement, we simulate systems with N_c = 150, 200, 300, 600, or 1200 chains of M = 10 monomers each (for a total of N = N_c × M monomers). These sizes correspond to thicknesses in the range from approximately 4 to 32 monomer diameters, using a lateral system size L_x = L_y = 20σ ≈ 14R_g, where R_g is the chain's radius of gyration R_g. We use periodic boundary conditions in the lateral directions. We simulate a bulk polymer melt at zero pressure with 400 chains of M = 10 monomers each for comparison purposes. All results are reported in reduced units, with length in units of σ, temperature in units of ε/k_B (k_B is Boltzmann's constant), and time in unit of $\sqrt{m{\sigma }^2/\epsilon }$. In physical units relevant to real polymer materials, the size of a chain segment σ is typically about 1–2 nm, and ε ≈ 1 kJ/mol for a polymer (like polystyrene) with T_g ≈ 100 °C.

THICKNESS DEPENDENCE OF T_g AND FRAGILITY

We first quantify the overall changes to glass formation with changing film thickness to establish the basic parameters in question. To characterize the dynamics of films, we evaluate the relaxation time τ of the film in equilibrium as a function of temperature T approaching T_g from above. We quantify structural relaxation using the coherent intermediate scattering function

$$F(q,t)\equiv \frac{1}{NS\left(q\right)}⟨\sum _{j,k=1}^N{e}^{-iq.[r_k\left(t\right)-r_j\left(0\right)]}⟩,$$ (2)

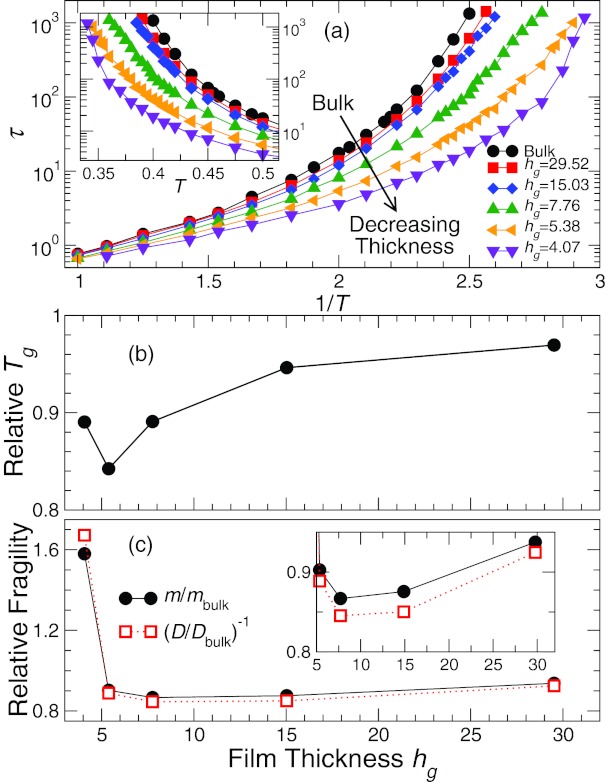
where r_j is the position of monomer j and S(q) is the static structure factor. We define the characteristic time τ by F(q₀, τ) = 0.2, where q₀ = 7.0 is the location of the first peak of S(q). To evaluate F(q₀, τ), we use q-vectors in all three directions, except as explicitly noted when we evaluate relaxation parallel and perpendicular to the plane of the film. Relative to the pure system, we find that τ decreases as we decrease the thickness of the film (Fig. 1a). Significantly, the data for τ show that τ increases more rapidly on cooling for the thinnest film. Thus, both the shift and the T dependence of τ must play a significant role in T_g changes.

Figure 1.

Effect of film thickness on the glass transition temperature and fragility. (a) The temperature dependence of relaxation time τ(h, T) from the intermediate scattering function F(q₀, t). In this T range, τ decreases as we decrease the thickness of the film. The inset shows a magnification of the behavior of τ at low T. (b) Glass transition temperature T_g and (c) fragility m relative to the pure melt as a function of the thickness h_g ≡ h(T_g); the determination of h_g is explained when we present the film density profile. We find a depression of T_g and fragility up to a critical thickness, where the behavior is reversed. The inset of (c) shows a magnification of the data at large h_g.

To estimate changes of T_g and fragility, we fit τ with the Vogel-Fulcher-Tamman form,

$$\tau \left(T\right)={\tau }_0{e}^{D{T}_0/(T-T_0)}.$$ (3)

In a lab setting, T_g is often defined by the T at which τ reaches 100 s and we adopt this simple criterion here. To do so, we extrapolate our fit to Eq. 3 to obtain T_g, assuming a simulation time unit ≈1 ps (units are discussed in Sec. 2). Figure 1b shows that T_g decreases relative to the bulk for all systems. However, T_g varies non-monotonically with film thickness: T_g initially decreases for smaller confinement, but then grows for the thinnest film suggesting that competing effects of the solid and free interface are at play in our supported films.²⁰

We also calculate the fragility, which describes how rapidly τ changes with temperature near T_g, by the “steepness” index

$$m\left(T_g\right)={\left.\frac{\partial \ln \tau }{\partial (T/T_g)}\right|}_{T_g}.$$ (4)

We evaluate m based on the same fit (Eq. 3) used to determine T_g. Figure 1c shows similar non-monotonic behavior of m (relative to the bulk). As a consistency check, we also consider an alternate definition of fragility k = D⁻¹, which shows the same trend. As in the case of a free standing film having fixed thickness,^{10, 13, 22}T_g and fragility of our supported films decrease relative to the pure melt. The fragility reduction in our supported film is relatively modest in comparison to previous simulations of free-standing polymer films.¹³ Our results for T_g and m are qualitatively in agreement with experimental fragility changes in polystyrene films.³

The trends of fragility and T_g for our supported films are similar, which is not surprising since experimentally m is often found to be proportional to T_g for polymers.³⁰ Consequently, the reduction of T_g can be primarily associated with a reduction of fragility. However, from Figs. 1b, 1c it is apparent that the ratio T_g/m as a function of film thickness h_g is not constant for the thinnest films, so the quantitative correspondence between T_g and m is not as clean as in pure polymers³⁰ or polymer nanocomposites.³¹ Consequently, T_g alone is not sufficient to capture dynamical changes in thin films due to confinement; since fragility governs the rate of change of relaxation with T and can vary independently of T_g, it must also be specified.

TESTING THE FREE VOLUME LAYER PICTURE

We next consider to what degree the FVL description can explain the observed changes in overall T_g and fragility. To quantify the interfacial layers, we must evaluate both density and relaxation time as a function of distance z from the substrate boundary. We first examine density profile ρ(z) (Fig. 2a). Near the solid substrate (z = 0), we see strong density oscillations induced by the planar wall and a relatively more narrow and diffuse interface near the polymer free surface, just as anticipated by the layer model. We precisely define the film thickness h(T) from this density profile. Specifically, for each T, we fit ρ(z) near the polymer free surface to ρ(z) = ρ₀tanh [(z − h)/l], where h defines film thickness and l defines the interfacial region width.³² The resulting h(T) (Fig. 3) is well described by an Arrhenius form

$$h\left(T\right)-h_0=\Delta e^{-E/T}.$$ (5)

We extrapolate the Arrhenius fit h(T) to T_g (where T_g is determined from the dynamics in Sec. 3) to estimate the film thickness at the glass transition, h_g ≡ h(T_g). Upon cooling, the film thickness decreases, the overall density increases, the amplitude and the range of ρ oscillations near the solid substrate increase, and the polymer free-surface interface becomes progressively sharper. Based on the FVL model, ρ(z) suggests slow dynamics near the substrate, accelerated dynamics at the free surface, and a similar scale for the range of density and dynamical changes.

Figure 2.

Spatial dependence of the density and relaxation of films. (a) Representative monomer density profile of ρ(z) for a supported film on an attractive surface for a range of T for film thickness h_g = 15.03, corresponding to about 30 nm in physical polymer units. It is apparent from ρ(z, T) that the thickness of the film decreases on cooling. The inset shows the density profile of monomers for various thicknesses scaled by the bulk value. We see that the peaks are independent of film thickness and that there is a bulk-like region far from the interfaces. (b) Relaxation time τ_s as function of distance z from the wall for various T for h_g = 15.03. τ_s(z) is altered from the bulk, even near the center of the film where the density is the same as the bulk. The deviation of τ_s from the bulk becomes more significant at low temperature.

Figure 3.

Temperature dependence of film thickness. Thickness h is plotted relative to its low temperature limit h₀, which demonstrates an approximate Arrhenius behavior. We use this Arrhenius behavior to estimate h(T_g). Note that the color representation corresponds to that used for film thicknesses in Fig. 1a.

We check these expectations by examining the spatial dependence of relaxation. To quantify dynamics locally, we use the self (or incoherent) F_self(z, q, t) part (i.e., j = k) of Eq. 2 on the basis of the position z of a monomer at t = 0, and define the local relaxation time τ_s(z) in the same way as τ. We discretize the z coordinate in fixed intervals δz = 0.875 for all temperatures based on the width of oscillations in the density profile. Smaller or larger values of δz do not qualitatively affect our findings. Consistent with the overall decrease of τ shown in Fig. 1a, Fig. 2b shows that τ_s(z) decreases near both interfaces (as also found in Ref. 14).

Our results show that τ_s decreases approaching the substrate, even though the surface is attractive, and density increases locally. This change is inconsistent with the free volume picture. In comparison with the range of the density variations, it is apparent that the scale of substrate effects on dynamics is similar, but that the scale of effects near the free surface is much greater for the dynamics than for the density. Additionally, while the middle region of the film has a density comparable to that of the bulk, τ_s near the middle of the film deviates substantially from the bulk values as T decreases. These qualitative differences are also not consistent with the free-volume layer picture.

We next quantify the scales of the substrate, free, and middle layers based on ρ(z) and τ_s(z). To evaluate the layer size, we identify the positions where τ_s(z) and ρ(z) deviate from the near constant behavior in the middle of the film (see Fig. 2). Specifically, we define the scale ξ as the length where ρ(z) or τ_s(z) deviates by 15% from the mean value of the central region of the film. This fraction is chosen to minimize artifacts from noise in our data, and other reasonable choices do not affect our qualitative findings. Note that, for thin films, there may be no middle layer—especially for τ_s(z) at low T. In this case, we define ξ from the extremum separates substrate and free surface layers. In this latter case, ξ is dominated by the overall film thickness. Figure 4 compares the dynamical length scales ξ_τ and density length scale ξ_ρ for two representative film thicknesses, demonstrating that for the substrate ξ_τ ≈ ξ_ρ. Growth of ξ_τ and ξ_ρ upon cooling have been observed in other interfacial studies.^{22, 32} In stark contrast, ξ_τ and ξ_ρ for the free surface deviate substantially. Specifically, the sharpening of the free surface means that ξ_ρ of the free surface shrinks on cooling, while ξ_τ of the free surface grows on cooling, and this scale is qualitatively comparable to ξ_τ of the substrate. In other words, the dynamical length scales of both interfaces are comparable, while the density length scales are not. The difference between ξ_τ and ξ_ρ for the free surface also requires that the scales of the middle layer differ for density and dynamics. These quantitative differences between ξ_τ and ξ_ρ further demonstrate deviation from the simplistic free-volume layer picture. We note that the relaxation time gradients near the polymer substrate and polymer-air interfaces are qualitatively consistent with the gradients in the structural relaxation rate in thin poly-methyl methacrylate films.⁸

Figure 4.

Scale of the surface layers from relaxation and density. (a) Dynamical length scale ξ_τ of substrate and free surfaces function of T with two thicknesses. The dynamical length scales at both interfaces grow upon cooling, but ξ_τ of substrate is constrained when its value ≈h_g/2. (b) Length scale from density of substrate and free surface as function of T. We see that the length scale of the substrate grows, while the length scale of the free surface shrinks upon cooling.

Confinement effects become particularly pronounced on cooling, when the film thickness becomes comparable to that of the surface layer scales. For example, for h_g = 7.76, we see that the maximum value of ξ_τ is constrained to ≈h/2 on cooling. Consequently, for T where ξ_τ is constrained by film thickness, the behavior of the film can become radically different from the thicker films. This provides an insight into why T_g and m have non-monotonic dependence on thickness. We are presently examining if there may be a relationship between ξ_τ to the scale of collective motion as function of z, a quantity closely connected to fragility.³¹

Before continuing, we consider the fact that ξ_ρ provides a measure of the depth to which the film structure is perturbed by the supporting surface, but does not measure if the density is actually different at that depth. This is potentially important in a free-volume analysis, since the average density could possibly reflect the observed changes of τ_s(z). To address this point, we evaluate ρ(z), but discretize in bins δz equal to the monomer size (similar to the size used for τ_s(z). Figure 5 shows that (for a representative thickness) this more broadly averaged measure of density is nearly constant up to the substrate interface, and only weakly dependent on T. This observation raises two points in the context of our free-volume discussion: (i) the average density increases weakly near the substrate at low T, which is opposite to the changes of τ approaching the substrate, and (ii) the scale of deviation of the average density is nearly T-independent, and does not match the length scale of relaxation deviations. Thus, regardless of whether we examine density oscillations or the more broadly averaged local density, we do not find agreement with the expectations from free-volume theory.

Figure 5.

Spatial dependence of the density ρ(z) of the film averaged over intervals δz equal to the monomer size to eliminate the oscillatory behavior shown in Fig. 2a. Data are shown for a representative film thickness h_g = 15.03.

LOCAL VARIATION OF T_g AND FRAGILITY

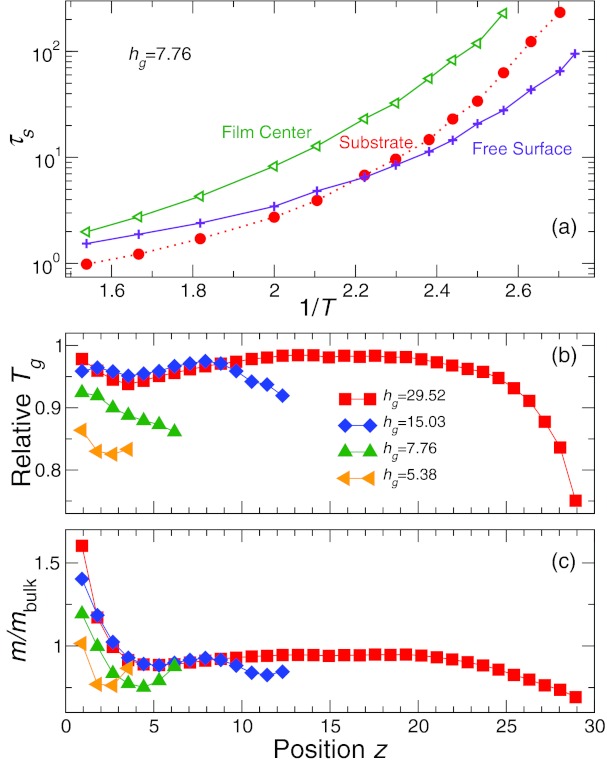
To more clearly explain the non-monotonic behavior dependence of T_g and m with film thickness, we consider the dependence of T_g and m as function z, based on the T-dependence of τ_s(z). The spatial variation of fragility is qualitatively apparent from Fig. 6a, which shows τ_s(z) for a representative h in three regions: (i) middle of the film, (ii) near the substrate, and (iii) near the free surface. The crossover behavior τ_s for the substrate and free surfaces requires a variation of local fragility. To extract T_g(z) and m(z), we fit τ_s(z, T) using Eq. 3, just as we did before for τ of the entire film; Figs. 6b, 6c show the resulting T_g(z) and m(z), respectively.

Figure 6.

The effect of film thickness on the local variation of T_g and fragility. (a) T dependence of the relaxation time τ_s for representative distances from the surface for h_g = 7.76. We observe that there is a rapid increase of τ_s near the attractive surface, consistent with an increase of fragility at the attractive surface. (b) T_g and (c) fragility as a function of distance z from the wall. The region closest to the attractive wall has a locally increased T_g, resulting from an increasing fragility near the wall. Hence, the high fragility near the supporting surface has a large effect on the overall film dynamics.

For relatively thick films, where the dynamical scale ξ_τ is not affected by film thickness, T_g and m near the film center are relatively weakly affected by confinement. At the free surface, τ is reduced compared to the center, and varies more slowly with T. Correspondingly, near the free surface T_g and m are reduced. Near the substrate, there is a seemingly paradoxical finding that τ_s near the substrate decreases relative to the film center, while T_g near the substrate increases. This is a direct consequence of the strongly increased fragility m near the substrate—apparent from the inversion of τ_s for the substrate relative to the free surface. That monomers near the attractive substrate have a lower T_g (relative to the bulk), but higher T_g relative to the film center, is consistent with the experimental observations on polystyrene films,⁵ providing an example of a situation where fragility and T_g can be anti-correlated—again emphasizing the importance of both quantities. This anti-correlation between T_g and m is predicted by the entropy theory of glass formation³³ when the cohesive interaction strength is varied, and the present substrate interaction should have such an effect.

Figurer 6c shows that the spatial variation of the fragility m(z) is similar to that of T_g(z), except that m(z) increases more rapidly near the substrate. If fragility were constant, the enhanced surface relaxation should only yield a decrease of T_g so we would not observe non-monotonic behavior of T_g(z). Thus, non-monotonic behavior of T_g(z) is dependent on similar non-monotonic behavior of fragility m(z). These affects are reflected in the overall thickness dependence of T_g. This emphasizes the practical importance of quantifying m variations, in addition to T_g. We also see that the fragility at the free interface drops by a factor of nearly 2 so that the dynamics of the free surface progressively approaches Arrhenius behavior, an effect noted in recent experimental studies.³⁴ This effect can be expected to lead an acceleration of the aging dynamics of thin polymer films and will also contribute largely to the overall film dynamics. Our findings for the thickness dependence of T_g at the interfaces (Fig. 6b) also qualitatively accord with the experiments of Ref. 5, where they found that the free surface T_g rose and subsequently dropped on decreasing film thickness.

The variation of T_g and m with z shown in Figs. 6b, 6c raises further questions about the quantitative validity of the FVL model. In the simplest form of this model, one would expect spatial variation to be independent of film thickness. However, for the thickness ⩽8, the interfacial effects dominate so that T_g(z) and m(z) are strongly dependent on film thickness. Additionally, an independent layer model only considers T_g to change in the density perturbed boundary regions of the film and does not account for the spatial variation of T_g(z) and m(z) away from the boundaries. In further contrast to the FVL model, the large drop in the apparent T_g near the polymer free-surface in Fig. 6b is not matched by a corresponding change in m. This means that the drop in T_g does not have the same physical consequences as in a bulk material, where m and T_g change in a proportional way.³⁰ Finally, the scales of the changes in T_g do not match the scales of changes in the density. A free volume interpretation of mobility changes is thus not well founded when one tries to apply this picture locally.³⁵

ANISOTROPY OF CHAIN CONFORMATION AND RELAXATION

Another common question is how the length scale of interfacial affect relates to the chain size. We examine the effect of confinement on the chain conformation by evaluating the mean square radius of gyration $⟨R_g^2⟩$, and its components perpendicular $⟨R_{g\perp }^2⟩$, and parallel $⟨R_{g\parallel }^2⟩$ to the surface; Fig. 7a shows that $⟨R_g^2⟩$ only slightly deviates from the bulk at the attractive surface. Near the interfaces, $⟨R_{g\parallel }^2⟩$ increases and $⟨R_{g\perp }^2⟩$ decreases. Thus, the polymers orient somewhat very near interfaces, an effect noted previously.^{28, 36, 37} These effects are only very weakly dependent on T. Combining ρ(z) and R_g, for thicker films (N_c ⩾ 600), we see that there is a substantial region of bulk-like density and chain conformation, even at the lowest T studied. Clearly, the chain radius of gyration is remarkably insensitive to confinement and we can then expect that polymer film to have little dependence on polymer mass (R_g), apart from the low molecular mass oligomeric regime where T_g and fragility are both strongly dependent on chain mass. Thus, finite size effects on T_g and fragility are primarily controlled by the relative size of the chain statistical segments σ (beads in our model) in comparison to film thickness.

Figure 7.

Chain conformation and anisotropy of relaxation. (a) Radius of gyration R_g of the polymer chains relative to the bulk as a function of position z of the center mass of the chain at T = 0.4 and thickness h_g = 15.03. We also resolve the perpendicular and parallel components to the surface, which we label by R_g⊥ and R_g∥. (b) Relaxation times in the perpendicular τ_⊥ and parallel τ_∥ directions at T = 0.6 and thickness h_g = 15.03. Near the substrate, we find that τ_⊥ is much larger than τ_∥.

Since it is widely appreciated that attractive surfaces typically slow the polymer dynamics near the surface, it may be initially surprising that Fig. 2b shows that the dynamics near the attractive substrate are actually enhanced. The same effect has been observed by Baschnagel and co-workers.¹⁴ We can understand this counter-intuitive result by resolving τ_s in the perpendicular and parallel directions (τ_⊥, τ_∥). Figure 7b shows that, near the substrate, relaxation parallel to the interface is enhanced relative to the film center (τ_∥ smaller), but relaxation perpendicular to the substrate is slowed (τ_⊥ larger). This implies a physical situation in which monomers are able to “slide” along the substrate due to its smoothness, but monomers are slowed down in the perpendicular direction because of the attractive interaction. For an attractive rough substrate,^{11, 12, 32} τ_s is slowed in both parallel and perpendicular directions so that substrate surface roughness is an important variable for the dynamic changes. In contrast, at the free surface, monomers relax more rapidly (τ_⊥, τ_∥ smaller) both parallel and perpendicular to the surface.

CONCLUSION

Our comparative analysis of density and relaxation changes of supported polymer films indicates that, while the density changes expected from the FVL model certainly arise, these density changes do not lead to any simple mapping to the observed relaxation dynamics that we find in our simulations.

From an alternate theoretical perspective, the mode-coupling theory (MCT) has recently been used to predict the effects of confinement by two hard walls on the glass transition of a hard sphere fluid.³⁸ That work indicates a non-monotonic behavior of the non-ergodic packing fraction (analogous to T_g) for very thin films, but the origin of the non-monotonic behavior is rather different from what we observe. Specifically, in the case of two confining walls, the non-ergodic packing fraction has oscillatory (non-monotonic) thickness dependence for very thin films arising from packing frustration for non-integer wall spacings. In the case of our supported polymer films, there is no such packing frustration, since the films have a free surface that allow for expansion of the film. Consequently, we do not observe an oscillatory T_g. The non-monotonic behavior we see arises from the competition between enhanced surface relaxation and diminished relaxation as films become progressively thinner. Consequently, T_g initially decreases on confinement, and only increases for films that are extremely thin—similar to the scale on which effects are apparent in the MCT work (≈5 monomer spacings).

Evidently, non-local effects arising from confinement can significantly influence film dynamics, so that T_g and the fragility m vary in non-proportional ways for films of variable thickness, making knowledge of both critical for characterizing thin film dynamics. Given that the spatial variation of τ is difficult to access experimentally, the Debye-Waller factor, which has been shown to reflect changes in relaxation in the bulk,^{35, 39} may be a more effective measure than density for probing spatial variations of relaxation through the film.