Abstract
Purpose: Previous studies have shown that the mean absorbed dose to a tissue element may not be a suitable quantity for correlating with the biological response of cells in that tissue element. Cell survival can depend strongly on the distribution of radioactivity at the cellular and multicellular levels. Furthermore, when cellular absorbed doses are examined, the cross-dose from neighbor cells can be less radiotoxic than the self-dose component. To better understand how the nonuniformity of activity among cells can affect the dose response, a computer model of a 3D tissue culture was previously constructed and showed that activity distribution among cells is significantly more relevant than the mean absorbed dose for low-energy-electron emitters. The present work greatly expands upon those findings.
Methods: In the present study, we used this same computer model but restricted the number of labeled cells to a fraction of the whole cell population (50%, 10%, and 1%, respectively). The labeled cells were randomly distributed among the whole cell population.
Results: While the activity distribution is an important factor in determining the tissue response for low-energy-electron emitters, the fraction of labeled cells has an even more pronounced effect on survival response. For all electron energies studied, reducing the percentage of cells labeled significantly increases the surviving fraction of the whole population.
Conclusions: This study provides abundant information on killing tumor and normal cells under some conditions relevant to targeted radionuclide therapy of isolated tumor cells and micrometastases. The percentage of cells labeled, activity distribution among the labeled cells, and electron energy play key roles in determining their response. Most importantly, and not previously demonstrated, lognormal activity distributions can have a profound impact on the response of the tumor cells even when the radionuclide emits high-energy electrons.
Keywords: multicellular dosimetry, Monte Carlo, nonuniform activity, cell culture, survival curve, ionizing radiation, electrons, isolated tumor cells (ITC), micrometastasis
INTRODUCTION
Considerable progress has been made in correlating biological outcome with many of the variables that dictate the overall biological response of tissues that contain radioactivity.1 Among these variables are radiosensitivity of the tissue, distribution of radioactivity at the macroscopic,2, 3 multicellular,4, 5, 6, 7, 8 cellular, and subcellular levels,5, 9 relative biological effectiveness (RBE) of the radiations emitted (e.g., alpha, beta, Auger electrons),10 kinetics of uptake and clearance of the radionuclide, dose rate,11 repair mechanisms, and bystander effect.12, 13, 14, 15 However, recent studies show that there remains much to be learned about correlation of biological effects with nonuniform dose distributions that result from nonuniform distribution of radioactivity at the cellular and subcellular levels.8, 16, 17, 18, 19, 20 Even when the distribution of labeled cells appears to be uniform at the macroscopic level but is nonuniform at the multicellular level, the mean absorbed dose to a tissue element may not be a suitable predictor of biological effect.18, 19
In previous work, paired theoretical and experimental multicellular dose-response models were created to improve our understanding of, and modeling capabilities for, nonuniform distributions of radioactivity.8, 21, 22 Three-dimensional (3D) models of cell clusters have been developed for experimental as well as theoretical studies.8, 22 More recently, considerable effort has been devoted towards developing a 3D tissue culture model that more closely simulates human tissue in vivo. This 3D tissue culture model uses human cells grown in a Cytomatrix™ carbon scaffold and has been used to examine the impact of nonuniform distributions of radioactivity in both tumor and normal human tissues.23, 24, 25 The Cytomatrix™ model resembles naturally occurring cell growth. Taken together, the properties of the Cytomatrix™ scaffold make it suitable for verifying multicellular dose-response models.
There are several parameters that can determine the dose received by each individual cell in a cluster and its corresponding response. First, the cross-dose (resulting from radioactive decays in neighboring cells) is largely dependent on the geometrical location of the cell relative to its neighbors.26, 27 For instance, in cancellous bone, the presence of bone trabeculae acts as a shield for all cells sitting next to a bone surface. Second, the self-dose (resulting from radioactive decays that occur in the target cell itself) depends on the activity within that cell. It is typical for a given cell in a tissue to have more or less activity than the mean value across the tissue element. It was previously shown that the distribution of activity among the cells of a tissue is not uniform and often follows a lognormal distribution.1, 20 Third, self- and cross-doses can have different values of RBE both for beta-particle emitters19 and Auger electron emitters.28, 29, 30 Furthermore, the RBE can depend on the percentage of intracellular activity that is incorporated into the DNA in the cell nucleus.29 This does not, however, appear to be true for alpha-particle emitters.31
In order to better understand the contribution of a multitude of parameters on the dose response, our research groups recently developed a computer model that simulated the 3D tissue culture model.32 The computer model combines a micro-computed tomography (μCT) image of a Cytomatrix™ carbon scaffold with a 6-μm voxel size and a cluster of 106 cell nuclei randomly positioned throughout the pores of the carbon matrix. Coupling a Monte Carlo transport code to the computer model allows one to record both the self- and the cross-dose for each cell. The self- and cross-doses are then used to determine the surviving fraction of the 106 cell assembly.32 Survival curves are constructed by gradually increasing the number of decays per simulation. In the previous work, monoenergetic electron sources were considered and it was assumed that all the cells were labeled (100% labeled). The dependence of the survival curves on (1) the electron energy and (2) the distribution of radioactivity among the cells (i.e., uniform or lognormal distribution) was studied.32 This earlier study showed that the surviving fraction depends strongly on both electron energy and activity distribution. Still, the study did not explore how the response depended on the percentage of cells that were labeled. Accordingly, a limited study was subsequently undertaken to assess whether the combination of lognormal distribution and percentage of cells labeled had a substantial impact on the response of cells labeled with a hypothetical 100-keV monoenergetic electron emitter.33 Changes in the response were observed, thereby warranting a more in-depth exploration of the interdependence of electron energy, activity distribution, and cell labeling percentage on determining the dose-response of three-dimensional cell populations. Accordingly, our aforementioned computer model32 was used to answer the following questions. First, are the dose-response trends seen when all cells are labeled also seen when only a fraction of the cell population is labeled? This situation can occur when only a fraction of the targeted population is labeled or, perhaps more importantly, it also can occur when the targeted population of cells lies in the midst of a non-targeted population of normal cells. Second, how does electron energy affect the dose-responses of these two cell populations as the relative fractions of each cell population change? Third, and finally, how does the shape of the cellular activity distribution influence the dose-responses of the targeted and non-targeted cells? The studies described below shed considerable light on these previously unanswered questions over a broad range of electron energies (10–1000 keV).
MATERIALS AND METHODS
Theoretical model of the 3D Cytomatrix™ cell culture model
The same geometrical model reported earlier was used.32 Briefly, the model is composed of a μCT image of a Cytomatrix™ carbon scaffold within which a field of 106 cell nuclei is created. Cell nuclei are represented by 8-μm diameter spheres. The cytoplasm is not explicitly modeled; rather, nuclei are randomly positioned within the pores but are not allowed within 1 μm of the ligaments of the scaffold. Furthermore, the nuclei are separated from each other by at least 2 μm which corresponds to a minimum cytoplasm thickness of 1 μm. Because our personal computer cluster cannot support computations with 108 cells, modeling is limited to 106 nuclei in the central portion of the Cytomatrix and specifically within a cylinder with a diameter of 1.322 mm and height of 1.252 mm. This arrangement yields a cell packing density of 31% when the cell is assumed to be a sphere with diameter 10-μm (e.g., cytoplasm is a 1 μm thick shell around the 8-μm diameter nucleus).32 If the cytoplasms were assumed to occupy all space not occupied by the nuclei and ligaments, the packing density would be 100%. Regardless, the cellular cytoplasm was not explicitly modeled. The supplementary material (A)50 contains figures that depict this model.
In our earlier study, extensive dose-response simulations were conducted for a range of electron energies when 100% of the cells in the scaffold were labeled.32 A subsequent paper undertook a preliminary investigation to determine how dose-response to 100-keV electrons was affected by the percentage of cells labeled. In the present work, the modeling is extended to conditions wherein only 50%, 10%, or 1% of the cells were labeled. For each set, the labeled cells were assigned an activity based on four different activity distributions: uniform, lognormal with a shape parameter σ = 0.6, lognormal with σ = 1.0, and lognormal with σ = 2.0.32 The labeled cells were randomly distributed among the whole cell population.
Calculation of absorbed dose and surviving fraction
As in our earlier work, the surviving fraction calculation was a two-step process.32 The first step was assessment of the radiation absorbed dose to each of the cell nuclei based upon the EGSnrc Monte-Carlo radiation transport code.34 The same electron energies were considered here (i.e., 10, 30, 100, 300, and 1000 keV) and the energy depositions were recorded as self-deposition (energy deposited by an electron emitted from within the target cell itself) and cross-deposition (energy deposited by an electron emitted from a cell different than the target). The standard tissue compositions and transport parameters were kept the same as reported previously.32 The self-doses (Dself) and cross-doses (Dcross) to the cell nuclei were then calculated using the tallied self- and cross-depositions of energy. The absorbed doses were compartmentalized in this manner because of the differing radiotoxicities that have been observed for self- and cross-dose when radionuclides are incorporated into nuclear DNA.22
Once the self- and cross-dose were recorded for each individual cell, the second step was to compute the surviving fraction of cells. The probability that a given cell survives can be expressed as32, 33
| (1) |
where D37,self and D37,cross are the self- and cross-dose required to achieve 37% survival, respectively. For the current study, the parameters D37,cross and D37,self were assigned values of 4.0 Gy and 1.2 Gy, respectively. These values were experimentally determined for 131I-iododeoxyuridine incorporated into the DNA of V79 cells maintained in 3D clusters.22 Additional simulations were carried out with D37,cross = 4.0 Gy and D37,self = 4.0 Gy for comparison. This latter case would be more typical when radioactivity is distributed in the cytoplasm or on the cell surface. As described earlier,32 the surviving fraction of the cell population was determined as follows. For each cell, a survival probability was calculated by substituting its self- and cross-dose into Eq. 1. A random number between 0 and 1 was generated, compared with the survival probability, and the cell was scored as a survivor if the random number was smaller than the generated probability. Otherwise, it was scored as reproductively dead. This was repeated for each cell and the fraction of survivors among the population in question (i.e., labeled, unlabeled, or mixed) represents their surviving fraction.
Building theoretical survival curves
The calculation briefly described above, and detailed by Rajon et al.,32 provides the surviving fraction for a specific simulation and for a particular number of electron histories. In order to build a complete survival curve, it was necessary to execute the transport simulation several times, each time with an increasing number of electron histories to increase the absorbed dose. For each simulation, a mean dose to the cell nucleus was calculated and used to plot the surviving fraction. Note that an empirical technique was combined with the Monte-Carlo process to attain doses as high as 80 Gy. In this technique, only the low-dose portion of the curve was built directly with Monte-Carlo simulations. The high-dose portion of the curve was extrapolated from the last simulation that reached sufficient statistical power. The number of histories for the last simulation was determined by increasing histories until statistical fluctuations in the shape of the survival curve were negligible. About 1000 × 106, 300 × 106, 300 × 106, 100 × 106, and 100 × 106 histories are required for convergence of the survival curves for 10-, 30-, 100-, 300-, and 1000-keV electrons, respectively.32
RESULTS
In the present work, a total of 60 new simulations were performed that were composed of five electron energies, four activity distributions, and 50%, 10%, or 1% of the cell nuclei were labeled. The current results were combined with earlier results for 100% labeling32 to investigate the dependence of the survival curves on the percentage of labeled cells. Therefore, a total of 80 simulations are compared in this study. The resulting survival curves facilitate independent analysis of the behavior of the labeled and unlabeled cells and of the mixed population.
Dependence of labeled cell survival on labeled fraction for uniform distribution
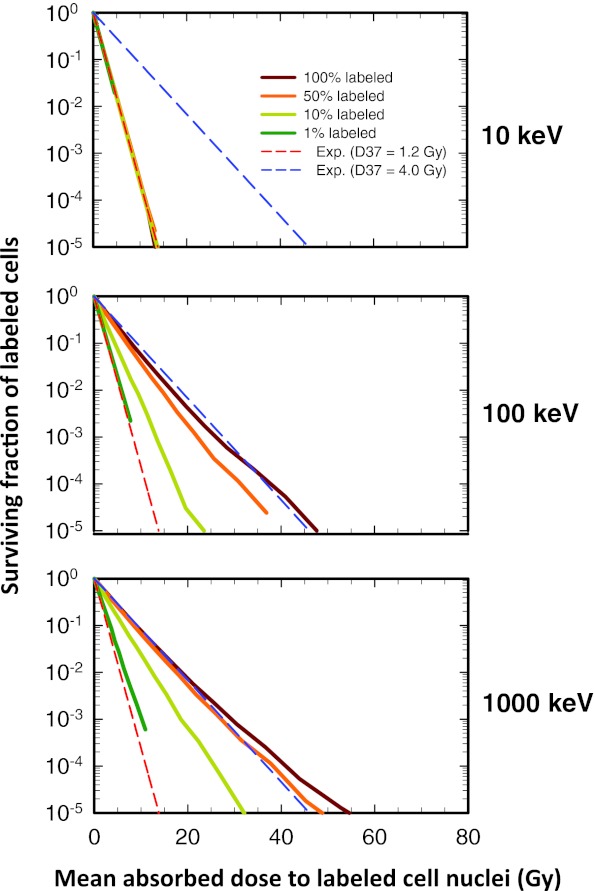
The labeled cells receive both self-dose from radiation emitted from within themselves and cross-dose from radiation emitted by their neighbors. Figure 1 shows the surviving fraction of labeled cells as a function of the mean absorbed dose (self-dose + cross-dose) to the labeled cell nuclei when the activity is uniformly distributed among the labeled cells. Note that the simulation is for 106 cells, hence, labeled cell surviving fractions smaller than 10−5 cannot be detected when 10% of the cells are labeled, and smaller than 10−4 when 1% of the cells are labeled. At these low surviving fractions, statistical uncertainties are an issue and no attempt was made to report results below these values or interpret results near these values. The survival curves in Fig. 1 are correspondingly truncated. The lack of smoothness in the latter portion of some curves is simply a sign of statistical uncertainty.
Figure 1.
Effect of electron energy and fraction of cells labeled on the shape of the survival curve for the labeled cell population when monoenergetic electron emitters are uniformly distributed among the labeled cells: (Top) 10 keV. (Middle) 100 keV. (Bottom) 1000 keV. The surviving fraction of labeled cells is plotted as a function of mean absorbed dose to the labeled cell nuclei when different fractions of the entire cell population are labeled: 100%, 50%, 10%, and 1%. The lower and upper dashed lines represent exponential survival curves with D37 = D37,self = 1.2 Gy and D37 = D37,cross = 4.0 Gy, respectively. At very low energies (10 keV), where the cross-dose to the nucleus is negligible, the curve expectantly follows that for D37 = D37,self = 1.2 Gy. Similarly, at high energies (1000 keV), where the cross-dose dominates, the curve expectantly follows that for D37 = D37,cross = 4.0 Gy. A complete set of curves including 10, 30, 100, 300, and 1000 keV is provided in Fig. 1 of the supplementary material (B) (Ref. 50). For the sake of comparison, the data for 100% labeling are reproduced from Rajon et al. (Ref. 32).
When the radioactivity emits 10-keV electrons (Fig. 1, top), the fraction of cells that are labeled has no effect on the surviving fraction of labeled cells. In this case, all survival curves are exponential with a D37,self = 1.2 Gy. The cross-dose is insignificant for 10-keV electrons because of their short range (2.5 μm in water). Accordingly, all cells respond solely according to the dose-response model for self-dose. As the electron energy increases (Fig. 1, middle and bottom), all curves shift towards the dose-response model for cross-dose (D37,cross = 4.0 Gy). However, for 100% labeling the shift is fully established by 100 keV, whereas for the 50%, 10%, and the 1% labeling the shift occurs progressively with electron energy. At high electron energies of 1000 keV, even though cross irradiation is substantial, the survival curve for labeled cells when 1% of the cells are labeled remains fairly close to the exponential at D37 = 1.2 Gy (Fig. 1, bottom). While the cross-dose is more uniformly distributed among the cells, the self-dose is only concentrated in that fraction of cells that are labeled. In summary, for uniform distribution of the radioactivity among a small fraction of cells (i.e., 1% labeling), the self-dose received by the labeled cells is the dominant factor in determining the response of the labeled cells at all electron energies—the role of cross dose is negligible.
Dependence of unlabeled cell survival on labeled fraction for uniform distribution
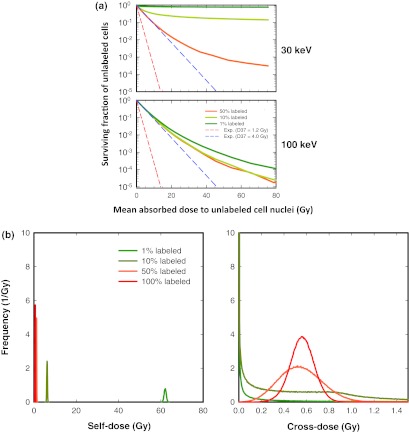
Unlabeled cells only receive cross-dose from their neighbors—by definition, they do not receive self-dose. Figure 2a shows the surviving fraction of unlabeled cells as a function of the mean cross-dose to the unlabeled cell nuclei when 30-keV and 100-keV monoenergetic electron emitters are uniformly distributed among the labeled cells. The data for 10-keV electrons are not shown here [Fig. 2 of the supplementary material (B)]50 because there is so little cross irradiation that the surviving fraction of unlabeled cells is 100% at all doses and all labeled fractions. In contrast, the labeled cells are efficiently killed (Fig. 1, top).
Figure 2.
(a). Effect of energy and fraction of cells labeled on the shape of the survival curve for the unlabeled cell population when monoenergetic electron emitters are uniformly distributed among the labeled cells. (Top) 30 keV. (Bottom) 100 keV. The surviving fraction of unlabeled cells is plotted as a function of mean absorbed dose to the unlabeled cell nuclei. The survival curves are shown for three different labeled fractions: 50%, 10%, and 1% (no unlabeled cells at 100%). The lower and upper dashed lines represent exponential survival curves with D37 = D37,self = 1.2 Gy and D37 = D37,cross = 4.0 Gy, respectively. A complete set of curves including 10, 30, 100, 300, and 1000 keV is provided in Fig. 2 of the supplementary material (B) (Ref. 50). (b) Frequency distribution of self- (Left) and cross-doses (Right) received by cells when a 30 keV monoenergetic electron emitter is distributed uniformly among 100%, 50%, 10%, or 1% of the cells. The Monte-Carlo simulation that generated this distribution transported 3 × 108 histories for a mean total dose of 1.17 Gy per cell.
The most interesting finding in Fig. 2a is that the unlabeled cell survival curves do not follow the theoretical exponential curves that correspond to a D37 = 4.0 Gy as one might expect from pure cross-dose. Apparently, the unlabeled cells do not all receive the same dose as the mean absorbed dose. Figure 2a clearly shows that, at 30 keV [Fig. 2a, top], some unlabeled cells (about 15% at 10%-labeled and 80% at 1%-labeled) receive sublethal doses and tend to survive even at high mean values of cross-dose. To understand that particular behavior, we constructed the self- and cross-dose distributions received by the cells during the Monte-Carlo simulations. Figure 2b shows these distributions for 30-keV electrons, uniform activity distribution, and for all labeling conditions (1%, 10%, 50%, and 100%). The mean self- and cross-doses per cell (i.e., labeled + unlabeled) were 0.62 Gy and 0.55 Gy, respectively, at all labeled fractions and correspond to the absorbed dose delivered by the largest number of histories that were required in our 30-keV simulations to minimize statistical fluctuations inherent in the Monte-Carlo process. For higher mean doses, the individual doses for each cell were scaled accordingly. Thus, the dose distributions are the same for all higher mean doses as shown in Fig. 2b except for the scale of the abscissae. The self-dose distributions [Fig. 2b, left] only include the labeled cells. As a consequence, the Gaussian shape of the distributions is centered at a mean that is inversely proportional to the labeled fraction. The cross-dose distributions [Fig. 2b, right] clearly show that, for small labeled fractions, a large number of cells receive a very small dose and, therefore, survive even at high mean doses. This is believed to be due to the local geometrical environment of each individual cell that arises as a consequence of random selection of cells that are labeled (i.e., edge effects). In our computer model, cells are static: they remain at the same place during the entire simulation. Electrons of 30 keV have a range of 17.5 μm in water. Compared with the 10-μm diameter of the cells, and when considering that only 1% of the cells are labeled, there are many unlabeled cells that are further than 17.5 μm from their closest labeled neighbor. These cells are never hit by an electron, no matter how many histories are simulated. As seen from Fig. 2a (bottom), this effect is reduced as the energy increases because the electron range increases with energy and reduces the probability for an individual cell to be seated at an unreachable location. As a consequence, the survival curves converge towards the theoretical exponential curve as the electron energy increases. A second consequence is that the three distinct survival curves seen at 30 keV [Fig. 2a, top] converge towards each other as one progresses upward in energy to 100 keV [Fig. 2a, bottom]. The convergence is complete for 300 keV and 1000 keV [Fig. 2 of the supplementary material (B)]50 because the dose becomes more uniform among the unlabeled cells. This also explains why the curves for 1000 keV [Fig. 2 of the supplementary material (B)]50 tend to retreat to the theoretical cross-dose exponential curve (D37 = 4.0 Gy). In summary, when electron emitters are uniformly distributed among a small fraction of cells (i.e., 1% labeling), some of the unlabeled cells receive doses below the mean dose. This results in cell survival curves that increasingly saturate with decreasing electron energy.
Dependence of mixed cell survival on labeled fraction for uniform distribution
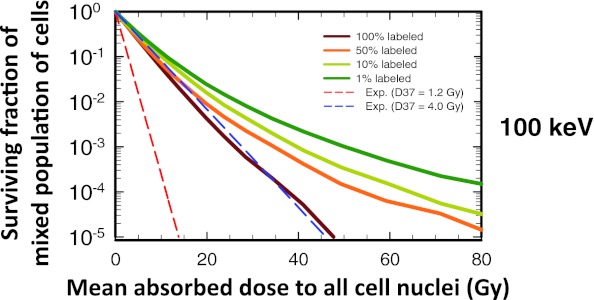
Survival curves for the mixed population of labeled and unlabeled cells are shown in Fig. 3. The mean dose on the abscissa is thus the average dose (cross-dose + self-dose) over the whole population of cells (labeled and unlabeled). The survival curves for this mixed population largely recapitulate those observed for unlabeled cells, so only the 100-keV data are shown in Fig. 3. Clearly, the percentage of cells labeled has a marked impact on the shape of the survival curve. Its impact is diminished at high electron energies and increased at low electron energies [Fig. 3 of the supplementary material (B)].50 In the latter case, as expected, the surviving fraction corresponds to the complement of the labeled fraction when they are labeled with a radionuclide that emits short-range 10-keV electrons [Fig. 3 of the supplementary material (B)].50 In summary, when the activity distribution is uniform among the labeled cells, the survival curves for the mixed population of cells follow the same trends seen for the unlabeled cells.
Figure 3.
Effect of fraction of cells labeled on the shape of the survival curve for the mixed cell population (labeled + unlabeled) when a 100-keV monoenergetic electron emitter is uniformly distributed among the labeled cells. The surviving fraction of mixed cells is plotted as a function of mean absorbed dose to all cell nuclei. The survival curves are shown for four different labeled fractions: 100%, 50%, 10%, and 1%. The lower and upper dashed lines represent exponential survival curves with D37 = D37,self = 1.2 Gy and D37 = D37,cross = 4.0 Gy, respectively. A complete set of curves for all combinations of energy and fraction of cells labeled is provided in Fig. 3 of the supplementary material (B) (Ref. 50). For the sake of comparison, the data for 100% labeling are reproduced from Rajon et al. (Ref. 32).
Dependence of labeled cell survival on labeled fraction for lognormal distribution
Figure 4 shows how combining lognormal activity distribution with labeled fraction affects the response of the labeled cells for 1000-keV electrons. It is apparent that a lognormal distribution of cellular activity among the labeled cells has little impact on the shape of the survival curves when 100% of the cells are labeled (Fig. 4, left), a conclusion reached earlier by Rajon et al.32 This remains true when only 50% of the cells are labeled (Fig. 4, left middle). In both cases, the survival curves essentially follow an exponential response corresponding to D37 = D37,cross = 4.0 Gy. However, lognormal distributions have a marked effect on dose response to a 1000-keV electron emitter when only 10% (Fig. 4, right middle) or 1% (Fig. 4, right) of the cells are labeled. It is interesting to note in the 1% case that some of the survival curves shift to the left of the exponential response corresponding to D37,self = 1.2 Gy. This is because the surviving fraction of labeled cells is plotted as a function of the mean absorbed dose to all cells. This does not occur when plotted as a function of the mean absorbed dose to the labeled cells. In summary, the importance of the lognormal distribution on survival of labeled cells increases as both the electron energy and the labeled percentage decreases [see Fig. 4 of the supplementary material (B)].50
Figure 4.
Combined effect of labeled fraction and of activity distribution on the cell survival-response of labeled cells when a 1000-keV monoenergetic electron emitter is lognormally distributed among the labeled cells. From left to right, the percentage of cells labeled is 100%, 50%, 10%, and 1%. The surviving fraction of mixed cells is plotted as a function of mean absorbed dose to all cell nuclei. The activity distribution is uniform (σ → 0) or lognormal with shape parameters of σ = 0.6, 1.0, and 2.0. The dashed lower and upper lines represent exponential survival curves with D37 = D37,self = 1.2 Gy and D37 = D37,cross = 4.0 Gy, respectively. A complete set of curves for all combinations of energy and fraction of cells labeled is provided in Fig. 4 of the supplementary material (B) (Ref. 50). For the sake of comparison, the data for 100% labeling are reproduced from Rajon et al. (Ref. 32).
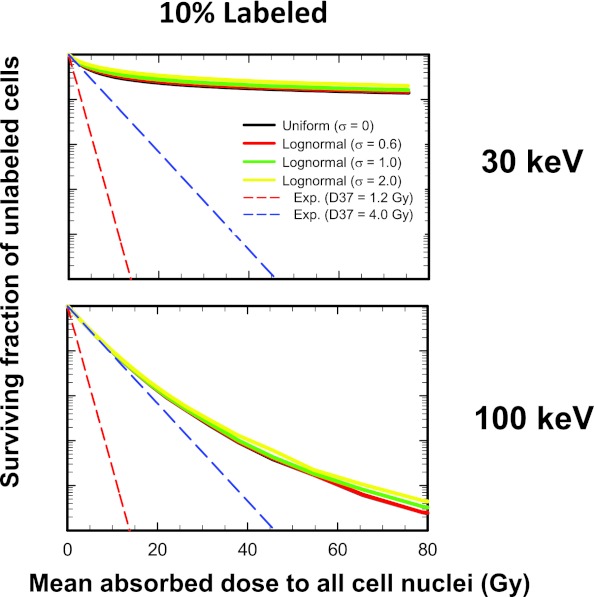
Dependence of unlabeled cell survival on labeled fraction for lognormal distribution
Figure 5 shows how combining lognormal activity distribution with labeled fraction affects the response of the unlabeled cells. The general trends are the same for 50%, 10%, and 1% labeling, namely, the activity distribution has a negligible impact on the shape of the unlabeled cell survival curves. However, electron energy and percent labeling does play a significant role in determining the degree of saturation of the survival curves. These trends are well represented by the unlabeled cell survival curves for 30- and 100-keV electron emitters when 10% of the cells are labeled (Fig. 5). Similar curves emerge when the survival of the mixed population of cells is plotted [Fig. 6 of the supplementary material (B)]50 except for the 100% labeling case which was published previously.32 In summary, activity distribution has a negligible impact on the shape of the unlabeled cell survival curves.
Figure 5.
Combined effect of labeled fraction and of activity distribution on the cell survival-response of unlabeled cells when 10% of the cells are labeled with 30-keV (Top) and 100-keV (Bottom) monoenergetic electron emitters. The surviving fraction of mixed cells is plotted as a function of mean absorbed dose to all cell nuclei. The activity distribution is uniform (σ → 0) or lognormal with shape parameters of σ = 0.6, 1.0, and 2.0. The dashed lower and upper lines represent exponential survival curves with D37 = D37,self = 1.2 Gy and D37 = D37,cross = 4.0 Gy, respectively. A complete set of curves for all combinations of energy and fraction of cells labeled is provided in Fig. 5 of the supplementary material (B) (Ref. 50).
Dependence on D37,self
The results above correspond to conditions wherein the self-dose is more lethal per unit dose than the cross-dose (i.e., D37,self = 1.2 Gy, D37,cross = 4.0 Gy). This reflects the well-known phenomenon of the dependence of relative biological effectiveness of Auger electron emitters on their subcellular distribution.29, 35 This has also been observed with beta-particle emitters such as 131I.19 These scenarios are relevant when such radionuclides are intercalated or incorporated into the DNA in the cell nucleus.35, 36, 37 It is also of interest to determine how the survival curves change when self- and cross-doses are equally effective (i.e., D37,self = 4.0 Gy, D37,cross = 4.0 Gy). This scenario corresponds to cases where the radiopharmaceutical localizes in the cytoplasm or on the cell membrane.28 Notably, the same general trends emerge for the labeled and unlabeled cells in this case too, although all of the labeled cell responses converge towards D37 = 4.0 Gy as the activity distribution becomes more uniform (σ → 0). These trends are shown in detail in the supplementary material (C) and (D).50 In summary, the value of D37,self relative to D37,cross plays an increasing role in the response of the labeled cells as the electron energy decreases.
DISCUSSION
The theoretical survival response of cell populations clustered within a Cytomatrix™ carbon scaffold and targeted with hypothetical monoenergetic electron emitters has been studied. The effects of electron energy, fraction of labeled cells, and activity distribution among the labeled cells were analyzed. In addition, the surviving fraction of labeled cells, unlabeled cells, and the mixed population of cells were compared. Analysis of these three cell populations extends the usefulness of these results to a variety of contexts. In the context of targeted radionuclide therapy, the labeled cells can be considered the target cells and the unlabeled cells considered as the normal cells. Alternatively, all of the cells can be considered as target cells but with only some of them labeled. In this latter scenario, the surviving fraction of the mixed population would be representative of their response. Other scenarios can also be envisioned within the extensive range of labeled percentage and activity distributions studied. Therefore, the results presented herein can be used broadly to understand how these variables affect the surviving fractions of various cell populations.
Malignant cells are continuously shed from primary tumors and dispersed through vessels to lymph nodes and organs such as bone marrow.38 Clinical trials have shown that the level of circulating tumor cells in peripheral blood can be related to both progression-free survival and to overall survival.39 Therefore, a key goal for targeted radionuclide therapy is to sterilize cells that have been shed from the tumor and are circulating or lodged within normal tissue. Within this context, one may consider applying the present model to such a tumor cell population that is dispersed among a population of normal cells and targeted with a radiopharmaceutical labeled with a monoenergetic electron emitter. Figures 45, in particular, provide important insights into how such cell populations might respond to targeted radionuclide therapy. Assuming that all malignant cells are labeled, Fig. 4 demonstrates that the percentage of malignant cells among the entire population has a major impact on their response when viewed in the framework of mean dose to the entire population (commensurate with mean voxel dose that can be obtained clinically). This applies to all electron energies [Fig. 4 of the supplementary material (B)].50 The same is true when viewed in the framework of mean dose to the labeled cells [Fig. 1 of the supplementary material (D)].50 These figures also highlight the strong dependence of response on the distribution of activity among the labeled cells even when the electron energy is as high as 1000 keV. The aforementioned conclusions apply even when the relative biological effectiveness of the self-dose is decreased (i.e., increase D37,self from 1.2 Gy to 4.0 Gy) [Fig. 4 of the supplementary material (C), Fig. 2 of the supplementary material (D)].50 It is apparent that lognormal activity distributions among dispersed malignant cells can introduce substantial limitations on our capacity to sterilize them with a single agent.40, 41 In contrast, the response of nontargeted normal cells to the cross-dose that they receive is not affected by the nature of the activity distribution among dispersed targeted cells (Fig. 5). However, their response is highly dependent on electron energy [Fig. 5 of the supplementary material (B)]50 with low energies affording substantial protection of normal cells due to their reduced capacity to cross-irradiate.
Now consider a tumor cell population consisting of 106 cancer cells that are clustered within spatial dimensions reasonably consistent with the American Joint Committee on Cancer (AJCC) definition of a micrometastasis (0.2 mm < diameter < 2.0 mm).42, 43 In this scenario, it may be appropriate to consider the response of the mixed population of labeled and unlabeled cells. The percentage of tumor cells that are labeled has a marked impact on the response of the tumor cell population when electron energies are 100 keV (Fig. 3) and lower [Fig. 3 of the supplementary material (B)].50 However, the distribution of activity among the labeled tumor cells has little impact under these conditions until the electron energy drops to about 30 keV. However, when tumor cells in a micrometastasis are loosely packed and interspersed with nontargeted normal cells (e.g., marrow, lymph tissues), a lognormal activity distribution among the tumor cells can have a profound impact on the response, depending on electron energy and relative percentage of tumor versus normal cells.
Not addressed here is how micrometastasis size and cell packing density influence the impact of activity distribution on response of the tumor cell population. There is evidence that the presence of isolated tumor cells (ITC), defined by the AJCC as consisting of single or clusters of tumor cells with diameter < 0.2 mm, in lymph nodes, bone marrow, and other sites, constitutes a significant risk factor in reducing the life expectancy of patients.42, 43 This is particularly prevalent in the case of sentinel nodes for invasive lobular carcinoma.44 Earlier work has shown that the size of ITCs and micrometastases can have a profound effect on the dosimetry3, 26, 27 and corresponding response of the population.6, 45 Similarly, cell packing density can have some effect on the response, particularly in the case of alpha particles which have ranges in soft tissue of only several cell diameters.6 In the setting of radionuclides that emit alpha particles with ranges 25–80 μm in water, Charlton6 found that changing the packing density from 40% to 70% reduced the surviving fraction by less than a factor of 2. One could anticipate similar results for low energy electrons with comparable ranges, noting that changes of a factor of 2 are relatively small when considering several logs of change. Also not considered here is how the surviving fraction depends on the spatial distribution of the labeled cells. In this work, the labeled cells were randomly distributed among the whole population of cells. If labeled cells were located in clumps of cells distributed among the whole population, one could anticipate differently shaped cell survival curves for the labeled, unlabeled, and mixed population plots. These are important areas for further study in the context of nonuniform distributions of radioactivity given the promise that targeted radionuclide therapy has for sterilizing ITCs.
Finally, it is important to project how the present model might be applied to clinical practice. It has been suggested that shape parameter values for different histologic types of tumors and different radiopharmaceuticals could be cataloged based on quantitative autoradiography of tumor specimens surgically harvested after tracer administrations to a limited number of patients.46 This information, along with supportive quantitative imaging, could be used to prescribe a cocktail of radiopharmaceuticals41, 47, 48 for a patient's specific histologic tumor type (i.e., shape parameter value).46 There is also for potential to use a combination of histology, multiparameter flow cytometry, and multicellular dose-response modeling to identify the optimal cocktail of therapeutic agents for a given patient.32, 41, 48, 49 These and other related approaches merit further investigation.
ACKNOWLEDGMENTS
This project was supported in part by National Institutes of Health (NIH) Grant No. R01 CA083838 (RWH) and NIH R01 CA116743 (WEB). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Cancer Institute or the National Institutes of Health.
References
- Howell R. W., Neti P. V., Pinto M., Gerashchenko B. I., Narra V. R., and Azzam E. I., “Challenges and progress in predicting biological responses to incorporated radioactivity,” Radiat. Prot. Dosim. 122, 521–527 (2006). 10.1093/rpd/ncl448 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwok C. S., Prestwich W. V., and Wilson B. C., “Calculation of radiation doses for nonuniformly distributed beta and gamma radionuclides in soft tissue,” Med. Phys. 12, 405–412 (1985). 10.1118/1.595752 [DOI] [PubMed] [Google Scholar]
- Howell R. W., Rao D. V., and Sastry K. S. R., “Macroscopic dosimetry for radioimmunotherapy: Nonuniform activity distributions in solid tumors,” Med. Phys. 16, 66–74 (1989). 10.1118/1.596404 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sastry K. S. R., Haydock C., Basha A. M., and Rao D. V., “Electron dosimetry for radioimmunotherapy: Optimal electron energy,” Radiat. Prot. Dosim. 13(1–4), 249–252 (1985). [Google Scholar]
- Goddu S. M., Howell R. W., and Rao D. V., “Cellular dosimetry: Absorbed fractions for monoenergetic electron and alpha particle sources and S-values for radionuclides uniformly distributed in different cell compartments,” J. Nucl. Med. 35(2), 303–316 (1994). [PubMed] [Google Scholar]
- Charlton D. E., “Radiation effects in spheroids of cells exposed to alpha emitters,” Int. J. Radiat. Biol. 76, 1555–1564 (2000). 10.1080/09553000050176315 [DOI] [PubMed] [Google Scholar]
- Malaroda A., Flux G., and Ott R., “The application of dose-rate volume histograms and survival fractions to multicellular dosimetry,” Cancer Biother. Radiopharm. 20, 58–65 (2005). 10.1089/cbr.2005.20.58 [DOI] [PubMed] [Google Scholar]
- Cai Z., Pignol J. P., Chan C., and Reilly R. M., “Cellular dosimetry of 111In using Monte Carlo N-particle computer code: Comparison with analytic methods and correlation with in vitro cytotoxicity,” J. Nucl. Med. 51, 462–470 (2010). 10.2967/jnumed.109.063156 [DOI] [PubMed] [Google Scholar]
- Faraggi M., Gardin I., de Labriolle-Vaylet C., Moretti J.-L., and Bok B. D., “The influence of tracer localization on the electron dose rate delivered to the cell nucleus,” J. Nucl. Med. 35(1), 113–119 (1994). [PubMed] [Google Scholar]
- Sgouros G., Howell R. W., Bolch W. E., and Fisher D. R., “MIRD commentary: Proposed name for a dosimetry unit applicable to deterministic biological effects–the barendsen (Bd),” J. Nucl. Med. 50, 485–487 (2009). 10.2967/jnumed.108.057398 [DOI] [PubMed] [Google Scholar]
- O’Donoghue J. A. and Wheldon T. E., “Dose-rate effects in biologically targeted radiotherapy,” Int. J. Radiat. Biol. 56, 745–749 (1989). 10.1080/09553008914551991 [DOI] [PubMed] [Google Scholar]
- Bishayee A., Rao D. V., and Howell R. W., “Evidence for pronounced bystander effects caused by nonuniform distributions of radioactivity using a novel three-dimensional tissue culture model,” Radiat. Res. 152, 88–97 (1999). 10.2307/3580054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kishikawa H., Wang K., Adelstein S. J., and Kassis A. I., “Inhibitory and stimulatory bystander effects are differentially induced by Iodine-125 and Iodine-123,” Radiat. Res. 165, 688–694 (2006). 10.1667/RR3567.1 [DOI] [PubMed] [Google Scholar]
- Persaud R., Zhou H., Baker S. E., Hei T. K., and Hall E. J., “Assessment of low linear energy transfer radiation-induced bystander mutagenesis in a three-dimensional culture model,” Cancer Res. 65, 9876–9882 (2005). 10.1158/0008-5472.CAN-04-2875 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Persaud R., Zhou H., Hei T. K., and Hall E. J., “Demonstration of a radiation-induced bystander effect for low dose low LET beta-particles,” Radiat. Environ. Biophys. 46, 395–400 (2007). 10.1007/s00411-007-0116-1 [DOI] [PubMed] [Google Scholar]
- Humm J. L. and Chin L. M., “A model of cell inactivation by alpha-particle internal emitters,” Radiat. Res. 134, 143–150 (1993). 10.2307/3578453 [DOI] [PubMed] [Google Scholar]
- Kvinnsland Y., Stokke T., and Aurlien E., “Radioimmunotherapy with alpha-particle emitters: Microdosimetry of cells with a heterogeneous antigen expression and with various diameters of cells and nuclei,” Radiat. Res. 155, 288–296 (2001). 10.1667/0033-7587(2001)155[0288:RWAPEM]2.0.CO;2 [DOI] [PubMed] [Google Scholar]
- Neti P. V. and Howell R. W., “When may a nonuniform distribution of 131I be considered uniform? An experimental basis for multicellular dosimetry,” J. Nucl. Med. 44(12), 2019–2026 (2003). [PMC free article] [PubMed] [Google Scholar]
- Neti P. V. and Howell R. W., “Isolating effects of microscopic nonuniform distributions of 131I on labeled and unlabeled cells,” J. Nucl. Med. 45(6), 1050–1058 (2004). [PMC free article] [PubMed] [Google Scholar]
- Neti P. V. and Howell R. W., “Log normal distribution of cellular uptake of radioactivity: Implications for biologic responses to radiopharmaceuticals,” J. Nucl. Med. 47(6), 1049–1058 (2006). [PMC free article] [PubMed] [Google Scholar]
- Humm J. L., Roeske J. C., Fisher D. R., and Chen G. T. Y., “Microdosimetric concepts in radioimmunotherapy,” Med. Phys. 20(2), 535–541 (1993). 10.1118/1.597049 [DOI] [PubMed] [Google Scholar]
- Howell R. W. and Neti P. V., “Modeling multicellular response to nonuniform distributions of radioactivity: Differences in cellular response to self-dose and cross-dose,” Radiat. Res. 163, 216–221 (2005). 10.1667/RR3290 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinto M., Azzam E. I., and Howell R. W., “Bystander responses in three-dimensional cultures containing radiolabeled and unlabeled human cells,” Radiat. Prot. Dosim. 122, 252–255 (2006). 10.1093/rpd/ncl460 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinto M., Azzam E. I., and Howell R. W., “Investigation of adaptive responses in bystander cells in 3D cultures containing tritium-labeled and unlabeled normal human fibroblasts,” Radiat. Res. 174, 216–227 (2010). 10.1667/RR1866.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinto M. and Howell R. W., “Concomitant quantification of targeted drug delivery and biological response in individual cells,” Biotechniques 43(64), 66–71 (2007). 10.2144/000112492 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Howell R. W., Rao D. V., and Haydock C., “Dosimetry techniques for therapeutic applications of incorporated radionuclides,” in Dosimetry of Administered Radionuclides, edited by Adelstein S. J., Kassis A. I., and Burt R. W. (American College of Nuclear Physicians, Washington, D.C., 1990), pp. 215–256. [Google Scholar]
- Goddu S. M., Rao D. V., and Howell R. W., “Multicellular dosimetry for micrometastases: Dependence of self-dose versus cross-dose to cell nuclei on type and energy of radiation and subcellular distribution of radionuclides,” J. Nucl. Med. 35(3), 521–530 (1994). [PubMed] [Google Scholar]
- Kassis A. I., Fayad F., Kinsey B. M., Sastry K. S. R., Taube R. A., and Adelstein S. J., “Radiotoxicity of I-125 in mammalian cells,” Radiat. Res. 111, 305–318 (1987). 10.2307/3576987 [DOI] [PubMed] [Google Scholar]
- Howell R. W., Narra V. R., Sastry K. S. R., and Rao D. V., “On the equivalent dose for Auger electron emitters,” Radiat. Res. 134, 71–78 (1993). 10.2307/3578503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Humm J. L., Howell R. W., and Rao D. V., “Dosimetry of Auger electron emitting radionuclides: Report No. 3 of the AAPM Nuclear Medicine Task Group No. 6,” Med. Phys. 21, 1901–1915 (1994). 10.1118/1.597227 [DOI] [PubMed] [Google Scholar]
- Azure M. T., Archer R. D., Sastry K. S. R., Rao D. V., and Howell R. W., “Biologic effect of 212Pb localized in the nucleus of mammalian cells: Role of recoil energy in the radiotoxicity of internal alpha emitters,” Radiat. Res. 140, 276–283 (1994). 10.2307/3578912 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rajon D., Bolch W. E., and Howell R. W., “Lognormal distribution of cellular uptake of radioactivity: Monte Carlo simulation of irradiation and cell killing in 3-dimensional populations in carbon scaffolds,” J. Nucl. Med. 52, 926–933 (2011). 10.2967/jnumed.110.080044 [DOI] [PubMed] [Google Scholar]
- Howell R. W., Rajon D., and Bolch W. E., “Monte Carlo simulation of irradiation and killing in three-dimensional cell populations with lognormal cellular uptake of radioactivity,” Int. J. Radiat. Biol. 88, 115–122 (2011). 10.3109/09553002.2011.602379 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kawrakow I., “Accurate condensed history Monte Carlo simulation of electron transport. I. EGSnrc, the new EGS4 version,” Med. Phys. 27, 485–498 (2000). 10.1118/1.598917 [DOI] [PubMed] [Google Scholar]
- Kassis A. I., Howell R. W., Sastry K. S. R., and Adelstein S. J., “Positional effects of Auger decays in mammalian cells in culture,” in DNA Damage by Auger Emitters, edited by Baverstock K. F. and Charlton D. E. (Taylor & Francis, London, 1988), pp. 1–14. [Google Scholar]
- Feinendegen L. E., Ertl H. H., and Bond V. P., “Biological toxicity associated with the Auger effect,” in Proceedings of the Symposium on Biophysical Aspects of Radiation Quality, edited by Ebert H. (IAEA, Vienna, 1971), pp. 419–430.
- ICRU, “ICRU Report No. 67. Absorbed-dose specification in nuclear medicine,” J. ICRU 2, 3–110 (2002). [Google Scholar]
- Chaffer C. L. and Weinberg R. A., “A perspective on cancer cell metastasis,” Science 331, 1559–1564 (2012). 10.1126/science.1203543 [DOI] [PubMed] [Google Scholar]
- Cristofanilli M., Budd G. T., Ellis M. J., Stopeck A., Matera J., Miller M. C., Reuben J. M., Doyle G. V., Allard W. J., Terstappen L. W., and Hayes D. F., “Circulating tumor cells, disease progression, and survival in metastatic breast cancer,” N. Engl. J. Med. 351, 781–791 (2004). 10.1056/NEJMoa040766 [DOI] [PubMed] [Google Scholar]
- Akudugu J. M. and Howell R. W., “Flow cytometry-assisted Monte Carlo simulation predicts clonogenic survival of cell populations with lognormal distributions of radiopharmaceuticals and anticancer drugs,” Int. J. Radiat. Biol. 88, 286–293 (2011). 10.3109/09553002.2012.638357 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akudugu J. M., Neti P. V. S. V., and Howell R. W., “Changes in lognormal shape parameter guide design of patient-specific radiochemotherapy cocktails,” J. Nucl. Med. 52, 642–649 (2011). 10.2967/jnumed.110.083584 [DOI] [PubMed] [Google Scholar]
- AJCC Cancer Staging Manual, 6th ed., edited by Greene F. L., Page D. L., Fleming I. D., Fritz A. G., Balch C. M., Haller D. G., and Morrow M. (Springer-Verlag, New York, 2002). [Google Scholar]
- Weaver D. L., “Pathology evaluation of sentinel lymph nodes in breast cancer: Protocol recommendations and rationale,” Mod. Pathol. 23(2), S26–S32 (2010). 10.1038/modpathol.2010.36 [DOI] [PubMed] [Google Scholar]
- Singletary S. E. and Connolly J. L., “Breast cancer staging: Working with the sixth edition of the AJCC Cancer Staging Manual,” Ca-Cancer J. Clin. 56, 37–47 (2006). 10.3322/canjclin.56.1.37 [DOI] [PubMed] [Google Scholar]
- O’Donoghue J. A., Bardies M., and Wheldon T. E., “Relationships between tumor size and curability for uniformly targeted therapy with beta-emitting radionuclides,” J. Nucl. Med. 36(10), 1902–1909 (1995). [PubMed] [Google Scholar]
- Zanzonico P., “Cell-level dosimetry and biologic response modeling of heterogeneously distributed radionuclides: A step forward,” J. Nucl. Med. 52, 845–847 (2011). 10.2967/jnumed.111.087841 [DOI] [PubMed] [Google Scholar]
- Milenic D. E., Brady E. D., Garmestani K., Albert P. S., Abdulla A., and Brechbiel M. W., “Improved efficacy of alpha-particle-targeted radiation therapy: Dual targeting of human epidermal growth factor receptor-2 and tumor-associated glycoprotein 72,” Cancer 116, 1059–1066 (2010). 10.1002/cncr.24793 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akudugu J. M. and Howell R. W., “A method to predict response of cell populations to cocktails of chemotherapeutics and radiopharmaceuticals: Validation with daunomycin, doxorubicin, and the alpha particle emitter 210Po,” Nucl. Med. Biol. 39, 954–961 (2012). 10.1016/j.nucmedbio.2012.01.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Leers M. P., Schoffelen R. H., Hoop J. G., Theunissen P. H., Oosterhuis J. W., vd Bijl H., Rahmy A., Tan W., and Nap M., “Multiparameter flow cytometry as a tool for the detection of micrometastatic tumour cells in the sentinel lymph node procedure of patients with breast cancer,” J. Clin. Pathol. 55, 359–366 (2002). 10.1136/jcp.55.5.359 [DOI] [PMC free article] [PubMed] [Google Scholar]
- See supplementary material at http://dx.doi.org/10.1118/1.4769409 for figures (Supplements A–D).