Power and Phase Properties of Oscillatory Neural Responses in the Presence of Background Activity

Abstract

Natural sensory inputs, such as speech and music, are often rhythmic. Recent studies have consistently demonstrated that these rhythmic stimuli cause the phase of oscillatory, i.e. rhythmic, neural activity, recorded as local field potential (LFP), electroencephalography (EEG) or magnetoencephalography (MEG), to synchronize with the stimulus. This phase synchronization, when not accompanied by any increase of response power, has been hypothesized to be the result of phase resetting of ongoing, spontaneous, neural oscillations measurable by LFP, EEG, or MEG. In this article, however, we argue that this same phenomenon can be easily explained without any phase resetting, and where the stimulus-synchronized activity is generated independently of background neural oscillations. It is demonstrated with a simple (but general) stochastic model that, purely due to statistical properties, phase synchronization, as measured by ‘inter-trial phase coherence’, is much more sensitive to stimulus-synchronized neural activity than is power. These results question the usefulness of analyzing the power and phase of stimulus-synchronized activity as separate and complementary measures; particularly in the case of attempting to demonstrate whether stimulus-phase-locked neural activity is generated by phase resetting of ongoing neural oscillations.

1. Introduction

Natural sensory inputs, such as speech, music and natural audio-visual scenes, are often rhythmic. Low frequency neural activity in the brain, either local field potential (LFP), electroencephalography (EEG) or magnetoencephalography (MEG), can synchronize to this input rhythm (Lakatos et al., 2008; Luo & Poeppel, 2007). The dominant rhythm of natural stimuli is usually below 10 Hz, and therefore the synchronized neural activity falls into the delta and theta bands of neural oscillations. From this, low frequency stimulus-synchronized activity is often hypothesized to be related to the intrinsic rhythm of large-scale neural oscillations. The main support for this hypothesis is that when a rhythmic sensory input is present, the phase of the oscillatory neural activity aligns with the input, as is demonstrated by the high trial-to-trial coherence of the phase of the neural response. In other words, similar response phases are observed when a stimulus repeats. In contrast to the phase, the power of the neural response is often not increased in the presence of the same stimulus (Schroeder and Lakatos, 2009) and may not follow the stimulus rhythm (Luo & Poeppel, 2007). In short, it appears at first that the phase, rather than the power, of a neural response is most sensitive to the stimulus. From this it is often concluded that stimulus-synchronized activity, without accompanying increases in power, must be caused by phase resetting of ongoing LFP/EEG/MEG oscillations (Shah et al., 2004)

Recently, however, Howard and Poeppel (2010) have suggested that even if the power of oscillatory neural activity is truly synchronized by the stimulus, it may not be at all observable experimentally, due to the presence of background, stimulus-irrelevant, neural activity. In this study we prove this mathematically, and characterize the statistical properties of the neural response phase and power, using a general model in which stimulus-synchronized activity is generated independently of background neural oscillations.

2. Phase synchronization in a general model

2.1 A linear model for stimulus-synchronized neural response

Suppose the neural activity tracking a sensory stimulus is S(f) and background neural activity is N(f), where both signals are represented in the frequency domain. The following discussion analyzes responses at only a single frequency, and therefore the symbol f is dropped. The results, however, hold without loss of generality to all frequencies, since any measured neural response, even if broadband, can be converted into its constituent frequencies using Fourier analysis. Since S and N are both complex Fourier coefficients, they can be conveniently denoted as phasors, i.e. S = r_Sexp(jθ_S) and N = r_Nexp(jθ_N), where r and θ represent the magnitude and phase respectively. For the stimulus-synchronized component S, r_S and θ_S are assumed to be constant over trials. Under the assumption that stimulus-synchronized activity S is generated independently of background activity N, the measured neural activity, M = r_Mexp(jθ_M), is modeled as the linear sum of the stimulus-synchronized and background activity, i.e. M = S + N (Sahani & Linden, 2003).

We assume at first the stimulus-irrelevant background activity to be independent identically distributed (i.i.d.) Gaussian noise in the time domain. Consequently, in the frequency domain, the phase of N, θ_N, is uniformly distributed (from 0 to 2π), and the real and imaginary parts of N are jointly Gaussian with equal variance, e.g. σ². For a more general case, we assume the stimulus-irrelevant background activity to be i.i.d. generalized Gaussian noise. Under this assumption, the probability distribution of the background activity, n(t), at any moment is p_n(n(t)) = C₀exp(−|n(t)/σ|^c), where C₀ is a normalization parameter and c is the shape parameter that determines the kurtosis of the distribution. The generalized Gaussian distribution reduces to a Gaussian distribution when c = 2, or a Laplacian distribution when c = 1.

2.2 Distribution of the neural response phase

When the real and imaginary parts of background activity N are jointly Gaussian, the real and imaginary parts of the measurement M, i.e. r_Mcos(θ_M) and r_Msin(θ_M), are also jointly Gaussian. The joint distribution of amplitude and phase of measured neural activity, i.e. r_M and θ_M, is then

$$p_{r\theta }(r_{\mathrm{M}},{\theta }_{\mathrm{M}})=\frac{\varphi \left(\frac{r_{\mathrm{M}}\text{cos}{\theta }_{\mathrm{M}}-r_{\mathrm{S}}\text{cos}{\theta }_{\mathrm{S}}}{\sigma },\frac{r_{\mathrm{M}}\text{sin}{\theta }_{\mathrm{M}}-r_{\mathrm{S}}\text{sin}{\theta }_{\mathrm{S}}}{\sigma }\right)}{\text{det}\left(\begin{array}{cc}\hfill \text{cos}{\theta }_{\mathrm{M}},\hfill & \hfill -r_{\mathrm{M}}\text{sin}{\theta }_{\mathrm{M}}\hfill \\ \hfill \text{sin}{\theta }_{\mathrm{M}},\hfill & \hfill r_{\mathrm{M}}\text{cos}{\theta }_{\mathrm{M}}\hfill \end{array}\right)}=\frac{r_{\mathrm{M}}}{2\pi \sigma }\text{exp}\left(-\frac{r_{\mathrm{M}}^2+r_{\mathrm{S}}^2-2r_{\mathrm{M}}{r}_{\mathrm{S}}\text{cos}({\theta }_{\mathrm{M}}-{\theta }_{\mathrm{S}})}{2{\sigma }^2}\right),$$

where ϕ (·,·) is the joint probability density function of two independent standard Gaussian variables. The marginal distribution of θ_M can then be calculated to be

$$p_{\theta }({\theta }_{\mathrm{M}})={\displaystyle {\int }_0^{\infty }}{p}_{r\theta }\left(r_{\mathrm{M}},{\theta }_{\mathrm{M}}\right)\mathrm{d}{r}_{\mathrm{M}}=\frac{1}{2\pi }\text{exp}\left(-\frac{{\gamma }^2}{2}\right)+\frac{1}{\sqrt{2\pi }}\mathrm{\Phi }(\gamma d)\gamma d\text{exp}\left(\frac{{\gamma }^2(d^2-1)}{2}\right),$$

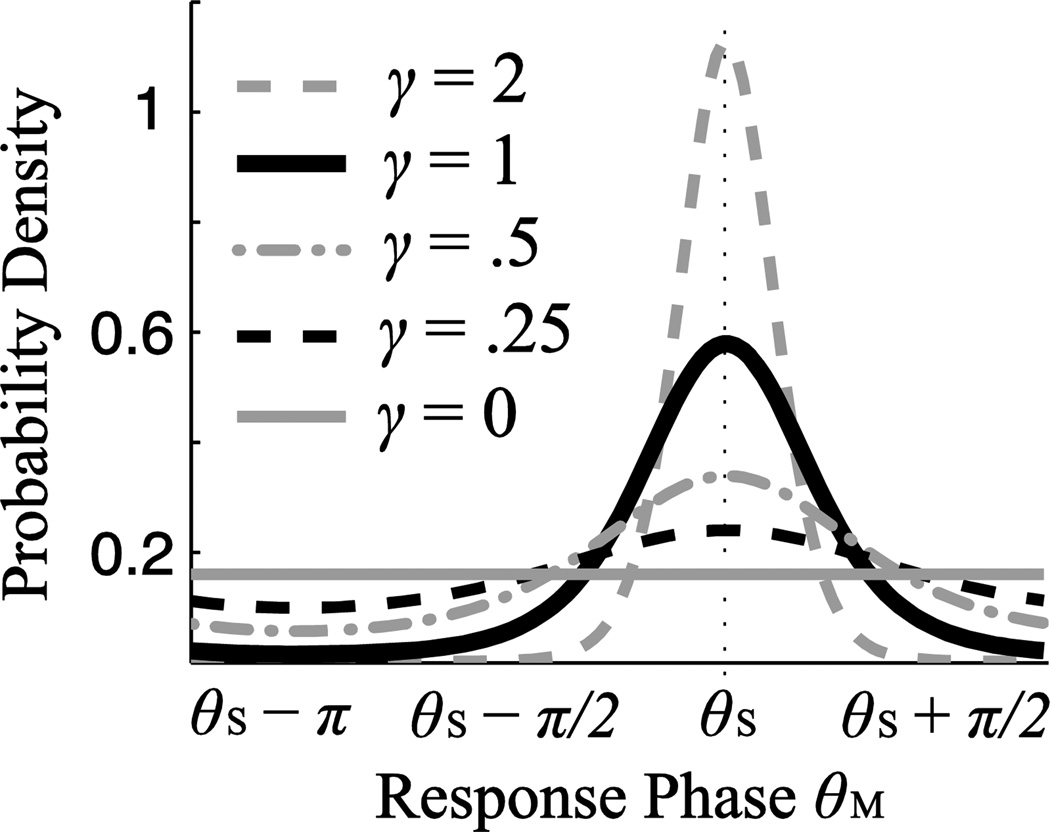
where d = cos(θ_M − θ_S), $\gamma =\sqrt{2}{r}_{\mathrm{S}}/\sigma$, and Φ(·) is the cumulative distribution function of a standard Gaussian random variable (zero mean and unit variance). γ is the ratio between the amplitude of the stimulus-related response and the amplitude of the stimulus-unrelated response, and can be interpreted as a signal to noise ratio (SNR). When the neural response amplitude is zero, γ is 0, and therefore p_θ (θ_M) = 1/(2π), i.e. θ is uniformly distributed across all phases. Nevertheless, as long as γ is not zero, p_θ (θ_M) is non-uniform and is maximal at θ_M = θ_S (Fig. 1a). When the background activity, N, is subject to a generalized Gaussian distribution, the analytical form of the probability density function of θ_M is unknown, but numerical results are shown in Fig. 2b.

Figure 1.

The probability density function of the phase of neural measurements when stimulus-synchronized activity is generated independently of background activity. The probability distribution is distinct from the uniform distribution (solid gray line), as long as stimulus-synchronized activity has non-zero amplitude.

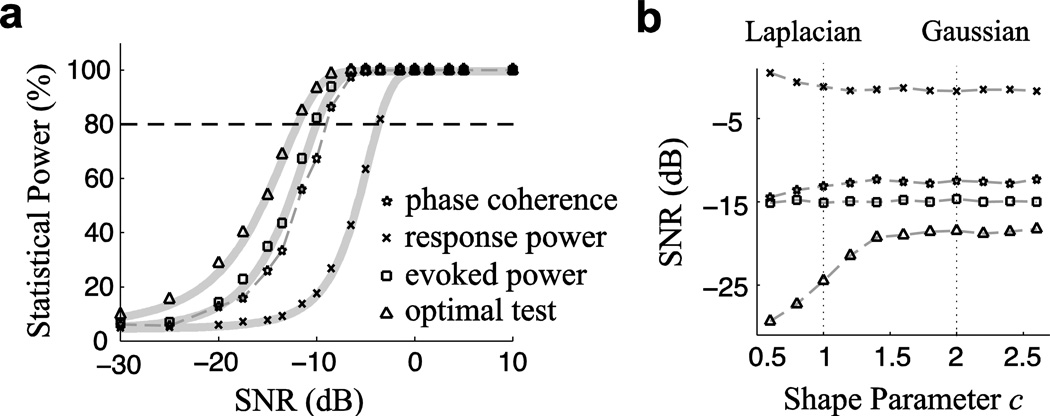
Figure 2.

(a) The statistical power of four significance tests as a function of SNR when background activity is subject to the Gaussian distribution. Each point in the figure is a Monte Carlo numerical result; the theoretical statistical power, when available, is plotted as a solid gray line. Test statistics whose curves lie more to the left possess greater statistical power at the same SNR than those to the right. Similarly, to achieve 80% statistical power, each test requires a different minimum SNR, where smaller SNR values demonstrate greater overall statistical power. (b) The SNR required for 80% statistical power, for background activity subject to the generalized Gaussian distribution (smaller SNR values demonstrate a more effective significance test). Phase coherence is much more effective than response power when testing the significance of a neural response.

3. Detecting oscillatory neural activity using power and phase

3.1 Detection of a neural response

In laboratory experiments, the existence of stimulus-synchronized activity must be validated with a significance test. Here, we analyze the statistical properties of the significance test based on the general model introduced in Section 2.1. In these significance tests the null hypothesis, H₀, is that there is no stimulus-synchronized neural response and therefore the neural measurement contains only background activity, e.g. M = N. The alternative hypothesis, H₁, is that there is indeed a non-zero stimulus-synchronized neural response, e.g. M = λS + N, with λ ≠ 0 the magnitude of stimulus-synchronized activity. The significance level of a test, α (fixed at 0.05 in this study) is the probability that the test reports the alternative hypothesis given that the null hypothesis is true, i.e. the false alarm rate. The performance of a test is evaluated based on the statistical power, defined as the probability that the test reports the alternative hypothesis when the alternative hypothesis is true, i.e. the detection rate.

The testing of stimulus-synchronized activity can be based on any random variable, called a test statistic, that is sensitive to the response, e.g. power or phase coherence. When the stimulus-synchronized activity is generated independently from background activity, it linearly increases with the power of neural responses, i.e. E(M²) = E(S²) + E(N²). Also, as demonstrated in Section 2.2, the phase of neural measurement deviates from the uniform distribution associated with H₀, when stimulus-synchronized activity exists. Therefore, power and phase based measures are both sensitive to stimulus-synchronized activity and are commonly used for significance test.

For K independent experimental measurements, M_i = r_icos(θ_i), i = {1, 2, …, K}, a few commonly used test statistics are listed in table 1, including phase coherence, mean response power and evoked power (Luo & Poeppel 2007; Shah et al., 2004). Phase coherence measures the consistency of the response phase over trials. It is maximal (1) when the response has the same phase in every single trial, and is minimal (0) when the response phase is uniformly distributed across all possible values. The evoked power is the power of the evoked response, i.e. the response averaged over trials, and approximates the power of the stimulus-synchronized response component, i.e. E(S²), when the trial number is large. The response power, an estimate of E(M²), on the other hand, averages the power of single trial responses and is independent of the phase consistency over trials. The response power is also called the total power of a response, since it includes both the power of phase-locked (evoked) activity and the power of non-phase-locked (induced) activity. Phase coherence and response power are usually viewed as complimentary measures, since they rely on, respectively, the phase and power of single trial responses. Nevertheless, they are statistically dependent in general, just as the power and phase of a neural signal (e.g. Kayser et al. 2009), and, critically, have very different statistical properties, as will be shown in the following.

Table 1.

Four random variables used for the detection of stimulus-synchronized activity, and their statistical power when background activity is Gaussian. The response power is proportional to the total power, i.e. summed over the individual power of every single trial response, while the evoked power is the power of the average response (i.e. the response averaged over trials). The optimal detector is optimal for the detection of phase-locked activity, i.e. S, from neural measurement M_i. See the text for symbol definitions.

	Expression	Statistical Power (Gaussian Prior)
Phase Coherence	$R^2={(\frac{1}{K}{\displaystyle \sum _{i=1}^K}\text{cos}({\theta }_i))}^2+{(\frac{1}{K}{\displaystyle \sum _{i=1}^K}\text{sin}({\theta }_i))}^2$	analytic form unknown
Response Power	$P_{\mathrm{A}}=\frac{1}{K}{\displaystyle \sum _{i=1}^K}{|M_i|}^2$	$1-\mathrm{\Gamma }(K,\frac{{\mathrm{\Gamma }}^{-1}(K,1-\alpha )}{1+{\gamma }^2})$
Evoked Power	$P_{\mathrm{E}}={\left|\frac{1}{K}{\displaystyle \sum _{i=1}^K}{M}_i\right|}^2$	1 − F (G−1 (1 − α), γ)
Optimal Detector	$D_o={\displaystyle \sum _{i=1}^K}\left(\text{Re}\right({\mathrm{M̂}}_i{S}^{*}\left)\right)$	1 − Φ(Φ−1(1 − α) − γ)

Notes:

Γ(·,·) is the incomplete gamma function (Poor 1994, Chapter 3).

G(·) and F(·,·) are the cumulative distribution functions of central and non-central Chi distributions with two degrees of freedom respectively (Johnson et al., 1995).

To quantify the theoretical limit for the performance of any significance test, we also compare all results with that of the locally optimal significance test (Miller & Thomas, 1972; Poor, 1994, Chapter 3). The locally optimal test is optimal when the neural signal contribution approaches zero amplitude, i.e. λ → 0. It requires a priori knowledge of the underlying amplitude and phase of the neural response and therefore is impractical experimentally. Under the generalized Gaussian noise assumption, based on a measured time series m(t) = λs(t) + n(t), the locally optimal test statistic is

$$D_{\mathrm{o}}=\partial \text{log}\left({\displaystyle {\prod }_t}{p}_n\left(m\left(t\right)-\lambda s\left(t\right)\right)\right)/{\partial \lambda |}_{\lambda =0}=\partial \text{log}\left(C_1\text{exp}\left(-{\displaystyle {\sum }_t}{\left|\left(m\left(t\right)-\lambda s\left(t\right)\right)\right|}^c\right)\right)/{\partial \lambda |}_{\lambda =0}=-\partial {\displaystyle {\sum }_t}{\left|\left(m\left(t\right)-\lambda s\left(t\right)\right)\right|}^c/{\partial \lambda |}_{\lambda =0}={\displaystyle {\sum }_t}{\left|\left(m\left(t\right)-\lambda s\left(t\right)\right)\right|}^{c-1}{\text{sign}\left(m\left(t\right)-\lambda s\left(t\right)\right)s\left(t\right)|}_{\lambda =0}={\displaystyle {\sum }_t}\mathrm{m̂}\left(t\right)s\left(t\right),$$

where m̂(t) = |m(t)|^c−1sign(m(t)), and C₁ is a constant. Since all discussions here focus on a single frequency, s(t) is taken to be a sinusoid, i.e. a single Fourier component. Under this assumption, the locally optimal test statistic can be easily computed using the Fourier transform of m̂(t). In other words, instead of directly taking the Fourier transform of m(t) to get M, the locally optimal test processes m(t) with a static nonlinearity, applies the Fourier transform, and then projects the Fourier coefficient at the response frequency, M̂_i, to the phase of the response.

3.2 Numerical detection results

The statistical power of each of the statistical variables listed in Table 1 is analyzed as a function of the neural response SNR in dB (i.e. 20log₁₀(γ)). Each Monte Carlo experiment uses 50 trials of the neural measurement. The results under the Gaussian assumption are shown in Fig. 2a. Each curve in there can be well fitted by a sigmoidal function and characterized by the SNR required for 80% statistical power. This SNR is shown in Fig. 2b under the generalized Gaussian prior. The numerical estimates of generalized Gaussian background activity use 5 second duration measurements m(t), but the results are not sensitive to the duration of neural measurements. The response power is the least effective statistic (of the four) for significance testing, and the phase coherence performs similarly to the evoked power for Gaussian background activity.

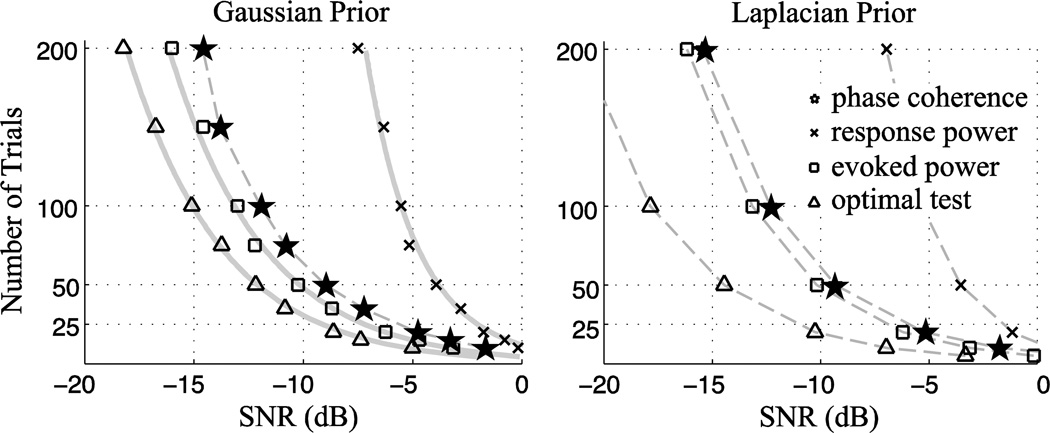
How the number of trials influences statistical power is illustrated in Fig. 3 for Gaussian and Laplacian background activity. For a given SNR, the averaged-response-power based significance test needs many more measurements to achieve similar performance to the phase coherence based significance test. The effect is particularly stark when the SNR of individual trials is poor (as is common in EEG/MEG measurements). In summary, when the stimulus-synchronized response is relatively weak compared to the ongoing background neural oscillation, it is very hard to detect an increase in the averaged response power, but easy to detect an increase in phase coherence, even when the stimulus-synchronized response is generated independently of background activity.

Figure 3.

The number of trials needed to achieve 80% statistical power at different SNR values, for background activity subject to a Gaussian (c = 2) or Laplacian (c = 1) distribution. Each point in the figure is a Monte Carlo numerical result. Theoretical values, when known, are plotted as solid gray lines. Test statistics whose curves lie more to the left possess greater statistical power at the same SNR than those to the right. To achieve similar statistical power, the response power test needs dramatically more measurement trials compared with other statistical tests.

3.3 Statistical properties of background neural activity

Appropriate values for the generalized Gaussian distribution’s shape parameter can be estimated experimentally. Here, as an example, it is estimated for MEG signals, either from an empty chamber, or from an experiment with human subjects listening to rhythmic stimuli, i.e. speech (Ding & Simon, 2012). When the subject is listening to speech, the recorded MEG signal contains both background activity and the response to the speech, but is dominated by background activity when not averaged over trials (Howard & Poeppel, 2010). The MEG activity is fitted to a generalized Gaussian distribution, with its shape parameter estimated as E(n(t)²)/E²(|n(t)|) (Mallat, 1999), where n(t) is the MEG recording from a sensor. Outliers corresponding to MEG activity stronger than 2 pT are removed from the analysis, as is routinely done in MEG analysis in the first step of artifact removal. The estimated shape parameter, the median over MEG sensors, is 1.2 for the empty chamber, and 1.8 ± 0.2 for 10 subjects during speech listening.

4. Discussion

4.1 Phase and power of neural activity

It is frequently observed that the phase of oscillatory LFP/EEG/MEG activity is aligned to rhythmic stimuli. This phenomenon could be a direct consequence of the “phase resetting” of ongoing massive neural oscillations but could also be an epiphenomenon caused by the generation of stimulus phase-locked activity, i.e. a stimulus phase-locked waveform. The decomposition of a response waveform into power (amplitude) and phase, e.g. through Fourier or Hilbert Transform, is nonlinear, and systematic characterizations of the statistical properties of power and phase has been lacking. The physiological meanings of the power-phase decomposition are also not established in general. In experiments, however, it is frequently observed that the power and phase of a neural response have distinct properties, e.g. the phase but not the power being sensitive to the stimulus. Here, we have demonstrated that such differences may simply be caused by the intrinsic statistical properties of the two measures rather than differences in underlying physiological mechanisms, and measured stimulus encoding in response phase may be simply a reflection of stimulus encoding in the entire response waveform, including amplitude. Therefore, the analysis of the response phase can be a powerful tool to extract and characterize stimulus-driven neural activity (e.g. Kayser et al. 2009; Lakatos et al. 2008; Luo & Poeppel, 2007), but its physiological indications should be treated with caution.

4.2 Relation to spatial synchronization of neural activity

The fundamental difference between the phase resetting theory and the background activity independent model presented here is whether the stimulus-synchronized neural response is generated independently of the background neural oscillations measured by LFP/EEG/MEG. However, it must be emphasized that LFP/EEG/MEG only measures spatially synchronized neural activity. Therefore, the model proposed here is an alternative to the hypothesis that the stimulus-synchronized neural activity is caused by the trial-to-trial phase resetting of spatially synchronized background activity, but is independent of the hypothesis that the LFP/EEG/MEG measurable response is caused by the spatial phase resetting of neural oscillations in local networks (Telenczuk et al., 2010).

More specifically, a stimulus-synchronized response can be generated through one of several mechanisms:

1. the excitation of new neural generators (excitation of new oscillators).

2. increased spatial synchronization between neural generators, while the power of each generator is constant (increased coupling between oscillators).

3. phase resetting of a single neural oscillator.

Mechanism (1) is clearly consistent with the linear model discussed in this study while mechanism (3) is the phase resetting model. For spatially synchronized neural measures, such as LFP, EEG, and MEG, mechanism (2) is also consistent with the linear model discussed here, since the power of spatially synchronized activity, in single trials, is influenced by both the power of individual neural generators and the synchronization between generators. Therefore, the current study distinguishes mechanism (3) from mechanisms (1) and (2). Of course, a stimulus can also lead to non-synchronized neural responses, i.e. induced activity, but such responses are not discussed in the current study.

4.3 Generation of stimulus-synchronized activity

The current model assumes stimulus-synchronized activity to be generated independently from background activity, i.e. that the neural measurement is a linear sum of stimulus-synchronized and stimulus-irrelevant activity (e.g. Ding & Simon, 2009, Howard & Poeppel, 2010, Sahani & Linden, 2003). How stimulus-synchronized activity is generated in the neural system, however, is not specified in the above model. In the following, we provide an additional simple linear-system model to demonstrate one way that stimulus-synchronized activity can be generated independent of stimulus-irrelevant activity. In this model, the neural generator is a damped oscillator that can be approximated as a linear system with a transfer function Tran(f), and so the response to stimulus Stim(f) is S(f) = Stim(f)Tran(f). The response S(f) is nonzero as long as the stimulus has energy at any frequency f₀ and the system responds at frequency f₀, i.e. Tran(f₀) ≠ 0. In this simple linear system model, the response is purely driven by the stimulus and therefore independent of any background activity.

4.5 Relation to the generation mechanism of the evoked response

The argument regarding the origin of the stimulus-synchronized neural response, discussed here, is very similar to the one regarding the origin of event-related potentials/fields (Sauseng et al., 2007; Shah et al., 2004): That is, whether the evoked response to a transient stimulus, e.g. an audio click or a visual flash, is generated independently of the background neural oscillations, or by the phase resetting of ongoing activity. Indeed, all the stimulus-synchronized activity discussed above is only assumed to be consistent over trials, and therefore generalizes to any evoked responses, even those generated by a transient, non-rhythmic stimulus. For event-related potentials/fields, simulations have shown that either of these two hypotheses may lead to phase synchronization of neural responses (Yeung et al., 2004). The analytical results obtained here validate and provide a theoretical basis for the results of those simulations.

4.6 Invariant null distribution for phase coherence

A distinct and important advantage of the phase coherence based significance test, over the others analyzed here, is that the null hypothesis is frequency independent and even experiment independent. Namely, the null hypothesis is always that the phase is uniformly distributed. In contrast, the null hypothesis of all other statistical variables discussed here, e.g. probability density function of the power of background activity, is data dependent and must be estimated from experiments.

4.7 Conclusion

This study characterizes the statistical properties of the power and phase of neural measurements based on a general model where stimulus-synchronized activity is generated independently from background activity. We analytically demonstrate that, even without phase resetting of background activity, the neural response phase is synchronized over trials and such phase synchronization is much more sensitive to the existence of stimulus-synchronized activity than response power. In other words, statistically, stimulus-synchronized activity may appear as a phase-resetting phenomenon, regardless of its underlying mechanism. These analytical and numerical results, together with earlier simulation results (Howard and Poeppel 2010; Yeung et al., 2004), question the validity of attempting to prove a phase resetting theory by showing the combination of response phase synchronization with the absence of power increase. Furthermore, the essence of the phase-resetting model is that intrinsic, ongoing neural activity contributes to the encoding of an external stimulus. This fundamental idea, however, does not even require the power of neural activity to be insensitive to external stimuli. Therefore, more advanced analysis methods, beyond simple power and phase analyses, would be required to establish any such phase resetting model.