Deletion of 1–43 amino acids in cardiac myosin essential light chain blunts length dependency of Ca²⁺ sensitivity and cross-bridge detachment kinetics

Abstract

The role of cardiac myosin essential light chain (ELC) in the sarcomere length (SL) dependency of myofilament contractility is unknown. Therefore, mechanical and dynamic contractile properties were measured at SL 1.9 and 2.2 μm in cardiac muscle fibers from two groups of transgenic (Tg) mice: 1) Tg-wild-type (WT) mice that expressed WT human ventricular ELC and 2) Tg-Δ43 mice that expressed a mutant ELC lacking 1–43 amino acids. In agreement with previous studies, Ca²⁺-activated maximal tension decreased significantly in Tg-Δ43 fibers. pCa₅₀ (−log₁₀ [Ca²⁺]_free required for half maximal activation) values at SL of 1.9 μm were 5.64 ± 0.02 and 5.70 ± 0.02 in Tg-WT and Tg-Δ43 fibers, respectively. pCa₅₀ values at SL of 2.2 μm were 5.70 ± 0.01 and 5.71 ± 0.01 in Tg-WT and Tg-Δ43 fibers, respectively. The SL-mediated increase in the pCa₅₀ value was statistically significant only in Tg-WT fibers (P < 0.01), indicating that the SL dependency of myofilament Ca²⁺ sensitivity was blunted in Tg-Δ43 fibers. The SL dependency of cross-bridge (XB) detachment kinetics was also blunted in Tg-Δ43 fibers because the decrease in XB detachment kinetics was significant (P < 0.001) only at SL 1.9 μm. Thus the increased XB dwell time at the short SL augments Ca²⁺ sensitivity at short SL and thus blunts SL-mediated increase in myofilament Ca²⁺ sensitivity. Our data suggest that the NH₂-terminal extension of cardiac ELC not only augments the amplitude of force generation, but it also may play a role in mediating the SL dependency of XB detachment kinetics and myofilament Ca²⁺ sensitivity.

force generation and muscle contraction is brought about by the ATP-dependent cyclic interactions between myosin heads (motor domain) and actin. One major feature of the motor domain, in addition to its ability to hydrolyze ATP, is its intricate linkage with the myosin lever arm. Upon strong binding of the motor domain to actin, the lever arm significantly swings to amplify small conformational changes in the motor domain and produce a power stroke (36). Stabilizing the lever arm is myosin essential light chain (ELC), which is considered to be essential for myosin function.

Two important reasons suggest that the function of ELC goes beyond that of just stabilizing the lever arm of the myosin cross-bridge (XB). First, it is well known that various isoforms of ELC exist (19), which differ not only in the sequence but also in length. Selective expression of these ELC isoforms in different tissue implies that its structure is important for tissue-specific motor domain function. Second, it is now becoming clear that during contractile activation, it is not just the motor domain that binds to actin but also the NH₂-terminal region of ELC (18, 30, 31, 41, 45). Although previous studies have shown a linkage between the binding of the NH₂-terminal region of ELC to actin and muscle function, the importance of this interaction in cardiac muscle function and the underlying mechanisms remains elusive. The cardiac-specific relevance of the NH₂-terminal extension of ELC is highlighted by the observation that a ∼40 amino acid longer isoform of ELC is expressed exclusively in the heart. On the other hand, smooth muscles express only the shorter isoform of ELC, and skeletal muscles express both the longer and the shorter isoforms of ELC simultaneously (19, 32, 43).

To understand how ELC functions, several investigators have used diverse experimental approaches. In vitro studies have shown that the NH₂-terminal region of ELC decreases the maximal fiber shortening velocity or the thin filament sliding velocity (3, 17, 25). Transgenic (Tg) mouse studies by Sanbe et al. (38) showed that the deletion of 5–14 amino acids in cardiac ELC had no effect on myofilament activation or XB cycling, whereas Miller et al. (29) evidenced decreased tension and faster cycling kinetics. Despite such extensive studies, a common theme for ELC function is yet to emerge. Regardless of what the physiological role of ELC is, there is little reason to doubt its importance in the structural stability of myosin heads. Low-angle X-ray diffraction studies by Muthu et al. (34) supports this argument because the expression of ELC-Δ43 (1–43 amino acids deleted at the NH₂-terminus) in the Tg-Δ43 mouse heart alters the disposition of myosin heads with respect to actin. Collectively, these observations are suggestive of a role for ELC in modulating the activity of myosin heads for optimal force production.

The structural effect of ELC on myosin head orientation takes on a new significance in cardiac muscle for two main reasons: 1) the extended NH₂-terminus of cardiac ELC has been suggested to influence the formation of strong XB (23, 29) and 2) strong XB are known to modulate the length-dependent activation of cardiac myofilaments (12, 39), a phenomenon that is more pronounced in cardiac muscles than in skeletal muscles (21, 28). In this regard, our goal was to determine the role of ELC in length-dependent activation of cardiac myofilaments. Therefore, we measured mechanical and dynamic properties of cardiac muscle fibers from Tg-wild-type (Tg-WT) and Tg-Δ43 mouse hearts at two different sarcomere lengths (SLs). To our knowledge, this is the first Tg mouse study that explicitly addresses the role of the NH₂-terminal extension of cardiac ELC in modulating SL dependency of cardiac muscle contraction. Our study demonstrates that Ca²⁺-activated maximal tension decreased significantly in Tg-Δ43 fibers without affecting the SL dependency of force generation. However, the SL dependency of myofilament Ca²⁺ sensitivity and XB detachment kinetics were ablated in Tg-Δ43 fibers.

METHODS

Animal protocols.

The handling of all the experimental animals followed the institutional guidelines and protocols approved by the Animal Care and Use Committee and the Office of Laboratory Animal Welfare, National Institutes of Health. Our muscle fiber study followed the established guidelines of the Washington State University Institutional Animal Care and Use Committee.

Tg mice.

We used two different groups of Tg mice that expressed different forms of the human ventricular ELC (hELC) in the heart: 1) Tg-WT control mice that expressed WT hELC and 2) Tg-Δ43 mice that expressed a modified form of hELC, in which 1–43 amino acids at the NH₂-terminus were deleted. Tg-WT mice expressed ∼76% of hELC in the left ventricles, and Tg-Δ43 mice expressed ∼35% of ELC-Δ43 in the left ventricles. We used ∼7-mo-old female mice for all experiments. Tg protein expression profiles, as well as the histopathological assessment of the hearts from Tg-WT and Tg-Δ43 mice, were previously described (23).

Preparation of detergent-skinned cardiac muscle fiber bundles.

Papillary muscle fiber bundles from Tg-Δ43 and Tg-WT mouse hearts were prepared, as previously described (8). Mice were deeply anesthetized using isoflurane, and their hearts were quickly excised. These hearts were immersed in an ice-cold high relaxing solution, which contained the following: (in mM) 20 2,3-butanedione monoxime, 50 N,N-bis-(2-hydroxyethyl)-2-amino-ethane-sulfonic acid (BES), 30.83 potassium propionate (K-propionate), 10 sodium azide (NaN₃), 20 EGTA, 6.29 magnesium chloride (MgCl₂), 6.09 Na₂ATP, 4 benzamidine-HCl, and 1 dithiothreitol (pH 7.0). The following protease inhibitors were also added to this solution: (in μM) 5 bestatin, 2 E-64, 10 leupeptin, 1 pepstatin, and 200 phenylmethylsulfonyl fluoride. Papillary muscle bundles were excised from the left ventricles of Tg-Δ43 and Tg-WT mouse hearts. Smaller bundles (2 to 3 mm in length and 150–250 μm in width and thickness) were dissected from larger bundles. Fiber bundles were detergent-skinned overnight at 4°C in high relaxing solution that contained 1% Triton X-100 (7).

pCa solutions.

The reagent concentrations of all pCa (pCa = −log₁₀ [Ca²⁺]_free) solutions were calculated based on a program (10). The relaxing solution (pCa 9.0) contained the following components: (in mM) 50 BES, 5 NaN₃, 10 phosphoenol pyruvate, 10 EGTA, 0.024 CaCl₂, 6.87 MgCl₂, 5.83 Na₂ATP, and 51.14 K-propionate. The maximal Ca²⁺-activating solution (pCa 4.3) contained the following: (in mM) 50 BES, 5 NaN₃, 10 phosphoenol pyruvate, 10 EGTA, 10.11 CaCl₂, 6.61 MgCl₂, 5.95 Na₂ATP, and 31 K-propionate. pCa solutions also contained 0.5 mg/ml pyruvate kinase and 0.05 mg/ml lactate dehydrogenase. The following cocktail of protease inhibitors were added to pCa solutions: (in μM) 10 leupeptin, 10 pepstatin, 100 phenylmethylsulfonyl fluoride, 20 A₂P₅, and 10 oligomycin. The ionic strength of the pCa solutions was 180 mM.

Measurement of steady-state isometric force.

Isometric steady-state force was measured using methods previously described (9). The ends of the muscle fiber were clipped using T-shaped aluminum foil clips, and the fiber was mounted between a force transducer and a servo motor. The baseline SL of the fiber was adjusted to either 1.9 or 2.2 μm using laser diffraction technique (9). The fiber was then subjected to two cycles of activation and relaxation. SL was readjusted to the baseline if necessary. The fiber was then bathed in a series of pCa solutions ranging from pCa 4.3 to 9.0, and the forces were digitally recorded. All measurements were made at 20°C (9).

Measurement of rate of tension redevelopment.

The rate constant associated with tension redevelopment, k_tr, was determined using a modification of the slack/restretch protocol, originally described by Brenner and Eisenberg (5). First, the baseline SL of the fiber was set to either 1.9 or 2.2 μm, and the fiber was allowed to reach steady-state force in pCa 4.3 solution. The fiber was then rapidly slackened by 10% of its baseline length. After 25 ms, the motor arm was commanded to stretch the fiber rapidly (within 0.5 ms) past the original set point by 10%. Then the fiber was brought back to its baseline length and was allowed to redevelop force. k_tr was estimated by fitting a monoexponential function given by the following equation:

$$\text{F}=({\text{F}}_{\text{s}\text{s}}-{\text{F}}_{\text{r}\text{e}\text{s}})(1-{\text{e}}^{-{\text{k}}_{\text{t}\text{r}}\mathit{\text{t}}})+{\text{F}}_{\text{r}\text{e}\text{s}}$$

where F is the force at time t, F_ss is the steady-state isometric force and F_res is the residual force.

Measurement of XB recruitment and XB distortion dynamics.

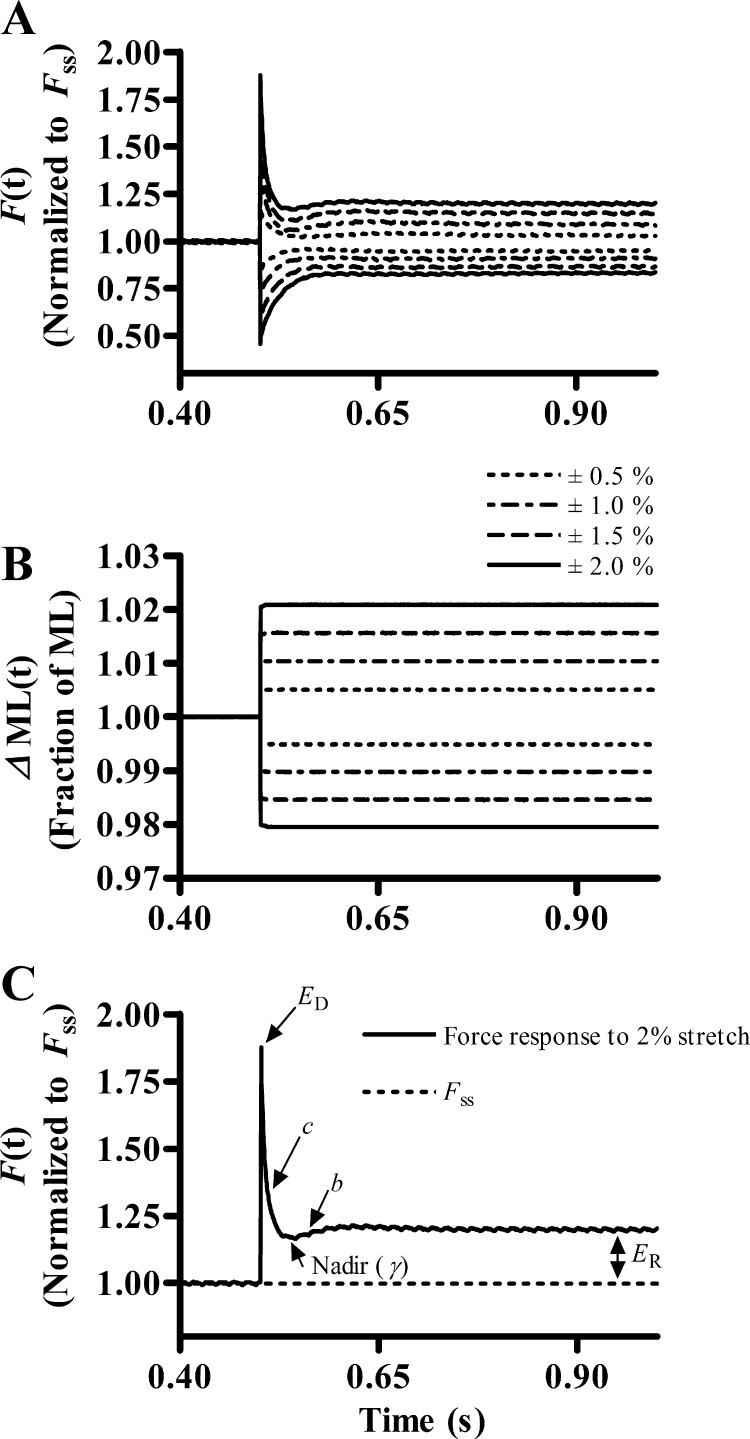
Upon attainment of steady-state isometric force in pCa 4.3 solution, step-like length changes were applied to the fiber (13). In brief, the motor arm was commanded to alter the muscle fiber length (ML) in a step-like manner (±0.5, ±1.0, ±1.5, and ±2.0% of the initial ML), as shown in Fig. 1B. Initially, the ML was rapidly increased by 0.5% and held at the increased length for 5 s. The motor arm was then commanded to rapidly return to the initial ML where it was held for 5 s. Step-like length changes were repeated for ± 1.0%, ± 1.5%, and ± 2.0% ML (Fig. 1B). A nonlinear recruitment distortion model (13) was fitted to the force responses to estimate several model parameters (see Fig. 1, A and C) and thereby determine XB recruitment and XB distortion dynamics.

Fig. 1.

Representative family of force responses of a muscle fiber to step-like length perturbations. A: force responses of a maximally activated (pCa 4.3) transgenic-wild-type (Tg-WT) cardiac muscle fiber at sarcomere length (SL) 2.2 μm normalized to isometric steady-state force (F_ss). B: length perturbation refers to the step-like stretch and release of the muscle fiber by ±0.5, ±1.0, ±1.5, and ±2.0% of the initial muscle length (ML). C: to highlight the significance of the 5 nonlinear recruitment distortion (NLRD) model parameters, only a representative sample of the force response of a maximally stretched (2%) Tg-WT fiber at SL 2.2 μm is shown. The NLRD model (13) parameters are as follows: the rate by which additional cross-bridge (XB) are recruited because of a change in ML (b); the rate by which the strain of distorted XB is dissipated, following a sudden change in ML (c); the magnitude of instantaneous fiber stiffness due to a sudden change in ML (E_D); the magnitude of change in stiffness from the initial steady state to the new steady state due to the length-mediated recruitment of XB (E_R); and the nonlinear term (γ) that represents the allosteric cooperative mechanisms by which distorted XB affect recruitment of additional XB. Arrows point to the regions on the force response trace from which the respective NLRD parameters were estimated.

Data analysis.

Data are shown as means ± SE. pCa₅₀ (−log of [Ca²⁺]_free required for half-maximal activation) and the Hill coefficient (n_H) were estimated by fitting the Hill's equation to normalized pCa tension data (20). The interpretation of our results involved two experimental factors: an ELC factor (WT-ELC and ELC-Δ43) and a SL factor (1.9 and 2.2 μm). Therefore, we used two-way ANOVA to test the hypothesis that the effect of the ELC factor on a given contractile parameter depends on the SL factor (interaction effect). When the interaction effect was significant, it showed that the differences between effects of WT-ELC and ELC-Δ43 were dissimilar at different SL. Therefore, to compare the effects of ELC on a specific parameter at a given SL, appropriate post hoc multiple comparisons were made using Holm-Bonferroni corrected t-tests. When the interaction effect was not significant, we interpreted only the main effect because of the ELC factor. The criterion for statistical significance was set at P < 0.05.

RESULTS

Effect of varied expression levels of hELC in Tg mice.

Kazmierczak et. al (23) generated several lines of Tg-WT and Tg-Δ43 mice where the expression levels of hELC varied among the different lines. Tg-WT mice of lines, L3 (∼36% expression of hELC) and L4 (∼71% expression of hELC), were compared by carrying out force and ATPase measurements. The results indicated that there were no statistically significant differences in the measured parameters between Tg-WT L3 and Tg-WT L4 fibers. Therefore, these observations suggested that varied expression levels of hELC in Tg mice did not affect the contractile properties of the fibers. Thus we were able to carry out valid comparisons between Tg-Δ43 mice that expressed ∼35% of ELC-Δ43 and Tg-WT mice that expressed ∼76% of hELC in the left ventricles.

Ca²⁺-activated maximal tension in Tg-WT and Tg-Δ43 fibers.

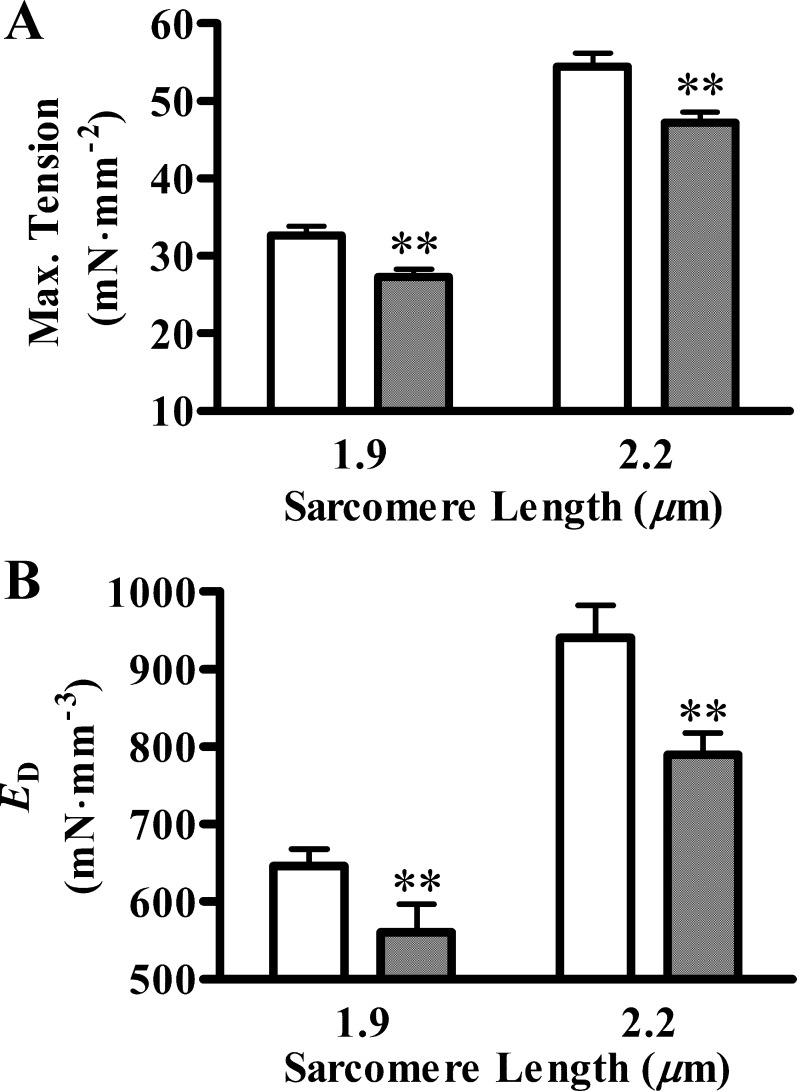
We measured Ca²⁺-activated maximal tension in Tg-WT and Tg-Δ43 fibers at short (1.9 μm) and long SL (2.2 μm). At SL of 1.9 μm, the Ca²⁺-activated maximal tension values (in mN·mm⁻²) were 32.64 ± 1.20 and 27.27 ± 1.03 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 2A). At SL of 2.2 μm, the respective values were 54.44 ± 1.80 and 47.22 ± 1.39 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 2A). Two-way ANOVA revealed that the expression of ELC-Δ43 altered maximal tension significantly (P < 0.01). This was indicated by a decrease in maximal tension in Tg-Δ43 fibers by ∼16% at SL of 1.9 μm and by ∼13% at SL of 2.2 μm, compared with Tg-WT fibers (Fig. 2A). These results confirmed earlier observations that the deletion of 1–43 amino acids in cardiac ELC leads to impaired tension development (23).

Fig. 2.

Ca²⁺-activated maximal tension and the magnitude of instantaneous stiffness due to distortion of bound XB (E_D). A: Ca²⁺-activated maximal tension (Max tension) was measured in pCa 4.3 solution. Two-way ANOVA showed that the main effect due to essential light chain (ELC) factor was significant (**P < 0.01), which indicated that ELC-Δ43 caused an overall decrease in maximal tension: ∼16% at SL of 1.9 μm and ∼13% at SL of 2.2 μm. B: E_D was measured as previously described (13). Two-way ANOVA showed that the main effect due to ELC factor was significant (**P < 0.01), which showed that ELC-Δ43 caused an overall decrease in E_D: ∼13% at SL of 1.9 μm and ∼16% at SL of 2.2 μm. White bars represent Tg-WT, and black bars represent Tg-Δ43 fibers. Values are denoted as means ± SE. At least 7 fibers were used for each group.

Approximation of strongly bound XB in Tg-WT and Tg-Δ43 fibers.

To determine a possible reason for the decrease in the Ca²⁺-activated maximal tension, we estimated the instantaneous stiffness parameter (E_D), as described in methods (Fig. 1C). E_D is proportional to the number of strongly bound XB, because it is a measure of the muscle fiber stiffness due to the strain of strongly bound XB, following an instantaneous length change. At SL of 1.9 μm, E_D values (in mN·mm⁻³) were 646 ± 21 and 561 ± 35 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 2B). At SL of 2.2 μm, the values were 940 ± 41 and 789 ± 27 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 2B). Two-way ANOVA revealed that ELC-Δ43 altered E_D significantly (P < 0.01). This was indicated by a decrease in E_D in Tg-Δ43 fibers by ∼13% at SL of 1.9 μm and by ∼16% at SL of 2.2 μm. A decrease in E_D is suggestive of a decrease in the number of strongly bound XB in Tg-Δ43 fibers. This observation substantiated our conclusion from maximal tension data that the deletion of 1–43 amino acids of ELC attenuated maximal tension. A previous study has shown that the fraction of XB that bind to actin during maximal Ca²⁺ activation was lesser by ∼15% in ∼7-mo-old Tg-Δ43 mouse cardiac muscle fibers (23). Therefore, our data on E_D support those earlier findings and suggest that the decrease in Ca²⁺-activated maximal tension might be a consequence of a fewer strongly bound XB in Tg-Δ43 versus Tg-WT fibers.

Myofilament Ca²⁺ sensitivity in Tg-WT and Tg-Δ43 fibers.

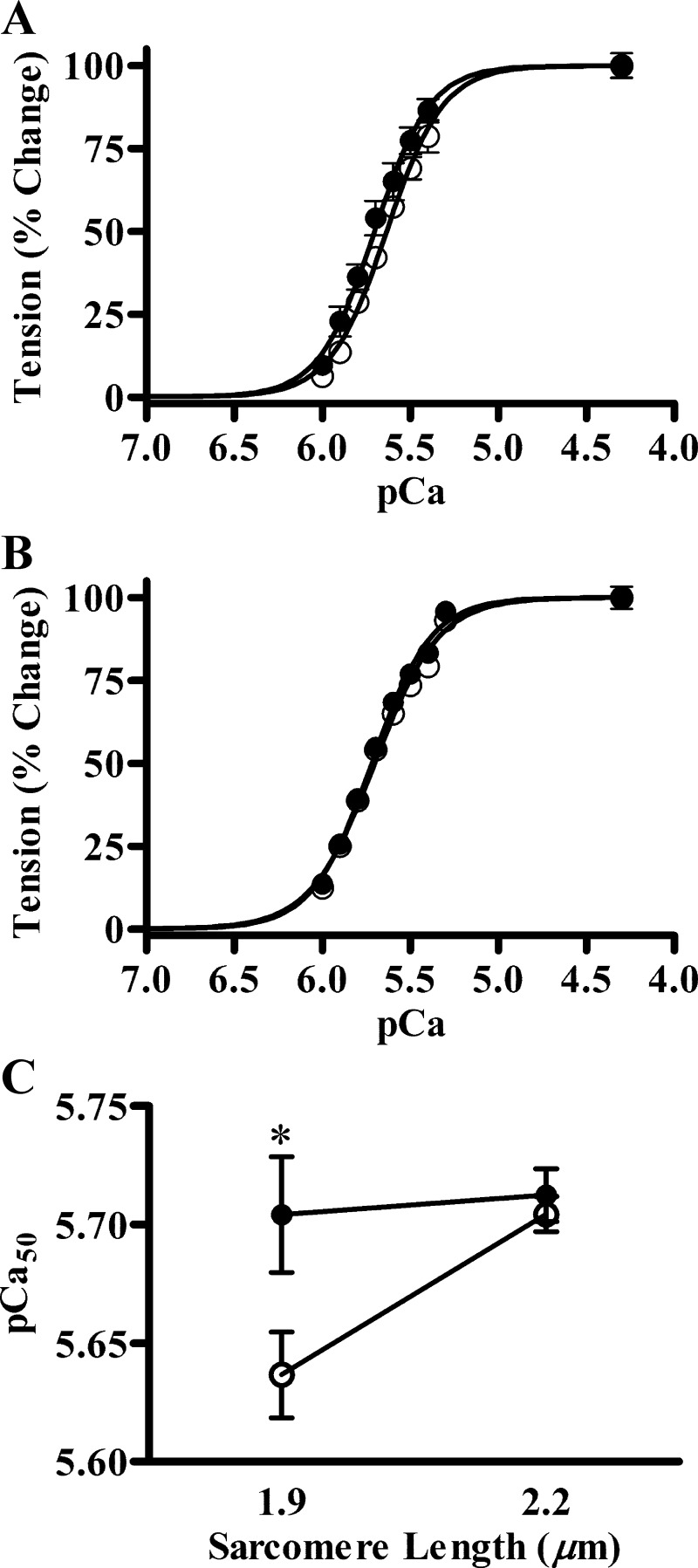
Normalized pCa tension data of Tg-WT and Tg-Δ43 fibers were analyzed by using the Hill equation (20). The myofilament Ca²⁺ sensitivity (pCa₅₀) and cooperativity (n_H) were estimated, as previously described (8). pCa-tension relationships at SL of 1.9 and 2.2 μm are shown in Fig. 3, A and B, respectively. At SL of 1.9 μm, pCa₅₀ values were 5.64 ± 0.02 and 5.70 ± 0.02 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 3A). At SL of 2.2 μm, the values were 5.70 ± 0.01 and 5.71 ± 0.01 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 3B). Two-way ANOVA revealed that the expression of ELC-Δ43 significantly (P < 0.05) altered the effect of SL on pCa₅₀ (Fig. 3C). To probe the cause of this significant interaction, we used Holm-Bonferroni corrected t-tests to compare the effect of ELC-Δ43 on pCa₅₀ at each SL. The post hoc Holm-Bonferroni tests indicated that pCa₅₀ at SL 1.9 μm was significantly higher in Tg-Δ43 fibers (P < 0.05), whereas this was unaffected at SL 2.2 μm. These results suggest that the SL dependency of myofilament Ca²⁺ sensitivity was abolished in Tg-Δ43 fibers (Fig. 3C). n_H values at SL 1.9 μm were 2.72 ± 0.07 and 2.92 ± 0.09 in Tg-WT and Tg-Δ43 fibers, respectively. At SL 2.2 μm, the values were 2.35 ± 0.14 and 2.54 ± 0.13 in Tg-WT and Tg-Δ43 fibers, respectively. Two-way ANOVA revealed that ELC-Δ43 had no impact on myofilament cooperativity.

Fig. 3.

Normalized pCa-tension relationships and SL dependency of myofilament Ca²⁺ sensitivity. Isometric steady-state tension values were normalized to the maximal tension generated in pCa 4.3 solution. The Hill equation was fitted to the normalized data to estimate pCa₅₀ and n_H. A: pCa-tension relationships at SL 1.9 μm. B: pCa-tension relationships at SL 2.2 μm. C: SL dependency of myofilament Ca²⁺ sensitivity. Two-way ANOVA showed that the ELC-SL interaction effect on pCa₅₀ was significant (P < 0.05). Subsequent post hoc Holm-Bonferroni tests revealed that the increase in pCa₅₀ caused by ELC-Δ43 was significant (*P < 0.05) only at SL 1.9 μm, indicating that SL dependency of myofilament Ca²⁺ sensitivity was ablated in Tg-Δ43 fibers. White circles represent Tg-WT, and black circles represent Tg-Δ43 fibers. Values are denoted as means ± SE. At least 7 fibers were used for each group.

The rate of XB detachment in Tg-WT and Tg-Δ43 fibers.

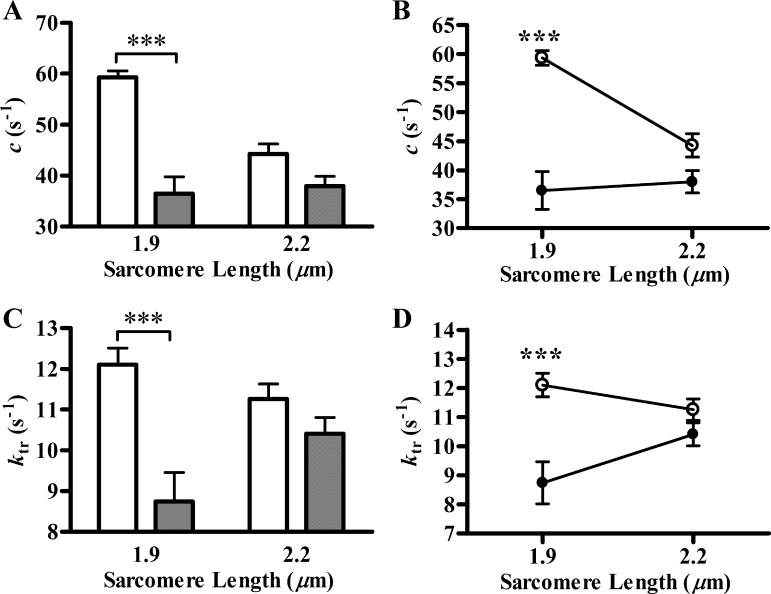
We wanted to test whether ELC-Δ43 also altered XB detachment rate in addition to its attenuating effect on the number of strong XB. Therefore, we estimated the rate constant of muscle length-mediated XB distortion, c, in Tg-WT and Tg-Δ43 fibers. c was estimated by fitting the nonlinear recruitment distortion model to a family of force responses elicited by step-like length perturbations, as described in methods (13). c values (in s⁻¹) at SL of 1.9 μm were 59.31 ± 1.25 and 36.49 ± 3.27 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 4A). At SL of 2.2 μm, the values were 44.25 ± 1.99 and 37.98 ± 1.90 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 4A). Two-way ANOVA revealed that the expression of ELC-Δ43 significantly (P < 0.01) altered the effect of SL on c. Subsequent post hoc Holm-Bonferroni tests indicated that c decreased significantly (∼38%; P < 0.001) in Tg-Δ43 fibers at SL 1.9 μm. On the other hand, the decrease in c (∼14%) was not significant between Tg-WT and Tg-Δ43 fibers at SL 2.2 μm (Fig. 4B). This demonstrated that ELC-Δ43 had no effect on c at long SL, whereas c was preferentially reduced at the short SL (Fig. 4B). Because c is an approximate measure of the rate of XB detachment (13), our results suggest that ELC-Δ43 blunts the SL dependency of XB detachment kinetics in Tg-Δ43 fibers.

Fig. 4.

Length-mediated XB distortion rate constant (c) and tension redevelopment rate constant (k_tr). A and B: c was measured as previously described (13). Two-way ANOVA revealed that the ELC-SL interaction effect on c was significant (P < 0. 01). Subsequent post hoc Holm-Bonferroni tests revealed that the decrease in c caused by ELC-Δ43 was significant (***P < 0.001) only at SL 1.9 μm, indicating that SL dependency of XB distortion rate constant was ablated in Tg-Δ43 fibers. At least 7 fibers were used for each group. C and D: k_tr was measured as previously described (5). Two-way ANOVA revealed that the ELC-SL interaction effect on k_tr was significant (P < 0. 05). Subsequent post hoc Holm-Bonferroni tests revealed that the decrease in k_tr caused by ELC-Δ43 was significant (***P < 0.001) only at SL 1.9 μm, indicating that SL dependency of k_tr was ablated in Tg-Δ43 fibers. At least 6 fibers were used for each group. White bars and circles represent Tg-WT, and black bars and circles represent Tg-Δ43 fibers. Values are denoted as means ± SE.

XB turnover rate and XB recruitment kinetics in Tg-WT and Tg-Δ43 fibers.

Because the Ca²⁺-activated maximal tension and the rate of XB detachment were significantly affected in Tg-Δ43 fibers, we wanted to determine whether the XB turnover rate, as assessed by k_tr, was also altered. k_tr represents the rate by which XB are recruited from a nonforce bearing pool to a force-bearing pool (4). At SL of 1.9 μm, k_tr values (in s⁻¹) were 12.10 ± 0.41 and 8.74 ± 0.72 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 4C). At SL of 2.2 μm, the values were 11.26 ± 0.37 and 10.41 ± 0.40 in Tg-WT and Tg-Δ43 fibers, respectively (Fig. 4C). Two-way ANOVA revealed that ELC-Δ43 significantly (P < 0.05) altered the effect of SL on k_tr. Subsequent post hoc Holm-Bonferroni tests indicated that k_tr decreased significantly (∼28%; P < 0.001) in Tg-Δ43 fibers at SL 1.9 μm. On the other hand, the decrease in k_tr (∼8%) was not significant between Tg-WT and Tg-Δ43 fibers at SL 2.2 μm (Fig. 4D). This demonstrated that ELC-Δ43 had no effect on k_tr at long SL, whereas k_tr was preferentially reduced at the short SL. The model-estimated values of E_R, b, and γ are listed in Table 1 (Fig. 1C). Two-way ANOVA showed that E_R, b, and γ were not altered in Tg-Δ43 fibers at either SL.

Table 1.

Effect of ELC-Δ43 on E_R, b, and γ in Tg-Δ43 fibers

	SL (1.9 μm)		SL (2.2 μm)
	Tg-WT	Tg-Δ43	Tg-WT	Tg-Δ43
ER, mN/mm3	100.12 ± 3.25	103.07 ± 8.25	189.90 ± 9.92	171.20 ± 13.58
b, s−1	36.91 ± 2.47	35.01 ± 2.10	33.89 ± 1.30	33.03 ± 1.15
γ, s−1	88.72 ± 7.67	73.64 ± 10.68	57.12 ± 5.51	49.48 ± 3.38

Values are means ± SE. E_R, b, and γ were estimated by fitting the NLRD model to the force responses elicited by the muscle fiber to step-like length changes, as previously described (13). Two-way ANOVA showed no significant essential light chain-sarcomere length (ELC-SL) interaction effect on E_R, b, and γ. Furthermore, the main effect due to mutant ELC lacking 1-43 amino acids (ELC-Δ43) factor did not affect E_R, b, and γ at either SL. At least 7 fibers were used for each group.

DISCUSSION

We investigated the role of the NH₂-terminal extension of cardiac ELC in the SL dependency of cardiac muscle contraction. New findings from our Tg-Δ43 mouse cardiac fiber studies demonstrate that ELC-Δ43 attenuates the SL dependency of myofilament Ca²⁺ sensitivity and XB detachment kinetics. It is likely that the decrease in the XB detachment rate, in combination with structural alterations of myosin heads (34), manifests as altered SL dependency of myofilament response to Ca²⁺ in Tg-Δ43 fibers.

The effect of ELC-Δ43 on Ca²⁺-activated maximal tension and the magnitude of instantaneous muscle fiber stiffness.

An overall decrease in Ca²⁺-activated maximal tension was observed in Tg-Δ43 fibers when compared with Tg-WT fibers (Fig. 2A). This is in agreement with previous observations made by Kazmierczak et al. (23). E_D also decreased significantly (Fig. 2B), indicating that the drop in tension is most likely due to a reduced number of strongly bound XB in Tg-Δ43 fibers. This correlation is made because our previous studies have demonstrated that E_D is a measure of the number of strongly bound XB (13). The decrease in stiffness observed in our study is an apparent contradiction to the observation made by Muthu et al. (34), who showed that stiffness was not affected in Tg-Δ43 fibers. However, it must be noted that their observations were carried under rigor and relaxed conditions (26), where all XB were either in the ADP-bound state (rigor) or in the unbound state (relaxed). Therefore, they interpreted unaltered stiffness to suggest that stiffness per XB was unaltered. In contrast, the E_D measurements in our study were carried out on maximally Ca²⁺-activated fibers, where the XB were cycling. Therefore, we interpret a decrease in E_D to suggest that ELC-Δ43 decreases the number of force-generating XB. In agreement with our finding, Kazmierczak et al. (23) have shown that the fraction of XB that binds to actin during maximal Ca²⁺ activation was lesser by ∼15% in ∼7-mo-old Tg-Δ43 mouse cardiac muscle fibers.

An alternative explanation for the decrease in tension is provided by low-angle X-ray diffraction studies on Tg-Δ43 fibers at SL of 2.2 μm by Muthu et al. (34). They observed a shift in the mass of myosin heads away from the thick filaments but closer to the actin filaments in Tg-Δ43 fibers. Therefore, they hypothesized that the angle between the long axis of myosin heads and actin would decrease because of the increased proximity of the myosin heads to the actin filament (34). This hypothesis provides a mechanical basis for the decrease in force caused by the inability of ELC-Δ43 to hold myosin heads in an optimal configuration. An interesting observation in their study is that the interfilament spacing does not change, which adds further credence to the assertion that ELC has a direct effect on myosin heads. Collectively, these observations highlight the role of the interaction of the NH₂-terminus of ELC with actin in maintaining the structural integrity of the myosin heads for optimal force production. One limitation of our study was that we used a Tg mouse model that expressed hELC. However, Kazmierczak et al. (23) observed that there were no significant differences between non-Tg and Tg-WT mice. Therefore, we believe that functional differences between Tg-WT and Tg-Δ43 mice could be directly attributed to the lack of residues 1–43 in ELC.

The effect of ELC-Δ43 on XB detachment kinetics.

Using a diverse set of in vitro assays, several studies have suggested that the interaction between the NH₂-terminus of ELC and actin either augments or decreases XB detachment rate (33, 35, 40, 42, 44). In contrast, two lines of Tg mouse studies show no effect on XB detachment kinetics (23, 29, 34). For example, Miller et al. (29) showed that the unloaded shortening velocity was not altered in fibers from Tg mouse hearts that expressed a mutant version of ELC in which residues 5–14 were deleted. Kazmierczak et al. (23) and Muthu et al. (34) observed no significant differences between Tg-WT and Tg-Δ43 fibers. Since the above-mentioned kinetic studies on Tg mouse fibers were carried out at longer SL, we tried to discriminate the effects of ELC-Δ43 on XB kinetics at two different SL (1.9 and 2.2 μm). The importance of measuring XB detachment kinetics at different SL is highlighted by the observation that the allosteric/cooperative mechanisms in the thin filament are tightly coupled to both Ca²⁺- and XB-induced changes in the thin filament [for review, see Gordon et al. (16)]. Therefore, SL-mediated effects on the thin filament will have an impact on XB detachment dynamics because XBs themselves affect the balance between regulatory unit (Tm-Tn) “on” and “off” states through cooperative activation. Interestingly, our results show that the SL dependency of both c and k_tr are ablated in Tg-Δ43 fibers because the decrease in both parameters was significant only at the short SL (Fig. 4). This suggests that ELC-Δ43 modulates c and k_tr differently at different SL. Since c approximates XB detachment rate g (6, 9, 13), our results demonstrate that ELC-Δ43 selectively decreases g at the short SL. According to the two-state model (22), since k_tr = f + g, a significant decrease in g provides a basis for a significant decrease in maximal k_tr at short SL (Fig. 4). If the effect of ELC-Δ43 was such that it decreased only g, the two-state XB model (22) would predict an increase of force in Tg-Δ43 fibers instead of the decrease that we observed (Fig. 2A). The rationale for this argument is that according to the two-state model, force is proportional to f/(f + g). Our results, however, show that ELC-Δ43 does not affect the SL dependency of maximal force development, i.e., ELC-SL interaction effect was not significant (Fig. 2A); therefore, we anticipate that f may also decrease differently at both short and long SL. However, the lack of any significant differences in b (rate of recruitment of additional XB in response to a change in muscle length) between Tg-WT and Tg-Δ43 fibers precluded us from making any valid conclusion regarding changes in f (Table 1). The decrease in k_tr can also be explained by the effect of ELC-Δ43 on the number of cycling XB and the extent of thin filament activation (27, 37). Our results indicate that during maximal Ca²⁺ activation, fewer XB are brought into force-bearing state in Tg-Δ43 fibers (Fig. 2), thereby suggesting that the decreased activation of thin filament could also contribute to slower k_tr.

The effect of ELC-Δ43 on the SL dependency of myofilament Ca²⁺ sensitivity.

According to the Frank-Starling law of the heart, cardiac myocytes are equipped with a length-sensing mechanism that adjusts the activity of myosin XB to the volume of blood in the ventricle: SL dependence of myofilament Ca²⁺ sensitivity has been considered a key component of this mechanism (2, 24). Our results show that the SL-dependent increase in myofilament Ca²⁺ sensitivity was blunted in Tg-Δ43 fibers (Fig. 3C). This observation can be explained by considering that a decrease in g at short SL increases XB dwell time and, therefore, leads an increase in myofilament response to Ca²⁺ at short SL (1, 12, 15). This hypothesis is well supported by results from our dynamic studies, which show that the SL dependency of XB detachment kinetics is also ablated in Tg-Δ43 fibers (Fig. 4, A and B).

Another clue as to how the SL dependency of Ca²⁺ sensitivity is ablated in Tg-Δ43 fibers is provided by the structural data obtained from Muthu et al. (34). Using low angle X-ray diffraction measurements, they studied the structural impact of ELC-Δ43 on myosin heads in Tg-Δ43 fibers at SL of 2.2 μm. Their results show that the proximity between actin and myosin increases in Tg-Δ43 fibers, albeit without any changes in interfilament spacing. If this effect is an intrinsic property of ELC-Δ43, it is likely to have similar structural effects on myosin heads at SL of 1.9 μm. Thus we would expect myosin heads in Tg-Δ43 fibers to be closer to actin than those of Tg-WT fibers at SL of 1.9 μm. Myofilament Ca²⁺ sensitivity is augmented by bringing actin and myosin closer together (14). Therefore, it is reasonable to predict an increase in myofilament Ca²⁺ sensitivity in Tg-Δ43 fibers at SL of 1.9 μm, but the same was not observed at 2.2 μm (Fig. 3). Why is it that the Ca²⁺ sensitivity at long SL is not affected although actin and myosin in Tg-Δ43 fibers are presumably much closer to each other than in Tg-WT fibers? The answer to this question may be found in observations that the orientation of myosin heads, as well as the distance between actin and myosin, is optimal at the longer SL, where cardiac myofilaments are known to display maximum sensitivity to Ca²⁺ (11, 46). Thus any further reduction in the distance between actin and myosin in Tg-Δ43 fibers at 2.2 μm will not increase myofilament Ca²⁺ sensitivity above that of Tg-WT fibers (Fig. 3C).

Conclusions.

Our results provide the following new information regarding the effects of the lack of the NH₂-terminus of ELC on cardiac muscle function: 1) SL dependency of XB detachment kinetics is ablated in Tg-Δ43 fibers and 2) SL dependency of myofilament Ca²⁺ sensitivity is also blunted in Tg-Δ43 fibers. Based on these observations, we conclude that the NH₂-terminal extension of cardiac ELC is not only important for regulating the XB detachment kinetics, but it may also participate in modulating SL-dependent activation of cardiac myofilaments.

GRANTS

This work was supported, in part, by National Heart, Lung, and Blood Institute Grants HL-075643 (to M. Chandra) and HL-108343, HL-071778, and HL-090786 (to D. Szczesna-Cordary).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

J.J.M., S.K.G., K.K., D.S.-C., and M.C. conception and design of research; J.J.M. and S.K.G. performed experiments; J.J.M., S.K.G., and S.J.F. analyzed data; J.J.M., S.K.G., S.J.F., D.S.-C., and M.C. interpreted results of experiments; J.J.M. and S.K.G. prepared figures; J.J.M., S.K.G., and M.C. drafted manuscript; J.J.M., S.K.G., S.J.F., K.K., D.S.-C., and M.C. edited and revised manuscript; J.J.M., S.K.G., S.J.F., K.K., D.S.-C., and M.C. approved final version of manuscript.