Predicting Development of Mathematical Word Problem Solving Across the Intermediate Grades

Abstract

This study addressed predictors of the development of word problem solving (WPS) across the intermediate grades. At beginning of 3rd grade, 4 cohorts of students (N = 261) were measured on computation, language, nonverbal reasoning skills, and attentive behavior and were assessed 4 times from beginning of 3rd through end of 5th grade on 2 measures of WPS at low and high levels of complexity. Language skills were related to initial performance at both levels of complexity and did not predict growth at either level. Computational skills had an effect on initial performance in low- but not high-complexity problems and did not predict growth at either level of complexity. Attentive behavior did not predict initial performance but did predict growth in low-complexity, whereas it predicted initial performance but not growth for high-complexity problems. Nonverbal reasoning predicted initial performance and growth for low-complexity WPS, but only growth for high-complexity WPS. This evidence suggests that although mathematical structure is fixed, different cognitive resources may act as limiting factors in WPS development when the WPS context is varied.

Mathematical word problem solving (WPS) is complex because it requires students to read and understand written material that expresses numerical relations. In addition, WPS requires a process of translating text to mathematical equations or a series of computations (i.e., using informal strategies, see Kieran, 1990, 1992; Koedinger & Nathan, 2004). According to theories of WPS, as part of this translational process, problem solvers construct two types of mental representations: problem models and situation models (Kintsch & Greeno, 1985; Nathan, Kintsch, & Young, 1992; Staub & Reusser, 1995).

Problem models are representations that contain only the elements essential for representing the mathematical structure of the problem (Kintsch & Greeno, 1985). For example, in the change problem, “Joe won 3 marbles. Now he has 5 marbles. How many marbles did Joe have in the beginning?” (see Kintsch & Greeno, 1985; Staub & Reusser, 1995), the problem model, which is influenced by education and problem-solving experience, includes three sets: marbles beginning (?), marbles won (3), marbles now (5), and the relations between those sets (? + 3 = 5). The problem model may be associated with an arithmetic strategy (e.g., counting up).

Situation models are qualitative representations of the problem, which include inferences based on real-world experiences. In the problem just described, the situation model allows the problem solver to make the inference that Joe had some marbles initially and the marbles he won were in addition to the marbles he initially had (Staub & Reusser, 1995). In fact, when the problem is reworded as, “Joe had some marbles. He won 3 more marbles. Now he has 5 marbles,” a greater proportion of first-grade students produce correct responses (33%) than when the problem is worded as described above (13%; De Corte, Verschaffel, & De Win, 1985).

Theoretically, the degree to which problem and situation models influence WPS behavior varies both as a function of the parameters of the word problem and the experience of the problem solver (Nathan et al., 1992; Reusser, 1990). Consequently, academic skills and cognitive resource requirements may also vary as a function of these two factors. The purpose of the present study was to examine the relations between WPS and academic skills and cognitive resources as students mature and gain experience in WPS. Specifically, our goal was to determine which of these skills and resources are most critical in predicting performance and growth when controlling for the others and to determine whether these “limiting factors” differ as a function of the situational complexity of the word problems. Interpretations of these limiting factors in the context of theories about WPS and the roles of situation and problem model representations in WPS skill have implications for WPS instruction and intervention.

Problem and Situation Models

Theories of WPS stem primarily from studies of elementary school students (typically kindergarten through third grade) solving one-step addition and subtraction word problems (for review, see Verschaffel & De Corte, 1993). Riley and colleagues (Riley & Greeno, 1988; Riley, Greeno, & Heller, 1983) hypothesized that WPS skill is a function of the ability to map components of word problems onto knowledge structures or problem models that represent quantities (i.e., sets) and their relations. They based this hypothesis on evidence that performance on WPS tasks varies with semantic relations between sets (i.e., change vs. combine vs. compare) and with location of the unknown in the mathematical equation (e.g., Carpenter, Hiebert, & Moser, 1981). Performance varies with the semantic relations even when the mathematical equations that represent the problems are the same. In addition, students’ strategies vary depending on the semantic relations (Carpenter et al., 1981), and their recall of the semantic relations is consistent with the errors they make (Cummins, Kintsch, Reusser, & Weimer, 1988). Problem model representations are “rigid” structures stored in long-term memory that have “slots” for the various components of the word problems and are retrieved on the basis of key words or phrases (e.g., altogether, more, or give) that suggest semantic relations (Thevenot, Devidal, Barrouillet, & Fayol, 2007).

Some patterns of WPS performance cannot be fully explained by a strictly mathematical representation of the problem scenario (Staub & Reusser, 1995). For example, among first- and second-grade students, performance varies substantially on problems as a function of wording that makes the situation more or less explicit, but does not change other characteristics of the problem, including the semantic relations (De Corte et al., 1985). One explanation is that in solving word problems, individuals construct an episodic situation model that represents the “temporal and functional structures of the situations and actions depicted in the problem texts” (Staub & Reusser, 1995, p. 293). Situation models are temporary (i.e., not stored in long-term memory), fluid, and suggest algorithms (Thevenot et al., 2007).

Among individuals for whom the link between text and a problem model is not salient or in contexts in which this link is not transparent, the situation model may play a more prominent role than the problem model. One explanation for the advantage of the situation over the problem model, especially among relatively inexperienced or low-ability students, is that the stories may “elicit … effective solution strategies” (Koedinger & Nathan, 2004). These informal solution strategies may be “more accessible for novice learners” than formal computational methods (Koedinger & Nathan, 2004, p. 135). For example, only 25% of kindergarten students correctly solve the problem “Here are some birds [5] and here are some worms [3]. How many more birds than worms are there?” (Hudson, 1983). When the problem is modified with the following situational information, “Suppose the birds race over and each one tries to get a worm. Will every bird get a worm? How many birds won’t get a worm?” 96% of kindergarten students solve the problem primarily by counting out equivalent sets or using a pairing strategy.

For school textbook word problems (i.e., low-complexity problems with minimal extraneous information), the situation models that students are likely to develop include contextual elements related to problem solving in the school environment (Reusser, 1988). Students may be primed to perform calculations on the basis of the numerical information (e.g., relative sizes of numbers determining which ones get subtracted from others) and certain cue words even if they are inexperienced in the specific problem type. As expertise develops, situation models may be bypassed or become automatic, and students are less likely to rely on them or be affected by apparent contradictions when developing the problem model. Reusser (1990) suggested that expert problem solvers may skip the situation model and translate directly from the text to the problem model. Alternatively, Nathan et al. (1992) argued that for experts, the inferences associated with the situation model may occur automatically. Both arguments are consistent with the hypothesis that as individuals gain experience, WPS may depend more on the problem model than the situation model. However, for highly complex problems with elaborate scenarios and extraneous information, experienced students may not recognize the connection with problem types they have seen before, and consequently they may rely on more “real world” situation models.

Problem and situation models are theoretically based on different but overlapping sets of knowledge (e.g., mathematical vs. real world), experiences (e.g., classroom vs. nonclassroom), and mental processes (e.g., procedures vs. inferences). Consequently, the construction and application of problem and situation models may require different but overlapping sets of academic skills and cognitive resources. If the relative influence of problem and situation models on WPS performance changes with the complexity of the word problem and with the WPS experience of the student (e.g., less complex and more experience = more reliance on mathematical knowledge and procedures and classroom experiences), then the combination of academic skills and cognitive resources that best predict WPS performance may also change as a function of these two factors.

Academic Skills, Cognitive Resources, and WPS

Although a variety of academic skills and cognitive resources have been theoretically and empirically related to WPS, the present study focused on computation, language, nonverbal reasoning, and attentive behavior. WPS manifestly begins and ends with language and computation. Language is the medium through which the problem is presented (whether presented orally or through text), and computation (formal or informal) is the mathematical process through which the numerical information is manipulated to produce a solution. Less obvious, but still evident, WPS requires nonverbal reasoning and attentive behavior. Nonverbal reasoning and attentive behavior are processes through which instructions are followed, information not evident in the problem presentation is inferred, essential information is targeted and organized, and irrelevant information is excluded. These are also processes through which the verbal and numerical information is converted to mathematical representations of the problem, through which procedural or nonprocedural algorithms are implemented in producing a solution from the mathematical representation, and through which all the steps in the WPS process are organized, followed, and monitored for careless mistakes.

Although each of these four processes is an apparent underlying component of WPS, the degree to which students recruit and apply skills and abilities consistent with these processes is an empirical question. They hypothetically occur as a function of several factors including the context of the WPS situation (e.g., classroom, real world, low- or high complexity) and the WPS experience of the student. Furthermore, as a function of the complexity of the problem and the experience of the student, one or more of these skills or abilities may act as limiting factors. For example, for students who have highly developed WPS skills and rely primarily on well-developed problem models, efficiency (of problem model identification, retrieval, and associated computational algorithms implementation) may have the strongest effect on WPS performance. In this case, attentive behavior and computational skill may be the best predictors of WPS performance even when controlling for other skills and resources. However, for inexperienced problem solvers who must rely on situation models, the ability to integrate verbal information, make inferences, and adapt strategies from real-life experiences to the problem scenario may have a stronger effect on WPS performance. In this case, language and nonverbal reasoning processes may be the best predictor of WPS performance.

Empirically, computation, language, nonverbal reasoning, and attentive behavior are each moderately related (.40 to .60) to WPS among elementary-age students (Fuchs et al., 2005, 2006, 2010). These four constructs also predict change in WPS among first-grade students when controlling for each other as well as processing speed and working memory (Fuchs et al., 2010). However, these simple relations do not capture the likely complex interplay between problem-solving context, age and WPS experience of the student, and the cognitive processes students recruit and apply to WPS. For example, among third-grade students, although all four skills and abilities have direct effects on simple WPS, computation also mediates the relation between attentive behavior and WPS (Fuchs et al., 2006). However, among fifth-grade students, conceptual knowledge about fractions, but not whole number computation, mediates the effect of attentive behavior on WPS involving fractions (Hecht, Close, & Santisi, 2003). In this case, whole number computation did not have an effect on WPS when controlling for conceptual knowledge, attentive behavior, and working memory (although whole number computation had a direct effect on fraction computation when controlling for these same abilities).

Rationale and Hypotheses

In prior studies relating WPS to academic achievement and cognitive abilities, WPS has typically been based on one or two measures that contain relatively simple problems (i.e., a few sentences in length, minimal or no extraneous information, represented with a single arithmetical equation) and with which students are likely to have had some experience. That is, the word problems can be solved through retrieval of problem models that students are likely to have stored in long-term memory. We identified no studies that examined the relation between WPS and academic skills and cognitive resources as a function of WPS complexity. Although we have identified two studies that have examined predictors of growth in WPS (Fuchs et al., 2010; H. L. Swanson, Jerman, & Zheng, 2008), neither study evaluated whether predictors of growth differ as a function of the complexity of the word problems. We therefore evaluated growth models for low- and high-complexity word problems from the beginning of third through fifth grade.

We hypothesized that third-grade computation, language, non-verbal reasoning, and attentive behavior predict initial WPS performance. We also hypothesized that computation is the limiting factor (i.e., the strongest predictors when controlling for the others) for low-complexity problems, whereas nonverbal reasoning is the limiting factor for high-complexity problems.

We hypothesized a similar pattern of predictors for growth. However, because attentive behavior in this study was based on teacher assessments of student behavior in the classroom, we predicted that attentive behavior is more likely to be related to growth in low-complexity problems (i.e., problems most aligned with school learning), whereas nonverbal reasoning is more likely to be related to growth in high-complexity word problems.

Method

Participants

Participants were 261 students from four cohorts who were followed from third through fifth grade. At the beginning of third grade, the mean age of this sample was 8.5 years (SD = 0.39) and the mean performance was 98.76 (SD = 13.94) on the Wechsler Abbreviated Scale of Intelligence (WASI; Wechsler, 1999) and 104.34 (SD = 13.23) on the Woodcock–Johnson III Tests of Achievement (WJ-III; Woodcock, McGrew, & Mather, 2001) Applied Problems. Of the 261 students, 50.6% were female, 53.6% qualified for free or reduced lunch, and 2.3% had a school-identified disability (i.e., learning disability, speech impairment, language impairment, attentive behavior-deficit/hyperactivity disorder, health impairment, or emotional-behavioral disorder). Race was distributed as 44.8% African American, 35.6% White, 11.1% Hispanic, and 8.5% “other.”

The data described in this article were collected as part of a prospective 4-year study assessing the effects of mathematics word-problem instruction and examining the cognitive predictors of WPS (see Fuchs et al., 2006, 2008). For this article, students from the 42 third-grade classrooms were selected who had been randomly assigned at the beginning of third grade to participate in the condition that received business-as-usual mathematics instruction (i.e., students in the other 81 classrooms, who received third-grade experimental intervention according to random assignment, were not included because we were interested in the predictors of typical development of WPS). The 42 classrooms were in a mix of Title 1 and non-Title 1 schools (one to three teachers per school) in a southeastern metropolitan school district.

From the 42 third-grade classrooms, students were sampled for participation on the basis of performance on the Test of Computational Fluency (Fuchs, Hamlett, & Fuchs, 1990) with which students have 3 min to write answers to 25 second-grade addition and subtraction arithmetic and procedural computation problems. From the children on whom we had consent (N = 653), we randomly sampled 438 students, blocking within three strata (selecting 25% of students with scores 1 SD below the mean of the entire distribution, 50% of students with scores within 1 SD of the mean of the entire distribution, and 25% of students with scores 1 SD above the mean of the entire distribution). Sixty-five of these students were randomly selected for participation in experimental WPS tutoring, so were excluded from this sample because as stated above, we were interested in typical development without researcher intervention.

From the 373 students receiving regular classroom instruction and no experimental tutoring, 112 students were excluded from analyses because they did not complete all 3 years of the study (n = 110) or were missing an assessment (n = 2). The excluded students did not differ significantly from the sample students on demographics: age, t(371) = −1.82, p > .05; cohort, χ²(3) = 5.90, p > .05; gender, χ²(1) = 0.47, p > .05; race, χ²(5) = 9.18, p > .05; or free-lunch status, χ²(2) = 4.05, p > .05. They also did not differ significantly on WASI IQ, t(371) = 0.82, p > .05.

Measures

Word-problem measures

The Word-Problem Battery (Fuchs, Hamlett, & Powell, 2003) has subtests of varying complexity that sample problems from four word-problem types addressed in the third- through fifth-grade curriculum (see the Appendix for example items). These problem types involve (a) buying varying quantities of one to four types of items, each at a different price (we refer to this problem type as adding multiple quantities of items with different prices); (b) finding half of a quantity (we refer to this problem type as half); (c) purchasing items sold in packages with fixed units (we refer to this problem type as step-up function); and (d) deriving relevant information from pictographs within the context of a multistep problem (we refer to this problem type as pictograph). Two forms (A and B) of each subtest were counterbalanced across the third-grade assessment waves at the classroom level. The same form (A) was used for all students in subsequent waves (i.e., students were tested with forms ABAA or BAAA across the four waves). Across the two forms, problems require the same operations, incorporate the same numbers, and present text with the same number and length of words. There were no consistent form effects across the waves for this sample.

Although each subtest samples the same four problem types, the subtests represent two levels of complexity in terms of contextual realism. Low-Complexity Word Problems comprise nine problems, each of which requires one to four steps. Each problem conforms to a single problem type. Problems are scored according to a rubric that assigns points for correct intermediate calculations and final solutions. Reported scores and scores used in the growth models were percent correct out of 19 possible points. For this sample, across the four assessment waves, Cronbach’s alpha was estimated to be .85–.89. Concurrent validity based on the correlation between the subtest and WJ III Applied Problems (Woodcock et al., 2001) was estimated to be .50 –.76. Interscorer agreement, computed on 20% of protocols by two independent scorers, was estimated to be .98.

High-Complexity Word Problem is a more complex and novel context than low-complexity word problem and resembles real-world problem solving. It simultaneously assesses all four problem types (multiple times) within a single problem narrative but with multiple questions. Questions build on preceding questions; require students to find relevant information across the problem narrative, previous question stems, and the student’s own previous work; and require students to contribute relevant information from their own prior experiences as would be the case in real life. Problems are scored according to a rubric which assigns points for showing intermediate steps, as well as correct calculations. Reported scores and scores used in the growth models were percent correct out of 20 possible points. For this sample, across assessment waves, Cronbach’s alpha was estimated to be .78 –.84. Concurrent validity based on the correlation between the subtest and WJ III Applied Problems (Woodcock et al., 2001) was estimated to be .40 –.61. Interscorer agreement, computed on 20% of protocols by two independent scorers, was estimated to be .91–.95. Given the deleterious effects of student unfamiliarity with performance assessments (Fuchs et al., 2000), research assistants delivered a 45-min lesson on test-taking strategies prior to the High-Complexity subtest at each wave.

Computation

A weighted average of three assessments was used to derive a computation score. The Grade 3 Math Battery (Fuchs et al., 2003) incorporates two subtests of fluency with math facts: Addition Fact Fluency and Subtraction Fact Fluency. Each subtest comprises 25 problems with answers from 0 to 12, and students have 1 min to write answers. On the Test of Computational Fluency (Fuchs et al., 1990), students have 3 min to write answers to 25 second-grade addition and subtraction arithmetic and procedural computation problems. A problem-correct-per-minute score was computed by averaging a third of the Computational Fluency score with the Addition and Subtraction Fact Fluency scores. The maximum score possible was 19.4 problems correct per minute. Concurrent validity, evaluated by correlating the derived computation score with the Tennessee Comprehensive Assessment Program (TCAP; Tennessee Department of Education, 2005) Achievement Test–Computation, was estimated to be .46, and with WJ III Applied Problems (Woodcock et al., 2001) was estimated to be .42. Computational Fluency was not assessed in Grades 4 or 5, so computation for Grades 4 and 5 were based on the average of Addition and Subtraction Fact Fluency. The test–retest reliability coefficients based on Grade 3 computation compared with Grades 4 and 5 computation were estimated to be .64 in both cases.

Language

WASI Vocabulary (Wechsler, 1999) measures expressive vocabulary, verbal knowledge, and foundation of information with 42 items. The first four items present pictures; the student identifies the object in the picture. For the remaining items, the tester says a word that the student defines. Responses are awarded a score of 0, 1, or 2, depending on the quality of response. Testing is discontinued after five consecutive scores of 0. As per the test developer, based on a standardization sample representative of the U.S. English-speaking population, split-half reliability coefficients are estimated to be .86 and .88 for 8- and 9-year-olds, and test–retest reliability coefficients are estimated to be .84 for 6-to 11-year-olds. Age-corrected T-scores were used in all analyses with expected M (SD) = 50 (10) for the representative sample described above.

Nonverbal reasoning

WASI Matrix Reasoning (Wechsler, 1999) measures nonverbal reasoning with four types of tasks: pattern completion, classification, analogy, and serial reasoning. Examinees look at a matrix from which a section is missing and complete the matrix by selecting among five options. Testing is discontinued after four errors on five consecutive items or after four consecutive errors. As per the test developer, based on a standardization sample representative of the U.S. English-speaking population, split-half reliability coefficients are estimated to be .94 and .93 for 8- and 9-year-olds, and test–retest reliability coefficients are estimated to be .77 for 6- to 11-year-olds. Age-corrected T-scores were used in all analyses with expected M (SD) = 50 (10) for the representative sample described above.

Attentive behavior

The SWAN (J. Swanson et al., 2004) is an 18-item teacher rating scale, nine of which assess the inattentive behavior (largely distractibility) criteria for attention-deficit/hyperactivity disorder (ADHD) from the Diagnostic and Statistical Manual of Mental Disorders, fourth edition (American Psychiatric Association, 1994). The measure was designed to approximate the normal distribution (as opposed to earlier measures designed to identify pathology but not representative of population norms; see J. Swanson et al., 2004). The items are rated on a 7-point scale (3 = Far Below Average, 2 = Below Average, 1 = Slightly Below Average, 0 = Average, −1 = Slightly Above Average, −2 = Above Average, −3 = Far Above Average). A cutoff score of 2.48 (1.65 SD above the mean, based on averaging the scores on the nine inattentive items) identified 3.98% extreme cases in a sample of 327 elementary school students, which was not statistically different than the expected value of 5% for ADHD predominantly Inattentive Type (J. Swanson et al., 2004). In order for the measure to reflect “attentive behavior” and to more easily interpret the relations between this scale and WPS, the coding was reversed so that positive numbers reflect more attentive behavior than negative numbers. The summary score is the sum across the nine items, with possible scores ranging from −27 to 27 points. On the basis of the cutoff score described above, scores less than −22 would be considered clinically significant for ADHD. Cronbach’s alpha in the present study was estimated to be .98.

Procedure

Students were consented and screened for participation using the Test of Computation Fluency in August of third grade. They were assessed on the Word-Problem Battery (Fuchs et al., 2003) in September and April of third grade, and in March of fourth and fifth grades. At each assessment wave, administration required three sessions, each lasting 30 – 60 min. In fall and spring of third grade, administration occurred in whole-class format. In Grades 4 and 5, administration occurred in small groups because students had dispersed to many classrooms. In fall of third grade, students were also assessed on computational skill (Grade 3 Math Battery; Fuchs et al., 2003) within the whole-class testing sessions.

For the Low-Complexity subtest of the Word-Problem Battery, research assistants read aloud each item while students followed along on their own copies of the problems; the tester progressed to the next problem when all but one to two students had their pencils down, indicating they were finished. Students could ask for re-reading(s) as needed. For the High-Complexity subtest of the Word-Problem Battery, research assistants read the entire assessment and reread portions to individuals, at their request, as they worked.

In fall of third grade, students also completed two individual 45-min test sessions in which trained research assistants administered achievement and cognitive measures according to standard instructions. The individually administered measures used in this study were WASI Vocabulary and Matrix Reasoning (Wechsler, 1999). The individual test sessions were audiotaped, and 17.9% of tapes, distributed equally across testers, were selected randomly for accuracy checks by an independent scorer. Agreement estimates exceeded 98.8%.

To assess attentive behavior, in October of third grade, teachers completed the SWAN Rating Scale (J. Swanson et al., 2004) on each student.

Results

Descriptive Information

Table 1 shows sample means and correlations for the WPS measures from third through fifth grade and the achievement and cognitive measures from the beginning of third grade. The students in this study demonstrated average performance (as compared with a nationally representative sample) in language (M = 47.6, SD = 9.8) and nonverbal reasoning (M = 50.3, SD = 11.1) and average attentive behavior (M = 2.21, SD = 12.2). Their mean computational fluency was 8.2 (SD = 3.4) problems correct per minute. Beginning third-grade performance on low- and high-complexity word problems was 27% (SD = 22.2) and 11% (SD = 16.7), indicating inexperience with the problems. They demonstrated substantial growth by the end of fifth grade (nearly 40 percentage points on both problem types, on average).

Table 1.

Means, Standard Deviations, and Correlations for all Measures Used in the Growth Models

Variable	M	SD	Correlations
			1	2	3	4	5	6	7	8	9	10	11
Low-complexity word problems
1. Grade 3 Fall	27	22.2	—
2. Grade 3 Spring	39	28.2	.66	—
3. Grade 4 Spring	57	27.9	.59	.73	—
4. Grade 5 Spring	64	26.8	.56	.68	.77	—
High-complexity word problems
5. Grade 3 Fall	11	16.7	.53	.46	.42	.41	—
6. Grade 3 Spring	26	22.6	.50	.59	.51	.46	.45	—
7. Grade 4 Spring	42	29.1	.52	.58	.63	.60	.44	.53	—
8. Grade 5 Spring	50	29.9	.49	.57	.61	.62	.42	.47	.62	—
Achievement, cognitive, and behavioral measures
9. Computation	8.16	3.40	.47	.42	.40	.42	.29	.35	.35	.32	—
10. Nonverbal reasoning	50.31	11.11	.34	.41	.43	.44	.27	.39	.35	.36	.26	—
11. Language	47.57	9.77	.43	.49	.47	.47	.42	.45	.40	.49	.25	.32	—
12. Attentive Behavior	2.21	12.19	.34	.45	.46	.42	.35	.33	.47	.49	.38	.22	.40

Note. For the word-problem measures, scores are percent correct of 19 (low-complexity) and 20 (high-complexity) points. For Computation, the score represents the number of problems solved in 1 min (average of three tests of single-digit addition, subtraction, and mix of single-digit and algorithmic computations). Nonverbal reasoning and Language scores are T-scores. For Attentive Behavior, 0 represents a teacher rating of average attentive behavior (range = −27 to 27); a higher score means the student is more attentive. All correlations are significant (p < .05).

Correlations within time points between the two levels of WPS were on the high end of moderate (.53 to .63). Correlations among the achievement and cognitive variables were low (.26 to .40), and they tended to be more highly correlated with WPS than with each other. This suggests the four constructs are distinct and each is moderately related to WPS. Descriptively, beginning third-grade low-complexity WPS was more highly correlated with computation (.47) and language (.43) than with nonverbal reasoning (.34) or attentive behavior (.34), but all four abilities were equally (and moderately) predictive of end-of-fifth-grade low-complexity WPS (.42 to .47). For high-complexity problems, WPS was more highly correlated with language (.42) than with the other abilities (.27 to .35), but both language (.49) and attentive behavior (.49) were moderately predictive of end-of-fifth-grade performance.

Unconditional Growth Models

We evaluated multilevel growth models for low- and high-complexity WPS in SAS using PROC MIXED (The SAS Institute, 2009). Time was scaled so that the intercept could be interpreted as expected performance on September 1 of the third-grade school year. For each student, time for each subsequent assessment was the number of years between that assessment date and September 1 of third grade. Mean time in years across students for the four measurement time points were 0.1, 0.6, 1.6, and 2.5 years.

To determine the best unconditional growth models, we evaluated linear and quadratic models with five different residual covariance structures: variance components, compound symmetry, autoregressive, banded main diagonal, and unstructured. We also evaluated class effects based on third-grade class assignments. We used Akaike’s (AIC) and the Bayesian (BIC) information criteria to determine the best fitting models.

The best fitting models for both low- and high-complexity WPS were quadratic with random intercept and linear growth effects, but fixed quadratic effects and banded main diagonal residual covariance structures (see Table 2; low complexity: AIC = −387, BIC = −362; high complexity: AIC = −282, BIC = −257). The banded main diagonal models estimated different residual variances for each time point. There were low to moderate class effects for low-complexity WPS (Intercept ICC = 4%, Slope ICC = 2%) and high-complexity WPS (Intercept ICC = 7%, Slope ICC = 13%). Including class effects made no difference in the estimates for the unconditional and subsequent conditional growth models.

Table 2.

Unconditional Growth Models for Low- and High-Complexity WPS

Parameter	WPS performance
	Low complexity	High complexity
Fixed effects
Average performance, Fall G3 (Intercept)	24.5	8.4
Initial linear growth, Fall G3 (Time)	27.5	30.8
Deceleration in growth from G3 through G5 (time squared)	−4.6	−5.6
Random effects
Intercept variance	4.1	1.5
Time variance	0.5	0.7
Intercept/time covariance	−0.1a	0.2a
Error variance
Fall G3	1.7	1.3
Spring G3	2.6	3.0
Spring G4	2.2	3.8
Spring G5	0.9	2.3

Note. The numbers reported are unstandardized coefficients, percent correct (out of 19 for low complexity and 20 points for high complexity) on the WPS tasks. WPS = word problem solving; G3–G5 = Grade 3–Grade 5.

^aNot significantly different from zero. All other effects are significant (p < .05).

As Table 2 shows, the growth model estimate for initial (beginning third grade) low-complexity WPS performance is 24.5%. The estimate for initial growth rate is 27.5% per year; however, the growth rate decreases by 9.2% per year (2 times the deceleration shown in Table 3) such that by the end of fifth grade, the estimated growth rate in low-complexity WPS is relatively flat at 1.5% per year. The growth model estimate for initial high-complexity WPS performance is 8.4%. The estimated initial growth rate is 30.8% per year, which decreases by 11.2% per year such that by the spring of Grade 5, the estimated growth rate in high-complexity WPS is 2.8% per year.

Table 3.

Cognitive Effects on Growth for Low- and High-Complexity WPS

Effect	Low complexity	High complexity
Intercepta	24.6*	8.4*
Computation	2.2*	0.6
Language	0.6*	0.5*
Nonverbal Reasoning	0.3*	0.1
Attentive Behavior	0.1	0.2*
Linear growth intercepta	27.3*	30.7*
Computation	−0.8	0.9
Language	0.2	0.0
Nonverbal Reasoning	0.4*	0.6*
Attentive Behavior	0.6*	0.3
Quadratic growth intercepta	−4.6*	−5.6*
Computation	0.2	−0.4
Language	−0.1	0.1
Nonverbal Reasoning	−0.1	−0.2*
Attentive Behavior	−0.2*	0.0

Note. The numbers reported are unstandardized coefficients, percent correct (out of 19 for low complexity and 20 points for high complexity) on the WPS tasks. Each effect represents the percentage of change in performance or growth rate for a unit change in the achievement or cognitive measure. For example, for low-complexity problems, a difference of one problem correct/minute in computational skill causes a 2.2% difference in initial WPS scores, a difference of 10 T-score points (1 SD) in nonverbal reasoning causes a difference of 4% (10 × 0.4) per year initial growth rate in WPS scores, and a difference of 12 points (1 SD) in attentive behavior causes a difference of 4.8% (12 × 0.2 × 2) per year in deceleration (i.e., yearly decrease in growth rate). WPS = word problem solving.

^aThe Intercept is average performance beginning third grade at sample mean levels of computation, language, nonverbal reasoning, and attentive behavior. Linear and quadratic growth intercepts are the average growth rates beginning third grade at sample mean levels of the achievement and cognitive measures.

^*p < .05.

Achievement and Cognitive Effects on Growth in WPS

To examine more directly whether computation, language, non-verbal reasoning, and attentive behavior have different effects on low- and high-complexity problems, we evaluated growth models that included these variables (see Table 3). For all models, the achievement/cognitive variables were centered on sample means.

Low-complexity WPS

Both computation and language were significantly related to beginning WPS performance, t(517) = 5.52, p < .05; t(517 = 4.24, p < .05), but were not significantly predictive of growth: linear, t(517) = −1.25, p > .05; t(517) = 0.85, p > .05; quadratic, t(517) = 1.02, p > .05; t(517) = −0.71, p > .05. Attentive behavior was not significantly related to beginning performance, t(517) = 0.95, p > .05, but was significantly predictive of growth: linear, t(517) = 3.52, p < .05; quadratic: t(517) = −3.24, p < .05. Nonverbal reasoning was significantly related to beginning performance, t(517) = 2.60, p < .05, and significantly predicted linear but not quadratic growth: linear, t(517) = 2.08, p < .05; quadratic, t(517) = −1.58, p > .05.

High-complexity WPS

Similar to low-complexity WPS, language was significantly related to beginning performance, t(517) = 4.38, p < .05, but was not significantly predictive of growth: linear, t(517) = −0.03, p > .05; quadratic, t(517) = 0.60, p > .05. However, computation was not significantly related to beginning performance, t(517) = 1.84, p > .05, nor did it significantly predict growth: linear, t(517) = 1.29, p > .05; quadratic, t(517) = −1.29, p > .05. Although not significant using strict criteria, inattentive behavior was marginally related to beginning performance, t(517) = 1.93, p < .055, but was not significantly predictive of growth: linear, t(517) = 1.25, p > .05; quadratic, t(517) = −0.06, p > .05. Nonverbal reasoning was the only significant predictor of growth: linear, t(517) = 2.60, p < .05; quadratic, t(517) = −2.11, p < .05, although it was not significantly related to initial performance, t(517) = 1.45, p > .05.

Summary of Achievement and Cognitive Effects on WPS Growth

Language was the only achievement/cognitive skill or behavior significantly related to initial performance on both low- and high-complexity WPS. A one standard deviation difference in language ability was related to 5.9% and 4.9% differences in initial WPS scores for low- and high-complexity problems, respectively. Computation had the largest (significant) effect on initial low-complexity WPS performance (7.5% difference for each SD difference in computational skill), but had a much smaller (nonsignificant) effect on initial high-complexity performance (2% difference for each SD difference in computational skill). Neither language nor computation significantly predicted growth in WPS.

Relative to computation and language, nonverbal reasoning had the smallest (significant) effect on initial low-complexity WPS (3.4% difference for each SD difference in nonverbal reasoning ability). Other than language, only attentive behavior had a marginally significant effect on initial high-complexity performance (2.2% difference for each SD difference in attentive behavior).

Only attentive behavior and nonverbal reasoning were significantly predictive of growth in WPS. However, attentive behavior significantly predicted growth only for low-complexity WPS. For low-complexity WPS, attentive behavior had a greater numerical effect than nonverbal reasoning on initial growth (beginning third grade, 7.8% vs. 4.3% per year for each SD difference in attentive behavior and nonverbal reasoning). Because nonverbal reasoning had less of a numerical effect than attentive behavior on deceleration (5.2% vs. 2.4% per year decrease in growth for each SD difference in attentive behavior and nonverbal reasoning), it had a greater numerical effect on long-term growth (third through fifth grade). However, as Figure 1 illustrates, these numerical differences are not practically meaningful. Practically speaking, for two students with similar levels of computational skill and language but one with higher nonverbal reasoning and the other with a comparable advantage in attentive behavior, their growth in low-complexity WPS from third through fifth grade was similar.

Figure 1.

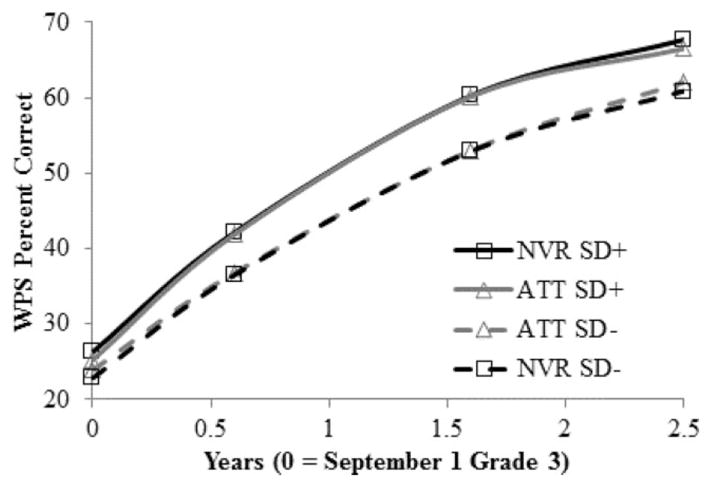
The effects of nonverbal reasoning (NVR) and attentive behavior (ATT) on low-complexity word problem solving (WPS). SD+/− represents WPS performance for students at 0.5 standard deviations above/below mean on specified measure, with other measures at mean levels.

Only nonverbal reasoning significantly predicted growth in both low- and high-complexity WPS, and the long-term effect on growth was similar in both cases. Although nonverbal reasoning had a greater numerical effect on initial growth for high- than low-complexity WPS (beginning third grade, 6.3% vs. 4.3% per year for each SD difference in nonverbal reasoning), it also had a greater effect on deceleration (3.9% vs. 2.4% per year decrease in growth for each SD difference in nonverbal reasoning) for high-versus low-complexity WPS such that, all other abilities equal, a one standard deviation difference in nonverbal reasoning resulted in virtually no difference (0.08%) on high- versus low-complexity WPS gains from beginning third through end of fifth grade.

Discussion

The purpose of this study was to evaluate growth models for low- and high-complexity WPS to determine whether predictors differ as a function of WPS complexity. We found that predictors of both WPS performance and growth do differ as a function of WPS complexity. Nonverbal reasoning is related to initial performance on low- but not high-complexity WPS; by contrast, attentive behavior is related to initial high- but not low-complexity WPS. Whereas both attentive behavior and nonverbal reasoning predict growth in low-complexity WPS performance, only nonverbal reasoning predicts growth in high-complexity WPS. Computation predicts initial performance in WPS for low- but not high-complexity WPS. The one cognitive ability with similar effects on WPS regardless of complexity is language. Language is related to initial performance regardless of WPS complexity but does not predict growth in low- or high-complexity WPS. In this discussion, we interpret the findings for predictors of performance (i.e., intercepts) and growth separately. We interpret these findings in relation to our hypotheses and reconcile findings with other research on cognitive correlates of WPS. Finally, we interpret results in the context of theories about WPS.

Predictors of Performance

With respect to predictors of performance, we hypothesized that third-grade computation, language, nonverbal reasoning, and attentive behavior are all related to initial third-grade WPS performance when controlling for each other. We also hypothesized that computation is most strongly related to low-complexity word problems when controlling for the other abilities, whereas nonverbal reasoning is most strongly related to high-complexity WPS. Our hypotheses were only partially supported by the results. For low-complexity WPS, although computation, language, and nonverbal reasoning are related to initial WPS, attentive behavior is not when controlling for the other abilities. For high-complexity WPS, neither computation nor nonverbal reasoning is related to initial WPS when controlling for language and attentive behavior. Computation has the strongest effect on initial low-complexity WPS as hypothesized. Counter to our hypothesis, language and attentive behavior, not nonverbal reasoning, are the strongest predictors of initial high-complexity WPS performance.

Results are consistent with prior research in that computation, language, nonverbal reasoning and attentive behavior are each moderately related to WPS. However, Fuchs et al. (2006) found that all four abilities are related to WPS when controlling for the others. In Fuchs et al., as in most studies of WPS, problems were of relatively low-complexity, and the mathematical structure (e.g., combine, change) were such that the third-grade students were likely to have had more experience with them than the third-grade students at the beginning of our study had with our word-problem tasks. So our study is unique in that the WPS tasks varied by complexity, and initially, students were relatively inexperienced with the problem types, regardless of complexity.

Predictors of Growth

In terms of predictors of growth, we hypothesized that that computation, language, nonverbal reasoning, and attentive behavior predict growth in WPS when controlling for the other abilities. We also hypothesized that attentive behavior is more likely related to growth in low-complexity problems (i.e., problems most aligned with school learning), whereas nonverbal reasoning is more likely related to growth in high-complexity word problems. Our hypotheses were partially supported in that attentive behavior predicted growth in low- but not high-complexity WPS. Nonverbal reasoning predicts WPS growth regardless of level of complexity. However, neither computation nor language predicted growth in WPS when controlling for the other abilities, regardless of complexity.

Fuchs et al. (2010) found that numerical cognition, language, attentive behavior, and nonverbal reasoning predicted gains in WPS during first grade. Similar to the third-grade students in this study, the first-grade students were also likely to have been relatively inexperienced in the problem types used in that study. However, the first-grade students were also likely to have been relatively inexperienced at WPS in general, whereas third-grade students likely have experience solving word problems even if they are not familiar with the specific problem types. Perhaps as students become more experienced at solving word problems in general, language becomes less a factor than other cognitive abilities in predicting growth, although it continues to be a strong predictor of overall performance.

Attentive behavior appears to be a key predictor of growth in low-complexity problems. In fact, students high on attentive behavior are likely to show as much gains on low-complexity problems as students high in nonverbal reasoning. The measure of attentive behavior was based on teacher reports of students’ classroom behavior (e.g., gives close attention to detail and avoids careless mistakes, sustains attention on tasks or play activities, listens when spoken to directly). Therefore, it is possible this measure represents several constructs (e.g., “good student”) aside from or in addition to attentive behavior. As hypothesized, attentive behavior appears to be a powerful predictor of WPS learning in the classroom (i.e., specific to learning to solve problem types taught in the classroom). It is also the only predictor besides language of initial performance in high-complexity WPS. Given the key role attentive behavior plays in predicting WPS performance and growth, it should be studied more carefully to determine the nature of the measure and what aspects of WPS it is influencing.

Interpretation of Results in the Context of Theories of WPS

The different pattern of predictors of initial performance and growth in WPS, depending on complexity of the word problems, provides some insight into theories of WPS. First, computation is less relevant (when controlling for other abilities) for higher than lower complexity problems. Second, attentive behavior is as strong a predictor of growth as nonverbal reasoning for low-complexity WPS, whereas only nonverbal reasoning predicts growth in high-complexity WPS. Theoretically, two forms of mental representations (problem and situation models) are thought to influence WPS and the degree to which they influence WPS is thought to differ depending on the situational complexity of the problem and the experience of the problem solver (Nathan et al., 1992; Reusser, 1990). Young children who lack WPS experience, but who are provided with enough situational information to understand the task in the context of their own experiences, appear to rely less on formal computational methods and use more informal strategies and reasoning processes to successfully solve word problems (Koedinger & Nathan, 2004). Our results suggest that a similar process may occur among elementary school students. At beginning of third grade, students had little experience with our WPS tasks (i.e., mathematical structure such as half problems). However, they were likely to have had experience with textbook type word problems in general (i.e., one or two sentences, only relevant numerical information, sparse situational information). The low-complexity word problems, although novel in terms of mathematical structure, were similar to textbook problems more generally. Students may have automatically used formal computational skills for solving some of the problems even if they did not have formal problem model representations of those problems. For these students, specific words (e.g., how much = add) or characteristics (e.g., [1/2] = divide by 2) may have triggered computational procedures even if they did not understand the problem.

The form of the high-complexity problems differed from the low-complexity problems, including elaborate situational information (e.g., extensive extraneous detail related to shopping for pets). The detailed problem scenarios may have evoked real-life experiences and perhaps informal strategies and reasoning processes for problem solving in real-world contexts. Although students had developed problem models for low-complexity word problems that were mathematically the same as the high-complexity word problems, the surface differences may have been sufficiently different to keep students from spontaneously relating the high-complexity problems to the formal problem models they were acquiring over 3 years of instruction. If the students were unable to retrieve the problem models for the high-complexity problems, they would have failed to make the association between problem models and formal computational procedures.

The finding that nonverbal reasoning is the only predictor of growth in high-complexity WPS may also be attributed to stronger reliance on situation models as problems become more complex. It may be that students rely more on situational models developed from learning in real-world contexts than problem models to improve performance on high-complexity problems. As a consequence, they may need to recruit general reasoning skills to solve more complex word problems on which they have not received classroom instruction.

In terms of limitations, because our WPS measures were experimental, interpretations about the trajectory of growth and comparison of performance levels across the two levels of complexity need to be treated with caution. These measures should be evaluated with larger samples and using item response theory methods to statistically validate that they are equated in terms of mathematical requirements but vary by complexity and that they are on a ratio scale. Although we found quadratic growth trajectories for the two measures, we cannot determine whether this was because improvement in ability was in fact quadratic or because each unit increase in performance represents different increases in ability. Although some measures have more suitable technical properties for evaluating growth trajectories (e.g., WJ-III Applied Problems; Woodcock et al., 2001), these are general measures of problem solving (including more than word problems) and cannot be used to answer specific questions related to theories of WPS (e.g., measures designed to vary items by problem and situation model requirements).

A second limitation is that other cognitive abilities related to WPS were not examined in this study. In particular, working memory is related to WPS (Fuchs et al., 2005, 2006; H. L. Swanson, Cooney, & Brock, 1993) and growth in WPS (Fuchs et al., 2010; H. L. Swanson et al., 2008). Yet, whether the effect of working memory on WPS is direct, indirect, or not significant varies across studies that themselves vary in age and experience of the participants, WPS context, and the other skills and cognitive resources included in the model of WPS. A further complication is that computation, language, nonverbal reasoning, and attentive behavior each relies on working memory. Working memory is commonly (across studies and populations) found to be a key component in computation (DeStefano & LeFevre, 2004; Geary, 1993; H. L. Swanson & Jerman, 2006). It is also strongly linked to attentive behavior. The central executive component of working memory, particularly controlled attention, is the primary source of attentive behavior deficits in children with ADHD (Kofler, Rapport, Bolden, Sarver, & Raiker, 2010). Although not the focus of this study, the role working memory in computation and attentive behavior as well as in language and nonverbal reasoning and the varying role of working memory in WPS, depending on problem solving context and student WPS experience, illustrates how these factors may influence the degree to which computation, language, nonverbal reasoning, and attentive behavior act as limiting factors in WPS. Finally, we evaluated the achievement/cognitive skills and attentive behavior at only one time point. It seems likely that the development of these skills and behaviors are related to the development of WPS.

Pending future related work, present findings do have some implications for educational practice. WPS is a substantial part of school curricula and high-stakes tests. WPS is perceived as difficult for students to master (Nathan & Koedinger, 2000a, 2000b) but as essential for situations outside of the school environment. Word problems occur in a variety of forms and contexts, and WPS performance can vary substantially due to differences in both surface and structural features as well as differences in student experience and resources. This study represents one important step in developing models of the interaction between word-problem factors and student characteristics. Understanding the nature of this interaction is critical to developing curricula and interventions that improve WPS performance across forms and contexts.

Appendix Example Items

Low-Complexity Problem Examples

[SUBTRACT Problem Model]

Becky collects stickers. She had 58 stickers in her collection. Then, she gave 7 scratch-n-sniff stickers to her best friend. How many stickers does Becky have now?

[ADD Problem Model] Adding Multiple Quantities of Items with Different Prices:

Jenny needs money to buy things for her art class. She needs 2 coloring books, 5 markers, and 4 pencils. The coloring books cost $6 each, the markers cost $3 each, and the pencils cost $2 each. How much money does Jenny need for her art class?

[PICTOGRAPH Problem Model] Deriving Relevant Information from Pictographs:

Billy wanted to make his mom a card. He made a chart to show how many crayons he had. Each picture of a crayon stands for 4 crayons.

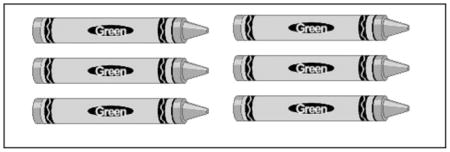
Billy found 3 more crayons in his closet. How many crayons does he have now?

[STEP Problem Model] Purchasing Items Sold in Packages with Fixed Units:

You want to buy some balloons. Balloons come in bags with 6 balloons in each bag. How many bags of balloons do you need to buy to get 17 balloons?

High-Complexity Problem Example

Note: The following is only the text from the problem. The actual problem was presented on four pages including a price chart, pictograph, pictures of cages, etc.

Class Pet

Your class decides to buy some parakeets as the class pets. You’ll have to buy the birds, a cage, swings, and food dishes for the cage, and enough parakeet food to last for the rest of the year. Your teacher told you that you can also buy other things for the pet center in your classroom.

After talking to the pet shop owner, your class decides to buy four parakeets, a large cage, three bird swings, and four food dishes for the cage. Your teacher figures out that you’ll need eight pounds of food to last for the rest of the year.

Your class raised one hundred nine dollars from a bake sale and ninety-five dollars from the book fair to buy the birds and supplies. Sixty-two people came to the book fair.

1. How much money do the students have for this project?

2. How much money will the students spend on the birds, the cage, the swings, the food, and the food dishes for the cage? Show all your work.

3. What other things will the students buy for the pet center in their classroom? How much will the students spend on these other things? What money could they use to pay for these things? (For example, how many $1 bills, how many $5 bills, how many $10 bills.)

4. A book on taking care of birds costs $35. After buying everything else for their pet center, do the students have enough money to buy the book? Explain how you got your answer.