Abstract
Understanding the relationship between the adiabatic free energy profiles of chemical reactions and the underlining diabatic states is central to the description of chemical reactivity. The diabatic states form the theoretical basis of Linear Free Energy Relationships (LFERs) and thus play a major role in physical organic chemistry and related fields. However, the theoretical justification for some of the implicit LFER assumptions has not been fully established by quantum mechanical studies. This study follows our earlier works1,2 and uses the ab initio frozen density functional theory (FDFT) method3 to evaluate both the diabatic and adiabatic free energy surfaces and to determine the corresponding off-diagonal coupling matrix elements for a series of SN2 reactions. It is found that the off-diagonal coupling matrix elements are almost the same regardless of the nucleophile and the leaving group but change upon changing the central group. Furthermore, it is also found that the off diagonal elements are basically the same in gas phase and in solution, even when the solvent is explicitly included in the ab initio calculations. Furthermore, our study establishes that the FDFT diabatic profiles are parabolic to a good approximation thus providing a first principle support to the origin of LFER. These findings further support the basic approximation of the EVB treatment.
Keywords: proton transfer, density functional theory, diabatic state, free energy surface, linear free energy relationships
I. Introduction
Linear free energy relationships (LFERs) that correlate rate constants with equilibrium constants represent on some level a unifying theory of organic reactivity. Such rate-equilibrium relationships were formulated quite early (e.g., see 4–6) and have found major use in analyzing various chemical reactions (e.g., 7–9). Although these concepts originate from studies in organic chemistry, they are now also widely used in applications of important empirical descriptors in biological systems10.
Arguably the most rigorous derivation of LFER comes from the generalization of Marcus’s theory11,12 of electron transfer (ET) treatment to adiabatic cases10. This was formulated by the modified Marcus-relationship10,13–17 (see also section II). The validity of this relationship has been examined empirically in several works (e.g., 15,18) and used extensively in studies of chemical reactions in solutions and proteins using the empirical valence bond approach (EVB)19 in its fully microscopic version15 to obtain the adiabatic free-energy functionals. The traditional use of bond order-bond length relationship7,20 to describe adiabatic reactions also provided interesting insight, but have been less straightforward in terms of its relationship to LFER and other physical features.
The realization of the fact that the LFER reflects the relationship between diabatic and adiabatic states led to several attempts to capture these relationships by ab initio quantum mechanical treatments (e.g., 1,21–23). There were also attempts to explore LFER in condensed phase by ab initio studies without relating it to the diabatic states24–26. Our own main direction in correlating diabatic and adiabatic states on the ab initio level has been based on constructing the diabatic states by using the frozen DFT approach (FDFT)3 or the constraint DFT (CDFT)1, and then using the difference between the FDFT and the full adiabatic DFT to extract the off diagonal coupling terms (see section II).
A CDFT approach that reflects some of the FDFT ideas has also been developed to obtain restricted charge-localized diabatic states27,28. This method introduces additional constraints on the solution of the Kohn-Sham equations by also decomposing the density into subsystems and restraining the total charge of each subsystem. Using this approach can lead to results that are sensitive to the choice of the external potential (i.e. definition of the charge) in situations where the distance between the nuclei of the subgroups is small (on the order of 1–2 covalent bond lengths) 29,30. This method was successfully applied to study electron transfer reactions31–33.
The issue of the nature of the off-diagonal element has been a central point in studies of diabatic reactions in ET reactions34 and the quantum mechanical evaluation of such terms have a long history (see e.g. 35–37), where different approaches have been used including direct calculations (e.g., 35,38,39) extracting the coupling from the behavior of the adiabatic states40 and applying the Mulliken-Hush method using the dipole moment of the system, and methods based on ab initio valence bond theory41, or directly calculating these elements from the diabatic states obtained by CDFT28,32. Note, however, that the main interest in the present work is in the dependence of Hrp on the environment and in its role in adiabatic LFER and not in the traditional issues addressed in the ET literature.
Here we focused on the nature of the Hrp for adiabatic chemical reactions with different substituent and different environments. This is done in the framework of the generalized Marcus expression (see 10,14 and section II). We concentrate on the SN2 class of reactions42, applying the FDFT formulation as was suggested first in Ref. 3 and implemented in Refs. 1,2, where we provided evidences that Hrp-s are phase independent using first principle-based calculations without any additional empirical parameters. Here, we extend the above studies and show that Hrp is very robust and does not change significantly even when some solvent molecules are included explicitly in the quantum region and even to some respect with the nature of the substituent. This finding further supports the basic assumption behind the Empirical Valence Bond (EVB) method10,43 that these off-diagonal matrix elements are phase-independent. We also use various nucleophiles in SN2 reactions and show that the corresponding Hrp are approximately considered constant.
Our present results and those obtained in our previous studies justify the use of the same off-diagonal matrix elements obtained for a given reaction in solution to a whole class of reactions with the same LFER in gas phase, in solution or in protein media. They also provide a fundamental justification to the existence of LFER in related chemical reactions.
II. Theory and Computational Methods
Our strategy of describing adiabatic reaction in condensed phases is based on the EVB approach and the corresponding modified Marcus formulation. In this approach, which is described here for simplicity for the two-state case, we represent the system by two diabatic states that correspond to the reactant and product states. For example, a generic reaction of the form:
| (1) |
can be described by the two diabatic wave functions (representing the reactant and product states, respectively):
| (2) |
The wave function for the ground state of the entire system can also be written in the adiabatic representation as
| (3) |
Although there are different ways of obtaining the diabatic states,44–46 the FDFT method provides a particularly useful way of producing both the diabatic states and the adiabatic state. Since the details on the FDFT method can be found elsewhere, we will provide below only a brief description.
The total energy of an N-electron system is defined within the Kohn-Sham formulation as follows:
| (4) |
where Vext(r) is the external potential, Exc[ρ(r)] is a density functional of the exchange-correlation energy and Ts[ρ(r)] is the Kohn-Sham kinetic energy expressed in terms of the Kohn-Sham orbitals:
| (5) |
| (6) |
The FDFT/CDFT embedding approach3,21,47 divides the system into subsystems, and applies Kohn-Sham formulation to each subsystem separately, taking into account the interaction with the other subsystems. For instance, if we divide the whole system into two subsystems with NI and NI′ electrons, respectively, then the total energy of the system is defined as follows:
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
where Ts[ρ] is defined as the orbital-independent kinetic energy functional of the electron density of the system. Fixing the electron density of region I′ and minimizing the total energy with respect to the orbitals of region I leads to the following one-electron embedding equation3:
| (12) |
where the effective potential Veff, I (r) is defined as follows:
| (13) |
Here, is approximated as described in Refs. 3,48, and the Kohn-Sham potential, , is given by the following:
| (14) |
Once ρI(r) is known, a counterpart equation for region I′ could be derived. These two coupled equations can be solved iteratively in a freeze-and-thaw procedure until convergence is reached47. In case a part of the system is described classically we use a QM(FDFT)/MM formulation where the effect of the MM part is incorporated in the FDFT Hamiltonian as described in Ref. 49.
At this point, it is useful to mention two other approaches related to FDFT/CDFT, which have been aimed, however, at the description of a system consisting of subsystems, namely the subsystem formulation of DFT (SDFT)50,51. These approaches provide an alternative to the conventional supermolecular Kohn-Sham framework. However, these approaches target the exact ground-state electronic density of the total collection of subsystems, in contrast to only targeting the density of subsystem A in a way that minimizes the Hohenberg Kohn energy functional of the total system using a fixed form of the environment density in the presence of constraints (see discussion in 52). Here the main conceptual difference is that the FDFT introduced the key idea of consistent embedding (in analogy to QM/MM), thus allowing one to focus on the system of interest while representing the environment quantum mechanically. This type of idea has not emerged from the other alternative approaches.
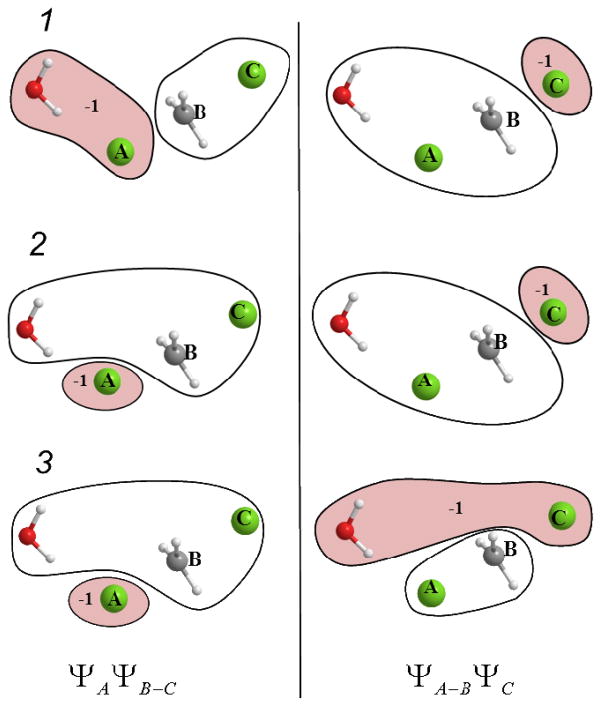
In order to use the FDFT approach to describe the diabatic states1 of Eq. (2), we divide the total density in the reactant and product states to (ρA and ρBC−) and (ρAB and ρC), respectively (see Fig. 1), and use
Figure 1.
Possible choices of assigning a QM water molecule to the partitions of the diabatic states illustrated for the Cl− + CH3Cl system. The water molecule can be either assigned to group A, B or C when defining the reactant and product diabatic states, resulting in the above depicted three possibilities: 1, 2, and 3. The first column shows the reactant state decompositions with ΨA ΨB–C, and the second column corresponds to the product state partitioning, ΨA–B ΨC. The three choices for the partitioning of the water molecule are 1: including the water molecule in the same partition with group A, 2: including the water molecule in the same partition with the central group B, or 3: including the water molecule in the same partition with group C. The negatively charged partition is indicated by colored background and the displayed charge value (e).
| (15) |
where EFDFT is defined in Eq. 7. In each case, we treat both ρI and ρI′ as being embedded in the rest of the system using a QM/MM procedure. In the present treatment, we used the constrained DFT (CDFT) approach47,49 with the freeze-and-thaw procedure. The same QM/MM approach is used for the adiabatic state, where we describe the whole reacting system by a regular DFT approach and embed this system in the classical MM surroundings. The energy of the adiabatic system is designated here as Eg.
In formulating the form of the adiabatic energy we are not constrained by any relationship between the diabatic densities of the reactant and product states, because these are arbitrary mathematical definitions and the only “real” measurable quantity here is the adiabatic electron density or adiabatic energy and the εr and εp are used as a tool for the free energy mapping (see below). As the adiabatic energy is known, we should focus on the most stable selection of the diabatic states and it is thus beneficial to consider them as formally orthogonal valence bond states, avoiding the need to introduce the complex overlap effect. The FDFT approximates such diabatic states by defining two different separations of the electrons: one partitioning for the reactant diabatic state, and a distinct partitioning of the product diabatic states. These differing separations correspond to Hamiltonians of the subsystems with different number of electrons that formally produce orthogonal diabatic states due to the changing number of electrons involved in the subsystems. Thus (see also below) we can define in a formally rigorous way a connection between the two representations by requiring that our two-state diabatic energies will satisfy the effective secular equation:
| (16) |
from which we have:
| (17) |
We use our FDFT to evaluate Hrp, but not to obtain a correct overlap or coupling elements, rather to address the question whether for reasonably defined εr and εp we would get a constant Hrp through Eq. (17) with the correct adiabatic surface. One may still ask whether the ideal diabatic states that correspond to the FDFT are actually orthogonal (as implied by the operational definition of Eq. (17)) but, first our approach guarantees some approximate orthogonality, and second it would not change our conclusion, as the key issue is to prove that for our chosen diabatic states we obtain constant Hrp through Eq. (17). For those who are interested in looking for a more mathematical proof we note that recent studies also showed that the VB overlap integral53 is rather constant at different regions of the surface. However, our approach is to use the Hrp defined by Eq. (17) and evaluate whether this arbitrarily defined Hrp is constant or not. We also like to clarify that we (and others) cannot have an exact mathematical proof for the postulate that the off diagonal element is relatively constant (regardless of the representation), but rather accumulation of numerical verifications.
Now our task is to evaluate the free energy that corresponds to the surface Eg. This is done by the EVB mapping procedure using
| (18) |
where λm is a mapping parameter, which is gradually changed according to a standard FEP approach. The ground state free energy surface is then obtained using the umbrella sampling expression54,55
| (19) |
where β = 1/kbT (kb is the Boltzmann constant and T is the absolute temperature) and x = εr − εp = Hrr − Hpp, the reaction coordinate.
This specialized treatment of the microscopic Marcus parabolas and the energy gap coordinate has been introduced originally by Warshel54 for generating the microscopic equivalent of the Marcus parabolas (see also Refs. 54,56,57), and has since been used extensively by many other workers (e.g., 58–61, 31–33,62,63). However, the extension to the adiabatic case has been somewhat less appreciated. In many cases the diabatic functionals follow the harmonic approximation, which is what has been assumed in Marcus macroscopic derivation of the ET theory and what has been established to be an excellent approximation in our microscopic simulations14,64,65, and in many subsequent simulations.
For adiabatic chemical reactions Hrp is usually large and its effect on the adiabatic surface cannot be neglected as in ET. In this case we must use the adiabatic free energy barrier to determine the reaction rates, which is given from Eq. (16) (in the two state case) as:
| (20) |
This relationship can be extended along a generic reaction coordinate, x, (e.g. using the EVB/umbrella sampling energy mapping10 with the choice of x = εr − εp) to obtain a rigorous adiabatic free energy profile, Δḡ(x) (which corresponds to Eg), using the reactant (Δgr(x)) and product (Δgp(x)) free energy functions that correspond to the εr and εp surfaces:
| (21) |
We can now exploit the fact that the Δgr(x) and Δgp(x) curves can be approximated by parabolas of equal curvature (an approximate relationship, which was found to be valid by many microscopic simulations55,66), we can express this approximation by:
| (22) |
where λ is the so-called “reorganization free energy”, ΔG0 is the reaction free energy, and are the minima of the reactant and product parabolas such that the origin for x is chosen at . From Eqs. (21) and (22), one obtains the free energy at the crossings of the parabolas, x‡ the following:
| (23) |
Similarly, at the reactant state, where approaches zero as the diabatic state equals to the adiabatic state, the free energy can be approximated as:
| (24) |
This gives the Hwang-Åqvist-Warshel (HAW) equation, which is given in the general case by:
| (25) |
where ΔG‡ is the activation free energy. The validity of Eq. (25) has been established through repeated quantitative EVB studies of reactions in solution and in proteins (such as those of Refs. 55,67). Thus, these equations can be seen as a quantitative correlation between ΔG‡ and ΔG0 .
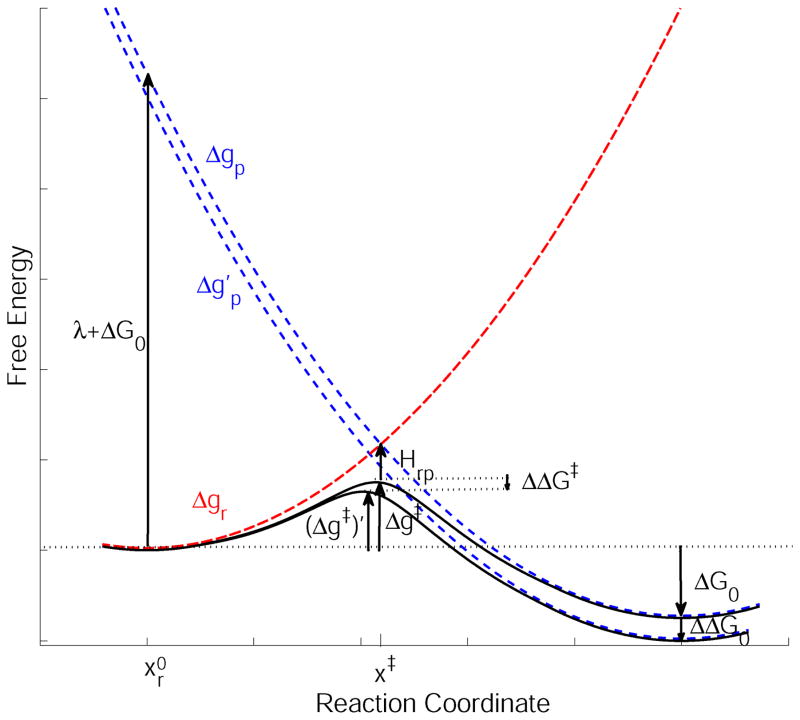
The nature of this relationship is illustrated in Fig. 2, where we show how the activation barrier changes with the reaction free energy. As is apparent from the figure we should expect a very clear relationship between ΔG‡ and ΔG0. In fact by examining Eq. (25) we obtain a linear relationship between ΔΔG‡ and ΔΔG0 if the reorganization energy and the off-diagonal terms are unchanged. The resulting relationship (which is linear for the range where ΔΔG0 is much smaller than λ) is simply obtained by differentiating the ΔG‡ of Eq. (25) with respect to ΔG0 can be expressed by:
| (26) |
where the contribution from the last term of Eq. (25) is neglected. Here, the linear correlation coefficient depends on the magnitudes of ΔG0 and λ, and it is close to ½ when λ is much larger than ΔG0. This linear free energy relationship (LFER) or free energy relationship (FER) as well as its performance in actual studies of chemical and biochemical problems has been discussed in detail elsewhere10,15,18,55,68,69. It is clear from the HAW relationship that it is essential to take into account the effect of the coupling Hrp in LFER studies that involve actual chemical (and not ET) reactions. Here we aimed at obtaining a numerical verification of the assumption that λ and Hrp are approximately constants for reactions that can be classified by a single LFER.
Figure 2.
A schematic description of the relationship between the free-energy difference between the reactant and product states (ΔG0), and the activation free energy (Δg‡). This figure illustrates how shifting εp by ΔΔG0 (which changes εp to εp′ and ΔG0 to ΔG0 + ΔΔG0) changes Δg‡ by a proportional amount.
We must emphasize at this point that for adiabatic reactions the effect of Hrp is frequently significant, and neglecting it leads to an incorrect estimate of the relevant free energies. This is illustrated in the systematic analysis of hydride transfer reactions by Kong and Warshel18 and in studies of proton transfer reaction (e.g., 70). The activation free energy can then be converted to the corresponding rate constant using transition state theory (TST) (see e.g. Ref. 10).
It might also be useful to expand here on the energy gap coordinate. This coordinate introduced by one of us in 198254 provided probably the most unique way of capturing the microscopic nature of Marcus macroscopic idea. It is based on looking for the probability of surface crossing at the hyperspace where x ≡ εr − εp =0 (see 56) and on the probability of having different values of x. This coordinate appears to capture in a remarkable way the effect of the solvent polarization and to demonstrate that the solvent follows the linear response approximation trend and this leads to the apparent quadratic feature of the diabatic states. The power of using the energy gap coordinate has been widely recognized and used by many research groups.
Here, our FDFT calculations were done with a modified version of the deMon program package71. The Becke88 exchange potential, Perdew86 correlation potential, and the gradient-dependent approximation of Ref. 48 for the nonadditive kinetic energy functional of Eq. 11 were used in all the calculations with standard 6–31+G(d) basis set. The QM/MM implementation was done by using a script to interface between the modified deMon and the MOLARIS package72. The simulation systems for the solvated TS calculations were set up by immersing the solute in a 18 Å water sphere, centered on the geometric center of the solute molecules.
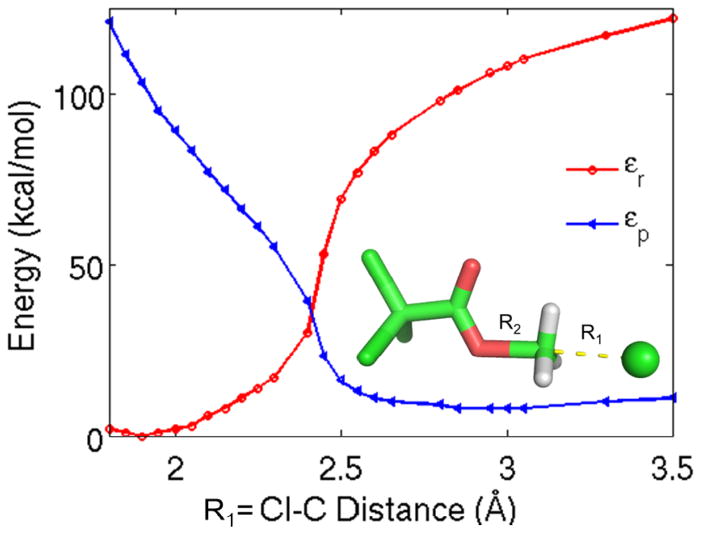
We started our calculations by generating gas phase geometries using the Gaussian0373 package with B3LYP74 DFT method and 6–31+G(d) basis set. Subsequently we performed FDFT and full FDT calculations, using the obtained geometries with the MOLARIS and deMon packages. The TS geometries were obtained by geometry optimization to a transition state. The corresponding single-imaginary-frequency motions were visually inspected. The geometries along the full reaction profiles were obtained by constrained geometry optimizations using Gaussian03. We used the breaking (R1 in Fig. 3) or the forming (R2 in Fig. 3) bond distances to constrain the geometries. In a series of geometry optimizations we used a distance constraint on R1, changing it from 1.75 Å to 3.5 Å in 0.05 Å increments, to obtain 35 geometries along the reaction profile. Similarly, we also obtained constraint minimized geometries using R2. In addition to constraining the bond distance, an angle constraint corresponding to the linear attack at the transition state was also applied in specific cases to ensure the stability of the molecular species of interest. Both sets of geometries were then used to calculate the FDFT and DFT energies with the deMon and MOLARIS programs in the gas phase. That is, we generated at each region of the reaction coordinate a grid of the one dimensional space defined by the central C – attacking Cl or the central C – leaving group distances (minimizing the energy with respect to all other coordinates) and then sorting form the generated diabatic energies the configurations that correspond to different values of x. The scanning for both the bond breaking and bond forming distances was set up by starting with a distance constraint of 1.7 Å, and after obtaining the structure with constrained optimized geometry increasing the constraint for each consecutive geometry optimization by 0.05 Å resulting in a total of 35 structures. Out of the 70 structures in total that were obtained only the successfully optimized structures were used for the FDFT calculations.
Figure 3.
Showing the diabatic energies as a function of a standard (distance based) reaction coordinate for the CCl3COO−+CH3Cl reaction. The R1=C-Cl distance was used to obtain the optimized geometries along the reaction pathway.
We then obtained solution structures at the solute transition state by running 0.5 ns molecular dynamics (MD) simulations with fixed solute geometry, where snapshots at 0.1 ns interval were collected (see results in SI). The fluorine van der Waals parameters in the MD simulations were set to the standard values of the chlorine to avoid extra parameterization effort (such an effort was not needed as it would not change our conclusions).
The FDFT and DFT energies were also obtained independently for the gas phase reaction profiles (see results in SI) using the ADF program75. We used the LDA exchange potential for the diabatic and adiabatic DFT calculations with DZ basis set76. The nonadditive kinetic exchange potential for the diabatic calculations was described by the Thomas-Fermi model50,77, and the freeze-and-thaw implementation47 was used to iteratively relax the densities of the two regions.
III. Results and Discussion
III.1 Calculated Trend
The present work considered as a benchmark SN2 reactions with various nucleophiles, X:
| (27) |
Defining diabatic reactant (r) and product (p) states, respectively, as:
| (28) |
The same system have been considered in our previous study1 (see also Ref. 2) that focused on the effect of the environment. That work examined the exchange reaction where X is Cl− and obtained the results presented in Fig. 4 using the FEP/US procedure of Eq. 19. These results established that Hrp is almost solvent independent.
Figure 4.
Diabatic and adiabatic FDFT free energy profiles for the reaction Cl− + CH3Cl → ClCH3 + Cl− in the gas phase (open symbols) and in solution (filled symbols). The reaction coordinate is defined as the free energy difference between the diabatic surfaces. The reactant diabatic free energies are shown with circles (gas phase red, solution pink), the product state diabatic free energies are shown with triangles (blue (gas), light blue (solution)). The full lines represent the corresponding parabolic fits (see also table 3). The adiabatic free energies are shown with symbols (x (gas), square (solution)), the fitted polynomial lines are given to guide the eye. The actual results were obtained in Ref. 1.
Here we turn our attention to effects, which are associated with tighter coupling than that of the solvent environment. That is, we focus here on the effect of the substituent and a nearby solvent molecule. The corresponding sets of calculations were done in a less rigorous way in terms of free energy dependence emphasizing just first order QM effects. These calculations used constrained-minimized geometries to calculate the full Marcus parabolas along the energy gap reaction coordinate together with the ground-state adiabatic DFT energies. We constrained the bond breaking or bond forming atomic distances and minimized the geometries of the reaction profiles for the reactions Cl− + CH3X → ClCH3 + X−, with X groups of Cl−, F−, CH3COO−, CH2ClCOO−, CHCl2COO−, CCl3COO−, HCOO−, OCl−, and the neutral NH3. The constrained and optimized structures of the SN2 reaction systems, at various leaving group or attacking group distances, were then used to obtain both the diabatic and the adiabatic energies, which were plotted along the energy-gap coordinate (e.g. Fig. 5). The energy gap was calculated as the energy difference between the two diabatic states for each structure, where the FDFT calculations provided the εr and εp diabatic energies, from which the x ≡ εr − εp value of the reaction coordinate was calculated. The ground state adiabatic energies (Eg) of the same structures were obtained by standard DFT method using the same level of theory as for the FDFT calculations. From the above three ab initio calculations we determined the Hrp values as defined in Eq (17).
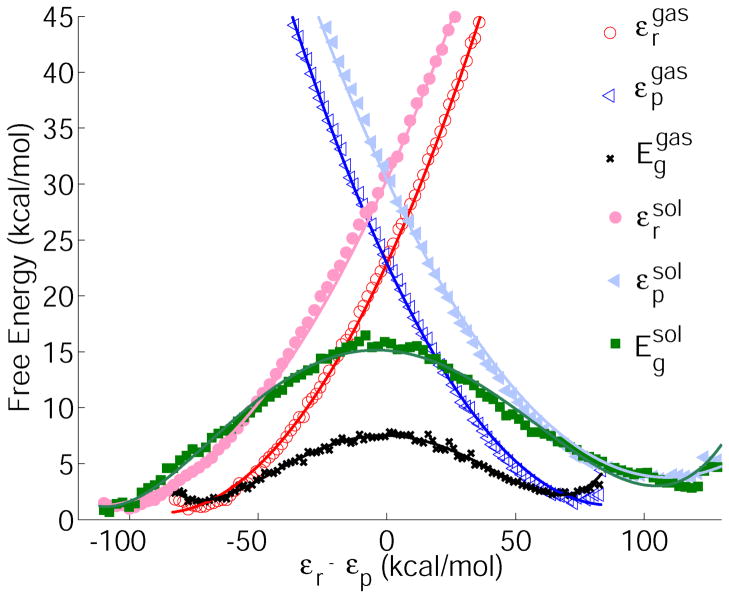
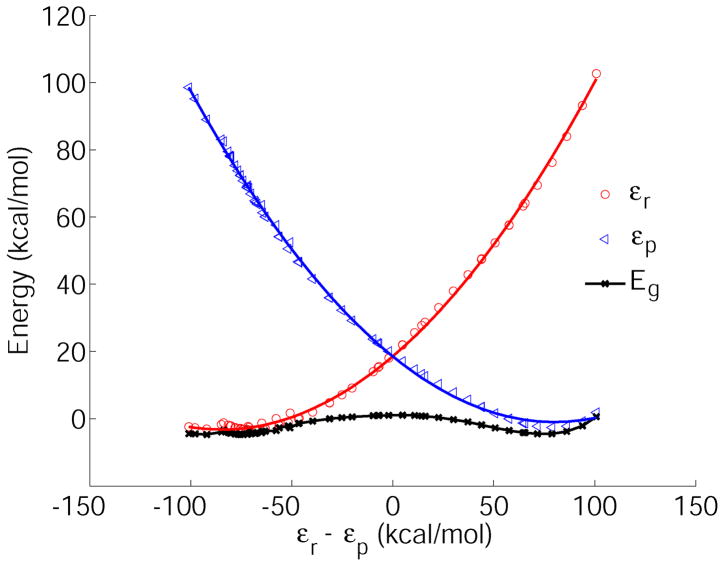
Figure 5.
The adiabatic energy (Eg, black) profiles as a function of the energy gap reaction coordinate. The quadratic fit is shown for the reactants (εr red) and for the products (εr, blue) for the gas phase Cl− + CH3Cl → ClCH3 + Cl− reaction.
The adiabatic barrier of the Cl− self-exchange reaction is known to be about 9 kcal/mol underestimated with the use of the BP method in the gas phase78. Taking this into consideration, our free energy estimates from previous work1 agreed well with the experimental result in solution79,80. In the current calculations we have evaluated the gas phase energy profiles (Fig. 5), and the adiabatic energy barrier only differed from our earlier the free energy calculations (Fig. 4) by about 0.5 kcal/mol, whereas the diabatic energies differed by about 1 kcal/mol. Therefore, taking into consideration the gas phase optimized structures rather than performing the full free energy calculations provides satisfactory accuracy for the barrier height. Additional calculations were performed by using different diabatic energy functional. Here we used the ADF program package and performed FDFT calculations using LDA exchange potential and Thomas-Fermi approximation as described in the previous section. We obtained different Hrp values compared with the ones obtained using DeMon, however the Hrp values were all very close to about 33 kcal/mol for the calculated LFER reactions (see Supplementary Materials for results). We note here that both higher and lower FDFT energies can be obtained as compared with the full DFT energies that will result in different coupling values. However, a constant shift of both diabatic states would leave the parabolic fit parameters unchanged and, therefore, the reorganization energies are insensitive to such effects. By analyzing the parabolic fits of the diabatic states, we estimated the reorganization energy (see SI) as λ(ΔG0) ≈ 122, which is very close to the values obtained using DeMon (Fig. 6).
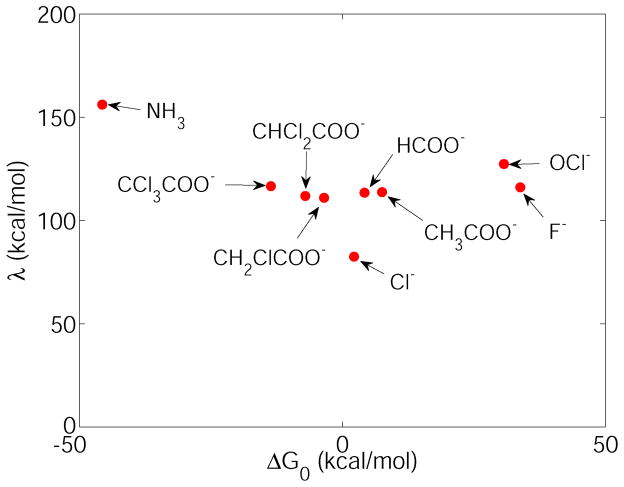
Figure 6.
The reorganization energy (λ) for the gas phase XCH3 + Cl− → X− + CH3Cl SN2 reactions as a function of the reaction energy (in this case we look at the energy rather than the free energy). The X groups are specified by arrows for each data point.
Obtaining an accurate parabolic fit to our data from minimizations nevertheless limits the accuracy of the determined reorganization energies. We observed that X = Cl− and NH3 seem to be outliers in Fig 6., and these large deviations of the reorganization energies from the mean subsequently also result in deviations in the LFER for the same substituents in Fig. 8. This may be due to several reasons. There could be a different extent of the self-interaction error that is particularly substantial for Cl−. To fully address this problem, and to quantitatively evaluate the reorganization energies also in solution, more accurate free energy simulations are required using also different functionals, which is outside of the scope of our current work. Given that in our results the Hrp is essentially unchanged with different leaving groups regardless of the self-interaction error, investigating the reorganization energy could potentially lead to new strategies for eliminating the self-interaction error in a non-system-specific way.
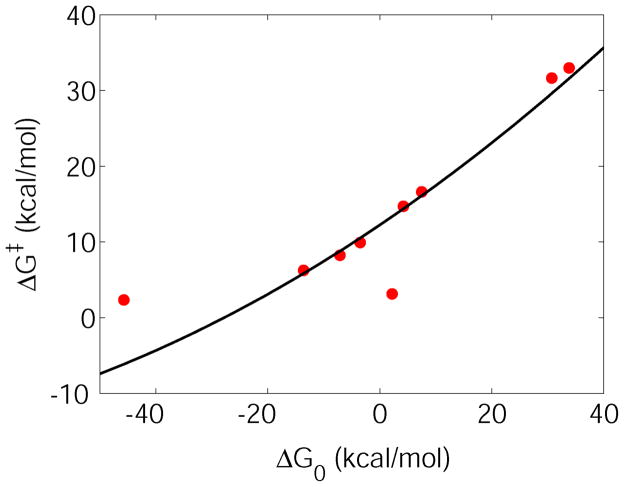
Figure 8.
Adiabatic gas phase energy barriers for the XCH3 + Cl− → X− + CH3Cl SN2 reactions as a function of the reaction energy. Please note that the free energies here are approximated with results from energy minimizations. The results shown are based on Table 1 and Table 2. The black curve corresponds to the parabola obtained from Eq. (25), assuming constant reorganization energy of 116.6 kcal/mol, and assuming negligible coupling in the reactant or product states, and a constant off-diagonal coupling matrix element of 16.9 kcal/mol.
Our calculations used the following nucleophiles (the X in Eq. (27)): Cl−, Cl−·H2O, CN−, CCl3COO−, CH2ClCOO−, CH3COO−, CHCl2COO−, F−, HCOO−, OCl−, and the neutral NH3. We also considered a single water molecule added to the QM region for X=Cl−. The transition state was optimized together with the water molecule with the obtained geometry as shown in Fig. 1 and in the inset of Fig. 7. The water molecule was assigned to the diabatic states according to the partitions 1, 2, or 3 of Fig. 1.
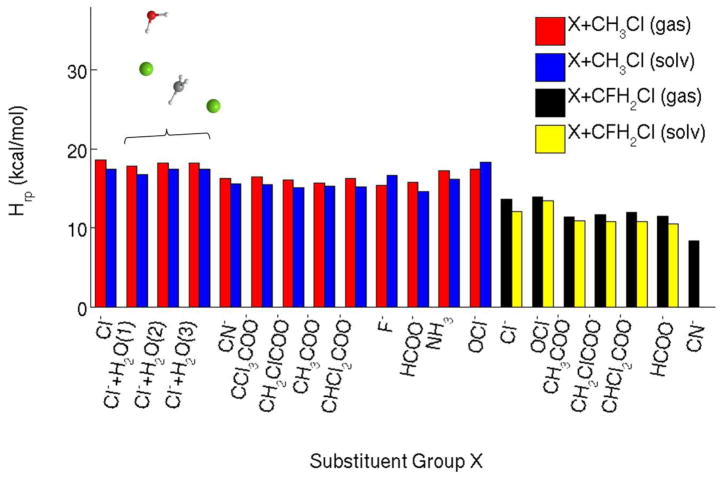
Figure 7.
Off-diagonal coupling constants (Hrp) obtained for the transition state geometries in the gas phase (red and black) and in solution (blue and yellow). The results are shown for two series of SN2 reactions defining two LFERs: X−+ CH3Cl → XCH3 + Cl− and X−+ CH2FCl → XCH2 + Cl− with the X groups as specified on the x-axis and in the text.
In the solution phase MD calculations, we used the gas phase optimized transition state structures for most of the systems. We used the structures that correspond to the solution phase transition states, when the gas phase structures did not yield an energy gap value in solution that was in the transition state region (|εr − εp|) < 22 kcal/mol). In these cases, geometries close to the transition states were chosen from the structures along the gas phase reaction profiles by visual inspection, except for [CN··CH2F··Cl]−, where such structure was not available due to the failed constrained minimizations. This type of treatment with fixed solute geometry is simpler than the more fundamental free energy calculations explored in Fig. 4, where the focus was on the difference between the effective Hrp in different environments and also at different regions of the reaction coordinate. Nevertheless, in the current work we aimed to discuss the Hrp only in the TS, to justify the assumptions implied in the derivation of the LFERs.
Our calculations are demonstrated in Fig. 5 for X=Cl− and then summarized in Tables 1–2, Figs. 6–8, where we provide results for 10 different nucleophiles in the gas phase and in solution. The average values in the gas phase and in solution are very close to each other: 16.9 kcal/mol and 16.3 kcal/mol for the gas phase and with solvent molecules, respectively, with a small standard deviation (1.1 kcal/mol in both gas phase and in solution). These results demonstrate numerically that the off-diagonal matrix elements are nearly constant for SN2 reactions belonging to the same LFER, regardless of the reaction media.
Table 1.
Fitting parameters obtained from the quadratic fit A(εr − εp)2 + Br/p (εr − εp) + C to the diabatic states for XCH3 + Cl− → X− + CH3Cl SN2 reactions. The reorganization energies (λ=1/(4A)) and reaction energies (ΔG0=λ(Br+Bp)) calculated from the parabolic fit are also givena.
| SN2 reaction | Reactant state | Product state | ΔG0 | λ | ||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| A | Br | C | A | Bp | C | |||
| F−+CH3Cl | 0.0022 | 0.65 | −17.9 | 0.0022 | −0.35 | −17.9 | 33.8 | 116.1 |
| Cl−+CH3Cl | 0.0030 | 0.51 | 18.5 | 0.0030 | −0.49 | 18.5 | 2.2 | 82.5 |
| OCl−+CH3Cl | 0.0020 | 0.62 | −47.6 | 0.0020 | −0.38 | −47.6 | 30.7 | 127.4 |
| HCOO−+CH3Cl | 0.0022 | 0.52 | −26.2 | 0.0022 | −0.48 | −26.2 | 4.2 | 113.5 |
| CH3COO−+CH3Cl | 0.0022 | 0.53 | −27.4 | 0.0022 | −0.47 | −27.4 | 7.5 | 113.7 |
| CH2ClCOO−+CH3Cl | 0.0023 | 0.48 | −58.1 | 0.0023 | −0.52 | −58.1 | −3.5 | 111.0 |
| CHCl2COO−+CH3Cl | 0.0022 | 0.47 | −89.7 | 0.0022 | −0.53 | −89.7 | −7.1 | 111.9 |
| CCl3COO−+CH3Cl | 0.0021 | 0.44 | −121.3 | 0.0021 | −0.56 | −121.3 | −13.6 | 116.6 |
| NH3+CH3Cl | 0.0016 | 0.35 | −12.2 | 0.0016 | −0.65 | −12.2 | −45.7 | 156.2 |
Energies in kcal/mol
Table 2.
Calculated off-diagonal elements (Hrp) at the TS structures. The solutions results represent the average values obtained from all five snapshots of the 0.5 ns long simulations (see also SI)a.
| Moiety | Gas phase | Solution | ||||||
|---|---|---|---|---|---|---|---|---|
| Hrp | Eg | εr | εp | Hrp | Eg | εr | εp | |
| [Cl··CH3··Cl]− | 18.6 | 0 | 18.6 | 18.6 | 17.4 | −78.7 | −60.0 | −62.2 |
| [Cl··CH3··Cl]−+H2O(A) | 17.8 | 0 | 15.8 | 20.2 | 16.8 | −79.7 | −65.4 | −59.6 |
| [Cl··CH3··Cl]−+H2O(B) | 18.2 | 0 | 21.1 | 15.8 | 17.4 | −79.7 | −57.9 | −65.4 |
| [Cl··CH3··Cl]−+H2O(C) | 18.2 | 0 | 21.1 | 15.7 | 17.4 | −80.7 | −57.9 | −65.3 |
| [CN··CH3··Cl]− | 16.3 | 0 | 17.9 | 14.9 | 15.6 | −80.8 | −76.7 | −82.9 |
| [CCl3COO··CH3··Cl]− | 16.5 | 0 | 15.6 | 17.5 | 15.5 | −77.2 | −57.9 | −51.5 |
| [CH2ClCOO··CH3··Cl]− | 16.1 | 0 | 18.2 | 14.3 | 15.1 | −79.4 | −69.2 | −67.8 |
| [CH3COO··CH3··Cl]− | 15.7 | 0 | 21 | 11.8 | 15.3 | −80.1 | −77.6 | −86.8 |
| [CHCl2COO··CH3··Cl]− | 16.3 | 0 | 16.6 | 16 | 15.2 | −79.2 | −65.3 | −59.7 |
| [F··CH3··Cl]− | 15.4 | 0 | 13.8 | 17.1 | 16.7 | −85.8 | −69.8 | −67.6 |
| [HCOO··CH3··Cl]− | 15.8 | 0 | 20 | 12.5 | 14.6 | −81.0 | −81.8 | −93.4 |
| [NH3··CH3··Cl]− | 17.2 | 0 | 10.4 | 28.3 | 16.2 | −74.4 | −3.4 | −21.3 |
| [OCl··CH3··Cl]− | 17.4 | 0 | 30.9 | 9.8 | 18.3 | −75.2 | −77.6 | −83.0 |
|
| ||||||||
| [Cl··CH2F··Cl]− | 13.6 | 0 | 13.8 | 13.6 | 12.1 | −74.0 | −66.2 | −67.5 |
| [CN··CH2F··Cl]− | 8.4 | 0 | 19.7 | 3.5 | ||||
| [OCl··CH2F··Cl]− | 13.9 | 0 | 25.2 | 7.7 | 13.4 | −74.4 | −55.7 | −67.9 |
| [CH3COO··CH2F··Cl]− | 11.4 | 0 | 16.3 | 7.9 | 10.9 | −70.9 | −74.2 | −81.1 |
| [CH2ClCOO··CH2F··Cl]− | 11.7 | 0 | 14.1 | 9.8 | 10.8 | −77.6 | −72.3 | −73.9 |
| [CHCl2COO··CH2F··Cl]− | 12.0 | 0 | 12.8 | 11.2 | 10.8 | −77.3 | −69.1 | −66.4 |
| [HCOO··CH2F··Cl]− | 11.5 | 0 | 15.5 | 8.5 | 10.5 | −77.4 | −42.5 | −50.5 |
Energies in kcal/mol. Note that the ground state and diabatic state energies are shifted for each system separately, by the reference energy of Eg for the gas phase transition state structure (See SI).
Using the numerically obtained average reorganization energy and the mean value of Hrp at the transition state, we obtained from Eq. (25) a nearly linear FER that matches the actual data (Tables 1 and 2) well (Fig. 8). This numerically verifies the theoretical derivation that LFERs can be obtained from the linear regime of the quadratic function that is given in Eq. (25). Interestingly, several recent calculations reported data where a quadratic fit would better describe the FERs rather than a linear relationship81,82. These could largely be associated with a distinctively changing underlying reaction mechanism.
We also addressed the effects of changing the central group in the SN2 reaction and changed CH3 to CH2F considering now X− + CH2FCl → XCH2F + Cl−. The calculated values of Hrp for the following X groups: Cl−, OCl−, CN−, HCOO−, CH3COO−, CH2ClCOO−, CHCl2COO− are given in Table 2 and Fig. 7. As seen from the figure, the Hrp values were nearly identical for the second set of reactions regardless of the media and the nucleophile, but distinct from the first set of reactions. The average Hrp value in gas phase was 11.8 kcal/mol with a standard deviation of 1.8 kcal/mol, and 11.4 kcal/mol in solution with a standard deviation of 1.1 kcal/mol.
III.2 The nature of the off diagonal elements
Our results suggest that the Hrp values depend mainly on the nature of the central (transferred) group. That is, the off-diagonal elements were close to constant for different nucleophiles, but differed by about 35% between the transfer groups CH3+ and CH2F+.
In agreement with our earlier study1, the gas phase results and those with solvent are very similar (Table 3). Here we also observe the same media-independence of Hrp with a solvent water molecule explicitly included in the QM region.
Table 3.
Parameters calculated from the quadratic fit A(εr − εp)2 + B(εr − εp) + C to the diabatic states for our earlier free energy simulations of the ClCH3 + Cl− → Cl− + CH3Cl SN2 reaction in the gas phase and in solution1. Hrp values reported here represent the maximum numerical value of the coupling obtained along the reaction coordinate, and in practice this corresponds to the transition state with Δε= 0.
| λ | Hrp | |
|---|---|---|
| Gas | 87.9 | 16.0 |
| Solution | 111.6 | 15.3 |
The finding of the remarkable stability of the off-diagonal element, obtained with formally orthogonal diabatic states, has a major significance in terms of the validity of LFER in general and the assumptions of the EVB in particular. Obtaining constant off-diagonal coupling means that if the diabatic states are approximately parabolic we have a well-defined and predictable LFER. It also means that the EVB idea of using the same off-diagonal element in different environments is valid even when we have different substituents.
The ability to evaluate Hrp by the CDFT is particularly useful in view of the capacity of this method to provide numerical coupling in different environments and different conditions. This feature can also be used in studies of electron transfer reaction where Hrp is much smaller. This may be very useful in exploring medium effect on electronic coupling, in particular if the environment is represented by the FDFT embedding approach.
It is useful to point out that other research groups27,83–85 also explored some of the ideas based on our CDFT and FDFT methods (reviewed in detail in Refs. 52,86,87). In this respect it is useful to clarify that despite the interest raised (e.g. 29,88–91) by the elegant work of Wu and Van Voorhis92, the main innovation of this work seems to be the emphasis on fixing the diabatic densities by using Lagrange multipliers, rather than by our physically based idea. Here, it should be remembered that diabatic states neither are nor should be unique. Rather, they are simply a useful mathematical representation in order to solve the physics of the real adiabatic system. The key issue is to force the diabatic states to reproduce the physics of the reactant and products, and, at least in the case of the crucial charge transfer reactions, our approach is far more effective than the (otherwise seemingly rigorous) use of Lagrange multipliers. That is, the CDFT approach follows the EVB philosophy, and considers the wave functions as being orthogonalized wave functions, and, of course, the corresponding Hij is completely different from the one used by Ref. 92, with both providing correct physics if one uses the corresponding diabatic states (see Ref. 93).
IV. Concluding remarks
This work explored the nature of Hrp in adiabatic reactions and the validity of LFER in describing chemical reactions. Our study starts by reviewing the HAW relationship that provided the basis for LFER in adiabatic reaction. After being proved by earlier studies that the free energy functionals are approximately quadratic in solution, we can obtain rigorous LFER if Hrp is medium-independent and substituent-independent, and the reorganization energies are substituent independent. Our previous study1 used the FDFT approach to establish that Hrp is nearly solvent independent and thus to provide overwhelming justification of the main ad hoc assumption behind the EVB. However, it remains to be proved that Hrp is insensitive to substituents and this has been the focus of the computations reported here. More specifically, we used here the FDFT approach to evaluate Hrp for a full series of SN2 reactions. It was found that these off diagonal elements are constant to a very good approximation, independent of the various nucleophiles used in the SN2 reactions. This finding was further verified by calculating the Hrp values for a second set of SN2 reactions that also exhibit LFERs. Here the middle transferred group was changed from a methyl group to a fluoro-methyl group. Despite the relatively small change between the two sets of reactions, our results showed a consistent, nearly 35% decrease in the Hrp values for the second set of reactions, providing a statistically significantly different mean value for the Hrp, as compared with the first set. We have seen no statistically significant difference, however, between the gas phase and the solution reactions, even if some of the solvent was explicitly included in the ab initio description.
Although this work focused on the off diagonal matrix elements, it also shed some light on the intramolecular contribution to the reorganization energy (the so called “inner sphere“ reorganization energy). This was done by calculating the approximate gas phase Marcus parabolas for the SN2 reactions using the FDFT approach. In this respect, it must be mentioned that in contrast to the treatment of Eq. (19) that led to Fig. 4 we explored the gas phase reorganization energies in a very approximate way but, nevertheless, the conclusions about the reorganization energy were consistent as also suggested by the fact that very different diabatic energy functions provided very similar values (see Fig. 6 and SI).
Our approach of using the FDFT also provides a powerful way of evaluating the effective off-diagonal element in charge transfer reactions in different environments1. This ability is of a generally fundamental and practical interest1,28,94. Here it is useful to note that in contrast to possible implications of Ref. 27, there is no problem with the use of Eq. (17) to obtain or examine the EVB off-diagonal elements. These off-diagonal elements are rigorously defined by Eq. (16) and do not have to be equal to the coupling terms between the nonorthogonal diabatic wave functions that are used in studies of the rates of the electron transfer processes.
The FDFT/CDFT can be used in exploring additional fundamental studies of molecular interactions. For example, one challenging issue is the nature of the environmental effects on long-range electron transfer. Here, for example, one can include the environment with the FDFT treatment and examine issues that are notoriously difficult to address, such as a partial charge transfer to the environment.
Supplementary Material
Acknowledgments
This work was supported by the NIH grant GM24492, and by the Intramural Research Program of the National Institute of Diabetes and Digestive and Kidney Diseases. The computational work was supported by the University of Southern California High Performance Computing and Communication Center (HPCC), and by the Biowulf Linux cluster at the NIH. We thank Dr. Attila Szabo for many helpful suggestions and Dr. Gongyi Hong for useful help in the calculations. This paper is dedicated to Wilfred F. van Gunsteren on the occasion of his 65th birthday.
Footnotes
Supporting Information Available: Detailed results using the ADF, and DeMon programs. This information is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Hong G, Rosta E, Warshel A. Using the Constrained DFT Approach in Generating Diabatic Surfaces and Off Diagonal Empirical Valence Bond Terms for Modeling Reactions in Condensed Phases. J Phys Chem B. 2006;110:19570–19574. doi: 10.1021/jp0625199. [DOI] [PubMed] [Google Scholar]
- 2.Xiang Y, Warshel A. Quantifying Free Energy Profiles of Proton Transfer Reactions in Solution and Proteins by Using a Diabatic FDFT Mapping. J Phys Chem B. 2008;112:1007–1015. doi: 10.1021/jp076931f. [DOI] [PubMed] [Google Scholar]
- 3.Wesolowski TA, Warshel A. Frozen Density Functional Approach for Ab Initio Calculations of Solvated Molecules. J Phys Chem. 1993;97:8050–8053. [Google Scholar]
- 4.Maskill H. Mechanisms of organic reactions. Oxford University Press; 1996. [Google Scholar]
- 5.Hammett LP. Some Relations between Reaction Rates and Equilibrium Constants. Chem Rev. 1935;17:125–136. [Google Scholar]
- 6.Pedersen KJ. The theory of protolytic reactions and prototropic isomerization. J Phys Chem. 1934;38:581–600. [Google Scholar]
- 7.Marcus RA. H and other transfers in enzymes and in solution: Theory and computations, a unified view. 2. Applications to experiment and computations. J Phys Chem B. 2007;111:6643–6654. doi: 10.1021/jp071589s. [DOI] [PubMed] [Google Scholar]
- 8.Haim A, Sutin N. Reactions Of Isothiocyanatobis(Ethylenediamine)Cobalt(3) Complexes With Chromium(2) And Linkage Isomerization Of Monothiocyanate Complex Of Chromium(3) J Am Chem Soc. 1966;88:434. [Google Scholar]
- 9.Wladkowski BD, Brauman JI. Application of Marcus Theory to Gas-Phase SN2 Reactions - Experimental Support of the Marcus Theory Additivity Postulate. J Phys Chem. 1993;97:13158–13164. [Google Scholar]
- 10.Warshel A. Computer Modeling of Chemical Reactions in Enzymes and Solutions. John Wiley & Sons; New York: 1991. [Google Scholar]
- 11.Marcus RA. On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer I. J Chem Phys. 1956;24:966–978. [Google Scholar]
- 12.Marcus RA. Chemical and electrochemical electron transfer theory. Ann Rev Phys Chem. 1964;15:155–196. [Google Scholar]
- 13.Warshel A, Russell ST. Calculations of Electrostatic Interactions in Biological Systems and in Solutions. Q Rev Biophys. 1984;17:283–421. doi: 10.1017/s0033583500005333. [DOI] [PubMed] [Google Scholar]
- 14.Warshel A, Hwang JK, Aqvist J. Computer Simulations of Enzymatic Reactions: Examination of Linear Free-Energy Relationships and Quantum-Mechanical Corrections in the Initial Proton-transfer Step of Carbonic Anhydrase. Faraday Discuss. 1992;93:225. doi: 10.1039/fd9929300225. [DOI] [PubMed] [Google Scholar]
- 15.Hwang JK, King G, Creighton S, Warshel A. Simulation of Free Energy Relationships and Dynamics of SN2 Reactions in Aqueous Solution. J Am Chem Soc. 1988;110:5297–5311. [Google Scholar]
- 16.Warshel A. Computer Simulations of Enzymatic Reactions. Curr Opinion in Struct Biol. 1992;2:230–236. [Google Scholar]
- 17.Warshel A. In: Molecular Aspects of Biotechnology; Computational Models and Theories. Bertran J, editor. Kluwer Academic Publishers; The Netherlands: 1992. pp. 175–191. [Google Scholar]
- 18.Kong YS, Warshel A. Linear Free Energy Relationships with Quantum Mechanical Corrections: Classical and Quantum Mechanical Rate Constants for Hydride Transfer between NAD+ Analogs in Solutions. J Am Chem Soc. 1995;117:6234–42. [Google Scholar]
- 19.Warshel A, Weiss RM. An Empirical Valence Bond Approach for Comparing Reactions in Solutions and in Enzymes. J Am Chem Soc. 1980;102:6218–6226. [Google Scholar]
- 20.Marcus RA. Enzymatic catalysis and transfers in solution. I. Theory and computations, a unified view. J Chem Phys. 2006;125:9. doi: 10.1063/1.2372496. [DOI] [PubMed] [Google Scholar]
- 21.Wesolowski T, Muller RP, Warshel A. Ab Initio Frozen Density Functional Calculations of Proton Transfer Reactions in Solution. J Phys Chem. 1996;100:15444–15449. [Google Scholar]
- 22.Shaik S, Hiberty PC. VB Mixing and Curve Crossing Diagrams in Chemical reactivity and Bonding. Adv Quant Chem. 1995;26:99–163. [Google Scholar]
- 23.Gao J, Truhlar DG. Quantum Mechanical Methods for Enzyme Kinetics. Annu Rev Phys Chem. 2002;53:467–505. doi: 10.1146/annurev.physchem.53.091301.150114. [DOI] [PubMed] [Google Scholar]
- 24.Florian J, Aqvist J, Warshel A. On the Reactivity of Phosphate Monoester Dianions In Aqueous Solution: Brønsted Linear Free-Energy Relationships Do Not Have an Unique Mechanistic Interpretation. J Am Chem Soc. 1998;120:11524–11525. [Google Scholar]
- 25.Klahn M, Rosta E, Warshel A. On the Mechanism of Hydrolysis of Phosphate Monoesters Dianions in Solutions and Proteins. J Am Chem Soc. 2006;128:15310–15323. doi: 10.1021/ja065470t. [DOI] [PubMed] [Google Scholar]
- 26.Rosta E, Kamerlin SCL, Warshel A. On the Interpretation of the Observed Linear Free Energy Relationship in Phosphate Hydrolysis: A Thorough Computational Study of Phosphate Diester Hydrolysis in Solution. Biochemistry. 2008;47:3725–3735. doi: 10.1021/bi702106m. [DOI] [PubMed] [Google Scholar]
- 27.Wu Q, Van Voorhis T. Direct Calculation of Electron Transfer Parameters through Constrained Density Functional Theory. J Phys Chem A. 2006;110:9212–9218. doi: 10.1021/jp061848y. [DOI] [PubMed] [Google Scholar]
- 28.Wu Q, Van Voorhis T. Extracting electron transfer coupling elements from constrained density functional theory. J Chem Phys. 2006;125:164105–9. doi: 10.1063/1.2360263. [DOI] [PubMed] [Google Scholar]
- 29.Oberhofer H, Blumberger J. Charge constrained density functional molecular dynamics for simulation of condensed phase electron transfer reactions. J Chem Phys. 2009;131:064101. doi: 10.1063/1.3190169. [DOI] [PubMed] [Google Scholar]
- 30.Migliore A. Nonorthogonality Problem and Effective Electronic Coupling Calculation: Application to Charge Transfer in pi-Stacks Relevant to Biochemistry and Molecular Electronics. J Chem Theory Comput. 2011;7:1712–1725. doi: 10.1021/ct200192d. [DOI] [PubMed] [Google Scholar]
- 31.Oberhofer H, Blumberger J. Insight into the Mechanism of the Ru2+-Ru3+ Electron Self-Exchange Reaction from Quantitative Rate Calculations. Angew Chem, Int Ed. 2010;49:3631–3634. doi: 10.1002/anie.200906455. [DOI] [PubMed] [Google Scholar]
- 32.Oberhofer H, Blumberger J. Electronic coupling matrix elements from charge constrained density functional theory calculations using a plane wave basis set. J Chem Phys. 2010;133:10. doi: 10.1063/1.3507878. [DOI] [PubMed] [Google Scholar]
- 33.Tipmanee V, Oberhofer H, Park M, Kim KS, Blumberger J. Prediction of Reorganization Free Energies for Biological Electron Transfer: A Comparative Study of Ru-Modified Cytochromes and a 4-Helix Bundle Protein. J Am Chem Soc. 2010;132:17032–17040. doi: 10.1021/ja107876p. [DOI] [PubMed] [Google Scholar]
- 34.Gray HB, Winkler JR. Electron Transfer in Proteins. Annu Rev Biochem. 1996;65:537–561. doi: 10.1146/annurev.bi.65.070196.002541. [DOI] [PubMed] [Google Scholar]
- 35.Newton MD. Electronic coupling in electron transfer and the influence of nuclear modes: theoretical and computational probes. Theor Chem Acc. 2003;110:307–321. [Google Scholar]
- 36.Cave RJ, Newton MD. Generalization of the Mulliken-Hush treatment for the calculation of electron transfer matrix elements. Chem Phys Lett. 1996;249:15–19. [Google Scholar]
- 37.Newton MD. Quantum chemical probes of electron-transfer kinetics: the nature of donor-acceptor interactions. Chem Rev. 1991;91:767–792. [Google Scholar]
- 38.Warshel A, Creighton S, Parson WW. Electron-Transfer Pathways in the Primary Event of Bacterial Photosynthesis. J Phys Chem. 1988;92:2696–2701. [Google Scholar]
- 39.Zhang LY, Friesner RA, Murphy RB. Ab initio quantum chemical calculation of electron transfer matrix elements for large molecules. J Chem Phys. 1997;107:450–459. [Google Scholar]
- 40.Larsson S. Electron transfer in chemical and biological systems. Orbital rules for nonadiabatic transfer. J Am Chem Soc. 1981;103:4034–4040. [Google Scholar]
- 41.Kurnikov IV, Beratan DN. Ab initio based effective Hamiltonians for long-range electron transfer: Hartree-Fock analysis. J Chem Phys. 1996;105:9561–9573. [Google Scholar]
- 42.Shaik SS, Schlegel HB, Wolfe S. Theoretical Aspects of Physical Organic Chemistry. Application to the SN2 Transition State. Wiley Interscience; NY: 1992. [Google Scholar]
- 43.Warshel A, Florian J. In: The Encyclopedia of Computational Chemistry. von Ragué Schleyer P, Allinger NL, Clark T, Gasteiger J, Kollman PA, Schaefer HF III, Schreiner PR, editors. John Wiley & Sons; Chichester, UK: 2004. [Google Scholar]
- 44.Mo YR, Gao JL. An ab initio molecular orbital-valence bond (MOVB) method for simulating chemical reactions in solution. J Phys Chem A. 2000;104:3012–3020. [Google Scholar]
- 45.Shurki A. Valence bond - rebirth of the phoenix or relic from the stone age. Theo Chem Acct. 2006;116:253–261. [Google Scholar]
- 46.Blancafort L, Celani P, Bearpark MJ, Robb MA. A valence-bond-based complete-active-space self-consistent-field method for the evaluation of bonding in organic molecules. Theo Chem Acct. 2003;110:92–99. [Google Scholar]
- 47.Wesolowski TA, Weber J. Kohn-Sham equations with constrained electron density: an iterative evaluation of the ground-state electron density of interacting molecules. Chem Phys Lett. 1996;248:71–76. [Google Scholar]
- 48.Wesolowski TA. Density functional theory with approximate kinetic energy functionals applied to hydrogen bonds. J Chem Phys. 1997;106:8516–8526. [Google Scholar]
- 49.Strajbl M, Hong G, Warshel A. Ab-initio QM/MM Simulation with Proper Sampling: “First Principle” Calculations of the Free Energy of the Auto-dissociation of Water in Aqueous Solution. J Phys Chem B. 2002;106:13333–13343. [Google Scholar]
- 50.Cortona P. Self-Consistently Determined Properties of Solids Without Band-Structure Calculations. Phys Rev B. 1991;44:8454–8458. doi: 10.1103/physrevb.44.8454. [DOI] [PubMed] [Google Scholar]
- 51.Senatore G, Subbaswamy KR. Density Dependence of the Dielectric-Constant of Rare-Gas Crystals. Phys Rev B. 1986;34:5754–5757. doi: 10.1103/physrevb.34.5754. [DOI] [PubMed] [Google Scholar]
- 52.Fradelos G, Lutz JJ, Wesolowski TA, Piecuch P, Wloch M. Embedding vs Supermolecular Strategies in Evaluating the Hydrogen-Bonding-Induced Shifts of Excitation Energies. J Chem Theory Comput. 2011;7:1647–1666. [Google Scholar]
- 53.Sharir-Ivry A, Shurki A. A VB/MM View of the Identity S(N)2 Valence-Bond State Correlation Diagram in Aqueous Solution. J Phys Chem A. 2008;112:13157–13163. doi: 10.1021/jp801722e. [DOI] [PubMed] [Google Scholar]
- 54.Warshel A. Dynamics of Reactions in Polar Solvents. Semiclassical Trajectory Studies of Electron-Transfer and Proton-Transfer Reactions. J Phys Chem. 1982;86:2218–2224. [Google Scholar]
- 55.Aqvist J, Warshel A. Simulation of Enzyme Reactions Using Valence Bond Force Fields and Other Hybrid Quantum/Classical Approaches. Chem Rev. 1993;93:2523–2544. [Google Scholar]
- 56.Warshel A, Hwang JK. Simulation of the Dynamics of Electron Transfer Reactions in Polar Solvents: Semiclassical Trajectories and Dispersed Polaron Approaches. J Chem Phys. 1986;84:4938–4957. [Google Scholar]
- 57.King G. Warshel, Investigation of the free-energy functions for electron-transfer reactions. J Chem Phys. 1990;93:8682–92. [Google Scholar]
- 58.Mones L, Kulhanek P, Simon I, Laio A, Fuxreiter M. The Energy Gap as a Universal Reaction Coordinate for the Simulation of Chemical Reactions. J Phys Chem B. 2009;113:7867–7873. doi: 10.1021/jp9000576. [DOI] [PubMed] [Google Scholar]
- 59.Kuharski RA, Bader JS, Chandler D, Sprik M, Klein ML, Impey RW. Molecular model for aqueous ferrous ferric electron transfer. J Chem Phys. 1988;89:3248–3257. [Google Scholar]
- 60.Zhou HX, Szabo A. Microscopic formulation of Marcus theory of electron-transfer. J Chem Phys. 1995;103:3481–3494. [Google Scholar]
- 61.Jayendran CR, Jianjun Z. Reaction coordinates for electron transfer reactions. J Chem Phys. 2008;129:214503. doi: 10.1063/1.3026365. [DOI] [PubMed] [Google Scholar]
- 62.Cascella M, Magistrato A, Tavernelli I, Carloni P, Rothlisberger U. Role of protein frame and solvent for the redox properties of azurin from Pseudomonas aeruginosa. Proc Natl Acad Sci USA. 2006;103:19641–19646. doi: 10.1073/pnas.0607890103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Blumberger J, Sprik M. Quantum versus classical electron transfer energy as reaction coordinate for the aqueous Ru2+/Ru3+ redox reaction. Theor Chem Acc. 2006;115:113–126. [Google Scholar]
- 64.Kong Y, Warshel A. Linear Free Energy Relationships with Quantum Mechanical Corrections: Classical and Quantum Mechanical Rate Constants for Hydride Transfer Between NAD+ Analogues in Solutions. J Am Chem Soc. 1995;117:6234–6242. [Google Scholar]
- 65.Warshel A. Computer Simulations of Enzyme Catalysis: Methods, Progress, and Insights. Annu Rev Biophys Biomol Struct. 2003;32:425–443. doi: 10.1146/annurev.biophys.32.110601.141807. [DOI] [PubMed] [Google Scholar]
- 66.Marcus RA. On theory of electron-transfer reactions 6. Unified treatment for homogeneous and electrode reactions. J Chem Phys. 1965;43:679. [Google Scholar]
- 67.Warshel A. Simulating the Energetics and Dynamics of Enzymatic Reactions. Pontificiae Academiae Scientiarum Scripta Varia. 1984;55 [Google Scholar]
- 68.Schweins T, Warshel A. Mechanistic Analysis of the Observed Linear Free Energy Relationships in p21 ras and Related Systems. Biochemistry. 1996;35:14232–14243. doi: 10.1021/bi961119g. [DOI] [PubMed] [Google Scholar]
- 69.Warshel A, Schweins T, Fothergill M. Linear Free Energy Relationships in Enzymes. Theoretical Analysis of the Reaction of Tyrosyl-tRNA Synthetase. J Am Chem Soc. 1994;116:8437–8442. [Google Scholar]
- 70.Schutz CN, Warshel A. Analyzing Free Energy Relationships for Proton Translocations in Enzymes; Carbonic Anhydrase Revisited. J Phys Chem B. 2004;108:2066–2075. [Google Scholar]
- 71.Stamant A, Salahub DR. New Algorithm For The Optimization Of Geometries In Local Density Functional Theory. Chem Phys Lett. 1990;169:387–392. [Google Scholar]
- 72.Chu ZT, Villa J, Strajbl M, Schutz CN, Shurki A, Warshel A. MOLARIS version beta9.05. 2004. [Google Scholar]
- 73.Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, Montgomery JA, Vreven T, Kudin KN, Burant JC, Millam JM, Iyengar SS, Tomasi J, Barone V, Mennucci B, Cossi M, Scalmani G, Rega N, Petersson GA, Nakatsuji H, Hada M, Ehara M, Toyota K, Fukuda R, Hasegawa J, Ishida M, Nakajima T, Honda Y, Kitao O, Nakai H, Klene M, Li X, Knox JE, Hratchian HP, Cross JB, Bakken V, Adamo C, Jaramillo J, Gomperts R, Stratmann RE, Yazyev O, Austin AJ, Cammi R, Pomelli C, Ochterski JW, Ayala PY, Morokuma K, Voth GA, Salvador P, Dannenberg JJ, Zakrzewski VG, Dapprich S, Daniels AD, Strain MC, Farkas O, Malick DK, Rabuck AD, Raghavachari K, Foresman JB, Ortiz JV, Cui Q, Baboul AG, Clifford S, Cioslowski J, Stefanov BB, Liu G, Liashenko A, Piskorz P, Komaromi I, Martin RL, Fox DJ, Keith T, Laham A, Peng CY, Nanayakkara A, Challacombe M, Gill PMW, Johnson B, Chen W, Wong MW, Gonzalez C, Pople JA. 2003 [Google Scholar]
- 74.Becke AD. Density-functional thermochemistry. III. The role of exact exchange. J Chem Phys. 1993;98:5648–5652. [Google Scholar]
- 75.te Velde G, Bickelhaupt FM, Baerends EJ, Fonseca Guerra C, van Gisbergen SJA, Snijders JG, Ziegler T. Chemistry with ADF. J Comput Chem. 2001;22:931–967. [Google Scholar]
- 76.Van Lenthe E, Baerends EJ. Optimized Slater-type basis sets for the elements 1–118. J Comput Chem. 2003;24:1142–1156. doi: 10.1002/jcc.10255. [DOI] [PubMed] [Google Scholar]
- 77.Neugebauer J, Jacob CR, Wesolowski TA, Baerends EJ. An Explicit Quantum Chemical Method for Modeling Large Solvation Shells Applied to Aminocoumarin C151. J Phys Chem A. 2005;109:7805–7814. doi: 10.1021/jp0528764. [DOI] [PubMed] [Google Scholar]
- 78.Yang SY, Fleurat-Lessard P, Hristov I, Ziegler T. Free Energy Profiles for the Identity SN2 Reactions Cl− + CH3Cl and NH3 + H3BNH3: A Constraint Ab Initio Molecular Dynamics Study. J Phys Chem A. 2004;108:9461–9468. [Google Scholar]
- 79.Albery JK, MM Methyl transfer reactions. Adv Phys Org Chem. 1978;16:87–157. [Google Scholar]
- 80.Olsson MHM, Warshel A. Solute Solvent Dynamics and Energetics in Enzyme Catalysis: The SN2 Reaction of Dehalogenase as a General Benchmark. J Am Chem Soc. 2004;126:15167–15179. doi: 10.1021/ja047151c. [DOI] [PubMed] [Google Scholar]
- 81.Blumberger J. Cuaq+/Cuaq2+ Redox Reaction Exhibits Strong Nonlinear Solvent Response Due to Change in Coordination Number. J Am Chem Soc. 2008;130:16065–16068. doi: 10.1021/ja805471a. [DOI] [PubMed] [Google Scholar]
- 82.Kaila VRI, Hummer G. Energetics of Direct and Water-Mediated Proton-Coupled Electron Transfer. J Am Chem Soc. 2011;133:19040–19043. doi: 10.1021/ja2082262. [DOI] [PubMed] [Google Scholar]
- 83.Wu Q, Kaduk B, Van Voorhis T. Constrained density functional theory based configuration interaction improved the prediction of reaction barrier heights. J Chem Phys. 2009;130:034109(1–7). doi: 10.1063/1.3059784. [DOI] [PubMed] [Google Scholar]
- 84.Jackson TA, Karapetian A, Miller A-F, Brunold TC. Probing the geometric and electronic structures of the low-temperature azide adduct and the product-inhibited form of oxidized manganese superoxide dismutase. Biochemistry. 2005;204405:1504–1520. doi: 10.1021/bi048639t. [DOI] [PubMed] [Google Scholar]
- 85.Neugebauer J, Baerends EJ. Exploring the ability of frozen-density embedding to model induced circular dichronism. J Phys Chem A. 2006;110:8786–8796. doi: 10.1021/jp0622280. [DOI] [PubMed] [Google Scholar]
- 86.Wesolowski TA. Embedding a multideterminental wave function in an orbital-free environment. Phys Rev A. 2008;77:012504(1)–012504(9). [Google Scholar]
- 87.Wesolowski TA. Computational Chemistry: Reviews of Current Trends. World Scientific; 2006. [Google Scholar]
- 88.de la Lande A, Salahub DR. Derivation of interpretative models for long range electron transfer from constrained density functional theory. J Mol Struct: THEOCHEM. 2010;943:115–120. [Google Scholar]
- 89.Schmidt JR, Shenvi N, Tully JC. Controlling spin contamination using constrained density functional theory. J Chem Phys. 2008;129:114110. doi: 10.1063/1.2978168. [DOI] [PubMed] [Google Scholar]
- 90.Cembran A, Song L, Mo Y, Gao J. Block-localized density functional theory (BLDFT), diabatic coupling and their use in valence bond theory for representing reactive potential energy surfaces. J Chem Theory Comp. 2009;5:2702–2716. doi: 10.1021/ct9002898. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Blumberger J. Free energies for biological electron transfer from QM/MM calculation: method, application and critical assessment. Phys Chem Chem Phys. 2008;10:5651–5667. doi: 10.1039/b807444e. [DOI] [PubMed] [Google Scholar]
- 92.Wu Q, Van Voorhis T. Direct optimization method to study constrained systems within density-functional theory. Phys Rev A. 2005;72:024502. [Google Scholar]
- 93.Kamerlin SCL, Cao J, Rosta E, Warshel A. On unjustifiably misrepresenting the EVB approach while simultaneously adopting it. J Phys Chem B. 2009;113:10905–10915. doi: 10.1021/jp901709f. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 94.Cave RJ, Newton MD. Calculation of electronic coupling matrix elements for ground and excited state electron transfer reactions: Comparison of the generalized Mulliken-Hush and block diagonalization methods. J Chem Phys. 1997;106:9213–9226. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.