Imaging Models of Valuation During Social Interaction in Humans

Abstract

The role of dopamine neurons in value-guided behavior has been described in computationally explicit terms. These developments have motivated new model-based probes of reward processing in healthy humans, and in recent years these same models have also been used to design and understand neural responses during simple social exchange. These latter applications have opened up the possibility of identifying new endophenotypes characteristic of biological substrates underlying psychiatric disease. In this report, we review model-based approaches to functional magnetic resonance imaging in healthy individuals and the application of these paradigms to psychiatric disorders. We show early results from the application of model-based human interaction at three disparate levels: 1) interaction with a single human, 2) interaction within small groups, and 3) interaction with signals generated by large groups. In each case, we show how reward-prediction circuitry is engaged by abstract elements of each paradigm with blood oxygen level– dependent imaging as a read-out; and, in the last case (i.e., signals generated by large groups) we report on direct electrochemical dopamine measurements during decision making in humans. Lastly, we discuss how computational approaches can be used to objectively assess and quantify elements of complex and hidden social decision-making processes.

Every aspect of the survival of an organism requires intact decision-making machinery. Human choices include those regarding basic needs (e.g., survival, security, and reproduction); however, human environments also require complex and abstract decisions unique to our species. Human decision-making is particularly guided by our ability to learn from experience and generate predictions about future events. Reinforcement learning algorithms (1) have been used to explain physiological data at the level of single neurons during relatively simple Pavlovian learning tasks (2,3). More recently, these models of value-guided learning have framed functional magnetic resonance imaging (fMRI) experiments in human decision-making in game theoretic paradigms (4,5). The burgeoning field of neuroeconomics (6-9) seeks to use neuroscientific tools (neuroimaging, neural recordings, etc.) to further develop “economic theory” about human decision-making (10). Recent developments suggest that neuroscience and psychiatric medicine might actually have much to gain as well from this merging of disciplines (8,11,12). Game theory provides a mathematical framework to investigate social interaction in humans with quantitatively controlled behavioral spaces and notions of optimal play. Comparing game play (economic games) in individuals diagnosed by DSM-IV standards with that in healthy control subjects is providing insight into the neurobiological responses associated with objectively quantifiable game behavior (12-16). These early steps suggest a newly developing paradigm in psychiatric medicine where computer-assisted objective measurements and analysis might augment the art of psychiatric diagnosis and treatment (12). We propose that the introduction of computer-assisted game play and objective neuroimaging signatures (yet to be established) might lead to the development of a new class of diagnostic variables for the diagnosis of psychiatric illness. Such biomarkers might include measurements of expressed behavior, parameters derived from models of learning and game play, or illness-specific brain responses. For example, King-Casas et al. (14) used a simple two-person exchange to show that subjects with Borderline Personality Disorder demonstrated a distinct neural correlate in anterior insula during game play that might be used as just such a biomarker. In general, this work is in its very early days and will require large-scale data collection and validation in healthy populations; however, the possibilities of augmenting traditional views of mental disease remain provocative.

Herein, we will first give a brief description of the theoretical framework for a particularly successful reinforcement learning algorithm, the temporal difference (TD) learning model, and then describe recent developments in applying this framework to valuation problems in decision-making during three levels of social exchange: 1) interaction between two humans (Figure 1), 2) interaction within a small group of humans (Figure 2), and 3) interaction with signals derived from large populations of humans (Figure 3). Each of these levels of social interaction challenges decision-making machinery in interesting and novel ways, each of which might be used to identify quantifiable endophenotypes in patients with psychiatric disorders.

Figure 1. Reputation formation during two-person trust game.

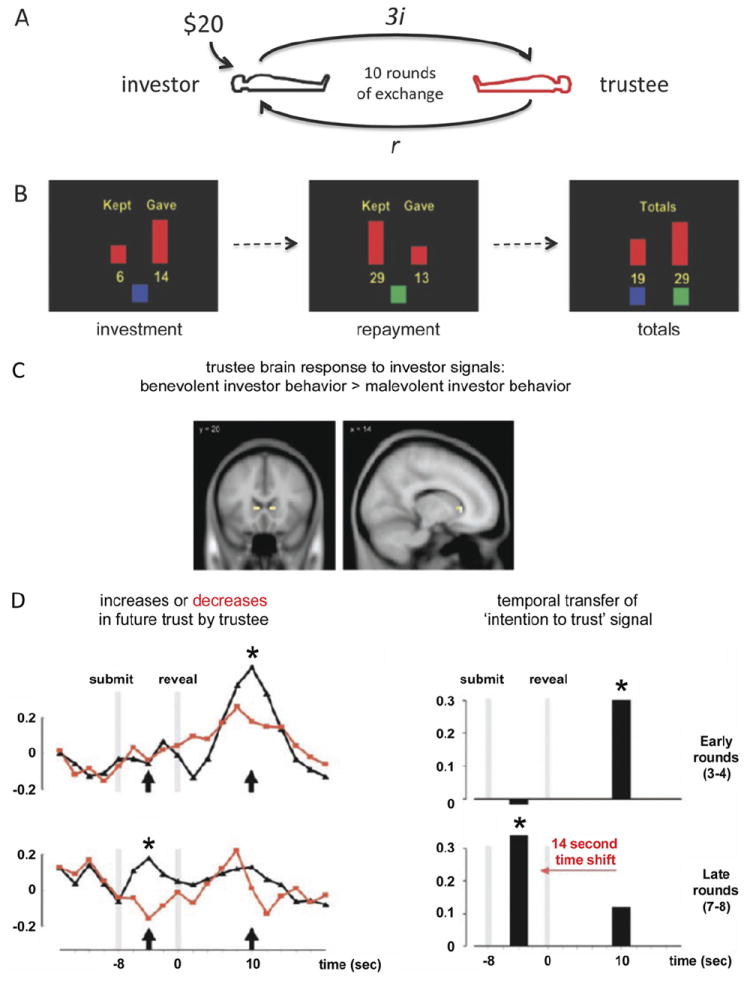
(A, B) Two-person multiround trust game. Pairs of subjects are hyperscanned (36) while playing 10 rounds of exchange. The total points earned during each round are tallied up at the end of the 10 rounds of exchange, and subjects are paid according to the total points earned. (C) Blood oxygen level–dependent correlates in the brains of the trustees to the reciprocity of the investors. Statistical parametric map showing only one region, the head of the caudate nucleus (bilateral), with responses greater for “benevolent” gestures relative to “malevolent” gestures (n = 125 gestures). (D) Neural correlates of reputation building. Region of interest blood oxygen level–dependent time series response in trustee brains from voxels defined in panel C. Responses in trustee brains around “investment” revelation (“reveal”) were separated on the basis of the next decision of the trustees (black: future increase in trust; red: future decrease in trust). Top row shows response in early rounds, bottom row shows responses in late rounds. A temporal transfer in the peak hemodynamic response (bar plots on right for time points highlighted with arrows in time series on left) after revelation of the decision of the investor is observed in late rounds where the peak response is predictive of positive investor gestures. This temporal shift is consistent with the formation of expectations in the brain of the trustee about the future behavior of the investor. Adapted, with permission, from King-Casas et al. (24).

Figure 2. Expectation error signals in the ventral striatum to changes in social rank in a small group.

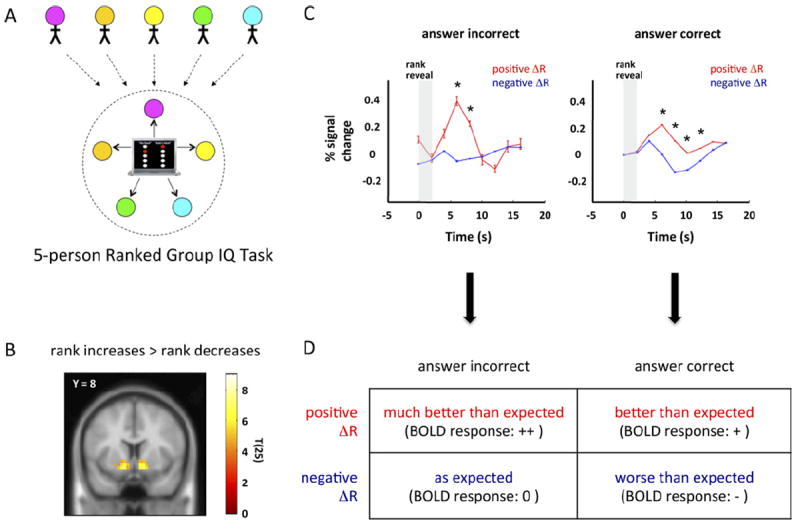
(A) Depiction of 5-person Ranked Group IQ task. Five subjects are recruited per group experiment. Subjects answer questions and are given feedback in the form of a ranking within the group of five. Two of the five subjects in each group are randomly selected to have their brains scanned with functional magnetic resonance imaging during this portion of the experiment. (B) Nucleus accumbens parametrically responds to positive changes in rank: a random-effects general linear model analysis for responses that correlated with changes in rank identified only the bilateral nucleus accumbens for positive changes in rank (random effects, n = 27, p < .0001, uncorrected). (C) Blood oxygen level dependent (BOLD) responses in nucleus accumbens to changes in rank after incorrect (left) or correct (right) responses to test questions. Horizontal-axis: time (seconds); vertical-axis: BOLD response expressed as the percentage change from baseline after the revelation of one’s own rank (vertical grey bar); red traces: BOLD responses (mean ± SEM) in the nucleus accumbens associated with rank increases (positive ΔR); blue traces: BOLD responses (mean ± SEM) in the nucleus accumbens associated with rank decreases (negative ΔR). Although subjects did not have explicit feedback about whether they answered the last question correctly or incorrectly, the responses observed in the nucleus accumbens are consistent with an expectation error over the effect of answering trials correctly and the effect it should have on one’s rank. *Significantly different at corresponding time points between red and blue traces (p < .05, two-sample t test). (D) Summary of prediction error interpretation of BOLD responses in nucleus accumbens after rank revelations. A 2 × 2 table summarizing BOLD responses in panel C after a prediction error interpretation. When subjects answer incorrectly or correctly (columns), the prediction error depends on the change in rank of the subject (ΔR, rows). A positive change in rank (top row) elicits a positive BOLD response in the nucleus accumbens, which is approximately twice as large in peak amplitude when the subject answered the question wrong (left column) compared with when the subject answered the question correctly (right column). By contrast, a negative change in rank resulted in no change in BOLD response when subjects answered incorrectly (left column) but saw a negative dip when preceded by a correctly answered question (right column). Adapted, with permission, from Kishida et al. (34).

Figure 3. Guidance signals in response to market fluctuations revealed in the dorsal striatum with functional magnetic resonance imaging and in situ sub-second measurements of dopamine (DA).

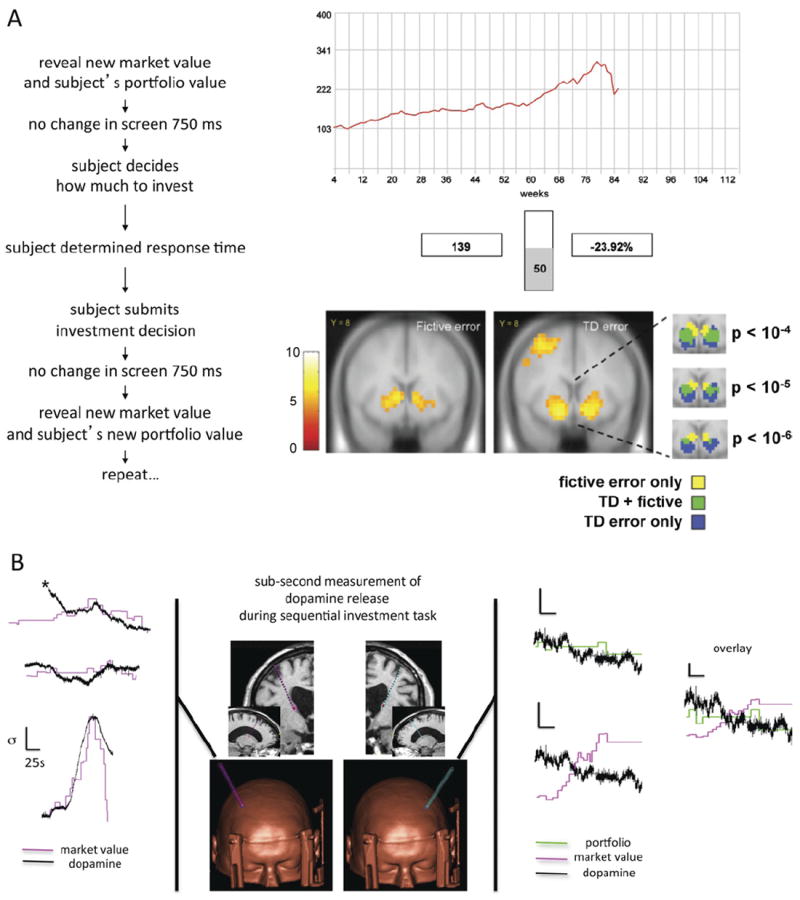
(A) Sequential investment task and blood oxygen level– dependent (BOLD) imaging of learning signals in humans. For each decision in the game, the subject is presented three pieces of information: 1) market trace (red), 2) portfolio value (bottom left, “139” in this example), and 3) the most recent fractional change in portfolio value (bottom right, “−23.92%” in this example). Inset, bottom right: Statistical parametric T-maps of two learning signals computed during the sequential investment task: fictive error signal (left) and the TD regressor (right). Call-out shows fictive error only, TD and fictive overlapping, and TD error only responsive voxels at three levels of significance. Panel adapted, with permission, from Lohrenz et al. (26). (B) Sub-second DA release in the caudate during the sequential investment task. Fast-scan cyclic voltammetry on a carbon fiber microsensor adapted for use in a human brain was used to measure cyclic voltammograms once every 100 msec in the human striatum. Insets: Middle, top: T1 weighted magnetic resonance image showing predicted electrode placement; middle, bottom: 3-dimensional rendering of the head of a patient with trajectory of carbon-fiber microsensor shown; left inset: three representative markets (magenta trace: normalized market value, N = 20 investment decisions) and DA measurement (black trace: normalized DA response in human caudate [right hemisphere]); right inset: representative market (magenta trace: normalized market value, N = 20 investment decisions), corresponding portfolio value (green trace: normalized portfolio value given N = 20 investment decisions), and DA measurement (black trace: normalized DA response in human caudate [left hemisphere]). Scale bars for all insets: normalized units (vertical bar = 1 SD: market, portfolio or DA, respectively) and time (horizontal bar = 25 sec). Panel adapted, with permission, from Kishida et al. (33).

Reinforcement Learning, Dopamine, and a “Common Neural Currency” for “Basic” and “Social” Rewards

In general, reinforcement learning algorithms make assumptions that are well-matched to the behavior of biological organisms (1). In these models, abstract agents are assumed to possess goals and the ability to represent decision spaces (i.e., options). These spaces might be conceived as a network of states that the agent traverses according to some policy. Importantly, it is assumed that the agent maintains representations of values associated with each state in the decision space and these values are updated after each decision. Learning takes place as the agent makes choices, receives immediate rewards, and observes the resulting change in value associated with the various available states. The exploration of the decision space and observation (or estimation) of values associated with the various states in the space can occur in actuality or through simulation. Importantly, all aspects of the problem as described have representations in mathematical forms. The updating signal in this framework is the reinforcement signal, which guides learning on the basis of observed changes. For a more comprehensive review on the application of these models see (1,17,18).

The “TD learning model” is a particular reinforcement learning algorithm that uses the TD error as its learning signal:

$$\mathrm{TD\; error}=\mathrm{reward\; prediction\; error}=r\left(S_t\right)+\mathrm{\gamma }V\left(S_{t+1}\right)-V(S_t)$$

Here, r(S_t) is the immediate reward the agent receives when it moves into state “S” at time “t”. V(S) reflects the long-term value function over states “S” at times “t” and future time points (i.e., “t+1”). The TD error signal is used in a reinforcement learning scenario to evaluate the action taken by evaluating the obtained state. The evaluation takes into account the expected reward, the actual reward received, and the new, updated values for all other states (now and into the future) and the expectations generated. Such a signal can be used to direct future decisions, given some policy function; for instance, softmax is a commonly used algorithm that chooses the transition probabilistically but is weighted toward the maximization of value (1).

Dopamine (DA) neurons in nonhuman primates have been shown to generate firing activity predicted by the TD learning algorithm (2,3,19). In these experiments, monkeys performed a simple Pavlovian conditioning task while microelectrodes recorded spike activity in DA neurons (3). Recent human fMRI experiments have demonstrated that similar “simple” instrumental (20) and passive conditioning (21) paradigms elicit blood oxygen level–dependent (BOLD) responses in the dorsal (20) and ventral striatum (21) consistent with TD learning model predictions and dopaminergic anatomical projections (20-23). These initial experiments set the groundwork for using fMRI to study human learning and decision-making with paradigms framed by computational models of valuation and choice behavior. These models in combination with game theoretic probes of human decision-making have recently been applied to study reward-processing, motivation, learning, and choice evaluation in social contexts (24-34).

Reinforcement Learning During Two-Party Social Exchange

King-Casas et al. (14,24,35) used hyperscanning (36) to investigate neurobehavioral responses elicited in two brains engaged in live social exchange. Participants played a simple exchange game, the multi-round trust game (Figure 1A). Participants play 10 rounds of sequential exchange as an “investor” or a “trustee”; the investor is given, for example, $20 at the start of a round and must decide what fraction (“i” in Figure 1A) of those points they will “invest” with their partner. This value can range from $0 to the full $20. Both partners know that the amount that the investor shares will be tripled on the way to the trustee. Both partners also know that the trustee would then have the opportunity to repay (“r” in Figure 1A) the investor from the total amount that the trustee received in the tripled investment (in Figure 1A: “r” = a fraction of the tripled investment, “3i”) and end the round. Multiple rounds of play between the partners allow the observation of learning, reputation formation, and associated brain responses (24).

The multiround trust game dramatically reduces two-party social exchange. The only communication between the partners comes in the form of points sent back and forth, which is communicated to the participants with simple displays on a computer screen (for examples: Figure 1B). Despite this, interesting social signals such as “benevolent” and “malevolent” investor behavior can be operationally defined (24). A contrast of brain responses in the trustee brain over rounds of “better than expected” (i.e., “benevolent”) versus “worse than expected” (i.e., “malevolent”) responses reveals guidance signals only in the head of the caudate nucleus (bilateral) (Figure 1C). In the trustee brain, large responses in this region were observed in early rounds after the revelation of investor gestures that resulted in future increases in trust by the trustee (i.e., increased reciprocation) (Figure 1D top row). These responses exhibited a temporal transfer in later rounds of the game (Figure 1D bottom row) that coincided with increased prediction accuracy about what the investor was going to do next (24), consistent with reputation building and TD prediction error models. Subsequent studies explored other dimensions of the value of social information, including social comparison (25), social status (29,30,34), reliability of social information (27), and social conformity (32). Each of these tasks implicates the mesolimbic dopaminergic system in processing social signals in a manner analogous to basic reward, suggesting a common neural currency (7). The connection between the observed BOLD responses in these experiments and the dopaminergic system continues to be the mathematically expressed model for reinforcement learning; however, new experiments aimed at directly measuring DA release in human brains (see following discussion) (Figure 3B) promises to test the hypothesized role of DA in human decision making directly.

Reinforcement Signals in Small Group Interactions

Relatively simple two-party exchange games are at the forefront of neuroimaging experiments investigating disorders that alter typical social exchange (12-16). However social behavior in many species typically involves small to large groups of individuals. This is certainly true of humans. BOLD responses in the ventral striatum consistent with reinforcement learning during small group interaction have recently been demonstrated (Figure 2, adapted from Kishida et al. [34]). Here, social status within the group was the valued commodity, and its magnitude was dynamically manipulated by the performance of the subjects during the Ranked Group IQ task (Figure 2). In this task, five subjects were recruited and introduced to each other by first name and performed a group IQ test with feedback in the form of their rank within the group of five (example screen shown in Figure 2A). Responses in the nucleus accumbens showed a parametric response in the nucleus accumbens to changes in social rank consistent with a reward related response (Figure 2B) in a random-effects general linear model analysis (n = 27 subjects, p < .0001, uncorrected). Further analysis of these responses revealed that the magnitude of the BOLD responses was correlated with a TD error over expected changes in rank, given the correctness of the last question (Figure 2C). The hypothesized error signal is derived by assuming the participants generate an expectation about their change in rank (expected change in rank: E[ΔR]), which is subtracted from their actual experienced change in rank (ΔR):

$$\mathrm{TD\; error\; signal}=\mathrm{\Delta }R-E\left(\mathrm{\Delta }R\right)$$

The model can be formulated by considering that participants form expectations about their change in rank, given their ability to answer questions correctly or incorrectly. The response in the nucleus accumbens (Figure 2C) shows four categorical responses that match predictions of the TD model and are summarized in Figure 2D.

The use of “model based” approaches in neuroimaging experiments take on at least two general forms. One approach is to identify patterns of behavioral exchange that are modified during experience and after feedback and to use a mathematical model to frame the observed responses. Thus, this more traditional trial-based comparison of responses can be framed by expectations from model behavior and used to explain the observed responses in a coherent hypothesis as exemplified in Figures 1 and 2. An additional approach starts where the former ends and generates an experiment to test specific parameters in a model or to test different models against expected biological responses (response magnitudes or anatomical differences in the expression of model parameters). The latter approach derives regressors from the combination of measured behavior and the computational model(s) being tested. These regressors are then used to search for correlated neural responses. In the following text we describe work comparing the role alternative learning signals (TD error and fictive error) play in value-guided behavior.

Reinforcement Learning with “Fictive Errors” Guide Investment Behavior

The role of the dopaminergic system in guiding behavior during simple reward harvesting behavior and more complex social interactions is bridged in an interesting way by Lohrenz et al. (26) and Kishida et al. (33) (Figure 3). Lohrenz et al. designed a sequential investment task, which uses historical stock market data and pits subjects against these fluctuating abstract signals. This task was designed to test computational models of learning and dopaminergic function and probes choice behavior in the context of a history of successful and failed gambles. This task takes advantage of the natural statistical structure that emerges during market-level exchanges.

In the sequential investment task (Figure 3), subjects are given a starting portfolio of $100 and are allowed to invest a fraction of their portfolio in the market (increments of 10%). Once the subject submits their decision, the market updates and reveals a new section of the market. The first imaging results from the sequential investment task demonstrated that the striatum responds to at least two mathematically defined guidance signals. The TD learning model and a fictive error model were shown to correlate with BOLD responses in overlapping and non-overlapping tissue in the caudate (Figure 3A, inset, adapted from Lohrenz et al. [26]). The fictive error derives from a variation of TD reinforcement learning algorithms, called “Q-learning.” Q-learning assesses more than just the relationship between states and value; rather, “state-action pairs” and value are assessed. Here a policy function determines what action, a_t, to take given the current state, s_t, (at time, “t”) and the expected value associated with those state-action pairs:

$$\mathit{policy}\left(S_t\right)=\underset{a}{\max }\widehat{Q}\left(s_t,a_t\right)$$

The policy taken is determined by finding the maximum of the estimated Q-value function, Q̂, for the range of state-action pairs (s_t, a_t). Q-learning takes advantage of the experiential learning in a similar manner as TD learning (by including such a term) but also takes into account other learning signals such as off-policy counter-factual signals (i.e., the fictive error signal). Here the “fictive error signal” resembles the subjective experience of “what could have been” but has a formal definition in the machine learning literature. In the context of Q-learning, the fictive error term speeds up the process of learning by taking into account the missed reward for all actions not taken (i.e., “fictive” actions, ã_t) from a given state, s_t:

$$\mathit{fictive\; critic}=\sum _{\mathit{fictive\; actions},{\stackrel{\sim }{a}}_t}\mathrm{\Delta }\widehat{Q}\left(s_t,{\stackrel{\sim }{a}}_t\right)$$

which adds to the update signal provided by experiential learning:

$$\mathit{experience\; critic}=\widehat{Q}\left(s_t,a_t\right)$$

In the context of the use of the sequential investment task of Lohrenz et al. (Figure 3A), the fictive error calculation accounts for the market fluctuation (state change: s_t → s_t+1) and the size of the bet of the player (action taken: a_t) and determines the magnitude of what the earnings could have been had the subject maximized their bet (fictive action: ã_t). This depiction quantifies the counterfactual signal within this paradigm and can be used to track brain responses correlated with the predictions of this model. Here the demonstration that the striatum calculates an additional guidance signal supports the hypothesis that computations about value-guided choice are reflected in metabolic demands in the striatum and are multifaceted. Subsequent work has shown that nicotine addicts (i.e., smokers) compute the fictive error signal in the same region as the non-addicts, but unlike the non-addicts, their subsequent decisions are not driven by fluctuations in this counterfactual signal (26,28).

Measuring DA Release in the Human Brain

The relationship between BOLD responses that track TD error computations and the underlying physiology is hypothesized to involve fluctuations in the neurotransmitter DA. The early studies that identified the relationship between the TD error model and DA neuron activity in the ventral tegmental area and substantia nigra of nonhuman primates (2,3) were followed by a jump into humans with fMRI and paradigms framed by the same model that predicted DA neuron activity (21,37-39). The body of literature investigating these signals is identifying multiple regions in the brain where DA neurons are known to send a high density of projections (e.g., dorsal and ventral striatum and the orbital frontal cortex). A consistent pattern is emerging for dorsal and ventral striatal responses observed for active versus passive learning, respectively (reviewed by Montague et al. [19]). The striatal responses reviewed here are consistent with this literature, but the link between the BOLD response and DA release is currently theoretical and remains an exciting opportunity for investigation.

Recently, a microsensor capable of measuring DA release in freely behaving rodents (40) was adapted for use in human patients undergoing deep brain stimulating electrode implantation for the treatment of Parkinson’s disease (Figure 3B) (33). These “first of their kind” measurements of sub-second DA release in humans were carried out in the caudate while the patient performed the sequential investment task. With the microsensor placed in the right hemisphere (Figure 3B left) DA is observed to track the value of the market over 100 decisions made by the patient (p < .000001; regression slope = .91; and r² = .549, N = 100 decisions) (33). In the left hemisphere, the DA was observed to track the portfolio of the investor (Figure 3B right). Additionally, work by Zaghloul et al. (41) has demonstrated a consistent picture between models of DA neuron activity in nonhuman primates and measurement of DA neuron activity in humans. They also recorded from human patients undergoing deep brain stimulating electrode implantation for Parkinson’s disease and showed that neural spike activity in the substantia nigra responded to unexpected financial rewards in a gambling task.

Deep brain stimulation electrodes are beginning to be used in a growing number of neurological disorders. The microsensor developed by Kishida et al. (33) has the ability to reach deep structures in the human brain during these surgical procedures, thus opening the door to a wide range of possibilities in investigating dopaminergic release in human cognition. Likewise the sharp electrodes used by Zaghloul et al. (41) are capable of recording electric activity deep in the brain and can be used to validate and discover new relationships between neural spike activity and human strategies. These technologies paired with economic probes of decision-making and social interaction promise to provide a new understanding of mechanisms underlying psychiatric disease.

Alternative Computational Approaches

Reinforcement learning models have proven to be successful in explaining neural and behavioral data at multiple levels of description. Here we have focused on the role of the dopaminergic system, due to its suspected role in a number of mental disorders; thus reinforcement learning models, with TD learning and its relationship with dopaminergic activity as one particular example from this genre, has offered an exemplary starting point. However, theoretical developments in many aspects of neurobiology have undergone an explosive growth in recent years (42), and so efforts to understand mental disease in computational terms will gain from similar computational approaches directed at other levels of organization in the nervous system. Particularly promising developments include the use of mathematical models depicting other processes required for social exchange. Recent work has led to the development of models that describe hypothesized computational processes underlying “mentalization” (43). These models are framed and tested within the context of economic games, thus taking full advantage of the quantitative, reduced, and value-guided behavioral environment these games provide. For example, Hampton et al. (44) identify brain responses that correlate with separable computations underlying strategic thinking; they compare three models—a reinforcement learning model, a fictitious play model, and an influence model—and identify neural correlates to the various signals these different computations generate. Another model-based approach toward mentalization and processes underlying the psychological construct known as “theory of mind” are included in a collection of articles by Yoshida et al. (16,45,46), where they develop a computational “game theory of mind” (45), identify neural correlates with the underlying computations (46), and demonstrate alterations in behavioral parameters in a cohort of participants diagnosed with autism spectrum disorder (16) with a two-party coordination game. Finally, the use of models to probe data generated in neuroeconomic tasks is not the only maneuver available to computational biologists interested in game theoretic probes of healthy and unhealthy behavior. Koshelev et al. (15) used data generated in the multi-round trust game where different patient populations were placed in the trustee role and asked whether a “model-free” computational approach could identify clusters of playing style that could differentiate the different populations input into the analysis. This approach was able to discover natural clusters of behaviors expressed by the healthy investors playing different trustee populations using objective and algorithmic procedures with surprising accuracy and very interesting “errors.”

Future Directions

The notion of a “common currency” for valuation in the human brain across decision spaces that include basic needs (food and water), proxies for later reward (points and monetary cues), and more abstract social signals (reputation and status) is held together by a relatively simple thread, mathematical depictions of reinforcement learning theories. Valuation models from the machine learning literature (1) and initially explored in animal models in simple learning and choice paradigms (2,3,40) have begun to provide quantitative insight about signals in human brains during choice behavior in social contexts. Framing experimental paradigms in mathematical theory can provide access to parameters and new concepts that are not directly available to our conscious psyche. The fruits of these maneuvers are beginning to express themselves as new insight into longstanding issues in psychiatric populations. The ability to track mathematically defined and objectively estimable parameters in games might provide a new set of quantitative phenotypes and insight into the biology of choice behavior. These developments in neuroeconomics are already showing promise for the development of new models of psychiatric disease (12). At least one major issue that characterizes psychiatric disorders is the observed aberrant social behavior and the inability to adjust these behaviors after various forms of positive and negative feedback from the environment. The mathematical models that capture important learning signals that have been used identify responses in neural structures consistent with a core valuation network. However, this network does not exist in isolation, and those extending this early work into psychiatric populations must keep this in mind. Hypothetical differences in patient populations might be discovered in the core valuation machinery, but it is also very likely that information processing at other stages might be affected as well. For example, neural tissue engaged during the representation of game states (i.e., perceptual machinery) or neural tissue engaged during the execution of an action “post”-evaluation might show alterations. Further developing mathematical models for other elements of the game process (mental representations and inferences) will be needed to fully understand and tease apart the decision-making process and how it can be altered in mental disorders.

Whether these initial steps in computational and neuroeconomic approaches to understand the biology underlying mental disorders will lead to improvements in diagnosis and treatment remains to be seen, but the insight gained into the biology of valuation and decision-making thus far is promising and suggests a picture that is much simpler than previously thought (e.g., a core valuation system vs. multiple specialized systems). Identifying the specific neural processes and behavioral characteristics that characterize and differentiate psychiatric conditions in the economic game environment will require much more work and a community of researchers and clinicians dedicated to understanding the underlying biology. Computational approaches are poised to handle formally explicit hypotheses about the behaviors expressed in these games and the computations that are likely executed during the decision making process. These computations might be discovered to match some of our intuitions, but we should be prepared to be open to the possibility that there might be underlying computations carried out that are removed from our conscious psychological experience. Framing these problems in mathematically explicit terms provides a language to develop new theories that are not limited by the restricted space of words we use to express our conscious experiences. Social behavior is immensely interesting, which might be driven in part by its sometimes overwhelming complexity. Neuroeconomic combined with computational approaches are providing a new window to observe, simplify, and experiment on important aspects underlying the biology of choice during social exchange; these developments possesses the potential to develop a new paradigm of diagnosing and treating psychiatric disease.