On the efficiency of nonparametric variance estimation in sequential dose-finding

Abstract

Dose-finding in clinical studies is typically formulated as a quantile estimation problem, for which a correct specification of the variance function of the outcomes is important. This is especially true for sequential study where the variance assumption directly involves in the generation of the design points and hence sensitivity analysis may not be performed after the data are collected. In this light, there is a strong reason for avoiding parametric assumptions on the variance function, although this may incur efficiency loss. In this article, we investigate how much information one may retrieve by making additional parametric assumptions on the variance in the context of a sequential least squares recursion. By asymptotic comparison, we demonstrate that assuming homoscedasticity achieves only a modest efficiency gain when compared to nonparametric variance estimation: when homoscedasticity in truth holds, the latter is at worst 88% as efficient as the former in the limiting case, and often achieves well over 90% efficiency for most practical situations. Extensive simulation studies concur with this observation under a wide range of scenarios.

1. Introduction

We consider quantile estimation in the context of dose-finding study where patients are tested in successive groups of size m. Precisely, let X_i denote the dose given to the patients in the ith group, and Y_ij denote a continuous biomarker from the jth patient in the group. A response is said to occur if the outcome Y_ij exceeds a threshold t₀. The objective is to estimate the dose θ such that π(θ) = p for some pre-specified p, where π(x) ≔ pr(Y_ij > t₀ | X_i = x). This clinical setting is not uncommon, and there is also a wide range of applications in other areas such as reliability testing and bioassay. However, quantile estimation based on continuous data has received relatively little attention in the literature. In practice, this problem is often dealt with by using sequential methods based on the dichotomised data V_ij ≔ I(Y_ij > t₀), where I(A) is indicator of the event A, such as the logit-MLE (Wu, 1985) or the continual reassessment method (O’Quigley et al., 1990). These methods, using the binary data to estimate θ, provide general solutions without imposing strong assumptions on the characteristics of Y_ij. On the other hand, this approach can result in substantial information loss due to dichotomisation. Cheung (2010) demonstrates that, with group size m = 3 and normal data, the asymptotic efficiency of an optimal logit-MLE using the dichotomised data V_ij is at most 80% of a corresponding Robbins-Monro (1951) procedure using the continuous data Y_ij; and the efficiency loss becomes more substantial with a larger m or a more extreme target p. Having said this, we acknowledge that there is an ongoing need for designs and models for clinical situations with truly binary outcomes that are not results of dichotomisation of continuous outcomes. This paper, however, focuses on the relative efficiency of a least squares recursion using the continuous data under various assumptions on Y_ij. Generally, we consider the regression model

$$Y_{\mathit{\text{ij}}}=M(X_i)+\sigma (X_i)Z_{\mathit{\text{ij}}},$$ (1)

where the noise Z_ij is standard normal. Among the earliest proposals to address this problem, Eichhorn and Zacks (1973) study sequential search procedures for θ under the assumptions that the mean function M(x) is linear in x and the standard deviation is known and is constant, i.e., σ(x) = σ. Recently, Cheung and Elkind (2010) describe a novel application of the stochastic approximation method that leaves both M(x) and σ(x) unspecified subject to the constraint that θ is uniquely defined, and propose to estimate σ(x) nonparametrically. These two sets of assumptions represent two extreme approaches, and raise the question whether there is a reasonable middle ground. Specifically, this article focuses on the estimation of the standard deviation function, and investigates how much efficiency may be retrieved by imposing stronger assumptions on σ(x) than that in Cheung and Elkind (2010) while keeping the mean M(x) unspecified. Our investigation will be conducted in the context of a sequential least squares recursion described in Section 2. Section 3 derives the asymptotic distribution of an proposed estimator for θ. Section 4 reviews Wu’s (1985) logit-MLE as a comparison method of the least squares recursion. Efficiency comparison is given in Section 5, and concluding remarks in Section 6. Technical details are put in the Appendix.

2. Least squares recursion

Under model (1), Cheung and Elkind (2010) show that solving π(θ) = p is equivalent to solving f(θ) = t₀, where f(x) ≔ M(x) + z_pσ(x) and z_p is the upper pth percentile of standard normal. For brevity in discussion, we may assume here that the objective function f is continuous and strictly increasing so that the solution θ exists uniquely. An important class of models that satisfies this assumption is models with increasing mean M(x) and constant coefficient of variation across doses. Conditions 1–3 below make precise statements of the assumptions that are much less restrictive.

Now, pretend that f(x) = t₀ + b(x − θ) for some b > 0, and suppose also that we can observe an asymptotically unbiased variable U_i,n of f(X_i) for group i. A least squares estimate θ̂_n of θ based on the first n groups of observations can be obtained by solving

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n}[U_{i,n}-\{t_0+b(X_i-{\mathrm{\theta ̂}}_n)\}]=0.$$ (2)

Then we may set the next dose

$$X_{n+1}={\mathrm{\theta ̂}}_n.$$ (3)

The least squares recursion formed by (2) and (3) in essence is identical to the adaptive design proposed by Lai and Robbins (1979). A subtle difference is that the unbiased variable U_i,n is chosen based on the assumption about the variance function σ(x).

Case 1 (known variance): When σ(x) is completely known, a natural choice is to define U_i,n = Ȳ_i + z_pσ(X_i), where ${Ȳ}_i=m^{-1}{\displaystyle {\sum }_{j=1}^m}{Y}_{\mathit{\text{ij}}}$ is the average of the measurements in group i.

Case 2 (heteroscedasticity): When σ(x) is unknown and unspecified, we may define $U_{i,n}=Ȳ+z_p{\lambda }_m^{1/2}{s}_i$, where $s_i^2$ is the sample variance of the measurements in group i,

$${\lambda }_m=\frac{(m-1){\mathrm{\Gamma }}^2\{(m-1)/2\}}{2{\mathrm{\Gamma }}^2(m/2)}$$ (4)

and Γ(·) is the gamma function. Note that the form of λ_m in (4) ensures $E({\lambda }_m^{1/2}{s}_i)=\sigma (X_i)$ so that U_i,n is unbiased for f(X_i).

Under both Cases 1 and 2, the observed variable U_i,n is unbiased for f(X_i), and U_i,n and U_j,n are mutually independent for i ≠ j. Therefore, using the same techniques as in Lai and Robbins (1979), we can then verify that the least squares recursion formed by (2) and (3) is identical to the nonparametric Robbins-Monro procedure under these two cases: X_n+1 = X_n − (nb)⁻¹(U_n,n − t₀), where b > 0 is the same as the assumed slope used in the least squares estimation (2). Hence, the standard convergence results of stochastic approximation apply so that X_n → θ with probability one; for example, see Sacks (1958). In addition, if b < 2f′(θ), the distribution of $\sqrt{n}(X_n-\theta )$ will converge weakly to a mean zero normal with variance equal to α₁σ²(θ) under Case 1 and α₁α₂σ²(θ) under Case 2, where α₁ = [mb{2f′(θ) − b}]⁻¹ and ${\alpha }_2=1+{\mathit{\text{mz}}}_p^2({\lambda }_m-1)$. In other words, the asymptotic relative efficiency due to the knowledge of σ(x) is equal to α₂. To illustrate the magnitude, the efficiency α₂ = 2.87, 2.35, 2.17 for m = 2, 3, 4 and p = 0.10. The efficiency gain is quite substantial, and is not surprising because Cases 1 and 2 in a sense represent two extremities of assumptions.

Case 3 (homoscedasticity): When σ(x) is identical to an unknown constant σ for all x, we may choose U_i,n = Ȳ_i + z_pσ̂_n where ${\mathrm{\sigma ̂}}_n^2=n^{-1}{\displaystyle {\sum }_{i=1}^n}{s}_i^2$.

Under Case 3, we can rewrite the least squares recursion as follows:

$$X_{n+1}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{X}_i-\frac{1}{b}(\frac{1}{n}{\displaystyle \sum _{i=1}^n}{Ȳ}_i-{\mathrm{\mu ̂}}_n),$$ (5)

where μ̂_n = t₀ − z_pσ̂_n.

We note that homoscedasticity may not be a viable assumption in many practical situations, and it is arguably the strongest parametric assumption one can impose on σ(x) besides complete knowledge assumed under Case 1. The consideration of Case 3 is intended to serve as a reference for Case 2, so as to shed light on how much efficiency one may lose due to nonparametric estimation of σ(x).

3. Asymptotic normality under homoscedasticity

Convergence for the recursion formed by (2) and (3) does not trivially follow the standard results of stochastic approximation under Case 3, because the summands are correlated in a complex way via U_i,n. The following lemma is a key result that transforms the least squares recursion (5) into a Robbins-Monro-type recursion with a target μ ≔ t₀ − z_pσ. Note that the estimand θ also solves M(θ) = μ under homoscedasticity.

Lemma 1. The design sequence {X_n} generated by (5) under homoscedasticity can be represented as

$$X_{n+1}=X_n-\frac{1}{\mathit{\text{nb}}}\{{Ȳ}_n+\frac{z_p}{2\sigma }(s_n^2-{\sigma }^2)-\mu \}+{\xi }_n$$ (6)

where ${\displaystyle {\sum }_{n=1}^{\mathrm{\infty }}}E(|{\xi }_n\Vert {ℱ}_{n-1})<\mathrm{\infty }$ a.s. and ℱ_n−1 denotes the σ-field generated by (X_i, Z_i1, Z_i2, …, Z_im) for i = 1, …, n − 1.

In words, the recursion (6) is generated by the mean function M(x) and independent errors ē_ns with bias ξ_n, where ${ē}_n=\sigma \{{\mathrm{Z̄}}_n+0.5z_p(s_n^2/{\sigma }^2-1)\}\text{ and }{\mathrm{Z̄}}_n=m^{-1}{\displaystyle {\sum }_{j=1}^m}{Z}_{\mathit{\text{nj}}}$. It is also easy to verify that E(ē_n) = 0 and var(ē_n) = α₃σ²/m, where ${\alpha }_3=1+{\mathit{\text{mz}}}_p^2{\{2(m-1)\}}^{-1}.$. Hence, if the bias ξ_n is adequately small, we expect the convergence properties of (6) will be similar to that of the Robbins-Monro procedure without the bias term.

Condition 1. The mean function M(x) is weakly increasing in that (x − θ){M(x) − μ} > 0 for all x ≠ θ.

Condition 2. There exists a constant C₁ > 0 such that |M(x) − μ| ≤ C₁|x − θ| for all x.

Theorem 1. Suppose Conditions 1 and 2 hold and σ(x) ≡ σ. The sequence {X_n} generated by the least squares recursion (5) converges to θ with probability one.

Condition 1 is weaker than requiring an increasing mean M(x), and is often reasonable in dose-finding study. Condition 2 puts a bound on the tails of M(x) and requires it to be flat on the tails. Particularly, while lab measurements of a bioassay in theory take on values from the real line (after taking log), they are typically confined to a finite range in practice. This implies that the mean function is bounded, which in turn satisfies Condition 2. Thus, the conditions for the consistency of the least squares recursion are quite mild and can often be verified from the clinicians. To obtain asymptotic normality of X_n, we also need:

Condition 3. The mean function can be expressed as M(x) = μ + β(x − θ) + τ(x, θ) for all x such that β > 0 and τ(x, θ) = o(|x − θ|) as x → θ.

Condition 3 ensures that the local slope of M(x) around θ is equal to β, while allows very flexible form of functions via τ(x, θ). Note that under homoscedasticity, β = M′(θ) = f′(θ) because σ′(x) ≡ 0.

Theorem 2. Suppose Conditions 1–3 hold and σ(θ) ≡ σ. If b < 2β, the distribution of $\sqrt{n}(X_n-\theta )$ converges weakly to a mean zero normal with variance α₁α₃σ².

4. Dosing finding with dichotomised data

Instead of using the continuous data Y_ij, a convenient alternative using the dichotomised data V_ij by the logit-MLE recursion that solves

$${\displaystyle \sum _{i=1}^n}[{\displaystyle \sum _{j=1}^m}{V}_{\mathit{\text{ij}}}-\frac{\mathit{\text{mp}}\text{exp}\{\mathrm{b̃}({\mathrm{X̃}}_i-{\mathrm{\theta ̃}}_n)}{1-p+p\text{ exp}\{\mathrm{b̃}({\mathrm{X̃}}_i-{\mathrm{\theta ̃}}_n)}]=0$$ (7)

and sets X̃_n+1 = θ̃_n. In practice, we need to consider a two-stage approach (Cheung, 2005) that assigns doses initially via the stochastic approximation based on the dichotomised data: ${\mathrm{X̃}}_{n+1}={\mathrm{X̃}}_n-{(n\mathrm{b̃})}^{-1}(m^{-1}{\displaystyle {\sum }_{j=1}^m}{V}_{\mathit{\text{ij}}}-p)$ and switches to logit-MLE when a unique solution to (7) exists, i.e., when V_ij ≠ V_i′j′ for some i ≠ i′ or j ≠ j′.

Using the results in Ying and Wu (1997), we can show that X̃_n → θ with probability 1, and that if b̃ < 2βϕ(z_p){σp(1 − p)}⁻¹, $\sqrt{n}({\mathrm{X̃}}_n-\theta )$ converges weakly to a mean zero normal distribution with variance

$$\frac{\sigma }{m\mathrm{b̃}\{2\beta \varphi (z_p)-\sigma \mathrm{b̃}p(1-p)\}}$$ (8)

where ϕ(z) is the standard normal pdf. The asymptotic variance (8) achieves its minimum when b̃ = β̃ ≔ βϕ (z_p){σp(1 − p)}⁻¹.

5. Efficiency comparisons

As a consequence of Theorem 2, the asymptotic efficiency of the least squares recursion assuming heteroscedasticity (Case 2) relative to that assuming homoscedasticity (Case 3) equals α₃/α₂, when homoscedasticity in truth holds. As shown in the left panel of Fig. 1, the ratio α₃/α₂ is uniformly less than 1. Such efficiency loss is not surprising because no parametric assumption on σ(x) is made under Case 2, whereas homoscedasticity amounts to a single-parameter model. Generally, the efficiency worsens as p becomes extreme, and converges to {2(m − 1)(λ_m − 1)}⁻¹ in the limiting case p → 0 or 1 where the ratio reaches a minimum of 0.88 when m = 2. The efficiency improves as the group size m increases, and always stays above 0.90 with m ≥ 3.

Fig. 1.

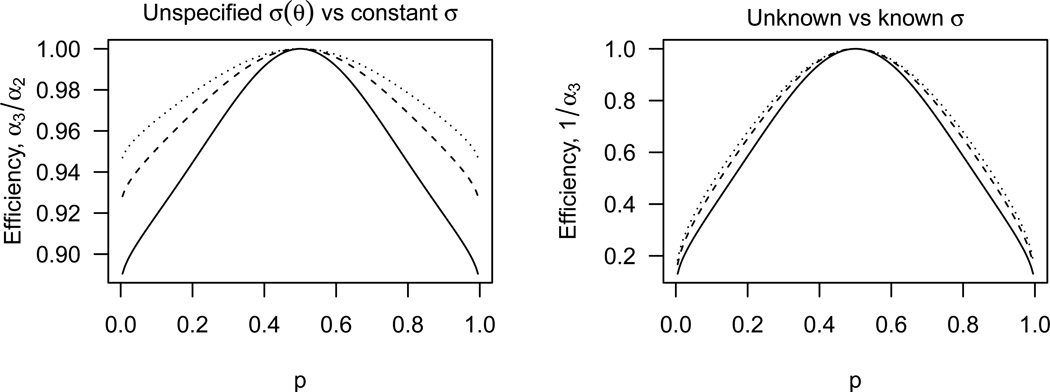
Asymptotic relative efficiencies under homoscedasticity for m = 2 (solid), 3 (dashed), and 4 (dotted).

In contrast, the efficiency of the least squares recursion assuming homoscedasticity (Case 3) against that assuming a known σ (Case 1) is plotted in the right panel of Fig. 1, which shows a great efficiency loss. The efficiency is about 0.40 for p = 0.10 and becomes arbitrarily close to 0 as p → 0 or 1. These comparisons demonstrate that efficiency loss due to incomplete knowledge about σ is far more substantial than that due to relaxing the parametric assumptions on the variance function.

We conducted a series of simulation studies to compare efficiency in finite-sample settings. The outcomes are generated with mean

$$M(x)=2{\{1+\text{exp}(\theta -x)\}}^{-1}\{-c_p+2\text{ log}(x-\theta +1)+1.5{(x-\theta )}^3\}$$ (9)

where c_p is the upper pth percentile of the cdf of Z_ij. We note that all methods in the simulation make the working assumption that Z_ij arises from a standard normal, even though we may generate noise from other distributions (see details below). This allows us to evaluate the impact of violation of the normality assumption. In the simulation, we set the variance σ²(x) ≡ 1 for x ∈ [0, 1] and t₀ = 0 so that θ as specified in (9) is the target pth percentile that we want to estimate under model (1). We consider p = 0.1, 0.2 and θ = 0.25, 0.50, 0.75.

The simulation include the least squares recursion procedures described in Section 2 and the logit-MLE in Section 4. For the least squares recursion, we consider b = β, which corresponds to the optimal choice in terms of asymptotic variance, and b = β/2 in order to investigate the relative performance of the methods when we fail to choose a good b. For the logit-MLE, we set b̃ = β̃ and β̃/2 respectively.

In the first set of simulations, we ran the four procedures with m = 3 and n = 15, and also considered the fully sequential version of the logit-MLE, i.e., m = 1 and n = 45. Each simulated trial will have a starting dose X₁ = 0.25 or 0.50. We apply truncation to the subsequent doses and set the next dose at X_n+1 = max{min(θ̂_n, 1), 0} instead of (3) for the least squares recursion. Likewise, for the logit-MLE, we set X̃₁ = 0.25 or 0.50, and set X̃_n+1 = max{min(θ̃_n, 1), 0}. Such truncation does not affect the asymptotic property of the recursion (see appendix), and is often done in practice.

Table 1 summarizes the results of the first simulation study. Overall, the biases are small when compared to the variances for all methods. In line with the asymptotic comparison in Fig. 1, the efficiency against assuming known σ is quite low for the other procedures, especially when the target percentile is extreme, i.e., p = 0.1. Also as expected, assuming heteroscedasticity instead of homoscedasticity yields further drop in efficiency—but the drop is slight. In contrast, the logit-MLE shows a marked efficiency loss when compared to the least squares recursion procedures that use the continuous data. The fully sequential logit-MLE retrieves some information loss from the small-group logit-MLE, but the gain in efficiency does not completely recover the loss due to the use of dichotomised data.

Table 1.

Bias(×10) and variance(×10²) of the least squares recursion and the logit-MLE with m = 3, n = 15, and the fully sequentially logit-MLE(f), i.e., m = 1, n = 45. The mean squared error ratio (rmse) is calculated relative to the method assuming known σ.

p	θ	Method assumes	X1 = 0.25, b = β†			X1 = 0.25, b = 0.5β‡			X1 = 0.50, b = β†			X1 = 0.50, b = 0.5β‡
			bias	var	rmse	bias	var	rmse	bias	var	rmse	bias	var	rmse
0.1	0.25	Known σ	−0.05	1.05	—	−0.10	1.51	—	−0.06	1.05	—	−0.10	1.52	—
		Unspecified σ	−0.09	2.11	0.50	−0.20	2.99	0.50	−0.09	2.11	0.50	−0.21	2.99	0.50
		Constant σ	−0.04	2.03	0.52	−0.18	2.88	0.52	−0.05	2.03	0.52	−0.19	2.88	0.52
		logit-MLE	−0.04	2.71	0.39	−0.44	3.09	0.46	−0.12	2.38	0.44	−0.54	3.01	0.46
		logit-MLE(f)	−0.02	2.59	0.41	−0.35	3.19	0.46	−0.11	2.41	0.44	−0.43	3.11	0.46
	0.50	Known σ	0.00	1.03	—	0.00	1.48	—	−0.01	1.03	—	0.00	1.48	—
		Unspecified σ	−0.01	2.25	0.46	−0.01	3.33	0.45	−0.01	2.25	0.46	−0.01	3.33	0.45
		Constant σ	0.04	2.14	0.48	0.00	3.15	0.47	0.03	2.14	0.48	−0.01	3.15	0.47
		logit-MLE	−0.11	3.60	0.29	−0.20	4.88	0.30	−0.09	3.13	0.33	−0.43	4.27	0.33
		logit-MLE(f)	−0.09	3.39	0.30	−0.21	4.58	0.32	−0.09	3.09	0.33	−0.40	4.17	0.34
	0.75	Known σ	0.10	1.04	—	0.12	1.49	—	0.04	1.03	—	0.09	1.48	—
		Unspecified σ	0.13	2.12	0.49	0.23	3.01	0.49	0.09	2.12	0.49	0.19	3.01	0.49
		Constant σ	0.18	2.02	0.51	0.24	2.88	0.51	0.13	2.02	0.51	0.20	2.88	0.51
		logit-MLE	−1.35	4.96	0.15	−0.29	4.74	0.31	−0.19	3.11	0.33	−0.04	4.11	0.36
		logit-MLE(f)	−0.98	4.32	0.20	−0.09	4.24	0.35	−0.15	2.96	0.35	−0.11	4.04	0.37
0.2	0.25	Known σ	−0.03	0.81	—	−0.06	1.16	—	−0.04	0.81	—	−0.07	1.16	—
		Unspecified σ	−0.05	1.23	0.66	−0.11	1.77	0.65	−0.06	1.23	0.66	−0.12	1.78	0.65
		Constant σ	−0.02	1.19	0.68	−0.10	1.72	0.67	−0.02	1.19	0.68	−0.11	1.73	0.67
		logit-MLE	−0.04	1.59	0.51	−0.24	2.13	0.53	−0.06	1.53	0.53	−0.27	2.17	0.52
		logit-MLE(f)	−0.04	1.57	0.51	−0.21	2.13	0.54	−0.07	1.58	0.51	−0.24	2.14	0.53
	0.50	Known σ	0.00	0.79	—	0.01	1.13	—	0.00	0.79	—	0.00	1.13	—
		Unspecified σ	0.00	1.22	0.65	0.00	1.77	0.64	0.00	1.22	0.65	0.00	1.77	0.64
		Constant σ	0.03	1.18	0.67	0.01	1.70	0.66	0.02	1.18	0.67	0.00	1.70	0.66
		logit-MLE	0.00	1.84	0.43	−0.15	2.37	0.47	−0.05	1.65	0.48	−0.19	2.32	0.48
		logit-MLE(f)	0.00	1.81	0.44	−0.16	2.32	0.48	−0.05	1.68	0.47	−0.17	2.33	0.48
	0.75	Known σ	0.08	0.80	—	0.09	1.15	—	0.03	0.80	—	0.07	1.14	—
		Unspecified σ	0.10	1.23	0.66	0.14	1.77	0.65	0.05	1.22	0.65	0.11	1.76	0.65
		Constant σ	0.13	1.19	0.67	0.15	1.71	0.67	0.08	1.18	0.67	0.11	1.70	0.67
		logit-MLE	0.11	2.09	0.39	0.19	2.52	0.45	0.00	1.77	0.45	−0.01	2.34	0.49
		logit-MLE(f)	0.09	1.90	0.42	0.06	2.44	0.47	0.00	1.75	0.46	−0.06	2.33	0.49

^† b~ = β~ for logit-MLE;

^‡ b~ = 0.5 β~.

Also in line with the asymptotic theory, setting b = β and b̃ = β̃ respectively for the least squares recursion and the logit-MLE generally yields better results than b = β/2 and b̃ = β̃/2. The only exception is when p = 0.1 and θ = 0.75, the logit-MLE with a low starting dose (X₁ = 0.25) has worse mean squared error when b̃ = β̃ than when b̃ = β̃/2. It is known that logit-MLE with a large b̃ corresponds to small changes in subsequent doses; therefore, with a finite sample size, it will have difficulty climbing to a high θ if the starting dose is low, and can be improved with the use of a smaller b̃.

The impact of the starting dose X₁ on the operating characteristics is comparatively nuanced, although the logit-MLE tends to have smaller variance when the starting dose X₁ is closer to the target dose θ.

The second simulation study further studies the effects of group sizes. Specifically, we consider designs with a bigger group size, namely, m = 5 and n = 9, so that the total sample size remains 45. Using bigger group sizes can be appealing in practice because it reduces the study duration and administrative burdens. We also consider random group sizes generated by permuting {2, 2, 2, 3, 3, 3, 4, 4, 5, 5, 6, 6} so that there are n = 12 groups and a total of 45 subjects in each simulated trial.

A bigger group size seems to have a slightly negative effect on the logit-MLE when comparing the results in Table 1 (m = 1, 3) and Table 2 (m = 5). Specifically, the fully sequential logit-MLE seems to outperform the small-group logit-MLE in finite sample size. Note that the asymptotic variance of the logit-MLE does not depend on group as long as the total sample size nm is the same. In contrast, the impact of group size on least squares recursion is relatively small. There is in fact slight improvement in relative efficiency of Case 2 and Case 3 against Case 1 when m = 5: this is in line with the fact that bigger group size improves asymptotic efficiency of the least squares recursion with unknown variance; cf. Fig. 1. The relative performance of the four procedures follows the same pattern under varying group sizes.

Table 2.

Bias(×10) and variance(×10²) of the least squares recursion and the logit-MLE with starting dose X₁ = 0.25. The mean squared error ratio (rmse) is calculated relative to the method assuming known σ.

p	θ	Method assumes	m = 5, n = 9 b = β†			varying group sizes b = β†			m = 5, n = 9 b = 0.5β‡			varying group sizes b = 0.5β‡
			bias	var	rmse	bias	var	rmse	bias	var	rmse	bias	var	rmse
0.1	0.25	Known σ	−0.04	1.04	—	−0.04	1.17	—	−0.15	1.55	—	−0.11	1.73	—
		Unspecified σ	−0.06	1.94	0.53	−0.05	2.42	0.48	−0.22	2.80	0.55	−0.20	3.40	0.51
		Constant σ	−0.02	1.90	0.55	0.00	2.30	0.51	−0.21	2.74	0.57	−0.17	3.24	0.54
		logit-MLE	−0.02	2.65	0.39	−0.03	2.71	0.43	−0.56	3.12	0.46	−0.48	3.32	0.49
	0.50	Known σ	0.01	1.03	—	0.02	1.16	—	−0.01	1.53	—	0.01	1.72	—
		Unspecified σ	0.02	2.03	0.50	0.02	2.68	0.43	0.00	3.03	0.50	0.00	4.04	0.43
		Constant σ	0.06	1.98	0.52	0.08	2.52	0.46	0.01	2.96	0.52	0.01	3.81	0.45
		logit-MLE	−0.09	3.71	0.28	−0.07	3.73	0.31	−0.22	5.17	0.29	−0.22	5.26	0.32
	0.75	Known σ	0.15	1.04	—	0.14	1.18	—	0.18	1.57	—	0.17	1.75	—
		Unspecified σ	0.19	1.97	0.53	0.18	2.45	0.48	0.30	2.80	0.55	0.28	3.48	0.50
		Constant σ	0.23	1.92	0.54	0.23	2.32	0.51	0.31	2.74	0.56	0.30	3.33	0.52
		logit-MLE	−1.57	5.26	0.14	−1.49	5.16	0.16	−0.48	5.25	0.29	−0.34	5.05	0.34
0.2	0.25	Known σ	−0.02	0.80	—	−0.02	0.91	—	−0.10	1.19	—	−0.08	1.35	—
		Unspecified σ	−0.03	1.15	0.70	−0.03	1.42	0.64	−0.13	1.70	0.70	−0.12	2.07	0.65
		Constant σ	0.00	1.13	0.71	0.01	1.36	0.67	−0.13	1.68	0.71	−0.11	1.99	0.67
		logit-MLE	−0.04	1.60	0.50	−0.02	1.57	0.58	−0.34	2.16	0.53	−0.29	2.18	0.60
	0.50	Known σ	0.01	0.79	—	0.02	0.90	—	−0.01	1.16	—	0.01	1.31	—
		Unspecified σ	0.02	1.15	0.69	0.03	1.43	0.63	0.01	1.67	0.69	0.01	2.13	0.62
		Constant σ	0.04	1.13	0.70	0.06	1.37	0.65	0.01	1.65	0.71	0.01	2.04	0.64
		logit-MLE	0.01	1.85	0.43	0.03	1.84	0.49	−0.19	2.51	0.46	−0.18	2.54	0.51
	0.75	Known σ	0.13	0.81	—	0.12	0.92	—	0.14	1.21	—	0.14	1.36	—
		Unspecified σ	0.15	1.16	0.69	0.14	1.43	0.64	0.20	1.71	0.70	0.20	2.11	0.64
		Constant σ	0.17	1.14	0.70	0.18	1.37	0.66	0.21	1.69	0.71	0.20	2.04	0.66
		logit-MLE	0.09	2.37	0.35	0.09	2.23	0.42	0.28	2.66	0.45	0.22	2.67	0.51

^†b~ = β~ for logit-MLE;

^‡b~ = 0.5 β~.

The third simulation study aims to examine the robustness of the least squares recursion when Z_ij is non-normal. While the methods use normality as the working assumption, we generated noises from other distributions with mean 0 and unit variance. Table 3 summarizes the results under the logistic distribution with mean 0 and scale 0.55, and the t-distribution with 6 degrees of freedom (scaled to have unit variance).

Table 3.

Bias(×10) and variance(×10²) of the least squares recursion and the logit-MLE with m = 3, n = 15, and the fully sequentially logit-MLE(f), i.e., m = 1, n = 45, with starting dose X₁ = 0.25. The mean squared error ratio (rmse) is calculated relative to the method assuming known σ.

p	θ	Method	Logistic, b = β†			t6, b = β†			Logistic, b = 0.5β‡			t6, b = 0.5β‡
			bias	var	rmse	bias	var	rmse	bias	var	rmse	bias	var	rmse
0.1	0.25	Known σ	−0.50	1.00	—	−0.74	0.90	—	−0.56	1.43	—	−0.81	1.29	—
		Unspecified σ	−0.30	2.11	0.57	−0.40	2.02	0.67	−0.40	2.87	0.58	−0.50	2.78	0.64
		Constant σ	−0.40	2.10	0.55	−0.54	2.02	0.62	−0.53	2.79	0.57	−0.68	2.70	0.62
		logit-MLE	−0.04	2.74	0.46	−0.08	2.57	0.56	−0.49	3.16	0.51	−0.52	3.12	0.58
		logit-MLE(f)	−0.06	2.64	0.47	−0.11	2.56	0.56	−0.43	3.11	0.53	−0.46	3.04	0.60
	0.50	Known σ	−0.45	1.01	—	−0.69	0.93	—	−0.46	1.45	—	−0.70	1.40	—
		Unspecified σ	−0.25	2.40	0.49	−0.36	2.36	0.57	−0.26	3.51	0.46	−0.38	3.53	0.51
		Constant σ	−0.37	2.49	0.46	−0.55	2.58	0.49	−0.43	3.63	0.44	−0.62	3.75	0.46
		logit-MLE	−0.18	3.71	0.32	−0.19	3.68	0.38	−0.31	5.06	0.32	−0.36	4.91	0.38
		logit-MLE(f)	−0.18	3.62	0.33	−0.16	3.47	0.40	−0.37	4.76	0.34	−0.35	4.61	0.40
	0.75	Known σ	−0.36	1.03	—	−0.60	0.95	—	−0.37	1.50	—	−0.63	1.43	—
		Unspecified σ	−0.09	2.30	0.50	−0.20	2.31	0.56	−0.02	3.29	0.50	−0.15	3.36	0.54
		Constant σ	−0.21	2.40	0.47	−0.39	2.57	0.48	−0.18	3.42	0.47	−0.39	3.71	0.47
		logit-MLE	−1.19	4.89	0.18	−1.22	4.89	0.21	−0.27	4.92	0.33	−0.35	4.90	0.36
		logit-MLE(f)	−0.90	4.38	0.22	−0.95	4.36	0.25	−0.12	4.50	0.36	−0.15	4.46	0.41
0.2	0.25	Known σ	−0.47	0.78	—	−0.62	0.72	—	−0.52	1.12	—	−0.68	1.05	—
		Unspecified σ	−0.35	1.23	0.74	−0.43	1.17	0.82	−0.43	1.73	0.72	−0.51	1.66	0.78
		Constant σ	−0.42	1.24	0.71	−0.53	1.20	0.75	−0.52	1.72	0.70	−0.64	1.67	0.72
		logit-MLE	−0.08	1.47	0.68	−0.11	1.35	0.82	−0.30	1.98	0.67	−0.32	1.92	0.74
		logit-MLE(f)	−0.09	1.46	0.68	−0.11	1.34	0.82	−0.28	1.94	0.69	−0.28	1.90	0.76
	0.50	Known σ	−0.44	0.78	—	−0.58	0.72	—	−0.44	1.11	—	−0.60	1.07	—
		Unspecified σ	−0.31	1.27	0.71	−0.39	1.22	0.77	−0.32	1.83	0.68	−0.40	1.81	0.72
		Constant σ	−0.38	1.30	0.67	−0.50	1.33	0.67	−0.42	1.87	0.64	−0.56	1.95	0.63
		logit-MLE	−0.05	1.72	0.56	−0.05	1.58	0.67	−0.23	2.26	0.56	−0.25	2.18	0.64
		logit-MLE(f)	−0.08	1.67	0.58	−0.10	1.52	0.69	−0.23	2.15	0.59	−0.25	2.04	0.68
	0.75	Known σ	−0.36	0.79	—	−0.51	0.74	—	−0.38	1.14	—	−0.54	1.10	—
		Unspecified σ	−0.22	1.28	0.69	−0.29	1.23	0.76	−0.20	1.85	0.68	−0.30	1.84	0.72
		Constant σ	−0.28	1.31	0.66	−0.40	1.33	0.67	−0.30	1.89	0.65	−0.45	1.96	0.64
		logit-MLE	0.04	2.06	0.45	0.04	1.98	0.50	0.10	2.47	0.52	0.07	2.39	0.58
		logit-MLE(f)	0.05	1.85	0.50	0.04	1.76	0.57	−0.04	2.29	0.56	−0.06	2.20	0.63

^†b~ = β~ for logit-MLE;

^‡b~ = 0.5β~.

Overall, the least squares recursion procedures induce larger biases under misspecified distribution (cf. Table 1). However, the biases are generally small when compared to the variances. Interestingly, assuming heteroscedasticity (Case 2) seems to mitigate the increase in bias due to misspecification, and as a result, leads to smaller mean squared error than the procedure assuming homoscedasticity (Case 3). It is also important to note that the least squares recursion procedures are generally superior to the logit-MLE in terms of mean squared error, even though the latter did not require normality to be valid. This suggests that variability, rather than bias, is the limiting factor of performance when sample size ranges from small to moderate. In other words, the information retrieved via the use of continuous data outweighs the potential bias induced by misspecification. Having said this, we recommend using pilot data to assess the noise distribution in the planning stage; see Cheung and Elkind (2010) for example.

6. Concluding remarks

The contribution of this paper is two-fold. First, it provides a unified least squares recursion approach (2) for sequential quantile estimation using continuous data. Second, and importantly, in the context of this least squares recursion (2), we investigate the issue of variance modeling in the context of an important biomedical application in dose finding. By asymptotic comparison and simulation studies, we show that the efficiency loss due to nonparametric variance estimation is small when compared to parametric estimation under the correct model (i.e. variance is an identity function of dose). Furthermore, the simulation study suggests that nonparametric variance estimation leads to improved robustness when the normality assumption is violated.

For the non-sequential settings, Fedorov and Leonov (2004) give a detailed and insightful discussion on parameter estimation for normal data with unknown variance, and study the behaviors of an iterated estimator under a parametric model. They show that the iterated least squares estimators may not be efficient without adjustment; this may bear implications on the use of nonparametric variance estimation for which no adjustment is needed. Having said this, the focus of this paper differ from that of Fedorov and Leonov (2004) in two ways. First, we avoid parametric assumptions on the mean M(x). Second, we focus on situations with sequential accrual of the data. The sequential nature of our problem renders the correctness of the parametric assumptions all the more crucial for the validity of statistical inference: in reality where modeling the variance function is difficult, the working assumption on σ(x) has a direct impact on the design {X_i} so that it is not possible to perform sensitivity analysis after the data are collected. As such, a misspecified σ(x) will affect the final estimate of θ in an irreconcilable way, and thus parametric structure on the variance function should be avoided unless there are compelling reasons—and, as we show in this paper, the advantage of parametric estimation is very modest even when the assumption is correct.

Appendix A. Proofs

This section provides the proofs of Lemma 1, Theorems 1 and 2.

Proof of Lemma 1. Applying Taylor’s expansion in σ̂_n about σ gives

$${\mathrm{\sigma ̂}}_n-\sigma =\frac{1}{2\sigma }({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)-\frac{1}{8{\sigma }^3}{({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)}^2+\frac{1}{16{\sigma }_n^{*5}}{({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)}^3$$

where ${\sigma }_n^{*}$ is between σ and σ̂_n. Therefore, we can rewrite (5) as

$$X_{n+1}=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{X}_i-\frac{1}{b}\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{Ȳ}_i+\frac{z_p}{2\sigma }({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)-\mu \}+{\eta }_n$$ (A1)

where

$${\eta }_n=\frac{z_p}{8{\sigma }^{3}b}\{1-\frac{{\sigma }^3}{2{\sigma }_n^{*5}}({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)\}{({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)}^2.$$

Next, consider the design {$X_n^{\prime }$} generated with $X_1^{\prime }=X_1$ and

$$X_{i+1}^{\prime }=X_i^{\prime }-\frac{1}{\mathit{\text{ib}}}[{Ȳ}_i^{\prime }+\frac{z_p}{2\sigma }(s_i^2-{\sigma }^2)-\mu ]+{\xi }_i$$

where ${Ȳ}_i^{\prime }=M(X_i^{\prime })+\sigma {\mathrm{Z̄}}_i$. Multiplying i on both sides then gives

$$i{X}_{i+1}^{\prime }-(i-1)X_i^{\prime }=X_i^{\prime }-\frac{1}{b}\{{Ȳ}_i^{\prime }+\frac{z_p}{2\sigma }(s_i^2-{\sigma }^2)-\mu \}+i{\xi }_i.$$

Iterating the above equation, we get

$$X_{n+1}^{\prime }=\frac{1}{n}{\displaystyle \sum _{i=1}^n}{X}_i^{\prime }-\frac{1}{b}\{\frac{1}{n}{\displaystyle \sum _{i=1}^n}{Ȳ}_i^{\prime }+\frac{z_p}{2\sigma }({\mathrm{\sigma ̂}}_n^2-{\sigma }^2)-\mu \}+\frac{1}{n}{\displaystyle \sum _{i=1}^n}i{\xi }_i.$$ (A2)

Matching the last terms in (A1) and (A2) gives

$$\left(\begin{array}{ccccc}\hfill 1\hfill & \hfill 0\hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill 0\cdots \hfill & \hfill \cdots \hfill & \hfill 0\hfill \\ \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill & \hfill \cdots \hfill \\ \hfill 1\hfill & \hfill 2\hfill & \hfill \cdots \hfill & \hfill \mathrm{n}-1\hfill & \hfill \mathrm{n}\hfill \end{array}\right)\left(\begin{array}{c}\hfill {\xi }_1\hfill \\ \hfill {\xi }_2\hfill \\ \hfill ⋮\hfill \\ \hfill {\xi }_n\hfill \end{array}\right)=\left(\begin{array}{c}\hfill {\eta }_1\hfill \\ \hfill 2{\eta }_2\hfill \\ \hfill ⋮\hfill \\ \hfill n{\eta }_n\hfill \end{array}\right),$$ (A3)

and inverting (A3), we have $X_n\equiv X_n^{\prime }\text{ and }{Ȳ}_n\equiv {Ȳ}_n^{\prime }$ with nξ_n = nη_n − (n − 1)η_n−1. To complete the proof and show ${\displaystyle {\sum }_{n=1}^{\mathrm{\infty }}}E(|{\xi }_n\Vert {ℱ}_{n-1})<\mathrm{\infty }$ a.s., it suffices to show that

$${\displaystyle \sum _{n=1}^{\mathrm{\infty }}}E(|{\xi }_n|)=E\left\{{\displaystyle \sum _{n=1}^{\mathrm{\infty }}}E(|{\xi }_n\Vert {ℱ}_{n-1})\right\}<\mathrm{\infty }.$$

Let $D_n={\mathrm{\sigma ̂}}_n^2-{\sigma }^2$. Thus, ${\mathit{\text{nD}}}_n=(n-1)D_{n-1}+(s_n^2-{\sigma }^2)$ and

$$n{\eta }_n-(n-1){\eta }_{n-1}=\frac{(n-1)z_p}{8n{\sigma }^{3}b}\left[-D_{n-1}^2+2(s_n^2-{\sigma }^2)D_{n-1}+\frac{{(s_n^2-{\sigma }^2)}^2}{n-1}-\left\{\frac{{\sigma }^3}{2{\sigma }_n^{*5}}{\left(\frac{n-1}{n}\right)}^2-\frac{{\sigma }^3}{2{\sigma }_{n-1}^{*5}}\right\}{\mathit{\text{nD}}}_{n-1}^3-\frac{3{\sigma }^3}{2n{\sigma }_n^{*5}}\left\{(n-1)D_{n-1}^2(s_n^2-{\sigma }^2)+D_{n-1}{(s_n^2-{\sigma }^2)}^2+\frac{{(s_n^2-{\sigma }^2)}^3}{3(n-1)}\right\}\right].$$

Thus, $E(|n{\eta }_n-(n-1){\eta }_{n-1}\Vert {ℱ}_{n-1})\le K_0|D_{n-1}|+K_1{D}_{n-1}^2+K_{2}n|D_{n-1}{|}^3+O(n^{-1})$ for some K₀, K₁, K₂ > 0. Since $E(D_n^2)=O(n^{-1}),E(|D_n|)\le {[E(D_n^2)]}^{1/2}=O(n^{-1/2}),\text{ and }E(|D_n{|}^3)\le {[E(D_n^4)]}^{3/4}=O(n^{-3/2})$,

$${\displaystyle \sum _{n=1}^{\mathrm{\infty }}}E(|{\xi }_n|)={\displaystyle \sum _{n=1}^{\mathrm{\infty }}}O(n^{-3/2})<\mathrm{\infty }.$$

Proof of Theorem 1. Following from Condition 2 and recursion (6) in Lemma 1, there exist K₃, K₄ > 0 such that E{(X_n+1 − θ)² | ℱ_n−1} ≤

$${(X_n-\theta )}^2-\frac{2}{\mathit{\text{nb}}}(X_n-\theta )(M(X_n)-\mu )+K_{3}E(|{\xi }_n||{ℱ}_{n-1})+K_{4}E({\xi }_n^2|{ℱ}_{n-1})+O(n^{-2}).$$

It is easy to show that ${\displaystyle {\sum }_{n=1}^{\mathrm{\infty }}}E({\xi }_n^2|{ℱ}_{n-1})<\mathrm{\infty }$ a.s. by verifying ${\Sigma }_{n}E({\xi }_n^2)<\mathrm{\infty }$. Therefore, Theorem 1 of Robbins and Siegmund (1971) implies that lim_n→∞(X_n+1 − θ)² exists and ${\displaystyle {\sum }_{n=1}^{\mathrm{\infty }}}{n}^{-1}(X_n-\theta )\{M(X_n)-\mu \}<\mathrm{\infty }$ a.s. Since (X_n−θ){M(X_n)−μ} > 0 under Condition 1, we conclude that X_n → θ a.s.

Proof of Theorem 2. We will follow the approach of Sacks (1958). First, define

$${\gamma }_{\mathit{\text{in}}}={\displaystyle \prod _{j=i+1}^n}\left(1-\rho j^{-1}\right)\text{ and }{h}_n={\left({\displaystyle \sum _{i=1}^n}{\rho }^2{i}^{-2}{\gamma }_{\mathit{\text{in}}}^2\right)}^{-1/2},$$ (A4)

where ρ ≔ β/b, with the following properties:

• Property 1. $(1+{\epsilon }_i)i^{\rho }{n}^{-\rho }\le {\gamma }_{\mathit{\text{in}}}\le (1+{\epsilon }_i^{\prime })i^{\rho }{n}^{-\rho }\text{ where }{\epsilon }_i,{\epsilon }_i^{\prime }\to 0\text{ as }i\to \mathrm{\infty }$.

• Property 2. lim_n→∞ h_nγ_in = 0 for fixed i and ρ > 1/2.

• Property 3. h_n ~ {b(2β − b)}^1/2β⁻¹n^1/2.

Properties 1–3 are respectively Equation (2.3), Lemma 2, and Lemma 5 of Sacks (1958). Now, under Condition 3, we can rewrite (6) as

$$X_{n+1}-\theta =(X_n-\theta )-\frac{1}{\mathit{\text{nb}}}\{\beta (X_n-\theta )+\tau (X_n,\theta )+{ē}_n\}+{\xi }_n$$

$$\iff X_{n+1}-\theta =\left(1-\frac{\beta }{\mathit{\text{nb}}}\right)(X_n-\theta )-\frac{\tau (X_n,\theta )}{\mathit{\text{nb}}}-\frac{{ē}_n}{\mathit{\text{nb}}}+{\xi }_n$$ (A5)

$$\iff X_{n+1}-\theta ={\gamma }_{0n}(X_1-\theta )-\frac{1}{b}{\displaystyle \sum _{i=1}^n}{i}^{-1}{\gamma }_{\mathit{\text{in}}}\tau (X_i,\theta )-\frac{1}{b}{\displaystyle \sum _{i=1}^n}{i}^{-1}{\gamma }_{\mathit{\text{in}}}{ē}_i+{\displaystyle \sum _{i=1}^n}{\gamma }_{\mathit{\text{in}}}{\xi }_i.$$ (A6)

Equation (A6) is obtained by iteration of (A5). If we show that h_n(X_n+1−θ) is asymptotically normal with mean 0 and variance α₃σ²(mβ²)⁻¹, then the desired result will follow from Property 3. Corresponding to the terms in (A6), the limiting results

1. h_nγ_0n(X₁ − θ) → 0 a.s.

2. $h_n{b}^{-1}{\displaystyle \sum _i}{i}^{-1}{\gamma }_{\mathit{\text{in}}}\tau (X_i,\theta )\to 0$ in probability

3. $h_n{b}^{-1}{\displaystyle \sum _i}{i}^{-1}{\gamma }_{\mathit{\text{in}}}{ē}_i{\to }^{ℒ}N(0,{\alpha }_3{\sigma }^2{m}^{-1}{\beta }^{-2})$

can be derived by mimicking the proof of Theorem 1 in Sacks (1958) under an additional assumption:

Condition 2b. There exists 0 < C₀ < C₁ such that C₀|x − θ| ≤ |M(x) − μ|. Finally, following from Properties 1–3,

$$h_n{\displaystyle \sum _{i=1}}{\gamma }_{\mathit{\text{in}}}{\xi }_i~{\{b(2\beta -b)\}}^{1/2}{\beta }^{-1}{n}^{-1/2}{n}^{1-\rho }{\displaystyle \sum _{i=1}^n}{i}^{\rho -1}(i{\xi }_i)\to 0$$

when ρ > 1 by Kronecker Lemma; and,

$$h_n{\displaystyle \sum _{i=1}}{\gamma }_{\mathit{\text{in}}}{\xi }_i~{\{b(2\beta -b)\}}^{1/2}{\beta }^{-1}{n}^{-1/2-\rho }n{\eta }_n{\displaystyle \sum _{i=1}^n}\left\{\frac{i{\eta }_i-(i-1){\eta }_{i-1}}{n{\eta }_n}\right\}{i}^{\rho -1}\to 0$$

if 1/2 < ρ < 1, because ${\displaystyle {\sum }_{i=1}^n}i{\eta }_i-(i-1){\eta }_{i-1}=n{\eta }_n$ The desired result is thus obtained under Conditions 1–3 and 2b.

Suppose now that M(x) satisfies Condition 1–3 but not 2b. Since b < 2β, there exists t > 0 such that b < 2(β − t). Let C₀ = β − t < C₁. Then under Condition 3, we can find δ > 0 such that C₀|x − θ| ≤ |M(x) − μ| ≤ C₁|x − θ| for |x − θ| ≤ δ.

Next, define M_δ(x) = M(x) if |x − θ| ≤ δ and M_δ(x) = μ + C₀(x − θ) if |x − θ| > δ, and let $X_1^{(\delta )}=X_{N_{\delta }+1}$ and

$$X_{n+1}^{(\delta )}-\theta =(X_n^{(\delta )}-\theta )-\frac{1}{(n+N_{\delta })b}\{M_{\delta }(X_n^{(\delta )})-\mu \}-\frac{{ē}_n+N_{\delta }}{(n+N_{\delta })b}+{\xi }_{n+N_{\delta }}$$

where N_δ > 0 is determined such that, for a given u, pr(|X_n−θ| ≤ δ for all n ≥ N_δ) > 1−u. We can find such an N_δ because X_n → θ a.s. under Conditions 1 and 2. Observing that M_δ(x) satisfies Condition 2b, we can verify $n^{1/2}(X_n^{(\delta )}-\theta ){\to }^{ℒ}N(0,{\alpha }_1{\alpha }_3{\sigma }^2)$. Furthermore, $X_{n+N_{\delta }}\equiv X_n^{(\delta )}$ a.s. on the event {|X_n+Nδ − θ| ≤ δ all n ≥ 1}. Thus,

$$\text{lim }\underset{n\to \mathrm{\infty }}{\text{sup }}\text{pr}\{n^{1/2}(X_n-\theta )<w\}=\text{lim }\underset{n\to \mathrm{\infty }}{\text{sup }}\text{pr}\{{(n+N_{\delta })}^{1/2}(X_{n+N_{\delta }}-\theta )<w\}$$

$$\le \text{ lim }\underset{n\to \mathrm{\infty }}{\text{sup }}\text{pr}\{{(n+N_{\delta })}^{1/2}(X_n^{(\delta )}-\theta )<w,|X_{n+N_{\delta }}-\theta |\le \delta ,n\ge 1\}+u$$

$$\le \underset{n\to \mathrm{\infty }}{\text{ lim }}\text{pr}\{{(n+N_{\delta })}^{1/2}(X_n^{(\delta )}-\theta )<w\}+u.$$

Similarly, we obtain

$$\text{lim }\underset{n\to \mathrm{\infty }}{\text{inf }}\text{pr}\{n^{1/2}(X_n-\theta )<w\}\ge \underset{n\to \mathrm{\infty }}{\text{lim }}\text{pr}\{{(n+N_{\delta })}^{1/2}(X_n^{(\delta )}-\theta )<w\}-u.$$

Since u is arbitrary, we conclude that n^1/2(X_n−θ) and $n^{1/2}(X_n^{(\delta )}-\theta )$ have the same limiting distribution. This completes the proof of Theorem 2.

Appendix B. Asymptotic irrelevance of truncation

This section discusses the asymptotic equivalence of the truncated least squares recursion and its non-truncated counterpart.

Under Cases 1 and 2, the least squares recursion is identical to the Robbins-Monro procedure, whose truncated version is known to be asymptotically equivalent to the non-truncated design; see Lai and Robbins (1981) for example.

Under Case 3, the true standard deviation σ is consistently estimated by σ̂_n, and we can re-write (2) as

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n}{Ȳ}_i+z_p\sigma -\{t_0+b(X_i-{\mathrm{\theta ̂}}_n)\}=-z_p({\mathrm{\sigma ̂}}_n-\sigma ).$$

Since σ̂_n − σ → 0 with probability one, by Martingale convergence theorem, we have

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n}f(X_i)-\{t_0+b(X_i-{\mathrm{\theta ̂}}_n)\}\to 0$$

with probability one. Therefore, we can use the arguments in the proof of Theorem 2 in Ying and Wu (1997) to show that X_n+1 = θ̂_n eventually with probability 1. Thus, in view of asymptotic efficiency, we can focus on the non-truncated design formed by (2) and (3) recursively.