An involuntary stereotypical grasp tendency pervades voluntary dynamic multifinger manipulation

Abstract

We used a novel apparatus with three hinged finger pads to characterize collaborative multifinger interactions during dynamic manipulation requiring individuated control of fingertip motions and forces. Subjects placed the thumb, index, and middle fingertips on each hinged finger pad and held it—unsupported—with constant total grasp force while voluntarily oscillating the thumb's pad. This task combines the need to 1) hold the object against gravity while 2) dynamically reconfiguring the grasp. Fingertip force variability in this combined motion and force task exhibited strong synchrony among normal (i.e., grasp) forces. Mechanical analysis and simulation show that such synchronous variability is unnecessary and cannot be explained solely by signal-dependent noise. Surprisingly, such variability also pervaded control tasks requiring different individuated fingertip motions and forces, but not tasks without finger individuation such as static grasp. These results critically extend notions of finger force variability by exposing and quantifying a pervasive challenge to dynamic multifinger manipulation: the need for the neural controller to carefully and continuously overlay individuated finger actions over mechanically unnecessary synchronous interactions. This is compatible with—and may explain—the phenomenology of strong coupling of hand muscles when this delicate balance is not yet developed, as in early childhood, or when disrupted, as in brain injury. We conclude that the control of healthy multifinger dynamic manipulation has barely enough neuromechanical degrees of freedom to meet the multiple demands of ecological tasks and critically depends on the continuous inhibition of synchronous grasp tendencies, which we speculate may be of vestigial evolutionary origin.

successful dexterous manipulation requires dynamic collaborative use of our fingers. Clearly, the neural controller must actuate the system properly to satisfy the mechanical constraints of the task. Numerous studies have investigated how we adapt grasp to different friction contact (Johansson and Westling 1984), object curvature (Jenmalm et al. 2003), fingertip positions (Baud-Bovy and Soechting 2001), perturbations (Eliasson et al. 1995; Kim et al. 2006; van de Kamp and Zaal 2007), object manipulations (Flanagan et al. 1999; Shim et al. 2005; Winges et al. 2008), and dexterity requirements (Johanson et al. 2001; Valero-Cuevas et al. 2003; Venkadesan et al. 2007). These prior studies have identified voluntary and involuntary collaborative force interactions among fingertips to reduce task variability when pressing or grasping rigid objects (e.g., Baud-Bovy and Soechting 2001; Latash and Zatsiorsky 2009; Scholz et al. 2002; Shim et al. 2005; see for review Schieber and Santello 2004).

This study, however, examines the behavior of collaborative, multifinger interactions during more ecological dynamic reconfiguration of a grasp requiring the simultaneous control of fingertip motions and forces. Common tasks requiring such simultaneous control include folding paper, unscrewing a bottle cap, or rotating an object in the hand. This study is motivated by prior work aiming to clarify an apparent and long-standing paradox between the scientific concepts of muscle redundancy and robustness and the clinical reality of motor development and dysfunction (Keenan et al. 2009; Kutch and Valero-Cuevas 2011; Venkadesan and Valero-Cuevas 2008). If, say, hand musculature is so redundant, why then is dynamic manipulation so vulnerable to developmental problems (Forssberg et al. 1991), mild neurological pathologies, and aging (Schreuders et al. 2006)? This paradox may arise simply because experiments and models often use simplified tasks for which the musculature is indeed redundant (Loeb 2000). In contrast, everyday ecological grasp behavior often involves tasks that require meeting multiple mechanical constraints and transitioning between constraints. Our prior work on single fingers indicates that even ordinary manipulation tasks can push the neuromuscular system to its limit of performance when they require combinations of, or transitions between, motion and force constraints (Keenan et al. 2009; Kutch and Valero-Cuevas 2011; Venkadesan and Valero-Cuevas 2008). Here we extend that prior work to multifinger function by investigating ordinary, yet critical, multifinger tasks: dynamic manipulation of deformable objects requiring continuous and simultaneous regulation of fingertip motions and forces.

MATERIALS AND METHODS

Experimental Procedure

We designed a novel instrumented apparatus with three hinged finger pads to be held by using a tripod grasp with the thumb, index, and middle fingers (Fig. 1), initially without any support to the device. Each finger pad consisted of a six-axis load cell (Nano 17, ATI/Industrial Automation, Apex, NC) at one end of a rigid link to measure forces used to grasp and manipulate the object, with the other end connected by a common planar hinge (Valero-Cuevas and Brown 2006). The grip surface of the load cell was 30 mm from the hinge axis and covered with fine (360 grit) sandpaper. The object's mass is ∼60 g to mitigate fatigue. Finally, in order to ensure rotation of the thumb pad at the appropriate frequency, we used a software metronome (Metronome 1.1, Keaka Jackson, The World, 2008).

Fig. 1.

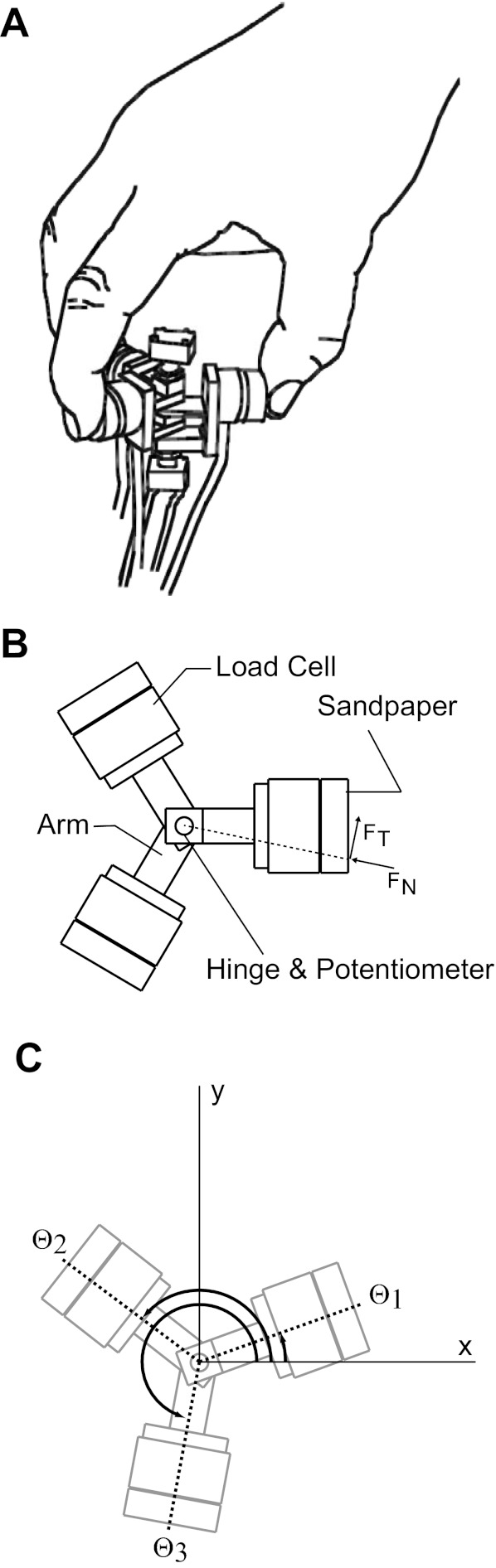
Experimental setup. A: subjects held the object in a precision tripod grasp. B: the test object connected 3 load cells with a central hinge that allowed movement of the fingers. Normal force in this work is defined as the force directed at the hinge. C: coordinates used in deriving the equations of motion.

Mechanics dictates that the direction of fingertip force vectors for a static grasp must intersect at a point or the forces would create a net moment about the center of mass and cause a rotation (see, e.g., Flanagan et al. 1999; Yoshikawa and Nagai 1991). The location of this point is arbitrary as long as the conditions imposed by the friction cones at the fingertips are satisfied and the zero net force constraint is met. In this study, in contrast, the fingertip forces are constrained to intersect at a specified point (a central hinge) or else the finger pads will rotate. Holding the apparatus with a given total grasp force while reconfiguring the angles between the hinged finger pads requires collaborative multifinger interactions to control fingertip motions and force vectors. Thus this apparatus explicitly distinguishes the multifinger interactions needed to hold the object against gravity (i.e., total grasp force) from those needed to dynamically reconfigure the grasp (i.e., compensating for thumb oscillations). Total grasp force is an independent task constraint from compensations in fingertip force vectors when reconfiguring the grasp: one can squeeze tighter without moving the pads or reconfigure the grasp while producing the same total grasp force.

We tested six subjects (1 women, 5 men; 21–31 yr; 5 right-handed, 1 left-handed) who gave their informed consent to participate in a protocol approved by the USC Institutional Review Board. Subjects held the test object with the thumb, middle, and index fingers of the dominant (Oldfield 1971) hand in a tripod grasp (Fig. 1A; the subject flexed the ring and little fingers out of the way). For all trials, subjects were seated comfortably in a chair and their arm rested on a surface.

Subjects were instructed to maintain 10 N of total grasp force, defined as the sum of the normal forces at each fingertip, while oscillating the thumb pad in time to an audible metronome. The visual feedback consisted of a line and a cross hair presented on a computer screen at a distance ∼1 m from the subject. The horizontal line represented the 10 N target total grasp force (sum of the 3 normal forces), which is consistent with the grasp force to lift a 400-g object with three fingers (Flanagan et al. 1999), while the cross hair represented the sum of normal forces actually applied by the subjects. Simultaneously, subjects were asked to oscillate the thumb pad of the grasping device in time with the audible metronome at 1 Hz, such that the leftmost and rightmost angular displacements of the thumb pad were reached on the metronome beat, at a frequency of 0.5 Hz. The angular displacement of the thumb was left to the subjects' preference. In the following, we refer to this task as the “original task.”

Subjects had several practice trials, repeated with 60-s rest between trials until they reported being comfortable with the task (from 2 to 6 repetitions, 3 typical). We did not do additional training because subjects reported being very satisfied with their performance, likely because humans perform such tasks regularly and our task was designed to be similar to many ecological tasks as mentioned above. We then recorded 95 s of force and angle data at 400 samples/s (PCI 6025, National Instruments, Austin, TX) for each subject to obtain up to 47 full task cycles per subject. Data acquisition and visual feedback were provided with a program written in MATLAB with the Data Acquisition Toolbox (MathWorks, Natick, MA). Subject visual feedback on the force magnitude was updated at a rate of 50 Hz. The needed forces were so low that subjects did not report fatigue, but 60 s of mandatory rest was always enforced before each trial.

To rule out potential confounds or alternative interpretations of our results, six different control tasks (Table 1) were performed in addition to the original task—all of which were done in block-randomized order and repeated three times each for 95 s, and for which subjects had practice trials as in the original task. These control tasks establish baseline performance for a variety of combinations of fingertip motion and force constraint and were added after the initial pilot work to better understand the performance of the original task.

Table 1.

Explanation of tasks and simulations used to support hypothesis

Task	Hinge State	Thumb Motion	Object Displacement	Target Force	Goal
Original	Free	0.5 Hz	Free	10-N grasp	Characterize multifinger interactions during dynamic manipulation requiring simultaneous control of fingertip motions and forces.
Control 1	Free	0.5 Hz	Fixed	10-N grasp	Same as original task, but with object fixed to ground to remove slip-grip response and behavioral fear of dropping object.
Control 2	Fixed	None	Free	0.5-Hz oscillating compensation	Voluntarily produce the Compensation Mode (alternating index and middle finger forces) as seen in original task, but with a locked object to remove hinge instability and voluntary finger motions.
Control 3	Free	None	Free	1-Hz oscillating grasp	Voluntarily produce the oscillations in the Grasp Mode (synchronous normal force modulation across fingers) as seen in original task, but without voluntary finger motions.
Control 4	Fixed	None	Free	1-Hz oscillating grasp	Same as in control task 3, but with a locked object to remove hinge instability.
Control 5	Free	None	Free	10-N grasp	Simple static grasp with visual feedback to assess effect of visuomotor feedback loop on grasp force variability.
Control 6	Fixed	None	Free	10-N grasp	Same as in control task 5, but with a locked object to remove hinge instability.
Simulation 1	Free	Oscillating	Free but stationary	10 N	Mechanical constraints of successful task performance dictate variability.
Simulation 2	Free	Oscillating	Fixed	10 N + noise	Signal-dependent noise informs force variability patterns more than the task mechanics.
Simulation 3	Free	Oscillating	Free but stationary	10 N + noise	Task mechanics govern force variability patterns.
Simulation 4	Free but stationary	None	Free but stationary	10 N + noise	Task mechanics govern force variability patterns.

Control task 1.

The subjects performed the above-described original task, but with the instrumented object attached to ground. Doing this enabled us to distinguish force fluctuation correlations across fingers due to neuromuscular causes from purely mechanical causes associated with motion or reaction forces. Furthermore, this task removes the need for force dynamics that could be attributed to behavioral responses to dropping the object or vertical slip-grip responses.

Control task 2.

The instrumented object was handheld, but we locked the pads in a configuration comfortable for the subjects (making it a rigid object) and asked them to oscillate the normal force between index and middle finger at a frequency of 0.5 Hz, while holding the thumb still, thus mimicking the oscillations in normal forces the subjects needed to apply to compensate for thumb pad motion. The visual feedback in this condition consisted of two 0.5-Hz sinusoidal curves, phase shifted by 180°, and two cross hairs, representing the individual normal forces applied by index and middle finger. There was no explicit feedback on the total grasp force in this condition, but the amplitude of the sinusoidal curves corresponded to the amplitude of the oscillations in the original task. This control task helps to elucidate the coupling of two dimensions of force, which are at least mathematically independent (Gao et al. 2005): the grasp force that counteracts gravity and the force compensating for thumb motion. It removes an explicit enforcement of a target total grasp force, as long as it is sufficient to hold the object.

Control task 3.

The instrumented object was handheld, but with unlocked pads, and we asked subjects to oscillate the total grasp force, that is, oscillate in phase the normal forces of thumb, index, and middle finger at 1 Hz, thus voluntarily reproducing the synchronous grasp variability (i.e., Grasp Mode, see results) observed experimentally in the original task. Here, the visual feedback consisted of a sinusoidal, whose amplitude we determined for each subject from his or her actual performance of the original task trials. While control task 2 above removed the target total grasp force enforcement, this task removes the requirement to modulate force variability compensating for thumb motion. It complements control task 2 in that it quantifies the coupling of the two force components, i.e., synchronous and compensatory normal force variability.

Control task 4.

Control task 3 was repeated, but this time with the pads locked as a rigid object to investigate the effect of removing the instability of the hinged pads on the Grasp Mode.

Control tasks 5 and 6.

The final two tasks consisted of simple static grasps (handheld object with no oscillation of the thumb), with the target sum of normal forces to be maintained at 10 N, with pads either free (control task 5) or locked (control task 6) to separate force variability caused by visual processing from other contributors. These tasks allow us to quantify the contribution to the total force variability by corrective action vis-à-vis the visual feedback.

Mechanical Analysis

We found the closed-form analytical solution to the necessary fingertip forces and motions to perform the task. Comparing experimental forces to the analytical solution disambiguates mechanically necessary from neurally driven interactions. We modeled the system as a planar, rigid-body mechanism with five degrees of freedom: x and y location of the hinge axis on the plane and the absolute angle of each pad. All three finger pads (which are each reduced to a point collocated with the center of pressure of the finger pad) and their links are in the horizontal plane, and gravity acts perpendicular to the plane in a downward direction, eliminating the vertical force from the analysis. The six control inputs in the plane of the finger pads are the normal (toward the hinge) and tangential components of fingertip forces for each of the three fingers. The normal and tangential forces of both the model and the experimental data are measured with respect to the hinge rather than the grip surface to reflect the task goals and to more easily separate the grasp force and compensation to thumb oscillation modes (Fig. 1B).

Equations of Motion for a Two-Dimensional System of Three Links Connected via a Common Hinge

We derived the dynamic equations of motion for a simplified planar model of the grasper setup with the Lagrange method (see, e.g., Williams 1996). The Lagrange method requires generalized coordinates (q_i) that describe the configuration of the object. The kinetic and potential energy (T and V) are expressed as functions of the q_i and generalized forces (F_i) that act on each generalized coordinate. The Lagrangian is the kinetic minus potential energy, L = T − V, and is inserted into Lagrange's equation:

$$\frac{d}{dt}\left(\frac{\delta }{\delta {\dot{q}}_i}L\right)-\frac{\delta }{\delta q_i}L=F_i$$

The grasp-device system has two translational degrees of freedom relative to an inertially fixed coordinate reference frame and three rotational degrees of freedom—one for each pad. Since we observed very limited motion in the vertical direction and rotation of the device itself, we disregarded these four dimensions (1 translational, 3 rotational) in our modeling analysis. For the generalized coordinates, we selected x and y position of the hinge and the absolute angle of each pad relative to the fixed coordinate system θ_i, i = 1, 2, 3 (see Fig. 1C). With these coordinates, the two-dimensional vector for the position of each pad is

$$r_i=\left[\begin{array}{c}x\\ y\end{array}\right]+d_i\left[\begin{array}{c}\cos {\theta }_i\\ \sin {\theta }_i\end{array}\right]$$

where d_i is the distance from the hinge to the center of mass of the ith pad. Differentiating this expression yields the velocity

$$v_i=\left[\begin{array}{c}\dot{x}\\ \dot{y}\end{array}\right]+d_i{\dot{\theta }}_i\left[\begin{array}{c}-\sin {\theta }_i\\ \cos {\theta }_i\end{array}\right]$$

where the overdot represents the derivative with respect to time. The velocity determines the kinetic energy of each body. Let m_i be the mass of the ith pad and I_i be the scalar moment of inertia of the ith pad about a vertical (out of the page) axis through the center of mass of link I. The kinetic energy of the system is given as the sum of the energy of the individual parts. The partial derivatives in Lagrange's equations eliminate potential energy terms from the equation because gravity acts perpendicular to the system. Thus the Lagrangian is given by the kinetic energy:

$$L=T={\displaystyle \sum \frac{1}{2}{m}_i\left(v_i·v_i\right)+\frac{1}{2}{I}_i{\dot{\theta }}_i^2}$$

The generalized forces for this simple system are the resultant forces or torques when all generalized coordinates are fixed except one. Fixing all coordinates and allowing x to vary gives us the generalized force for x:

$$F_x={\displaystyle \sum F_{N_i}\cos {\theta }_i-F_{T_i}\sin {\theta }_i}$$

which is all the forces in the x-direction. The forces F_Ni and F_Ti are the normal and tangent forces at the grip surface on each pad (Fig. 1B). Likewise for the y-direction, the generalized force is

$$F_y={\displaystyle \sum F_{N_i}\sin {\theta }_i-F_{T_i}\cos {\theta }_i}$$

The generalized forces corresponding to the angles are physically torques. The resultant torque when allowing only one angle to vary is given by

$$T_{{\theta }_i}=lz·F_{T_i}$$

Where lz represents the length of a device arm, i.e., the distance between the pad surface and the center of the hinge. The component parts are arranged according to Lagrange's equation to arrive at the following equations of motion, written in matrix form for computational ease:

$$\left[\begin{array}{ccccc}M& & -m_1{d}_1{s}_1& -m_2{d}_2{s}_2& -m_3{d}_3{s}_3\\ & M& m_1{d}_1{c}_1& m_2{d}_2{c}_2& m_3{d}_3{c}_3\\ -m_1{d}_1{s}_1& m_1{d}_1{c}_1& m_1{d}_1^2+I_1& & \\ -m_2{d}_2{s}_2& m_2{d}_2{c}_2& & m_2{d}_2^2+I_2& \\ -m_3{d}_3{s}_3& m_3{d}_3{c}_3& & & m_3{d}_3^2+I_3\end{array}\right]·\left[\begin{array}{c}\ddot{x}\\ \ddot{y}\\ {\ddot{\theta }}_1\\ {\ddot{\theta }}_2\\ {\ddot{\theta }}_3\end{array}\right]+\left[\begin{array}{ccc}-d_1{c}_1& -d_2{c}_2& -d_3{c}_3\\ -d_1{s}_1& -d_2{s}_2& -d_3{s}_3\end{array}\right]·\left[\begin{array}{c}{\dot{\theta }}_1^2\\ {\dot{\theta }}_2^2\\ {\dot{\theta }}_3^2\end{array}\right]=\left[\begin{array}{cccccc}{c}_1& c_2& c_3& -s_1& -s_2& -s_3\\ s_1& s_2& s_3& c_1& c_2& c_3\\ & & & l_z& & \\ & 0& & & l_z& \\ & & & & & l_z\end{array}\right]·\left[\begin{array}{c}{F}_{N_1}\\ F_{N_2}\\ F_{N_3}\\ F_{T_1}\\ F_{T_2}\\ F_{T_3}\end{array}\right]$$

This can be written compactly by using matrix and vector notations with obvious meaning as

$$M\ddot{x}+C{\dot{x}}^2=D·F$$

The model takes the dynamics of the position and angles as inputs and outputs the normal and tangential forces. This gives us a one-parameter subspace of the possible forces. The grasp force is added to the equations to completely determine the forces necessary for successful completion of the experimental task. In simulation, we fix x and y at the origin, maintain the middle and index angles at 130° and 230°, respectively, and prescribe the grasp force as either constant or noisy. The reduced model with these assumptions is

$$\left[\begin{array}{c}-d_1{c}_1·{\dot{\theta }}_1^2\\ -d_1{s}_1·{\dot{\theta }}_1^2\\ \left(m_1{d}_1^2+I_1\right)·{\ddot{\theta }}_1\\ 0\\ 0\\ F_{grasp}\end{array}\right]=\left[\begin{array}{cccccc}{c}_1& c_2& c_3& -s_1& -s_2& -s_3\\ s_1& s_2& s_3& c_1& c_2& c_3\\ & & & l_z& & \\ & 0& & & l_z& \\ & & & & & l_z\\ 1& 1& 1& 0& 0& 0\end{array}\right]·\left[\begin{array}{c}{F}_{N_1}\\ F_{N_2}\\ F_{N_3}\\ F_{T_1}\\ F_{T_2}\\ F_{T_3}\end{array}\right]$$

The last row of this equation comes from the definition of grasp force as the sum of the normal forces.

Simulations

In the closed-form inverse dynamics solution we calculate fingertip forces necessary to produce the desired motion and total grasp force. The desired motion maintains the index and middle finger angles fixed at 130° and 230° while the thumb angle oscillates through an arc with amplitude of 30° following a sine function with a period of 2 s (0.5 Hz; see ideal angles in Fig. 2A). In this way we defined a comfortable configuration that would reveal clear changes in forces, shown in Fig. 1A. For comparison, a plot of the measured angles from one representative subject is shown in Fig. 2B. Note that in the subject's data the angle between the middle and index finger pads also changed slightly during the trial (Fig. 2B), but the motion of the thumb is much greater and the mechanical solutions retain their same form in the plot of the normal forces (Fig. 3B). The experimental apparatus was built to have very low friction at the hinge; thus the modeled and experimentally measured tangential forces are very small relative to the normal forces (3,000× smaller in the frictionless model and 20× smaller in the experimental data) and were excluded from the analysis. Instead, the adaptation of the normal forces to the changing configuration captures the relevant behavior due to the thumb oscillations. We further justify using only the three normal forces to characterize the task because they fully account for the two active degrees of freedom of the system: grasp force and compensation to thumb oscillation. A system or study designed to consider additional degrees of freedom would need to include the tangential forces for the very low frictions.

Fig. 2.

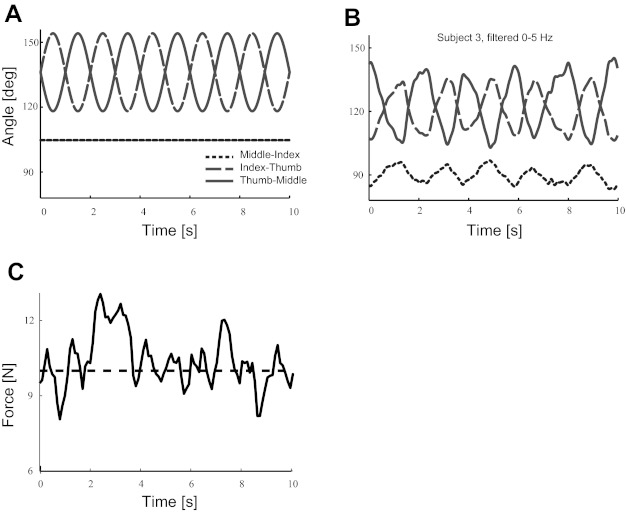
Sample time histories. A: ideal interfinger angles used in the model. The equations reference all angles to a fixed ground but are shown relative to one another here to be consistent with the experimental data. B: measured angles from a representative subject's data. C: measured grasp force from the same data as B. Note the quasiperiodicity in the measured data.

Fig. 3.

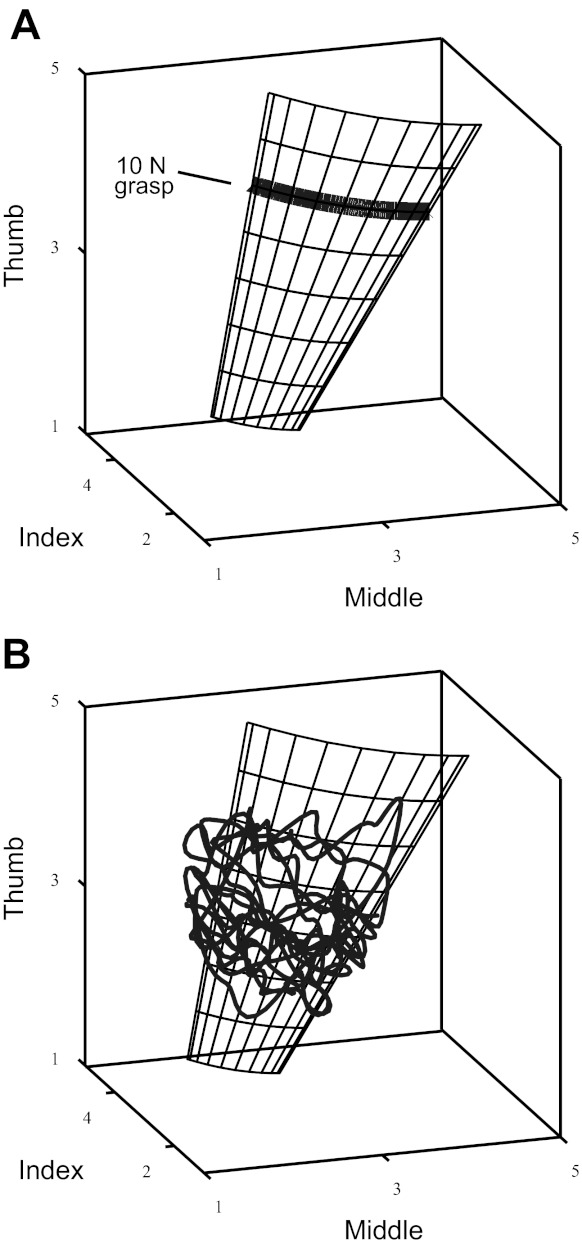
Force space. A: a perfectly executed task traverses the thick line shown here. Connecting the lines created by a variety of grasp forces (from 5 to 12 N) illustrates the manifold of allowable forces. B: the subject data lie on the manifold described by the model, but with varying grasp force magnitude. The subject data and the manifold have slight curvature when viewed from the [1 1 1] direction.

We simulated four conditions for the grasp force (Table 1).

Simulation 1.

This condition was an idealized original task, where the grasp force was ideally constant while the index and middle finger generated the exact normal forces necessary to compensate for the reconfiguration of the grasp as the thumb pad oscillated.

Simulation 2.

This was the same as simulation 1, but with the object fixed to ground and each finger generating a zero mean Gaussian-distributed noisy normal force, whose standard deviation was adjusted such that either the experimentally observed grasp force variability magnitude or the error between target grasp force and the actual grasp force was reproduced. The noise was not band limited to the 8–12 Hz frequency band, however, with which signal-dependent noise is commonly associated. This condition simulates the effects of signal-dependent noise (Jones et al. 2002) at each fingertip, but since it does not consider reaction forces at the other fingertips, this condition in effect simulates control task 1, in which the device was attached to ground.

Simulation 3.

Simulation 3 consisted of the noisy normal forces acting on the object and inducing reaction forces in the other fingers, thus simulating correlations between fingers that would arise purely due to mechanics. This condition simulates the original task with noise.

Simulation 4.

This was a simple static grasp without thumb oscillations, but including the requirement to generate a 10 N sum of normal forces, which considers correlations due to mechanics (simulating control tasks 5 and 6 for simple static grasp). This condition helps to separate contributions to visual feedback error by corrective actions and by signal-dependent noise.

In simulations 3 and 4 there is no unique mechanical solution, so we computed the reaction forces by solving a underconstrained system of linear equations, solving for zero force and moment using the pseudoinverse matrix (i.e., the least-squares energy solution). In simulation 1 we modeled constant total grasp forces ranging from 5 N to 12 N to find the full solution manifold (i.e., the set of all mechanically feasible fingertip forces to accomplish the task). This set of mechanically feasible forces is the slightly curved manifold shown as a curved surface in Fig. 3.

Data Analysis

Plotting the normal component of the fingertip forces (i.e., the component of fingertip force acting on the finger pad and directed toward the hinge) against each other in the three-dimensional (3D) space of normal forces is an effective way to visualize the experimental and simulation results. Each coordinate axis in this 3D space represents the normal force of a given finger (thumb, index, and middle), and a combination of three forces is represented as a point in this space. The analytical solution to the task shows that the feasible set of fingertip forces lies on a slightly curved, nearly planar surface in force space (Fig. 3). This is because lines or nearly planar surfaces in the force space represent the mechanical constraints of the task, such as the equilibrium equations for different finger pad configurations. That is, only combinations of forces that lie on the constraint lines or surfaces are valid solutions to the grasp problem, and linear analysis tools may be used, such as principal components analysis (PCA; Clewley et al. 2008).

We used the 3D force vector and torques on each finger pad (Fig. 1B) to extract the center of pressure location and force components in the normal, tangent, and vertical (F_N, F_T, F_V) directions relative to the hinge (Fig. 1B). The normal force covariance patterns completely determine the grasp force and manipulation force components; the others are not included in the analysis as discussed above. The first 5 s and last 1 s of data were removed to eliminate transient behavior in the data.

The data, represented by a 3 × N matrix where N is the number of samples, were filtered with a sliding band-pass Butterworth filter of width 1 Hz and 99% overlap between filter windows, starting from 0.1 Hz up to 10 Hz, to extract the normal force dynamics in each of these frequency bins. We performed PCA on the 3 × 3 normal force covariance matrix computed from each set of filtered data associated with a particular filter window and computed the loadings of the three resulting principal component (PC) vectors (r-mode PCA, computed from covariances between variables) as well as the percentage of variance explained by each PC. Next, we compared the loadings of each PC to the theoretical grasp force mode and compensation-to-thumb-oscillation mode for each frequency range, by computing the angle between the experimentally observed PC and the PC associated with the mechanical simulation of the task.

Because we know the structure of the solution space from our simulations, we could have projected the task variability directly onto the major directions of variability representing it. However, this approach has two problems: first, the normal force solution manifold for this task corresponds to a slightly curved surface and not a strictly two-dimensional plane. While it would be possible to describe the location on this plane in terms of polar coordinates, i.e., distance from origin and orientation, it would not be easily possible to compare variability along these two dimensions. Therefore, we decided to use PCA as the optimal linear approximation, in a least-squares sense, to this plane to easily capture and compare the variability along the directions of interest without loss of generality. Second, the use of PCA allows us to find these directions of interest in each subject despite inevitable experimental differences and inaccuracies across trials such as slightly different postures across subjects.

Finally, to determine whether variability along a PC in the original task changed in a state-dependent manner, e.g., variability at the extreme points of thumb motion versus at the middle point, we computed the variance over a window, whose length was one-third of the thumb oscillation period, i.e., 0.6 s, and slid the window over the trial data. This tests the hypothesis that increased grasp force variability reflects the action of a purposeful mechanism, such as guarding against drop of the object by squeezing it at critical locations in the state space.

RESULTS

Analytical Solution and Simulations

The analytical solution to the manipulation task, with interfinger angles as in Fig. 2A, shows that the feasible set of fingertip forces lies in a tilted and slightly curved plane in the force space (Fig. 3A). It is to be expected, therefore, that the PCA of the subjects' data will naturally approximate this manifold well and that subjects' PCs will align with the manifold's PCs, for the following reasons.

First, grasp force is the sum of the fingertip normal forces and is equal to the projection of the current force vector [F_middle F_index F_thumb]^T onto the [1 1 1]^T direction¹ (Fig. 4, column I). Changes in grasp force magnitude cause movement toward or away from the origin in force space, while not moving the object. Therefore a PC of the subjects' data with loadings of the same sign and similar magnitude indicates a changing grasp force. We say this PC aligns with the Grasp Mode.

Fig. 4.

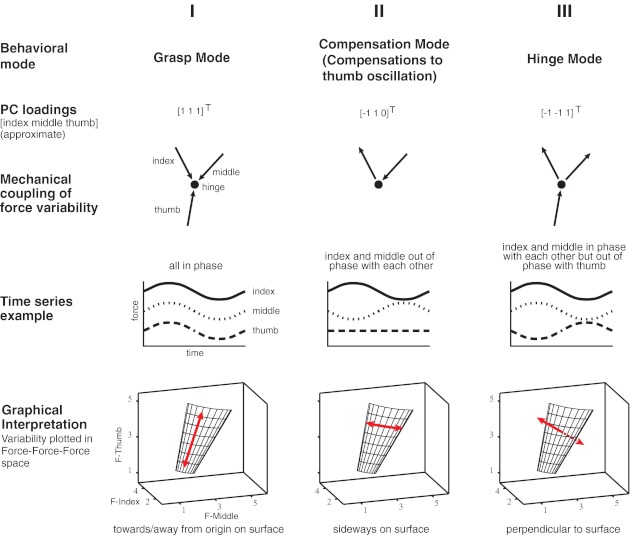
Overview over the 3 force variability modes. The grasp force mode (I) is the dimension of force variability that is associated with simultaneous, or in-phase, increases and decreases by all 3 finger normal forces. Graphically (bottom), this can be expressed as motion along a line in 3-dimensional (3D) normal force space, which has components in every dimension. The compensation force mode (II) explains out-of-phase variation of index and middle finger force, with no contribution by the thumb. In 3D normal force space, this corresponds to motion at a constant thumb force level, between index and middle finger axes, along a slightly curved line. Finally, the hinge force mode (III) explains that force variability whereby middle and index finger vary their normal force in phase while varying out of phase with the thumb normal force. This will lead to accelerations of the object.

Second, as the thumb oscillates from side to side, the relative magnitude of the middle and index fingers' forces alternates to compensate for the change in direction of the thumb's force vector during the task. Thus the “manipulation force” is the projection of the current force vector onto the [−1 1 0]^T direction (Fig. 4, column II). The changing force magnitudes of the index and middle fingers for a given thumb force magnitude causes lateral movement in force space as described by the compensations to thumb oscillation mode. The mechanics of the task result in grasp force and compensations to thumb oscillation being orthogonal modes in force space. This is the mathematical way of saying that one can produce the same magnitude of grasp force while moving the thumb or, conversely, vary the grasp force without affecting the thumb's positional control. We say this PC aligns with the Compensation Mode.

The third mode of force interactions is variability perpendicular to the constraint plane and represents errors in maintaining the hinge constraint. Namely, the task requires that the force vectors intersect at or near the hinge, and this constraint is violated if the point of intersection of forces moves in toward or away from the thumb [−1 −1 1]^T direction (Fig. 4, column III). Variability along this dimension is associated with translations and rotations of the grasped object. We say this PC aligns with the Hinge Mode.

Principal Components Associated with Modeled Ideal Performance of Task

The fingertip forces necessary to produce motion of the thumb while maintaining a perfectly constant grasp force create a horizontal line that is slightly curved in force space (Fig. 4, column II), and the family of lines for a variety of grasp force magnitudes creates a slightly curved surface defining all feasible solutions to the task. For this ideal case (simulation 1; see Fig. 3A) the variability in normal forces is associated purely with compensations for movement of the thumb (i.e., Fig. 4, column II, which is seen as traveling back and forth along the thick line as the thumb moves from side to side). The loadings of each PC for this ideal case are shown in Fig. 4, column II, top, and, as expected, the Compensation Mode is the PC that explains >99% of the variance (i.e., [−1 1 0]^T). The small contribution of the hinge constraint mode PC (i.e., [−1 −1 1]^T direction) reflects the slight curvature of the force trajectory in force space. The grasp force mode PC (i.e., [1 1 1]^T direction) shows zero variance in the grasp force by construction (i.e., the ideal task has no variability in grasp force). This result applies equally to all frequency bands.

Summary of Experimental PCA Result and Comparison with Modeled Ideal Performance of Task

Figure 5 summarizes our findings. As expected by the mechanical requirements of the task shown in simulation 1 and Figs. 3 and 4, the Compensation Mode dominates in the original task. But whereas simulation 1 only shows residual levels of the Grasp and Compensation Modes (because of the linear approximation to the slightly curved solution manifold), the performance of the original task by the subjects was accompanied by mechanically unnecessary variability in the form of substantial amounts of the Grasp Mode and small amounts of the Hinge Mode. The control tasks (Table 1) go on to demonstrate that the Grasp Mode strongly pervaded manipulation tasks requiring different fingertip motion and force constraints (Fig. 5 shows only control tasks 1 and 2 for clarity, others are presented below in detail). Only simple static grasp (control tasks 5 and 6) exhibits much small levels of force variability in general. Importantly, these results cannot be explained by signal-dependent noise (simulations 2–4), whether the object is deformable versus rigid (hinge state) or handheld versus attached to ground (object displacement). Taken together, these results demonstrate that stereotypical grasp-and-release synchronous interactions (i.e., Grasp Mode) pervade multifinger manipulation when the manipulation task requires orchestrating individuated fingertip motions and forces, as explained in discussion.

Fig. 5.

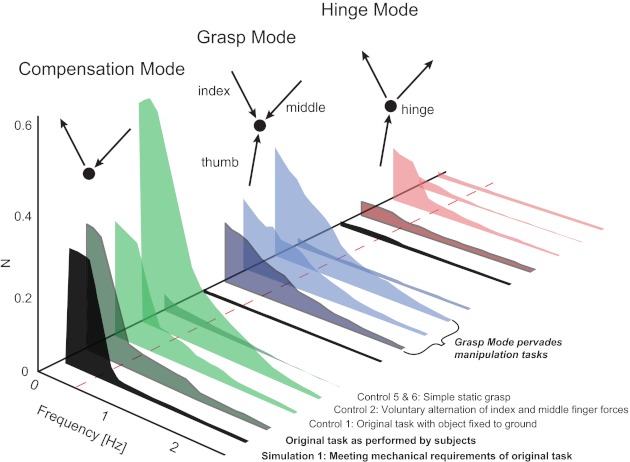
Summary figure showing the normal force variability magnitudes of the 3 force modes (Compensation, Grasp, and Hinge Modes) across the low frequency range, found through principal components analysis (PCA) in the original and control tasks as well as simulation 1. The results are grouped by mode, and in each group the first graph shows the magnitudes found in simulation 1 (noiseless, ideal performance). Note that because of the curvature of the solution manifold (Fig. 3), the Hinge Mode is not exactly zero even in the simulation. Most importantly, the original task and control task 1 both reproduce the expected magnitude of the Compensation Mode, while they exhibit much larger and mechanically unnecessary Grasp Mode magnitude.

Experimental PCA Result and Comparison with Modeled Ideal Performance of Task

We can see from Fig. 6C that, on average, subjects were able to meet the 10 N sum of normal forces requirement, with a standard deviation of 0.5 N. Across the physiologically plausible frequency range for control of force production (Johansson and Birznieks 2004), the modes observed in the experimental data match the theoretical ones quite well: the median angle difference between the experimental and theoretical modes never exceeds 30°, indicating that the simulations predict the structure of variability faithfully (Fig. 6B). Beyond 12 Hz (not shown), and thus at timescales shorter than those of the shortest sensorimotor loops for sensory mediated force production (Johansson and Birznieks 2004), the predicted structure breaks down, i.e., it converges to a purely white noise process in a 3D space, which suggests that the structure of variability is plausibly imposed by the neural drive to alpha motoneuron pools and thus of physiological origin. Figure 6A shows that the magnitude of the Compensation Mode PC is in agreement with that found in the simulated task (Fig. 7). The Compensation Mode dominates the variability below and at the oscillation frequency, and then falls off sharply above. While this is not surprising, since the task determines this magnitude of variability, the magnitudes of the Grasp Mode show a very different picture, compared with simulation 1, the modeled ideal performance of the task. The simulations suggest that there should be no Grasp Mode and very little Hinge Mode variability across the physiologically plausible frequency range. However, near the oscillation frequency, the Grasp Mode in the experimental data explains ∼30% of the overall normal force variance or, alternatively, has a standard deviation of almost 0.2 N. Beyond the task-relevant frequency of 0.5 Hz, the Grasp Mode explains most of the force variance and thus dominates its variability, even though the Compensation Mode magnitude does not fall off as sharply with frequency as in simulation 1. The milder roll-off can be explained by imperfect matching of the task frequency by subjects over the course of an entire 95-s trial. The strong contribution of the Grasp Mode at all frequencies, on the other hand, is plausibly a consequence of neural and biomechanical coupling between the control of forces that compensate for object manipulation and that of forces required to hold it. On the other hand, grasp force variability does not reflect a safety mechanism: at the most critical locations of thumb oscillation, i.e., the turning points, it is not increased compared with the middle points, based on the results of our analysis of computing the variance of a 0.6-s sliding window of the data across every trial (result not shown).

Fig. 6.

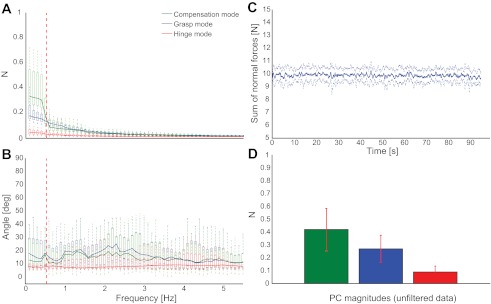
A: measured magnitudes of the 3 principal components (PCs) vs. frequency in the original object manipulation task. Not surprisingly, near the task-relevant frequency of 0.5 Hz (vertical red dashed line), the Compensation Mode dominates the overall force variability, as suggested by simulation 1. However, at those frequencies, subjects exhibit considerable contributions to force variability from the Grasp Mode. Box plots indicate the distribution of these variability contributions across the 7 subjects. B: difference in angle between the directions of the measured and the analytical PCs. Box plots reflect the fact that the 3 normal force correlation modes did not vary much across subjects and were closely aligned with the theoretical correlation modes. Differences across subjects and between observed and theoretical modes mostly indicate the variability of object orientation during task performance. C: average sum of normal forces across the 7 subjects in the original object manipulation task. Subjects were well able to meet the 10 N target. D: 3 force mode magnitudes computed from the unfiltered data (square root of the eigenvalues), showing that, overall, the Compensation Mode contributes most of the force variability and the Hinge Mode contributes the least, reflecting successful task performance. (Note that the values are in Newtons and do not represent proportions of variance. No statistical tests are done on these data because they simply show the total variance across all frequencies.)

Fig. 7.

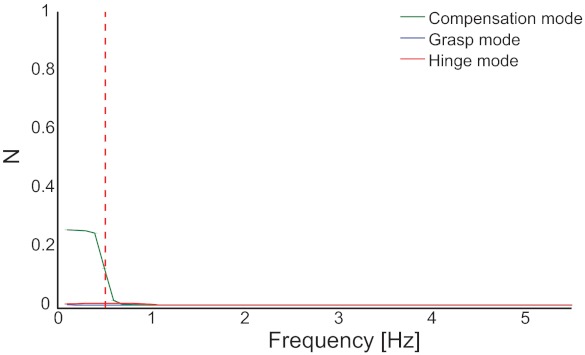
The 3 mode magnitudes vs. frequency in the noiseless simulation of the original task (simulation 1). The Compensation Mode explains almost all the force variability and only near the task frequency of 0.5 Hz (vertical red dashed line). The remaining variability is explained by the Hinge Mode, near the task frequency, which can be attributed to the curvature of the solution manifold (Fig. 3). The Grasp Mode does not contribute to force variability at any frequency.

There are two objections that can be made against the interpretation that the control of force modes is coupled. First, the strong contribution of the Grasp Mode to the overall normal force variability could be attributed to the interplay between mechanics of the task- and signal-dependent noise at the fingertips (Jones et al. 2002), whose magnitude scales with the mean force. According to this objection, noise generated by each of the fingertips will show up as reaction force at the other two fingertips, thus giving rise to positive correlations (theoretically instantaneous but perhaps with small delay due to tissue deformation and compression) across fingertips and thereby causing the Grasp Mode variability observed in the experiments. Second, the large variability along the Grasp Mode direction could be attributed to the visuomotor loop involving the visual feedback, which instructed subjects to generate a constant 10 N sum of normal forces, and subjects' efforts to maintain this force after seeing the visual feedback. The simplest strategy to correct for displayed deviations from the target force is to increase or decrease forces across all fingertips simultaneously, hence in alignment with the observed Grasp Mode. It should be noted, however, that 1) subjects were encouraged to make their best possible effort at maintaining this force and that 2) the visuomotor loop has a defined latency, operates at timescales considerably shorter than that of the thumb oscillation frequency, and, in particular, cannot be expected to be present across the entire range of frequencies. We investigate both of the above objections in the following two paragraphs.

Comparison with modeled imperfect performance and experimentally grounded task.

To address the first objection, we added signal-dependent noise to the simulated forces generated by each fingertip, whose magnitude was proportional to that force (simulation 2). The noise proportionality constant was chosen so that the resulting grasp force mode variability would match experimental observations near the frequency of thumb oscillation, i.e., either the magnitude of the grasp force mode or, instead, the magnitude of the visual feedback error. Since there is no connection between fingertips, neural or mechanical, PCA does not reveal any correlation structure and the sum of normal forces either varies wildly about the 10 N mean or the grasp force mode magnitude is not reproduced (results not shown). This is what we would expect in an experiment in which the device is attached to ground, and all the variability observed was due to signal-dependent noise at the fingertips. As a refinement, we introduced mechanical connection between fingertips and computed and added the reaction forces at the other fingertips (simulation 3). Figure 8A shows that the magnitudes of Compensation and Hinge Modes are unaffected at low frequencies, while the Grasp Mode magnitude is increased and matches the experimental observations. However, its magnitude does not roll off across the entire frequency range, thus differing significantly from the experimental observations. This is not surprising, since we did not band-limit the noise. However, band-limiting the noise in our simulations to the frequency range observed by Jones et al. (2002), i.e., 8–12 Hz, does not reproduce the results either, as the tracking error is still vastly larger than in the original experimental task. On the other hand, matching the noise to the visual feedback error again does not reproduce the grasp force mode magnitude. Most importantly, however, comparing the results of the original task with control task 1 in which the device was attached to ground, we find that the experimental Grasp Mode magnitude is equally large (Fig. 5 and Fig. 9A). This is surprising because the device is attached to ground and correlations across fingertips cannot be explained by mechanical coupling (i.e., force variability and errors are shunted to ground and do not affect the other fingers), and mismatches in forces do not accelerate the object. Moreover, simulation 2 above predicted a complete absence of correlation modes. In summary, these results challenge the alternative interpretation that signal-dependent noise in conjunction with mechanics explains the experimentally observed, yet mechanically unnecessary, Grasp Mode variability.

Fig. 8.

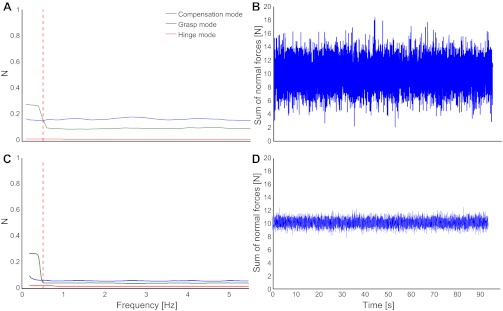
A: simulated magnitudes of the 3 PCs vs. frequency in the original object manipulation task, including signal-dependent noise, whose standard deviation is proportional to the mean force. The proportionality factor was chosen such that the grasp force magnitude at the task frequency of 0.5 Hz (vertical red dashed line) matches that measured in the original task. However, the noise is not band-limited to the low frequencies, since signal-dependent noise is associated with higher-frequency bands, and thus the grasp force mode magnitude is considerably larger than the measured one at all other frequencies. B: the simulation also exhibits much greater variability in terms of the sum of normal forces, making signal-dependent noise an unlikely source of the grasp force variability. C and D: if, on the other hand, the signal-dependent noise magnitude is scaled to the error observed in the sum of normal forces (D), the resultant grasp force magnitude does not match the experimentally observed one (C).

Fig. 9.

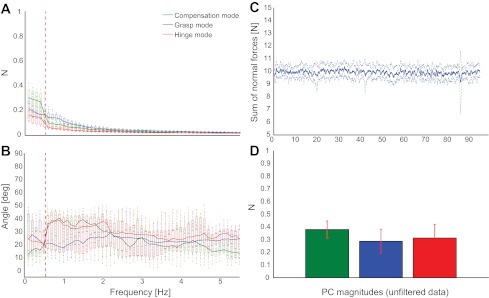
A: measured force mode magnitudes vs. frequency in the original task, in which the device was attached to ground (control task 1). Although the load cells are now mechanically decoupled and thus noise originating at one finger does not get transmitted to the other fingers, and moreover, dropping the device is not a concern, the Grasp Mode contribution in this case is just as strong as in the original task. B: the measured PC directions agree with the theoretical across the frequency range, although to a lesser extent than in the original task. Note, however, that the measured Grasp Mode shows the greatest agreement (vertical red dashed line indicates 0.5-Hz frequency of thumb oscillation). C: average subject performance at maintaining the 10 N target force. D: force variability analysis reveals that even though the object is attached to ground, and safety or signal-dependent noise is not an issue, the grasp force variability is as present as in the original task. Note, however, that the Hinge Mode contributes more strongly, too.

Comparison with simple static hold control tasks.

To investigate the second objection, that Grasp Mode variability is attributable solely to corrections to drifts in the visual feedback, we analyzed the normal force data of control tasks 5 and 6, in which subjects simply held the object statically (did not oscillate the thumb) and only tracked the 10 N sum of normal force visual feedback. As in the other experiments, the three modes of force variability match those predicted by simulation 1, the modeled ideal performance, across the low frequency range (Fig. 10B). Furthermore, while the Compensation Mode is now contributing less to the force variability near the frequency of thumb oscillation, the variability magnitude along the Grasp Mode is also reduced by ∼50%. This can be seen in Fig. 5 and Fig. 10A. Similarly, the standard deviation of the sum of normal forces is reduced by half (Fig. 10C). These results suggest that voluntary (i.e., visuomotor) corrective action does explain some of the variability in the Grasp Mode, since this control task failed to abolish Grasp Mode variability altogether—but a large proportion (as much as 50%) of that variability needs to be attributed to causes other than voluntary modulation of force and the limitations of the visuomotor loop associated with it.

Fig. 10.

A: force mode magnitudes vs. frequency in the simple hold task (control tasks 5 and 6). Although for this task grasp force variability is also unnecessary, we see some contribution to force variability by it. However, it is much smaller than in the original task, indicating that force corrections to the visual feedback are not the sole cause of Grasp Mode contribution. B: the measured modes agree with the hypothesized modes across all frequencies (vertical red dashed line indicates 0.5-Hz frequency of thumb oscillation). C: subject performance at maintaining the 10 N target force in the simple hold task. D: analyzing the unfiltered simple grasp data, we find that the order of force modes in the original task is preserved, but there is much less force variability. The amount of grasp force variability in this task indicates the variability arising from tracking the constant visual feedback.

Comparison with Alternating Index/Middle Finger Normal Force Task

One can argue that cognitive load may explain the higher corrective activity (i.e., dominant Grasp Mode) seen when the thumb is being oscillated, since moving the thumb could consume resources that could otherwise be fully devoted to the maintenance of the task requirements. Using the range of compensation force magnitudes observed in each subject, we asked them to voluntarily generate alternating index and middle finger forces of the same frequency and magnitude, but without oscillating the thumb and while the pads were locked into a rigid object (control task 2). Once again, the experimental force variability structure matches the predictions in terms of the relative magnitudes of force modes' variability (Fig. 11, B and D). Furthermore, we see that despite the absence of any finger motion in this task, the contribution of the Grasp Mode is just as strong as in the original task (Fig. 5, Fig. 11, A and D). Furthermore, the feedback in this control task was based on the alternation of index and middle finger normal forces and no explicit feedback about the force error was presented for the sum of normal forces. Hence, despite the absence of an explicitly enforced requirement on the grasp force, variability along this mode is just as present and thus likely to be linked to the explicitly enforced Compensation Mode requirements.

Fig. 11.

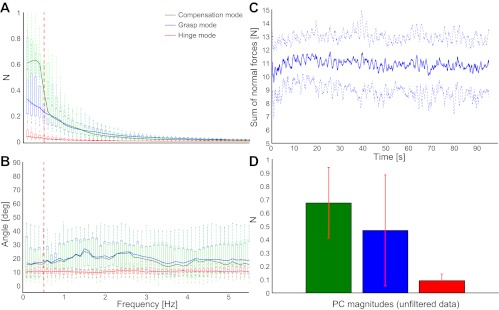
A: force mode magnitudes vs. frequency in the index/middle finger alternating normal force task (control task 2). Since in this task production of alternating index and middle fingers was encouraged, not surprisingly, we see a large contribution from the Compensation Mode. There was no motion component in this task, and yet the grasp force contribution near the task frequency of 0.5 Hz (vertical red dashed line) is quite considerable, too. B: measured force mode directions are in agreement with the simulation directions. C: the visual feedback did not represent the 10 N target force but instead represented the sinusoids that mimicked the thumb force Compensation Mode. Hence, greater error on the target force (which is the sum of the individual normal forces) is to be expected, but also a reduced need to correct via the Grasp Mode. D: while the magnitude of force mode variability computed from the unfiltered data is approximately twice of that observed in the original task, the order of force modes in terms of magnitude and their relative magnitudes is preserved.

Comparison with Voluntarily Oscillated Grasp Force

So far, we have shown that the Grasp Mode is present when performing a voluntary compensatory task. We next used control tasks 3 and 4 to test the inverse, i.e., whether voluntary Grasp Mode produces a corresponding involuntary Compensation Mode. While, for the sake of brevity, we do not show the results here, we find that such coupling is not present. In other words, generating voluntary grasp force does not increase the magnitude of compensation force variability beyond what is seen in static grasp in control tasks 5 and 6 (Fig. 5 and Fig. 10A). This is in contrast to the voluntary production of the Compensation Mode (control task 2, previous paragraph), which even in the absence of thumb motion gives rise to even larger magnitudes of grasp force variability than observed in the original task (Fig. 5 and Fig. 11).

DISCUSSION

While it is clear that the human nervous system has distinct adaptations that enable dexterous manipulation—a functional hallmark of our species—we demonstrate that multifinger manipulation exposes strong limitations even for ordinary and ecological tasks requiring the simultaneous control of individuated finger motion and force, such as unscrewing a bottle cap. We systematically explored the potential confounds that could explain our results of unnecessary grasp-and-release force variability pervading the original task of holding the object while reconfiguring the grasp. Now we discuss why we can now confidently argue that the underlying cause of such pervasive Grasp Mode variability is likely a context-sensitive coupling in the actual drive to the alpha motoneuron pools across fingers. Moreover, our control experiments and numerical simulations, when put in the context of seminal work by human neuroanatomists, help interpret those limitations as consequences of evolutionarily vestigial properties of cortical projections to hand muscles. We speculate that the results reveal strong competition between descending commands to grasp versus manipulate, likely driven by competition between the phylogenetically older reticulospinal and the newer corticospinal tracts. This suggests that, for all its neuro-musculo-skeletal uniqueness and versatility, the healthy human hand critically depends on maintaining a delicate balance between competing descending commands. This may explain the disproportionately severe disruption of manipulation after neurological injury such as stroke, or even with healthy aging.

We begin by emphasizing that holding and reconfiguring our novel hinged apparatus defines an unstable mechanical system that requires the nervous system to generate fingertip force vectors that intersect at or close to the hinge at all times (Flanagan et al. 1999). For a variety of magnitudes of total grasp force, the set of valid combinations of fingertip forces defines a slightly curved manifold (Fig. 3). We provided subjects with visual feedback to produce a constant sum of 10 N of total grasp force while oscillating the thumb.

We studied multifinger interactions in the context of grasp and manipulation. We did not study nongrasp multifinger tasks because others have done so in detail (Latash et al. 2001). They find that the variability during table presses with multiple fingers tends to be appropriately structured to compensate for errors across fingers during nongrasp tasks and does not show a context-dependent pervasive Grasp Mode. Combining their and our results leads us to believe that our findings are likely primarily seen in the context of grasp and manipulation. Moreover, the fact that the pervasiveness of the Grasp Mode arises in the absence of thumb motion (control task 2, Fig. 5 and Fig. 11)—or that it does not increase at the critical turning points of thumb motion—also strongly suggests that the observed behavior is not a direct result of a low-frequency intermittent switching between controlling motion (or posture) and force (Keenan et al. 2009; Kurtzer et al. 2005; Mah and Mussa-Ivaldi 2003). Had such switching mechanisms been the dominant ones, we would have seen the pervasiveness of the Grasp Mode disappear in the control cases where the thumb did not move.

The fact that our analytical model of the task revealed the solutions to be well approximated by a linear manifold (see discussion in Clewley et al. 2008) both justifies and motivates the use of PCA, which in turn allows us to disambiguate mechanically necessary from neurally driven (and mechanically unnecessary) variability in the experimental data (Kutch and Valero-Cuevas 2012; Tresch and Jarc 2009). Variability in the Compensation Mode (PC [−1 1 0]^T in Fig. 4) represents the instructions given to the subjects to oscillate the thumb, which results in compensatory alternating force magnitudes of the index and middle fingers as they maintain equilibrium. It is not surprising, therefore, that this PC explains the greatest variance in the data near the thumb oscillation frequency of 0.5 Hz because it is driven by the mechanical requirements of the task. On the other hand, since the subjects succeeded at the task and did not greatly translate or rotate the object, the data exhibited the lowest variability along the Hinge Mode (PC [−1 −1 1]^T). In fact, the mechanical requirements of the task explain both the low variability in the hinge constraint and the high variability in the Compensation Mode near 0.5 Hz. Had we not modeled the analytical dynamical solution to the task, we might have been tempted to interpret the Compensation Mode force variability as indicative of properties of the neural controller, such as coherence modes in the control of motoneuron pools across fingers, for which there is some evidence (Schieber and Santello 2004; Tresch and Jarc 2009). Contrast this to the Grasp Mode PC [1 1 1]^T, which represents unnecessary grasp-and-release force variability that is not part of the mechanical requirements of the task, which in turn leads to the population of a manifold of mechanically feasible solutions (Fig. 3B). Its lack of mechanical relevance renders the Grasp Mode critically informative of the neural controller's performance and limitations.

Ruling Out Potential Confounds

The additional six systematic control tasks, plus four simulations of mechanically driven correlations between clean and noisy fingertip forces (Table 1), strongly indicate that the variability along the Grasp Mode cannot be attributed to signal-dependent noise and only to a limited extent—if at all—to visuomotor corrective actions along the grasp force direction at low frequencies. That is, 1) signal-dependent noise is associated with a higher frequency band (8–12 Hz; Jones et al. 2002) than that in which we observed large and unnecessary grasp force fluctuations, and 2) control task 1, with the apparatus fixed to ground to abolish—by shunting to ground—any fingertip force correlations arising from reaction forces driven by signal-dependent noise, exhibited the same unnecessary contribution by the Grasp Mode (Fig. 5 and Fig. 9). Therefore, we conclude that signal-dependent noise in conjunction with instantaneous action-reaction mechanics cannot explain this unnecessary variability.

Second, simple static grasp in control tasks 5 and 6, in which a 10 N sum of normal force was to be maintained, exhibits greatly diminished variability along the Grasp Mode direction (Fig. 5 and Fig. 10A). This variability reflects, among other things, the corrective activity in response to visual feedback error. Its small magnitude here suggests that the much stronger presence of Grasp Mode in the original task is not primarily driven by the interaction with visual feedback. Importantly, control tasks 2, 3, and 4, involving voluntary generation of grasp and compensation forces, show that voluntary production of Compensation Mode variability leads to involuntary Grasp Mode variability, but not vice versa. We therefore conclude that the mechanically unnecessary (and potentially counterproductive?) Grasp Mode variability is of involuntary neural origin, and that such stereotypical grasp-and-release synchronous interactions pervade multifinger manipulation when the manipulation task requires individuated fingertip motions and forces.

What could be the causes of this neurally driven, context-sensitive involuntary variability in the Grasp Mode? A behavioral explanation is that subjects may have simply chosen not to track the constant visual feedback despite our encouragement to do so. However, all subjects reported performing the task in all conditions to the best of their ability and satisfaction with using visual feedback to explicitly help them maintain a given grasp force level (recall that we have ruled out visuomotor corrective actions as the main source of the Grasp Mode). Moreover, subjects are familiar with and adept at common motor tasks requiring the reconfiguration of grasp during their daily activities, such as rotating an object in the hand or unscrewing a bottle cap.

Alternatively, one can be tempted to attribute such variability to the principle of minimal intervention, giving rise to an uncontrolled manifold (Scholz and Schöner 1999; Todorov and Jordan 2002). Having dedicated most of its control efforts to meeting the critical constraint of not accelerating or rotating the object (hinge constraint mode PC [−1 −1 1]^T) while also visibly moving the thumb (Compensation Mode PC [−1 1 0]^T), the nervous system may have chosen to assign the regulation of the grasp force PC [1 1 1]^T the lowest priority. After all, increasing total grasp force does not immediately lead to mechanical failure of the task and is a task variable (i.e., constraint) that might be given lower priority (i.e., an “uncontrolled manifold”). However, constant total grasp force is an explicit task constraint that is part of our instructions and visual feedback. In fact, control task 2 shows that Grasp Mode variability does not increase even when it is not an explicit part of the instructions (i.e., demoting the relevance of the Grasp Mode does not increase it). Conversely, control task 1 shows that Grasp Mode variability is not decreased when the object is attached to ground either, even though there is no concern of dropping the object or involuntary slip-grip response. Therefore, the observed Grasp Mode variability arguably does not reflect controller prioritization à la minimal intervention or uncontrolled manifold.

Grasp Mode Variability Reveals Fundamental Challenges to Controlling Dynamic Multifinger Manipulation

This leads to the intriguing third explanation that manipulating an object while dynamically reconfiguring the grasp is challenging enough to expose limitations in the neuromuscular control of multifinger manipulation. That is, when performing certain multifinger tasks requiring individuated finger actions to meet multiple requirements (i.e., maintaining hold of an object while also reconfiguring the grasp), the nervous system is physiologically bound to violate some task constraints. We see this here as a pervasive grasp force variability. This is quite different from choosing to prioritize some task constraints as in the first two explanations above. In fact, this agrees well with other work with single fingers, where even “ordinary” manipulation tasks can push the neuromuscular system to its limit of performance when they require combinations of, or transitions between, motion and force constraints (Keenan et al. 2009; Venkadesan and Valero-Cuevas 2008). Thus we are compelled to conclude that, when manipulating an object with individuated finger actions such as dynamically reconfiguring the grasp, the neural controller must carefully and continuously overlay individuated finger actions over unavoidable and mechanically unnecessary, yet strongly structured, synchronous interactions.

This superposition of the Grasp Mode should not be confused with the notion of functional coupling as in the context of the “principle of superposition” (Gao et al. 2005). In that functional superposition, necessary internal forces (such as the grasp forces) are coupled to manipulation forces (required to accelerate an object) in a simultaneous, appropriate, and intentional fashion. Such coupling is determined by the goals of the task, such as the simultaneous increase of grip and load force to prevent slip, or deceleration forces at the extreme points of an oscillating motion. Here, in contrast, we showed that our multifinger manipulation task is unavoidably accompanied by functionally unnecessary (and even inappropriate) synchrony across fingertip forces. This pervasive synchrony is neither an epiphenomenon of the task nor a desired feature of the task.

In fact, in agreement with Schieber and Santello (2004), who review the literature on peripheral and central limitations of multifinger manipulation, we argue that the nervous system has to superimpose finger individuation over a propensity to modulate fingertip forces in synchrony.

From the mechanical perspective, many extrinsic flexor and extensor muscles are multitendoned or have multiple compartments subject to a certain level of common neural inputs [but the thumb and index finger are largely independent (Brand and Hollister 1999)]. This provides a level of mechanical coupling across fingers—which is mostly known to prevent large individuated finger motions (Agee et al. 1991; Brand and Hollister 1999; Zilber and Oberlin 2004), as reviewed by Schieber and Santello (2004). Our task and control cases were in fact designed to consider these potential confounds by requiring no large or small individuated index and middle finger motions so that their interconnections do not play a dominant role. Their common neural inputs also do not seem to be a confound because, as reported by others (Latash et al. 2001), those common drives are not reported to produce the kind of variability that leads to a pervasive dynamic Grasp Mode in the low frequency range during nongrasp force production tasks. Moreover, we replicate those results in the simple static grasp (control tasks 5 and 6), where pervasiveness of the Grasp Mode is not present. Thus we can conclude that the pervasiveness of the Grasp Mode is strongly contextual to our grasp and manipulation tasks and does not arise primarily from known neuroanatomical interactions among extrinsic finger muscles.

A potential explanation for this is the emerging picture from seminal and recent work (Lang and Schieber 2004; Lawrence and Kuypers 1968; Lemon 2008; for a review, see Baker 2011) on different neural pathways that project on hand motoneuronal pools and segmental interneurons. The divergent projections to flexor muscle motoneuronal pools by the reticulospinal tract seem to be in competition with corticospinal projections (Riddle et al. 2009). A major finding of Riddle et al. (2009) is the existence of the previously unknown, and divergent, excitatory reticulospinal projections to intrinsic hand muscles. Therefore we speculate that the contextual pervasiveness of the Grasp Mode reflects competition between the well-known corticospinal projections necessary for muscle individuation for dexterous manipulation (Baker 2011) and those divergent reticulospinal projections that would prevent muscle individuation. Whether that competition is one based on inhibitory or excitatory mechanisms is unknown. Furthermore, we do not consider the rubrospinal tract in this context because it has been shown to be almost absent in humans (Nathan and Smith 1955). Thus the constant presence of the Grasp Mode perhaps reflects the inability of the (evolutionarily younger?) corticospinal tract to completely override divergent projections from the reticular formation [one of the phylogenetically oldest portions of the human brain (Ranson 1921)]. Thus the strongly structured stereotypical interactions that pervade voluntary dynamic multifinger manipulation may be the modern echoes of an evolutionarily vestigial tendency for grasp so critical to brachiation or early tool use (Baker 2011; Lawrence and Kuypers 1968). As a consequence, the human hand might not have enough neuromechanical, as opposed to strictly mechanical, degrees of freedom to meet both the constraints of grasp (i.e., holding the object steadily against gravity) and manipulation (i.e., reconfiguring the grasp).

This interpretation that, despite its complexity and redundancy, a neuromuscular system can “run out” of neuromechanical degrees of freedom if the task is sufficiently demanding has been proposed elsewhere (see, e.g., Keenan et al. 2009; Kutch and Valero-Cuevas 2011; Loeb 2000; Venkadesan and Valero-Cuevas 2008). That is, despite the evolutionary adaptations and apparent versatility and redundancy of the human hand, our results strongly suggest that it has barely enough neuromechanical degrees of freedom to meet the multiple simultaneous mechanical demands of ecological tasks. This helps explain the apparent paradox (Keenan et al. 2009) that, for all the neuromechanical redundancy of the human hand, multifinger manipulation is susceptible to even mild neurological conditions, takes years to develop in childhood, and degrades in healthy aging.

GRANTS

This material is based upon work supported by National Science Foundation Grant EFRI-COPN 0836042 and National Institute of Arthritis and Musculoskeletal and Skin Diseases Grants AR-050520 and AR-052345 to F. J. Valero-Cuevas.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: K.R., D.B., and F.J.V.-C. conception and design of research; K.R., D.B., and F.J.V.-C. performed experiments; K.R., D.B., and F.J.V.-C. analyzed data; K.R., D.B., and F.J.V.-C. interpreted results of experiments; K.R., D.B., and F.J.V.-C. prepared figures; K.R., D.B., and F.J.V.-C. drafted manuscript; K.R., D.B., and F.J.V.-C. edited and revised manuscript; K.R., D.B., and F.J.V.-C. approved final version of manuscript.