Sensitivity of cochlear nucleus neurons to spatio-temporal changes in auditory nerve activity

Abstract

The spatio-temporal pattern of auditory nerve (AN) activity, representing the relative timing of spikes across the tonotopic axis, contains cues to perceptual features of sounds such as pitch, loudness, timbre, and spatial location. These spatio-temporal cues may be extracted by neurons in the cochlear nucleus (CN) that are sensitive to relative timing of inputs from AN fibers innervating different cochlear regions. One possible mechanism for this extraction is “cross-frequency” coincidence detection (CD), in which a central neuron converts the degree of coincidence across the tonotopic axis into a rate code by preferentially firing when its AN inputs discharge in synchrony. We used Huffman stimuli (Carney LH. J Neurophysiol 64: 437–456, 1990), which have a flat power spectrum but differ in their phase spectra, to systematically manipulate relative timing of spikes across tonotopically neighboring AN fibers without changing overall firing rates. We compared responses of CN units to Huffman stimuli with responses of model CD cells operating on spatio-temporal patterns of AN activity derived from measured responses of AN fibers with the principle of cochlear scaling invariance. We used the maximum likelihood method to determine the CD model cell parameters most likely to produce the measured CN unit responses, and thereby could distinguish units behaving like cross-frequency CD cells from those consistent with same-frequency CD (in which all inputs would originate from the same tonotopic location). We find that certain CN unit types, especially those associated with globular bushy cells, have responses consistent with cross-frequency CD cells. A possible functional role of a cross-frequency CD mechanism in these CN units is to increase the dynamic range of binaural neurons that process cues for sound localization.

the spatio-temporal pattern of auditory nerve (AN) activity, i.e., the relative timing of spikes across the tonotopic axis, provides cues to important features in sounds. In particular, the cochlear traveling wave generates spatio-temporal cues to the pitch of harmonic complex tones that are more consistent with psychophysical observations than traditional rate-place and temporal representations of pitch (Cedolin and Delgutte 2010; Shamma 1985). Local spatio-temporal features of AN activity may also play a role in loudness (Carney 1994), timbre (Patterson and Green 1970), masking (Carlyon and Datta 1997; Kohlrausch and Sander 1995), and detection of interaural time differences (Day and Semple 2011; Shamma et al. 1989), even when the distribution of average firing rates along the tonotopic axis contains little information.

In principle, these spatio-temporal cues could be extracted centrally by a mechanism that is sensitive to the relative timing of spikes across AN fibers tuned to different characteristic frequencies (CFs). One way to extract these cues is a network of “cross-frequency” coincidence detector (CD) cells, which would increase their firing rates when their AN fiber inputs with different CFs fire in synchrony. Our goal is to evaluate whether cochlear nucleus (CN) neurons implement a cross-frequency CD mechanism by examining their responses to stimulus manipulations that alter the AN spatio-temporal response pattern without changing overall firing rates.

Anatomical evidence indicates that most types of cells in the CN receive inputs from multiple AN fibers. Estimates for the number of afferent inputs for CN cells range from one to hundreds, depending on the cell type (Cant and Morest 1979; Liberman 1993; Spirou et al. 2005). Less is known about the range of tonotopic locations of the input AN fibers and their relationship to the CF of the CN cell. The dendrites of octopus cells run orthogonal to iso-frequency surfaces, suggesting that these cells may perform cross-frequency processing (McGinley et al. 2012; Oertel et al. 2000). On the other hand, Young and Sachs (2008), using spike-train correlations to identify functional AN inputs to CN cells, find that the CFs of chopper and primary-like neurons in the ventral CN do not differ from the CF of their presumed AN inputs by more than one-quarter octave, which would limit opportunities for cross-frequency CD. There is nevertheless indirect physiological evidence for coincidence detection (CD) in the ventral CN based on enhanced onset responses and enhanced phase locking to pure tones (Joris et al. 1994a, 1994b; Joris and Smith 2008; Kalluri and Delgutte 2003a, 2003b; Rothman et al. 1993). However, to our knowledge, there has not been a systematic physiological effort to identify the CF range of AN inputs for CN units that appear to perform CD.

The most direct attempt to assess sensitivity of CN cells to local changes in the spatio-temporal pattern of AN activity (Carney 1990) used “Huffman stimuli” (Huffman 1962; Patterson and Green 1970; Patterson et al. 1969). Because these stimuli have a flat power spectrum, they excite all cochlear regions with nearly the same energy while allowing for control of the frequency and bandwidth of a 2π transition in the phase spectrum. In principle, varying the bandwidth of this phase transition should elicit systematic changes in the AN spatio-temporal pattern for CFs near the phase transition frequency, with minimum changes in overall firing rates. Using Huffman stimuli, Carney (1990) found that some CN units (in particular those corresponding to globular bushy cells) are sensitive to local changes in the spatio-temporal pattern of AN activity. The sensitive neurons typically showed an overall rate preference for Huffman stimuli with a gradual phase transition over stimuli with a sharp transition at low stimulus levels. Because Huffman stimuli with a broad phase transition have less cross-frequency dispersion in group delays than sharp-transition stimuli, Carney (1990) interpreted this preference as evidence for a cross-frequency CD mechanism.

The present paper extends Carney's work by directly and rigorously testing whether a cross-frequency CD mechanism occurs in some CN units. To do so, we compare responses of CN units to Huffman stimuli with responses of model CD cells operating on spatio-temporal patterns of AN activity. We use a quantitative method to determine the CD model cell parameters (such as the CF range of AN inputs) most likely to produce the measured CN unit responses. We show that the overall rate difference between responses to Huffman stimuli with sharp versus broad phase transitions used by Carney (1990) is not a reliable indicator of cross-frequency CD, even at low stimulus levels. We instead base our identification of CD behavior on a set of metrics characterizing both rate and temporal aspects of responses; these metrics were motivated by a detailed analysis of the spatio-temporal pattern of AN responses to Huffman stimuli. We also make more complete use of the systematic changes in these metrics over a wide range of stimulus levels to identify responses that are consistent with cross-frequency CD behavior. Like Carney (1990), we find that certain CN unit types, especially those associated with globular bushy cells, behave like cross-frequency CD cells. We specifically provide evidence that the responses of these cells are not produced by a “same-frequency” CD model in which all inputs would have the same CF, thereby providing strong evidence for cross-frequency CD in the CN.

METHODS

Neurophysiology

All surgical and experimental procedures for recording from single units in the AN and CN were approved by the Animal Care and Use Committees of both the Massachusetts Eye and Ear Infirmary and the Massachusetts Institute of Technology. Surgery and preparation were similar to those described by Cedolin and Delgutte (2010). Cats were anesthetized with either diallyl-barbituric acid (75 mg/kg) or Nembutal (37.5 mg/kg) mixed with urethane (100 mg/kg), with supplementary doses given to maintain an areflexic state. After removal of the posterior portion of the skull, the cerebellum was either retracted to expose the AN or partially aspirated to expose the surface of the dorsal CN and the posterior portion of the antero-ventral CN. The tympanic bullae and middle ear cavities were opened to expose the round window. Throughout the experiment the cat was given injections of dexamethasone (0.26 mg/kg im every 4 h) to prevent brain swelling and Ringer solution (50 ml/day iv) to prevent dehydration.

The cat was placed on a vibration-isolated table in an electrically shielded, sound-proof chamber. A silver electrode was positioned near the round window to record the AN compound action potential (CAP) in response to click stimuli in order to assess the condition and stability of cochlear function. The experiment was terminated if the CAP click-evoked threshold increased by >10 dB from its initial value (typically ∼40 dB peak SPL).

Sound was delivered to the cat's ear through a closed acoustic assembly driven by an electrodynamic speaker (Realistic 40-1377). The acoustic system was calibrated to allow accurate control over the sound pressure level and waveform at the tympanic membrane. Stimuli were generated by a 24-bit digital-to-analog converter using sampling rates of either 20 kHz (Huffman stimuli) or 100 kHz (pure tones). Stimuli were digitally filtered to equalize the transfer characteristics of the acoustic system.

Action potentials were recorded with glass micropipettes filled with 2 M KCl for AN experiments and parylene-insulated tungsten electrodes for CN experiments. The electrode was inserted posterodorsally to anteroventrally into the CN (and slightly laterally into the AN) at an angle of 45° from the coronal plane and mechanically advanced with a micropositioner (Kopf 650). For CN experiments, the electrode was typically aimed for the antero-ventral CN directly, although sometimes it was necessary to first traverse parts of the dorsal CN. The electrode signal was band-pass filtered (1–3 kHz) and input to a software spike detector triggering on level crossings. Detected spike times were saved for off-line processing.

A click at ∼60 dB peak SPL was used to search for single AN units, and wideband noise at 75 dB SPL was used to search for CN units. Once a unit was isolated, its frequency tuning curve was measured by a tracking algorithm (Kiang et al. 1970) to determine the CF and the threshold at CF. The neuron's spontaneous activity was then measured over 20 s. For CN units, the response to tone bursts at CF with 30-ms duration was measured as a function of stimulus level. The CN unit type was determined according to established classification methods (Blackburn and Sachs 1989; Bourk 1976; Young et al. 1988) based on tone-burst poststimulus time histograms (PSTHs), first-order interspike interval (ISI) histograms, regularity analysis (using the coefficient of variation of the ISI), and first spike latency. The responses to Huffman stimuli were then studied in detail.

Stimulation Paradigms

“Huffman sequences” (Huffman 1962; Carlyon and Shamma 2003; Patterson and Green 1970) have a flat magnitude spectrum and a 2π phase transition centered at a transition frequency FT (Fig. 1A). They are completely characterized by two parameters: FT and r. The parameter r is bounded between 0 and 1 and is inversely related to the phase transition bandwidth. An r close to 1 results in a sharp phase transition and a long group delay. This is illustrated in Fig. 1A, which shows the magnitude and phase spectra and temporal waveforms of Huffman stimuli with FT at 1 kHz for a 20-kHz sampling rate. The stimulus with a greater r (0.95) has a sharper phase transition than the stimulus with a smaller r (0.85). Over the range of FT investigated, the −π/2 to −3π/2 phase transition bandwidths are 1,017 Hz for r = 0.85 and 326 Hz for r = 0.95 when the sampling rate FS is 20 kHz. In contrast, Carney (1990) used lower sampling rates (6–10 kHz) and also covaried FS and FT to keep the number of samples in each waveform fixed at 100. As a result, Carney's stimuli had smaller transition bandwidths than ours for a given r: 503 Hz vs. 1,017 Hz for r = 0.85 and 161 Hz vs. 326 Hz for r = 0.95, with FS = 10 kHz and 20 kHz, respectively. To allow a direct comparison, we determined the r values that match Carney's phase transition bandwidths for FS = 20 kHz (r = 0.92 and 0.98) and studied a subset of AN fibers with these matched-bandwidth stimuli. We return to this point in discussion.

Fig. 1.

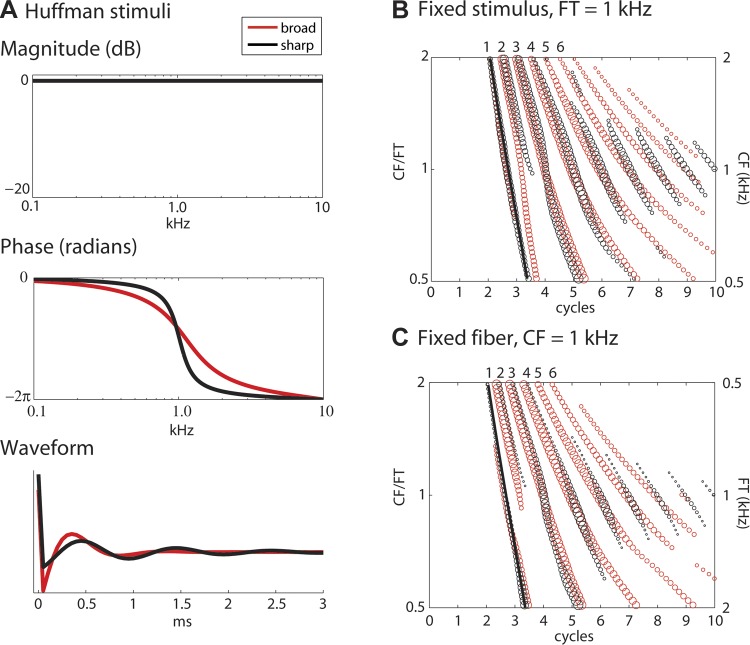
Huffman sequences and auditory nerve (AN) model response patterns. A: waveforms and magnitude and phase spectra of 2 Huffman sequences with transition frequency (FT) 1,000 Hz and r values 0.85 (“broad phase transition,” red) and 0.95 (“sharp phase transition,” black). The phase spectrum shows a 2π phase transition centered at FT whose bandwidth is controlled by the parameter r. B: spatio-temporal response pattern of a tonotopic array of model AN fibers (Zilany and Bruce 2006) to the 2 Huffman stimuli in A at 36 dB SPL. Local maxima of the response pattern are shown by circles, with the relative area of each circle indicating the height of the corresponding response peak. The y-axis represents characteristic frequency (CF) and is shown both in kHz (right) and in normalized frequency units CF/FT (left). The x-axis represents time in cycles of FT. The black line is the delay of the cochlear traveling wave estimated from the first peak in model responses to 0.1-ms clicks at 50 dB peak SPL. C: responses of a single model fiber with CF 1 kHz to Huffman stimuli with varying FT (right y-axis). The range of FT was chosen to obtain the same range of normalized frequencies CF/FT as in B (left y-axis).

Our Huffman stimuli decayed to nearly zero within a few milliseconds, but at least a 30-ms interstimulus interval was used to ensure recovery of responses to successive stimuli. Stimulus level is defined as the r.m.s. sound pressure over a 3-ms interval (expressed in dB re. 20 μPa). This 3-ms interval included at least 99% of the energy in the stimulus waveform for all Huffman stimuli. Carney (1990) instead defined stimulus level for Huffman stimuli by reference to the peak amplitude expressed in dB SPL, with the consequence that the energy in her stimuli was dependent on r. Thus Carney's stimulus levels are 11.9 dB lower than ours for the broad-transition stimulus (r = 0.85) and 13.9 dB lower for the sharp-transition stimulus (r = 0.95). When the different conventions are taken into account, the stimulus levels used in this study are very comparable to those used by Carney (1990).

For neurons with low spontaneous firing rates, the threshold for Huffman stimuli was found by listening for an audible response just above spontaneous activity from the electrode signal. For neurons with high spontaneous rates, responses to Huffman stimuli were sometimes measured as a function of stimulus level to find the lowest, “threshold” level where the peak response was at least 5 standard deviations above the mean background activity measured over the last 10 ms of each interstimulus interval. Huffman threshold levels for AN fibers ranged from −4 to 66 dB SPL, with a median of 26 dB SPL and an interquartile range of 16–39 dB SPL. Thresholds for CN cells were somewhat higher, ranging from 16 to 71 dB SPL, with a median of 46 dB SPL and an interquartile range of 34–56 dB SPL.

Once the threshold was determined, responses of AN fibers and CN units to Huffman stimuli were studied as a function of stimulus level and the bandwidth parameter r (see details below). The stimulus level was initially set near threshold and then increased in 10- or 15-dB increments; at least three stimulus levels were tested for each neuron. In 44 AN fibers, responses were additionally measured over a one-octave range of FT centered at the CF in 1/6th octave steps. Level, and when applicable FT, was interleaved randomly across trials to minimize any effect of stimulus order on neural responses.

For detailed study of the effect of r on responses to Huffman stimuli, each 300-ms stimulus trial consisted of a sequence of either 6 Huffman stimuli (3 ascending and 3 descending r values: 0.85, 0.9, 0.95, 0.95, 0.9, and 0.85) with 50-ms interstimulus intervals or 10 stimuli (r = 0.85, 0.9, 0.92, 0.95, 0.98, 0.98, 0.95, 0.92, 0.9, 0.85) with 30-ms interstimulus intervals. This was done to minimize any possible effect of the order in which the stimuli were presented. Since we observed no systematic differences between the ascending and descending parts of the sequence, spike data obtained with the same r from both parts were combined. Responses to these sequences were recorded for at least 100 trials (and typically between 200 and 300 trials) with no interruption. In the following, we only describe responses to the two stimuli with r = 0.85 and 0.95. Responses to stimuli with intermediate r fell in between these two cases.

AN Model

To guide the interpretation of the physiological AN responses, we used one of the latest in an evolving family of computational models of the auditory periphery (Bruce et al. 2003; Carney 1993; Carney and Yin 1988; Zhang et al. 2001; Zilany and Bruce 2006, 2007; Zilany et al. 2009) that have been shown to be consistent with a wide range of AN data in the cat. The model (Zilany and Bruce 2006) takes as input an arbitrary stimulus waveform and outputs either spike times or firing probabilities for AN fibers with arbitrarily chosen CFs. The model consists of a middle ear filter followed by three signal paths representing cochlear processing (Fig. 1 in Zilany and Bruce 2006). One path represents the low-level, sharply tuned processing through inner hair cells. The gain and bandwidth of this first path are controlled by a second path representing active cochlear processes in outer hair cells. A third path, out of phase with the first path, represents the broadly tuned inner hair cell response obtained at high sound levels. The summed outputs of the first and third paths are then processed through a model for the inner hair cell ribbon synapse followed by a spike generator.

Cochlear Scaling Invariance

To physiologically measure the spatio-temporal response pattern to Huffman stimuli across the tonotopic array of AN fibers would be experimentally challenging because it would require a fine and uniform sampling from AN fibers with differing CF. To get around this challenge, we applied the principle of local scaling invariance in cochlear mechanics (Zweig 1976), which has previously been used similarly in studies of the neural coding of pitch (Cedolin and Delgutte 2010; Larsen et al. 2008). In a completely scaling-invariant cochlea, the basilar membrane impulse response h(t,CF) at location CF and time t is the same as $h\left(t\beta ,\frac{CF}{\beta }\right)$, where β is an arbitrary scalar. This means that the impulse response at location CF is a time-scaled (by β) version of the response at a different cochlear location $\frac{CF}{\beta }$.

To illustrate how scaling invariance is used, we define β as the ratio of the fiber CF to the transition frequency FT of a Huffman stimulus. It then follows that the basilar membrane response at the cochlear location tuned to CF is a scaled (in time by β) version of the basilar membrane response at the location tuned to FT. Therefore, scaling the Huffman stimulus waveform in time so as to vary FT while recording the responses from a fixed location allows us to infer the responses of different cochlear locations to a fixed Huffman stimulus having its transition frequency at the CF of the recording site. Importantly, scaling invariance only holds locally (Shera and Guinan 2003; van der Heijden and Joris 2006), so FT must be near CF for this method to be valid.

To scale the Huffman stimuli in time, both FT and r (which sets the decay of the stimulus envelope) should be covaried. For simplicity we only varied FT, while keeping r fixed in our recordings from AN fibers. We used the AN model to address differences in the two scaling methods. Figure 1B shows the peak locations in the spatio-temporal response pattern of a tonotopic array of AN model fibers responding to a pair of Huffman stimuli with fixed FT of 1 kHz and r values of 0.85 and 0.95, respectively. Figure 1C shows the responses of a single model fiber with CF of 1 kHz to a set of Huffman stimuli with varying FT, and with the same two r values as in Fig. 1B. The vertical axes have been chosen such that the normalized frequencies CF/FT are the same in Fig. 1, B and C, and the horizontal axes are in units of cycles of FT. We use the term “virtual” spatio-temporal response pattern to refer to scaled responses to varying FT stimuli as in Fig. 1C. The patterns shown in Fig. 1, B and C, are very similar, consistent with cochlear scaling invariance.

To quantify the similarity between virtual and actual model spatio-temporal response patterns, we computed the correlation coefficients between the two over a certain range of CF/FT. When scaling invariance was rigorously applied (by covarying r and FT, not shown), the correlation coefficients were somewhat higher (ranging between 0.97 and 0.99) than when only FT was varied (ranging between 0.94 and 0.99). The correlations were lower when a wider range of normalized frequencies was included (up to 1 octave tested), consistent with the notion that scaling invariance is local. The correlations between the patterns for both methods of scaling were very high over the frequency range considered, supporting the use of scaling invariance in our experiments.

AN Data Analysis

We used cochlear scaling invariance to create virtual spatio-temporal patterns of AN activity from the responses of a single fiber to a set of Huffman stimuli with FT varying over approximately one octave centered at the CF (Fig. 2, B and E). We first constructed a PSTH for each FT with bin width 1/25 cycle of FT, and then aligned all the PSTHs on a normalized timescale representing cycles of FT. Figure 2, B and E, show virtual spatio-temporal response patterns obtained from an AN fiber (CF = 972 Hz) in response to a set of Huffman stimuli with {FT} ranging from 645 to 1,448 Hz. Using scaling invariance, we infer that these patterns correspond to the responses to a stimulus with fixed FT_virt = 972 Hz of a set of fibers with virtual CFs {CF_virt} matching the ratios CF/FT in the data: {CF_virt} = CF²/{FT}, i.e., 652–1,465 Hz.

Fig. 2.

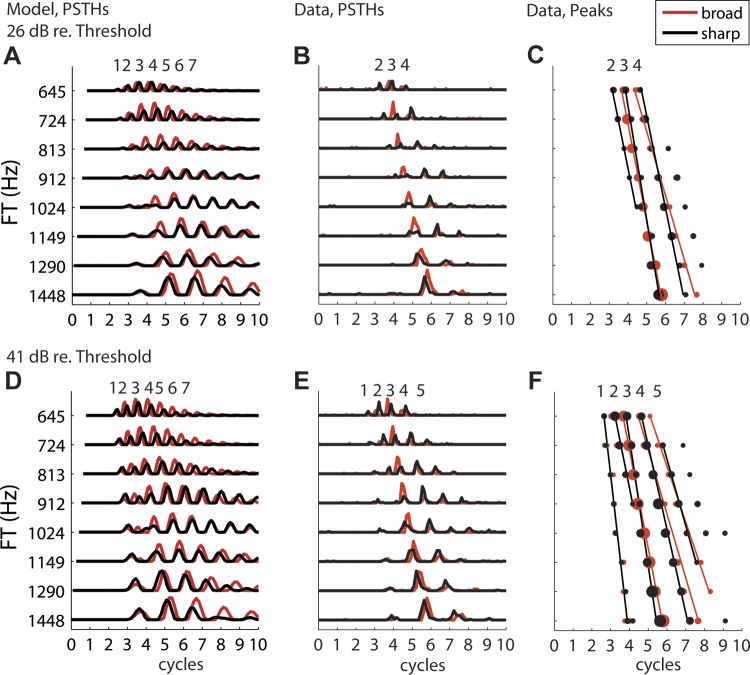
Response patterns of real and model AN fibers with CF 972 Hz to Huffman stimuli with varying FT on the y-axis and time in cycles of FT on the x-axis: responses to stimulus with broad phase transition in red and sharp phase transition in black. A: model fiber response poststimulus time histograms (PSTHs) at 26 dB re. CF tone threshold (41 dB SPL). B: real fiber response PSTHs at 26 dB re. CF threshold (61 dB SPL). C: peak locations and fitted lines for AN fiber response in B. D–F: same as A–C at 41 dB re. CF threshold (56 dB SPL for model fiber, 76 dB SPL for real fiber).

The cochlear traveling wave creates CF-dependent delays, here defined as the time to the first peak in the AN model response to a 0.1-ms condensation click at 50 dB peak SPL. To take these delays into account when generating virtual spatio-temporal patterns, the cochlear delay corresponding to the fiber's CF (972 Hz in Fig. 2) was first subtracted from the Huffman PSTH for each FT, and then the cochlear delays appropriate for each virtual CF were added back.

To visualize essential features in the virtual spatio-temporal patterns, response peaks were found by detecting all local maxima in the PSTH that exceeded 5 standard deviations above baseline activity measured over the last 10 ms of each interstimulus interval (long after the response had decayed). The peak times are plotted against FT in Fig. 2, C and F. Peaks were grouped together into sets across virtual CFs based on a matching algorithm that finds the best alignment, accounting for temporal offsets and warping. Specifically, for each pair of adjacent virtual CFs, the peak times for one were held fixed while the peak times for the other were iterated over to find the closest (in time) matching pairs. This process was repeated until all adjacent pairs were aligned, and peaks were grouped into sets across virtual CFs. Peak sets were discarded if they contained fewer than three peaks, or if there was no peak in the set when FT = CF. For each peak set, line segments (at most 3) were fit to the peak locations by the least-squares method. The slopes of these line segments (in normalized frequency/time units) quantify the degree of coincidence across virtual CFs that each stimulus elicited. The slopes were then compared for different r to evaluate the relative degree of coincidence for each phase transition width (see Fig. 4).

Fig. 4.

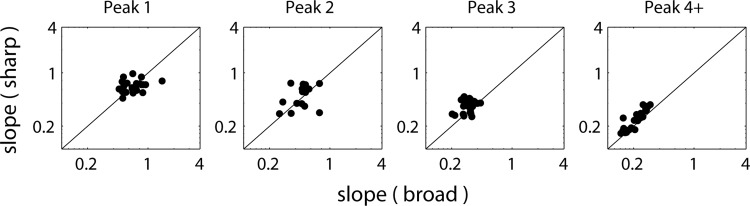
Scatterplots of absolute slopes of fitted lines to sets of response peaks for sharp-transition stimulus against slopes for broad-transition stimulus across sample of AN fibers. Slopes for peaks 1, 2, 3, and 4+ (4 and higher) are shown in separate panels. Slopes were measured from AN fibers responding to varying FT stimuli as in Fig. 2 and are expressed as frequency ratios (CF/FT) divided by normalized time in cycles of FT. Peak numbers are evaluated by reference to the closest model peak.

Coincidence Detector Model Cells

Our goal was to identify likely cross-frequency CD cells by comparing responses of CN neurons to Huffman stimuli with those of CD models receiving inputs from AN fibers with different CFs. Ideally, the CD model cells would operate on true spatio-temporal patterns (across CF) of AN activity. As stated above, this would be experimentally difficult because of the need for a fine, regular sampling of CF and because of variability in response properties across animals and across fibers in each animal. Alternatively, the CD model cells could operate on spatio-temporal activity patterns produced by the AN model. We also rejected this approach because there were substantial differences between responses of AN fibers and those of the model to Huffman stimuli (Fig. 2). Instead, we simulated responses of CD model cells operating on virtual spatio-temporal patterns (across FT) of real AN fibers, including the cochlear traveling wave delays introduced as described above. We interpret the responses of these CD model cells to be equivalent to those operating on true spatio-temporal patterns of AN activity (see discussion).

We used an analytical point process model of neural CD cells (Krips and Furst 2009) to compute the responses of neurons that receive inputs from several AN fibers. This model provides a convenient framework for studying responses of CD cells because, rather than using spike times (which can be computationally slow), the model analytically derives the instantaneous firing rate of the CD cell from the instantaneous rates of its inputs (estimated from measured PSTHs). The model CD cell receives excitatory inputs from a total of N virtual AN fibers, whose CFs are distributed uniformly over a range of w octaves. The cell produces a spike when at least L out of its N inputs discharge within a coincidence window of 0.1 ms. The three parameters N, L, and w completely characterize the CD cell model.

The CD cell parameters were systematically varied to determine which parameter sets produce responses most resembling those measured from CN neurons. N was restricted to 4, 10, or 16 because obtaining responses for larger values of N became computationally prohibitive. To determine realistic values of L and w for each N, frequency tuning curves were measured from CD cells receiving inputs from model AN fibers (Zilany and Bruce 2006), using the same automatic tracking algorithm used in the experiments. When the CD parameters were too strict (if L or w were too large), the CD cell was unresponsive to the 100-ms tone bursts at any level. Table 1 shows the range of w for different values of N and L for which the model cells had a reasonable tuning curve with thresholds at CF below 50 dB SPL. These parameters were used in the CD models. The frequency range of AN inputs w was limited to no more than 1 octave because that is the range over which FT of Huffman stimuli was varied in the experiments, and therefore the range of available virtual CFs.

Table 1.

Maximum CF range of inputs for CD model cells to have realistic tuning curves

	N = 4	N = 10	N =16
L = 2	1	1	1
L = 3	0.25	1	1
L = 4	X	0.5	1
L = 5	X	0.25	0.5
L = 6	X	X	0.1

Values are maximum characteristic frequency (CF) range of inputs (w, in octaves). CD, coincidence detector; N, no. of inputs; L, no. of inputs discharging.

Interpolating Responses Across FT

In implementing the CD cell models, it was necessary to sample the virtual CF axis of the AN inputs with fine resolution. The 1/6th octave sampling of FT used in the AN recordings was not always adequate for this purpose, especially for large N. We therefore used dynamic time warping to interpolate between responses to each pair of consecutive FTs to obtain responses at a finer sampling of FT (1/36th octave).

The dynamic time warping algorithm (Sakoe and Chiba 1978) begins by taking the distance (absolute difference) between each time point in a first signal and each point in a second signal, generating a two-dimensional matrix of distances. Here the two signals are the time-scaled PSTHs for two FTs separated by 1/6th octave. Starting at the bottom left corner (the first time sample in both signals) and ending at the top right (the last sample in both signals), the optimal path is traced by iteratively choosing the mapping with the lowest cumulative distance. The result is a nonlinear mapping in time between the two signals. To interpolate responses, we assume that both the mapping generated by the dynamic time warping algorithm and the response amplitudes depend logarithmically on FT (or, equivalently, the virtual CF). Specifically, for each pair of measured FT, the algorithm maps each time t_l in the response to the lower FT to a time t_h in the response to the higher FT. To interpolate, for example, the response to an FT halfway between the two FT (on a logarithmic scale), the response amplitude at time $\frac{t_l+t_h}{2}$ is set to the average of the response to the lower FT at t_l and the response to the higher FT at t_h. In most cases, the interpolation algorithm generates response patterns that change smoothly with FT, such that line segments could readily be fit to sets of peaks across FT with small residual error. See Fig. 5, A and C, for two examples of interpolated virtual spatio-temporal patterns obtained by dynamic time warping from PSTHs of an AN fiber for Huffman stimuli. The patterns vary smoothly with FT and show no discontinuities at the FT values where responses were actually measured.

Fig. 5.

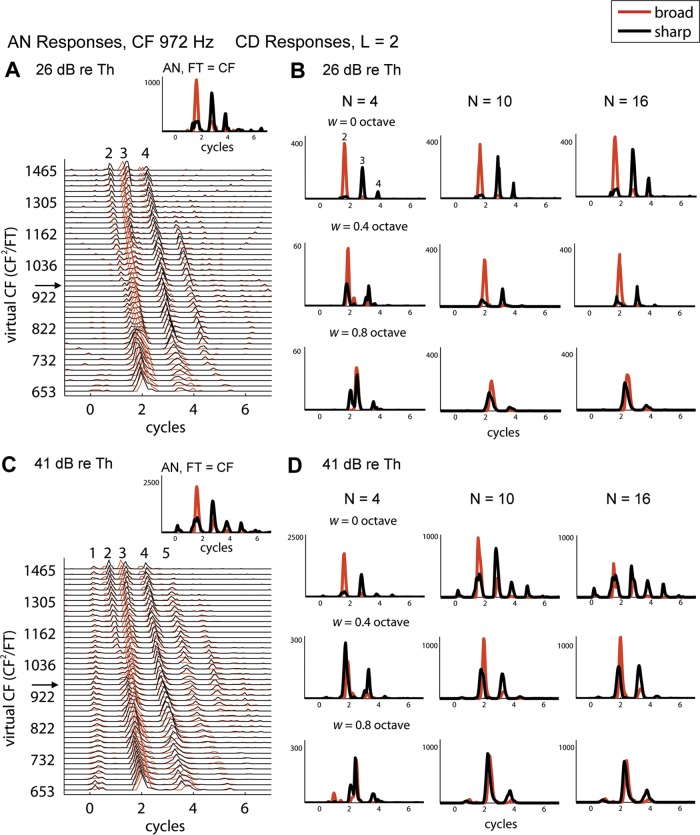
Responses of AN fiber and model coincidence detector (CD) cells to Huffman stimuli with broad (red) and sharp (black) phase transitions. A, inset shows responses (spikes/s) of the 972-Hz AN fiber when FT = CF (same fiber as in Fig. 2). Main panel shows interpolated AN response patterns in fine steps of virtual CF on the y-axis (arrow points to the pattern shown in inset). Stimulus level is 26 dB re. CF tone threshold (61 dB SPL). B: responses of model CD cells with N = 4 (left), 10 (center), and 16 (right) inputs taken from the AN response pattern in A. The output cell produces a spike if at least L = 2 of its inputs fire within a 0.1-ms coincidence window. Responses are shown for model cells with different CF ranges of inputs: w = 0 (same-frequency CD, top), 0.4 (midrange CD, middle), and 0.8 (wide-range CD, bottom) octaves. y-Axes are in spikes/s. C and D: same as in A and B but for 41 dB re. CF tone threshold (76 dB SPL).

Quantifying Sensitivity to Phase Transition and Temporal Characteristics

We used a maximum likelihood approach to quantitatively assess the similarity between responses of CN neurons to Huffman stimuli and responses of CD model cells, including AN fibers. (An AN fiber is equivalent to a CD cell with N = L = 1.) The maximum likelihood method is described in detail in the appendix. The likelihood maximization is done for six response metrics chosen because of their sensitivity to CD cell parameters. Specifically, we use two rate difference (RD) metrics to quantify sensitivity to phase transition bandwidth for the early and late (defined below) portions of the response and two metrics that quantify temporal characteristics (normalized duration ND and peak width PW) for each transition width, giving the following set: RD_Early, RD_Late, ND_Broad, ND_Sharp, PW_Broad, and PW_Sharp.

Carney (1990) used the overall rate difference in spikes per second between the broad- and sharp-transition stimuli to quantify sensitivity to phase transition bandwidth. To factor out differences in firing rates across units, we normalize this rate difference by the rate sum to get a dimensionless metric $RD=\frac{r_{broad}-r_{sharp}}{r_{broad}+r_{sharp}}$. In addition, it proved necessary to separate early and late portions of responses because these two components behaved differently as a function of FT. We defined the border between early and late responses to be halfway between peaks 3 and 4 in AN responses. This border varies with CF and occurs around 1.5–2 CF cycles after the cochlear delay. Since the CD model introduces no additional delay, the same early-late border was used for CD cells. CN neurons have longer and more variable latencies than AN fibers, making it difficult to determine which CN response peaks correspond to the early part of AN responses and which correspond to the late response. We found that, on average, 25% of the spikes in the CD models occurred before the early-late border as defined above. Thus the early-late border in individual CN responses was set at the peristimulus time when 25% of the spikes have occurred.

While RD_Early and RD_Late quantify preference for phase transition width and thus sensitivity to the AN spatio-temporal pattern, there is additional information in the responses not captured by these two metrics. Specifically, temporal characteristics of the responses change systematically as parameters of the CD model are varied. At one extreme, a CD cell with strict requirements (if L = N) performs a multiplication of the instantaneous firing rates of its inputs, resulting in temporally sharpened response patterns relative to those of AN fibers. Therefore, we expected responses of CD cells with strict parameters to have shorter overall duration and narrower peaks than those of AN responses. At another extreme, if the requirements for the CD cell to fire are lenient (L ⪡ N), the cell behaves as if it were summing the instantaneous firing rates of its inputs, resulting in a longer response duration and wider peaks if the inputs are not temporally aligned. Thus evaluating the temporal characteristics of CN responses should provide insight into whether a CN unit performs an operation similar to coincidence detection, and the CD parameters that characterize that operation.

The normalized duration (ND, in cycles of FT) of each response PSTH was measured by taking the distance from the first time bin to the last time bin in which the response exceeded an amplitude threshold (5 standard deviations above baseline activity). Peak width (PW) was measured by taking the width (in cycles of FT) of each response peak, measured by the time interval centered at the peak that exceeded threshold. PW was then averaged over all response peaks to obtain a single metric.

RESULTS

Model AN Fiber Responses to Huffman Stimuli

We used a peripheral auditory model (Zilany and Bruce 2006) to simulate the discharge patterns of a tonotopic array of AN fibers in response to Huffman stimuli in order to determine how manipulation of the phase transition bandwidth alters these spatio-temporal patterns. To help visualize changes in the spatio-temporal patterns, the response patterns were reduced to their local maxima (Carney 1990). Figure 1B shows these maxima plotted together for both a broad-transition stimulus (r = 0.85) and a sharp-transition stimulus (r = 0.95) with transition frequency FT of 1,000 Hz.

In Fig. 1B, peak 1 lines up nearly perfectly with the “cochlear delay” estimated from model responses to clicks at 50 dB SPL for both sharp and broad phase transition stimuli, and the height of peak 1 is similar across CFs. In contrast to peak 1, the later peaks differ in both amplitude and latency between the two transition widths. As CF decreases from 2 kHz, peak 2 for the sharp-transition stimulus decreases in amplitude and ultimately disappears when the CF is just below FT. In contrast, peak 2 for the broad-transition stimulus maintains a roughly constant amplitude for all CFs. Thus, when CF is near or below FT, peak 2 is small (or nonexistent) for the sharp-transition stimulus compared with the broad-transition stimulus. Peak 3 remains fairly constant in amplitude across CF for the broad-transition stimulus, while it shows a minimum when CF is near FT for the sharp-transition stimulus. As a result, peak 3 is smaller for the sharp-transition stimulus than for the broad-transition stimulus over a CF range near FT. When considering peaks 1, 2, and 3 together, which we call the “early response,” the overall response is smaller for the sharp-transition stimulus than for the broad-transition stimulus over a CF range near FT. On the other hand, the heights of peaks 4 and later, which form the “late response,” tend to be larger for the sharp-transition stimulus than for the broad-transition stimulus when CF is near FT, with an opposite pattern when CF is far from FT. The contrasting behaviors of the early and late responses to the two Huffman stimuli when CF is near FT are a consequence of the shorter group delay for the broad-transition stimuli compared with the delay for the sharp-transition stimulus (Fig. 1A, bottom).

Responses of cross-frequency CD cells to Huffman stimuli are expected to depend not only on the amplitudes of the early and late AN responses but also on the temporal alignment of the individual response peaks across the tonotopic axis. While peak 1 for the two transition bandwidths are aligned with each other and with the cochlear delay, peak 2 gradually occurs earlier for the broad-transition stimulus than for the sharp-transition stimulus as CF decreases towards FT. Peaks 3 and later all have approximately the same temporal relationship between the two transition widths. Specifically, responses to the two stimuli align in time only when CF is near FT and diverge when CF is far from FT. When CF is above FT, responses to the sharp-transition stimulus occur slightly later than responses to the broad-transition stimulus. This trend reverses for CF below FT, where responses to the sharp-transition stimulus occur slightly earlier than responses to the broad-transition stimulus. As a result, the stimulus with sharp transition excites more coincidentally across CF than the broad-transition stimulus. These observations are consistent with the phase spectra of the two stimuli (Fig. 1A, middle), in that the phase lag is smaller for the sharp-transition stimulus than for the broad-transition stimulus for frequencies below FT but the opposite pattern holds for frequencies above FT.

To summarize, analysis of model AN fibers responses suggests two important differences between Huffman stimuli differing in transition bandwidth. First, the early response (peaks 1–3) is smaller for the sharp-transition stimulus than for the broad-transition stimulus when CF is near FT and increases as CF moves away from FT. Second, for peaks 3 and later, the sharp-transition stimulus gives rise to better temporal alignment across CF than the broad-transition stimulus.

These observations are consistent with model AN responses in Fig. 2 from Carney (1990), which were obtained with a simpler model (Carney and Yin 1988) based on linear cochlear filters rather than the more sophisticated nonlinear model of Zilany and Bruce (2006). Carney reasoned that the broad-transition stimulus would introduce smaller variations in group delays across CF, resulting in greater coincidence across CF and greater responses of cross-frequency CD cells. Indeed, the envelope of the model response to the broad-transition stimulus is more concentrated toward early latencies than the response to the sharp-transition stimulus for CFs near FT. However, the behavior of the response envelope does not predict the temporal alignment of individual response peaks across CF, to which cross-frequency CD cells are likely to be sensitive because of their short time constants. Peaks 3 and later are clearly more coincident across CF for the sharp-transition stimulus than for the broad-transition stimulus.

Although Fig. 1B only shows model responses for FT = 1,000 Hz, a similar pattern was observed for FT ranging from 250 to 3,000 Hz (not shown). Moreover, the key observations for the model spatio-temporal response pattern (across CF) in Fig. 1B also hold for the model virtual spatio-temporal pattern (across FT) in Fig. 1C when viewed in normalized frequency (CF/FT) and time (t × FT) coordinates, further supporting the use of cochlear scaling invariance in the experiments. Next we test whether these model predictions hold for virtual spatio-temporal patterns constructed from responses of real AN fibers.

Physiological AN Fiber Responses to Huffman Stimuli

Our analysis of AN fiber responses to Huffman stimuli is limited to low-CF fibers within the range of phase locking to the temporal fine structure, so that the relative timing of discharges across CF can be manipulated. Our results are based on recordings from 147 AN fibers with CFs ranging from 107 Hz to 2,565 Hz in 11 cats. Of these, 94 fibers (64%) had high (>18 spikes/s) spontaneous rates (SR), 44 (30%) had medium SR (0.5–18 spikes/s), and 9 (6%) had low SR (<0.5 spikes/s). In 44 fibers, responses were measured as a function of FT varying from a half octave below CF to a half octave above CF. These data were used to infer responses of an array of AN fibers with different CFs to a Huffman stimulus with fixed FT using cochlear scaling invariance (see AN Data Analysis) and were also used as inputs to CD cell models. In another 103 AN fibers, we measured the responses to Huffman stimuli with different r in which FT was set at the CF to serve as a reference for comparison to responses of CN neurons and CD model cells described later.

In this section, we first describe an example fiber's responses when FT is varied and verify that essential features of these responses resemble those of a model fiber with the same CF and same inputs. We introduce rate difference metrics to quantify the preference for Huffman stimuli with sharp versus broad transition widths. We also use a slope metric to quantify the degree of alignment in response peaks across FT, which we interpret as cross-CF coincidence. These metrics serve as a reference for comparison to responses of CN neurons and CD model cells.

Example responses when transition frequency is varied.

As described in methods, cochlear scaling invariance allows us to approximately infer the response pattern of an array of fibers with different CFs to a stimulus with a specific FT from the responses of a single fiber to varying FT stimuli. PSTHs comprising the virtual spatio-temporal pattern of an AN fiber (CF = 972 Hz) are shown in Fig. 2 in response to Huffman stimuli at two stimulus levels (26 and 41 dB re. pure tone threshold at CF). Figure 2, B and E, show the measured PSTHs, while Fig. 2, A and D, show responses of a 972-Hz model AN fiber to the same stimuli. Figure 2, C and F, show the response peaks for the real fiber's PSTHs, using a similar format as for the AN model in Fig. 1, B and C. The numbers above Fig. 2, A–F, correspond to the model peaks that most closely match in time.

The model fiber responses tend to last longer, ringing for several more cycles than observed in the real AN fiber, suggesting that the model overestimates the frequency selectivity at this cochlear place. The response peaks for the model also tend to be broader than those in the data. In this particular fiber, which had a medium spontaneous rate and therefore a relatively high threshold, these differences may partly be a consequence of using ∼20 dB lower absolute stimulus levels (in dB SPL) in the model in order to match the levels re. threshold. However, similar differences between responses of the model and real AN fibers were also observed with other fibers for which the absolute stimulus levels were well matched.

Despite the poor match in response duration and peak widths, the peak locations and their temporal alignment across FT are similar for the model and real fibers at both levels. Response latencies increase as FT increases and therefore the virtual CF decreases. Peak 2 for the sharp-transition stimulus is only observed when FT is below CF, and its height decreases as FT approaches CF. For the broad-transition stimulus, peak 2 in the model response also gradually vanishes and merges into peak 1 with increasing FT. The same effect is observed at the higher level in the real fiber (Fig. 2E), but the response at the lower level (Fig. 2B) lacks peak 2 for the broad-transition stimulus. For peaks 3 and later, the temporal relationships between the two transition widths are the same for model and data: when FT is below CF, the responses to the sharp-transition stimulus occur slightly later than the responses to the broad stimulus. This trend reverses direction when FT is above CF, causing the responses to be overall more coincident across FT for the sharp-transition stimulus. Furthermore, for both the model and real fibers, the peak 3 height remains roughly constant across FT for the broad-transition stimulus, while it shows a minimum when FT is near CF for the sharp-transition stimulus. In contrast, peaks 4 and later in the real AN fiber are larger for the sharp-transition stimulus than for the broad-transition stimulus when FT is near CF. These observations result from the longer group delay induced by the stimulus with the sharper phase transition (Fig. 1A). All of the effects described in Fig. 2 were also observed in many fibers in our sample across the range of CFs investigated.

Rate differences between sharp- and broad-transition stimuli.

We used normalized rate difference (RD) metrics to quantify the relative responsiveness of AN fibers to Huffman stimuli with broad versus sharp transition bandwidths. Separate RD were computed for the early (RD_Early, peaks 1–3) and late (RD_Late, peaks 4+) parts of the response because these two components had different dependencies on FT. Figure 3, A and B, show RD_Early and RD_Late as a function of normalized frequency CF/FT for the fiber of Fig. 2 at stimulus levels of 26 and 41 dB re. threshold at CF, respectively. At both stimulus levels, RD_Early tends to be positive (indicating preference for the broad-transition stimulus) when FT is near the CF and becomes smaller or even negative when FT is far from CF. This preference for the broad-transition stimulus is more pronounced at the lower level than at the higher level. RD_Late shows the opposite pattern, with a preference for the sharp-transition stimulus (negative RD) for FT near CF.

Fig. 3.

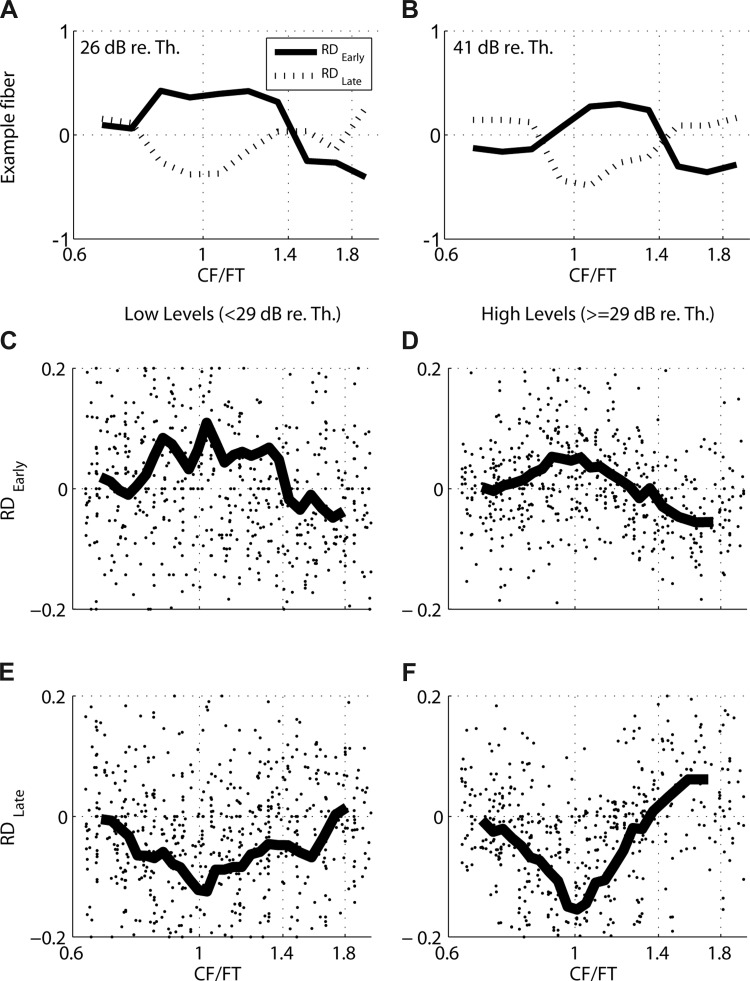
Normalized rate differences between responses to broad- and sharp-transition stimuli (Broad − Sharp)/(Broad + Sharp) for example fiber (A and B) and sample of 44 AN fibers (C–F). A: early (RD_Early) and late (RD_Late) rate differences vs. CF/FT for example AN fiber from Fig. 2 at 26 dB re. CF threshold (61 dB SPL). B: same as in A, but at 41 dB re. CF threshold (76 dB SPL). C: RD_Early against CF/FT for the sample of AN fibers at low stimulus levels (<29 dB re. CF threshold). Each dot shows data from 1 individual fiber, while lines indicate moving averages across the sample. x-Axes are truncated to emphasize trends in the moving averages. D: same as in C, but at higher levels (≥29 dB re. CF threshold). E: RD_Late for AN sample at low levels (<29 dB re. CF threshold). F: same as in E, but at higher levels (≥29 dB re. CF threshold).

The RD trends shown in Fig. 3, A and B, for the 972-Hz example fiber are also apparent for the entire sample of AN fibers in Fig. 3, C–F. RD_Early (Fig. 3C for levels < 29 dB re. threshold at CF and Fig. 3D for levels ≥ 29 dB re. threshold) and RD_Late (Fig. 3E for low levels and Fig. 3F for high levels) are plotted as a function of CF/FT. Despite the large amount of scatter across individual fibers, the moving averages show clear trends. At both low and high levels, RD_Early tends to be positive and RD_Late negative when CF is near FT, but early and late responses tend to converge when FT is far from CF. Furthermore, the normalized frequency range for which the mean RD_Early is positive and RD_Late is negative is wider at low levels than at high levels. This pattern of results (which is consistent with the model responses in Fig. 1, B and C) arises because, compared with the broad-transition stimulus, the sharp-transition stimulus has a longer group delay for frequencies near FT (Fig. 1A). This difference in group delay gives rise to stronger early responses for the broad-transition stimulus and stronger late responses for the sharp-transition stimulus when CF is near FT.

Quantifying cross-frequency coincidence.

While all CD cells will partly inherit their response preference for Huffman stimuli with broad versus sharp transition bandwidths from those of their AN inputs (as quantified by the RD metrics), the preference of cross-frequency CD cells (which receive inputs from AN fibers with different CFs) should also depend on the alignment (coincidence) of AN response peaks across the tonotopic axis. To quantify the degree of cross-frequency coincidence we fit line segments to sets of homologous peaks in the response patterns to Huffman stimuli across FT (Fig. 2, C and F). We used the slopes of the fitted lines when FT is near the CF as a measure for the degree of cross-CF coincidence in the virtual spatio-temporal pattern. Overall, the fit of the lines to the data was quite good: across 125 peak sets from 44 fibers, the mean absolute error was 0.030 cycles of FT. Slopes were always negative because the peaks always occurred later for higher FT (lower virtual CF), consistent with the direction of the cochlear traveling wave, but we use the absolute values of the slopes for simplicity. A slope of 1 means that the response peak shifts in time by 1 cycle of FT for a unit shift in normalized frequency CF/FT. A higher slope means greater cross-frequency coincidence (more vertical alignment). For example, in Fig. 2C, the slope of peak 4 is 0.33 for the sharp-transition stimulus, which is larger than the 0.27 slope for the broad-transition stimulus, indicating a higher degree of coincidence for the former. The slopes of peak 3 are also higher for the sharp-transition stimulus than for the broad-transition stimulus in Fig. 2, C and F.

Figure 4 shows scatterplots of the absolute slopes for the sharp-transition stimulus against absolute slopes for the broad-transition stimulus across our sample of 44 AN fiber responses to varying-FT stimuli. For both transition widths, the responses are more coincident (the slopes are higher) for the earlier peaks than for the later peaks. Despite some scatter in the data, mean slopes for peak 1 do not significantly differ between the two phase transition widths (paired t-test, P = 0.77). On the other hand, mean slopes for all other peaks were significantly larger for the sharp-transition stimulus than for the broad-transition stimulus (P < 0.01 for peaks 2, 3, and 4+). These results indicate that for peaks 2 and later, the sharp-transition stimulus excites more coincidentally across virtual CFs.

The data shown in Fig. 4 are pooled across all CFs and levels. There was no significant dependence on CF. The slopes tended to increase with level, consistent with widening of the cochlear filters at higher levels. However, there was no effect of level on the slope difference between the two transition widths (not shown).

Predictions for coincidence detector cells.

The above observations from AN fibers on rate differences and peak slopes for Huffman stimuli lead to two predictions about responses of cross-frequency CD cells.

1) The early AN response (peaks 1–3) is larger for the broad-transition stimulus than for the sharp-transition stimulus when CF is near FT, but this difference becomes less pronounced as CF moves away from FT (Fig. 3). Thus we expect the preference of cross-frequency CD cells for the broad-transition stimulus in their early response to be attenuated or even reversed as their CF range of inputs increases.

2) For peaks 2 and later, we observed greater cross-CF coincidence in the AN for the sharp-transition stimulus compared with the broad-transition stimulus. However, peaks 2 and 3 have lower amplitude for the sharp-transition stimulus than for the broad-transition stimulus when FT is near CF (Fig. 3), while the opposite effect is observed for peaks 4+. Because the response of a CD cell is expected to increase with both input amplitude and the degree of cross-CF coincidence of its inputs, it is unclear which of these opposing effects would dominate in the early CD response. Thus we make a conservative prediction that the late responses of cross-frequency CD cells should have an enhanced preference for the sharp-transition stimulus over the broad-transition stimulus compared with AN fibers.

Responses of Coincidence Detector Model Cells

We implemented CD model cells operating on virtual spatio-temporal response patterns of AN fibers to Huffman stimuli. Our goals were twofold: 1) to test whether CD cells are sensitive to manipulations of the AN spatio-temporal pattern produced by changing the transition width of Huffman stimuli and 2) to develop rigorous criteria for distinguishing the responses of cross-frequency CD cells from those “same-frequency” CD cells (i.e., for which all the AN inputs have the same CF).

Coincidence detector cell example.

Figure 5, A and C, show the responses of the same AN fiber as in Fig. 2 (CF 972 Hz) to Huffman stimuli with different FT presented at 26 dB (Fig. 5A) and 41 dB (Fig. 5C) re. threshold. While the measurements were made for FT separated by 1/6th octave steps, the responses in Fig. 5 were interpolated to 1/36th octave steps so as to sample the virtual spatio-temporal response pattern with fine frequency resolution (see methods). Figure 5, B and D, show responses of nine model CD cells with different parameters operating on these virtual spatio-temporal patterns as inputs. Columns correspond to different values of the total number of AN inputs N, while rows differ in the CF range of inputs w. The top row shows responses of same-frequency CD cells (w = 0), while middle and bottom rows show responses of cross-frequency CD cells (w > 0). The AN inputs to the CD model all had CF/FT ranges centered around 1, meaning that the virtual CFs of the inputs to the CD cell were centered at the CF of the AN fiber from which the recording was made. All CD responses in Fig. 5 were obtained with L = 2, meaning at least two inputs have to fire within the 0.1-ms coincidence window for the CD cell to produce a spike.

On the basis of our observations from AN responses, we had two predictions for cross-frequency CD cells. First, we expected the preference of cross-frequency CD cells for the broad-transition stimulus in their early response to be attenuated and even reversed as the CF range of inputs increases. This prediction qualitatively holds in Fig. 5, B and D. To test the prediction more directly, Figure 6 shows RD_Early and RD_Late versus input range w for the CD cells with N = 10 shown in Fig. 5 at 26 dB (Fig. 6A) and 41 dB (Fig. 6B) re. CF threshold. RD_Early is positive for small w and decreases with increasing w, becoming negative when w is larger than 0.6 octave at the lower level and 0.4 octave at the higher level. This means that narrow-range CD cells show a preference for the broad-transition stimulus in their early response, whereas wide-range CD cells show a preference for the sharp-transition stimulus. Therefore, the early rate difference can provide information about the input frequency range of a CD cell and in particular distinguish same-frequency CD cells from wide-range cross-frequency CD cells.

Fig. 6.

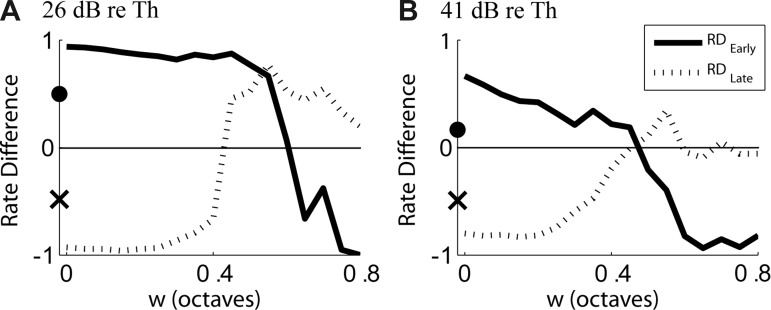
Normalized rate differences to Huffman stimuli with broad vs. sharp transition widths for AN fiber and CD cells from Fig. 5, as a function of CF range of inputs w to the CD cell. A: RD_Early (CD solid line, AN filled circle on y-axis) and RD_Late (CD dashed line, AN × on y-axis) at 26 dB re. CF tone threshold. B: same as in A but for 41 dB re. CF tone threshold. The CD cells were driven by virtual spatio-temporal patterns of the example fiber in Fig. 2.

Second, we predicted that CD cells would have an enhanced preference for the sharp-transition stimulus compared with AN fibers in their late response. Consistent with this prediction, Fig. 6 shows that RD_Late is more negative for CD cells than for the input AN fiber so long as w < 0.4 octave at both levels. However, contrary to our prediction, RD_Late increases with increasing w and becomes larger than RD_Late for the AN fiber for w > 0.4. This increase in RD_Late results from a slight shift in response latencies of CD cells as w increases (Fig. 5, B and D), which causes an increasing number of spikes to occur within the late response window, which has a fixed temporal position for all w. The longer latencies for large w arise because the AN inputs with lower virtual CFs, which have long latencies, increasingly drive the CD cell with increasing w. Even though the results are not entirely consistent with our prediction, the important point is that RD_Late can also provide information about the input CF range of a CD cell.

CD population: rate difference metrics.

We used six metrics to characterize responses of AN fibers and CD cells to Huffman stimuli: RD_Early, RD_Late, ND_Broad, ND_Sharp, PW_Broad, and PW_Sharp. These metrics were selected both to quantify the sensitivity of CD cells to phase transition width and to distinguish CD cells with different parameters, especially cross-frequency from same-frequency CD cells. Images in Fig. 7 show the probability distributions of these metrics as a function of w for CD cell responses (N = 10, L = 2) across 125 input virtual spatio-temporal patterns measured from 44 AN fibers. The distributions are shown separately for low levels (<29 dB re. CF threshold; Fig. 7A) and high levels (≥29 dB re. CF threshold; Fig. 7B). Distributions from CD cells with different input frequency ranges are plotted along the vertical axes. Bar plots below each image show distributions of the six metrics across the original 125 AN fiber responses when FT is set to the CF.

Fig. 7.

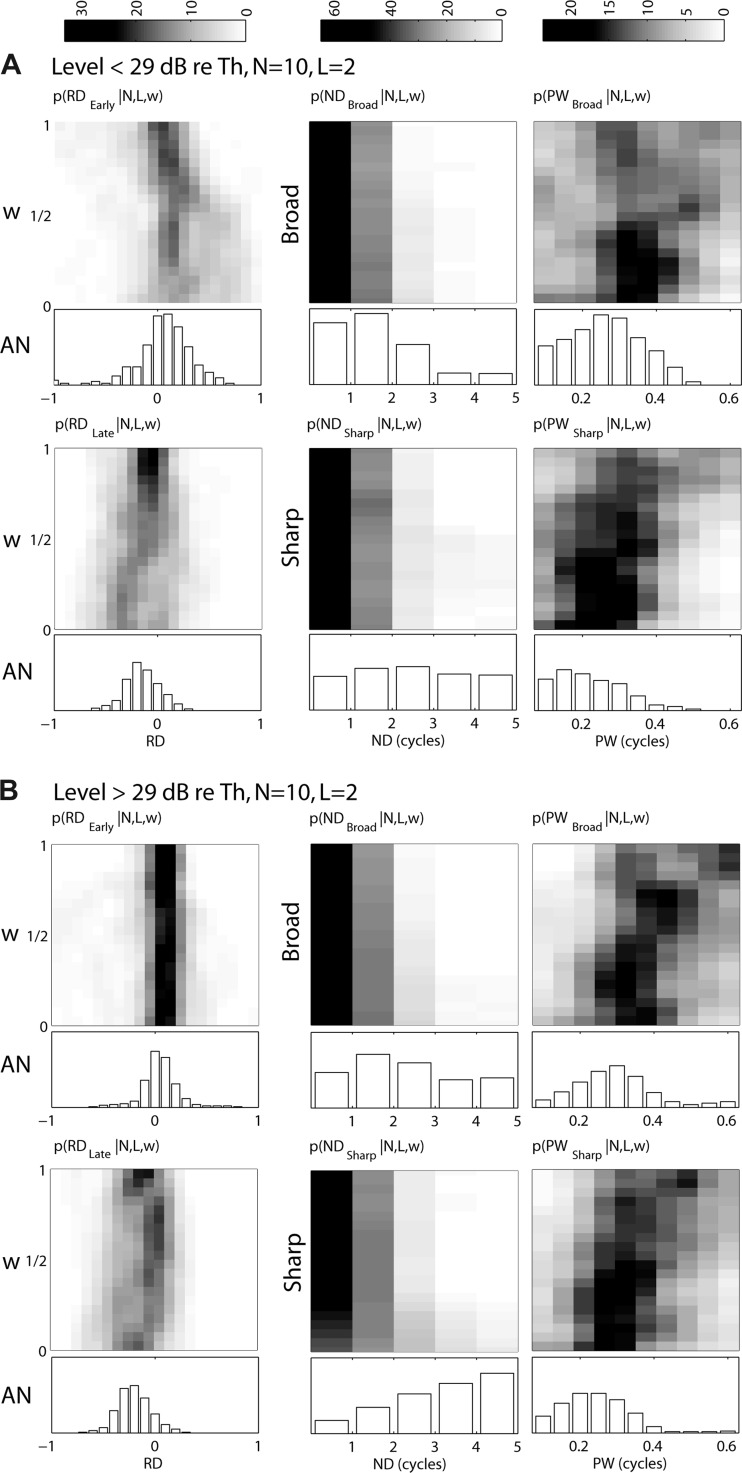
Histograms of the distributions of 6 metrics used to characterize responses of AN fibers and CD cells to Huffman stimuli for low (<29 dB re. CF tone threshold, A) and high (≥29 dB re. CF tone threshold, B) stimulus levels. Histograms are based on 125 recordings from 44 AN fibers, each used as input to CD model cells. Images show distributions for CD cells (N = 10, L = 2) as a function of the CF range of inputs w; gray scale (see maps at top of figure) represents % of recordings for each w. Bar plots below each image show the corresponding distributions for AN fibers when FT = CF. Left: distributions of RD_Early and RD_Late are shown at top and bottom, respectively. Temporal metrics normalized response duration (ND) and mean peak width (PW) in cycles of FT are shown at center and right, respectively. For ND and PW, broad transition responses are shown at top and sharp transition responses at bottom.

Consistent with the example responses shown in Figs. 5 and 6, RD_Early at low levels tends to be positive for narrow-range CD cells and decrease to near zero or become slightly negative for wider-range CD cells. At high levels, RD_Early for the population tends to remain roughly unchanged near zero for all input ranges, even though some individual CD cells showed a systematic decrease in RD_Early with increasing input range (Fig. 6). In contrast, RD_Late is usually negative for both levels and tends to be more negative for narrow-range CD cells than for wide-range CD cells, again consistent with the example in Fig. 6.

CD population: temporal metrics.

While RD_Early is useful for distinguishing between CD cells with narrow versus wide input ranges, the normalized response duration ND is useful for distinguishing AN responses from CD responses. The ND histograms for CD cells and AN fibers are shown in Fig. 7, middle. ND (which is expressed in cycles of FT) is always an integer because the responses of low-frequency, phase-locking AN fibers and CD cells tend to show peaks at intervals of 1/FT. For both transition widths, CD cells, regardless of w, tend to have shorter ND than their AN inputs, usually lasting just 1 or 2 cycles of FT, while AN responses frequently last for 3 or more cycles. For both AN fibers and CD cells, ND tends to be longer for the sharp-transition stimulus than for the broad-transition stimulus, especially at high levels. This is consistent with the longer ringing in the stimulus waveform with the sharp transition (Fig. 1A).

At both levels, the average width of response peaks PW (Fig. 7, right) for both CD cells and AN fibers tends to be narrower for the sharp-transition stimulus compared with the broad-transition stimulus. This result was expected for cross-frequency CD cells because the sharp-transition stimulus results in better temporal alignment of AN discharges across virtual CF for all but the first response peaks. Cross-frequency CD cells should convert this temporal alignment into precisely timed response peaks. While this prediction is verified, response peaks are also narrower for the sharp-transition stimulus in AN fibers and same-frequency CD cells. This means that the differences in peak width observed in CD cells are partly inherited from their AN inputs. The small late peaks observed in response to sharp-transition stimuli for both AN fibers and CD cells tend to be very narrow and likely decrease the mean width across all peaks.

We expected a strict CD cell (L ≈ N) to have shorter ND and PW than AN fibers because strict coincidence detection leads to temporal sharpening. Indeed, as L increases, CD cell responses have shorter ND and narrower PW regardless of input range (not shown). However, for the relatively lenient set of parameters used in Fig. 7 (N = 10, L = 2), PW tends to be larger for cross-frequency CD cells than for AN fibers. In the response of a lenient (L ⪡ N) cross-frequency CD cell, the early portion of a peak may originate from its high-CF_virt (low FT) inputs, while the later portion of the same peak may originate from its low-CF_virt (high FT) inputs. As the input range increases, more asynchronous activity is included, which would tend to increase PW. Therefore, PW can provide information about the input range of CD cells as well as their degree of strictness.

Responses of Cochlear Nucleus Units

Having established how responses of model CD cells to Huffman stimuli depend on cell parameters, we next compare responses of CN units to those of model CD cells with the goal of inferring which cell parameters (if any) are the most likely to have produced the observed CN responses. For this purpose, we recorded from 126 single CN units (with CFs 151–2,639 Hz) in 19 cats. In all units, we recorded the responses to Huffman stimuli with FT set to the CF for at least two phase transition widths (r = 0.85 and 0.95). Stimulus level was initially set near threshold (see methods) and then increased in 10- or 15-dB steps. We used a maximum likelihood test (see appendix) to objectively determine whether the responses of each CN unit most resemble responses of AN fibers or model CD cells and, for the latter, infer the CF range of inputs w to the CD cell. Table 2 lists the total number of units studied from each CN unit type and the number of units whose responses were found to resemble those of AN fibers, narrow-range CD cells (w < 1/3 octave), and wide-range CD cells (w > 1/3 octave). As a control, the same test was performed on the responses of 103 AN fibers when FT = CF; 97 of these were correctly recognized as coming from AN fibers, while 6 fibers were found to resemble CD cell responses, yielding a false alarm rate of just 6%. Importantly, none of the test AN fibers was used in generating the probability distributions of response metrics on which the maximum likelihood test is based, in order to avoid overfitting the model.

Table 2.

Total number of units found to have responses to Huffman stimuli most like AN fibers, narrow-range CD cells, and wide-range CD cells

	AN	Pri	Pri-N	PhL	HiS	On
AN-like	97	36	2	19	3	2
Narrow CD-like ^w < 1/3	3	3	0	9	2	0
Wide CD-like ^w > 1/3	3	1	8	3	1	1
Total number of units	103	40	10	31	6	3

AN, auditory nerve; Pri, primary-like; Pri-N, primary-like with notch; HiS, high synchrony; PhL, phase locker; On, onset.

Primary-like units.

In response to short tone bursts at CF, the PSTHs of CN primary-like (Pri) units for tone burst stimuli are characterized by a high onset response followed by a gradual decline to a steady discharge, resembling the PSTHs of AN fibers. Pri units are associated with spherical bushy cells, which receive only 1–3 excitatory inputs from the AN through large synapses called endbulbs of Held (Cant and Morest 1979; Ryugo and Sento 1991; Sento and Ryugo 1989). Because of the small number of convergent inputs and the secure synapses, we expected the responses of these cells to resemble those of AN fibers.

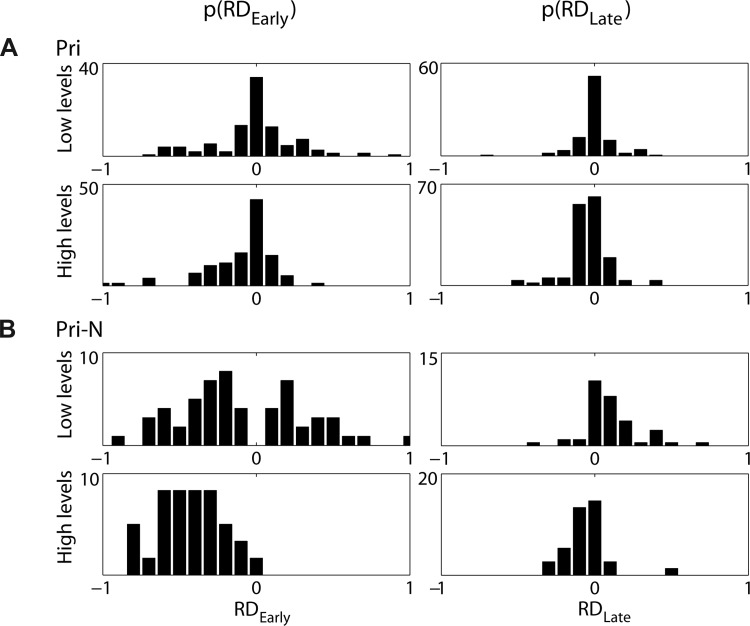
Figure 8A, top, shows the response of a Pri unit to a 30-ms tone burst at CF (1,293 Hz) at 80 dB SPL; the response exhibits clear phase locking to the stimulus. Responses of this unit to Huffman stimuli are shown in the lower panels of Fig. 8A at three different stimulus levels. The Pri responses resemble those of AN fibers with similar CFs (Fig. 5, A and C, insets). The response lasts for 3–4 cycles of FT, and the earliest peak is higher for the broad-transition stimulus, while the later peaks are higher for the sharp-transition stimulus. With the maximum likelihood test, the responses of this unit were found to most closely resemble responses of an AN fiber rather than those of any CD cell. These characteristics were typical for Pri units in our population. Of 40 Pri units studied, 36 had responses that matched most closely with AN responses, while only 4 units resembled CD cells. Figure 9A shows the distributions of RD_Early and RD_Late measured from the 40 Pri units in two level ranges. For both levels, the RD_Early and RD_Late distributions are centered near zero and are similar to the distributions from AN fibers (Fig. 7).

Fig. 8.

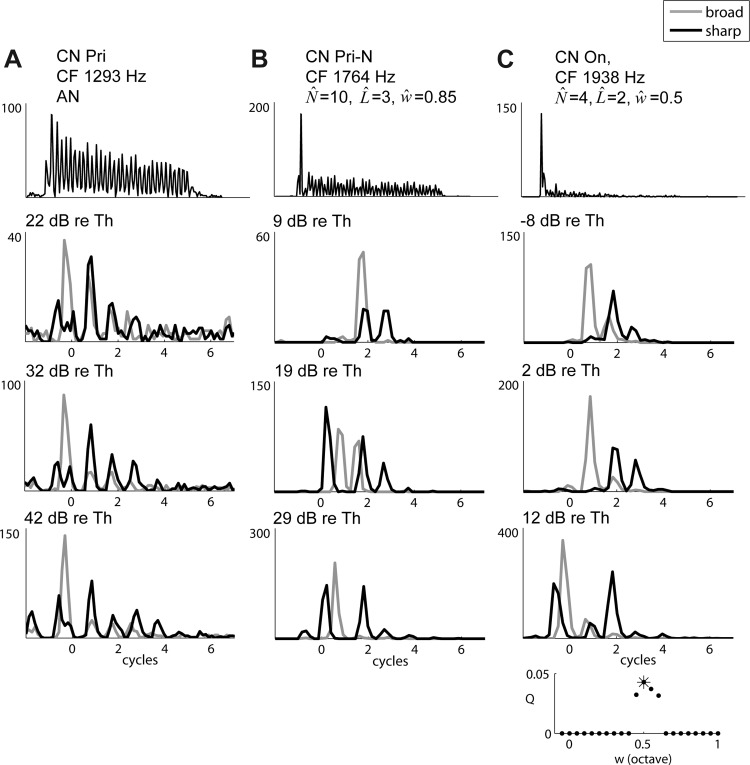
Example responses of cochlear nucleus (CN) units to Huffman stimuli. Top: responses to 30-ms tone bursts at CF at 80 (A), 70 (B), and 60 (C) dB SPL. Bottom 3 rows show responses to Huffman stimuli with FT = CF at 3 different stimulus levels expressed in dB re. CF tone threshold. Broad transition response is shown in gray, sharp transition response in black. All y-axes are in spikes/s. A: primary-like (Pri) unit, CF tone threshold = 24 dB SPL. B: primary-like-with-notch (Pri-N) unit, CF tone threshold = 32 dB SPL. C: onset (On) unit, CF tone threshold = 49 dB SPL. Inset, bottom right: likelihood that the responses observed in the On unit result from a CD cell (N = 10, L = 2) as a function of CF range of inputs w.

Fig. 9.

Distributions of RD_Early (left) and RD_Late (right) measured from responses of 40 Pri (A) and 10 Pri-N (B) units at low (<29 dB re. CF tone threshold, top) and high (≥29 dB re. CF tone threshold, bottom) stimulus levels.

Of the four Pri units that resembled CD cells, two had low CFs (896 and 1,078 Hz) and relatively high vector strengths in response to tone bursts at CF, meaning that they precisely phase locked. These units are likely to form a continuum with the high-synchrony (HiS) units described below.

Primary-like-with-notch units.

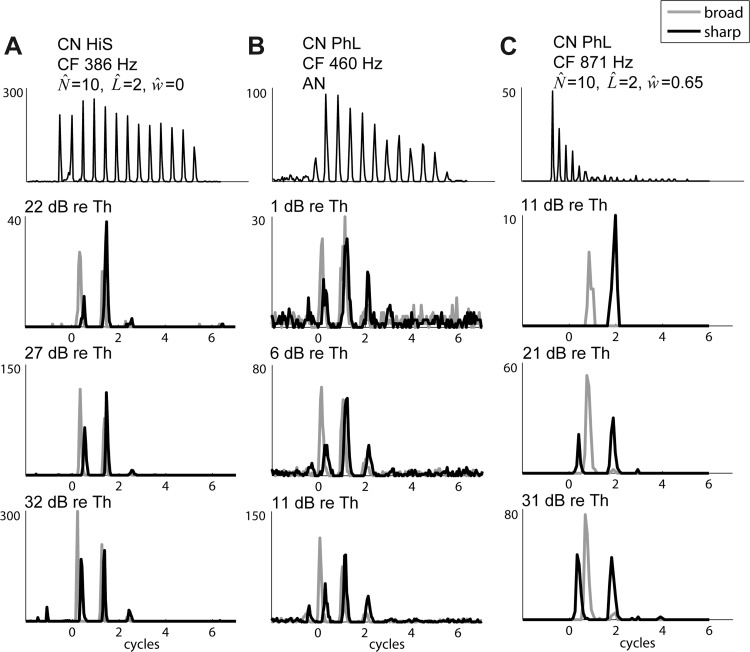
Primary-like-with-notch (Pri-N) units are characterized by a strong onset response to tone bursts, followed by a brief notch of inactivity (or decreased response) and recovery to a plateau (Fig. 8B, top). Pri-N response patterns are recorded from globular bushy cells, along with onset-with-late-activity (On-L, Fig. 8C) or HiS (Fig. 10A) response patterns (Smith and Rhode 1987). Globular bushy cells receive a large number of AN inputs: 15–23 somatic inputs (Spirou et al. 2005) and >60 dendritic inputs (Liberman 1993). The somatic inputs are via modified endbulbs (Tolbert and Morest 1982a, 1982b), which largely preserve the temporal firing precision of the AN inputs (Paolini et al. 2001; Spirou et al. 2005). The relatively large number of precisely timed AN inputs suggests that globular bushy cells could potentially perform cross-frequency coincidence detection (Carney 1990).

Fig. 10.

Example responses of low-CF CN units, using the same format as in Fig. 8. Top: responses to 30-ms tone bursts at CF at 80 (A), 80 (B), and 65 (C) dB SPL. A: high-synchrony (HiS) unit, CF tone threshold = 24 dB SPL. B: phase locking (PhL) unit, CF tone threshold = 40 dB SPL. C: PhL unit, CF tone threshold = 30 dB SPL.

Responses of a Pri-N cell to Huffman stimuli are shown in the lower three panels of Fig. 8B. The response duration is shorter (1–3 cycles) than those of AN and Pri responses (3–4 cycles). At the lowest level, the earliest peak is larger for the broad-transition stimulus than for the sharp-transition stimulus. In contrast, at higher levels there is a strong early response to the sharp-transition stimulus. This behavior is similar to that of the cross-frequency CD cells in Fig. 5, B and D, middle and bottom. Based on the maximum likelihood test, this unit's responses most closely resemble those of a CD cell with a wide input range (w = 0.85 octave).

The characteristics of the example Pri-N unit in Fig. 8B were typical across our sample of 10 Pri-N units. Figure 9B shows distributions of RD_Early (Fig. 9B, left) and RD_Late (Fig. 9B, right) across this sample. At low levels RD_Early is negative slightly more often than it is positive, and at high levels it is almost always negative. AN fibers and narrow-range CD cells rarely exhibit negative RD_Early, but moderately strict wide-range CD cells often have an early preference for the sharp-transition stimulus (negative RD_Early). Moreover, RD_Late in Pri-N units is mostly positive at low levels and negative at high levels, in contrast to AN fibers and Pri units, where RD_Late is rarely positive. With the maximum likelihood test, 8 of 10 Pri-N units studied were found to resemble CD cells with relatively wide input range (w > 1/3 octave). Two units resembled AN fibers, and none resembled a narrow-range CD cell.

Onset units.

Onset (On) units are characterized by a temporally precise onset response followed by little or no sustained activity. Because of their wide tuning curves and very precise onset response, On units are thought to receive input from a wide range of CFs (Oertel et al. 2000). Simple CD cell models receiving a large number (>100) of weak synaptic inputs from AN fibers produce responses resembling those of On units (Kalluri and Delgutte 2003a, 2003b). We recorded from three On units, which all displayed some late activity (On-L). Because both On-L and Pri-N response patterns have been recorded from globular bushy cells, these units may form a continuum with Pri-N units.

In response to Huffman stimuli, the On-L unit shown in Fig. 8C displayed responses similar to the Pri-N example at even lower levels. At −8 and 2 dB re. CF tone threshold, the early peak was larger for the broad-transition stimulus, while the later peaks were larger for the sharp-transition stimulus. At the highest level shown (12 dB re. CF threshold), an early response to the sharp-transition stimulus appears, consistent with cross-frequency CD cells. This On unit was found to most closely match a CD cell with wide input range (0.5 octave). Unexpectedly, the other two On-L units were found to have responses to Huffman stimuli more similar to those of AN fibers than CD cells. However, the responses of these units to short tone bursts did not resemble those of AN fibers. This failure of On units to be consistently identified as CD cells is addressed in discussion.

High-synchrony units.

Low-CF (<1 kHz) CN units usually strongly phase lock to tone bursts at CF. This strong phase locking obscures the other features of the response pattern that are used to classify CN units. One metric that may help to distinguish between cell types at these low frequencies is the strength of phase locking. We split low-CF CN units into two groups based on the synchrony index (vector strength) for tone bursts at CF: high-synchrony (HiS, n = 6) units have synchrony indexes higher than observed in the AN (>0.9; Joris et al. 1994a), while we call the other units phase lockers (PhL, n = 31).

HiS units have been associated with both spherical and globular bushy cells (Smith et al. 1991, 1993; Joris et al. 1994a). For the 386-Hz HiS unit shown in Fig. 10A, the sharpened temporal response is apparent in the narrow peak widths for both tone bursts and Huffman stimuli. At all levels, the responses to Huffman stimuli displayed two large, narrow peaks, with an early preference for the broad-transition stimulus and, at lower levels, a late preference for the sharp-transition stimulus. The unit had responses most similar to a same-frequency CD cell based on the maximum likelihood test. Three of the six HiS units most resembled AN fibers, while two resembled narrow-range CD cells (0 and 0.25 octave) and one resembled a wide-range CD cell (0.65 octave).

We used the onset-to-sustained ratio in response to 30-ms tone bursts at CF (the ratio of the firing rate for the first 10 ms of the response to the firing rate for the later 20 ms) in an attempt to predict the CD cell classification for HiS units. The three HiS units that resembled AN fibers had the lowest ratios (the weakest onset responses), while units with higher ratios resembled wide-range CD cells, suggesting a correlation between this ratio and the CF range of inputs for this small sample of HiS units.

Phase locking units.

Figure 10, B and C, show the responses of two PhL units (CF 460 Hz in Fig. 10B, 871 Hz in Fig. 10C). These examples illustrate the variety of characteristics that units in this group can exhibit. In response to short tone bursts at CF, the 460-Hz PhL unit in Fig. 10B shows a strong onset response, which gradually decreases throughout the stimulus. In contrast, the 871-Hz PhL unit in Fig. 10C has a very strong onset response that rapidly decays to nearly zero over just a few cycles.

The PhL unit in Fig. 10B has responses to Huffman stimuli similar to those of AN fibers. The responses last for 3 cycles, and the early response has a strong preference for the broad-transition stimulus at all three stimulus levels. In contrast, the PhL unit in Fig. 10C has a shorter duration, only displaying one peak at the lowest level and one or two peaks at the higher levels. Furthermore, the early response to the sharp-transition stimulus increases with level, consistent with a cross-frequency CD cell. The maximum likelihood test found the PhL unit in Fig. 10B most resembled an AN fiber, while the unit in Fig. 10C resembled a wide-range (0.65 octave) cross-frequency CD cell.

Of our sample of 31 PhL units, 19 had responses that most resembled AN fibers, 9 resembled narrow-range CD cells (w < 1/3 octave), and 3 resembled wide-range CD cells (w > 1/3 octave). Our finding that some PhL units resemble AN fibers while others resemble CD cells is not surprising considering that we cannot infer much information about these cells' inputs from the tone-burst response pattern. We attempted to further categorize PhL units based on the ratio of early to late responses for tone burst stimuli. However, unlike for HiS units, we found no correlation between this ratio and the best matching CD parameters for these PhL units.

Chopper units.

CN chopper units have a distinctive response pattern to short tone bursts at CF, where the spikes tend to occur at regular intervals unrelated to the stimulus frequency. As a result, these units have poor phase locking. Choppers are associated with stellate cells (Cant 1981) and have been modeled as integrate-and-fire neurons (Hewitt et al. 1992; Laudanski et al. 2010; Molnar and Pfeiffer 1968; van Gisbergen et al. 1975). The coefficient of variation (CV) of the first-order ISI quantifies irregularity in the unit's discharge pattern and is used to distinguish between two classes of choppers (Bourk 1976; Young et al. 1988). Sustained choppers (Ch-S; Fig. 11B) display regular chopping intervals and low CVs throughout the tone burst stimulus. In contrast, transient choppers (Ch-T; Fig. 11A) only display a chopping pattern during the early portion of the response, and the later responses have CVs higher than those of Ch-S units.

Fig. 11.

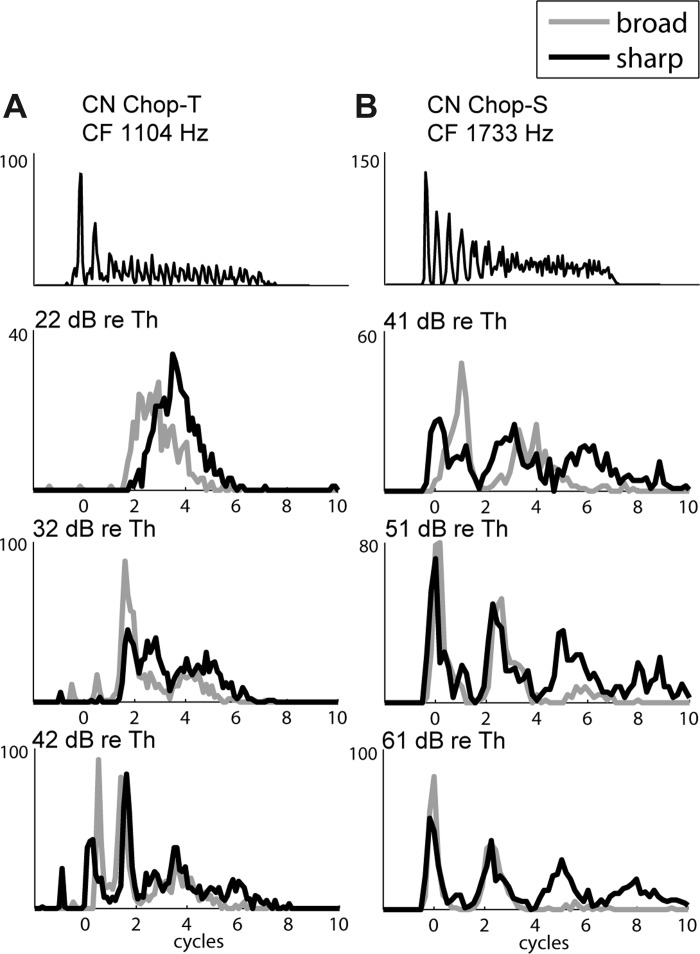
Example responses of CN chopper units, as in Fig. 8. Top: responses to 30-ms tone bursts at CF at 55 (A) and 60 (B) dB SPL. Bottom 3 rows show responses with FT = CF at 3 different stimulus levels expressed in dB re. CF tone threshold. A: transient chopper (Chop-T) unit, CF tone threshold = 14 dB SPL. B: sustained chopper (Chop-S) unit, CF tone threshold = 20 dB SPL.

Responses of chopper units to Huffman stimuli tend to have very wide peaks, sometimes wider than a cycle of FT. For example, the Ch-T unit in Fig. 11A has a long latency and a very wide (∼3 FT cycles) unimodal response at low levels. At the highest level, the unit's latency is shorter and the early response displays chopping. The Ch-S unit in Fig. 11B displays two to four wide peaks in response to Huffman stimuli, which are enhanced at higher stimulus levels. Unlike responses of other cell types, the intervals between peaks in the PSTHs of Ch-T and Ch-S units are not related to FT, and the average peak width is very wide, greater than 1 cycle. These responses are representative of the 20 chopper units in our sample (10 Ch-T, 10 Ch-S).

CD cells strongly phase lock and do not produce regular chopping patterns, whereas chopper units tend to produce spikes at intervals unrelated to the stimulus. Therefore, choppers are unlikely to have the very short time constants required for a CD mechanism as implemented here, and so the maximum likelihood test was not performed on these units. Nevertheless, Carney (1990) inferred that some Ch-T units behave like cross-frequency CD cells by determining that these units have larger (positive) overall rate differences (RD_Total) than AN fibers at low stimulus levels. Figure 12A shows the distribution of RD_Total at low (Fig. 12A, top) and high (Fig. 12A, bottom) stimulus levels for our sample of 10 Ch-T units. In contrast to Carney's results, RD_Total is mostly centered around zero at low levels and mostly negative at high levels. Figure 12B shows the distributions of RD_Total for Ch-S units, which rarely met Carney's criteria for CD cells. While the distribution of RD_Total for Ch-S units is broadly centered around zero at low levels (as for Ch-T units), RD_Total is even more negative for Ch-S units than for Ch-T units at high levels.

Fig. 12.

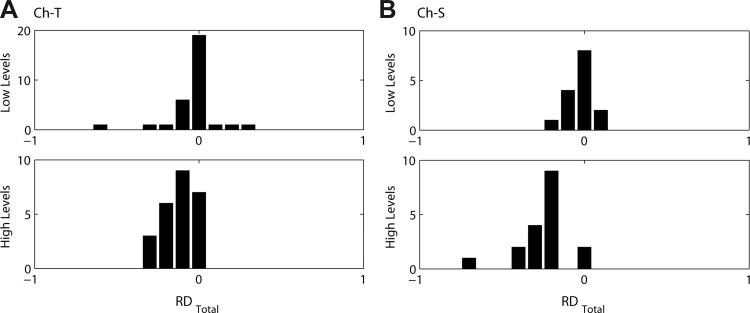
Distributions of total rate differences (RD_Total) measured from 10 transient (Ch-T; A) and 10 sustained (Ch-S; B) chopper units at low (<29 dB re. CF tone threshold, top) and high (≥29 dB re. CF tone threshold, bottom) stimulus levels.

Unusual units.

Sixteen CN units could not be classified into one of the above categories and displayed characteristics such as low firing rates, poor phase locking, long latencies, flat PSTHs, or unusual chopping patterns in response to tone bursts at CF. Because of the difficulty of relating these response patterns to those of model CD cells, responses of these units to Huffman stimuli were not analyzed in detail.

DISCUSSION

We measured responses of AN fibers and CN cells to Huffman stimuli, which have an all-pass magnitude spectrum and a 2π phase transition around a specific frequency FT. We showed that these stimuli can be used to systematically manipulate the spatio-temporal pattern of activity in the AN while causing minimum changes in overall firing rate. We found that the early AN response is larger for broad-transition stimuli than for sharp-transition stimuli for CF near FT, and that the range of CF where this holds is wider at low levels than at higher levels. We then implemented model CD cells operating on virtual spatio-temporal patterns of AN activity and used a quantitative framework to compare responses of CN units to those of CD model cells and identify the CD parameters that were most likely to give rise to the measured CN responses. The level dependence observed in the AN spatio-temporal pattern was reflected in the early responses of cross-frequency CD model cells, which increasingly preferred the sharp-transition stimulus at high levels. In contrast, early responses of same-frequency CD cells and AN fibers maintained a preference for broad-transition stimuli over a wide range of levels. We found that most CN Pri-N units and some HiS and PhL units had responses consistent with those of cross-frequency CD cells, while responses of Pri units and a majority of PhL units resembled those of AN fibers. Responses of CN chopper units resembled neither those of AN fibers nor those of CD cells and showed no preference for either transition width in their overall firing rate at low stimulus levels.

Comparison with previous results.

The present study is closely based on that of Carney (1990), who was the first to use Huffman stimuli for manipulating the spatio-temporal pattern of AN activity in order to identify CN cells that behave like cross-frequency CDs. Carney concluded that the rate responses of some CN unit types (particularly those corresponding to globular bushy cells) are sensitive to the spatio-temporal patterns of AN fibers in a direction consistent with cross-frequency CD. These conclusions are similar to our own, and the proportions of sensitive units across the CN unit classes are similar across the two studies (compare our Table 2 with Table 1 in Carney 1990). However, these similar conclusions were reached through very different analyses, and we show below that our detailed analysis of the behavior of model CD cells does not support some of the assumptions underlying Carney's analysis.

Carney's analysis was based primarily on the overall unnormalized rate difference RD_Total = r_broad − r_sharp between responses to Huffman stimuli with broad and sharp transitions, measured over the entire duration of the response. She interpreted an overall preference for the broad-transition Huffman stimulus in a CN neuron at low stimulus levels as evidence for cross-frequency CD. Her reasoning was that a more gradual phase transition introduces smaller variations in group delays across CF than a sharp transition (Fig. 1A), and therefore should result in greater coincidence across CF. Subsequently, Carney (1992) implemented a cross-frequency CD model that resembles our CD model with N = 16, L = 2, and w = 0.4. Consistent with our results with this model (Fig. 5B, middle right), her model cell displayed an overall preference for the broad-transition stimulus, especially at low levels. However, this overall preference for broad-transition stimuli does not hold for our CD cells in general.

Before discussing the usefulness of RD_Total as an indicator for cross-frequency CD cells, we must address the fact that Carney's Huffman stimuli had smaller transition bandwidths than ours for a given r because her stimuli were synthetized with a lower sampling rate (6–10 kHz vs. 20 kHz, see methods). To allow a direct comparison, we measured the responses of 28 AN fibers to 20-kHz Huffman stimuli with r values (0.92 and 0.98) selected to match Carney's phase transition bandwidths for r = 0.85 and 0.95, respectively. The maximum RD_Total across stimulus levels in this sample of fibers was nearly the same when comparing r = 0.92 vs. 0.98 (mean 4.0 spikes/s) as when comparing r = 0.85 vs. 0.95 (P = 0.96, unpaired t-test), suggesting that the effect of transition bandwidth differences on this metric is minimal. Nevertheless, the maximum RD_Total across levels for r = 0.92 vs. 0.98 tended to be somewhat smaller than the mean RD_Total for the bandwidth-matched stimuli in Carney's data (14.4 spikes/s), and the difference was statistically significant (P < 0.001, t-test). This small difference may arise because Carney's broad-transition stimuli had a slightly higher overall energy (by ∼2 dB) than her sharp-transition stimuli, possibly contributing to the slight preference she observed for the broad-transition stimulus. Importantly, all three sets of data concur, in that RD_Total is minimal for AN fibers, consistent with the goal of manipulating the spatio-temporal patterns without producing major changes in firing rate. Therefore the primary difference with Carney's study is not in the AN data but in how responses of CN neurons were analyzed.

To evaluate the usefulness of RD_Total as an indicator of cross-frequency CD cells, images in Fig. 13 show the distributions of normalized RD_Total as a function of w for a sample of 125 model CD cells (using N = 10 and L = 2 as in Fig. 7). Results were similar for other values of N and L. Bar plots below each image show the distributions of RD_Total measured from the 44 AN fibers for which FT was varied with r = 0.85 and r = 0.95. Using this metric alone, it is difficult to distinguish AN fibers from CD cells, because both tend to have slightly negative RD_Total at low and high levels. Moreover, it is difficult to distinguish between same-frequency and cross-frequency CD cells based on RD_Total because the distributions do not greatly depend on w. A one-way ANOVA revealed no significant differences in the mean RD_Total between AN fibers, narrow-range CD cells (w < 1/3), and wide-range CD cells (P = 0.24). Importantly, we find no evidence for an overall preference for the broad-transition stimulus (positive RD_Total), for wide-range CD cells, even at low stimulus levels. The same lack of preference for either transition width is obtained when the RD_Total distribution is plotted for those CN cells that were identified as wide-range CD by the maximum likelihood test (not shown). Thus RD_Total does not appear to be a reliable indicator of cross-frequency CD cells at any stimulus level.

Fig. 13.

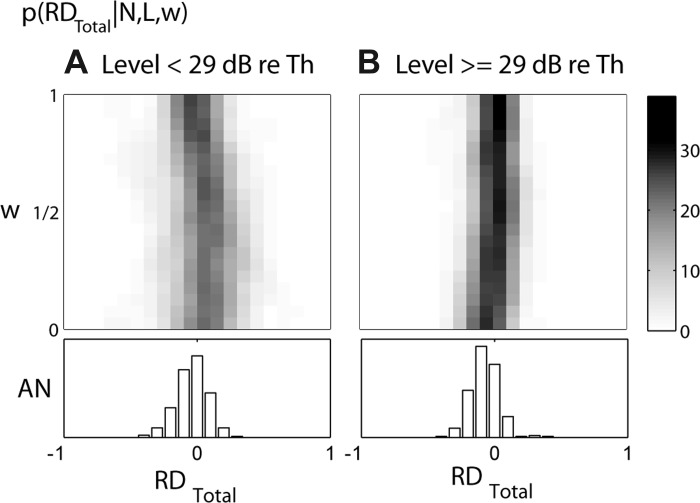
Images show distributions of RD_Total for model CD cells (N = 10, L = 2) at low (<29 dB re. CF tone threshold, A) and high (≥29 dB re. CF tone threshold, B) levels. Distributions are based on 125 recordings from 44 AN fibers and are shown as a function of CF range of inputs w on the y-axis; gray scale (see map at right) represents % of recordings for each w. Bar plots below each image show the corresponding distributions for AN fibers when FT = CF.

Why is RD_Total not a reliable indicator of cross-frequency CD? As argued by Carney (1990), the shallower frequency dependence of group delays for the broad-transition Huffman stimulus (Fig. 1A, middle) does result in a shorter overall latency and smaller across-CF dispersion in the envelope of the AN response to the broad-transition stimulus compared with the sharp-transition stimulus (Fig. 1, B and C, Fig. 2). This difference in the response envelopes for the two transition widths is, in turn, reflected in the opposing behaviors of the early and late rate differences as a function of CF (Fig. 3). These observations are consistent with the fact that the group delay is a property of the envelope of a signal (Papoulis 1962). However, CD cells, with their short time constants, are not directly sensitive to the envelope of response patterns of their AN inputs, but rather to the temporal fine structure of these input patterns. [This holds for CD cells with low CFs within the frequency range of phase locking to the temporal fine structure, which was the focus of both the present study and the Carney (1990) study; CD cells with CFs above 3 kHz may be more sensitive to the envelope of the input response patterns.] Specifically, cross-frequency CD cells are likely to be sensitive to both the amplitudes and the temporal alignment across CF of individual peaks in the response patterns of their AN inputs. Our results show that the temporal alignment of individual response peaks does not always behave in the same way as the alignment of the response envelopes: Specifically, peaks 2, 3, 4, and higher show greater alignment across CF (higher slopes) for the sharp-transition stimulus than for the broad-transition stimulus (Fig. 4), in contrast to the greater alignment of the response envelopes for the broad-transition stimulus.

The unreliability of RD_Total as an indicator of cross-frequency CD cells and the complex behavior of individual AN response peaks as a function of the Huffman parameters FT, r, and stimulus level led us to devise a set of metrics that distinguish between early and late rate responses and also take into account temporal response properties in order to quantitatively determine whether individual CN units resemble CD cells. Because some of these metrics systematically varied with the parameters of the CD model (Figs. 6 and 7), we were able to not only characterize CN units as resembling CD cells or AN fibers but also gain insight into the nature of the AN-to-CN convergence. Specifically, for CN units that resembled CD cells, key parameters such as the input range and relative strictness of coincidence detection (relationship between L and N) could be estimated.

Carney (1990) reported that the CN cells sensitive to phase transition width (based on RD_Total) sometimes switched their overall rate preference at high levels, where they fired more for the sharp-transition stimulus. For this reason, she excluded high-level responses in determining spatio-temporal sensitivity. We also observed an increased response to the sharp-transition stimulus at high levels in almost all of our Pri-N (Figs. 8B and 9B), some On-L (Fig. 8C), and some PhL (Fig. 10C) units that were identified as cross-frequency CD cells by the maximum likelihood test. At low levels (Fig. 5B), the early response of midrange (w = 0.4 octave) cross-frequency CD cells is much smaller for the sharp-transition stimulus than for the broad-transition stimulus. At higher levels (Fig. 5D), the CD early response to the sharp-transition stimulus increases, and sometimes exceeds the early response to the broad-transition stimulus. Because the range of virtual CFs over which the early AN response shows a preference for the broad-transition stimulus decreases with increasing level (Fig. 3), the early preference of cross-frequency CD cells is attenuated and sometimes reversed at high levels (Fig. 5D), consistent with Carney's observation from phase-sensitive units. Rather than discarding the high-level responses, the maximum likelihood test uses this strong level dependence in the early response preference as a defining feature of cross-frequency CD cells.

Cochlear Scaling Invariance

We used the principle of cochlear scaling invariance (Zweig 1976) to obtain virtual statio-temporal patterns of AN activity for a given Huffman stimulus from the responses of a single AN fiber to a set of stimuli with varying FT. These virtual spatio-temporal patterns were used to drive CD model cells that receive inputs from a varying range of CF. The validity of the scaling invariance assumption has been discussed in detail in previous publications (Cedolin and Delgutte 2010; Larsen et al. 2008). Briefly, two kinds of errors result from this assumption. One type of error arises because cochlear filters are not perfectly scaling invariant in that their Q (the ratio of CF to bandwidth) is not constant across tonotopic positions (CF). The other type of error arises because some temporal parameters of cochlear processing such as the upper frequency limit of phase locking and neural refractory periods does not scale with tonotopic position. Both types of error are fairly small so long as the frequency range over which scaling invariance is used to generate virtual spatio-temporal patterns is restricted. The strong similarity of virtual (Fig. 1C) and actual (Fig. 1B) spatio-temporal patterns for the AN model suggests that this is the case for the 1-octave range over which we varied FT around the CF. The use of virtual spatio-temporal patterns to drive model CD cells requires no additional assumption so long as these patterns are valid approximations to the true spatio-temporal patterns. Nevertheless, the CD model cells are undoubtedly oversimplified in that the response properties of their AN inputs are homogeneous except for their virtual CF. The inputs to real CD cells would likely also differ in other response properties such as threshold, spontaneous rate, and maximum firing rate.

Carlyon et al. (2012) have questioned the validity of cochlear scaling invariance based on their reanalysis of phase vs. frequency curves for pure-tone stimuli measured by Palmer and Shackleton (2009) from a large sample of AN fibers in guinea pig. By combining data from many animals, Carlyon et al. converted the raw measurements of phase against frequency from single fibers into smoothed patterns of phase against CF for a pure tone at a specific frequency. In their Fig. 12, they compare the smoothed phase vs. CF curves for two pure tones (500 and 1,516 Hz) separated by 1.6 octave after shifting the curve for the lower tone up by 1.6 octave along the CF axis in order to bring the two curves in alignment if scaling invariance holds. [1.6 octave is the range of frequencies over which Cedolin and Delgutte (2010) applied scaling invariance in their study of the spatio-temporal coding of the pitch of harmonic complex tones in the AN.] The two phase curves (whose y-axes were arbitrarily matched at 2,000 Hz) differed by as much as 0.8 cycle at 500 Hz, which Carlyon et al. (2012) interpret as a substantial deviation from scaling invariance. However, the correct way to test scaling invariance as used here and in earlier papers from our laboratory (Cedolin and Delgutte 2010; Larsen et al. 2008) would be to compare the phase vs. CF curve for a 871-Hz pure tone (the center of the 1.6-octave frequency range of interest, which serves as a pivot) with the phase vs. frequency curve for a single fiber with a 871-Hz CF. An examination of the data in Carlyon et al. (2012) suggests that the phase errors resulting from this method would be well within two standard deviations of the phase measurements in their Fig. 4 over the 1.6-octave frequency range of interest, and would be even smaller if the frequency range was reduced to 1 octave as in the present study. Thus the relatively large phase errors reported by Carlyon et al. (2012) result from a misunderstanding of how scaling invariance is applied.

Effect of Cochlear Traveling Wave Delays

In generating virtual spatio-temporal patterns of AN activity to drive the CD models, cochlear traveling wave delays were accounted for by first removing the delay corresponding to the CF of the fiber from which the recordings were made, and then reintroducing a delay appropriate for the CF of each virtual fiber. This was done so that the inputs to the CD model represent the relative timing present in the true AN spatio-temporal pattern.

This “cochlear-aligned” method of delay compensation contrasts with the method of Carney (1992), who aligned the responses so that the initial response to a click stimulus would be coincident across CF. In terms of generating a virtual spatio-temporal pattern, this “click-aligned” method effectively subtracts the constant delay but does not reintroduce a CF-dependent delay into the pattern. Some CN units have large responses to click stimuli, suggesting that these units may prefer to fire when AN responses across CF align with the cochlear delay. However, the click-aligned method effectively assumes a compensation mechanism in which the AN-to-CN conduction delay systematically varies with CF so as to keep the total delay (cochlear delay + conduction delay) constant across the entire tonotopic axis. A global cochlear delay compensation is unlikely because 1) latencies of CN neurons show a CF dependence roughly paralleling that found in the AN (Rhode and Smith 1986) and 2) chirp stimuli that equalize the frequency dependence of cochlear delays evoke larger auditory brain stem responses (ABR) than click stimuli (Elberling and Don 2008; Fobel and Dau 2004), indicating that cochlear delay compensation has not occurred for the brain stem neurons that contribute to the ABR. However, these data do not rule out a local form of delay compensation operating at the level of the AN inputs to a single CN cell or small cluster of cells, and there is evidence for such local compensation in the inputs to octopus cells (McGinley et al. 2012; Oertel et al. 2000).

To address the possibility of local cochlear delay compensation, the analysis of the CD cell model responses was repeated using the click-aligned method of delay compensation used by Carney (1992). The effect of such compensation is to remove an overall tilt (corresponding to the CF-dependent latency of peak 1, which matches the cochlear delay for both transition widths) in spatio-temporal response patterns to Huffman stimuli as shown in Fig. 1, B and C. The slopes of the fitted lines that characterize the degree of temporal alignment of AN response peaks across CF (Fig. 2, C and F) were increased in magnitude, but the relative pattern of alignment between the broad- and sharp-transition stimuli was largely unchanged. Specifically, the mean slopes of peaks 3 and 4+ across our AN sample remained significantly larger (P < 0.01, paired t-test) for the sharp-transition stimulus than for the broad transition. The largest effect was observed for peak 2, whose slope preference for the sharp-transition stimulus went from being highly significant (P < 0.001) with the cochlear-aligned method to just missing significance (P = 0.07) with the click-aligned method. Thus the overall tendency for most response peaks to be better aligned across CF for the sharp-transition stimulus was not fundamentally altered by cochlear delay compensation, and neither were the probability distributions for the six metrics characterizing CD responses. Most importantly, the categorization of CN units as AN-like versus CD-like did not change drastically, although there were some changes in the estimate of the CF range of inputs for the CN units identified as CD-like. For example, of eight Pri-N units that were identified as CD-like, four were found to have a narrow range of inputs (w < 1/3 octave) with the click-aligned method of delay compensation, whereas all had a wide input range with the cochlear-aligned method. Overall, the exact method for handling cochlear delays mattered less than the rate differences in the CD cell responses to the two phase transition widths and the temporal characteristics of the CD responses.

Refractoriness in the CD Model

The CD model used in this work does not include refractory effects. Refractoriness refers to the period of time following an action potential before a cell can fire again. For Pri-N units that have very precisely timed onsets, the subsequent notch of inactivity likely arises from the cell's refractory period. Johnson and Swami (1983) described an iterative method for introducing refractory effects in point process models of neurons such as our CD model. We implemented their method on CD cell responses to approximate the effects of absolute refractoriness not included in the CD model. Introducing refractoriness resulted in response peaks that were slightly skewed in favor of earlier times; however, it did not substantially alter the rate and temporal metrics used to characterize CD cell responses. Furthermore, the characterization of CN units as resembling CD cells or AN fibers based on their responses to Huffman stimuli remained unchanged after simulating refractory effects.

Role of Inhibitory Inputs to CN Cells

In this work, all inputs to the CD model cells were assumed to be excitatory and from AN fibers, even though many CN cells also receive inhibitory inputs from sources other than the AN. The sources of inhibitory inputs are diverse and include the dorsal CN (Oertel and Wickesberg 1993; Wickesberg and Oertel 1990), the contralateral CN (Babalian et al. 2002; Needham and Paolini 2003; Wenthold 1987), and descending input from the superior olivary complex (Ostapoff et al. 1997). There is evidence that inhibition plays an important role in shaping the responses of some CN unit types (Evans and Zhao 1993; Gai and Carney 2008; Kopp-Scheinpflug et al. 2002). In contrast to the excitatory inputs from AN fibers, the inhibitory inputs to the CN arrive indirectly, resulting in longer delays that are difficult to estimate without knowing the specific source of these inputs. Because the responses of CN units to the click-like Huffman stimuli decay after only a few milliseconds, delayed inhibitory inputs may not play a major role in shaping the responses to such transient stimuli. On the other hand, if some of the inhibitory inputs have a slow time course so as to provide sustained inhibition to CN cells, their main effect would be to increase the firing threshold of the CN cells, an effect that can be mimicked to a degree by increasing the parameter L in our CD models.

CF Range of Inputs to Primary-Like Units

Our estimates of the CF range of inputs to CN cells based on the maximum likelihood test are only in partial agreement with those of Young and Sachs (2008) based on correlations between simultaneously recorded pairs of spike trains from AN fibers and individual units in the ventral CN. Young and Sachs only observed significant correlation when the CFs of the AN fiber and the paired CN cell differed by <0.25 octave, suggesting that the functional range of inputs to their CN cells is limited to ∼0.25 octave. This estimate is consistent with our maximum likelihood results for Pri units, which were typically found to resemble AN fibers rather than CD cells (implying w ∼0), but not for Pri-N units, where our estimate of CF range of inputs typically exceeded 1/3 octave and even 2/3 octave in some cases. Unfortunately, Young and Sachs (2008) did not report the number of Pri-N units in their sample (which included 17 correlated pairs comprising either a Pri or Pri-N unit), so it is difficult to assess the reliability of this apparent discrepancy. The Young and Sachs sample consists almost entirely of units with CFs above 3 kHz, while we only studied units with CFs below 3 kHz; it is possible that the CF range of inputs is wider in low-CF regions than in high-CF regions, consistent with the wider bandwidths (in octaves) of cochlear tuning at low CF. It is further possible that our broadband Huffman stimuli were effective in recruiting a wider range of inputs to Pri-N cells than the pure-tone stimulation used by Young and Sachs (2008). Their data typically failed to show any correlation at higher sound levels, even for AN-CN pairs that showed strong correlation near threshold, suggesting that the correlation technique is ineffective at detecting the effects of AN inputs in certain conditions.

Onset Units and Coincidence Detection

The failure of the maximum likelihood test to consistently identify On units as CD cells in our small sample (n = 3) was unexpected because On units are usually modeled as coincidence detectors (Cai et al. 1997; Kalluri and Delgutte 2003a, 2003b; Levy and Kipke 1998; Rothman et al. 1993). This discrepancy may arise through our use of stimuli and models that are not optimal for characterizing the responses of On units. The CN cells that give rise to On responses may receive inputs from a wider range of CFs than the maximum 1 octave considered in this study. Specifically, McGinley et al. (2012) estimate that octopus cells (one of the CN cell types giving rise to On units) receive AN inputs from one-third of the extent of the tonotopic axis in the mouse, which corresponds to a CF range of 1.6 octaves. Huffman stimuli only manipulate the spatio-temporal pattern in the AN over a restricted CF range near FT. If a cell receives input from AN fibers beyond this CF range, its responses to Huffman stimuli may be relatively insensitive to changes in spatio-temporal pattern limited to this narrow FT region. Thus Huffman stimuli may not be ideal for assessing the spatio-temporal sensitivity of On units. Furthermore, the maximum number of AN inputs to CD cells examined in this work was 16, while cells giving rise to On patterns may receive a much larger number of inputs (>60 for octopus cells in mice; Oertel et al. 2000). The analytic CD model used here (Krips and Furst 2009) is very efficient for a small number of inputs, but its computational requirements increase exponentially with N, so that running the CD model with large values of N was not practical. More realistic models of On neurons would take into account the membrane properties of these cells and use a larger number of inputs with explicit spiking (Cai et al. 1997; Kalluri and Delgutte 2003a, 2003b; Levy and Kipke 1998).

Chopper Units and Coincidence Detection

We did not apply the maximum likelihood test to chopper units because their responses to Huffman stimuli clearly differed from those of CD model cells in that responses of chopper neurons rarely showed clear peaks indicative of phase locking to the temporal fine structure. Nevertheless, some chopper units showed clear differences in their response patterns to Huffman stimuli with different transition widths, suggesting they may be sensitive to the spatio-temporal pattern of AN activity, albeit by a mechanism distinct from simple coincidence detection. Stellate cells (which give rise to chopper response patterns) receive multiple inputs from the AN in the form of small bouton endings (Cant 1981; Redd et al. 2002). In principle, these cells could implement spatio-temporal sensitivity in their dendrites if they receive inputs from a range of CFs, even if precise timing and phase locking is subsequently lost as the postsynaptic potentials propagate to the cell body. Indeed, Carney (1990) identified a majority (6/8) of transient chopper (Ch-T) neurons in her sample as phase sensitive based on an overall rate preference for the broad transition at low stimulus levels. Although we have shown that RD_Total is not a reliable indicator of cross-frequency CD for neurons sensitive to the temporal fine structure, it may be a more useful metric for neurons such as choppers that are more sensitive to the envelope (Sayles and Winter 2007; Shofner 1999) because of the smaller envelope dispersion across CF for the broad-transition stimulus (Carney 1990).

Contrary to Carney (1990), our sample of 10 Ch-T neurons did not show an overall rate preference for the broad-transition stimulus at low stimulus levels (Fig. 12). Both Ch-T and Ch-S neurons (n = 10) showed an overall rate preference for the sharp-transition stimulus at higher stimulus levels, consistent with the longer duration of the stimulus waveform (Fig. 1A) and AN response patterns (Fig. 1B) for the sharp-transition stimulus and the idea that chopper neurons act as integrate-and-fire neurons (Hewitt et al. 1992; Laudanski et al. 2010; Molnar and Pfeiffer 1968; van Gisbergen et al. 1975). Possible reasons for the differences between the Carney (1990) study and ours are the relatively small sample sizes, variability among Ch-T units, and sampling biases in the regions of the CN that were studied. Also, as already mentioned, the energy in Carney's broad-transition stimuli was ∼2 dB higher than the energy in her sharp-transition stimuli, which could contribute to the increased occurrence of positive RD_Total in her data.

Functional Implications of Cross-Frequency Coincidence Detection

Our main finding is that the majority of Pri-N and some PhL and HiS units have responses consistent with those of cross-frequency CD cells. This monaural cross-frequency CD mechanism results in a temporal sharpening across frequency channels that has functional implications for the processing of sound.

The cell types associated with Pri-N and HiS response patterns are globular bushy cells, which project to the contralateral medial nucleus of the trapezoid body (MNTB) via thick axons and giant synapses (calyces of Held), thereby ensuring accurate transmission of their temporal response patterns (Smith et al. 1991, 1998). MNTB neurons in turn form glycinergic inhibitory projections to binaural neurons in the ipsilateral medial superior olive (MSO) and lateral superior olive (LSO) (Smith et al. 1998). MSO neurons are tuned to interaural time differences (ITD) primarily by detecting the coincidence of bilateral excitatory inputs from CN spherical bushy cells (Yin and Chan 1990). Their ITD tuning appears to be influenced in vivo by inhibitory inputs ultimately originating from globular bushy cells (Brand et al. 2002; Pecka et al. 2008), although a role for inhibition in ITD tuning of MSO neurons has been questioned based on in vitro experiments (Roberts and Golding 2012). As shown by our results, these inhibitory inputs are largely derived from cross-frequency CD cells, suggesting that the ITD tuning of MSO neurons might be sensitive to the local spectro-temporal features of the sound stimuli in the vicinity of their CF. Testing the ITD tuning of MSO neurons with Huffman stimuli may prove informative in exploring the functional consequences of cross-frequency CD.

LSO neurons are sensitive to interaural level differences (ILDs) through comparison of ipsilateral excitatory inputs from spherical bushy cells and contralateral inhibitory inputs derived from globular bushy cells via the MNTB (Glendenning et al. 1985, 1991). Our results suggest that the contralateral inhibitory inputs are derived from cross-frequency CD cells, while the ipsilateral, excitatory inputs arise from Pri units, which behaved much like AN fibers in response to Huffman stimuli. This asymmetry may have consequences for the dependence of ILD sensitivity of LSO neurons on overall sound level. Specifically, at high sound levels, the cochlear filters widen, the firing rates of AN fibers saturate, and the degree of coincidence across CF increases in the spatio-temporal pattern of AN activity (Carney 1994). Cross-frequency CD cells have higher thresholds than AN fibers and convert the degree of cross-CF coincidence in the AN into a temporally sharpened rate response. Thus, if the contralateral inhibitory inputs to LSO neurons saturate less than the ipsilateral excitatory inputs, the inhibition should become relatively more potent at high levels. This should cause the steep portions of ILD functions of LSO neurons to shift toward the excitatory ear as overall stimulus level increases. There is evidence for such shifts at low levels in both the LSO and the inferior colliculus, which receives input from the LSO (Park et al. 2004; Tsai et al. 2010; Wenstrup et al. 1988). However, at higher stimulus levels, ILD functions tend to shift toward the inhibitory ear (Irvine and Gago 1990; Joris and Yin 1995; Semple and Kitzes 1987), contrary to our prediction. These physiological results were all from high-frequency units (>3 kHz), which are above the range of CFs considered in the present study. Responses of low-CF (<3 kHz) LSO neurons also show contralateral inhibition (Finlayson and Caspary 1991; Tollin and Yin 2005), but whether the ILD functions of these neurons shift with overall stimulus level has yet to be addressed.

In summary, our results suggest that some of the inhibitory inputs that shape sensitivity to binaural cues in MSO and LSO are derived from a circuit that performs monaural cross-frequency coincidence detection. This observation leads to testable predictions about how ITD and ILD tuning depend on the overall sound level and local spectro-temporal features of the stimulus. Cross-frequency CD cells in the CN may also play a role in pitch, loudness, masking, and timbre perception, although it is difficult to pinpoint a specific role for globular bushy cells in these phenomena because the underlying neural circuits are more poorly understood than those involved in binaural interactions.

GRANTS

This work was supported by National Institute on Deafness and Other Communication Disorders Grants R01 DC-002258 and P30 DC-005209.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: G.I.W. and B.D. conception and design of research; G.I.W. and B.D. performed experiments; G.I.W. analyzed data; G.I.W. and B.D. interpreted results of experiments; G.I.W. prepared figures; G.I.W. and B.D. drafted manuscript; G.I.W. and B.D. edited and revised manuscript; G.I.W. and B.D. approved final version of manuscript.

APPENDIX: MAXIMUM LIKELIHOOD TEST

We used a maximum likelihood test to quantitatively assess the similarity between responses of CN neurons to Huffman stimuli and those of CD model cells and AN fibers. The similarity was quantified based on six metrics measured from the responses of AN fibers, CD model cells, and CN neurons. These metrics are described in methods and, for each recording, can be represented by a vector y = [RD_Early, RD_Late, ND_Broad, ND_Sharp, PW_Broad, PW_Sharp].

We first characterized the responses of CD cells with different model parameters (each characterized by the vector x = [N, L, w]) by computing the distributions (histograms) of the six response metrics across a set of CD models driven by different AN inputs (125 responses from 44 fibers). For each vector x of CD parameters, six histograms (1 for each metric in y) across all 125 inputs were computed. We also computed the six histograms for AN fiber responses when FT was equal to the CF, which can be thought of as a CD cell with N = L = 1 and w = 0. Since the responses markedly varied with stimulus level, separate histograms were constructed for responses measured at low and high levels, with a cutoff at 29 dB re. CF tone threshold. The distributions are plotted as images in Fig. 7 for N = 10, L = 2 as a function of the CF range of inputs w. The distributions are normalized so that each row sums to 100%. Beneath each image is the histogram computed from the AN responses. Histogram images were smoothed twice with a three-point filter in both dimensions.

Our goal with the maximum likelihood test was to determine the CD model parameters x̂ that maximize the joint probability p(y_CN; x) of observing the six response metrics y_CN measured from a given CN cell. Since we did not have enough data to directly estimate the joint probability, we assumed statistical independence among the six metrics so that the joint probability is simply the product of the marginal probabilities shown in Fig. 7. Because responses of each CN cell were available at several stimulus levels, we also assumed statistical independence between recordings made at different levels, such that the overall probability of the observations made from a cell is the product of the distributions across metrics and across stimulus levels:

$$p\left(y_{CN};x\right)={\displaystyle \prod _{t=1}^{\#\text{levels}}{\displaystyle \prod _{m=1}^{6}p\left(y_{C{N}_{l,m}};x\right)}}$$

This overall likelihood is maximized with respect to the CD cell parameters x to estimate the model x̂ most likely to have produced the observed CN responses:

$$\widehat{x}=\underset{x\in X}{\arg \max }\left(p\left(y_{CN};x\right)\right)$$

The inset in Fig. 8, bottom right, shows the likelihood as a function of input range w for an example On unit, with N and L set at their most likely values, 4 and 2, respectively. The likelihood shows a well-defined maximum for w = 0.5 with a half-width of 0.22 octaves, showing that this CN neuron most resembles a wide-range CD cell. The likelihood functions for other CN units resembling CD model cells had similarly well-defined global maxima with median half-widths of 0.17 octaves (interquartile range 0.17–0.29 octave).