Electrophysiological characterization of Grueneberg ganglion olfactory neurons: spontaneous firing, sodium conductance, and hyperpolarization-activated currents

Abstract

Mammals rely on their acute olfactory sense for their survival. The most anterior olfactory subsystem in the nose, the Grueneberg ganglion (GG), plays a role in detecting alarm pheromone, cold, and urinary compounds. GG neurons respond homogeneously to these stimuli with increases in intracellular [Ca²⁺] or transcription of immediate-early genes. In this electrophysiological study, we used patch-clamp techniques to characterize the membrane properties of GG neurons. Our results offer evidence of functional heterogeneity in the GG. GG neurons fire spontaneously and independently in several stable patterns, including phasic and repetitive single-spike modes of discharge. Whole cell recordings demonstrated two distinct voltage-gated fast-inactivating Na⁺ currents with different steady-state voltage dependencies and different sensitivities to tetrodotoxin. Hodgkin-Huxley simulations showed that these Na⁺ currents confer dual mechanisms of action potential generation and contribute to different firing patterns. Additionally, GG neurons exhibited hyperpolarization-activated inward currents that modulated spontaneous firing in vitro. Thus, in GG neurons, the heterogeneity of firing patterns is linked to the unusual repertoire of ionic currents. The membrane properties described here will aid the interpretation of chemosensory function in the GG.

the grueneberg ganglion (GG) is a specialized olfactory subsystem located at the far-anterior end of the nasal cavity in many mammals (Fleischer et al. 2006a; Fuss et al. 2005; Grüneberg 1973; Koos and Fraser 2005; Roppolo et al. 2006; Storan and Key 2006). The subsurface neuronal clusters that comprise the GG are ensheathed by glial-like satellite cells (Brechbuhl et al. 2008; Liu et al. 2009; Tachibana et al. 1990). Axons of the GG in mice form 8–12 glomeruli in the caudal, necklace-like domain in the olfactory bulb (Fuss et al. 2005; Koos and Fraser 2005; Liu et al. 2009). GG neurons express olfactory marker protein (OMP) (Fleischer et al. 2006a; Koos and Fraser 2005; Liu et al. 2009; Storan and Key 2006) and signal transduction components necessary to utilize cGMP as the primary second messenger (Fleischer et al. 2009; Liu et al. 2009).

GG neurons in mice function in a variety of contexts. Most GG neurons exhibit increases in cytosolic [Ca²⁺] when exposed to a so-called alarm pheromone, composed of water-soluble compounds collected during the asphyxiation of mice (Brechbuhl et al. 2008). The vast majority of neurons in both in vivo (Mamasuew et al. 2008) and in vitro studies (Schmid et al. 2010) respond to cold with increased c-Fos levels and [Ca²⁺] bursts, respectively. Thermosensitive [Ca²⁺] bursts rely on tetrodotoxin (TTX)-sensitive Na⁺ channels (Schmid et al. 2010), supporting the idea that GG neurons encode and process information by firing action potentials. It also has been shown that GG neurons respond to dimethylpyrazine and related urinary compounds in vivo (Mamasuew et al. 2011).

The largely homogeneous responses in the GG organ within each sensory context suggest that a single GG neuron functions multimodally. Gene expression studies indicate that GG neurons express various potential odor receptors, including the membrane-bound guanylate cyclases pGC-G and pGC-A (Liu et al. 2009), the pheromone receptor V2r83 (Fleischer et al. 2006b), and several trace amine-associated receptors (Fleischer et al. 2007). In particular, pGC-G and V2r83 are expressed on the same sets of neurons (Fleischer et al. 2009). In vivo studies demonstrate that both cold temperatures and dimethylpyrazine are detected by the pGC-G/V2r83 neuronal subset (Mamasuew et al. 2010, 2011).

Previous studies on GG function have inferred neuronal activity from immediate-early gene expression (Mamasuew et al. 2008, 2011), cytosolic [Ca²⁺] elevations (Brechbuhl et al. 2008; Schmid et al. 2010), and alterations in animal stress behavior (Brechbuhl et al. 2008). It is not known if the responses seen in these assays correspond to uniform electrical behaviors in GG neurons. The anatomic properties of the GG have posed severe challenges to electrophysiological recordings. The glial sheath prevents access of microelectrodes. The surrounding cartilage precludes gentle dissociation of GG neurons. Even in organotypic preparations, a thin keratinized epithelium makes microelectrode recordings quite difficult (Brechbuhl et al. 2008; Liu et al. 2009). As a result, our knowledge about the membrane properties and electrical outputs of GG neurons is limited.

In the present study, patch-clamp experiments in acute slices were undertaken to gain an initial understanding of electrical transduction in the GG. We found evidence of functional heterogeneity in the receptor neurons. In extracellular recordings, we detected spontaneous firing that could be categorized into three intrinsic patterns. Whole cell recordings enabled an identification of two subtypes of fast-inactivating voltage-gated Na⁺ currents with different sensitivities to TTX and one type of hyperpolarization-activated cationic current (I_h). These Na⁺ currents confer two different modes of action potential generation based on membrane status and may underlie heterogeneous interpretations of evoked activity. We also incorporated the Na⁺ currents into a Hodgkin-Huxley computer model and analyzed their potential contributions to the spontaneous discharge pattern of a simulated GG neuron.

MATERIALS AND METHODS

Animal Care

Mice were maintained as per a Caltech Institutional Animal Care and Use Committee-approved protocol. Genetically modified mice that express green fluorescent protein (GFP) in mature olfactory neurons (OMP-GFP mice) were a gift from P. Mombaerts. Their generation and characterization have been previously described (Liu et al. 2009; Potter et al. 2001). All animals used were postnatal.

Electrophysiology

Recordings were performed on acute slices of the far-anterior nasal vestibule from OMP-GFP heterozygous mice aged postnatal days 4–14 (P4–P14). To prevent dissociation of protease-treated slices and neuronal activation artifacts resulting from CO₂ exposure (Chao et al. 2010), most recordings were performed in a bicarbonate-free extracellular solution, instead of the usual 95% O₂-5% CO₂ (carbogen)-saturated artificial cerebrospinal fluid (ACSF). Using the following protocol, we could obtain membrane seals of gigaohm resistance from the somata of >10 neurons per recording session.

Mice were transported from the Caltech animal facility to the dissection station, euthanized, and decapitated. The nasal vestibules were skinned, separated from the rest of the nasal cavity, and trimmed of excess tissue. Dissection and subsequent sectioning were performed in a cold glycerol-based saline solution (glycerol HEPES-buffered saline, or gHBS), to promote neuronal viability, containing (in mM) 272 glycerol, 2.5 KCl, 10 HEPES, 2 CaCl₂, 1.3 MgCl₂, and 10 d-glucose, pH 7.4 (adjusted with KOH).

After dissection, nasal vestibules were infiltrated with 4.5% low-melt agarose (LMA) in Ringer solution for 10 s at 37°C and immediately embedded in additional 4.5% LMA. LMA-embedded noses were allowed to solidify on ice for 1 min and were cut into 100-μm transverse slices containing GG neurons (5–7 slices per animal) in cold gHBS with the use of a Vibratome (VT-1000S; Leica).

Slices were washed with room-temperature HEPES-buffered saline (HBS) containing (in mM) 136 NaCl, 2.5 KCl, 10 HEPES, 2 CaCl₂, 1.3 MgCl₂, and 10 d-glucose, pH 7.4 (adjusted with NaOH). They were incubated with 0.1% prewarmed type II collagenase (Invitrogen) in HBS for 10 min at 37°C in a tissue culture incubator infused with 5% CO₂. Slices were rinsed with warmed HBS and recovered at 37°C in HBS for 5–25 min, depending on the animal's age. Slices were stored at room temperature for 5–300 min before recording. Recordings were performed in HBS at room temperature (23–25°C). Several slices were prepared with a glycerol-based artificial cerebrospinal fluid (gACSF) and recorded in ACSF superfused with 95% O₂-5% CO₂ as control experiments, according to recipes described previously (Xiao et al. 2009).

GG neurons were visualized with an upright microscope (BX50WI; Olympus) and blue-light (GFP) illumination. Slices were positioned and anchored in a perfusion chamber. Cell-attached and whole cell patch-clamp techniques were used to record electrophysiological signals with a MultiClamp 700B amplifier (Axon Instruments, Molecular Devices), Digidata 1322 analog-to-digital converters (Axon Instruments), and pClamp 9.2 software (Axon Instruments). Data were sampled at 10 kHz and low-pass filtered at 2 kHz. Junction potential was nulled just before seal formation.

The patch electrodes had resistances of 3–8 MΩ when filled with intrapipette solutions. For characterization of Na⁺ and putative Ca²⁺ currents, we used a CsCl-based intrapipette solution containing (in mM) 110 CsCl, 30 tetraethylammonium chloride, 10 HEPES, 1 CaCl₂, 2 MgCl₂, 2 Mg-ATP, and 5 EGTA, pH 7.4 (adjusted with CsOH). For current-clamp studies and characterization of K⁺ currents, we used a KCl-based intrapipette solution containing (in mM) 140 KCl, 10 HEPES, 1 CaCl₂, 2 MgCl₂, 2 K-ATP, and 5 EGTA, pH 7.4 (adjusted with KOH). Na⁺-free extracellular solution contained (in mM) 136 N-methyl-d-glucamine (NMDG), 2.5 KCl, 10 HEPES, 10 d-glucose, 2 CaCl₂, and 1.3 MgCl₂, pH 7.4 (adjusted with HCl). Predicted junction potentials between the patch pipette and the HBS bath solution were 2.7 mV for the CsCl-based intrapipette solution and 4.0 mV for the KCl-based intrapipette solution. Predicted junction potential for the KCl-based intrapipette solution in extracellular NMDG-based Na⁺-free solution was 9.3 mV. Junction potentials were corrected off-line during data analysis. Capacitance compensation was not performed unless otherwise noted; the capacitance of the patched cells was estimated off-line by integration of the exponential discharge function induced by a 5-mV voltage step from the holding potential. Series resistance compensation was not performed unless otherwise noted, when it was compensated to 50–90% by the MultiClamp 700B amplifier. Series resistances were normally in the range of 10–40 MΩ. Data were discarded when series resistances exceeded 40 MΩ.

GG neurons were selected for recording on the basis of 1) the presence of GFP, 2) a protruding surface amenable to patch pipette approach, and 3) the absence of intracellular granularity. Spontaneous firing was recorded in cell-attached mode, before breakthrough of the cell membrane. Current-voltage (I-V) relationships were derived from 0.1- to 2-s depolarizing pulses from various holding potentials (−55, −70, −85, or −120 mV) to test potentials between the holding potential and +50 mV at increments of 10 mV. I_h were evoked by 3-s hyperpolarizing pulses to test potentials between −55 and −135 mV with a decrement of 10 mV. Current-clamp studies were performed with 0.3- to 10-s current pulses.

TTX (50 nM–2 μM; Calbiochem) application and ion substitutions were performed by bath perfusion. Responses to 8-Br-cGMP were tested by 10-psi pressure ejection (Parker Instrumentation) from a filled patch pipette placed 20 μm from the cell soma. Unless otherwise noted, all chemicals were obtained from Sigma.

Immunohistochemistry

Immunohistochemistry was performed as previously described (Liu et al. 2009). Briefly, adult mice (age: >6 wk) were euthanized with CO₂ and decapitated. Nasal vestibules were dissected and fixed overnight in cold 4% paraformaldehyde in phosphate-buffered saline (PBS). After cryoprotection in ascending sucrose-PBS (maximum sucrose: 30% wt/vol) mixtures, nasal vestibules were rapidly frozen in Tissue-Tek O.C.T. (Sakura) and cryosectioned at 12-μm thickness at −23°C. Sections were adhered to glass slides and thawed in PBS. Slides were incubated with rabbit anti-HCN1 antibody (1:400; cat. no. APC-056; Alomone Labs) without Triton-X for 18 h at 4°C. After several washes with PBS, slides were incubated with biotinylated anti-rabbit antibodies and streptavidin-bound Alexa Fluor 555 probes (Invitrogen). Results were imaged on a Zeiss LSM510 upright confocal microscope with laser excitation at 488- and 543-nm wavelengths. Optical sectioning was performed at 2-μm thickness. Images were processed and reconstructed in ImageJ (NIH, Bethesda, MD). Other antibodies used were rabbit anti-S100β (1:1,000; Abcam, catalog no. ab52642) and rabbit anti-GFAP (1:600; Abcam, catalog no. ab7260).

RT-PCR

Adult mice (age: 2–3 mo) were euthanized with CO₂ and decapitated. Nasal vestibules were dissected and trimmed of excess tissue. GG organs and surrounding epithelium were carefully separated from the cartilaginous nasal septum and collected in 600 μl of Trizol reagent (Invitrogen) on ice. The solution was vigorously vortexed for 5 min or until the tissue was observed to dissociate. Chloroform (125 μl) was added to separate RNA from proteins, and after centrifugation the aqueous phase was preserved for subsequent isopropanol precipitation and ethanol cleaning. RNA pellets were redissolved in water at 50°C. First-strand synthesis was performed with 1 μg of RNA template using oligo-dT DNA primers with the SuperScript III kit (Invitrogen). The first-strand cDNA library (2 μl) was used for gene amplification using PCR with HotStar Taq (Qiagen). For control experiments, the RNA from a single cerebrum from an adult mouse (age: 2 mo) was extracted.

Primers for gene amplification were as follows (from 5′ end to 3′ end): Omp, forward ACTGGAACGTGGTTCTGGAC, reverse CACAGAGGCCTTTAGGTTGG; Hcn1, forward ACCAGCTGACATGCGCCAGAA, reverse GCTTCACGATCTGCTTCAGGATCTCGT; Hcn2, forward GAAGATGTTTGATGAGGACAGCAT, reverse GCACGCCGCATCATGGGGTAT; Hcn3, forward GGCGCCACGTGTTATGCCATG, reverse TCAGAGCGTTTCCGCTGCAG; and Hcn4, forward CAGCGACCAGATCCTCCCCGA, reverse GCGCAGAGCCCTAGCGGTTTT.

Data Analysis

Electrophysiological data were analyzed with Clampfit 9.2 and with custom-written routines in MATLAB 7.4.0. Current-voltage curves for inward Na⁺ currents were obtained by measuring the peak inward current amplitude within 1 ms after the depolarization command, to exclude the activation of axonal currents. For Ca²⁺ and K⁺ currents, peak currents during the depolarizing pulse were used. Data were then imported to MATLAB for off-line leak current subtraction. Activation and inactivation curves for Na⁺ and K⁺ channels were fit to a two-state (open or closed) Boltzmann sigmoid model with a single voltage-dependent transition. Half-activated voltages (V_1/2) were derived from the Boltzmann fit in MATLAB. Inactivation time constants (τ_h) were calculated by fitting Na⁺ currents to Hodgkin-Huxley equations (Hodgkin and Huxley 1952) for Na⁺ current (see Simulations). Action potential (AP) rise times were obtained from Clampfit. Unless otherwise indicated, values are means ± SE.

Spontaneous APs were extracted from >3-min traces using the template search feature of Clampfit 9.2. Templates were developed by visual identification of APs at the start of each trace, according to their rise time (<1 ms). APs were automatically scanned, and erroneous identifications were removed. Calculations of instantaneous firing frequencies, binned (total) firing frequencies, and clustering of firing rates were performed in MATLAB with custom-written routines. Clustering of instantaneous firing rates used to distinguish patterns of spontaneous discharge was performed with a Gaussian mixture expectation-maximization algorithm, with two expected means. Phasic and sporadic patterns of discharge were distinguished by the overlap of the two Gaussian functions that provided the resultant density estimation.

The time-dependent activation of I_h and inactivation of K⁺ currents were fitted to a two-component exponential function of the form

$$I_{\text{h}}=A{e}^{-\frac{t}{{\tau }_{\text{f}}}}+B{e}^{-\frac{t}{{\tau }_{\text{s}}}+C}$$

with t denoting time, I_h denoting current amplitude, A, B, and C indicating constants, and τ_f and τ_s representing the fast and slow time constants of activation and inactivation, respectively. Correlation coefficients were derived from fitting procedures in Clampfit 9.2.

Simulations

Currents recorded in voltage-clamp experiments were modeled with NEURON 7.1 (Hines and Carnevale 1997). Unless otherwise mentioned, we used the default settings of NEURON for modeling. The modeled currents were the TTX-resistant (TTX-R) Na⁺ current, TTX-sensitive (TTX-S) Na⁺ current, a single voltage-gated K⁺ current, and a nonspecific leak current. The data were fitted to Hodgkin-Huxley rate equations (Hodgkin and Huxley 1952). APs were simulated within a single somatic cylindrical compartment with a radius of 6 μm and a length of 6 μm. The effects of current injections on membrane potential were simulated with a stimulating electrode placed at the center of the soma. Table 1 describes the main topological and electrical parameters used in the construction of the model. These parameters were derived from the voltage-clamp data. All programming code was deposited to ModelDB (http://senselab.med.yale.edu/modeldb/).

Table 1.

Constants used in NEURON simulations of GG neurons

Constant	Value Chosen	Estimation Method
Cm, μF/cm2	1.0	Hodgkin and Huxley (1952)
r, μm	6.0	Capacitance measurements in whole cell mode, 5-mV test pulse
VNa, mV	+50	Voltage-clamp data, depolarization protocols
VK, mV	−80	Voltage-clamp data, tail currents
Vleak, mV	−60	Chosen so ionic current is 0 at V = −55 mV
ḠTTX-S, S/cm2	0.00244	Voltage-clamp data, depolarization protocols from a holding potential of −70 mV, divided by h∞ at −70 mV
ḠTTX-R, S/cm2	0.00244	Fractional shift of activation curve (G/Gmax) from −120-mV holding potential, with and without TTX
ḠK, S/cm2	0.00455	Voltage-clamp data, depolarization protocols from −70-mV holding potential
Ḡleak, S/cm2	8.98 × 10−6	Chosen so ionic current is 0 at V = −55 mV

Values are constants used in simulations of Grueneberg ganglion (GG) neurons. C_m, membrane capacitance; r, spherical radius. See text for other definitions.

Na⁺ currents.

Na⁺ currents were modeled using the Hodgkin-Huxley formalism (Hodgkin and Huxley 1952)

$$I_{\text{Na}}={\overline{G}}_{\text{Na}}{m}^{3}h\left(V-V_{\text{Na}}\right)$$

with I_Na representing the Na⁺ current, Ḡ_Na the maximal Na⁺ conductance, m and h the parametric activation and inactivation gates, respectively, V the membrane potential, and V_Na the reversal potential of Na⁺. G/G_max activation curves (shown in Fig. 5E) were set equal to m_∞³; I/I_max inactivation curves in the same figure were set equal to h_∞. Estimates for τ_h and τ_m were obtained by fitting depolarization-evoked Na⁺ currents in voltage-clamp recordings to the functional form

$$I_{\text{Na}}=A+B{\left(1-e^{-\frac{t}{{\tau }_{\text{m}}}}\right)}^3{e}^{-\frac{t}{{\tau }_{\text{h}}}}$$

with t representing time (ms) and values for A, B, τ_h, and τ_m determined in MATLAB. The values of the rate constants α_m, β_m, α_h, and β_h could be calculated using the relations described by Hodgkin and Huxley (1952) (e.g., α_m = m_∞/τ_m).

Fig. 5.

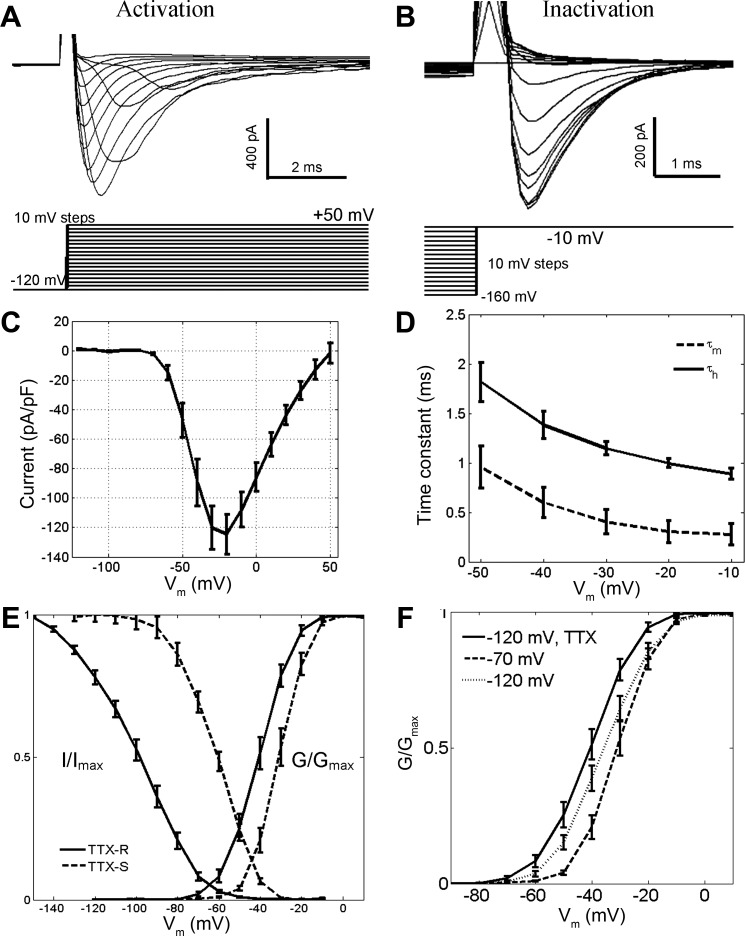
Activation and steady-state inactivation properties of Na⁺ currents in GG neurons. A: selective activation of fast-inactivating TTX-resistant (TTX-R) Na⁺ currents (top) was achieved with depolarizing pulses from a holding potential of −120 mV (bottom) in 0.1 μM TTX. B: steady-state inactivation of TTX-R currents (top) was characterized by depolarizing pulses to a test potential of −10 mV from various prepulse potentials (bottom) in 0.1 μM TTX. C: the current-voltage (I-V) relationship for TTX-R currents demonstrates their reversal potential near +50 mV. D: Hodgkin-Huxley activation (τ_m) and inactivation (τ_h) time constants for TTX-R currents were fast and voltage dependent. E: activation and steady-state inactivation curves of TTX-R and TTX-S currents. Fits are reported in text. Activation properties of TTX-S currents were characterized by test depolarizations from holding potentials more positive than −70 mV; steady-state inactivation properties were calculated by subtraction of TTX-R currents from total Na⁺ currents. F: the total activation curve of Na⁺ currents, derived from depolarizing pulses from a holding potential of −120 mV in saline, shows contributions from activation curves of isolated TTX-R (−120 mV, TTX) and TTX-S currents (−70 mV). Error bars in C–F represent SE. V_m, membrane potential.

Currents evoked by depolarizations from a holding potential of −70 mV, in cells patched with pipettes filled with a CsCl-based solution, were used to determine the Hodgkin-Huxley rate equations for TTX-S currents. The rates depended on membrane potential such that

$$\begin{array}{c}{\alpha }_{\text{m}}=\frac{0.5\left(-V-33\right)}{e^{\frac{-V-33}{4}}-1},{\beta }_{\text{m}}=2.4e^{\frac{-V-65}{21}}\\ {\alpha }_{\text{h}}=1.1e^{\frac{-V-65}{8}},{\beta }_{\text{h}}=\frac{1}{1+e^{\frac{-V-50}{4}}}\end{array}$$

Currents evoked by depolarizations from a holding potential of −120 mV, in cells bathed in 0.1 μM TTX and patched with pipettes filled with a CsCl-based solution, were used to determine the rate equations for TTX-R currents. The rates were

$$\begin{array}{c}{\alpha }_{\text{m}}=\frac{0.25\left(-V-54\right)}{e^{\frac{-V-54}{2.3}}-1},{\beta }_{\text{m}}=0.86e^{\frac{-V-66}{29}}\\ {\alpha }_{\text{h}}=0.025e^{\frac{-V-65}{10.5}},{\beta }_{\text{h}}=\frac{1.6}{1+e^{\frac{-V-43}{31}}}\end{array}$$

K⁺ currents.

K⁺ currents were modeled using the Hodgkin-Huxley formalism (Hodgkin and Huxley 1952)

$$I_{\text{K}}={\overline{G}}_{\text{K}}{n}^4\left(V-V_{\text{K}}\right)$$

with I_K representing the K⁺ current, Ḡ_K the maximal K⁺ conductance, n the parametric activation gate, V the membrane potential, and V_K the reversal potential of K⁺. A G/G_max activation curve was calculated from the sustained depolarization-activated K⁺ currents observed in voltage-clamp recordings (from a holding potential of −65 mV); this activation curve was set equal to n_∞⁴. Estimates for τ_n were computed by fitting K⁺ currents obtained from GG neurons bathed in Na⁺-free saline, patched with pipettes filled with a KCl-based solution. The fitting equation was

$$I_{\text{K}}=A+{\left(B-B{e}^{-\frac{t}{{\tau }_{\text{n}}}}\right)}^4$$

Rates were described by the following relations:

$${\alpha }_n=\frac{0.007\left(1-V-66\right)}{e^{\frac{-V-66}{1.4}}-1},{\beta }_{\text{n}}=0.37e^{-\frac{-V-66}{35}}$$

Leak currents.

Leak currents were represented by the following equation:

$$I_{\text{leak}}={\overline{G}}_{\text{leak}}\left(V-V_{\text{leak}}\right)$$

with I_leak representing the leak current, Ḡ_leak the maximal leak conductance, V the membrane potential, and V_leak the reversal potential of the nonspecific ions assumed to comprise the leak current. Ḡ_leak was calculated with V_leak = −60 mV such that the total ionic current equaled 0 (I_i = 0) at V = −55 mV, the average resting potential of GG neurons. This was performed by using the equation

$$I_{\text{i}}=I_{\text{Na}}+I_{\text{K}}+I_{\text{leak}}$$

and using the steady-state values m_∞, h_∞, and n_∞ for m, h, and n, respectively.

Analysis of neuronal excitability.

Simulations of 300-ms duration were performed inside nested loops that iterated over increasing amplitudes of depolarizing current injection (inner loop), various initial membrane potentials (middle loop), and different permutations of values for maximal membrane conductances (step size of 5%) of Na⁺ channels (outer loop). Sampling frequency was 40 kHz. Maximal leak conductance and E_leak were continually adjusted such that 1) the tested initial membrane potential was stable for the first 25 ms of the simulation, 2) maximal leak conductance always exceeded 0, and 3) |V_i − V_leak| ≤ 5 mV, where V_i denotes the initial membrane potential. This produced a different maximal leak conductance at different membrane potentials. However, the differences in the resultant leak currents were small (<1%) compared with stimulating current amplitudes. APs were collected in an unbiased manner as time points when V > −20 mV within 10 ms following the injection of current. Shifts in the modeled activation and inactivation curves of TTX-R currents were achieved by shifting the abscissa (V_m) in the plot of kinetic parameters α_m, β_m, α_h, and β_h and repeating the fitting procedure. In individual experiments that involved modification of maximal Na⁺ conductances, either Ḡ_TTX-R or Ḡ_TTX-S was changed, but not both. Data were exported to text files and analyzed in MATLAB.

RESULTS

We investigated the membrane biophysics of mouse GG neurons by performing patch-clamp electrophysiological recordings from acute slices of the far-anterior mouse nose. These slices were prepared from young (P4–P14) OMP-GFP mice, in which all mature olfactory neurons, including the GG collection, are highlighted by GFP expression (Potter et al. 2001). Even in these young animals, the glial ensheathing layer was evident in immunolabeling experiments with antibodies raised against S100β and GFAP (data not shown). The brief exposure of slices to diluted collagenase facilitated the access of micropipettes to GG neurons (Fig. 1, A and B) but did not cause neuronal damage. GG neurons retained the ciliary localization of the membrane-bound guanylate cyclase pGC-G (Liu et al. 2009) and continued to express GFP (Fig. 1, B and C). Extracellular recordings showed that the neurons were excited by 20-s pressure ejections of 1.3 mM 8-Br-cGMP (Fig. 1D). Thus GG neurons functionally retain their identities as cGMP-transducing cells in this acute slice preparation.

Fig. 1.

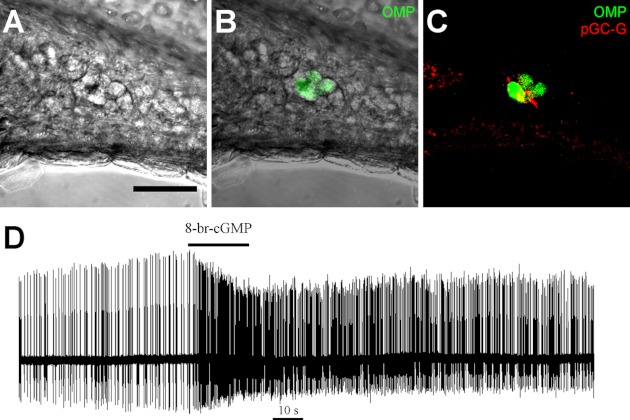
Grueneberg ganglion (GG) neurons in acute slices. Transverse slices of the young mouse nasal vestibule were treated with collagenase. A: protruding surfaces of GG neurons were visible with brightfield optics. B: their identity could be verified with green fluorescent protein (GFP) expression in olfactory marker protein (OMP)-GFP mice. C: GG neurons retained expression of the guanylate cyclase pGC-G on cilia. D: in cell-attached recordings, GG neurons were excited by 20-s puffs of a membrane-permeable cGMP analog (1.3 mM 8-Br-cGMP). The trace shows spontaneous firing. The horizontal black line indicates puff onset and duration. Scale bar, 40 μm.

Spontaneous Firing

In extracellular loose-seal recordings, we observed that GG neurons discharged APs in the absence of stimulation. The temporal patterns of discharge of 89 neurons were grouped into three categories: 1) repetitive single spike (RSS), 2) phasic, and 3) sporadic.

The RSS pattern was found in 34 neurons (38%). This pattern was characterized by a continuous discharge of APs at regular intervals (Fig. 2A), resulting in firing frequencies of 10–25 Hz (mean: 15.2 ± 0.9 Hz). A single mean instantaneous firing rate is visible on representative frequency vs. time plots of RSS firing (Fig. 2B).

Fig. 2.

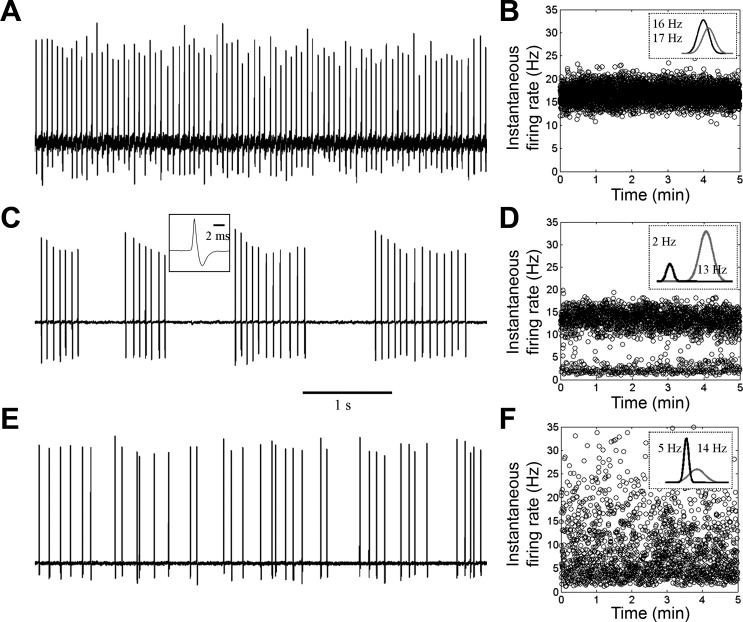
Spontaneous firing in GG neurons. Extracellular recordings revealed that GG neurons spontaneously discharge action potentials (APs) in repetitive single-spike (RSS; A and B), phasic (C and D), or sporadic patterns (E and F). A, C, and E show 5-s typical traces. B, D, and F show representative frequency vs. time plots of each firing pattern over 5 min. Insets within frequency vs. time plots show Gaussian density estimates of instantaneous frequencies with annotated means. Inset in C shows a typical AP waveform.

The phasic pattern was found in 26 neurons (29%). This pattern consisted of bursts of APs followed by periods of electrical quiescence (Fig. 2C), resulting in an interburst frequency of 0.5–3 Hz (mean: 2.4 ± 0.3 Hz) and a variable intraburst frequency of 10–40 Hz (mean: 19.5 ± 0.6 Hz). Two mean firing rates whose difference is >5 Hz are evident on representative frequency vs. time plots of phasic firing, with lower and higher mean values corresponding to interburst and intraburst frequencies, respectively (Fig. 2D). The coefficients of variation of these two distributions are small, allowing unambiguous fits to the firing frequencies with Gaussian functions.

The sporadic pattern was found in 29 neurons (33%). This pattern was composed of randomly discharged APs (mean firing frequency: 4.9 ± 0.7 Hz) (Fig. 2E). There are two mean firing rates on representative frequency vs. time plots of sporadic firing (Fig. 2F). The lower mean value is <75% of the higher mean value. Because of higher variation in firing frequencies, density estimation is provided by overlapping Gaussian descriptors of the data.

In extracellular recordings of up to 20 min, we observed no instances of spontaneous transition between firing patterns in a single neuron. Examples of all three major firing patterns could be found in separate neurons within a single slice originating from a single animal. We observed that neighboring neurons within a ganglionic cluster fired in different patterns.

Intracellular recordings, obtained from the whole cell patch-clamp configuration, demonstrated the effects of current injections on the firing pattern. Although breakthrough could alter firing rate, it did not alter the spontaneous firing pattern (data not shown). Figure 3 shows the electrical manipulation of distinct GG neurons that exhibited the various patterns of spontaneous discharge. From the resting potential, we injected currents of 10-s duration in serial steps of 10-pA magnitude in the range between −30 and +50 pA. Figure 3, A–C, shows that hyperpolarization of the resting potential inhibited repetitive firing. In contrast, injection of depolarizing current evoked a burst of APs. After burst termination, the rates and patterns of spontaneous firing could be monitored at a steady-state membrane potential.

Fig. 3.

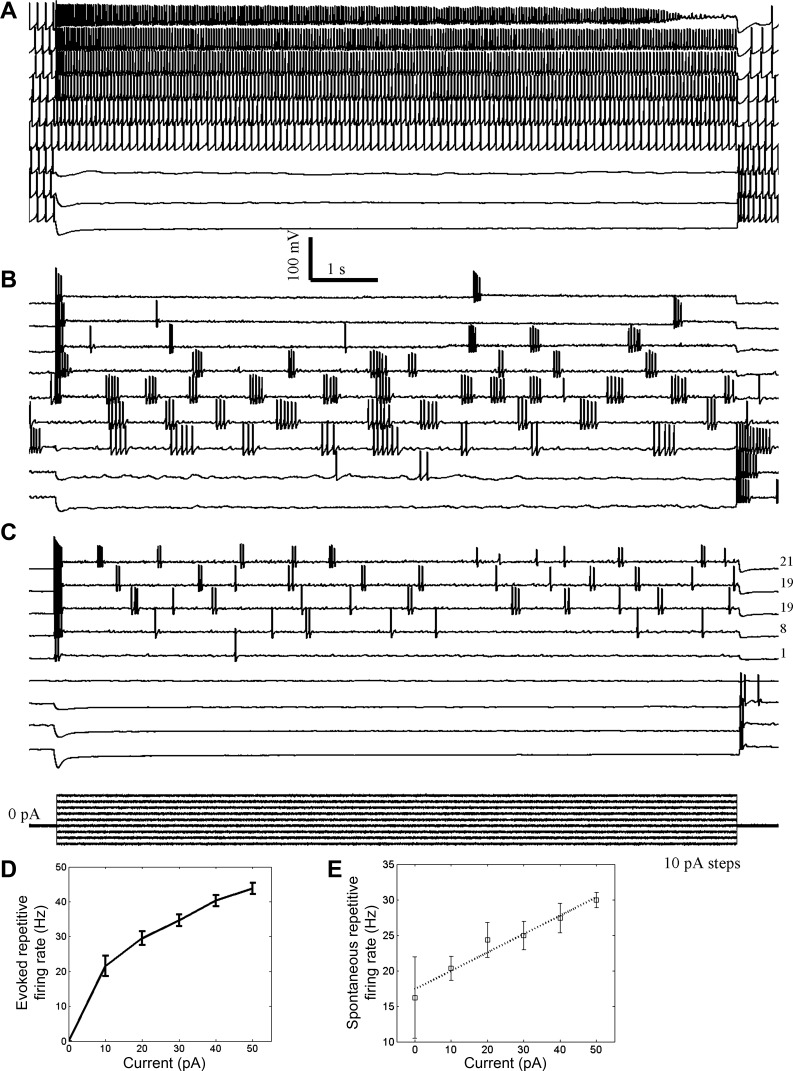
The pattern of spontaneous discharge is an intrinsic property of a GG neuron. In intracellular current-clamp recordings, 10-s serial hyperpolarizing and depolarizing currents (10 pA per step) were injected from the resting membrane potential (defined as 0 pA, approximately −55 mV). The effects of current injections were observed on RSS firing (A), phasic firing (B), and sporadic firing (C). Numbers at right in C indicate the total number of spikes evoked from the steady-state membrane potential. Note anode-break excitation. The stimulus waveform is shown in C (bottom). The relationship of depolarizing current injection to firing rate is shown for evoked firing (D) and spontaneous firing (E) from the new membrane potential baseline. The dotted line in E is a linear fit to the data.

The three main firing patterns observed in GG neurons represent intrinsic modes of discharge. Figure 3, A and B, demonstrates the mutual stabilities of RSS and phasic firing, respectively, in that depolarization of the resting potential does not convert RSS firing to phasic firing, and vice versa. At strongly depolarized resting potentials, the repetitive firing of RSS- and phasic-firing neurons was inhibited and could give the outward appearance of sporadic discharge. However, Fig. 3C shows that sporadic firing can also be an intrinsic state of GG neurons. Phasic or RSS firing was not observed with stronger depolarization in this neuron. A small fraction (4/28, 14%) of neurons manipulated in this manner did not exhibit spontaneous activity at any tested resting potential.

Successive injections of depolarizing current were associated with increases in firing frequency. All three firing patterns putatively consist of repetitive elements, whose frequencies are represented by the total firing rate, intraburst rate, and higher mean value in the RSS, phasic, and sporadic patterns, respectively. The repetitive firing frequency is depicted relative to current injection for the depolarization-evoked burst (Fig. 3D) and for the spontaneous discharge (Fig. 3E) from the new steady-state baseline potential (n = 9). The firing frequency increased with stronger injections of depolarizing current.

Na⁺ Conductance

In voltage-clamp experiments, transient inward currents (with an exponential decay time <3 ms) and sustained outward currents were elicited by depolarizing pulses from a holding potential of −70 mV to test potentials more positive than −50 mV (Fig. 4A). The depolarizing pulses did not elicit outward currents when we used a Cs⁺-based intrapipette solution (Fig. 4B) and did not evoke inward currents in the presence of 50 nM TTX (Fig. 4C) or in Na⁺-free extracellular solution containing an equimolar substitution of NMDG for Na⁺ (data not shown). Therefore, the inward and outward currents are mediated by voltage-gated Na⁺ and K⁺ channels, respectively.

Fig. 4.

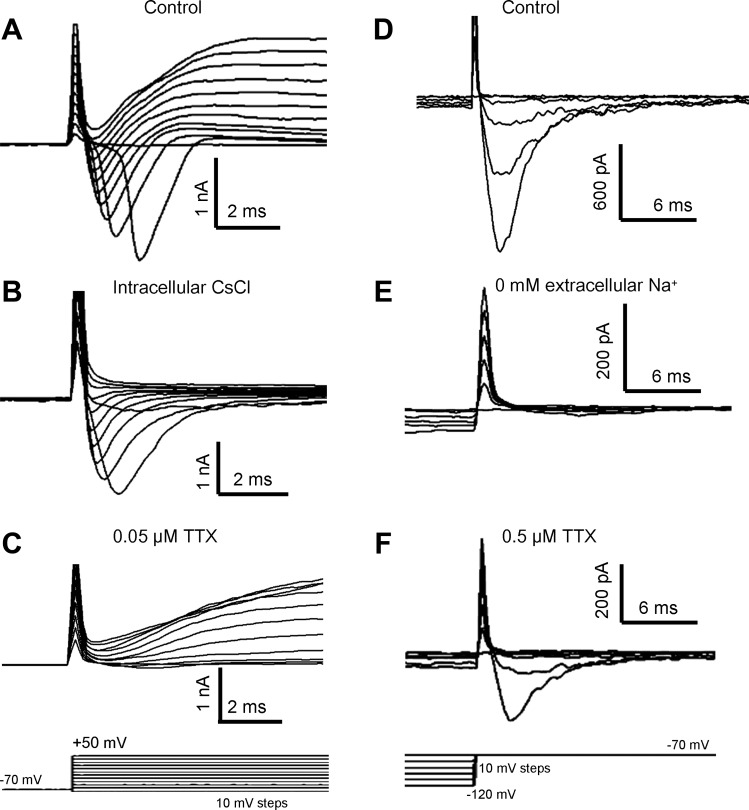
Whole cell voltage-dependent currents in GG neurons. A–C: depolarization to test potentials in the range of −50 to +50 mV from a holding potential of −70 mV (C, bottom) induced membrane currents in GG neurons. A: depolarization pulses evoked transient inward currents and sustained outward currents. B: outward currents were absent when patch pipettes were filled with 110 mM Cs⁺ and 30 mM tetraethylammonium. C: bath application of 50 nM tetrodotoxin (TTX) abolished most inward currents. D–F: repolarization back to −70 mV from hyperpolarized test potentials in the range of −120 to −100 mV (F, bottom) elicited transient inward currents (D). These inward currents were eliminated by removal of extracellular Na⁺ (E) but remained in the presence of 0.5 μM TTX (F). Traces shown are from different neurons but are representative.

To characterize Na⁺ currents, we used the Cs⁺-based intrapipette solution. Surprisingly, depolarizing pulses to a test potential of −70 mV from holding potentials in the range of −120 to −100 mV elicited inward currents in 69% (24/35) of GG neurons (Fig. 4D). These inward currents exhibited an exponential decay time <2 ms. They were still found in GG neurons recorded under alternate experimental conditions: without collagenase treatment in adult mice (age: 1.5 mo), with carbogen-bubbled ACSF serving as the extracellular medium and with capacitance and series resistance compensation up to 90%. Replacing extracellular Na⁺ with NMDG abolished these currents (Fig. 4E), identifying their conducting ion as Na⁺. They persisted in 0.5 μM TTX (Fig. 4F).

These results can be explained simply if the total inward Na⁺ current in GG neurons is composed of two distinct components. One component is activated at membrane potentials more positive than −50 mV and likely inactivated at potentials more positive than −65 mV. This component is TTX sensitive (TTX-S). The other component is activated at potentials more positive than −70 mV and inactivated at potentials more positive than −90 mV. This second component exhibits moderate TTX resistance (TTX-R). TTX-S and TTX-R currents have different steady-state voltage dependencies such that at a holding potential of −70 mV, TTX-R currents are inactivated and depolarizing pulses selectively activate TTX-S currents. TTX-R and TTX-S currents are likely conducted through two distinct Na⁺ channels with differential sensitivities to TTX. We performed experiments to examine systematically the I-V relationship of the Na⁺ conductance in GG neurons; the results described below support this interpretation of the phenomena.

To characterize the activation of TTX-R currents, we included 0.1 μM TTX in the extracellular solution and applied depolarizing pulses of 100-ms duration from a holding potential of −120 mV (Fig. 5A). TTX-R currents were found in all examined GG neurons at all times. The I-V curve in Fig. 5C shows that TTX-R currents had a reversal potential near +50 mV, consistent with a current carried by Na⁺. The time constants of activation (τ_m) and inactivation (τ_h) were fast (<1 ms and <2 ms, respectively) and were voltage dependent (Fig. 5D). The activation curve for TTX-R currents had a midpoint (V_1/2) of −44 ± 1.8 mV and a slope factor of 6.6 mV (n = 19) (Fig. 5E). TTX-R currents were not activated by depolarizing pulses in a higher extracellular concentration of TTX (2 μM; data not shown). To study steady-state inactivation of TTX-R currents, we depolarized TTX-perfused GG neurons to a test potential of −10 mV from various holding potentials more positive than −160 mV (Fig. 5B). As shown in Fig. 5E, the inactivation curve of TTX-R currents had a midpoint V_1/2 of −103 ± 2.0 mV and a slope factor of −13 mV (n = 17).

To study the I-V relationship for TTX-S currents, we applied depolarizing pulses from a holding potential of −70 mV, at which TTX-R currents are inactivated, in TTX-free extracellular saline. The activation curve for TTX-S currents exhibited a midpoint V_1/2 of −34 ± 1.6 mV and a slope factor of 5.0 mV (n = 19) (Fig. 5E). This V_1/2 value represents a positive 10 mV shift compared with the activation V_1/2 of TTX-R currents, a statistically significant difference (P = 0.0001; 2-sample t-test). The voltage activation midpoint of TTX-S currents was indistinguishable between its calculation by either the prepulse method or the subtraction of TTX-R currents from total Na⁺ currents at a −120-mV holding potential.

The activation curve derived from a holding potential of −120 mV in neurons perfused with extracellular saline exhibited a midpoint V_1/2 of −39 ± 1.6 mV (n = 43) (Fig. 5F). This value differed significantly from the activation V_1/2 of isolated TTX-R and TTX-S currents (P = 0.0027; 2-sample t-test), being more positive than the V_1/2 of TTX-R currents and more negative than the V_1/2 of TTX-S currents. The shape of the activation curve was approximated by the linear summation of the individual activation curves of TTX-R and TTX-S currents, with a ∼55% contribution from the TTX-R curve and a ∼45% contribution from the TTX-S curve. The inactivation curve of the TTX-S currents was calculated by subtracting the inactivation curve for TTX-R currents from the inactivation curve for the total Na⁺ currents. The midpoint V_1/2 of inactivation for TTX-S currents was −65 mV, with a slope factor of −9.5 mV (Fig. 5E). These results are consistent with the dual composition of Na⁺ currents in GG neurons.

On average, the TTX-R currents had more hyperpolarized activation and inactivation curves than their TTX-S counterparts. However, an examination of the activation curves of Na⁺ currents in single neurons revealed that this was not always the rule. Within 5 min after breakthrough, we obtained the total activation curve of inward Na⁺ currents from holding potentials of −55, −70, −85, and −120 mV. At more negative holding potentials, there was a greater contribution of the TTX-R current to the total activation curve. In 9/30 (30%) GG neurons examined in this manner, the activation V_1/2 values derived from all four holding potentials were within a range of 3 mV, suggesting that TTX-R and TTX-S currents have similar activation voltage dependencies in these neurons. In the other 21 GG neurons, the activation V_1/2 values were successively more negative as the holding potential was changed from −70 to −120 mV. In these neurons, the shifting of activation V_1/2 values in the negative direction likely reflected the increasing contribution of the hyperpolarized TTX-R activation curve to the total activation curve.

Voltage-Dependent K⁺ and Ca²⁺ Currents

A hyperpolarized activation threshold may be a nonspecific property of more negative holding potentials and may be found in other ionic conductances in the GG. With this idea, we examined the activation curves of K⁺ currents. GG neurons were studied in the whole cell configuration with a K⁺-containing intrapipette solution and a Na⁺-free extracellular solution.

Figure 6A shows that, from a holding potential of −90 mV, long (2 s) pulses to test potentials in the range between −50 and +40 mV evoked outward currents. The outward currents exhibited a reversal potential of approximately −80 mV (Fig. 6B). These outward currents were sustained throughout the 2-s pulse at test potentials in the range between −60 and −10 mV. However, at test potentials more positive than −10 mV, a partially inactivating component of the outward current was observed (Fig. 6A). At a test potential of +20 mV, this inactivation had an exponential τ_f of 210 ± 77 ms and a τ_s of 2,800 ± 710 ms (n = 7). The steady-state component represented ∼70% of the peak current. We previously showed that all of these outward currents were absent when Cs⁺ replaced K⁺ in the intrapipette solution (Fig. 4B); thus the currents are carried by K⁺. The total K⁺ current (I_K) in GG neurons is thus composed of sustained and inactivating components.

Fig. 6.

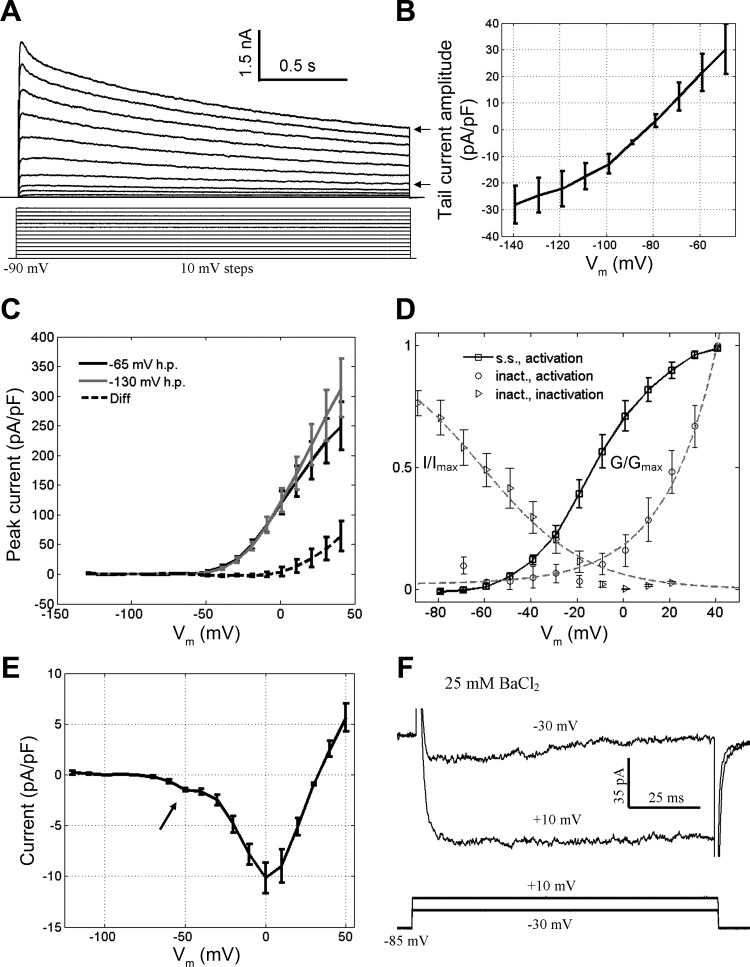
Properties of K⁺ and Ca²⁺ currents in the GG. A: 2-s depolarizing pulses from a holding potential of −90 mV evoked outward currents. Compare the inactivating current at more positive potentials with the steady-state current at less positive potentials (arrows). B: the I-V curve for the K⁺ tail currents (from a test potential of −20 mV) demonstrates a reversal potential near −80 mV. C: the I-V curves for K⁺ current activation from 2 different holding potentials (−65 and −135 mV) can be subtracted to isolate the I-V relationship for the inactivating component of I_K. D: approximate steady-state curves for the steady-state and inactivating components of I_K. Fits were as follows: steady-state activation: V_1/2 = −12 mV, slope = 14 mV (Boltzmann); inactivation: V_1/2 = −61 mV, slope = −22 mV (Boltzmann); activation of inactivating component: rise = 22 mV (exponential). E: the I-V curve of putative Ca²⁺ currents shows that a component is activated at resting potential (arrow). F: exposure of GG neurons to extracellular 25 mM BaCl₂ revealed that I_Ca consists of both inactivating (test potential of −30 mV) and persistent components (test potential of +10 mV). Data were collected from a holding potential of −85 mV. h.p., Holding potential; s.s., steady-state component; inact., inactivating component; G/G_max, normalized conductance; I/I_max, normalized current.

The inactivating component of I_K in GG neurons is dissimilar from the A-type current described by Connor and Stevens (1971b). We measured and subtracted the peak outward currents evoked by depolarizing pulses to test potentials in the range between −60 and +40 mV from two different holding potentials, −65 and −130 mV. Consistent with qualitative observations, the inactivating component of I_K was only activated at potentials more positive than −10 mV, well positive of the activation threshold of the sustained component of I_K (approximately −50 mV) (Fig. 6, C and D). We next applied depolarizing 2.5-s pulses to a test potential of +20 mV from prepulses in the range between −170 and +20 mV. Figure 6D shows full inactivation of the inactivating component of I_K only at membrane potentials more positive than 0 mV, well positive of resting potential. The K⁺ currents in GG neurons have the same activation threshold across different holding potentials (Fig. 6C). We did not explore pharmacological perturbations of the outward current.

In contrast to K⁺ currents and similar to Na⁺ currents, putative Ca²⁺ currents in the GG possess an inactivating low-threshold component. We examined the residual inward current, putatively the total Ca²⁺ current (I_Ca), using an intrapipette solution containing Cs⁺ and an extracellular solution containing 2 μM TTX. From a holding potential of −120 mV, 100-ms depolarizing pulses to test potentials in the range between −70 and +50 mV evoked inward currents. As shown in the I-V curve in Fig. 6E, the inward current magnitude exhibited two distinct components (n = 4). One component was activated near resting potential, and the other was activated at a value more positive than the resting potential. In 25 mM extracellular BaCl₂, the low-threshold component of I_Ca exhibited a gradual inactivation during a 100-ms depolarizing pulse (Fig. 6F); in contrast, the high-voltage-activated component did not appear to inactivate within 100 ms. The maximum magnitude of the observed inward I_Ca in physiological recording conditions was ∼70 pA, nearly 10-fold smaller than the tail currents observed in Fig. 4D.

Hyperpolarization-Activated Currents

In voltage-clamp experiments, hyperpolarizing pulses of 1.5-s duration from a holding potential of −55 mV revealed sustained inward currents (I_h) in most (26/30, 87%) GG neurons (Fig. 7A), suggesting the existence of hyperpolarization-activated cationic channels. I_h time-dependent activation could be described by a two-component exponential function (τ_f = 232 ± 27 ms; τ_s = 1,120 ± 690 ms, correlation = 0.98). The rate of onset (τ_f) was faster with larger currents (data not shown), consistent with previous descriptions of I_h (Lynch and Barry 1991). Similar to I_h in olfactory sensory neurons (Vargas and Lucero 1999), the currents in GG neurons were blocked by adding 5 mM CsCl to the extracellular solution (Fig. 7B). The I-V curve in Fig. 7C shows that the currents had a peak density of approximately −19 pA/pF at a test potential of −135 mV with an extracellular [K⁺] of 2.5 mM. The activation curve in Fig. 7D demonstrates an activation V_1/2 of −105 mV and a slope factor of −9.3 mV. In intracellular current-clamp experiments, we observed that injections of hyperpolarizing current induced voltage sags in GG neurons (Fig. 3, A–C), consistent with the predicted effect of I_h.

Fig. 7.

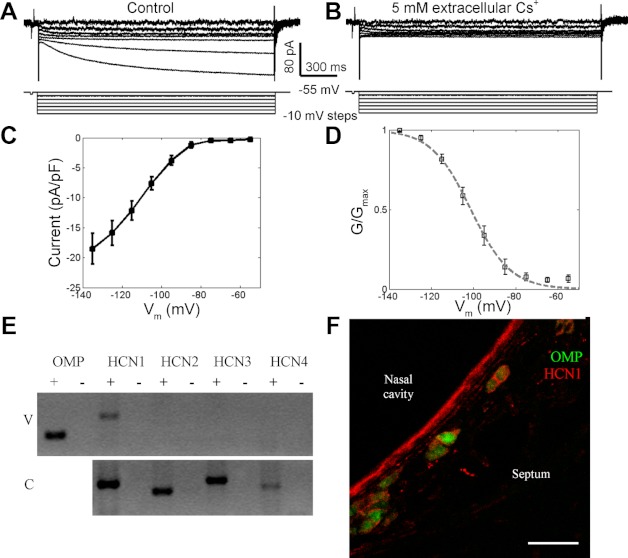
Hyperpolarization-activated currents (I_h) in GG neurons. A: hyperpolarizing pulses to test potentials in the range of −55 to −115 mV from a holding potential of −55 mV induced inward currents that developed over several hundred milliseconds. B: I_h was blocked by extracellular 5 mM Cs⁺. C: the I–V relationship for membrane hyperpolarization shows inward rectification at membrane potentials more negative than −90 mV. D: the activation curve of I_h has a midpoint of −105 mV and a slope factor of −9.3 (fit is shown by the dashed line). E: RT-PCR was used to detect mRNA of HCN (hyperpolarization- and cyclic nucleotide-activated channel) subtypes in the mouse nasal vestibule (V). Total RNA from a single mouse cerebrum (C) was used as a positive control for subtype cDNA amplification. + and − respectively denote reverse transcription reactions with and without reverse transcriptase. F: HCN1 antibody (red) labeled most GFP+ GG neurons (green) in OMP-GFP mice. The staining appears localized to the cell membrane. Scale bar, 30 μm.

Because hyperpolarization- and cyclic nucleotide-activated channels (HCN) mediate I_h (Biel et al. 2009), to test which channels mediated I_h, we performed RT-PCR in the nasal vestibule, where GG neurons reside, with cerebral tissue as a positive control (Fig. 7E). Only Hcn1 mRNA was detected in the nasal vestibule. To confirm the expression of HCN1 protein in GG neurons, immunofluorescence analyses were performed using an HCN1 antibody (Fig. 7F). HCN1 was detected in most GFP+ GG neurons. These results show that I_h in GG neurons was likely mediated by HCN1 channels.

Predictions and Measurements of Excitability

In whole cell recordings obtained with a K⁺ intrapipette solution, the mean V_m was −54 ± 2.4 mV (n = 31). At resting potential, the input resistance was 2.3 ± 0.5 GΩ. Because both TTX-R and TTX-S currents represent fast-inactivating Na⁺ conductance, they each can support APs. However, spontaneous APs were entirely absent when GG neurons were bathed with 0.1 μM TTX, suggesting that spontaneous APs were primarily mediated by TTX-S Na⁺ currents. This observation is consistent with the voltage-clamp data of Fig. 5E, showing the near-full inactivation of TTX-R currents at resting potential.

In the presence of 0.1 μM TTX, APs could be evoked from a resting potential of −90 mV, but not from −60 mV (Fig. 8A). This result agrees with the voltage-clamp data showing the deinactivation of TTX-R currents at negative potentials (Fig. 5E). In current-clamp recordings, we compared the APs supported by TTX-R currents only, TTX-S currents only, and both TTX-R and TTX-S currents by injecting 10-pA depolarizing current from baseline potentials of −120 mV in 0.1 μM TTX, −60 mV in saline, and −120 mV in saline, respectively. The three types of APs have similar shapes, with half-widths <2 ms. However, APs solely supported by TTX-R currents were not always followed by an afterhyperpolarization (AHP) (Fig. 8B).

Fig. 8.

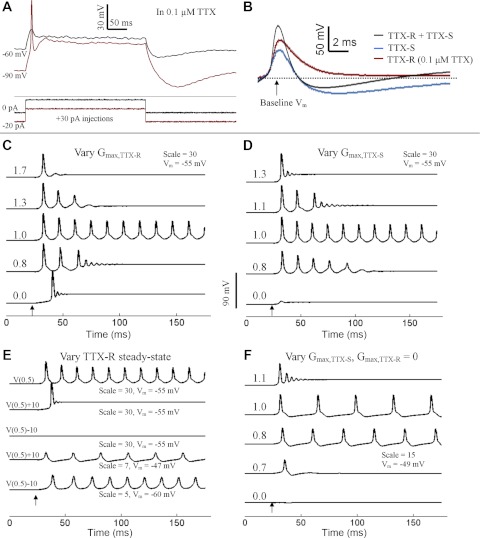
Experimental and computational measurements of excitability. A: in whole cell current-clamp recordings obtained in 0.1 μM TTX, an AP could be elicited by current injection from −90 mV but not from −60 mV. B: superimposition of AP waveforms that use both TTX-R and TTX-S currents (black), TTX-S currents only (blue), and TTX-R currents only (red; measured in 0.1 μM TTX). Baseline V_m differed between samples and was more negative in traces to elicit firing mediated by TTX-R currents. Computer simulations are shown in C–E. Arrows indicate the injection of a 10-ms, 1-pA depolarizing current. V_m indicates the initial membrane potential of the simulation. “Scale” denotes the multiplication factor of the total Na⁺ conductance over the values reported in Table 1. C: varying the maximal conductance of TTX-R current (Ḡ_max,TTX-R), with Ḡ_max,TTX-S = 0.073 S/cm³, generates graded repetitiveness of AP discharge. Numbers at the start of traces denote r_G, the ratio of Ḡ_max,TTX-R to Ḡ_max,TTX-S. D: experiment depicted is similar to that in C, except that Ḡ_max,TTX-S was varied with Ḡ_max,TTX-R = 0.073 S/cm³. Numbers at the start of traces indicate 1/r_G. E: with r_G = 1, shifting the inactivation and activation curves of the TTX-R current by +10 mV [in the depolarizing direction, V(0.5)+10] or by −10 mV [in the hyperpolarizing direction, V(0.5)−10] removes repetitive firing. V(0.5) indicates that the activation and inactivation curves reflect the average values shown in Fig. 5E. Repetitive firing could be restored in V(0.5)+10 and V(0.5)−10 conditions by changing the initial V_m and the scale factor. F: burst firing was eliminated with removal of TTX-R current. Ḡ_max,TTX-S was varied, and numbers on the traces indicate Ḡ_max,TTX-S = n × 0.037 S/cm².

What is the function of TTX-R Na⁺ currents that are mostly inactivated near resting potential? To address this question, we developed a Hodgkin-Huxley model of the GG neuron in silico and included a second Na⁺ current with the steady-state properties of the TTX-R current. Table 1 lists the parameters, including Ḡ_TTX-R (maximum TTX-R conductance), that were derived from the voltage-clamp data. In computer simulations, the injection of 0.1-nA current of 10-ms duration from a resting potential of −55 mV triggered a single AP. Setting Ḡ_TTX-R and Ḡ_TTX-S equal to 0 resulted in the removal of the AP. Selective restoration of Ḡ_TTX-S resulted in the recovery of the AP (data not shown). Thus the computer model replicates the experimental observation that APs elicited from a resting potential of −55 mV are dominantly supported by TTX-S currents.

Repetitive firing from a resting potential of −55 mV could be evoked with a 10-ms current injection of 1-pA amplitude by increasing Ḡ_TTX-R and Ḡ_TTX-S to levels that were 30 times (scale: 30) their values in Table 1. Ḡ_K was not changed in these simulations. Figure 8C demonstrates the effect on repetitive firing that resulted from modifying the ratio of TTX-R and TTX-S Na⁺ conductance. At a conductance ratio (r_G, the value obtained from Ḡ_TTX-R/Ḡ_TTX-S) of 1.0, the transient injection of depolarizing current evoked a long-running train of APs. However, at an r_G value of 1.3, obtained by modifying Ḡ_TTX-R, the current injection evoked a self-limiting burst of APs. The decreasing AP amplitudes observed with successive spikes in the burst in silico were consistent with observations in vitro. At r_G values exceeding 1.7, the current injection resulted in a single AP. The bursts of APs evoked at r_G values <0.9 led to a depolarized steady-state resting potential that was not observed in vitro. Similar results (Fig. 8D) were obtained when modifying 1/r_G (by changing Ḡ_TTX-S).

In the computer model, we tested the effects of shifting both the activation and inactivation curves of the TTX-R current. Figure 8E demonstrates that shifting both curves by +10 mV abrogated the repetitive firing from −55 mV. A −10-mV shift in the steady-state curves of the TTX-R current resulted in a similar cessation of repetitive firing. Repetitive firing could be initiated with these positively or negatively shifted curves at more positive and negative resting potentials, respectively. The most suitable membrane potentials for repetitive firing could be predicted by calculating the approximate rheobase at various potentials. We were unable to obtain the burst firing shown in Fig. 8, C and D, by changing r_G at these more suitable membrane potentials.

Finally, we simulated a TTX-R current ablation by setting Ḡ_TTX-R equal to 0. Repetitive firing could be achieved with a 10- ms injection of 1-pA depolarizing current from a resting potential of −49 mV (Fig. 8F). No burst activity was evoked at various tested values of Ḡ_TTX-S. Thus the TTX-R current is predicted to promote burst firing. Overall, this computer model of the “average” GG neuron suggests that the ratio and specific voltage dependencies of TTX-R and TTX-S conductances determine the repetitiveness of firing.

Pharmacological Modulation of Spontaneous Firing

To test the role of Na⁺ conductance on the degree of repetitive firing, we perfused 0.1 μM TTX onto GG neurons in extracellular recordings. The gradual increase in [TTX] should increase the ratio of TTX-R conductance to TTX-S conductance (r_G). Figure 9A demonstrates a neuron that initially fired in the RSS pattern (trace 1). At an intermediate exposure to TTX (trace 2), the firing converted to the less repetitive phasic pattern. At full exposure to 0.1 μM TTX, the firing was abolished (trace 3). Washout of TTX resulted in the recovery of the phasic pattern at an intermediate stage and, finally, restoration of the original RSS pattern (trace 4). Phasic-firing neurons converted to the least repetitive sporadic firing pattern at intermediate stages of the perfusion (Fig. 9B). None of the nine tested neurons exhibited an increase in the repetitiveness of firing at intermediate [TTX].

Fig. 9.

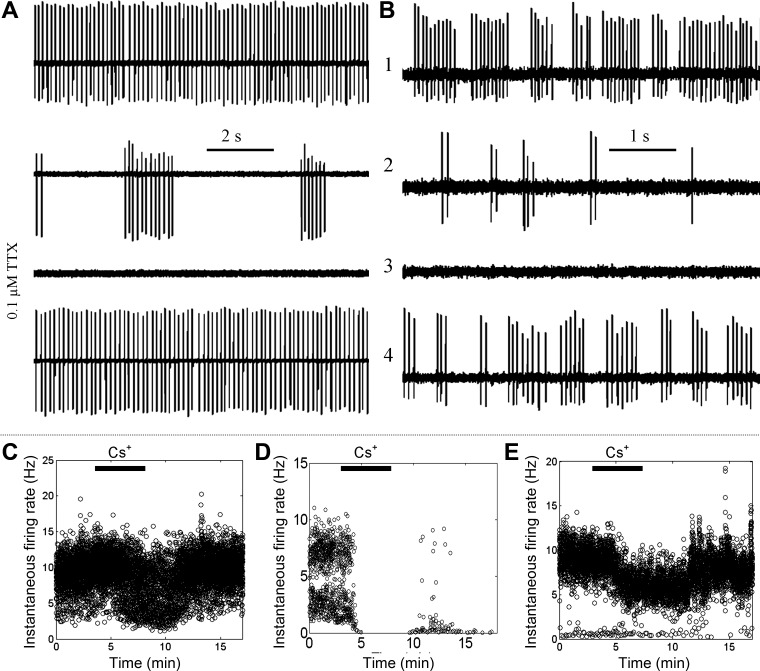
Pharmacological modulation of spontaneous firing. A: an RSS-firing GG neuron was slowly perfused with 0.1 μM TTX. Traces show firing pattern at different time points in the perfusion: 1, initial firing pattern; 2, intermediate [TTX]; 3, full effect of TTX; 4,- recovery. B: in an experiment similar to that in A, a phasic-firing GG neuron exhibited reduced repetitiveness of firing before being fully inhibited. C–E: frequency vs. time plots of spontaneous firing in different GG neurons perfused with 5 mM CsCl to inhibit I_h. I_h influenced firing rate of RSS (C), sporadic (D), and phasic firing patterns (E).

We next tested the contribution of I_h to spontaneous firing in GG neurons. In extracellular recordings, perfusion of 5 mM Cs⁺, which abolished I_h, reduced the rate of spontaneous AP discharge in 6/17 (35%) GG neurons. The Cs⁺-mediated inhibition was found in neurons representing each of the three identified spontaneous firing patterns. In RSS-firing and sporadically firing neurons, Cs⁺ reduced the total frequency of spontaneous discharge (Fig. 9, C and D). In GG neurons that fired in the phasic pattern, Cs⁺ reduced the intraburst firing frequency (Fig. 9E). Untreated GG neurons exhibited a stable firing pattern but could show small (<10%) and temporary changes in firing rate (data not shown). These temporary changes could be readily distinguished from Cs⁺-induced changes on the basis of their different time dependencies. In whole cell recordings, 5 mM CsCl resulted in the acute, reversible hyperpolarization of resting membrane potentials in 3/5 neurons (mean hyperpolarization: −6.0 ± 2.0 mV).

DISCUSSION

GG Neurons in Nasal Vestibule Slices

The electrophysiological characterization of GG neurons has been challenging, because the stiff surrounding tissue vitiates the access of recording electrodes to the neurons. We seldom obtained recordings from untreated slices. We have demonstrated that gentle collagenase treatment of transverse slices of the mouse nasal vestibule enables patch-clamp recordings from GG neurons. There are several reasons collagenase treatment helps. In electron micrographs of the mouse nasal vestibule, collagen fibrils appear to support adhesion of glial cells to neurons within clusters of GG cells (Brechbuhl et al. 2008; Liu et al. 2009). Digestion of these fibrils reduces the tension on the glial cell membranes and enables the glial cells to retract. Clusters of GG neurons, normally embedded within the tough extracellular matrix (ECM) of the slice, protrude after collagenase treatment. The reduction in ECM stiffness increases the compliance of the neuronal membrane to suction. The patch pipette also moves more readily through a softened ECM to the surfaces of the neurons. We observed no obvious differences in spontaneous firing patterns and Na⁺ currents in GG neurons between collagenase-treated and untreated slices (data not shown). These data suggest that protease digestion does not change the intrinsic properties of GG neurons. However, the treatment likely disrupted the interactions of GG neurons with other neurons or glial cells.

Voltage-Dependent Ionic Currents

In whole cell recordings from GG neurons, we activated distinct sets of fast-inactivating inward Na⁺ currents by depolarizing the membrane from either more (−120 mV) or less (−70 mV) hyperpolarized holding potentials. The former protocol induced the TTX-R Na⁺ currents that exhibited hyperpolarized shifts in both activation and inactivation curves relative to the TTX-S currents evoked by the latter protocol. Because hyperpolarization does not decrease TTX sensitivity of Na⁺ channels (Roy and Narahashi 1992), we suppose that TTX-R and TTX-S currents are mediated by different Na⁺ channels.

Three groups of voltage-gated Na⁺ channels are reported according to their high (IC₅₀: 10 nM), moderate (IC₅₀: 1 μM), or low (IC₅₀: 50 μM) TTX sensitivity (Catterall 2000; Goldin et al. 2000). Both TTX-sensitive and TTX-resistant Na⁺ currents are found in small dorsal root ganglion neurons (Akopian et al. 1996; Cummins et al. 1999; Roy and Narahashi 1992). The TTX-sensitive Na⁺ currents there exhibit more hyperpolarized activation and inactivation voltages than TTX-resistant ones. However, TTX-resistant Na⁺ currents in nociceptive neurons decay with a time constant ∼5 ms, more slowly than the fast-inactivating TTX-R currents found in this study. TTX-sensitive and TTX-insensitive fast-inactivating Na⁺ currents are also reported in vomeronasal sensory neurons (Liman and Corey 1996). The TTX-insensitive Na⁺ currents have hyperpolarized inactivation relations, but similar activation relations, compared with TTX-sensitive currents. The two subtypes of Na⁺ currents in GG neurons might operate differently from those expressed in both dorsal root ganglion neurons and vomeronasal sensory neurons.

GG neurons exhibit outward K⁺ currents that have sustained and inactivating components. The activation of the inactivating component was predominantly at membrane potentials more positive than −10 mV. GG neurons show graded firing rates vs. current injection and fire at lower rates than predicted by the Hodgkin-Huxley model, which are functional hallmarks the inactivating A-type K⁺ current. However, the activation and inactivation curves of the inactivating K⁺ current in GG neurons do not resemble the properties of A-type current originally reported by Connor and Stevens (1971b). Instead, the properties reported here are generally consistent with a partially inactivating delayed outward rectifier (Aldrich et al. 1979; Connor and Stevens 1971a; Ehrenstein and Gilbert 1966). Because the K⁺ current may require longer times to recover from inactivation (Aldrich et al. 1979), the inactivating K⁺ current may contribute to the early termination of repetitive firing by gradually reducing the AHP magnitude.

We detected I_h in most GG neurons in both voltage (Fig. 7)- and current-clamp experiments (Fig. 3). I_h contributes to pacemaker firing in several types of neurons in the central nervous system (CNS) (Biel et al. 2009; Heida et al. 2008; Neuhoff et al. 2002; Overton and Clark 1997; Wilson 2005) but not in others (Raman and Bean 1997, 1999). Blocking I_h inhibited only 33% of GG neurons, with no bias in firing pattern. In the responsive cells, I_h likely helped to maintain a depolarized resting potential. This is consistent with the observed Cs⁺-induced hyperpolarization. The activation curve presented in Fig. 7D predicts a small amount of I_h near the resting potential. In the unresponsive cells, the input resistance at rest may have been too low to reveal I_h contributions, or the resting potential may have been more depolarized than the mean value reported here. Because I_h is temperature sensitive (Vargas and Lucero 1999), a greater contribution may have been observed had the experiments been performed at 37°C.

Biophysical Basis for Spontaneous Firing

We observed that most GG neurons spontaneously fired in either an RSS, phasic, or sporadic pattern, as reported in CNS neurons (Grace and Bunney 1984; Swensen and Bean 2003; Wilson 2005). The RSS pattern usually exhibited a firing frequency >10 Hz, whereas the phasic pattern showed long (0.3–2 s) interburst intervals and high intraburst frequency (>10 Hz). Given that both firing rate and firing pattern modulate neurotransmitter release (Aosaki et al. 1994; Overton and Clark 1997), we assume that the neurons with different firing patterns might play different roles in chemosensory information encoding.

We were not able to interconvert between RSS and phasic firing patterns in GG neurons by simple injections of depolarizing current (Fig. 3), demonstrating that firing pattern is an intrinsic property of a GG neuron. The phasic discharge pattern cannot be solely mediated by the activity of an inactivating “T-type” voltage-gated Ca²⁺ channel (Llinas and Jahnsen 1982), because bursting behavior was observed at a resting membrane potential of −55 mV, at which T-type currents are inactivated (Huguenard 1996). The actions of Ca²⁺-activated K⁺ conductances are also insufficient to explain the bursting behavior, because the break hyperpolarizations indicative of their activity, seen in other bursting systems (Goldberg and Wilson 2005), were not observed in GG neurons (Fig. 3B).

We believe the finely tuned interaction of Na⁺ and K⁺ channels explains the three spontaneous firing patterns in GG neurons. This explanation requires a short (<10 ms) initiating current that triggers the first AP. The ionic basis of this proposed initiating current is presently unknown. As demonstrated in computer simulations, the proportion of the two main components of the total Na⁺ conductance is a critical parameter to specify the degree of repetitive firing that follows the initial AP. Sporadic firing would result from infrequent spike initiation combined with low repetitiveness. Phasic firing would arise from infrequent spike initiation combined with moderate repetitiveness. RSS firing would stem from either infrequent spike initiation with high repetitiveness or relatively frequent spike initiation with moderate repetitiveness.

The TTX-induced alterations in firing pattern lend confidence to the computer model. Because TTX acts primarily on the TTX-S current, perfusion of TTX should lead to a decrease in the maximal TTX-S conductance, effectively increasing the conductance ratio r_G. In extracellular recordings of RSS- and phasic-firing neurons, the spontaneous discharge pattern transitioned to phasic and sporadic patterns, respectively. This confirms the categorization of the three different firing patterns as variations of a repetitive firing tendency and suggests that the firing patterns have the same fundamental ionic basis whose components are differently tuned. Other assumptions and predictions of the model will require additional study. The firing frequency of repetitive spikes observed in the computer model is between 40 and 90 Hz, which is 3–6 times higher than the frequencies observed in patch-clamp experiments. The elucidation of different ionic currents, including Ca²⁺-activated currents, and the elaboration of inactivating K⁺ (Aldrich 1981) and voltage-dependent Ca²⁺ currents (Wang et al. 1991) into the model may be helpful in later versions. Because I_h only affected spontaneous firing in ∼35% of GG neurons, we excluded it from the model to focus on the contributions of the TTX-R current.

To achieve the repetitive firing patterns in the computer model, the maximal Na⁺ conductance had to be increased to 30 times the value obtained from voltage-clamp experiments. Recent studies of the axon initial segment (AIS), where APs originate, in other neuronal systems have shown a Na⁺ channel density in the AIS that can be 50 times the density found in the soma (Kole et al. 2008). In the voltage-clamp experiments presented here, the observed Na⁺ conductance is thus likely to be spatially nonuninform. The 30-fold increase in the Na⁺ conductance resulted in a value that approximated the Na⁺ conductance in the squid giant axon (0.14 S/cm² in this study vs. 0.12 S/cm² in the squid giant axon) (Hodgkin and Huxley 1952).

The experiments presented here demonstrate that two distinct Na⁺ currents can generate heterogeneous patterns of firing, including a pulsatile pattern. Molecular identification of the TTX-R Na⁺ channel in GG neurons will be critical. The computer model predicts that a genetic ablation of the TTX-R channel in GG neurons should reduce the proportion of neurons in the phasic firing state (see Fig. 8F). Future experimentation should also focus on potential ways in which an individual GG neuron can modulate or switch firing patterns. Our experiments suggest that endogenous modification of the Na⁺ conductance, in particular the TTX-R conductance, may drive pattern selection. Potential modifiers include mechanical stretch (Beyder et al. 2010), calmodulin (Young and Caldwell 2005), corticosteroids (Filatov and Rich 2004), protein kinase C activity (Watson and Gold 1997), and polyunsaturated fatty acids (Vreugdenhil et al. 1996). β-Subunits of Na⁺ channels also play important modulatory roles in steady-state Na⁺ channel properties (Patino and Isom 2010; Qu et al. 2001). Developmental or activity-induced changes in the expression of Na⁺ channels can affect the relative Na⁺ conductances and the pattern of spontaneous discharge.

Perspectives on Chemosensory Function

Although most GG neurons exhibit Ca²⁺ responses to alarm pheromone and cold, this study shows that the actual electrical outputs of GG neurons are diverse. GG neurons segregate into three equally represented classes by their basal firing pattern. Thus alarm pheromone and cold likely elicit changes in all three types of neurons.

GG neurons exhibit two mechanisms for AP generation, which is explained by the presence of two fast-inactivating Na⁺ currents. Beyond its proposed function in determining spontaneous firing pattern, the TTX-R current may be responsible for a different interpretation of evoked APs at more negative potentials. For example, APs evoked from a hyperpolarized baseline may activate Ca²⁺ influx through an inactivating voltage-gated Ca²⁺ channel. Thus, in GG neurons, hyperpolarizing stimuli may have a distinct signature beyond a mere reduction in firing rate. A recent report has shown that, in olfactory sensory neurons of the main olfactory epithelium, a second fast-inactivating Na⁺ channel is essential for the transduction of odor information to the olfactory bulb (Weiss et al. 2011). In GG neurons, spontaneous firing from a hyperpolarized resting potential may represent a distinct mode of odor transduction, due to the mobilization of TTX-R currents. Within a single neuron, multimodal detection can possibly be supported by the depolarization of the resting potential by some odors and its hyperpolarization by others.

In an earlier study, we demonstrated that GG neurons express a membrane-bound guanylate cyclase and downstream cGMP signaling components (Liu et al. 2009), similar to the GC-D olfactory subsystem, whose neurons are located in the caudal recesses of the nasal cavity (Juilfs et al. 1997) and respond to multimodal stimuli (Hu et al. 2007; Leinders-Zufall et al. 2007; Munger et al. 2010). Contrary to early observations on the electrical function of the GC-D subsystem (Leinders-Zufall et al. 2007; Munger et al. 2010), GG neurons appear to have diverse electrical outputs that can be potentially explained by an unusual set of underlying ionic conductances. This study shows that the GG has a variety of biophysical mechanisms that can potentially interact to produce complex and heterogeneous behaviors. For example, the cyclic nucleotides that are essential for olfactory signal transduction (Zufall and Munger 2001) could also modulate I_h in GG neurons (Biel et al. 2009). The GG should serve as a model experimental system to explore how a small number of neurons performs multiple sensory functions.

GRANTS

This project was supported by grants from the National Institutes of Health and the National Science Foundation.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

Author contributions: C.Y.L., H.A.L., and D.S.K. conception and design of research; C.Y.L. and C.X. performed experiments; C.Y.L. and C.X. analyzed data; C.Y.L., C.X., and H.A.L. interpreted results of experiments; C.Y.L. prepared figures; C.Y.L. drafted manuscript; C.Y.L., C.X., S.E.F., H.A.L., and D.S.K. edited and revised manuscript; S.E.F. and D.S.K. approved final version of manuscript.