Abstract
Nitric oxide (NO) research in biomedicine has been hampered by the absence of a method that will allow quantitative measurement of NO in biological tissues with high sensitivity and selectivity, and with adequate spatial and temporal resolution. 4-amino-5-methylamino-2′,7′-difluorofluorescein (DAF-FM) is a NO sensitive fluorescence probe that has been used widely for qualitative assessment of cellular NO production. However, calibration of the fluorescent signal and quantification of NO concentration in cells and tissues using fluorescent probes, have provided significant challenge. In this study we utilize a combination of mathematical modeling and experimentation to elucidate the kinetics of NO/DAF-FM reaction in solution. Modeling and experiments suggest that the slope of fluorescent intensity (FI) can be related to NO concentration according to the equation: where α is a proportionality coefficient that relates FI to unit concentration of activated DAF-FM, k1 is the NO oxidation rate constant, and k was estimated to be 4.3 ± 0.6. The FI slope exhibits saturation kinetics with DAF-FM concentration. Interestingly, the effective half-maximum constant (EC50) increases proportionally to NO concentration. This result is not in agreement with the proposition that N2O3 is the NO oxidation byproduct that activates DAF-FM. Kinetic analysis suggests that the reactive intermediate should exhibit NO-dependent consumption and thus is a more likely candidate. The derived rate law can be used for the calibration of DAF-FM fluorescence and the quantification of NO concentration in biological tissues.
Keywords: nitric oxide; 4-amino-5-methylamino-2′,7′-difluorofluorescein; reaction kinetics
1. Introduction
The measurement of nitric oxide (NO) in biological samples has been hampered by the lack of sensitive probes that can detect NO in nanomolar levels without interference from other species. The available methods for NO detection include the colorimetric Griess reaction, chemiluminescence, electron paramagnetic resonance, electrochemical and fluorometric analyses [1; 2; 3]. Available assays to asses NO availability measure free NO or NO oxidation products (i.e. , N2C3) and signaling derivatives (i.e. S-nitrosothiols, cGMP). Available methods vary in their sensitivity, specificity and interference from biological constituents. NO is highly reactive with other modalities and has a very short half-life and steep concentration gradients. Determining local availability and intracellular concentrations has proven to be quite challenging.
Fluorometric methods have been used to assess intracellular NO levels [4]. The development of fluorescent probes in recent years has provided sensitive and specific assays that are gaining wide applications in measuring nitrogen oxides [5; 6; 7; 8; 9; 10; 11]. NO-reactive fluorescent indicators allow bio-imaging of NO with high spatial resolution, permitting investigation of two-dimensional NO production in real time by digital fluorescence imaging, which is not possible with other methods [7]. These fluorescent probes may be used to measure nanomolar levels of NO in vitro and in vivo [12]. Diamine derivatives of fluorescein are the most widely used NO fluorescent probes (i.e. 4,5 Diaminofluorescein (DAF-2) and 4-amino-5-methylamino-2′,7′-difluorofluorescein (DAF-FM)). Exposure of these compounds to NO, generates highly fluorescent triazole derivatives (DAF-T) [13]. Fluorescence to NO, however, is achieved only under aerobic conditions, indicating that these fluorescent probes react with an oxidative product of NO, rather than NO itself [14]. The nature of the NO active derivative has not been established, although N2O3 has been proposed as a candidate for the reactive intermediate [14]. An alternative reaction scheme has also been proposed [15] where activation of DAF-FM occurs through a two step process by initially reacting with NO2 radical. Therefore, controversy exists as to the actual kinetic mechanism for the reaction between DAF-FM and NO.
The vast majority of studies incorporating the use of DAFs have only reported relative changes in fluorescent signal [16; 17; 18; 19; 20]. Quantification of NO concentration ([NO]) in biological tissues using fluorescent probes is hindered by a series of challenges, including uneven dye loading, dye leakage, motion artifacts, photoactivation and photobleaching [14; 21; 22]. In addition, the dye may also exhibit increase in fluorescence due to the presence of cations [23]. Most importantly, elucidating the kinetics of NO-dye interaction is a prerequisite for developing meaningful calibration protocols. In this study, we utilize mathematical modeling and experimentation to investigate the reaction of NO with DAF-FM and to gain further insight into the actual intermediate that activates DAFs. Based on the proposed mechanism and kinetic law, recommendations for calibration of DAF-FM fluorescence and the quantification of NO in biological tissues are provided.
2. Methods
2.1 Kinetic analysis
We investigated the kinetic mechanism that leads to activation of DAF-FM by NO and the formation of the triazole derivative, DAF-T. Assuming that the intermediate product of NO’s autoxidation reacting with DAF-FM is N2O3, [24] DAF-T formation will proceed through the following reactions [7; 20; 25].
| (Reaction 1) |
| (Reaction 2) |
| (Reaction 3) |
| (Reaction 4) |
Reaction rate constants k1 (3.15×106 M−2s−1), k2 (1.1×109 M−1s−1), k-2 (8.1×104s−1), and k3 (38130 s−1) have been previously reported [26]. Applying the law of mass action to this reaction scheme yields differential equations that can be solved numerically to describe the rates of change of NO, , N2O3, and DAF-T (see Appendix).
Activation of DAF-FM by an oxidation product of NO, rather than NO itself, will affect the functional dependence of the rate of DAF-T formation on the reactants. Assuming that the concentrations of unstable intermediates (i.e. N2O3 and ) are small relative to the reactants, and therefore show negligible rates of change, a Pseudo Steady State Approximation (PSSA) can be employed for their concentrations. This simplifies the proposed kinetic mechanism (Reactions 1–4) and yields Equation 1:
| (Equation 1) |
is the fraction of N2O3 that is utilized to activate DAF-FM at any given moment (i.e. rate of reaction 4 over reaction 3 and 4). Note that the kinetic mechanism and the simplified kinetic behavior depicted in Equation 1 are analogous to the kinetics of nitrosation of thiols by NO in [27]. Equation 1 simply states that the formation rate of the triazole derivative, DAF-T, will be limited by the rate of NO oxidation (Reaction 1) and the fraction of N2O3 that reacts with DAF-FM. This approximation was validated against the numerical solution of the system for the assumed parameter values for k1, k2, k-2, k3 and a wide range of values for k4. Assuming a constant fraction γ, Equation 1 can be integrated to give the increase in DAF-T after the addition of a bolus amount of NO. For limiting initial NO concentrations ([NO]i) this increase will be approximately equal to:
| (Equation 2) |
Thus, a linear dependence between fluorescent intensity (FI), and total amount of NO added, is possible under some conditions despite a square dependence of the increase in FI on [NO] at any particular instance.
2.2 Materials
Dulbecco’s phosphate buffered saline was purchased from Invitrogen (Grand Island, NY). DAF-FM was from Molecular Probes (Eugene, OR). Spermine NONOate (SPER/NO) was from Cayman Chemicals (Ann Arbor, MI). DMSO (dimethyl sulfoxide anhydrous) was purchased from Sigma-Aldrich (St. Louis, MO), and the sodium hydroxide (NaOH), 2N solution was from Fisher Scientific (Fair Lawn, NJ). A 7 mM stock solution of DAF-FM was made with DMSO. Dilutions to final working concentrations were done by the addition of DPBS. Spermine NONOate (t1/2= 230 minutes at 22–25°C) was chosen as a slow releasing NO donor. Final working concentrations were made with DPBS immediately prior to experimentation.
2.3 Measurement of NO
We investigated the NO released from a NO donor (SPER/NO) at 25°C, obtaining the resulting [NO] profile using a NO sensitive electrode (ISONOP, WPI; Sarasota, FL). Different concentrations of the NO donor (50 nM to 500 μM), were prepared in an aerated buffered solution (pH 7.4). The NO released was detected using the electrode. The reaction of DAF-FM with NO liberated from the NO donor was monitored using a computer controlled automatic microplate fluorometer (GENios; TECAN, Inc.; Durham, NC). Samples were loaded in black 96-well plates and fluorescence intensity (FI) was recorded at an emission wavelength 535 nm followed excitation at 485 nm. FI increase with time was recorded at different combinations of DAF-FM and NO donor concentrations to assess the dependency of FI on both DAF-FM and NO.
3. Results
3.1 The “Clamped NO” protocol
First, we examined the NO release pattern from SPER/NO in aerated solution. An NO donor, with a relatively long half-life, can provide continuous release of NO over the duration of a typical experiment (~ 15 minutes). Figure 1A shows representative model simulations (Eq. A.1) for the evolution of NO in an aerated solution ([O2] = 2.77×10−4 M) at three different SPER/NO concentrations (10, 500 and 1000 μM). Simulations were performed utilizing an Ordinary Differential Equation solver based on an explicit Runge-Kutta method in MATLAB. NO is released and accumulates until reaching a maximum concentration (represented by a circle) that is followed by a slowly decaying plateau. The time it takes to reach this plateau differs depending on the concentration of the NO donor and its assumed half-life. At higher concentrations, this plateau is established faster. This offers a relative steady level of NO which can be maintained over the duration of an experiment, similar to the “clamped NO protocol” in [28]. (Note that the “clamped NO protocol” of this earlier study utilizes CPTIO rather than dissolved O2 as the main route of NO consumption.)
Figure 1.
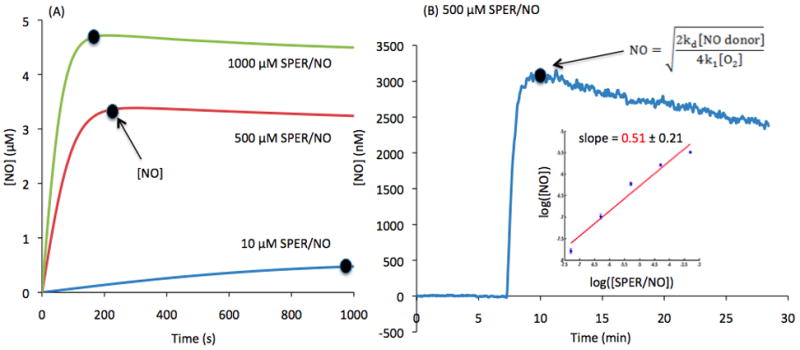
(A) Predicted continuous release by 1000, 500 and 10 μM SPER/NO. Maximum NO release is indicated by the dot with a constant increase until a pseudo steady-state plateau is reached. (B) NO release from 500 μM SPER/NO over time, detected by an NO electrode (n=4). The dot indicates when maximum [NO] is achieved. (B-Insert) Log-log plot displays the relationship between [NO] and [SPER/NO] using maximum [NO] from ranging [SPER/NO] detected by the electrode. The linear fit of the log-log plot has a slope of 0.508 with a standard deviation of 0.208. The slope is not significantly different than 0.5 (p=0.95).
This relative steady level of NO, during the plateau phase, is a result of the balance between NO release by the NO donor (S) and NO consumed by the rate limiting oxidation reaction of NO (R = ~ 4k1[NO]2[O2]), and can be approximated by Equation 3:
| (Equation 3) |
where kd is the dissociation rate constant (kd = ln 2/t1/2), and n is the moles of NO released for every mole of NO donor. In Equation 3 we have assumed a constant release rate for the NO donor which is a valid assumption for . Thus, a 100 times increase in [NO donor] (i.e. 10 and 1000 μM SPER/NO) should yield only a 10-fold increase in “clamped” [NO], given the square relationship.
The theoretical prediction for a square dependence between NO and NO donor concentration was verified experimentally. Figure 1B shows a representative tracing using the NO-sensitive electrode. NO evolves in a buffered solution of 500 μM SPER/NO. After a short accumulation phase, a maximum [NO] is reached. A slight decay after the peak is observed as the NO donor is slowly consumed over time. The maximum NO concentration reached was recorded and average values (n=4) at different SPER/NO concentrations (50 nM to 500 μM) are summarized in a log-log plot (Insert in Figure 1B). A linear fit of the data yields a slope of 0.51 ± 0.21. The slope is not significantly different than 0.5 (p=0.95). Thus, experimental data is in agreement with the theoretical predictions suggesting that the [NO] is proportional to the square root of [SPER/NO].
3.2 Dependence of fluorescence intensity on DAF-FM and NO concentrations
A representative numerical simulation from the model in the Appendix is presented in Figure 2A. DAF-T formation is depicted as a function of time, for 5 μM of DAF-FM and 50 μM of SPER/NO. At t=0, the slope of the curve is zero as a result of the absence of free NO initially. DAF-T formation begins to increase as NO evolves, until a maximum rate of change is reached (i.e. maximum slope, βmax). This corresponds to the point of maximum NO concentration in Figures 1A and 1B. Thus, the βmax of the DAF-T formation curve, can be correlated to the clamped NO concentration levels.
Figure 2.
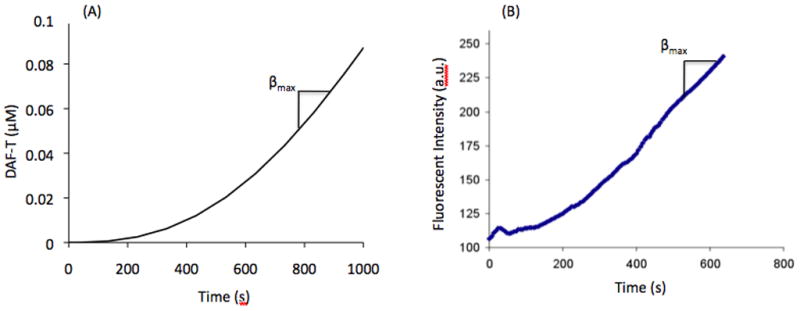
Fluorescent intensity curves obtained from solutions containing 5 μM DAF-FM and 50 μM SPER/NO (A) simulation (B) experimental, indicating when βmax is achieved.
Assuming that DAF-T is the main fluorescently active species in the solution, we expect that FI will be proportional to the DAF-T concentration. Thus, FI should exhibit a similar profile in time with the [DAF-T] generated from the model. Figure 2B depicts a representative experimental tracing of FI upon mixing of [DAF-FM] and [SPER/NO] (5 μM and 50 μM final concentrations respectively) in the fluorometer. The experimental tracing of FI and the model predictions for [DAF-T] show a similar profile in time.
Fluorescent Intensity vs. NO donor
In a series of experiments, we investigated the dependence of FI on [NO] by varying the concentration of SPER/NO, while keeping the concentration of DAF-FM constant at 5 μM. Fluorescence measurements were taken in the fluorometer and representative results are depicted in Figure 3A for SPER/NO concentrations of 10 μM, 100 μM and 1 mM. As expected, we observed an increase in maximum slope (βmax) when increasing [SPER/NO]. To test the relationship between NO donor and βmax, average maximum slopes (n=5) were calculated for six different SPER/NO concentrations (10 – 1000 μM). Data is summarized in Figure 3B as a log-log plot. A linear fit gives a slope of 0.99 ± 0.03. This slope is not significantly different than 1 (p=0.74). Therefore, experiments show a maximum slope in FI (βmax) that is proportional to NO donor concentration. Data in Figures 1–3 combined, suggests that βmax is also proportional to [NO]2. This is in agreement with the kinetic analysis (Equation 1).
Figure 3.
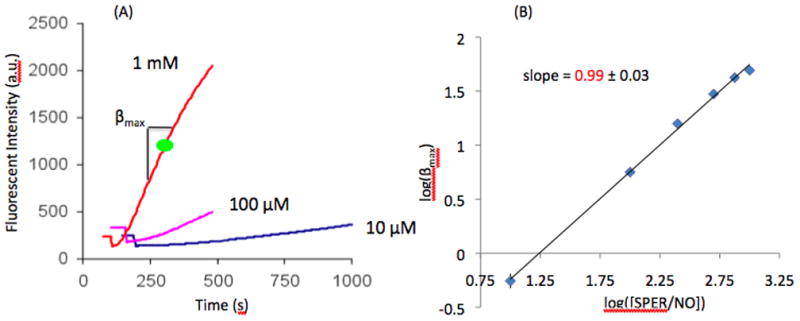
(A) Fluorescent intensity curves showing the dependence of [SPER/NO] (10 μM, 100 μM, and 1 mM) on slope (βmax). (B) Log-log plot of βmax and [SPER/NO] (n=5). A linear relationship is observed having a slope of 0.99 with a standard deviation of 0.03. This slope is not significantly different than 1 (p=0.74).
Fluorescent Intensity vs. DAF-FM
To investigate the dependence of the FI on DAF-FM, a series of experiments were performed by varying [DAF-FM] at constant [SPER/NO]. Experiments were repeated for different [SPER/NO]. For each combination of [DAF-FM] and [SPER/NO], the maximum slope βmax of the FI curve was recorded. Figure 4A depicts representative results. Average βmax values (n=5) are presented as a function of DAF-FM concentration and for two different NO donor concentration. We observe saturation dependence of βmax on DAF-FM and thus the following n equation was utilized to fit the data.
Figure 4.
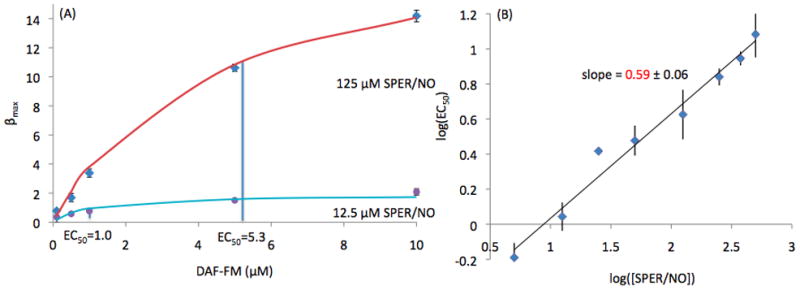
(A) Data fitting for βmax with respect to [DAF-FM] at 12.5 and 125 μM [SPER/NO] (n=5) indicating EC50 values of 1.0 and 5.3 respectively. (B) Log-log plot of EC50 and [SPER/NO] (n=5) with a linear relationship having a slope of 0.59 and a standard deviation of 0.06. The slope of this line is statistically different than 1 (p<5.5×10−5) and 0 (p<1.2×10−5) and close to 0.5.
| (Equation 4) |
where maxβmax is the maximum βmax at saturating DAF-FM concentrations, and EC50 is the concentration of DAF-FM for half-maximum βmax.
Fitting with Equation 4 allows us to estimate maxβmax and EC50 at each [SPER/NO]. maxβmax increases linearly with SPER/NO concentrations (i.e. maxβmax is 20.1 and 1.9 for 125 μM and 12.5 μM of SPER/NO respectively). This linear relationship has been previously noted [20; 29]. Therefore, the slope βmax of the FI curve shows a linear dependence on [SPER/NO] and thus exhibits a square dependence on [NO]. This is in agreement with Equation 1 (maxβmax=2k1[NO]2[O2]). Surprisingly, however, the estimated EC50 values also increase with NO donor concentrations (i.e. EC50 is 5.3 and 1.0 for 125 μM and 12.5 μM of SPER/NO respectively). This was not anticipated based on Equation 1 and thus, the observed dependence of EC50 on NO questions the proposed kinetic mechanism of DAF-FM activation by N2O3 (Reactions 1–4).
Experiments at eight different SPER/NO concentrations (5–500 μM) were performed. At each NO donor concentration, five different DAF-FM concentrations (0.1–10 μM) were utilized to estimate a single EC50 value for each combination. The log-log plot of the average EC50 values from n=5 repetitions are depicted in Figure 4B. A linear fit of this line has a slope of 0.59 ± 0.06. The slope of this line is statistically different than 1 (p<5.5×10−5) and 0 (p<1.2×10−5) and close to 0.5. Thus, our data points toward a EC50 that is proportional to [SPER/NO]1/2 and thus proportional to [NO].
Figure 5 shows the dependence of EC50 on NO. SPER/NO concentrations were translated to NO concentrations based on Equation 3 and NO-electrode recordings that show 500 μM NO donor correspond to 3.2 μM NO. A linear fit of the data in Figure 5 gives:
| (Equation 5) |
with k = 4.3 ± 0.6. Equations 1, 4 and 5 suggest the following rate law for DAF-T formation rate.
Figure 5.
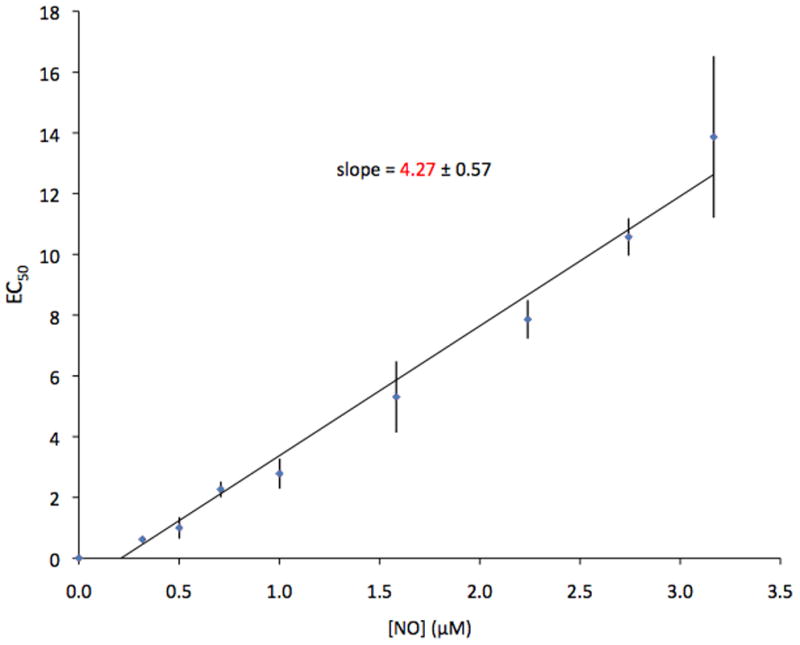
Relationship of the dependence of EC50 on [NO]. The linear slope of the line yields the value of k with a standard deviation of 0.57.
| (Equation 6) |
3.3 A Revised Kinetic Mechanism
Equation 6 suggests that the fraction of the unknown NO byproduct X that reacts with DAF-FM is . An effective EC50=k[NO] that is NO dependent can be achieved if this active intermediate is consumed through an NO-dependent pathway. (i.e. γ′ is the rate of reaction of X with DAF-FM over the rate of reaction with DAF-FM plus the rate of NO-dependent consumption of X).
Thus, our data argues against the proposition that this species is N2O3. Previous studies have argued for a different reaction mechanism where conversion of DAF-FM to DAF-T occurs after DAF-FM is initially oxidized [15; 22; 30]. is proposed to be this oxidating agent, and the measurement of the fluorescently derived triazole product reflects this oxidation. N2O3 has also been suggested as the active intermediate involved in thiol nitrosation [27]. However, recent work has provided evidence for a more important role of , rather than N2O3, in thiol nitrosation [31; 32; 33; 34]. The resemblance of the kinetic behavior between DAF-FM activation and GSH nitrosation, also makes an attractive candidate for the unidentified reactive intermediate in DAF-FM activation by NO. A potential kinetic mechanism that assumes as the oxidative product of NO that reacts with DAF-FM would include Reaction 1–3 as well as Reaction 5 instead of Reaction 4.
| (Reaction 5) |
Assuming the DAF-FM oxidation by is the rate limiting step in Reaction 5, a PSSA can be utilized to simplify Reactions 1,2,3, and 5 yielding the rate of DAF-T formation:
| (Equation 7) |
Comparing Equation 7 with Equation 6 we get . Based on the values for the other reaction rate constants, we can an estimate a value for k5 in the reaction of DAF-FM activation to be 8.2×107 M−1s−1. This value is of the same order as the oxidative rate constant of similar vicinal diamines by (i.e. rate constant for 1,4-phenylenediamine is 4.6×107 M−1s−1 [30; 35]).
4. Discussion
A number of methods have been employed to measure NO and related nitrogen oxides. NO sensitive fluorescent probes have often been used to detect NO levels, however, most studies provide data in relative fluorescence and quantification of NO concentration fluorescently has not been accomplished. This is due to several experimental limitations that may arise when utilizing DAF-FM in many systems (i.e. motion artifacts, uneven dye loading, photosensitivity and dye leakage) as well as due to an incomplete understanding of the kinetics of DAF-FM activation by NO. Characterizing the active intermediate for DAF-FM activation and analyzing the kinetic mechanism will aid in overcoming some of these limitations.
Active intermediate of DAF-FM activation
The dependence of DAF-FM fluorescence on the presence of O2, suggests that DAF-FM is activated by a byproduct of NO oxidation rather than NO itself. N2O3 has been previously proposed as an intermediate that can play this role. An alternative reaction mechanism has also been proposed according to which the activation of DAF-FM occurs as a two-step process [30]. The first step is the oxidation of DAF-FM via a one electron species such, as , yielding a nitrosamine intermediate that reacts further with NO to form the fluorescent triazole DAF-T. The data presented in this study supports the second mechanism of as the reactive intermediate in DAF-FM activation [15; 22; 30]. Although our data does not directly show a two-step activation process, it does suggest that the initial oxidation step of DAF-FM by to be rate-limiting.
A mechanism based on rather than N2O3 as the reactive intermediate would exhibit similar, but not identical kinetic behavior (Equation 1 vs. Equation 7). In both mechanisms, DAF-T formation is limited by the rate of NO oxidation and both exhibit saturation dependence on DAF-FM concentration. However, based on the second mechanism, the effective EC50 is NO dependent. Experimental data (Figure 4) demonstrates such a dependence of EC50 on [NO] and point towards as the active intermediate for DAF-FM activation. However, any NO oxidation byproduct, that would exhibit NO dependent consumption, could satisfy the observed behavior.
Several studies have proposed a significant role of NO2 radical in nitrosation of thiols [31; 32; 33; 34]. Given the similarities between the nitrosation of thiols and the observed activation of DAF-FM, we can assume that a similar kinetic mechanism is likely. It has also been suggested that the relative importance of NO2 vs N2O3 mediated thiol nitrosation will be dependent on the amount of [NO], with N2O3 becoming important only at high [NO] (i.e. greater than 20 μM is predicted in) [36]. Given the similar kinetic constants between the nitrosation of thiols and the activation of DAF-FM, we can assume that the maximum NO concentration of 5 μM utilized in our experiments favor the NO2 mediated nitrosation pathway.
Thus, our experimental data, corroborates earlier suggestion that is the intermediate that activates DAF-FM through the formation of a one electron oxidation product of DAF, which then combines with NO to form DAF-T [30]. However, this might suggest a major limitation for DAF-FM as a NO fluorescence probe as other strong one electron species could also affect DAF-FM oxidation and thus the resulting fluorescent signal. Evidence of this has been noted in a recent study by Zhang et al, where it was found that species such as dehydroascorbic acid and ascorbic acid can potentially affect the DAF-T fluorescent signal [37].
Use of NO Donors for calibration standards
Theoretical considerations, corroborated by experiments, suggest that slow releasing NO donors can provide steady levels of NO concentrations in aerated buffered solutions. This is ideally suited for creating calibration standards. The half-life of the NO donor needs to be significant relative to the duration of the experiment (i.e. t1/2 > 10texperiment) such as no significant consumption of NO donor occurs over this time frame. The “clamped NO” concentration will depend not only on the stoichiometry, half-life, and concentration of NO donor, but also on the rate of NO consumption. In the absence of other NO scavengers, the reaction with dissolved O2 will limit this rate and will lead to a square dependence between [NO donor] and [NO]. An appropriate time from the initiation of NO donor release is required for reaching this plateau NO concentration. This time can be approximated by the ratio of the NO plateau over the initial release rate (i.e. ιlag > (4k1[O2] nkd[No donor]−1/2. NO electrodes can validate these predictions and test the relationship between [NO] and [NO donor] in a particular system. Alternatively, NO standards can be created using NO gas as described in [38] and such methods may offer several advantages, particularly in cellular systems, at the expense of more complex instrumentation.
Calibration using bolus addition of NO
Studies have sometimes utilized the addition of a solution containing a known NO concentration for assessing NO fluorescence of a fast releasing NO donor [39; 40]. Such an addition of a bolus amount of NO will result in a change in NO fluorescence that will stop when NO (or DAF-FM) is consumed. This information is difficult to interpret as the [NO] and/or [DAF-FM] concentrations may change significantly during the course of the experiment. Thus, a linear increase in final fluorescence after addition of solutions with different NO concentration does not guarantee a linear dependence of fluorescence on [NO] at any particular instance. For example, Equation 2 shows that under some conditions the final change in NO fluorescence will be linearly dependent on the amount of NO added on the system, even though at any particular moment the increase in FI is proportional to [NO]2 (Equation 6). Thus, a calibration curve using solutions with different NO concentration standards may not be ideal for time-dependent monitoring of NO.
Kinetics of DAF-FM activation
Unlike many other fluorescence indicators that bind reversibly with the molecule of interest, DAF-FM reacts with the active NO derivative in an irreversible manner. The irreversibility of DAF-FM activation has two main implications. First, the fluorescence signal should remain constant and should not decrease when NO disappears. As a result, any observed drop in FI is an artifact that should be attributed to experimental limitations such as dye leakage, motion artifacts, photobleaching etc. Second, the NO concentration levels correlate with the rate of DAF-T formation and thus with the rate of FI increase (i.e. assuming a linear dependence of FI on [DAF-T]). Thus, a relationship between the slope of FI and [NO] (and not NO release rate) should be sought. This relationship will be governed by the reaction mechanism of DAF-FM with NO and based on our theoretical and experimental data can be approximated by:
| (Equation 8) |
where α is a proportionality coefficient that depends on the fluorescent yield per mole of DAF-T, and k is estimated from our experiments to be 4.3 ± 0.6 μM DAF-FM/μM NO. Inspection of Equation 8 suggests two limiting cases. In Case I, when [DAF-FM]≪ k [NO], Equation 8 reduces to:
| (Equation 8a) |
This would suggest a DAF-T formation rate that is proportional to [NO] and [DAF-FM] under these conditions.
In case II, when [DAF-FM]≫ k [NO], Equation 8 reduces to:
| (Equation 8b) |
This would yield a DAF-T formation that is independent of the [DAF-FM] and is proportional to [NO]2. Typical experimental protocols utilize μM concentrations of [DAF-FM], while in many biological tissues and conditions, nM levels of NO are anticipated. Thus, the second scenario is more likely to occur. Although the kinetic data was acquired from mixing DAF-FM and NO donor in aerated buffered solutions, similar behavior may hold in biological tissues. Ideally, the applicability of Equation 8a or 8b should be verified on a particular system and a method of analysis should be designed accordingly. For example, normalizing FI(t) with initial fluorescence may be required according to Equation 8a but not according to 8b to yield data slopes independent of [DAF-FM]. Nevertheless, phenomena such as uneven dye loading, motion artifacts or dye leakage can still affect fluorescence through their effect on coefficient α.
The absence of reliable methods for quantifying NO in biological tissues has provided a significant obstacle in elucidating NO functions in biomedicine. NO sensitive fluorescent probes are ideally suited for such investigations by allowing spatio-temporal NO monitoring. Despite several drawbacks associated with the use of DAFs, these fluorescent probes have adequate sensitivity for assessing physiological levels NO that are usually in the nanomolar range. The kinetic information provided in this study can assist in the development of calibration protocols that will enable us to quantify cellular NO levels in different systems. Future studies should test the kinetic behavior in assessing intracellular DAF-FM metabolism and validate fluorescent based quantification of NO against other established methods (i.e. Chemiluminescence, electrochemical).
We investigated the kinetics of DAF-FM activation by NO in aerated solutions.
-
Data suggest rather than N2O3 as the reactive NO oxidation intermediate.
The slope of DAF-T signal is related to [NO] according to: For [DAF-FM]≫[NO] the slope is proportional to [NO]2 and independent of [DAF-FM].
Recommendations for the calibration of DAF fluorescence are provided.
Acknowledgments
This work was funded by National Institutes of Health Grant SC1HL095101 (NT).
Abbreviations
- NO
nitric oxide
- FI
fluorescence intensity
- SPER/NO
Spermine NONOate
Appendix
Mathematical model of the proposed kinetic mechanism
Applying the law of mass action to the first reaction scheme (i.e. Reactions 1–4), yields four differential equations for the rates of change of NO, , N2O3, and DAFT as follows:
| (Eq.A.1) |
| (Eq.A.2) |
| (Eq.A.3) |
| (Eq.A.4) |
For the revised reaction mechanism, that assumes DAF activation by (i.e. Reactions 1,2,3, and 5), Eqs. A.2–A.4 are modified to reflect this change.
| (Eq.A.5) |
| (Eq.A.6) |
| (Eq.A.7) |
Differential equations can also describe the change in the O2 and DAF-FM concentrations. However, we can assume that due to the abundance of O2 its concentration will remain essentially constant while the total concentration of the dye is preserved. Eq. 5 can then estimate the concentration of DAF:
| (Eq.A.8) |
where [DAF]i is the initial dye concentration.
An NO donor, with a relatively long half-life, can provide continuous release of NO over the duration of the experiment. To model this scenario, Eq. A.1 is modified to incorporate the NO release:
| (Eq.A.9) |
where S is the NO release rate given by:
| (Eq.A.10) |
kd is the dissociation rate constant of the NO donor and is inversely proportional to the half-life (kd = ln 2/t1/2).
Although simulations exhibited in Figure 1A were performed for the proposed kinetic mechanism, an identical simulation is achieved for the revised kinetic mechanism (not shown). Similarly, the simulated evolution of DAF-T over time follows comparable profiles for both kinetic mechanisms. Figure 2A shows simulations for the first kinetic mechanisms (Eq. A.2, A.3, A.4, A.9) assuming a k4 value of 4.0×108 M−1s−1.
Modeling parameters utilized
| Parameters | Values |
|---|---|
| k1 | 3.15×106 M−2s−1 |
| k2 | 1.1×109 M−1s−1 |
| k-2 | 81000 s−1 |
| k3 | 38130 s−1 |
| k4 | 4.0×108 M−1s−1 |
| k5 | 8.2×107 M−1s−1 |
| Km | 4.27 |
| [O2] | 2.77×10−4 M |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Archer S. Measurement of nitric oxide in biological models. FASEB. 1993;7:349–360. doi: 10.1096/fasebj.7.2.8440411. [DOI] [PubMed] [Google Scholar]
- 2.Feelisch M, Rassaf T, Mnaimneh S, Singh N, Bryan NS, Jourd’Heuil D, Kelm M. Concomitant S-, N-, and heme-nitros(yl)ation in biological tissues and fluids: Implications for the fate of NO in vivo. Free Radic Biol Med. 2002;33:1590–1596. doi: 10.1096/fj.02-0363com. [DOI] [PubMed] [Google Scholar]
- 3.Marzinzig M, Nussler AK, Stadler J, Marzinzig E, Barthlen W, Nussler NC, Beger HG, Morris SM, Jr, Bruckner UB. Improved methods to measure end products of nitric oxide in biological fluids: Nitrite, nitrate, and S-nitrosothiols. Nitric Oxide. 1997;1:177–189. doi: 10.1006/niox.1997.0116. [DOI] [PubMed] [Google Scholar]
- 4.Stern JE, Zhang W. Cellular sources, targets and actions of constitutive nitric oxide in the magnocellular neurosectretory system of the rat. J Physiol. 2005;562:725–744. doi: 10.1113/jphysiol.2004.077735. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chvanov M, Gerasimenko OV, Petersen OH, Tepikin AV. Calcium-dependent release of NO from intracellular S-nitrosothiols. EMBO. 2006;25:3024–3032. doi: 10.1038/sj.emboj.7601207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Hempel SL, Buettner GR, O’Maller YQ, Wessels DA, Flaherty DM. Dihydrofluorescein diacetate is superior for detecting intracellular oxidants: Comparison with 2′,7′-dichlorodihydrofluorescein diacetate, 5(and 6)-caroxy-2′,7′-dichlorodihydrofluorescein diacetate, and dihydrorhodamine 123. Free Radic Biol Med. 1999;27:146–159. doi: 10.1016/s0891-5849(99)00061-1. [DOI] [PubMed] [Google Scholar]
- 7.Kojima H, Nakatsubo N, Kikuchi K, Kawahara S, Kirino Y, Nagoshi H, Hirata Y, Nagano T. Detection and imaging of nitric oxide with novel fluorescent indicators: Diaminoflurosceins. Anal Chem. 1998;70:2446–2453. doi: 10.1021/ac9801723. [DOI] [PubMed] [Google Scholar]
- 8.Kojima H, Sakurai K, Kikuchi K, Kawahara S, Kirino Y, Nagoshi H, Hirata Y, Nagano T. Development of a fluorescent indicator for nitric oxide based on the fluorescein chromophore. Chem Pharm Bull (Tokyo) 1998;46:373–375. doi: 10.1248/cpb.46.373. [DOI] [PubMed] [Google Scholar]
- 9.Lim MH, Lippard SJ. Fluorescent nitric oxide detection by copper complexes bearing anthracenyl and dansyl fluorophore ligands. Inorg Chem. 2006;45:8980–8989. doi: 10.1021/ic0609913. [DOI] [PubMed] [Google Scholar]
- 10.Sasaki E, Kojima H, Nishimatsu H, Urano Y, Kikuchi K, Hirata Y, Nagano T. Highly sensitive near-infrared fluorescent probes for nitric oxide and their application to isolated organs. J Am Chem Soc. 2005;127:3684–3685. doi: 10.1021/ja042967z. [DOI] [PubMed] [Google Scholar]
- 11.Soh N, Katayama Y, Maeda M. A flurescent probe for monitoring nitric oxide production using a novel detection concept. Analyst. 2001;126:564–566. doi: 10.1039/b101600h. [DOI] [PubMed] [Google Scholar]
- 12.Ji XB, Hollocher TC. Mechanism for nitrosation of 2,3-diaminonaphthalene by Escherichia coli: Enzymatic production of NO followed by O2-dependent chemical nitrosation. Appl Environ Microbiol. 1988;54:1791–1794. doi: 10.1128/aem.54.7.1791-1794.1988. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Nagano T. Practical methods for detection of nitric oxide. Luminescence. 1999;14:283–290. doi: 10.1002/(SICI)1522-7243(199911/12)14:6<283::AID-BIO572>3.0.CO;2-G. [DOI] [PubMed] [Google Scholar]
- 14.Kojima H, Hirata M, Kudo Y, Kikuchi K, Nagano T. Visualization of oxygen-concentration-dependent production of nitric oxide in rat hippocampal slices during aglycemia. J Neurochem. 2001;76:1404–1410. doi: 10.1046/j.1471-4159.2001.00161.x. [DOI] [PubMed] [Google Scholar]
- 15.Espey MG, Thomas DD, Miranda KM, Wink DA. Focusing of nitric oxide mediated nitrosation and oxidative nitrosylation as a consequence of reaction with superoxide. Proc Natl Acad Sci U S A. 2002;99:11127–32. doi: 10.1073/pnas.152157599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Nagy G, Barcza M, Gonchoroff N, Phillips PE, Perl A. Nitric Oxide-Dependent Mitochondrial Biogenesis Generates Ca 2+ Signaling Profile of Lupus T Cells. J Immunol. 2004;173:3676–3683. doi: 10.4049/jimmunol.173.6.3676. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Qian Y, Banerjee S, Grossman CE, Amidon W, Nagy G, Barcza M, Niland B, Karp DR, Middleton FA, Bank K, Perl A. Transaldolase deficiency influences the pentose phosphate pathway, mitochondrial homoeostasis and apoptosis signal processing. Biochem J. 2008;415:123–134. doi: 10.1042/BJ20080722. [DOI] [PubMed] [Google Scholar]
- 18.Grossini E, Molinari C, Mary DASG, Uberti F, Caimmi PP, Surico N, Vacca G. Intracoronary Genistein Acutely Increases Coronary Blood Flow in Anesthetized Pigs through beta-Adrenergic Mediated Nitric Oxide Release and Estrogenic Receptors. Endocrinology. 2008;149:2678–2687. doi: 10.1210/en.2007-1361. [DOI] [PubMed] [Google Scholar]
- 19.Nyberg M, Mortensen SP, Thaning P, Saltin B, Hellsten Y. Interstitial and Plasma Adenosine Stimulate Nitric Oxide and Prostacyclin Formation in Human Skeletal Muscle. Hypertension. 2010;56:1102–1108. doi: 10.1161/HYPERTENSIONAHA.110.161521. [DOI] [PubMed] [Google Scholar]
- 20.Planchet E, Kaiser WM. Nitric oxide (NO) detection by DAF fluorescence and chemiluminescence: A comparison using abiotic and biotic NO sources. J Exp Bot. 2006;57:3043–3055. doi: 10.1093/jxb/erl070. [DOI] [PubMed] [Google Scholar]
- 21.Berkels R, Dachs C, Roesen R, Klaus W. Simultaneous measurement of intracellular Ca(2+) and nitric oxide: A new method. Cell Calcium. 2000;27:281–286. doi: 10.1054/ceca.2000.0119. [DOI] [PubMed] [Google Scholar]
- 22.Bryan NS, Grisham MB. Methods to detect nitric oxide and its metabolites in biological samples. Free Radic Biol Med. 2007;43:645–657. doi: 10.1016/j.freeradbiomed.2007.04.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Broillet M, Randin O, Chatton J. Photoactivation and calcium sensitivity of the fluorescent NO indicator 4,5-diaminofluorescein (DAF-2): implications for cellular NO imaging. FEBS Lett. 2001;491:227–32. doi: 10.1016/s0014-5793(01)02206-2. [DOI] [PubMed] [Google Scholar]
- 24.Hong H, Sun J, Cai W. Multimodality imaging of nitric oxide and nitric oxide synthases. Free Radic Biol Med. 2009;47:684–98. doi: 10.1016/j.freeradbiomed.2009.06.011. [DOI] [PubMed] [Google Scholar]
- 25.Nakatsubo N, Kojima H, Kikuchi K, Nagoshi H, Hirata Y, Maeda D, Imai Y, Irimura T, Nagano T. Direct evidence of nitric oxide production from bovine aortic endothelial cells using new fluorescence indicators: diaminofluoresceins. FEBS Lett. 1998;427:263–6. doi: 10.1016/s0014-5793(98)00440-2. [DOI] [PubMed] [Google Scholar]
- 26.Williams DLH. Nitrosation reactions and the chemisty of nitric oxide. Elsevier B.V; Amsterdam: 2004. [Google Scholar]
- 27.Kharitonov VG, Sundquist AR, Sharma VS. Kinetics of nitrosation of thiols by nitric oxide in the presence of oxygen. J Biol Chem. 1995;270:28158–28164. doi: 10.1074/jbc.270.47.28158. [DOI] [PubMed] [Google Scholar]
- 28.Griffiths C, Wykes V, Bellamy TC, Garthwaite J. A new and simple method for delivering clamped nitric oxide concentrations in the physiological range: application to activation of guanylyl cyclase-coupled nitric oxide receptors. Mol Pharmacol. 2003;64:1349–56. doi: 10.1124/mol.64.6.1349. [DOI] [PubMed] [Google Scholar]
- 29.Nyberg M, Mortensen SP, Thaning P, Saltin B, Hellsten Y. Interstitial and plasma adenosine stimulate nitric oxide and prostacyclin formation in human skeletal muscle. Hypertension. 2010;56:1102–8. doi: 10.1161/HYPERTENSIONAHA.110.161521. [DOI] [PubMed] [Google Scholar]
- 30.Wardman P. Fluorescent and luminescent probes for measurement of oxidative and nitrosative species in cells and tissues: Progress, pitfalls, and prospects. Free Radic Biol Med. 2007;43:995–1022. doi: 10.1016/j.freeradbiomed.2007.06.026. [DOI] [PubMed] [Google Scholar]
- 31.Schrammel A, Gorren AC, Schmidt K, Pfeiffer S, Mayer B. S-nitrosation of glutathione by nitric oxide, peroxynitrite, and (*)NO/O(2)(*-) Free Radic Biol Med. 2003;34:1078–88. doi: 10.1016/s0891-5849(03)00038-8. [DOI] [PubMed] [Google Scholar]
- 32.Nedospasov AA. Is N2O3 the main nitrosating intermediate in aerated nitric oxide (NO) solutions in vivo? If so, where, when, and which one? J Biochem Mol Toxicol. 2002;16:109–20. doi: 10.1002/jbt.10029. [DOI] [PubMed] [Google Scholar]
- 33.Keszler A, Zhang Y, Hogg N. Reaction between nitric oxide, glutathione, and oxygen in the presence and absence of protein: How are s-nitrosothiols formed? Free Radic Biol Med. 2010;48:55–64. doi: 10.1016/j.freeradbiomed.2009.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jourd’heuil D, Jourd’heuil FL, Feelisch M. Oxidation and nitrosation of thiols at low micromolar exposure to nitric oxide - Evidence for a free radical mechanism. Journal of Biological Chemistry. 2003;278:15720–15726. doi: 10.1074/jbc.M300203200. [DOI] [PubMed] [Google Scholar]
- 35.Ross AB, Mallard WG, Helman WP, Buxton GV, Huie RE, Neta P. NDRL-NIST Solution Kinetics Database: Ver. 3. Notre Dame Radiation Laboratory and National Institute of Standards and Technology; 1998. [Google Scholar]
- 36.Lancaster JR. Protein cysteine thiol nitrosation: Maker or marker of reactive nitrogen species-induced nonerythroid cellular signaling? Nitric Oxide-Biology and Chemistry. 2008;19:68–72. doi: 10.1016/j.niox.2008.04.028. [DOI] [PubMed] [Google Scholar]
- 37.Zhang X, Kim WS, Hatcher N, Potgieter K, Moroz LL, Gillette R, Sweedler JV. Interfering with nitric oxide measurements - 4,5-Diaminofluorescein reacts with dehydroascorbic acid and ascorbic acid. Journal of Biological Chemistry. 2002;277:48472–48478. doi: 10.1074/jbc.M209130200. [DOI] [PubMed] [Google Scholar]
- 38.Dendroulakis V, Russell BS, Eric Elmquist C, Trudel LJ, Wogan GN, Deen WM, Dedon PC. A system for exposing molecules and cells to biologically relevant and accurately controlled steady-state concentrations of nitric oxide and oxygen. Nitric Oxide. 2012;27:161–8. doi: 10.1016/j.niox.2012.06.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Rathel TR, Leikert JJ, Vollmar AM, Dirsch VM. Application of 4,5-diaminofluorescein to reliably measure nitric oxide released from endothelial cells in vitro. Biol Proced Online. 2003;5:136–142. doi: 10.1251/bpo55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Thomas DD, Liu ZP, Kantrow SP, Lancaster JR. The biological lifetime of nitric oxide: Implications for the perivascular dynamics of NO and O(2) Proceedings of the National Academy of Sciences of the United States of America. 2001;98:355–360. doi: 10.1073/pnas.011379598. [DOI] [PMC free article] [PubMed] [Google Scholar]


