Comparison of latency and rate coding for the direction of whisker deflection in the subcortical somatosensory pathway

Abstract

The response of many neurons in the whisker somatosensory system depends on the direction in which a whisker is deflected. Although it is known that the spike count conveys information about this parameter, it is not known how important spike timing might be. The aim of this study was to compare neural codes based on spike count and first-spike latency, respectively. We extracellularly recorded single units from either the rat trigeminal ganglion (primary sensory afferents) or ventroposteromedial (VPM) thalamic nucleus in response to deflection in different directions and quantified alternative neural codes using mutual information. We found that neurons were diverse: some (58% in ganglion, 32% in VPM) conveyed information only by spike count; others conveyed additional information by latency. An issue with latency coding is that latency is measured with respect to the time of stimulus onset, a quantity known to the experimenter but not directly to the subject's brain. We found a potential solution using the integrated population activity as an internal timing signal: in this way, 91% of the first-spike latency information could be recovered. Finally, we asked how well direction could be decoded. For large populations, spike count and latency codes performed similarly; for small ones, decoding was more accurate using the latency code. Our findings indicate that whisker deflection direction is more efficiently encoded by spike timing than by spike count. Spike timing decreases the population size necessary for reliable information transmission and may thereby bring significant advantages in both wiring and metabolic efficiency.

to understand better how neural circuits represent and process sensory information, it is helpful to determine the fundamental relationship between sensory signals and the neural activity they evoke. It has long been known that neurons throughout the nervous systems of diverse species transmit significant information about sensory signals via a spike-count code: that is, the number of action potentials fired within a given time window (Adrian 1926). It has also long been known that substantial additional information is potentially available from the precise timing of action potentials within the time window (MacKay and McCulloch 1952). However, it is only more recently that this possibility has been established quantitatively. In the whisker system, precise spike timing conveys significant information beyond that available from spike count about stimulus location on the whisker pad (Panzeri and Diamond 2010; Panzeri et al. 2001; Petersen et al. 2002b) and kinetics of temporally varying whisker deflections (Ahissar et al. 2000; Arabzadeh et al. 2006; Jones et al. 2004; Montemurro et al. 2007a; Pinto et al. 2000; Wilent and Contreras 2005). Similar principles pertain to the dorsal column somatosensory system (Foffani et al. 2008, 2009; Johansson and Birznieks 2004; reviewed by Johansson and Flanagan 2009).¹

Analogously to almost all mammalian sensory systems, information from mechanoreceptors in the whisker follicle reaches the cerebral cortex via trisynaptic pathways. Primary sensory afferents, for which the cell bodies are located in the trigeminal ganglion, project in parallel to a cluster of nuclei, the brain-stem trigeminal complex. From here, at least three parallel pathways project from brain stem to thalamus [ventroposterior medial (VPM) and posterior medial nuclei] and onto primary/secondary somatosensory cortex (Diamond et al. 2008; Petersen et al. 2009).

The direction in which a rodent's whisker is deflected (hereafter “direction”) exerts a marked effect on the responses of many neurons in the whisker system, particularly in the subcortical, lemniscal pathway, and is a useful test case for studies of neural coding. The aim of this study was to compare candidate neural codes for direction, based on spike count and spike timing. Neurons at all levels of the whisker pathway convey information about direction by means of variations in spike count (Axelrad et al. 1976; Waite 1973; Zucker and Welker 1969). Recently, it was shown that neurons in the principal nucleus of the brain stem also convey directional information by means of latency (Bellavance et al. 2010). However, it is not known whether direction information is available from spike timing at other stages of the pathway nor is it known, quantitatively, how the information available from spike timing compares with that available from spike count.

The simplest type of spike-timing code is the first-spike latency code: here, it is the time between stimulus onset and the first spike evoked after stimulus onset that carries information. There is considerable evidence for latency coding in a number of sensory modalities: visual (Gawne et al. 1996; Gollisch and Meister 2008), auditory (Middlebrooks et al. 1994), dorsal column somatosensory (Foffani et al. 2009; Johansson and Birznieks 2004), and whisker (Panzeri and Diamond 2010; Panzeri et al. 2001; Petersen et al. 2002b). However, a potential problem with latency coding is that, unlike the experimenter, neurons in the brain of the experimental subject have no direct knowledge of stimulus onset time. For latency coding to be feasible, there must be a mechanism to estimate stimulus onset time either from sensory neural activity (reafference) or from motor neural activity (efference copy). A number of potential mechanisms have been proposed (Chase and Young 2007; Johansson and Birznieks 2004; Gollisch and Meister 2008; Panzeri and Diamond 2010; Vasserman et al. 2010; Zohar et al. 2011), but it is not known whether they are applicable to direction coding. A related point is that most previous studies of latency coding have considered either single neurons or pairs of neurons. However, neurons are embedded in populations and encode sensory information as integral members of ensembles. In general, properties of population codes cannot simply be inferred from the properties of individual neurons or small groups of neurons. It is not known how the relative properties of spike count and latency coding depend on population size.

In the present study, we quantitatively compared latency and spike coding for the direction of a whisker deflection. To determine the neural code at the first stage of the sensory pathway, we recorded from the trigeminal ganglion. To determine whether there might be a transformation in the neural code across the subcortical pathway, we also recorded from the ventroposterior thalamic nucleus. 1) For neurons in the trigeminal ganglion, we found diverse tuning characteristics: 58% of single units were spike-count coders, but 42% conveyed significantly more information by latency than by spike count. 2) 91% Of this latency information could be extracted by a mechanism relying entirely on neural activity with no knowledge of stimulus onset time. 3) A majority of units in the ventroposterior thalamus also conveyed significantly more information by latency compared with spike count. 4) For small populations (<6 neurons), direction could be decoded more accurately from latency than from spike count, whereas for larger populations decoding accuracy was similar. Collectively, our results suggest that first-spike latency conveys significant information about whisker deflection direction, which may enable this parameter to be effectively encoded even by small populations of subcortical neurons. A significant computational advantage of this coding strategy may be a reduction in wiring cost.

MATERIALS AND METHODS

Electrophysiology.

All experimental protocols were approved by both United Kingdom national authorities and institutional ethical review. Experimental procedures have been previously described (Bale and Petersen 2009). Briefly, adult Wistar rats (n = 19) were anesthetized with urethane (1.5 g/kg body wt) and placed in a stereotaxic instrument. In each rat, recordings were made from either the trigeminal ganglion or the VPM thalamus. A craniotomy was made over the structure of interest, the dura was reflected, and a tungsten microelectrode was inserted vertically into the brain. Extracellular signals were preamplified, digitized, and stored. Offline, single units were isolated by spike sorting. For VPM recordings, microelectrode placement was verified histologically.

Whisker stimulation.

At each recording site, the principal whisker was identified by deflection of individual vibrissae using a hand-held probe. Whiskers were cut at 10 mm from the skin, and the principal whisker was inserted into a snugly fitting tube attached to a multidirectional mechanical stimulator (Fig. 1A). At the start of each trial, the whisker was deflected by 400 μm in a given direction and held there for 250 ms before being returned to the starting position. This square-wave signal was smoothed by convolution with a Gaussian (1.6-ms SD). The direction was chosen at random from a uniform distribution. Each of 430 directions was presented once, at 0.5-s intervals, in a random sequence that was the same for every unit. The random stimulus design allowed us to classify flexibly the stimuli into a variable number of direction categories. We typically used 8 categories (0–45, 45–90°, etc.). 0° Corresponded to deflection in the ventral direction, 90° to the caudal, and −90° to the rostral. We verified that the apparatus accurately reproduced the desired stimuli using a custom-built light-emitting diode-phototransistor device (Fig. 1B). Rapidly adapting (RA) and slowly adapting (SA) cells in the trigeminal ganglion were discriminated based on the presence or absence of tonic response to whisker deflection (Bale and Petersen 2009).

Fig. 1.

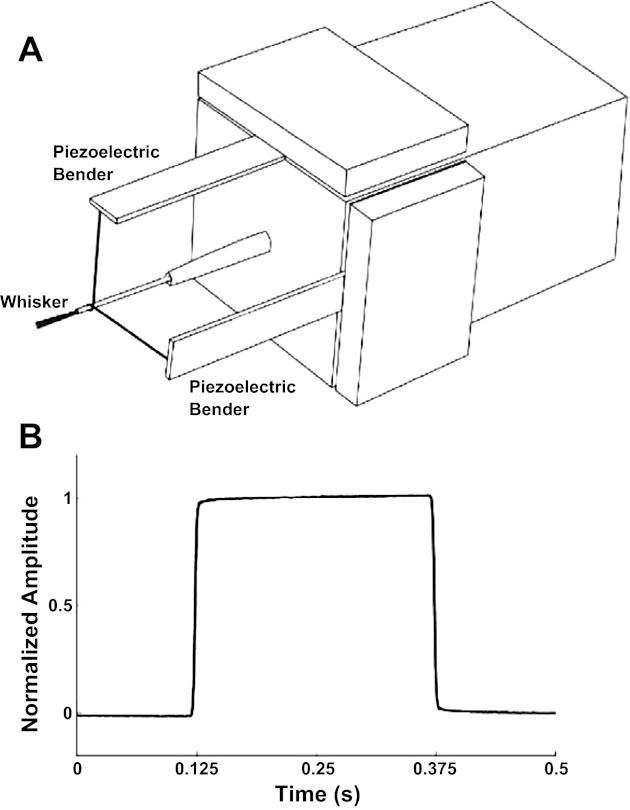
Directional whisker stimulation. A: schematic of the whisker stimulator, composed of 2 orthogonally mounted piezoelectric benders. B: optically measured movement of the stimulator.

Quantification and comparison of neural codes for single neurons.

Mutual information (MI) is a general measure of how well one variable predicts another. In studies of sensory coding, one variable is a sensory stimulus, and the other a neural response. The key advantages of MI are that it makes no assumptions concerning the probability distributions of stimulus/response and that it provides an objective yardstick that enables the information made available by alternative codes present in the response to be quantified and compared (reviewed in the context of the whisker system by Petersen et al. 2009).

We used MI to quantify the amount of information conveyed by neural codes based on spike count and first-spike latency, respectively. To this end, we first quantified the response of a neuron in a manner that captured the desired coding scheme. We denote the stimulus on a particular trial as s and the evoked response as r. The spike count response, on a given trial, was measured as the number of spikes fired within a time window of duration, T, starting from whisker deflection onset. To obtain the first-spike latency response, the response window was subdivided into L bins of width Δt ms (L = T/Δt). The latency, on a given trial, was measured as the time of the first bin that contained ≥1 spikes. If no spikes were fired within the response time window, the latency was set to the arbitrary value L+1.

We computed the marginal probability P(s) of each direction category s (typically 45° wide) as its relative frequency. Since the deflection directions were chosen from a uniform distribution, the P(s) were approximately equal. For each unit, we estimated the probability P(r∣s) of response r being evoked by stimulus s for each possible stimulus-response combination. The marginal probability, P(r), was estimated using the identity:

$$P\left(r\right)={\displaystyle \sum _{s=1}^{N_s}P\left(r|s\right)P\left(s\right)}$$ (1)

where N_s represents the number of direction categories. To estimate the MI for a given code, we substituted the corresponding probabilities into the MI definition:

$$I\left(S;R\right)=H\left(R\right)-H\left(R|S\right)$$ (2)

where H(R), the response entropy, and H(R∣S), the noise entropy are defined:

$$H\left(R\right)=-{\displaystyle \sum _{r=1}^{N_r}P\left(r\right){\log }_{2}P\left(r\right)}$$ (3)

$$H\left(R|S\right)=-{\displaystyle \sum _{r=1}^{N_r}{\displaystyle \sum _{s=1}^{N_s}P\left(s\right)P\left(r|s\right){\log }_{2}P\left(r|s\right)}}$$ (4)

and N_r represents the number of distinct neuronal responses. MI has units of bits and depends on the duration of the time window, T, and (for spike timing) on the bin size, Δt. Sampling error in the estimation of the probabilities P(r) and P(r∣s) typically leads to positive bias in estimates of MI (reviewed by Panzeri et al. 2007). To avoid this, we corrected our initial estimates using the shuffling estimator of Montemurro et al. (2007b):

$$I_{sh}\left(S;R\right)=H\left(R\right)-H_{ind}\left(R|S\right)+H_{sh}\left(R|S\right)-H\left(R|S\right)$$ (5)

H_ind(R∣S) is obtained by computing P_ind(r∣s) = ∏_iP(r_i∣s), where i indexes time bins, and substituting P_ind(r∣s) into Eq. 4. H_sh(R∣S) is obtained by computing a quantity P_sh(r∣s) and substituting that into Eq. 4. P_sh(r∣s) is a “shuffled” version of P(r∣s), calculated from pseudodata where the relationship between trials and responses has been randomized within each stimulus category. With an infinite number of trials, H_ind(R∣S) = H_sh(R∣S), so that I_sh(R;S) is an unbiased estimate of I(S;R). For a finite number of trials, the bias of H_sh(R∣S) is of the same order of magnitude as that of I(S;R), which results in a useful bias cancellation effect. Finally, we applied quadratic extrapolation to I_sh(S;R) (see Panzeri et al. 2007). We checked that bias correction was effective by verifying that the MI for pseudodata, where we randomized the relationship between trials and responses within a stimulus category, was within 1 SE of 0.

We denote as I_latency the MI conveyed by the first-spike latency response and as I_spikecount that conveyed by the spike count response. It is important to note that I_latency, as defined above, reflects not only stimulus-dependent modulations of spike timing, but also modulations of firing rate. For example, a unit that always fires one spike at the same latency to deflection in any direction has I_latency = 0 bits, since neither latency nor spike count is informative. In contrast, a unit that emits spikes always at the same latency, except that it fires to only half of the possible directions, has I_latency = 1 bit, since the spike count is informative. To distinguish these effects, we estimated how much of I_latency could be attributed entirely to differences in spike count. To this end, we first computed a unit latency response as defined above. On every trial for which the unit fired a spike within the response time window, the spike was randomly reallocated (using a uniform distribution) to one of the L bins. In this way, spike count information was preserved, but any additional spike-timing information was eliminated. Next, we calculated how much MI the randomized latency responses conveyed about the stimulus. The result quantifies how much of I_latency can be explained purely on the basis of stimulus-dependent modulations of the spike count. By repeating the calculation 1,000 times (using different randomizations), we calculated a 95% confidence interval. We classified a given unit as a “latency coder” if I_latency exceeded the upper limit of this confidence interval.

Clock-free decoding analysis.

The two measures of response (spike count and latency) were measured within a time window synchronized to whisker deflection onset. We term this the external stimulus “clock.” However, as noted in the Introduction, neural circuits in the experimental subject do not have direct knowledge of this external clock signal. A major aim of this study was to test the feasibility of avoiding this problem by calculating latencies in a “clock-free” manner. To this end, we adapted an approach originally introduced by Chase and Young (2007) to study sound localization in the inferior colliculus (Fig. 2).

Fig. 2.

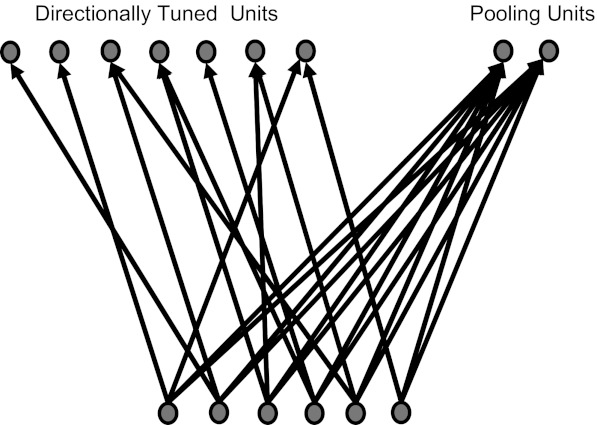
Internal clock mechanism. The mechanism posits a specialized subpopulation of neurons (“pooling units”) that integrate the activity of stimulus-coding units (“directionally tuned units”) to estimate stimulus timing.

Consider an idealized population of neurons where each unit responds at short latency to a particular, preferred stimulus direction and responds at longer latency to other directions. Assume that 1) all directions are represented (not necessarily homogeneously), and 2) the latency with which a neuron responds in its preferred direction is uncorrelated with direction. Whenever a stimulus is delivered, there will be a volley of spikes fired by neurons for which the preferred direction is similar to that of the stimulus. Because of assumption 2, the timing of this volley will be approximately independent of direction. Thus the volley onset can, in principle, be used as an “internal clock” signal. In this way, a downstream neural circuit could potentially estimate latency in a way that entirely avoids direct knowledge of the unknown, external stimulus clock.

In practice, real neuronal populations will deviate somewhat from these ideal properties. An internal clock signal computed as above will be subject to error, and, unless this error is small compared with the range of stimulus-induced modulations of response latency, the above mechanism will not work. Hence, it is important to evaluate it quantitatively. The key requirements for an effective internal clock mechanism are that it 1) measures a running average of the population firing rate (on a given time scale), and 2) generates a timing signal when this running average exceeds a given threshold. Here, we implemented the internal clock using a simple, leaky integrate-and-fire mechanism.

To be able to consider pool sizes comparable with the number of neurons that innervate a whisker follicle or that constitute one thalamic barreloid (100–300 neurons per whisker) and to avoid biases due to the limited number of recorded cells (n = 38 for ganglion, n = 25 for VPM), we generated a pseudopopulation. This population was generated by randomly selecting (with replacement) units from the recorded data set. The directional tuning curve of each selected unit was rotated by a random angle (chosen uniformly from the interval 0 to 360°). For some analyses, to test for possible sensitivity to inhomogeneity, we restricted the interval, for example to 0–120°. It is theoretically possible for this sampling procedure to produce spuriously synchronous spikes. However, in practice, the probability was low, and we verified that none of the data sets used in the study contained any such events.

To implement the pooling process, we used a leaky integrator:

$$\frac{dV}{dt}=-\frac{V}{\tau }+{\displaystyle \sum _{j=1}^{N_{pool}}{\displaystyle \sum _{i=1}^{N_j}{\delta }_{i,j}}}$$ (6)

Here, V denotes the pooled signal at time t, τ the time constant of the pooling process, N_j the number of spikes emitted by the jth unit on a given trial, and N_pool the number of units in the population: δ_i,j = 1 if the jth unit fires its ith spike at time t and 0 otherwise. The time at which V first crosses a threshold (θ) during a given trial was used as the internal estimate of stimulus onset time. This time was used to compute a “clock-free” measure of latency. MI conveyed by the clock-free latency was then calculated as detailed above.

Population decoding analyses.

Since the issue of sampling bias becomes much more severe as the number of dimensions increases, it is usually not possible to obtain accurate estimates of MI from populations of more than a few neurons. To assess latency and spike-count coding at the neuronal population level, we adopted a data-robust decoding approach.

We selected a population of units (either ganglion or VPM) and encoded the responses (20-ms time window) on each trial as either a spike count or latency. Since short latencies (corresponding to directions close to the preferred 1) tended to be more precisely timed than longer ones, we applied the following transformation to the latencies. For each unit, the latency t on a given trial was transformed logarithmically into the range (0–1):

$$t_{\log }=\frac{\text{In}\left(t_{\max }\right)-\text{In}\left(t\right)}{\text{In}\left(t_{\max }\right)-\text{In}\left(t_{\min }\right)}$$ (7)

where ln(x) denotes the natural logarithm of x; t_max and t_min denote the largest and the smallest latency for that unit across all direction categories. The transformation had the effect of making the distribution of t_log approximately Gaussian and better suited to artificial neural network (ANN) decoding (detailed below) than the raw latency values. The spike counts or transformed latencies were used as inputs to an ANN.

The ANN consisted of a single hidden layer of 20 hyperbolic tangent units and 1 linear output unit and was trained by a cross-validation procedure (75% of data trials used for training, 25% for testing). The ANN was trained using the Levenberg-Marquardt training algorithm (MATLAB function trainlm). Adding further hidden units or layers did not significantly improve decoding performance.

To compare the decoding performances of ANNs based on different neural codes, we trained the ANN using a given combination of N_set units. We evaluated decoding performance by computing the Pearson correlation coefficient, ρ, between delivered and decoded stimuli. For each population size N_set (range 2–10)_, this procedure was repeated for 250 randomly chosen unit combinations. To compare latency decoding to spike count decoding, we used the normalized index Δρ_norm = (ρ_latency − ρ_spikecount) / < ρ_spikecount >, where ρ_latency and ρ_spikecount indicate ρ values for first-spike latency and spike-count codes, respectively, and angled brackets indicate averaging across unit combinations of a given N_set.

RESULTS

Spike-count coding and latency coding in trigeminal ganglion.

We recorded the responses of single units from the trigeminal ganglion (hereafter ganglion; n = 38) and from the VPM nucleus of the thalamus (n = 25) to deflection of their principal whiskers in 430 different, randomly chosen directions (Fig. 1, A and B). To construct directional tuning curves, stimuli were divided into 8 categories (0–45, 45–90°, etc.). Consistent with previous reports, ganglion units responded robustly to this stimulus, and their responses were clearly modulated by the direction of deflection (Fig. 3, A and D). For each unit, we defined its preferred spike count direction as the direction category that evoked greatest average spike count (0–20 ms after stimulus onset) and the preferred latency direction as the category that evoked the shortest latency.

Fig. 3.

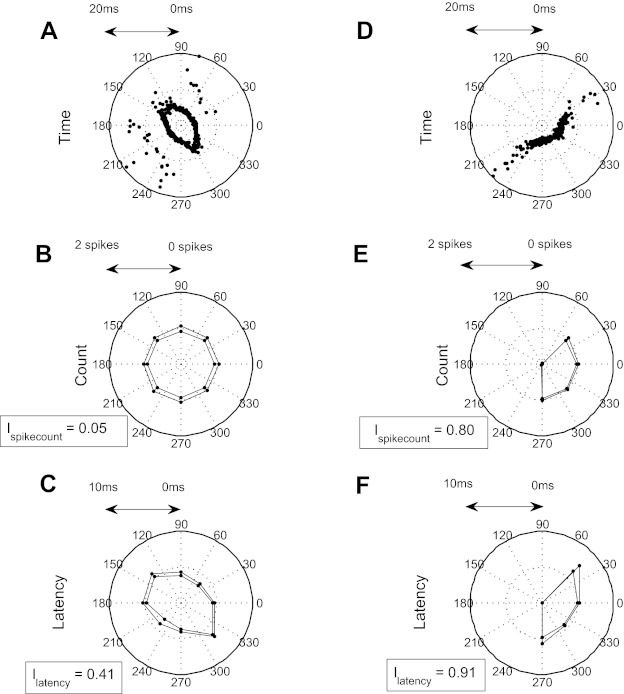
Latency vs. spike count in the trigeminal nucleus for 2 example units. A: response of an example latency coding unit to whisker deflection in different directions. B: median spike count ± SD. C: median 1st-spike latency ± SD. D–F: corresponding data for an example spike-count-coding unit. I, mutual information.

We observed striking diversity in how different ganglion units encoded whisker deflection direction. The unit illustrated in Fig. 3, A–C, fired spikes in response to deflection in every direction. Although evoked spike count (20-ms time window) was essentially independent of direction and hence uninformative (Fig. 3B), median latency (within a direction category) varied systematically from 3.6 ms for a deflection in the range 0–45° to 6.5 ms for a deflection in the range 270–315° (Fig. 3C). Thus, despite not being directionally tuned in terms of spike count, this unit was tuned in terms of latency. In contrast, the unit illustrated in Fig. 3D responded robustly only within a restricted range of directions (0–45 and 225–360°), and thus its spike count was strongly modulated by direction (Fig. 3E). Within the responsive range, the median latency varied between 4.5 ms (270–315°) and 6.8 ms (0–45°; Fig. 3F).

To quantify these observations, we measured the MI conveyed by both spike count (I_spikecount) and latency (I_latency). The unit of Fig. 3, A–C, conveyed eight times more MI by latency than by spike count (I_latency = 0.41 bits and I_spikecount = 0.05 bits; 2-ms bin size). In contrast, the unit of Fig. 3, D–F, conveyed a similar amount of MI by the two codes (I_latency = 0.91 bits and I_spikecount = 0.80 bits). For convenience, we classified each unit into one of two categories: as a latency coder if it conveyed significantly more information by latency than could be accounted for by stimulus-induced presence/absence of the first spike (P = 0.05; see materials and methods) and as a spike-count coder otherwise. However, it is important to note that there was a continuum between units that conveyed no significant additional information by latency and units that conveyed substantial additional information (Fig. 4). The unit of Fig. 3, A–C, exemplifies a latency coder, that of Fig. 3, D–F, a spike-count coder.

Fig. 4.

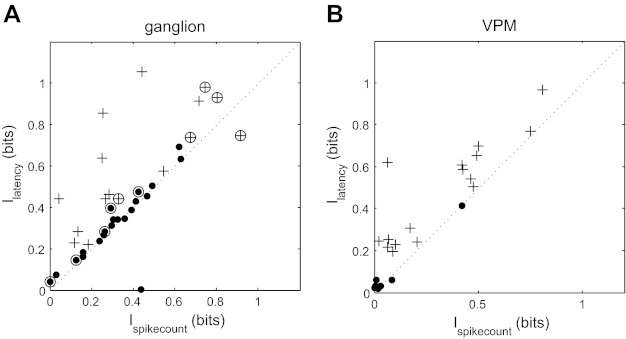
Information analysis of latency vs. spike-count coding. A: comparison between I_latency and I_spikecount for ganglion units. Dots and plus signs represent spike-count coders and latency coders, respectively. Slowly adapting (SA) neurons are marked with an open circle, and rapidly adapting (RA) neurons are unmarked. B: corresponding data for ventroposteromedial (VPM) units.

To assess the incidence of spike-count coding vs. latency coding in the ganglion, we carried out the MI analysis for each unit in our data set (Fig. 4A). Units conveyed 0.44 ± 0.27 bits (mean ± SD) by latency and 0.35 ± 0.23 bits by spike count. Forty-two percent of ganglion units were latency coders, and 58% were spike-count coders. The latency coders conveyed 48% more information by latency than spike count (I_latency = 0.62 ± 0.28 bits and I_spikecount = 0.42 ± 0.28 bits), whereas spike-count coders conveyed a similar amount (I_latency = 0.31 ± 0.19 bits and I_spikecount = 0.30 ± 0.18 bits).

To test whether the latency-/spike-count-coder distinction might relate to that between RA and SA cells, we classified each unit as RA (n = 27) or SA (n = 11). We found that 41% of RA units and 55% of SA units were latency coders. For RA units, I_latency = 0.42 ± 0.25 bits and I_spikecount = 0.33 ± 0.18 bits, whereas for SA units, I_latency = 0.47 ± 0.37 bits and I_spikecount = 0.42 ± 0.32 bits (Fig. 4A). Thus both SA and RA cell types exhibited latency and spike-coding subpopulations. Note that, due to our definition of a latency coder, a unit that conveys more information by the timing of the first spike than by the presence/absence of the first spike, it is possible for units that fire more than one spike within the response time window to have I_spikecount (which takes all spikes into account, not just the first) greater than I_latency; this occurred for two units in Fig. 4A.

Coding with an internally generated stimulus clock.

As noted in the Introduction, a potential problem with latency coding is that whereas latency is defined with respect to the onset of the stimulus (external stimulus clock), neural circuits in the subject's brain do not have direct access to this information. Thus it is important to consider whether latency can be effectively extracted by downstream neuronal populations.

As detailed in materials and methods, latency can potentially be estimated in a manner that does not depend on the external stimulus clock, provided that the neural responses are sufficiently precisely timed and that the latency with which a neuron responds in its preferred direction depends only weakly on direction. When these assumptions hold, any stimulus will tend to evoke a volley of population activity for which the onset time will depend little on the stimulus parameter. Thus the onset time of the population response can, in principle, be used as a reliable surrogate for the external stimulus clock.

Our aim was to investigate whether such a mechanism might be feasible for direction coding in the whisker system. To this end, we treated our database of ganglion units as if they were simultaneously recorded and resampled units from the population, as detailed in materials and methods, so that pseudopopulations of any desired size could be generated. The preferred direction of each resampled unit was obtained by applying a random shift (in the interval 0–360°) to that recorded unit. Figure 5A shows 3 examples of the population response (N_pool = 100 resampled units) to single trials of whisker deflections in each of 3 directions (70, 208, and 322°). Although the precise subset of neurons responding differed according to deflection direction, the overall response of the population was qualitatively similar (Fig. 5A).

Fig. 5.

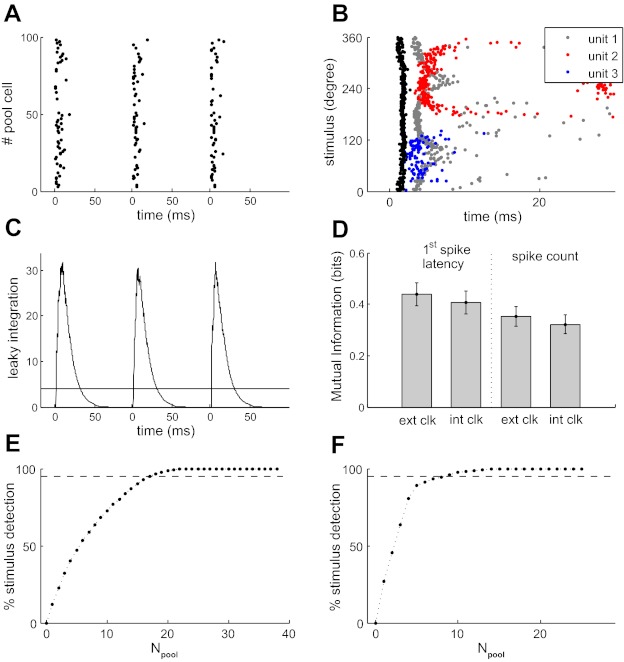
Decoding latency without an external stimulus clock. A: response of 100 resampled ganglion units to single whisker deflections in 3 different directions (70, 208, and 322°). Units are plotted along the y-axis in arbitrary order. B: times when the activity of the leaky integrator crossed threshold as a function of stimulus direction (black dots) and 1st-spike times from 3 example units (gray, blue, and red dots, respectively) C: output of the leaky integrator to the activity of A: threshold (θ) = 4, time constant of the pooling process (τ) = 10 ms, the number of units in the population (N_pool) = 100. D: mutual information (MI) conveyed by latency and spike count by ganglion units when neuronal response was measured either relative to actual stimulus onset time (ext clk; θ = 0) or relative to the threshold-crossing time of the leaky integrator (int clk; θ = 4). E: analysis, using the n = 38 recorded ganglion units, of the percentage of trials on which the stimulus was detected as a function of population size (θ = 1; τ = 10 ms; dashed line indicates 95%). F: corresponding results for VPM.

To detect the onset of the population response, we used a leaky integrator mechanism with time constant, τ (Eq. 6). The integrated population response was indeed very similar for the different directions (Fig. 5C). On each trial, the internal clock signal was generated when the population response first exceeded a threshold, θ.

We found a threshold, θ, in the range 1–5 to be effective. This indicates that an effective clock signal can be generated based on just the onset (1st 1–5 spikes) of the population response. On average, the integrated response reached threshold 2.4 ms after deflection onset (θ = 4, τ = 10 ms, N_pool = 100). Importantly, the threshold-crossing time varied very little with direction and exhibited submillisecond reliability (Fig. 5B, black dots): the SD was 0.38 ms, ∼2 orders of magnitude less than the typical variation in latency evoked by different directions (10–20 ms; Fig. 5B; gray, blue, and red dots).

In fact, only a subset of units was necessary for reliable detection of stimulus onset time. For the specific case of θ = 1, it is straightforward to count how many units, out of the whole population, contribute to stimulus onset detection. We found, using the recorded sample (n = 38 units), that 95% of stimulus onset detections were due to the 17 units (44%; θ = 1 and τ = 10 ms) that fired with shortest latencies (Fig. 5E).

To test the assumptions and reliability of the internal clock mechanism, we conducted a number of further tests. Since our resampled units were generated by applying a random 0–360° shift to the tuning curve of a recorded unit, the representation of direction in the resampled population could have been more homogeneous than the actual population. Since there is evidence that the distribution of preferred directions in ganglion is not entirely homogeneous (Lichtenstein et al. 1990), we tested the effect of relaxing the homogeneity. Instead of applying a random shift in the interval 0–360°, we restricted the range to 0–120, 0–180°, etc. We found that restricting the range to 120° did not substantially (<22%) affect the onset time SD. To test the parameter-dependence of the mechanism, we varied the pool size, N_pool (range 25–250, θ = 4, τ = 10 ms), threshold, θ (range 1–10, N_pool = 100, τ = 10 ms), and time constant, τ (range 1–100 ms, N_pool = 100, θ = 4). In each case, we measured the probability that a stimulus was detected and the SD of the detection time. We found that the mechanism was remarkably robust. Detection probability was constant at 1 throughout the range of parameter values tested; detection time SD was <1 ms.

These data indicate that a highly reliable estimate of stimulus onset time, differing primarily in a short submillisecond delay, can be obtained from the ganglion population response itself, without any knowledge of the external stimulus clock. In principle, this “internal stimulus clock” could be used to measure the response latency of individual units. We term this “internally clocked” latency in contrast to the standard “externally clocked” latency.

To evaluate the performance of the internally clocked latency code quantitatively, we compared the MI conveyed by the standard (externally clocked) latency reported above with that conveyed by the internally clock latency. We found that the internally clocked estimates were very similar (Fig. 5D). In terms of MI, I_latency = 0.44 ± 0.27 bits for externally clocked latency compared with 0.40 ± 0.28 bits for internally clocked latency (θ = 4, τ = 10 ms, N_pool = 100). The average information loss due to using the internal clock was thus 9%. For RA units, the information loss was 9.2%; for SA units, it was 3.4%. Spike-count coding was affected in a similar way (I_spikecount = 0.32 ± 0.23 bits, 8.5% loss).

Latency coding in VPM.

Our next aim was to determine whether there is any transformation in the neural code for whisker deflection direction along the subcortical lemniscal pathway. To address this, we recorded the response of units in the VPM thalamus (n = 25) to the whisker deflection protocol described above. We compared spike count and latency codes quantitatively using MI. Overall, for VPM units, I_latency = 0.35 ± 0.28 bits compared with I_spikecount = 0.23 ± 0.25 bits (P = 3.6 × 10⁻⁵, sign test; Fig. 4B). Seventeen VPM units (68%) were latency coders. For these units, I_latency was 0.48 ± 0.23 bits, and I_spikecount was 0.30 ± 0.26 bits. For spike-count coders (32% of VPM units), I_latency was 0.08 ± 0.14 bits, and I_spikecount was 0.07 ± 0.14 bits. The difference between I_latency and I_spikecount was statistically significant for latency coders (P = 1.5 × 10⁻⁵) but not for spike-count coders (P = 0.45). These results indicate that latency information is preserved along the trigeminothalamic pathway from ganglion to VPM.

As in the previous section, it is important to consider whether VPM latency information can be decoded without the need for external stimulus clock information. The nature of the problem is somewhat different in VPM since, unlike ganglion neurons, VPM neurons exhibit spontaneous activity, which could potentially degrade the performance of the internal clock mechanism.

We found, as in ganglion, that synchronous VPM population activity could be used to obtain a remarkably precise and reliable timing signal (4.8 ± 0.28 ms; θ = 4; τ = 10 ms, N_pool = 100). Thus, despite the presence of spontaneous activity, VPM responses are precise and robust enough to generate a reliable, internal stimulus clock. To test whether the internal clock precision was adequate to capture the latency information, we compared the MI conveyed by externally and internally clocked latency measures, as above. We found that the internally clocked latency preserved 90% of the information conveyed by the standard, externally clocked latency (θ = 4, τ = 10 ms, N_pool = 100). The internally clocked latency MI was 28% greater than that conveyed by the spike count.

As for the ganglion population, we found that a subset of units was sufficient for reliable detection of stimulus onset time. For example, for θ = 1, 9 of the recorded population of n = 25 neurons (36%) accounted for 95% of the stimulus onset detections since they had the shortest latencies (Fig. 5F). These results indicate that, in VPM, latency contains substantially more information about whisker deflection direction than spike count and that this latency information is potentially decodable even in the absence of external stimulus clock information using a small population.

Population coding of direction.

It is commonly accepted that neural circuits encode information at the level of neuronal ensembles rather than at the level of single neurons. Thus the final aim of this study was to investigate the code for whisker deflection direction at the population level. Since MI cannot typically be reliably estimated for large populations (Panzeri et al. 2007), we adopted a data-robust decoding approach.

A qualitative difference between spike count and spike latency codes is that spike count is a discrete quantity, whereas latency is a continuous one. This has significant implications for decoding. Figure 6A shows latency tuning curves for two hypothetical neurons. Because of the U-shaped form of the tuning function, direction cannot be unambiguously decoded from the latency response of one such neuron. However, direction can be unambiguously decoded from the two neurons illustrated (Fig. 6C). The situation for spike-count coding is very different. Most (RA) neurons in the whisker system typically respond to a whisker deflection by firing either one spike or no spikes (Fig. 6B). Because of the discrete (in this example, binary) nature of the code, it is possible only to decode at a much cruder resolution compared with the latency code (Fig. 6D). However, an increase in population size can compensate for the discreteness of the spike count so that, as population size increases, increasingly higher resolution spike count decoding becomes possible. For example, with a population of 30 neurons (with tuning curves similar to those of Fig. 6, A and B, and an even spread of preferred directions), decoding performance was similar for the population spike count and population latency codes (Fig. 6, E and F).

Fig. 6.

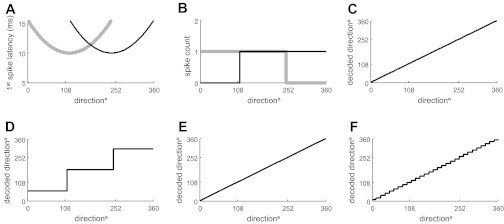
Decoding 1st-spike latency and spike count population codes: hypothetical illustration. A: latency response as a function of stimulus direction (tuning curve) for 2 hypothetical neurons with different preferred directions. B: spike count as a function of stimulus direction for the same neurons. C: actual vs. decoded stimulus direction based on the population latency code of A. D: actual vs. decoded stimulus direction for the spike-count code of B. E and F: corresponding decoding results for a population of 30 hypothetical neurons with identical tuning curve shape to those illustrated in A and B and preferred directions evenly distributed in the range 0–360°.

Of course, real neurons have more complicated responses than the idealized ones of Fig. 6, so it is necessary to consider decoding performance from populations of real neurons. We trained ANNs to decode stimulus direction using either spike count or latency responses of ganglion/VPM populations (materials and methods). An internal stimulus timing signal was generated as detailed above (θ = 4; τ = 10 ms, N_pool = 100). Figure 7A plots actual stimulus direction vs. decoded stimulus direction based on the latency responses of three ganglion units. Figure 7B shows corresponding data for the spike count responses of the same 3 units. Decoding was more accurate with the latency code: the ρ between the actual and the decoded stimulus directions was 0.89 for the latency code compared with 0.51 for the spike-count code. We repeated this analysis for 250 randomly selected populations of 2 or 3 neurons (Fig. 7, C and D). For populations of size 2, mean ρ was 0.42 ± 0.19 for latency and 0.34 ± 0.18 for spike count. For populations of size 3, mean ρ was 0.52 ± 0.17 for latency and 0.44 ± 0.17 for spike count. Very similar results were obtained from analysis of VPM units. For populations of size 2, ρ was 0.45 ± 0.22 for latency and 0.35 ± 0.26 for spike count; for populations of size 3, the corresponding results were 0.52 ± 0.19 and 0.46 ± 0.23, respectively. Thus, for small populations, there was a substantial decoding advantage for latency compared with spike count.

Fig. 7.

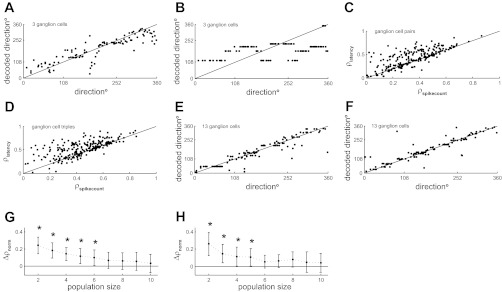
Decoding population codes based on 1st-spike latency and spike count. A: actual vs. decoded stimulus direction based on 1st-spike latency of 3 ganglion units. Each point represents data for a single trial. B: corresponding results using spike count responses for the same units. C: decoding accuracy for latency vs. spike codes based on 250 randomly selected pairs of ganglion units. Decoding accuracy was measured as the Pearson correlation coefficient between actual and decoded direction across all trials: denoted ρ_latency for the latency code and ρ_spikecount for the spike-count code. D: corresponding results for triples of ganglion units. E: actual vs. decoded stimulus direction based on latency of 13 ganglion units. F: corresponding data based on spike count. G: normalized difference in decoding accuracy between latency and spike-count codes (Δρ_norm); see materials and methods for ganglion populations of size 2–10 units. Bars denote SE. H: corresponding data for VPM. Asterisks denote statistically significant differences (P = 0.05).

However, as expected, this advantage was less with larger populations. For ganglion, even a population size of 13 was sufficient for decoding based on spike count to be as good as that based on latency (Fig. 7, E and F): ρ was 0.92 for latency, compared with 0.90 for spike count. To explore this effect systematically, we repeated these calculations for 250 randomly selected populations each of size 2–10 (Fig. 7, G and H). The difference in decoding accuracy steadily decreased with population size. The difference was statistically significant for population size up to 6 units for ganglion (Fig. 7G) and up to 5 units for VPM (Fig. 7H). These results indicate that, at least in the subcortical lemniscal pathway, spike timing potentially allows directional information to be accurately decoded from smaller neuronal ensembles than would be the case for a spike-count code.

DISCUSSION

The aim of this study was to evaluate alternative neural codes for the direction of whisker deflection based on either first-spike latency or spike count. Our main results were as follows. 1) Coding in both ganglion and VPM was diverse: there was a continuum, from units that conveyed substantially more information by latency than by spike count, to others that conveyed the same amount. 2) Ninety-one percent of the latency information could be extracted by an internally clocked mechanism, relying entirely on neural activity, with no knowledge of stimulus onset time. 3) The latency information was propagated along the trigeminothalamic pathway and was also available in the ventroposterior thalamus. 4) For small populations (≤6 neurons), direction could be decoded more accurately from latency than from spike count, whereas for larger populations (>6 neurons), decoding performance was equivalent.

Neural codes for the direction of whisker deflection.

It is well-established from previous work that neurons at all levels of the lemniscal whisker pathway code at least some information about the direction of whisker deflection by a spike-count code (Bale and Petersen 2009; Bellavance et al. 2010; Lichtenstein et al. 1990; Simons and Carvell 1989; Zucker and Welker 1969). Our findings show that a substantial subset of neurons code significant, additional information by latency. Evidence that neurons in the principal trigeminal nucleus also exhibit direction-tuned latencies (Bellavance et al. 2010) together with our finding that latency information is present in a subset of VPM neurons indicates that the latency code is preserved across the subcortical lemniscal pathway. Our result that latency information is already present in the ganglion indicates that this latency code arises from receptor mechanisms in the whisker follicle. However, the latency code is further sharpened by inhibitory circuitry in the brain stem (Bellavance et al. 2010). Most of the information that cortical neurons convey about direction is present in the first poststimulus spike (Bale and Petersen 2009), suggesting the possibility of a cortical latency code [as has previously been reported for other parameters of whisker stimulation (Panzeri et al. 2001; Petersen et al. 2002b)]. However, given that the information that each neuron conveys is substantially lower in barrel cortex than in the subcortical pathway (Bale and Petersen 2009), there appears to be a significant transformation in the neural code across the thalamocortical pathway in part due to cortical integration mechanisms (Puccini et al. 2006).

Latency coding in the somatosensory system.

Spike-timing codes have been previously reported in the whisker system for a variety of other sensory parameters: the location of whisker contact (Panzeri and Diamond 2010; Panzeri et al. 2001; Petersen et al. 2002b), white noise whisker motion (Jones et al. 2004; Montemurro et al. 2007a), and texture (Arabzadeh et al. 2006). Spike-timing codes have also been reported in the dorsal column somatosensory system (Foffani et al. 2008, 2009; Johansson and Birznieks 2004). The emerging picture is that coding by spike timing is a general principle of coding in the somatosensory system.

Coding in the whisker system is known to be heterogeneous: neurons exhibit diversity in their selectivity to kinetic features of whisker motion (Petersen et al. 2008), in their response to object contact (O'Connor et al. 2010; Yu et al. 2006), and in their synaptic dynamics (Martini et al. 2011). The present study shows that neurons are also diverse in the manner in which their spike trains encode information. An advantage of the MI method is that the contribution of alternative codes can be quantified and compared. In this way, we found surprising variety: some neurons (42% in ganglion, 68% in VPM) conveyed more information by latency than by spike count.

Decoding latency information.

Latency is the time delay between stimulus onset (external clock) and the first spike evoked after stimulus onset. This gives rise to a “clock problem” in that, unlike the experimenter, neurons in the brain of the experimental subject cannot have direct knowledge of this external stimulus clock. Hence, there is a general issue whether latency coding is neurobiologically viable. Both motor and sensory solutions are possible. In active sensory modalities, such as the whisker system or the saccadic eye movement system, sensory stimuli (e.g., whisker contacts) are typically evoked as a consequence of motor commands. In the whisker system, there is evidence that information about whisking phase is present in cortical circuits (Curtis and Kleinfeld 2009). In principle, efference copy of the motor command could be used as a clock signal with reference to which latencies could be extracted by neural circuits. Alternatively, when neural population activity is taken into account, it can be possible for neural circuits to compute latency information even in the absence of external clock information. This can be done either, as here, by using population activity to estimate stimulus onset time explicitly (Chase and Young 2007; Foffani et al. 2008; Vasserman et al. 2010) or by using population activity to extract measures such as relative latency or rank order that do not depend on the external clock (Gollisch and Meister 2008; Johansson and Birznieks 2004; Panzeri and Diamond 2010; Zohar et al. 2011). As an example of the second approach, Johansson and Birzneks (2004) showed that the direction of force on a human fingertip could be accurately decoded from the rank order of latencies within a population of primary sensory afferents. In these reports, the number of neurons required to detect the stimulus reliably varied from 2 to 100. This variation probably reflects differences in spike-timing reliability and spike counts in different sensory systems and different parts of the nervous system as well as differences in the algorithms employed.

Here, we tested the first strategy. The mechanism we used (Chase and Young 2007) relies on the precisely timed firing of neurons but makes the additional assumption that the latency with which a neuron responds to its preferred parameter value depends only weakly on that parameter. Under these circumstances, any stimulus will evoke a volley of activity, and the timing of this volley will be approximately independent of the stimulus value even though the particular neurons that make up the volley will be stimulus dependent. Thus, in principle, the time of the population volley can be used as an internal clock to substitute for the external one. However, for this to be feasible, it is critical that the population volley be precisely timed. Otherwise, the latency information will be degraded. Thus it is important to quantify the internally clocked latency information. Use of MI allowed us to do this. We found that the mechanism was remarkably effective for direction coding in both ganglion and VPM, with the internally clocked latency providing 91% of that provided by the standard (externally clocked) latency. The main reasons for this were the high spike-timing precision of neurons in the whisker system and the fact that latency in the preferred direction was not systematically dependent on direction. This meant that the population volley had submillisecond precision (0.2-ms SD) and thus could serve as a highly effective internal clock, provided that the population size was sufficient. Although the bulk of our analysis was done for populations of 100 neurons, we found that a minority, 17 in ganglion (44%) and 9 in VPM (36%), were responsible for 95% of stimulus detection events. It is important to note that our analysis does not capture all the information available about whisker direction in the responses of a population of neurons. Rather, our conclusion is that stimulus timing can be estimated from neuronal activity in an internally clocked manner and, therefore, that spike-timing information is potentially decidable by neural circuits.

For the nervous system to implement some form of this mechanism, it must be the case that spike-timing information is accurately relayed along the sensory pathway. Consistent with this, spike timing is conserved with millisecond precision along the lemniscal whisker pathway (Montemurro et al. 2007a; Panzeri et al. 2001). It must also be the case that there exist specialized neurons that accurately encode stimulus onset time. Cortical fast-spiking units (FSUs; putative inhibitory interneurons) have properties potentially well-suited to such a role: in contrast to regular-spiking units, FSUs tend to respond more reliably to whisker deflection, lack direction sensitivity, and more extensively pool convergent inputs (Bruno and Simons 2002; Swadlow and Gusev 2002). Thus we speculate that FSUs may have a role in stimulus onset detection. Interestingly, in the auditory system, direct evidence for stimulus onset detectors has recently been reported (Brasselet et al. 2012).

Our analysis assumed that the impact of noise correlation across neurons is negligible. Previous simultaneous recording studies in the whisker system have found these to be small (Petersen et al. 2002b), but it is important to note that, in principle, noise correlations might either improve or impair the function of a decoder (Petersen et al. 2002a). It would be interesting in future work to consider latency decoding with large-scale simultaneously recorded data.

Since precise spike timing is a general property of lemniscal somatosensory neurons (Arabzadeh et al. 2006; Foffani et al. 2009; Montemurro et al. 2007a; Panzeri and Diamond 2010; Panzeri et al. 2001; Petersen et al. 2002b; Tutunculer et al. 2006), the mechanism of latency decoding we propose may well be useful to not only direction coding, but also somatosensory coding in general.

Population coding of direction.

It is important to consider the coding of sensory parameters at the population level. Population coding schemes can be conceptually divided into those based on spike timing and those based on spike count. The first-spike latency scheme and the spike count scheme represent single members, respectively, of the first and of the second class. Since latency is a continuous quantity, whereas spike count is discrete, latency codes can be substantially more powerful, particularly when, as here, the encoded variable is itself continuous and hence requires a large bandwidth (Maass 1996). Thus, as illustrated in Fig. 6 for small populations, direction can only be decoded at very low resolution from a population spike-count code but at much higher resolution from a population latency code. For a discrete stimulus with few classes, the potential of a latency scheme could be underestimated.

Our final aim was to study coding of direction at the population level. We did this by considering how accurately direction could be decoded based on neuronal population activity. When considering the code for a single parameter such as direction, there will inevitably be a saturation effect as the population size increases since there is a limit to how far performance can increase. As expected, we found that decoding for both latency and spike-count codes became increasingly accurate and increasingly similar as population size increased. However, for small populations (2–6 in ganglion, 2–5 in VPM), decoding was significantly more accurate for the latency code.

These results indicate that population latency coding may permit the same amount of stimulus information to be processed by a neural circuit with fewer neurons than would be necessary with a spike-count code. This has significant potential advantages. First, neural processing incurs a substantial metabolic cost (Laughlin 2001; Laughlin et al. 1998), and latency coding could decrease the energetic cost of information transfer. Second, since the number of possible neural connections rises factorially with population size, latency coding may substantially reduce the wiring complexity of neural circuits, which studies indicate to be an important constraint on nervous system organization (Cherniak 1994; Laughlin and Sejnowski 2003; Shinbrot and Young 2008; Varshney et al. 2011). Third, sparser connectivity potentially reduces redundancy and promotes adaptability of neural circuits to novel and unexpected stimuli (Tononi et al. 1999). For cases such as the subcortical lemniscal pathway, where the number of afferent synaptic inputs is small (Arsenault and Zhang 2006; Deschenes et al. 2003), computation based on first-spike latencies may present significant computational advantages compared with those based on spike counts.

GRANTS

This work was supported by CARMEN e-science project (Engineering and Physical Sciences Research Council Grant EP/E002331/1) and Biotechnology and Biological Sciences Research Council Grant BB/G020094/1 to R. S. Petersen.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

R.S. and R.S.P. conception and design of research; R.S. analyzed data; R.S., G.E.M.B., and R.S.P. interpreted results of experiments; R.S. and R.S.P. prepared figures; R.S. and R.S.P. drafted manuscript; R.S., M.R.B., G.E.M.B., and R.S.P. edited and revised manuscript; R.S., M.R.B., G.E.M.B., and R.S.P. approved final version of manuscript; M.R.B. performed experiments.