Sacrificial layer technique for axial force post assay of immature cardiomyocytes

Abstract

Immature primary and stem cell-derived cardiomyocytes provide useful models for fundamental studies of heart development and cardiac disease, and offer potential for patient specific drug testing and differentiation protocols aimed at cardiac grafts. To assess their potential for augmenting heart function, and to gain insight into cardiac growth and disease, tissue engineers must quantify the contractile forces of these single cells. Currently, axial contractile forces of isolated adult heart cells can only be measured by two-point methods such as carbon fiber technique s, which cannot be applied to neonatal and stem cell-derived heart cells because they are more difficult to handle and lack a persistent shape. Here we present a novel axial technique for measuring the contractile forces of isolated immature cardiomyocytes. We overcome cell manipulation and patterning challenges by using a thermoresponsive sacrificial support layer in conjunction with arrays of widely separated elastomeric microposts. Our approach has the potential to be high-throughput, is functionally analogous to current gold-standard axial force assays for adult heart cells, and prescribes elongated cell shapes without protein patterning. Finally, we calibrate these force posts with piezoresistive cantilevers to dramatically reduce measurement error typical for soft polymer-based force assays. We report quantitative measurements of peak contractile forces up to 146 nN with post stiffness standard error (26 nN) far better than that based on geometry and stiffness estimates alone. The addition of sacrificial layers to future 2D and 3D cell culture platforms will enable improved cell placement and the complex suspension of cells across 3D constructs.

1. Introduction

Ischemic damage following myocardial infarction often leads to heart failure, contributing to cardiovascular disease's status as the number one killer in developed countries. This year an estimated 785,000 people in the United States alone will have their first heart attack (Roger et al. 2011). This underscores the critical need for cardiac therapies to actively repair damaged tissue. These therapies will be predicated upon knowledge of the mechanisms of cardiac growth and disease, including the development of contractile function in maturing heart cells.

The study of isolated cardiomyocytes enables observation of active and passive properties that can be attributed to cell autonomous mechanics, i.e. independent of the properties of cell matrix proteins and supporting cells such as fibroblasts. These mechanics are related directly to the alignment and organization of sarcomeres, the actin- and myosin-containing muscular subunits that enable cellular contraction. Cardiomyocytes are mechanosensitive and respond to environmental stimuli by remodeling that in turn can affect their contractile capacity (McCain and Parker 2011), and force measurements provide a direct measure of cardiomyocyte function or “health” that can be extrapolated up to scale of a tissue graft.

Currently, little is known about force production in single developing cardiomyocytes, while mature cardiomyocytes have been previously studied (Sivaramakrishnan et al. 2009; Bollensdorff et al. 2011; Curtis and Russell 2011). Their contractile forces have been measured by suspending single, isolated cardiomyocytes between pairs of carbon fibers (Le Guennec et al. 1990; Yasuda et al. 2001; Iribe et al. 2007), glass micropipettes (Brady et al. 1979; Fabiato 1981), or micromachined silicon grippers (Lin et al. 1995) that deflect during contraction; the resulting deflections can be used to calculate applied contractile forces. The two-point carbon fiber technique has been used with displacement feedback to perform both isometric and auxotonic contractile force measurements of adult rat cardiomyocytes (Yasuda et al. 2001; Nishimura et al. 2004; Iribe et al. 2007), leading to the measurement of peak contractile forces in the range of 0.7–12.6 μN (Lin et al. 2000; Yasuda et al. 2001; Nishimura et al. 2004; Iribe et al. 2007). Fiber-based two-point techniques are the gold standard for axial force measurement, and all similar techniques exploit the observation that adult cardiomyocytes maintain a persistent, elongated, cylindrical shape after enzymatic extraction from tissue. However, immature cardiomyocytes become spherical after extraction, resisting attempts to measure their contractile forces using current two-point techniques (Lam et al. 2002; Kolossov et al. 2005). Similarly, cardiomyocytes derived from either embryonic or induced pluripotent stem cells have similar spherical morphology when extracted from culture. Furthermore, these fiber-based techniques are very labor-intensive and incapable of being adapted to high-throughput analyses.

To date, there have been no purely axial force measurements of single neonatal or stem cell-derived cardiomyocytes, the cells that could provide useful models for fundamental studies of heart development and cardiac disease and form the basis for future cardiac therapies. Open questions regarding these cells include the affects of sarcomeric mutations on disease development (Sivaramakrishnan et al. 2009), regulatory mechanisms of the Frank-Starling relationship (Bollensdorff et al. 2011; Campbell 2011; Cazorla and Lacampagne 2011), strain-sensing by titin (Cazorla and Lacampagne 2011; King et al. 2011), and the role of microtubules in mechanosensing and cardiomyocyte resistance to compression (White 2011).

Recent studies have measured depolarizations and pace-response in cardiomyocytes differentiated from human induced pluripotent stem cells (Yazawa et al. 2011). In addition, optogenically modified human stem cell-derived cardiomyocytes have been created and offer the opportunity for non-invasive pacing with light (Abilez et al. 2011). Force generation studies on these cells have not been performed, and axial force measurements would provide critical information about the function of healthy and diseased stem cell derived cardiomyocytes at multiple points in time.

When force-related studies of immature heart cells have been conducted, they have primarily been achieved using traction force microscopy (Dembo et al. 1996; Butler et al. 2002) and arrays of elastomeric microposts (Tan et al. 2003). Both methods offer the potential for high-throughput analysis, unlike serial carbon fiber measurements, but these techniques measure distributed loads across the substrate as “heat maps” of applied forces. Per post measurements from 39 to 100 nN have been reported using neonatal and adult cardiomyocytes on elastomeric force post arrays (Zhao and Zhang 2006; Zhao et al. 2007; Kim et al. 2011). Although these forces can be summed into dipoles, the resulting sums are not equivalent to the gold standard axial measurements because the cellular loading conditions vary across traction force surfaces. As a result of these measurement differences and the large uncertainties inherent in most polymer-based force assays (Constantinides et al. 2008; Kim et al. 2011), prior investigations have focused on the effects of relative substrate stiffness rather than on comparisons of net force production (Engler et al. 2008; Jacot et al. 2008; Jacot et al. 2010; Tang et al. 2011).

In a study of neonatal rat cardiomyocytes on force posts, Rodriguez et al. showed that the cardiomyocytes generate increasing twitch power with increasing effective device stiffness up to 15 kPa (Rodriguez et al. 2011). They also argue that power is a more important metric than contractile force and use individual post displacements for those calculations. Here we suggest that it would be useful to develop an axial method that generates measurements of both power and force that are comparable with the current two-point literature. Further, without additional protein patterning, current traction force microscopy and micropost methods fail to prescribe a physiologically relevant elongated cardiomyocyte shape, which is critical to sarcomere alignment and thus cell contractility (Brady et al. 1979; McCain and Parker 2011). Kazjer et al. addressed these issues by culturing neonatal rat cardiomyocytes between large, widely separated micropost arrays, successfully measuring contractile forces for separations up to 30 μm (Kajzar et al. 2008). Since these cells attached to the sides of the posts, the forces were calculated based on distributed loading of the microposts instead of on two-point loading at the post tops, complicating direct comparison with other studies. Widely separated micropost arrays have also been used in a similar manner with REF52 fibroblasts to study cell spreading (Ghibaudo et al. 2011); this investigation was also unable to achieve a pure two-point loading condition, as the cells spread along the lengths of the posts instead of across the post tops.

Here we present the development of a sacrificial layer technique with widely separated microposts, an approach that promotes the maintenance of an elongated, physiologically relevant shape in primary neonatal cardiomyocytes and human embryonic stem cell-derived cardiomyocytes. A critical innovation allows our system to overcome previous cell adhesion issues without the need for an etching step: we utilize an aqueous deposition and hydrophobic backing layer to protect the post tops from coating with the sacrificial polymer. Our process does not require protein micropatterning and achieves pure two-point axial measurements of these cells, permitting direct comparison of our measurements with previous axial investigations of adult cardiomyocytes. Further, calibration of our microposts using piezoresistive cantilevers (Kim et al. 2011) improves device accuracy and precision and ensures that the variability observed is due to biological variation rather than device uncertainty. The use of video post-displacement imaging makes this an ideal high- throughput platform for testing both pharmacologic and gene therapies in isolated cardiomyocytes.

2. Experimental Methods

To suspend single cardiomyocytes across posts, force post arrays are filled with a dehydrated layer of a thermoresponsive polymer, functionalized with adhesion proteins, and seeded with cells. After the cells spread and adhere, the devices are cooled to dissolve away the sacrificial layer (Figure 1).

Fig. 1.

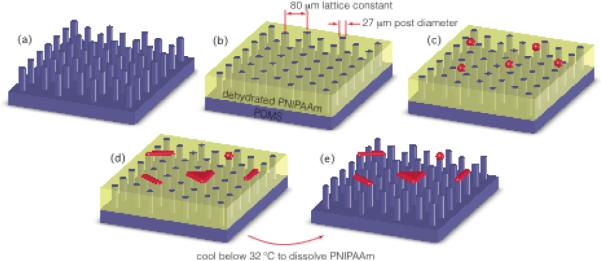
Device fabrication and cell suspension using a sacrificial layer. Our hybrid force assay platform is created by augmenting an elastomeric micropost array (a) with a dehydrated layer of the thermoresponsive polymer PNIPAAm (b). Isolated and balled immature cardiomyocytes (red) are seeded onto the platform (c) and allowed to spread for 4–7 days (d). Once the cells have spread across the posts, the sacrificial layer is dissolved away (e) by temporarily cooling the media to just below 32 °C, leaving the immature heart cells spread across pairs and triads of posts

2.1 Force post fabrication

Micropost arrays were made according to previously published replica molding techniques (Figure 2) (Tan et al. 2003; Sniadecki and Chen 2007). A master post array was first fabricated out of SU-8 2075 (MicroChem) on a silicon wafer using standard lithography techniques. Next, the array was silanized (chlorotrimethylsilane C72854, Sigma-Aldrich) overnight to minimize adhesion during molding. Polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning) was mixed in a 10:1 ratio of polymer base to curing agent, deposited on the master array, degassed to remove air bubbles, and baked in a 65°C oven for two hours. This negative mould was peeled from the master array to become the next mould for the replica arrays. The PDMS negative was then oxygen plasma-treated (Branson Barrel Asher) at 80 W for 40 s and silanized. The PDMS molding procedure was repeated to obtain PDMS duplicates of the original SU-8 master array. PDMS moulds can be reused several times to fabricate new replica post arrays. Post dimensions were optically measured using an upright microscope (Leica, DM RXA2) with a resolution of 0.395 μm/pixel; distances were calibrated using reference slides.

Fig. 2.

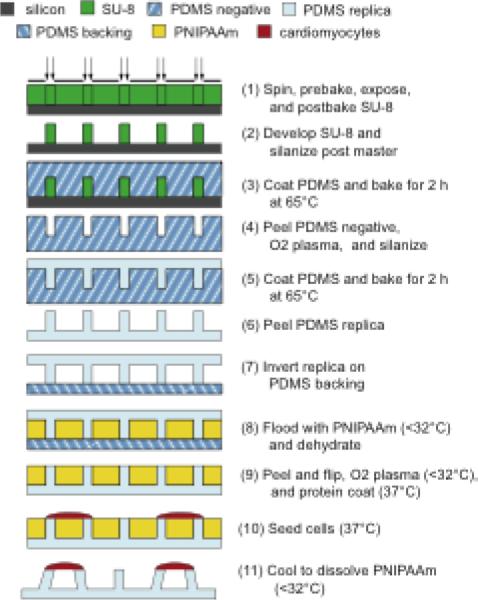
Device fabrication starts with replica molding of microposts (steps 1–6) followed by inversion of the replica on a PDMS backing (step 7), deposition of the thermoresponsive sacrificial layer (steps 8–9), cell seeding (step 10), and dissolution of the sacrificial support layer (step 11)

2.2 Calibration

Micropost stiffness is typically calculated using post geometry and estimates of the PDMS elastic modulus. This elastic modulus can be measured using nanoindentation or macroscale tensile tests, or an estimate can be obtained from the literature, which reports a stiffness range of 0.36–2.5 MPa for a 10:1 base to curing agent ratio (Armani et al. 1999; Mata et al. 2005; Zhao and Zhang 2005; Sniadecki and Chen 2007). However, there are challenges inherent to such strategies due to the wide variation in reported values and because bulk PDMS properties can vary from microscale properties (Miao et al. 2009; Xu et al. 2011).

In practice, batch-to-batch property variation of PDMS can be due to small differences in the ratio of elastomer base to curing agent, the baking time, the degree of mixing, and the duration of time from fabrication to use (Fuard et al. 2008; Cheng et al. 2010). Further, as we have reported previously (Kim et al. 2011), estimates of post stiffness based on geometry and assumed material properties can lead to large uncertainties of 50–100% or greater. Even commercial atomic force microscopy cantilevers provide at best 50% measurement uncertainty in force if used for direct calibration (Pratt et al. 2004). To improve the resolution of our force-generation assay, we directly calibrated each batch of microposts using well-characterized piezoresistive microcantilevers (Figure 3) (Park et al. 2007; Kim et al. 2011). This calibration enabled accurate quantitative measurements with our elastomer force posts, and we observed significant batch-to-batch stiffness variation between our devices, which suggests that the effective stiffness of microstructures may vary more than bulk measurements would indicate. (Figure 4).

Fig. 3.

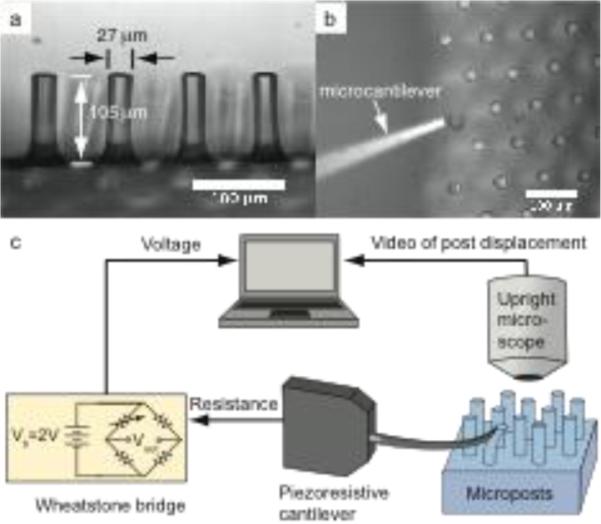
Microposts (a) are calibrated using a piezoresistive microcantilever (b). Force is calculated from voltage out of the Wheatstone bridge and displacement is measured optically using an upright microscope (c). Scale bar represents 100 μm. Panels A and B adapted from (Taylor et al. 2010)

Fig. 4.

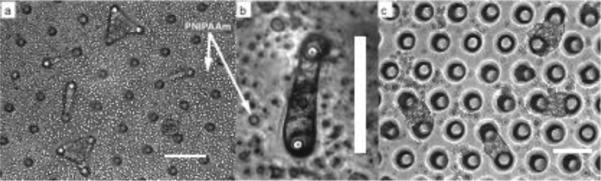
Single neonatal rat cardiomyocytes stretch across round-top microposts (a and b), as do primary neonatal rat cardiomyocytes across pairs of sharp cylindrical microposts (c). Arrows indicate clumps of PNIPAAm polymer that came out of solution after the media was rewarmed to 37 °C. Quantitative measurements were made with sharp cylindrical post geometries only, but we noted that microposts with rounded tops yielded narrower cell shapes. Scale bars indicate 100 μm. Panels a and c adapted from (Taylor et al. 2010)

All microposts were calibrated with a piezoresistive microcantilever with stiffness k_c = 0.0500 +/− 0.0037 N/m and displacement sensitivity 56.74 +/− 2.48 V/m at a 2-V bridge bias voltage with a gain of 1000, yielding a force sensitivity of 1134 +/− 50 V/N. For each calibration, programmable linear actuators (T-NA series, Zaber) were used to move the cantilever until it was just in contact with the top and side of the micropost. Displacement steps in 1 μm increments advanced the cantilever as it deflected the post, and the resulting micropost deflections were captured via an upright microscope (Leica, DM RXA2) with a 10× objective (Figure 3). From these calibrations, the microposts exhibit a linear force-displacement relationship for deflections less than 20 μm (Figure 5a).

Fig. 5.

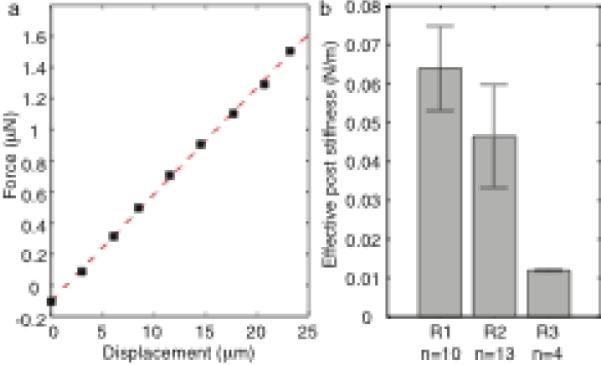
Force-displacement curves (a) for each micropost verify linearity within the desired measurement range up to 20 μm. Each device was made from a separate batch of PDMS according to the same recipe, and multiple posts were calibrated to determine device stiffness, which varied considerably from batch to batch (b). Error bars represent standard deviation

We calculate micropost stiffness (Figure 5b) from the following equation,

$$k_p=\frac{0.24\rho LWT{\left(2\pi {\omega }_n\right)}^2\Delta V}{G{V}_{b}R{S}_d\Delta x}$$ (1)

Where ρ is the density of silicon, L is the cantilever length, W is the cantilever width, T is the cantilever thickness, ω_n is the cantilever natural frequency, ΔV is the change in measured voltage, G is the gain of the Wheatstone bridge, V_b is the bridge bias voltage, R is the image resolution in microns per pixel, S_d is the displacement sensitivity, and Δx is the micropost displacement in pixels during calibration.

Cellular forces were determined by multiplying micropost stiffness by micropost displacement during cardiomyocyte contraction (details of this calculation are given in the Appendix). Random error was measured by repeating the calibration process on multiple microposts from the same batch.

2.3 Sacrificial layer application

A novel two-step technique for the application of the thermoresponsive polymer poly(N-isopropylacrylamide) (PNIPAAm, Polysciences) enables filling of the arrays up to the full height of the posts without coating the tops of the posts (Figures 1 and 2). Instead of dissolving the PNIPAAm in a polar solvent with higher solubility such as ethanol (Xi et al. 2005), isopropanol (Okano et al. 1993), or butanol (Feinberg et al. 2007), as commonly reported, we employed an aqueous solution. We then exploited the hydrophobic nature of PDMS to keep the PNIPAAm away from the post tops.

To prepare the PNIPAAm solution (1 wt %), we added 500 mg of PNIPAAm powder and cold deionized water to fill a 50-mL centrifuge tube. We vortexed this solution for 30–60 s. If the PNIPAAm did not fully dissolve, we cooled the solution in a 4° C refrigerator for 1 h. We ran the solution through a sterile 0.2 μm filter before use.

We inverted each post array onto a soft PDMS backing layer (30:1 or 40:1 ratio) and flooded the array with the PNIPAAm solution. When the inverted device was flooded with solution, the tops of the posts formed a hydrophobic seal with the backing layer, preventing the PNIPAAm from coating the post tops. The solution was allowed to evaporate for 2 d at room temperature, and the resulting devices, filled flush with the dehydrated PNIPAAm, were peeled from the backing layer (Figure 2).

2.4 Functionalization and cell seeding

The PDMS post tops of these hybrid devices must be functionalized with adhesion protein before cell seeding. To make the exposed PDMS post tops hydrophilic, devices were oxygen plasma-treated for 80 s at 40 W (Branson Barrel Asher). PNIPAAm remains in its dehydrated, hydrophobic solid state in water only at temperatures greater than its lower critical solution temperature of 32°C. Therefore, to keep the PNIPAAm structures from dissolving during the protein coating step, the devices were warmed to 37°C directly on a hotplate before being coated with a pre-warmed 10 μg/mL solution of laminin (Natural Mouse Laminin, Invitrogen). After 1 h of incubation at 37°C, the devices were washed in warmed distilled water to remove excess laminin, continually heated by the hotplate to maintain 37°C, and finally coated with a suspended cardiomyocyte solution at 37°C.

Protein micropatterning is unnecessary in this system because the cells selectively adhere to functionalized micropost tops rather than to PNIPAAm in between the posts; the filled array acts as if it has been microcontact-printed with circular islands of adhesion protein. Even without specific protein cues in the region between the posts, immature cardiomyocytes spread across the device to span pairs of posts (Figure 1), allowing the cardiomyocytes to subsequently be suspended between posts after sacrificial layer dissolution.

Two types of immature cardiomyocytes were used for our studies: primary neonatal rat cardiomyocytes (Lonza) and human embryonic stem cell-derived cardiomyocytes. Neonatal cardiomyocytes were thawed, suspended in rat cardiac myocyte basal medium (Lonza) supplemented with 10% fetal bovine serum, 10% horse serum, and GA-1000 (Gentamycin, Amphotericin-B, Lonza), then seeded directly on devices.

To prepare the human embryonic stem cell-derived cardiomyocytes, human embryonic stem cell line HES2 (ESI, Singapore) was maintained on feeder-free Matrigel (BD Biosciences)-coated culture dishes with mTESR-1 human ES/iPS cell culture medium (Stemcell Technologies). Differentiation of HES2 cells into the cardiomyocyte lineage was performed via a well-established protocol (Yang et al. 2008). Beating embryoid bodies were dissociated with collagenase I and seeded on devices for subsequent analysis. Cardiomyocytes were incubated and allowed to adhere to the devices for 2 d, at which point the devices were allowed to cool for 30 minutes to room temperature to dissolve the PNIPAAm (Figure 4). As a note, it is difficult to see the cells through the PNIPAAm using an inverted microscope, but they are clearly visible after dissolution. Cardiomyocytes were monitored for up to 7 d to observe beating.

Between days 4 and 7, beating cells were paced at 1 Hz in Tyrode's solution (Fisher Scientific) at room temperature with a 10 ms-wide biphasic pulse at 10–15 V electric field stimulation (Myopacer, IonOptix) using a platinum electrode with 1 cm spacing between signal and ground wires. Post deflections were optically measured at 8 frames/s using phase contrast microscopy on an inverted microscope (Leica, DMI 6000B) with 20× and 40× objectives with 0.645 and 0.3225 μm/pixel resolution.

2.5 Post displacement analysis

Cardiomyocyte post displacement was tracked and analyzed using custom MATLAB software that uses a frame subtraction scheme to determine the micropost deflections. Frame-to-frame movement is determined by a sum of squares differencing algorithm that determines which movement of a region of interest creates the smallest change in the sum of the squares of pixel intensity differences from frame to frame. Regions of interest were drawn at the edges of each post and in that way post displacement was tracked (Figure 6a). Contractile forces were calculated by multiplying micropost displacements by calibrated micropost stiffnesses. Peak forces and dynamic forces were extracted from each video (Figure 6b and 6c).

Fig. 6.

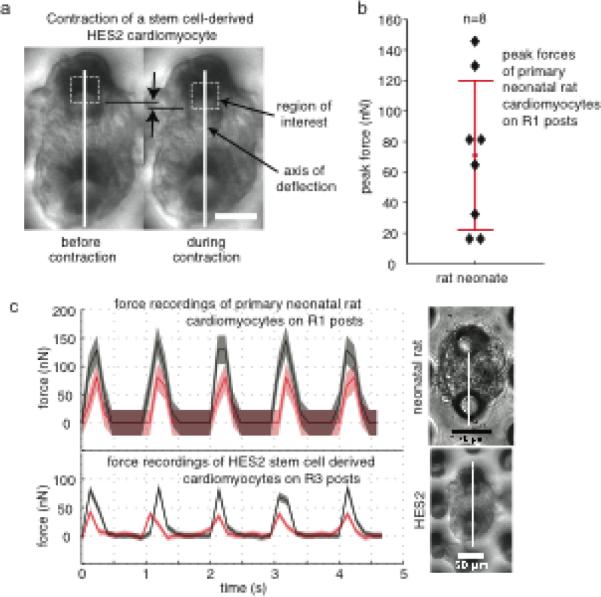
Contractile force measurements. (a) Micropost deflections were extracted from video microscopy still frames. Deflections were measured using custom MATLAB code that applies a least squares difference algorithm to the still frames to track displacements of specified regions of interest (dotted line boxes) along the axis of micropost pairs (white lines). (b) Peak forces up to 146 nN were observed with primary neonatal rat cardiomyocytes. Forces were calculated based on micropost stiffness and observed micropost deflections during contraction. (c) Representative plots for two primary neonatal rat and two human embryonic stem cell-derived hearts show contractile forces for 1 Hz pacing; red and gray curves represent two different cells; shaded regions indicate overall measurement uncertainty in accuracy (overall systematic error) and precision (one standard deviation of post stiffness variation). Scale bars indicate 50 μm

3. Results

Neonatal rat cardiomyocytes and human embryonic stem cell-derived cardiomyocytes were successfully suspended across elastomer posts (Figure 4). Online Resources 1 and 2 are videos showing the beating of each cell type, respectively, indicating that the cells were able to survive and exhibit physiological behavior in our system. Video still frames of cardiomyocytes contracting and relaxing were analyzed using custom MATLAB code to extract post deflections during contractions.

Although microposts were optically measured to be 27 μm in diameter and 105 μm tall with an 80 μm lattice constant (Figure 3a), these measurements are merely used as references. To extract forces from these post deflections accurately, we calibrated micropost stiffness and evaluated variability in each array (Figure 5). We propagated uncertainty through our analysis to determine how well we can quantify force. Systematic error in our reported forces was calculated using root mean sum of squares analysis of the measurement uncertainties (Holman 1988). For analysis of the micropost force measurements, we used a working definition of system accuracy to mean the total systematic uncertainty. Sources of this uncertainty include lithographic variations, the displacement sensitivity of the calibrated cantilever, and the optical measurements. We assumed that lithographic dimensions were accurate within 0.5 μm, that displacement sensitivity had 4.4% uncertainty based on cantilever calibrations (Park et al. 2007), and that optical measurements were accurate to 0.707 pixels, the root mean square of 0.5 pixel uncertainty in both the x- and y-directions. Error in micropost stiffness that was based on dimensional uncertainty of post length, width, and thickness contributed 7.3% error, while optical measurement error during calibration increased that error to 8.7% for posts in each calibration batch, which we will refer to as batches R1, R2, and R3. Uncertainties in the optical measurement of micropost deflections during cardiomyocyte contraction also contributed to the systematic error in cardiomyocyte force measurement. Deflections were small for the relatively stiffer posts from batch R1, and thus optical uncertainty increased the force measurement uncertainty to 17.9%; the relatively softer posts from batch R3 experienced larger deflections and increased systematic force measurement uncertainty to only 10.6%. These systematic errors are considerably smaller than the minimum 50–100% uncertainties in stiffness we would expect without calibration.

For each device we calibrated a sampling of microposts to determine our measurement precision, which we defined as the standard deviation of these measured stiffnesses. Therefore, the post-to-post variation is responsible for our cellular force measurement precision (Figure 5b). The standard deviations of post stiffness measurements for three batches were 17.1% for R1, 28.6% for R2, and 2.3% for R3. Micropost geometric defects and polymer mixing irregularities likely are the two main contributors to post-to-post variation.

Figure 6 shows the post deflections caused by contraction of two different types of single immature cardiomyocytes, primary neonatal cardiomyocytes and human embryonic stem cell-derived cardiomyocytes. Peak contractile forces for multiple primary neonatal cardiomyocytes are also shown, and the maximum peak force exerted by a neonatal rat cardiomyocyte, the main cell type investigated in this study, was 146 nN with an estimated precision of ± 26 nN and comparable accuracy of ± 25 nN. This value is a fraction of the micron-level contractile forces that have been reported in the literature for adult cardiomyocytes (Lin et al. 2000; Yasuda et al. 2001; Nishimura et al. 2004; Iribe et al. 2007). These differences could be due to their smaller size, to disorganized subcellular structures, or even to a nonideal resting length in culture.

We were able to demonstrate that our technique could be used on two different immature cell types: primary neonatal cardiomyocytes that once functioned in a neonatal rat heart and human stem cell-derived heart cells that were differentiated in vitro and were never part of a functional tissue. These differences may also contribute to variation in contractile forces. However, while the contractile forces we measured with primary neonatal rat cardiomyocytes (Figure 6b and 6c) were highly variable, they were on the same scale as forces we measured with stem cell-derived cardiomyocytes (Figure 6c). Such measurements are capable of distinguishing small functional differences that may exist between cells of different species (rat and human), developmental stages (embryonic and neonatal), sources (primary stem cell-derived) and condition (healthy and diseased).

Since the same cantilever was used for both calibrations, we use the precision (from micropost variability) alone as the relevant uncertainty for comparing between cells and populations. Our precision, which is tunable and can be further reduced, is small enough to differentiate the contractile forces observed in these studies from each other and we therefore attribute the variability to differences in the biology and handling of the cells.

4. Discussion

Here we have presented a technique for measuring the axial contractile properties of immature heart cells, reporting the first purely axial force measurements of single developing cardiomyocytes. This general technique achieves single-cell manipulation in a parallel fashion with minimal labor and enables the study of both developing neonatal cardiomyocytes and stem cell-derived cardiomyocytes, which can be used in cardiac cell and tissue graft therapies. To create this system we modified a traditional force post assay (Tan et al. 2003) by enlarging the posts and lattice constants and by filling the volume between the posts with a sacrificial layer of the biocompatible and thermoresponsive polymer, PNIPAAm. Previously PNIPAAm has been used as a release layer for creating contractile cell sheets (Okano et al. 1993) and beating muscular actuators (Feinberg et al. 2007) as well as a thick sacrificial layer for the creation of suspending multicellular cardiomyocyte constructs (Xi et al. 2005). No patterning of protein or other adhesion material was required as with polyacrylamide gels (Théry et al. 2006; Théry 2010), standard force post arrays (Liu et al. 2010), and multicellular cardiomyocyte systems (Xi et al. 2005; Feinberg et al. 2007). The aspect ratio (3:1) between large lattice constant and post diameter prescribed a physiological, elongated shape for the cardiomyocytes that has been shown to promote optimal sarcomeric alignment (Bray et al. 2008). While optical measurement errors are problematic in studies with small micropost displacements, our system is less sensitive to the optical measurement errors.

As we have discussed, device calibration is critical to quantify and detect small changes in force generation across samples and populations. As seen in figure 6a, large variation in micropost stiffness suggests that stiffness in microstructures may be more variable than bulk measurements. These micropost batch-to-batch stiffness variations may be caused by irregularities in bake temperature, time, and exposure to oxygen plasma. Post-to-post variations may be due to geometric irregularities in the microposts caused by mold degradation or imperfections in the original lithographic masks. Calibrations using piezoresistive cantilevers (Park et al. 2007; Kim et al. 2011) can be used to standardize cellular force transducer platforms and enable meaningful comparisons of measurements made using various techniques.

Absolute uncertainty in any given force measurement is the sum of the accuracy and precision. For studies in which the same cantilever was used for all calibrations, any offset errors due to accuracy are expected to be consistent. For these comparisons, the precision error due to post-to-post variation is the key parameter differentiating uncertainties between studies. When measurements using one technique are compared with measurements using other force sensors and calibrations, it is important to use the absolute uncertainty, because both the accuracy and precision will vary from system to system.

Previous experiments with adult cardiomyocytes and carbon fibers demonstrated peak isometric forces ranging from 2.42 μN (Yasuda et al. 2001) to 5.7 μN (Nishimura et al. 2004). Here we detected axial peak forces that were ten to one hundred times smaller. The axial forces generated by neonatal rat cardiomyocytes are smaller than the net forces measured on force post arrays with neonatal rat cardiomyocytes (Zhao and Zhang 2006; Rodriguez et al. 2011), but it is difficult to compare such measurements because in previous force post measurements the cells had spread out into shapes that are not physiologically realistic. These cardiomyocytes were applying forces in multiple axes and such irregularly spread shapes can exaggerate pre-stress and therefore enlarge contractile forces (Bollensdorff et al. 2011). Without a simple axial loading scheme, forces cannot readily be compared.

Our measurements were carried out under auxotonic conditions (mimicking ejection of blood from the heart); as the cells contract against the micropost “springs,” they experience increasing load. Differences in loading condition may contribute to between-study discrepancies in the observed force magnitude. As reported previously,(Iribe et al. 2007) isometric loading conditions (mimicking isovolumic contraction of the heart) in which the cell length is held constant during contraction produce larger forces than loaded contraction. If our devices were integrated into a micropost array stretching device (Bollensdorff et al. 2011) to control cell length during contraction, we might observe larger forces. However, large forces have also been measured under auxotonic conditions; using novel polysilicon microgrippers, Lin et al. (Lin et al. 2000) measured peak auxotonic loaded forces of 12.6 μN with device effective stiffness of 1.47 N/m, suggesting that loading condition alone is unlikely to underlie such a large discrepancy between immature and adult cardiomyocyte contractile forces. Therefore, the large difference between the magnitude of force produced by immature and adult heart cells may be due to biological differences between developing and adult cardiomyocytes.

There are several potential limitations in all of these studies. Cell shape, cell slippage, varying levels of initial pre-stress, and damage during handling may also contribute to this variation. By controlling cell shape, we expect that we have limited geometry-based variations in cell function. In addition, we did not observe cell slippage and believe slippage was not an issue for this study. Implementation of force feedback may enable initial pre-stress to be tuned and its effects studied, and standardization of the cell isolation and plating procedure may reduce differences due to subtle cell damage incurred during the isolation of immature cardiomyocytes and their subsequent plating onto the devices. Controlling for these factors should enable future studies to detect any biologically meaningful differences in contractile force generation between adult, neonatal, and stem cell-derived cardiomyocytes, and should highlight platform-dependent differences in cell health, adhesion, and slippage.

This approach provides cell-level functional information, so it is also an ideal complement for recent “microtissue” measurement platforms that utilize multicellular constructs of heart cells and extracellular matrix proteins (Feinberg et al. 2007; Legant et al. 2009; Grosberg et al. 2011) to measure the active and passive properties of heart-like tissue. Both platforms could be used in conjunction to study the role of cell-level mutations and tissue composition and organization in disease progression.

Future work should address sources of the differences in the forces generated by immature and adult cardiomyocytes. It will be important to identify potential cellular differences in behavior for this assay compared to other two-point methods. Additionally, future studies should address changes in contractile force generation as a function of cell age, morphology, sarcomere organization, and external environmental parameters. Ultimately we would like to be able to perform studies of immature and adult cardiomyocytes with our platform. Adhesion is extremely challenging with adult cardiomyocytes. The few micropost studies that have achieved it have required at least 24 hours in culture, and these studies have observed significant dedifferentiation and unhealthy contractility changes (Zhao and Zhang 2006; Zhao et al. 2007). For future studies we aim to develop a protocol for robustly adhering adult heart cells to microposts in less than an hour and thereby enable contractile measurements of “healthy” adult cardiomyocytes. We have reported the first steps towards this goal using a PNIPAAm-free adhesion process (Taylor et al. 2011).

This technique may also be applicable to other tension-sensitive cell types (such as neurons and fibroblasts), and to investigate changes in force production over time in healthy and diseased cells. Finally, this sacrificial layer technique is broadly applicable as a highly parallel technique for controlling cell placement and shape. We anticipate that our method will be suitable for tissue engineering applications such as co-culture on 3D topographies as well as high-throughput pharmaceutical screening.

5. Conclusions

We have demonstrated a new method for elevated self-assembly of cells on 3D microfabricated topographies, a method that is broadly applicable to functional diagnostics as well as general cellular and device assembly. We developed a two-point force assay for studying force generation in both immature and stem cell-derived cardiomyocytes. To achieve cell suspension across widespread micropost sensors, we introduced a sacrificial PNIPAAm support structure that elevates the cells as they self-assemble to spread across post tops. Once the thermoresponsive PNIPAAm layer is dissolved away, cardiomyocytes are left suspended across pairs of microposts. During contraction, post deflection can be used to measure cardiomyocyte force production. By directly calibrating our force posts with piezoresistive cantilevers, we achieved accurate, precise, and quantitative measurements of contractile forces of immature cardiomyocytes. We observed peak contractile forces of 146 ± 51 nN generated by rat neonatal cardiomyocytes, and these forces can be compared with measurements on adult cardiomyocytes made using carbon fiber methods.

6. Appendix

The natural frequency of the cantilever is related to its stiffness and mass using the classical equation for a translational mechanical harmonic oscillator, where k_c is the bending stiffness of the cantilever for a point load applied to its tip and m_eff is the mass of the cantilever:

$${\omega }_n=\frac{1}{2\pi }\sqrt{\frac{k_c}{m_{eff}}}$$ (2)

We substitute cantilever mass with density times volume. In the following equation, ρ is the density of silicon and L, W, and T are the cantilever length, width, and thickness, respectively:

$${\omega }_n=\frac{1}{2\pi }\sqrt{\frac{k_c}{0.24\rho LWT}}$$ (3)

The effective mass is only 0.24 times the overall mass of the cantilever beam due to the mode shape of the first eigenmode. If stiffness is calibrated from a higher-order eigenmode, then the effective mass should be calculated accordingly. Laser Doppler vibrometry was used to determine the natural frequency, ω_n, 2.37 kHz, and when we rearrange the previous equation we obtain the following expression for k_c:

$$k_c=0.24\rho LWT{\left(2\pi {\omega }_n\right)}^2$$ (4)

The force F applied by the cantilever is calculated from the amplifier output-referred differential voltage, ΔV, and the cantilever force sensitivity, S_f:

$$F_c=\frac{\Delta V}{G{S}_f}$$ (5)

where G is the overall gain of the signal-conditioning circuit. The force sensitivity scales linearly with the Wheatstone bridge bias voltage and depends on the cantilever design parameters. The force sensitivity is calculated from the product of the cantilever stiffness and displacement sensitivity.

The micropost stiffness, k_p, is the quotient of the applied force, F, and the optical displacement of the micropost. Since we measured micropost displacement in pixels, we multiply our resolution [microns/pixel], R, and our pixel deflection, Δx, to obtain the deflection in microns:

$$k_p=\frac{\Delta V}{G{S}_{f}R\Delta x}$$ (6)

Finally, we must express force sensitivity, S_f, in terms of the displacement sensitivity, S_d, since we do not measure force sensitivity directly during cantilever calibration. The displacement sensitivity is determined by driving the cantilever on resonance and measuring the ratio of the circuit voltage output to the tip deflection, again using laser Doppler vibrometry (Park et al. 2007). The micropost stiffness can finally be written in terms of experimentally measured parameters as follows:

$$k_p=\frac{k_c\Delta V}{V_{b}G{S}_{d}R\Delta x}$$ (7)

$$k_p=\frac{0.24\rho LWT{\left(2\pi {\omega }_n\right)}^2\Delta V}{V_{b}G{S}_{d}R\Delta x}$$ (8)

As we have detailed previously (Kim et al. 2011), uncertainty in the cantilever stiffness contributes to the accuracy or systematic error in our reported forces and is calculated using a root mean sum of squares analysis of the measurement uncertainties (Holman 1988). Lithographic variations and uncertainty in displacement sensitivity contribute to this device uncertainty (Park et al. 2007). We convolve this error with the error in optical measurements, which is limited by pixel resolution.