Generalization of unconstrained reaching with hand-weight changes

Abstract

Studies of motor generalization usually perturb hand reaches by distorting visual feedback with virtual reality or by applying forces with a robotic manipulandum. Whereas such perturbations are useful for studying how the central nervous system adapts and generalizes to novel dynamics, they are rarely encountered in daily life. The most common perturbations that we experience are changes in the weights of objects that we hold. Here, we use a center-out, free-reaching task, in which we can manipulate the weight of a participant's hand to examine adaptation and generalization following naturalistic perturbations. In both trial-by-trial paradigms and block-based paradigms, we find that learning converges rapidly (on a timescale of approximately two trials), and this learning generalizes mostly to movements in nearby directions with a unimodal pattern. However, contrary to studies using more artificial perturbations, we find that the generalization has a strong global component. Furthermore, the generalization is enhanced with repeated exposure of the same perturbation. These results suggest that the familiarity of a perturbation is a major factor in movement generalization and that several theories of the neural control of movement, based on perturbations applied by robots or in virtual reality, may need to be extended by incorporating prior influence that is characterized by the familiarity of the perturbation.

as we move and interact with the environment, we constantly update our sensorimotor behaviors to adapt to changing sensory feedback and forces on our limbs. Which aspects of these changes are learned and how these changes are represented in the nervous system have been studied extensively by examining how people generalize a behavior learned in one context to another. Traditionally, generalization studies have perturbed reaching movements by introducing visual distortion in a virtual-reality setting (Bock 1992; Ghahramani et al. 1996; Imamizu et al. 1995; Mattar and Ostry 2007; Paz et al. 2003) or by applying deflecting forces with robots (Donchin et al. 2003; Shadmehr and Mussa-Ivaldi 1994; Sing et al. 2009; Thoroughman and Shadmehr 2000). Participants usually adapt to these perturbations within a training session, and generalization is assessed by having participants make reaches with different joint configurations, spatial locations, effectors, or movement directions. Under these conditions, behavior often generalizes locally to contexts that are similar to the training condition (Shadmehr 2004). This is not surprising from a normative view, since the novel perturbations used in these laboratory settings are rarely encountered in our daily life, and the perturbations applied in a short experimental session might not be applicable to other contexts. If a perturbation is experienced frequently in daily life, can the nervous system generalize it easily and to widely varying contexts? How we generalize familiar perturbations has not been systematically examined.

For most types of perturbations, previous studies have found that generalization of planar reaching movements peaks around the training direction and decays with increasing angular separation from the training direction. For instance, force-field learning generalizes minimally beyond 90° (Donchin et al. 2003; Mattar and Ostry 2007), whereas learning of visuomotor rotations exhibits even narrower generalization, only to targets within ∼45° (Krakauer et al. 2000). In some cases, the degree of direction dependence may indicate how learning occurs and how perturbations might be represented in the brain. Generalization curves are often associated with the tuning properties of neurons in various brain areas. For example, neuropsychological, electrophysiological, and imaging studies have found that learning of visuomotor rotations is associated with changes in the cerebellum (Krakauer et al. 2004; Rabe et al. 2009; Tseng et al. 2007), ventral premotor cortex (Krakauer et al. 2004), primary motor cortex (Paz et al. 2003; Wise et al. 1998), and posterior parietal motor cortex (Diedrichsen et al. 2005; Inoue et al. 1997). Most theories emphasize a bottom-up view, where sensory errors lead to a reorganization of neural primitives and their connections, which directly determines generalization that is behaviorally observed (Poggio and Bizzi 2004; Tanaka et al. 2009; Thoroughman and Shadmehr 2000). Here, we postulate that generalization is also under top-down influence, where familiarity with the perturbation impacts generalization in analogy to the way that prior experience biases percepts in various perceptual systems (Mamassian and Goutcher 2001; Stocker and Simoncelli 2006). Our working hypothesis is that familiar perturbations should lead to more global generalization than that found previously when participants learn less-familiar perturbations created by virtual-reality feedback or robots.

Here, we investigate motor generalization with a novel experimental paradigm in which the weight of the participant's hand can be unexpectedly modified during center-out reaching. This paradigm allows us to impose naturalistic perturbations, similar to those experienced as we move objects of varying weights. By naturalistic perturbations, we mean that the perturbation is not generated by virtual-reality or robot-generated deflecting forces, as they are rarely encountered in our daily life. Hand-weight changes are common perturbations to the nervous system. For example, to transport a cup of coffee to our mouth, our nervous system needs to tailor motor commands according to the cup's weight. When we take a sip or add more coffee to the cup, the weight changes, and our motor commands must be updated to compensate. Here, we found that generalization to this type of familiar, naturalistic perturbation is global and unimodal across directions. Repeated exposure to the perturbation enhances this broad generalization, in contrast to other types of perturbations where repeated exposure does not change generalization or results in a narrowing of generalization (Donchin et al. 2003; Krakauer et al. 2000; Mattar and Ostry 2007; Tanaka et al. 2009; Thoroughman and Shadmehr 2000). These findings support our normative hypothesis and suggest that bottom-up explanations of generalization using neural tuning should be complemented with top-down mechanisms involving prior experience.

METHODS

Apparatus.

Participants were seated in front of a desk with a light paper box (∼10 g) firmly attached underneath the right hand (Fig. 1). A water-filled plastic bag was placed in the box and connected to a syringe (140-g capacity) through a 2.2-m light-weight plastic tube running underneath of the arm. Sitting behind the participant, the experimenter could change the weight of the participant's hand by injecting/removing water from the plastic bag with the syringe. A plastic palm brace was placed between the water box and the palm to minimize tactile cues, and participants wore noise-isolating biauricular headphones throughout the experiment to block possible auditory cues during weight changes. These procedures prevented participants from noticing changes in the weight of the hand between trials, while their hand rested on the support (a 10.5-cm-high, 3.0-cm-diameter cylinder fixed on the desk top) before each movement. The hand, the water box, and the palm brace were all wrapped together with medical bandage such that they could be treated as a rigid body. The pointed index finger was fixed on the palm brace, and fingertip location was measured throughout the experiment by an attached infrared marker (Codamotion; Charnwood Dynamics, UK; sampling rate at ∼200 Hz).

Fig. 1.

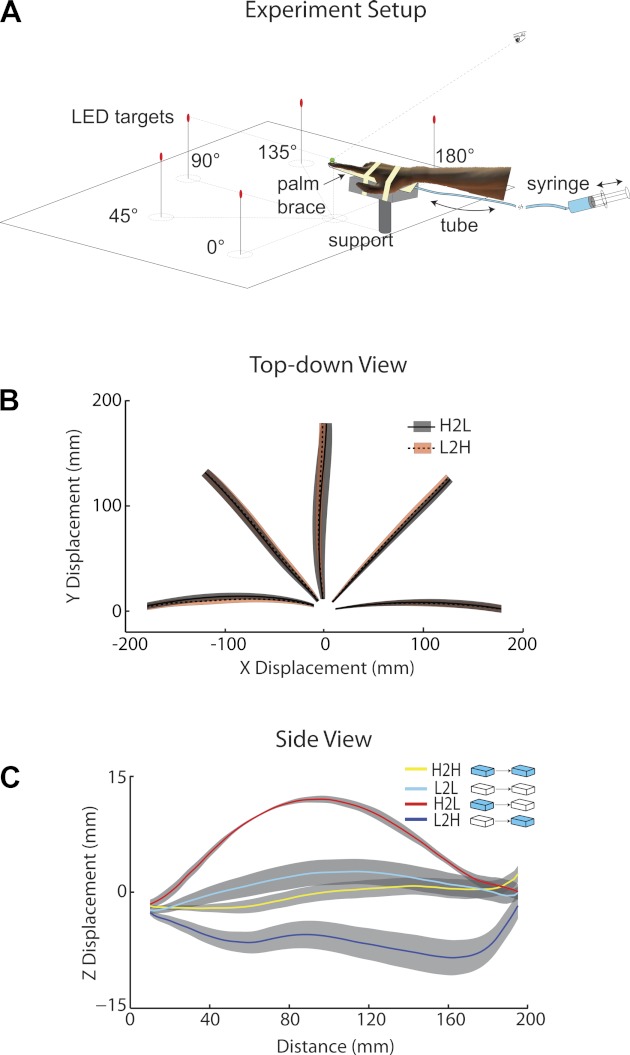
Experimental setup and exemplary trials. A: experimental setup. Participants made cued, unconstrained reaches to 5 targets, placed 15-cm high, 20-cm away from the starting position. Between each trial and without the participant's knowledge, the hand weight is modulated by changing a water load attached underneath of the hand. Behind the participant, the experimenter can change the volume of water and thus weight at the participant's hand using a syringe. LED, light-emitting diode. B: a top-down view of movement trajectories. Heavy-to-light (H2L) and light-to-heavy (L2H) trials are plotted for a typical participant in experiment 1. The shaded area denotes ± 1 SD across trials (same below). Positive X displacement stands for moving rightward and positive Y displacement for moving frontward. C: trajectory height as a function of distance from the starting position for the same participant in experiment 1 reaching for the 90° target with 0° angular separation between trials. Positive Z displacement stands for moving upward. H2H, heavy to heavy; L2L, light to light.

Before each trial, the participant rested his/her right hand on the support. With the tip of the index finger as a center, five red light-emitting diode (LED) targets (15 cm above the desk top and separated 45° apart) were placed on a 20-cm perimeter. The LED targets were at the same height as the fingertip given the height of the support. The basic task was to move the fingertip from the starting position to one of the LED targets. The illumination of a LED light was controlled by a programmable circuit board (Arduino Duemilanove). After each reach, to facilitate the participant's return to the starting position in three-dimensional space, the finger position was displayed as a cursor (1.5 cm in diameter) on a projection screen (projector model Optoma EX774), 1.5 m in front of the desk. A red circle (2.5 cm in diameter) was also displayed on the projection screen to indicate the starting position. When the distance between the actual fingertip and the starting position was <1.0 cm, the starting circle expanded to a red disc (5.0 cm in diameter) to notify the participant that the fingertip was in place. Participants subsequently attended to the table and waited for a LED target to be illuminated. Data acquisition and screen display were controlled by a customized Matlab program (Matlab 2009b; MathWorks, Natick, MA).

Basic movement.

Participants performed center-out, unsupported, point-to-point reaching movements to each of the five targets with varying hand weight. Each trial started off when participants placed their right hand on the hand support and aligned the index finger with the starting position. Once the hand was placed properly, the monitor of the data-acquisition computer, unseen by the participant, displayed an instruction to the experimenter who sat behind the participant. The instruction signaled the experimenter to inject or remove water using the syringe. Upon finishing water change, the experimenter pressed the space key on a wireless keyboard to light up one of the LED targets, signaling the participant to initiate a reach. Participants were instructed to move quickly and comfortably to the LED target with precision and hold at the target position briefly until the LED was off. Then, participants returned the hand to the starting position for the next trial. If the index finger was within 1.1 cm of the target, a monetary reward of 2 cents would be displayed on the projection screen to motivate participants. The hand movement from the starting position to the target usually lasted 800 ∼ 900 ms, and the trial-to-trial interval was approximately 2.6 ± 1.7 s (including the movement time and the resting time on the hand support). To prevent slow movements, we would warn participants with a sharp beep sound played by a loudspeaker if a reach lasted longer than 900 ms.

Protocols.

Experiment 1 used trial-by-trial weight changes to perturb reaching movements. Each trial was randomly assigned with a target direction and a hand weight, with the hand either loaded with 140 g water [heavy condition (H)] or without [light condition (L)]; the water bag with its containing box has a dead weight of ∼37 g without water load. Thus each trial is associated with one of four types of weight transitions, depending on the loading on the current trial and the trial immediately preceding: H to L (H2L), L to H (L2H), L to L (L2L), and H to H (H2H). To define the left-most target as 0° and the right-most target as 180°, the angular separation between two successive trials could take one of nine values: 0, ±45°, ±90°, ±135°, and ±180°. Before the experiment, participants were familiarized with the setup by practicing reaches without weight changes. The formal data collection consisted of 5 (targets) × 4 (weight transitions) × 50 (repetitions) = 1,000 trials. The experiment lasted ∼90 min with a 10-min mandatory break after the 500th trial. It should be noted that although each target was equally likely, the angular separations between trials were unevenly distributed: 0° separation was presented most frequently, whereas ±180° was least likely. On average, 0°, ±45°, ±90°, ±135°, and ±180° transitions should occur for 200, 320, 240, 160, and 80 times, respectively. As the target sequence was fully randomized in the experiment, actual numbers were slightly different.

Experiment 2 investigated block-based learning and generalization. Participants first learned to reach the same target with loading (H) for a number of trials. Immediately after this block learning, generalization was assessed by a test trial when participants reached to other directions with or without loading. These training trials and the subsequent test trial were counted as a block. This block-design or postadaptation-design experiment had 2-day data collection: on 1 day, participants were trained to reach to the target at 0° and on the other day at 180°. As such, the 0° training led to generalization to all positive angular separations (0, 45°, 90°, 135°, and 180°) and the 180° training to corresponding negative angular separations. Data collection on each day was further divided into three sessions that involved different lengths of training. In two-trial learning session (called Block2), the average number of training trials is two: 20% of the blocks had one training trial, 20% had three trials, and 60% had two trials. The same training-length distribution was applied to four-trial and six-trial sessions (called Block4 and Block6, respectively; e.g., Block4 sessions consist of 20% three-trial, 60% four-trial, and 20% six-trial blocks). The aim of this design was to investigate whether learning and generalization of hand-weight changes can be modulated by length of exposure. The orders of training directions (days) and of training length (sessions) were counter balanced and assigned randomly across participants.

Each session started with a block of 30 unloaded trials (washout block, six trials each target) to familiarize the participant with the apparatus and to wash out the effect from previous sessions. The rest of the session consisted of 50 blocks of trials: in each block, participants first reached for a single target repetitively with loading, and then they were tested by reaching for one of the five targets. The two-trial learning session had 30 (washout block) + 3 (average of two training and one test trial in a block) × 50 (blocks) = 180 trials. The four-trial and six-trial learning sessions had 280 and 380 trials, respectively.

As eight (out of 11) participants were tested in experiments 1 and 2, there is a possible carryover effect between experiments. To rule out this possible confound, we performed a control experiment with the same protocol as in experiment 1 but with a new set of nine participants. The only difference was that the finger position was sampled at 100 Hz by an infrared motion-capture system (OptiTrack, model V100:R2).

Participants.

Both main experiments had 11 volunteer participants, and eight of them were tested in both experiments. The average age of two participant groups was 21.9 ± 1.6 and 22.3 ± 1.8, respectively. The number of male participant was six and seven, respectively. All eight shared participants were examined for experiment 2 first. The control experiment had a separate group of nine participants (age 21.8 ± 2.0; four males). All participants provided informed consent before data collection, and they were naive to the purpose of the experiments. One participant in experiment 1 and two participants in experiment 2 were left handed, but they reached with the right hand. All participants had normal or corrected-to-normal vision. All procedures were approved by the Ethics Committee of Peking University.

Data analysis.

Changes in the weight of the hand primarily affect the vertical displacement of the hand during reaching (Fig. 1, B and C). Reaches were essentially horizontal toward the target if the hand weight was not changed from the previous trial. However, when the weight was changed unexpectedly, the movement trajectory was elevated or lowered depending on whether participants expected their hand to be heavier or lighter, respectively. Denoting trial types by the current and preceding hand weight, trials without weight changes are labeled as H2H and L2L and trials with unexpected weight changes as H2L and L2H. Changes in trajectory height thus represented an estimation error in hand weight and can be used to assess learning and generalization. An alternative way to quantify the influence of weight changes is to compute the peak height, either upward or downward, within a certain window of the hand trajectory. However, we noticed that a large portion of trials did not have a clear peak height in the mid of the trajectory (especially for L2H, H2H, and L2L trials; see Fig. 1C). Hence, it is best to use average height as the independent variable, as it captures the main effect of unexpected weight changes, independent of the specific shape of a trajectory. Before calculating the average height, the trajectories between 10 mm and 180 mm were interpolated to 100 data points. The first 10 mm of movement was omitted due to jitter of hand on the hand support during the reaction time period (the support has a radius of 10 mm), which made interpolation for some trials impossible. The last 20 mm of movement was also excluded, since for some trials, participants stopped movement early without reaching the full required distance of 20 cm. The last segment also tends to be less indicative of weight-related, feed-forward learning, since participants tend to home in on the target and make small, corrective movements at the end of the reach (Fig. 1C).

In experiment 1, learning of weight changes can be quantified by calculating the differences in height between different types of trials. The difference between L2H and H2H indicates how much is learned about an empty load, and the difference between L2L and H2L indicates how much is learned about a full load. In each pair of comparisons, the current reach has same load but differs in terms of the immediately preceding load. Hence, their difference can be attributed to influence of the preceding exposure. We further grouped these differences by angular separations between pairs of trials, allowing us to quantify directional generalization (see Eqs. 1 and 2 below). In experiment 1, two directional generalization functions (learning loading: H2L − L2L; learning unloading: H2H − L2H) can be derived for learning an empty load and a full load, respectively.

Experiment 2 mainly investigated the learning and generalization of a full load, and we are thus interested in the difference between L2L and H2L trials. The last five trials in the washout block (without loading) were used to estimate the height of L2L. The test trials without loading were used to estimate H2L. Thus the generalization function (H2L − L2L) can be calculated.

To compare learning across directions, we need to consider directional biases caused by the inertial anisotropy of the limb (Flanagan and Lolley 2001; Gordon et al. 1994; Mussa-Ivaldi et al. 1985). This inertial bias means that the height difference, the behavior observable in our experiment, may be different across directions even when the weight estimation error is the same. This bias, directly related to limb compliance, can be estimated by taking the average height of trials with a weight transition but without a direction transition. For example, consider all of the trial pairs that reach to the same direction but the first trial with load (H) and the next without (L). The average difference in heights can be viewed as a proxy for limb compliance in that direction, since it resulted from, on average, one unit of weight estimation error. This compliance measure is thus a 5 (direction) × 2 (weight change) matrix. In practice, we find that limb compliance is fairly consistent across participants (see results). We can then convert the observed height into a degree of learning (or generalization)

$$Learnin{g}_{unloading}=\left(H2H-L2H\right)/Complianc{e}_{direction,unloading}$$ (1)

and

$$Learnin{g}_{unloading}=\left(H2L-L2L\right)/Complianc{e}_{direction,loading}$$ (2)

Taking learning loading as an example (Eq. 2), the H2L trial involves a loading transition where a heavy loading has been learned in the previous trial, but the current trial has no loading. The L2L is the average height in the same direction of the current trial, and it serves as a baseline height for reaching without loading in this direction. The difference between H2L and L2L is thus caused by learning in the previous trial with loading. If this previous trial differs in direction than the current trial, then the computed learning is actually an estimate of directional generalization. It amounts to one if generalization is complete and zero if no generalization happens. Note that compliance is measured for absolute target directions, whereas generalization is estimated by dividing the compliance in the current target direction, and it is a function of relative target directions (angular separations).

The models.

A state-space model was formulated to derive a generalization function based on trial-to-trial changes in trajectory height. We assume that the weight estimate on the ith trial (X_i) is influenced by the previous estimate (X_{i − 1}) and the learning from the preceding trial

$$X_i=X_{i-1}+G_{\theta i,\theta i-1}\left(X_{i-1}-W_{i-1}\right)$$ (3)

$$Y_i=A\times X_i$$ (4)

where W_{i − 1} is the loading in the preceding trial, which takes a value of 1 or −1 for a heavy or a light load, respectively. Thus (X_{i − 1} − W_{i − 1}) is the error in weight estimation experienced during the preceding trial. Note that both X and W are 5 × 1 vectors to quantify simultaneous representations in five movement directions. G_{θi,θi − 1} captures the learning rate as a function of angular separation (θ_i,θ_{i − 1}), and it is a 5 × 5 matrix. Originally, there are nine kinds of angular separations. However, we can reduce the number of free parameters in G from nine to five by assuming that learning rates of negative angular separations are the same as those of corresponding positive separations. Finally, we include a scaling factor A to convert weight estimates into the observed hand height Y_i. The model (model 1) is an autoregressive model of order 1. From the data, we find that weight changes tend to be learned almost completely in a single trial and including higher-order, autoregressive terms, do not improve the model significantly.

As a control, we also examined whether a flat generalization function might be sufficient to explain our data. In this case, learning only depends on the weight changes and is independent of any differences in target direction. Assuming that generalization is equal in all directions and that the current estimate is influenced by four immediately preceding trials, we can rewrite Eq. 3 as

$$X_i=X_{i-1}+{\displaystyle \sum _{\Delta =1}^4{L}_{\Delta }\left(X_{\Delta }-W_{\Delta }\right)}$$ (5)

where L_{i − Δ} and (X_{i − Δ} − W_{i − Δ}) are the learning rate and the error-experienced Δ trials before the current trial, respectively. Thus the current estimate is affected by the immediately preceding estimate, as well as influences from previous trials. As we are only interested in the relative contributions from the previous trial, we set the learning rate as 1 for Δ = 1 to reduce the number of parameters. This flat-generalization model (model 2) is a standard state-space model with four free parameters (three learning rates and as in model 1, a scaling factor A that maps the weight estimates to hand height).

We fitted the models with the trial sequence and trajectory heights (normalized by their corresponding compliance) from each participant in experiment 1 to derive the generalization functions G (model 1) or the learning rates L (model 2). The data from experiment 2 were not sufficient to constrain the model, since the longest trial sequence contained only 380 trials (Block6), and there were only 50 trials with weight changes. Active set search algorithm (Matlab R2009, MathWorks) was used for model fitting.

RESULTS

Here, we have constructed an experiment that allows us to change the effective weight of the hand by pumping water in and out of a brace that is attached to the hand. This allows us to analyze, using both trial-by-trial and block-based paradigms, how these naturalistic force perturbations are generalized.

Experiment 1: trial-by-trial generalization.

Despite the fact that changes in hand weight are unexpected, trajectories in the horizontal plane showed negligible differences (Fig. 1B). The two types of weight-changing trials (H2L and L2H) are indistinguishable in the horizontal plane. However, during each trial, participants learn about the weight of their hand, and this information affects the height of their trajectory on the next trial (Fig. 1C). With unexpected loading (L2H), the hand moves lower than movements during an expected load (H2H). With unexpected unloading (H2L), the hand moves higher than movements during an expected load (L2L). Note that the conditions being compared (e.g., L2H vs. H2H) always have an identical hand weight (e.g., both being heavy), and the differences in trajectory can be attributed to the weight and direction of the immediately preceding trial. These differences suggest that the hand weight from the previous reach biases the estimate of hand weight and subsequently impacts the next movement. Hence, when the hand weight is unexpectedly changed, the reach is substantially elevated or lowered.

Trial-by-trial learning of weight changes generalizes across directions (Fig. 2A). The generalization function is mostly unimodal: the generalization is most prominent when moving in the same direction as the preceding trial and is reduced gradually with increasing angular separation. A 2 (type of generalization) × 5 (angle) two-way repeated-measures ANOVA reveals a significant main effect on loading, indicating that generalization for learning loading (H2H − L2H) is larger than generalization for learning unloading (H2L − L2L). However, the interaction fails to reach significance (P = 0.81), suggesting that the two generalization functions tend to have the same pattern against angles. Examining the average generalization curve over these two generalization functions, we find that the generalization is significantly higher at 0° and 45° angular separations than those at 135° and 180° (P < 0.05, two-tailed paired t-tests). The generalization among the 90°, 135°, and 180° angular differences is not significantly different (P > 0.05). On the other hand, the generalization is still significantly larger than zero, even at the largest angular separation of 180° (P < 0.05), indicating a strong global generalization component.

Fig. 2.

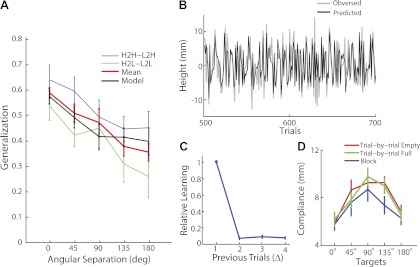
Results from experiment 1 with trial-by-trial hand-weight perturbations. A: generalization functions from learning loading (H2H − L2H) and unloading (H2L − L2L), the average across both conditions, and the corresponding model-predicted generalization function. Error bars denote SE across participants (same below). B: trial-by-trial changes of trajectory height for a typical participant and the corresponding model predictions. C: the relative learning (L_Δ) from previous trials, as estimated from model 2. D: compliance of vertical hand displacement as a function of movement direction. The compliance is estimated from unexpected loading and unloading trials from experiments 1 and 2.

The generalization function is also estimated by the state-space model (model 1; Fig. 2A). The model captures the overall height changes across trials with 40.2 ± 3.5% of variance explained (six free parameters and 1,000 data points), and it tracks trial-by-trial changes fairly well (Fig. 2B). More importantly, the generalization function exhibits a similar semiglobal unimodal pattern as in the data. Note that the generalization function from the model is comparable with the average generalization (over both unloading and loading generalization curves) from the data, since the model computes average learning from a previous trial, disregarding of the sign of weight changes. A 2 (model vs. data) × 5 (angle) two-way repeated-measures ANOVA does not find a significant main effect on the model-vs.-data comparison or significant interaction, indicating a good match between model predictions and the data.

In contrast to the full generalization model (model 1), model 2 with a flat-generalization function can account for only 27.7 ± 3.1% of variance in the data. The learning rate drops rapidly with elapsed time; it appears that most of the learning happens within one trial (Fig. 2C). We compared the performance of models 1 and 2 using Bayesian Information Criterion (BIC) (Schwarz 1978) to take different numbers of free parameters into account. Model 1 is significantly better than model 2 with a reduction of 168.5 ± 76.2 in BIC measures (P < 0.0001), indicating that a generalization function with direction dependency can better explain the data.

We find that the limb is more compliant during reaches to the target at 90° (where the hand is farther from the body) than reaches to targets at 0° and 180° (where the hand is closer to the body). In general, reaching forward is more influenced by an erroneously estimated hand weight than reaching laterally. Compliances for upward (unexpected unloading) and downward (unexpected loading) movements are not significantly different (Fig. 2D). These findings are confirmed by a 2 (vertical direction) × 5 (horizontal direction) two-way repeated-measures ANOVA where the main effect on horizontal direction is significant (P < 0.0001), but the main effect on vertical direction is not (P = 0.16). Similar direction dependence was observed in experiment 2, where a different set of participants was measured on different days (Fig. 2D). This similarity between experiments suggests that our estimation of compliance is reliable.

Experiment 2: block-based generalization.

Repetitive exposure of the same load leads to a similar unimodal generalization pattern as in the trial-by-trial experiment (Fig. 3A). Interestingly, different training lengths yield a similar generalization, as a 3 (block size) × 5 (angle) two-way repeated-measures ANOVA does not find a significant main effect on block size (P = 0.24) or interaction (P = 0.43). We thus pool over data from three training-length conditions for the following analyses. Generalization is significant for all directions (paired t-test, P < 0.0001). The generalization at 0° and 45° is not significantly different from one (P = 0.56 and 0.08, respectively), indicating a full learning and generalization around the training direction. Paired t-tests indicate that the generalization pattern is unimodal: generalization is significantly higher at 0° than at all other directions (P < 0.05), also higher at 45° than at 90° (P < 0.05), and it plateaus for other larger angles.

Fig. 3.

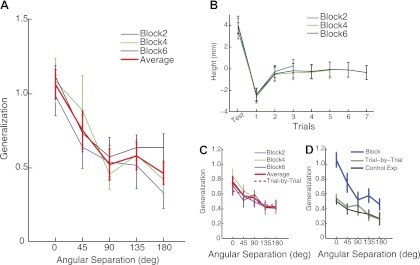
Results from experiment 2 with block-based training. A: generalization functions for unexpected unloading following training with 2 trials, 4 trials, 6 trials, and their average. B: trajectory heights within a training block with its preceding unloading trial. Blocks with different training lengths are plotted separated. C: similar generalization functions as in A but associated with the loading immediately following the unloaded test trials, i.e., generalization of de-adaptation. D: the generalization functions from experiments 1 and 2 and the control experiment. To make a direct comparison, only H2L − L2L (learning a heavy weight) is reported for experiment 1 and the control experiment.

We examine how learning evolved over training trials (Fig. 3B). Trajectory height increases at unexpected unloading trials, and it is then lowered substantially at the first training trial with loading. Both trials are significantly different from other trials, as indicated by paired t-tests. This sharp reversal is suggestive of one-trial learning from unexpected unloading. Participants manage to increase the height back to the baseline level in the next training trial as confirmed by paired t-test (P > 0.05). This fast learning is observed in all three training-length conditions. From another perspective, the learning from a single trial can also be viewed from the perspective of generalization: after experiencing an unexpected unloading in one direction (test trials), participants were tested in other directions (the training directions at 0° and 180°). By analyzing this first training trial after the test trial in each block, we can estimate a generalization function of de-adaptation embedded in the block paradigm (Fig. 3C). This generalization pattern shows a unimodal pattern with a strong global component, remarkably similar to its counterpart in the trial-by-trial design (H2H − L2H). In fact, they are statistically indistinguishable (two-way ANOVA, P = 0.53 for main effect of experiment comparisons). However, it is important to note that in this case, the load was not entirely unexpected, since reaches to the training target always used the H condition.

The generalization functions from the block-based learning and the trial-by-trial learning of a reduced load are compared directly (Fig. 3D). A 2 (experiment) × 5 (angle) two-way repeated-measures ANOVA yields a significant main effect on experiment (P < 0.01) and significant interaction (P < 0.05). These results indicate that more training in one direction tends to improve the overall generalization, and this improvement is especially more pronounced around the training direction.

One confound for direct comparison between experiments is that eight participants were tested in both experiments. The exposure to weight changes during one experiment might affect their generalization in the second experiment. However, we think this carryover effect is less likely given that the learning and its washout happen promptly on a time scale of one or two trials (Fig. 3B). Nevertheless, we performed a control experiment with a new set of nine participants with an identical protocol as in experiment 1. We find that the generalization function is similar to the one found in experiment 1 (Fig. 3D). A 2 (experiment) × 5 (angle) two-way repeated-measures ANOVA fails to find significant difference between experiments (main effect, P = 0.73). This result suggests that generalization of adaptation to weight changes is not affected by a short session of exposure to weight perturbations.

DISCUSSION

We have introduced a novel motor adaptation paradigm to perturb the hand's weight during center-out reaching. These changes in the hand's weight, similar to those encountered in everyday life, were quickly learned and generalized across reaching directions. We found a unimodal yet global generalization function for random trial-by-trial perturbations. With merely two training trials, generalization was enhanced in all directions, peaking around the training direction. These generalization patterns were dramatically different from those previously found in experiments using visuomotor or robotic-force perturbations which are rarely encountered in daily life.

Task complexity/familiarity and generalization.

Here, we have found that the generalization functions associated with hand-weight changes are much wider than those found previously with novel perturbations (Krakauer et al. 2000; Thoroughman and Shadmehr 2000). For directional generalization of learning to reach with visuomotor rotation and force fields, generalization drops to zero at ∼90° or even 45° angular separations (Krakauer et al. 2000; Paz et al. 2003; Tanaka et al. 2009), whereas our generalization persists at the farthest angular separation of 180°. These differences suggest that in addition to providing information about the neural representation of movement, generalization curves are affected by the familiarity of perturbations. In this case, the familiar situation of carrying a new weight is broadly generalized to subsequent hand movements. Thus generalization appears to have both a bottom-up component that depends on movement similarity and a top-down component that depends on the overall familiarity of the perturbation.

We interpret our results in terms of familiarity, but another way of thinking about this broad generalization is in terms of a neural locus with an unusually broad neuronal tuning property that specifically governs the generalization of adaptation to weight changes. Previous studies have argued that distinct areas are responsible for varying types of perturbations, such as narrowly tuned neurons in primary motor cortex corresponding to narrow generalization of visuomotor rotations (Paz et al. 2003) and broadly tuned neurons in cerebellum corresponding to bimodal generalization of force-field learning (Donchin et al. 2003; Shadmehr 2004). It is thus possible to locate an area or multiple areas representing broad generalization in weight learning. However, there is currently little neurophysiological evidence for these kinds of distinct circuits, and it certainly invites further investigations.

From a normative perspective, the purpose of the nervous system is to allow us to interact successfully with the environment (Körding 2007). In this light, the nervous system should generalize a perturbation only if the learned dynamics are likely to be present in a new context. Besides the familiarity of the perturbation, this probability may depend on the uncertainty of our state estimation or the feedback that we receive (Wei et al. 2010), how accurately we can attribute the perturbation to internal or external sources (Berniker and Körding 2008; Wei and Kording 2009), and the typical time scales of perturbations in the world (Körding et al. 2007; Smith et al. 2006). Although it is difficult to make precise conclusions about what perturbations are “likely” without measuring natural statistics of diverse perturbations (Ingram et al. 2008), distinct generalization curves observed for visuomotor rotations, force fields, and now, changes in hand weight are qualitatively consistent with this normative viewpoint.

Familiar perturbations might also be viewed as simple to learn. Most motor adaptation studies deliberately used novel perturbations to induce prolonged and gradual learning. Adaptation to these perturbations is usually associated with building an internal model of the new dynamics (Shadmehr and Mussa-Ivaldi 1994). For instance, learning of a velocity-dependent force field necessitates mastery of a mapping between the position and velocity of the hand with perturbation forces (Hwang et al. 2003; Shadmehr 2004; Sing et al. 2009). Learning these novel dynamics usually requires long exposure. For instance, learning visuomotor rotation needs at least 20 trials (Krakauer et al. 2000). In contrast, hand-weight changes are perturbations without dependency on spatiotemporal characteristics of the movement itself and presumably can be viewed as changes of a static parameter in an internal model. As such, these perturbations may be easier to learn and more readily generalized. Indeed, we found that the majority of adaptations to a weight change occurs in the first trial with near-complete adaptation within two trials, consistent with previous findings that people can adjust finger force properly with a novel object after several attempts (Johansson and Westling 1988; Johansson 1996). Consistent with a familiarity/simplicity hypothesis, a previous study found that complex force fields, compared with simple ones, showed much less generalization (Thoroughman and Taylor 2005). Similarly, experiments in perceptual learning also suggest that harder perceptual skills showed less generalization than easier ones (Ahissar and Hochstein 1997).

Global generalization patterns have also been found in learning of visuomotor gain, a scaling factor between hand-movement amplitude and its cursor representation (Bock 1992; Krakauer et al. 2000; Pine et al. 1996; Vindras and Viviani 2002). Interestingly, this visual perturbation is also frequently present in modern daily life when we use computer mice. Thus global generalization for visuomotor gain can also be explained by our simplicity/familiarity hypothesis. As extreme cases of unfamiliar perturbations, a recent study examined the learning of an arbitrary mapping from multi-finger movements to a cursor movement, a completely novel task where prior experience was minimally applicable (Liu et al. 2011). Not surprisingly, generalization across directions was found to be very narrow. In some sense, our perturbation and this novel perturbation sit on the two extremes of the familiarity continuum for the nervous system.

Our findings are quite different from the generalization observed in object manipulation tasks, although our weight perturbation is applied through a hand-held object. People have found that directional generalization of learning to manipulate a hammer in a virtual-reality setting is rather local with a narrow Gaussian pattern (Ingram et al. 2010). We postulate that limited generalization of this familiar object is expected, since representations of object dynamics are shown to be hard to generalize across orientations (Zhang et al. 2010). The other possible explanation is that the presentation of the hammer via augmented visual feedback and a robotic manipulandum prevents broad generalization across directions.

Top-down vs. bottom-up influence.

It is quite intriguing that the global generalization features a unimodal shape, as an equal generation across workspace is expected if the hand weight is a static parameter in an internal model. Single-cell recording during reaching with inertial loading showed that population activity in primate motor cortex had a systematic, load-dependent discharge (Kalaska et al. 1989). Interestingly, this discharge exhibited a smooth and broad tuning curve centered on the movement direction, suggesting that there exists a population of neurons modulated by both inertial load and movement direction with tuning that is consistent with the generalization curves observed here. We thus postulate that learning hand-weight changes involves neuronal activity with local tuning, which leads to the unimodal pattern on top of the global generalization.

The generalization functions, discovered from psychophysical experiments on perceptual or motor tasks, have been directly linked to neuronal tuning; i.e., broader generalization relies on neurons with broader tuning (Ahissar 2001; Amirikian and Georgopulos 2000; Chou and Lisberger 2002; Tanaka et al. 2009). Specifically, narrow generalization of visuomotor rotations has been associated with narrowly tuned neurons in primary motor cortex (Paz et al. 2003), whereas the bimodal generalization of force-field learning has been associated with broadly tuned neurons in the cerebellum (Donchin et al. 2003; Shadmehr 2004). Directional generalization patterns have also been related to the shape of learning primitives (Donchin et al. 2003; Paz et al. 2003; Thoroughman and Shadmehr 2000) and their connections (Poggio and Bizzi 2004; Tanaka et al. 2009). However, our study and some previous studies suggest that behaviorally observed generalization functions are flexible and under top-down influence. For example, although learning a single visuomotor gain generalizes globally, people can learn two conflicting gains simultaneously and effectively produce a different overall generalization function by flexibly reshaping and combining two separate functions (Pearson et al. 2010). Learning force fields with varying complexity induces distinct generalization functions where simpler force fields led to broader generalization (Thoroughman and Taylor 2005). These findings speak to the modifiability of generalization, given specific task demands. Our study reveals that generalization can be changed swiftly in a few trials—unimodal generalization increases and becomes more specific from one-trial to multiple-trial learning. This is a direct and strong support for rapid reshaping of generalization functions simply by varying durations of exposure to the same perturbation. Taken together, our results suggest that top-down effects clearly influence the exact shape of the generalization function. We thus propose that the approach of simply mapping the generalization function in behavior to neuronal tuning in various areas of the brain should be taken with caution.

Block-based vs. trial-by-trial generalization.

There have not been any previous experimental attempts to compare trial-by-trial generalization side by side with block-based generalization. However, piecing together evidence from separate studies, we find that generalization patterns from these two learning protocols vary greatly depending on the nature of the perturbation. For visuomotor rotation, both types of learning induced narrow unimodal generalization functions whose widths were indistinguishable (Krakauer et al. 2000; Tanaka et al. 2009). For force-field learning, trial-by-trial adaptation exhibits a broader bimodal generalization function than does block-based learning (Donchin et al. 2003; Mattar and Ostry 2007; Thoroughman and Shadmehr 2000). Our study instead finds that the global generalization is enhanced from trial-by-trial learning to block learning, especially in the proximity of the training direction. For the naturalistic perturbations used here, this enhancement saturated within two trials.

The enhanced generalization is consistent with the normative idea that repetitive exposure to the same weight reduces the participant's uncertainty about hand weight. In other words, the internal model of the hand weight is better formed and more readily to generalize to other directions after more exposure to the perturbation. If this is the case, why do visuomotor rotation and force-field learning not show enhanced generalization with repeated exposure to the same perturbation? Here, we would argue again that this is due to the top-down influence in motor generalization. As these are novel perturbations produced by virtual-reality and robotic manipulandums, the nervous system tends to view them as local or external perturbations (Berniker and Körding 2008). The more the nervous system learns about the exact dynamics of the perturbation, the more it is “aware” of its locality and the less it will generalize to other directions. Indeed, it has been found that the population activity in the motor cortex exhibits a gradual sharpening of the tuning curve during learning of a visuomotor rotation (Paz et al. 2003), suggesting that the neuronal representation of the learned perturbation became more specific. This hypothesis also predicts that learning in multiple directions should induce broader generalization, as the nervous system can extrapolate that perturbations are effective across directions, consistent with a previous finding that the generalization function is broadened with training in more directions (Krakauer et al. 2000). In sum, the difference between trial-by-trial and block-based generalization depends on the nature of the perturbation, and it reflects the fact that generalization is under top-down influence.

It is noteworthy to mention that our enhanced generalization in the block-based paradigm might be partially explained by use-dependent plasticity. Motor adaptation studies have found that repetition of movement can contribute to learning and bias subsequent movements in the direction of the perturbation (Diedrichsen et al. 2010; Huang et al. 2011). This use-dependent learning can at least contribute to the enhanced learning in the training directions, which has been observed in our generalization function. However, we also observed enhanced generalization in movement directions other than the training directions with training repetitions. Generalization of use-dependent learning has also been observed in the study by Huang et al. (2011), where repetition of reaching movements in the to-be-learned directions during visuomotor rotation adaptation can “attract” the subsequent movements when participants reach to untrained directions. Hence, this bias is a sign of use-dependent learning in the form of generalization. However, we note that in this study, the manipulation of repetition and its effect share the same variable: the learning (use) in this study is about movement direction, and the use-dependent generalization is also quantified as shifts in direction. Our study, instead, separates these two variables: the use is about weight perturbations, and the generalization is assessed across the horizontal directions. Thus our results might serve as a strong support for the effect of use-dependent plasticity on motor generalization. Recent advances in motor learning have started to examine separate contributions from error-based learning, use-dependent learning, and operant reinforcement (Huang et al. 2011). It remains an open question of how different types of learning, especially use-dependent learning, contribute to the behaviorally observed generalization.

Concluding remarks.

In the present study, we discovered a unique generalization pattern associated with hand-weight changes and propose that motor generalization involves top-down influence, where prior experience with a perturbation plays a critical role. This view complements the much-emphasized role of bottom-up learning, where a flexible combination of motor primitives essentially determines motor learning and generalization (Poggio and Bizzi 2004). The necessity of combining top-down and bottom-up phenomena suggests that a simple mapping between behaviorally observed generalization functions and neuronal activity in isolated brain areas cannot provide a full account of motor generalization. In addition, our findings suggest that insights from studying motor generalization of novel perturbations should be interpreted with caution, since they may not necessarily be applicable to more naturalistic types of perturbations. Lastly, our novel experimental paradigm may provide a useful tool for neurophysiologists to study the neural substrate underlying motor learning and generalization during naturalistic perturbations.

GRANTS

Funding for this work was provided by National Institute of Neurological Disorders and Stroke Grants R01NS-063399 and R01NS-057814, the National Natural Science Foundation of China (Nos. 61005082, 31000456, J1103602, and 61020106005), and the Fundamental Research Funds for the Central Universities.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

X.Y., I.H.S., K.K., and K.W. conception and design of research; X.Y., Q.W., Z.L., and K.W. performed experiments; X.Y., Q.W., and K.W. analyzed data; X.Y., I.H.S., K.K., and K.W. interpreted results of experiments; X.Y. and K.W. prepared figures; K.K. and K.W. drafted manuscript; I.H.S., K.K., and K.W. edited and revised manuscript; I.H.S., K.K., and K.W. approved final version of manuscript.