Sensorimotor feedback based on task-relevant error robustly predicts temporal recruitment and multidirectional tuning of muscle synergies

Abstract

We hypothesized that motor outputs are hierarchically organized such that descending temporal commands based on desired task-level goals flexibly recruit muscle synergies that specify the spatial patterns of muscle coordination that allow the task to be achieved. According to this hypothesis, it should be possible to predict the patterns of muscle synergy recruitment based on task-level goals. We demonstrated that the temporal recruitment of muscle synergies during standing balance control was robustly predicted across multiple perturbation directions based on delayed sensorimotor feedback of center of mass (CoM) kinematics (displacement, velocity, and acceleration). The modulation of a muscle synergy's recruitment amplitude across perturbation directions was predicted by the projection of CoM kinematic variables along the preferred tuning direction(s), generating cosine tuning functions. Moreover, these findings were robust in biphasic perturbations that initially imposed a perturbation in the sagittal plane and then, before sagittal balance was recovered, perturbed the body in multiple directions. Therefore, biphasic perturbations caused the initial state of the CoM to differ from the desired state, and muscle synergy recruitment was predicted based on the error between the actual and desired upright state of the CoM. These results demonstrate that that temporal motor commands to muscle synergies reflect task-relevant error as opposed to sensory inflow. The proposed hierarchical framework may represent a common principle of motor control across motor tasks and levels of the nervous system, allowing motor intentions to be transformed into motor actions.

muscle synergies have been proposed as a neural mechanism by which abstract, task-level motor goals (which do not have a direct, one-to-one mapping to lower-level variables such as joint angles) can be transformed into appropriate muscular patterns that achieve those goals (Cheung et al. 2005; d'Avella et al. 2003; Ivanenko et al. 2004, 2005; Saltiel et al. 2001; Ting 2007). As such, muscle synergies have been hypothesized to represent motor modules that provide the nervous system with a repertoire or library of actions that can be flexibly and robustly combined to produce movements (Chvatal et al. 2011; Ting and Macpherson 2005; Torres-Oviedo and Ting 2007, 2010; Tresch et al. 1999). In this scenario, a muscle synergy would be the most basic unit of motor output, where the descending temporal commands that recruit a muscle synergy reflect a desired task-level goal. In turn, the muscle synergy would specify a particular spatial pattern of muscle activation across the body to coordinate multiple body segments in a way that achieves the goal (van Antwerp et al. 2007; Zajac and Gordon 1989). This suggests that complex spatiotemporal patterns of muscle activity arise from a hierarchical arrangement whereby low-dimensional temporal signals reflecting task-level goals flexibly recruit a low-dimensional spatial set of muscle synergies, generating complex spatiotemporal muscle activation patterns for movement.

A number of studies have demonstrated that spatially fixed muscle synergies form a modular basis for movement control, allowing specific motor goals to be achieved. Spatially fixed muscle synergies have been identified in a variety of voluntary and reactive motor tasks in both humans (Cheung et al. 2009; Chvatal et al. 2011; Clark et al. 2010; Hug et al. 2011; Torres-Oviedo and Ting 2007) and other animal models (Hart and Giszter 2004; Overduin et al. 2008; Saltiel et al. 2001; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Tresch et al. 1999). The robustness of the low-dimensional spatial structure across tasks with different dynamics (Cheung et al. 2005; Chvatal et al. 2011; d'Avella and Bizzi 2005; Kargo et al. 2010) suggests that muscle synergies do indeed constrain the spatial structure of motor outputs. Muscle synergy recruitment has been further correlated to task-level motor outputs, such as producing forces (McKay and Ting 2008; Ting and Macpherson 2005; Torres-Oviedo et al. 2006) or moving the body center of mass (CoM) (Chvatal et al. 2011) in a particular direction during reactive balance control.

Recent evidence suggests that the temporal recruitment of muscle synergies is also low dimensional and modulated by task-level goals. While typical decomposition algorithms leave temporal recruitment patterns of spatially fixed muscle synergies unconstrained, they nonetheless appear to be modulated with task-level variables such as movement speed (Clark et al. 2010; d'Avella et al. 2008), mechanical constraints (Hug et al. 2011), and limb configuration (Cheung et al. 2009; Muceli et al. 2010; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2010). However, in these cases, the exact relationship between task-level variables and the temporal features of muscle synergy recruitment has not been examined. Alternately, low-dimensional structures of temporal patterns of muscle activity for walking have been demonstrated by identifying fixed temporal patterns of motor output while leaving spatial patterns unconstrained (Cappellini et al. 2006; Gizzi et al. 2011; Ivanenko et al. 2004, 2005). However, such fixed temporal structures cannot account for temporal modifications due to changing task-level goals, particularly in reactive tasks (Safavynia and Ting 2012). Others have used multiple algorithms to first identify spatial structure and then addressed the temporal recruitment of spatially fixed muscle synergies by fixed temporal structures associated with feedforward motor commands for voluntary and reactive movements (d'Avella and Bizzi 2005; d'Avella et al. 2008; Hart and Giszter 2004). Together, the results of the aforementioned studies suggest that there are low-dimensional neural constraints on the temporal as well as spatial generation of muscle activity for movement.

If muscle synergies provide a mapping between task-level goals and execution-level muscle activity patterns, it should also be possible to predict their recruitment based on task-level goals. However, in cyclic or feedforward tasks, there may be a stereotypical sequence of task-level goals from one movement to the next, making it difficult to demonstrate a clear relationship between the temporal recruitment pattern and task-level motor goals. In contrast, in reactive tasks, it is possible to experimentally administer different perturbations that alter the temporal patterns of muscle activity, allowing for the relationship between muscle synergy recruitment and task-level goals to be explicitly established. In reactive balance control, CoM has been identified as an important task-level variable because it is necessary to maintain the body CoM over the base of support to maintain an upright stance (Horak and Macpherson 1996; Massion 1994). Temporal patterns of individual muscles can be described by delayed task-level feedback of CoM kinematics (displacement, velocity, and acceleration) in both bipedal (Welch and Ting 2008, 2009) and quadrupedal (Lockhart and Ting 2007) balance control. In an initial study, we recently used this sensorimotor transformation to reconstruct but not predict temporal recruitment of muscle synergies in human responses to discrete sagittal plane perturbations during standing (Safavynia and Ting 2012). While promising, the generality of task-level feedback recruitment of muscle synergies to nonsagittal directions, its predictive power, and the robustness of the model to more dynamic conditions where the body does not start at the desired state remain unknown.

Here, we hypothesized that the temporal recruitment of muscle synergies could be robustly predicted based on the error between the actual and desired state of the CoM during standing balance control, where we assumed the desired state to be the upright, quasistatic condition. First, we hypothesized that task-relevant error feedback of muscle synergies previously demonstrated in the sagittal plane would generalize to nonsagittal directions. To test this, we administered multidirectional discrete perturbations in 12 horizontal plane directions when subjects were standing quietly. Next, we hypothesized that task-relevant error feedback of muscle synergies would robustly predict responses to perturbations in dynamic conditions. To test this, we designed biphasic perturbations that first perturbed the body in the sagittal plane from rest and then perturbed the body in 1 of 12 directions while the body was already moving (Fig. 1). In this case, the elicited motor response to achieve the desired, upright state must account for both the prior motion of the body as well as the effects of the perturbation. We first used the CoM feedback model to reconstruct the temporal structure of muscle synergy recruitment patterns throughout discrete perturbations in 12 horizontal plane directions. For each muscle synergy, the identified reconstruction parameters in a single direction were used to predict muscle synergy recruitment across all remaining 11 directions. Next, we identified a single set of feedback parameters based on the maximal tuning direction for each muscle synergy in biphasic perturbations and tested whether these parameters could predict complex temporal recruitment of muscle synergies across all biphasic perturbations. Together, our results demonstrate that sensorimotor feedback based on task-relevant error robustly predicts muscle synergy recruitment during standing balance control.

Fig. 1.

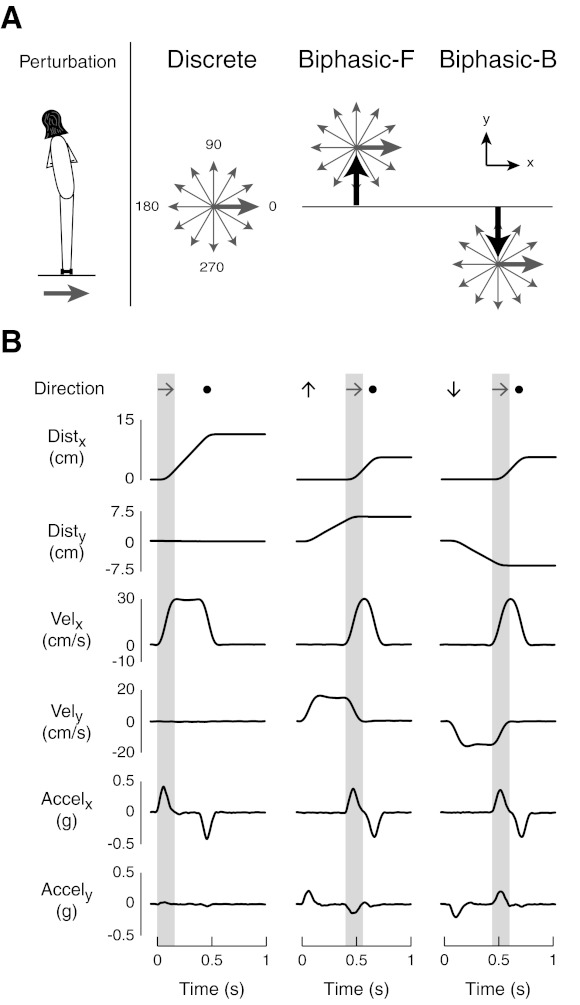
Example of perturbations. A: discrete ramp and hold perturbations were administered in 12 equally spaced directions in the horizontal plane. Biphasic perturbations featured either a forward or backward premovement before moving in one of the same 12 directions administered in discrete perturbations. B: example of kinematic characteristics for rightward perturbations. Black arrows indicate the time and direction of premovement, shaded arrows indicate rightward movement, and solid circles indicate platform deceleration. Shaded boxes indicate the periods of rightward acceleration. Dist, distance; Vel, velocity; Accel, acceleration.

METHODS

Experimental Design

Twelve healthy subjects (6 men and 6 women, mean age ± SD: 23 ± 4 yr) participated in the experimental protocol, which was approved by the Institutional Review Boards of Emory University and the Georgia Institute of Technology. All perturbations were administered using a custom two-axis perturbation platform commanded with a Baldor NextMove ESB controller (Fort Smith, AR) through a custom MATLAB interface.

Discrete ramp and hold translations were administered in 12 equally spaced directions in the horizontal plane; the direction of movement was specified in which 0° indicated rightward platform movement and the angle of perturbation increased in a counterclockwise manner. Discrete perturbations lasted 570 ms and were 12 cm in displacement, 30 cm/s in peak velocity, and 0.5 g in peak acceleration; data for a rightward perturbation are shown (Fig. 1B, left).

Biphasic perturbations were given in the same directions as discrete perturbations but with either a forward or backward premovement (Fig. 1A), similar to a target jump (Shafer et al. 2000). Biphasic perturbations lasted 760 ms and began with either a forward or backward premovement with an acceleration pulse of 0.25 g, resulting in an initial perturbation velocity of 15 cm/s (Fig. 1B, middle and right). A second acceleration was applied at 400 ms after the perturbation onset corresponding to the time that the platform had moved half of the total distance of discrete perturbations (6 cm). The second acceleration, ranging from 0.25 to 0.75 g, was applied in 1 of 12 directions such that the total distance travelled (12 cm) and peak velocity (30 cm/s) in biphasic perturbations was the same as in discrete perturbations.

Data Collection

We randomly presented 5 repetitions of discrete perturbations over 12 directions for a total of 60 trials, as has been done in previous studies (Safavynia and Ting 2012; Torres-Oviedo and Ting 2007). After the discrete perturbations, 120 biphasic perturbations were randomly presented (5 repetitions × 12 directions × 2 premovement directions). To eliminate confounding effects of fatigue, subjects were given a mandatory rest period of 5 min after every set of 60 trials.

Surface electromyographic (EMG) activity was recorded from 16 muscles over the right leg and trunk. The muscles recorded included the rectus abdominis (REAB), tensor fascia lata (TFL), tibialis anterior (TA), semitendinosus (SEMT), long head of the biceps femoris (BFLH), rectus femoris (RFEM), peroneus longus (PERO), medial gastrocnemius (MGAS), lateral gastrocnemius (LGAS), erector spinae (ERSP), external oblique (EXOB), gluteus medius (GMED), vastus lateralis (VLAT), vastus medialis (VMED), soleus (SOL), and adductor magnus (ADMG). In three subjects, SEMT activity was missing due to faulty leads. Muscles were recorded using bipolar electrodes placed ∼2.5 cm apart over the belly of each muscle and oriented in the direction of the muscle fibers (Basmajian et al. 1980). Raw EMG data were collected at 1,080 Hz and then processed according to custom MATLAB routines. Data were high-pass filtered at 35 Hz, de-meaned, rectified, and then low-pass filtered at 40 Hz.

Kinematic and kinetic data were collected for the estimation of CoM kinematic variables. Kinematic data were collected at 120 Hz using an eight-camera Vicon motion capture system (Centennial, CO) and a custom 25-marker set that included head-arms-trunk, thigh, shank, and foot segments. Kinetic data were collected at 1,080 Hz from force plates under the feet (AMTI, Watertown, MA). CoM displacement and velocity were calculated from kinematic data as a weighted sum of segmental masses (Winter 2005); to avoid uncertainty associated with second-order derivatives of kinematic data (Risher et al. 1997), CoM acceleration was computed with respect to the feet using ground reaction forces (force = mass × acceleration), as has been previously reported (Welch and Ting 2008, 2009).

Muscle Synergy Extraction

EMG data structure.

We extracted muscle synergies from EMG data in an epoch corresponding to the initial long-latency automatic postural response beginning 100 ms after the onset of multidirectional perturbation acceleration (Horak and Macpherson 1996). In discrete perturbations, we used a 170-ms epoch beginning 100 ms from the onset of the initial acceleration, corresponding to the initial burst of EMG activity elicited by that acceleration. In biphasic perturbations, we used a slightly shorter 160-ms epoch beginning 100 ms from the onset of the second acceleration because the acceleration duration was shorter (Fig. 2, shaded boxes). Within these epochs, EMG data were parsed into 10-ms bins, and mean activity in each bin was calculated. Three data matrices were assembled (one for each perturbation type: discrete, forward biphasic, and backward biphasic) that consisted of binned EMG activity normalized to peak activity in discrete perturbations. We constructed our three data matrices to have the dimensions of m × s, where m is the number of muscles and s is the number of samples (bins × directions × repetitions).

Fig. 2.

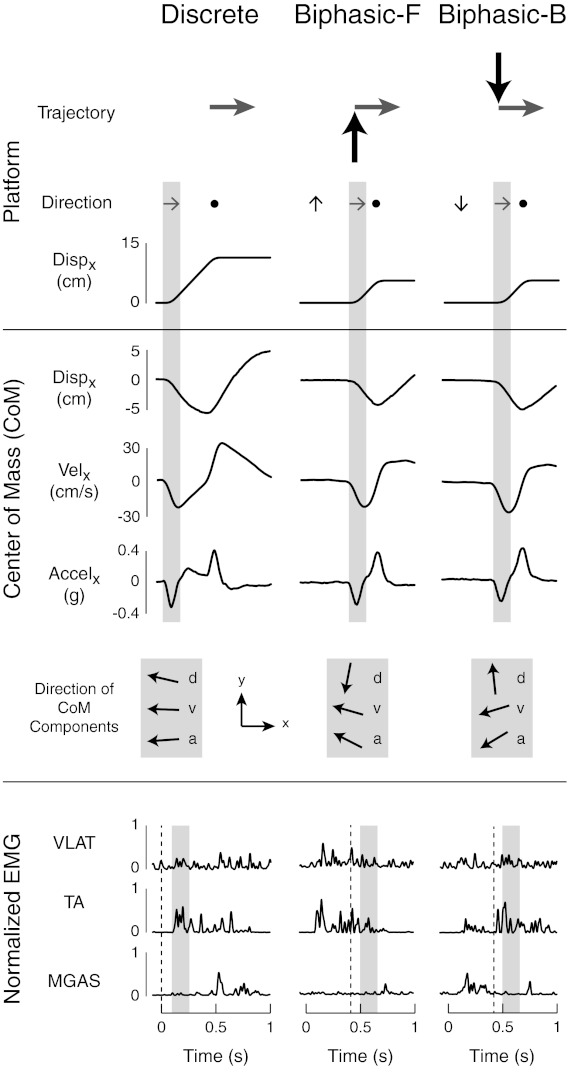
Example of postural responses to rightward discrete and biphasic perturbations. Kinematics of center of mass (CoM) motion in the frontal (x) plane are shown for discrete, forward biphasic, and backward biphasic perturbations. The directions of CoM kinematic components relative to the feet during rightward platform acceleration (shaded region) were oriented in similar directions during discrete perturbations. However, in biphasic perturbations, the direction and magnitude were more dissociated. Muscular responses lagged behind CoM acceleration onset by ∼100 ms (compare shaded boxes with black dotted lines) and varied across perturbation types. Disp and d, displacement; v, velocity; a, acceleration; EMG, electromyograph; VLAT, vastus laturalis; TA, tibialis anterior; MGAS, medial gastrocnemius.

Muscle synergy extraction algorithm.

We used non-negative matrix factorization to extract muscle synergies from EMG activity as previously reported (Chvatal et al. 2011; Lee and Seung 1999; Safavynia and Ting 2012). Briefly, the non-negative matrix factorization algorithm chooses non-negative matrices (W and C) such that the activity of a muscle (M_i) is reconstructed by linearly combining muscle weightings (W_i) with temporal recruitment patterns (C) according to the following equation:

$${\text{M}}_i={\displaystyle \sum _{j=1}^{N_{\text{syn}}}{\text{w}}_{i,j}{\text{C}}_j}$$ (1)

For the spatially fixed muscle synergies used here and in other studies (Chvatal et al. 2011; Hart and Giszter 2004; Kargo et al. 2010; Safavynia and Ting 2012; Torres-Oviedo and Ting 2007, 2010), the muscular composition W does not change, although the recruitment coefficient C can vary at each time point for each trial. We scaled the rows of the data matrices to have unit variance, weighting the variance of each muscle equally for muscle synergy extraction; this normalization factor was then removed after extraction to return the data to the original scaling between 0 and 1.

Choosing the number of muscle synergies.

As previously done, we used a combination of global and local criteria to determine the fewest number of muscle synergies (N_syn) to faithfully reconstruct the EMG data matrices (Chvatal et al. 2011; Safavynia and Ting 2012; Torres-Oviedo and Ting 2007, 2010). Goodness of fit between actual and reconstructed EMG was determined using variability accounted for (VAF), which is defined as 100 times the square of Pearson's uncentered correlation coefficient (Zar 1999). We increased N_syn as long as total VAF and VAF of individual muscles improved; these values were further validated using factor analysis (Tresch et al. 2006). Discrepancies in N_syn obtained from VAF and factor analysis were resolved by additional criteria based on individual muscle reconstruction VAF values. We further verified N_syn against a shuffled matrix of the same data using bootstrapping (Cheung et al. 2009; Chvatal et al. 2011) to ensure that the VAF confidence intervals of muscle synergies extracted from actual versus shuffled data were nonoverlapping.

Muscle Synergy Analysis

Muscle synergy tuning curves.

We constructed tuning curves for muscle synergies recruitment with respect to both platform and CoM acceleration direction based on the average magnitude during the middle eight bins of each EMG epoch. Previously, we have used platform direction rather than CoM acceleration direction as the independent variable in muscle synergy tuning curves (Chvatal et al. 2011; Ting and Macpherson 2005; Torres-Oviedo and Ting 2007, 2010). Because the CoM acceleration directly opposes the platform acceleration direction in discrete perturbations, they generate identical muscle synergy tuning curves but with opposite directional tuning. However, in biphasic perturbations, the body is already moving at the time of the perturbation and CoM kinematics (displacement, velocity, and acceleration) differ in both sign and direction compared with the perturbation. Therefore, to test whether CoM kinematics determine muscle synergy recruitment, we plotted muscle synergy recruitment versus CoM (and not platform) acceleration direction in a bin 100 ms before the EMG epoch. We defined the preferred direction of recruitment as the CoM acceleration direction that corresponded to the maximum averaged recruitment of a muscle synergy, rounded to the nearest multiple of 30°.

Comparison of muscle synergy structure.

We determined the structural consistency of muscle synergies across perturbation types as in previous studies (Chvatal et al. 2011; Safavynia and Ting 2012). We calculated Pearson's correlation coefficients (r) between pairs of muscle synergies: for subjects that had 16 muscle recordings, we considered a pair of muscle synergies to have consistent structure if r > 0.623, which corresponds to the critical value of r² for 16 elements at P = 0.01 (r² = 0.388); for the 3 subjects that had 15 muscle recordings, muscle synergies with r > 0.641 were considered consistent (r² = 0.411, P = 0.01). Critical values of r were validated against a distribution of chance r values (Berniker et al. 2009). Muscle synergies extracted from discrete perturbations were used to reconstruct EMG activity throughout all perturbation types and directions, yielding observed temporal recruitment patterns.

Feedback Model Reconstructions

We reconstructed muscle synergy recruitment patterns using a “jigsaw” model based on delayed feedback of CoM kinematics as in our previous studies (Welch and Ting 2009, Safavynia and Ting 2011) (Fig. 3). An implicit assumption in this model is that the desired body state is to remain in an upright body configuration, and the errors in CoM kinematics are continuously corrected in a manner that restores the desired state. Using CoM horizontal displacement, velocity, and acceleration, we reconstructed recruitment patterns for each muscle synergy [C_Wi(t), where t is time] according to the following equation:

$$C_{w_i}\left(t\right)=\lfloor k_{d}d\left(t-\lambda \right)+k_{v}v\left(t-\lambda \right)+k_{a}a\left(t-\lambda \right)\rfloor$$ (2)

where k_d is feedback gain on CoM displacement (d), k_v is feedback gain on CoM velocity (v), and k_a is feedback gain on CoM acceleration (a), λ is a common time delay representing delays in neural transmission and processing time, and the floor brackets designate half-wave rectification of the reconstructed muscle synergy recruitment pattern (Ting et al. 2012).

Fig. 3.

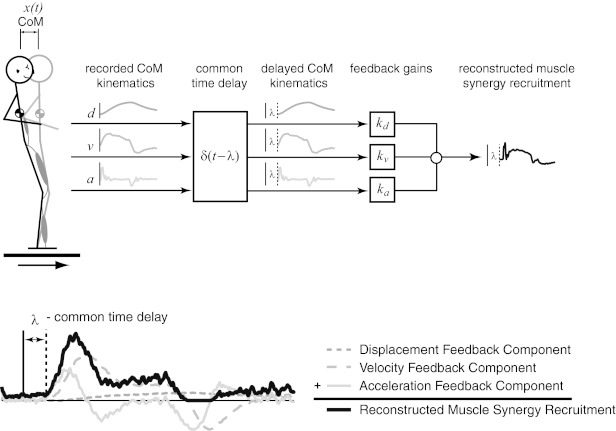
Reconstruction of temporal patterns of muscle synergy recruitment using delayed CoM feedback. Recorded CoM kinematic variables were multiplied by a feedback gain (k) at a common time delay (λ), summed, and half-wave rectified to reconstruct muscle synergy recruitment patterns. [Adapted with permission from Safavynia and Ting (2012).]

Temporal recruitments of muscle synergies were averaged across repeated trials for each direction and perturbation type. Because the frequency content of EMG reconstructed by muscle synergies was lower than that of measured EMG, observed muscle synergy recruitment patterns were low-pass filtered at 20 Hz to match the frequency content of input and output signals and resampled at 1,000 Hz. Each component of CoM motion was averaged, interpolated, and resampled at 1,000 Hz to match sampling rates of inputs and outputs to the model. All reconstructions were performed on muscle synergy recruitment patterns from 50 ms before the perturbation onset to 500 ms after the perturbation offset. This corresponded to a 1.07-s time interval for discrete perturbations and a 1.26-s time interval for biphasic perturbations.

We identified four model parameters that best reconstructed the average temporal recruitment of each muscle synergy. The model identified the three feedback gains (k_i) and λ that best reproduced the averaged muscle synergy recruitment pattern according to the following cost function:

$$\min \left[{\mu }_s{\displaystyle {\int }_0^{t_{\text{end}}}{e}_{\text{m}}^2\text{d}t+{\mu }_k\max \left(\left|e_{\text{m}}\right|\right)}\right]$$ (3)

The first term penalized the squared error (e_m) between recorded and simulated muscle synergy recruitment patterns throughout the perturbation. The second term penalized the maximum error between simulated and recorded data at any point in time. The ratio of weights (μ_s and μ_k) was 10:1 based on prior work (Welch and Ting 2009) and more heavily weighted the integrated error across time rather than the maximum error at any given time point.

We first reconstructed temporal recruitment patterns of each muscle synergy in its preferred tuning direction using the projection of CoM kinematics in the preferred tuning direction. We quantified the similarity between actual and reconstructed muscle synergy recruitment patterns using both r² and VAF, as r² is more sensitive to the contour of traces and VAF is more sensitive to the magnitude of traces. Muscle synergy recruitment patterns were considered well reconstructed when r² ≥ 0.5 or VAF ≥ 75% (Safavynia and Ting 2012).

Prediction of Temporal Recruitment of Muscle Synergies

For each perturbation type, we then predicted temporal muscle synergy recruitment patterns for the remaining 11 directions using feedback gains identified from reconstructions for each muscle synergy in the preferred CoM tuning direction. Based on a cosine tuning principle, we used the projection of CoM kinematic vectors along the preferred direction in Eq. 2 to generate a predicted muscle synergy recruitment pattern for all 11 nonpreferred perturbation directions. Feedback gains for each muscle synergy were fixed to the values identified in the preferred direction for each perturbation type. As in reconstructions, muscle synergy recruitment patterns were considered well predicted when r² ≥ 0.5 or VAF ≥ 75% (Safavynia and Ting 2012).

RESULTS

Differences in Postural Responses to Discrete and Biphasic Perturbations

Biphasic perturbations allowed us to test the robustness of our predictions because they evoked different combinations of CoM kinematics and EMG responses compared with discrete perturbations that began from rest. Whereas in discrete perturbations, the CoM displacement, velocity, and acceleration are always aligned, the premovements of the biphasic perturbations allowed us to examine conditions where these vectors could be oriented in different directions (e.g., Fig. 2, shaded boxes) and correlate them with differences in EMG activity. Moreover, the magnitude of the CoM kinematic vectors as well as evoked EMG activity in response to a multidirectional perturbation also varied based on the direction of premovement in biphasic perturbations. For example, TA was active during all rightward perturbations (Fig. 2, shaded boxes); however, the magnitude of activity was lower after forward premovements and higher after backward premovements compared with discrete perturbations. In contrast, MGAS was not active during rightward perturbations but active during backward premovements.

Structural Consistency of Muscle Synergies Across Perturbation Types and Subjects

Across all subjects, four to seven muscle synergies were independently identified in discrete and biphasic perturbations. For each perturbation type, muscle synergies yielded similar total and muscle VAF during the response to multidirectional platform accelerations (Table 1, within condition). VAFs of muscle synergies from actual data were 7.3 ± 3.3 confidence intervals higher than VAF of the same number of muscle synergies extracted from shuffled data (Fig. 4A).

Table 1.

VAF of muscle synergy reconstructions

	Discrete		Biphasic Forward		Biphasic Backward
VAF	Total	Muscle	Total	Muscle	Total	Muscle
Within condition	87 ± 3	83 ± 6	89 ± 3	85 ± 12	89 ± 3	82 ± 14
Discrete	87 ± 3	83 ± 6	85 ± 6	83 ± 5	82 ± 4	81 ± 6

Values (in %) are means ± SD of variability accounted for (VAF). Within condition, reconstructions of electromyographs using muscle synergies extracted from each condition individually; discrete, reconstructions of electromyographs using muscle synergies extracted from discrete perturbations.

Fig. 4.

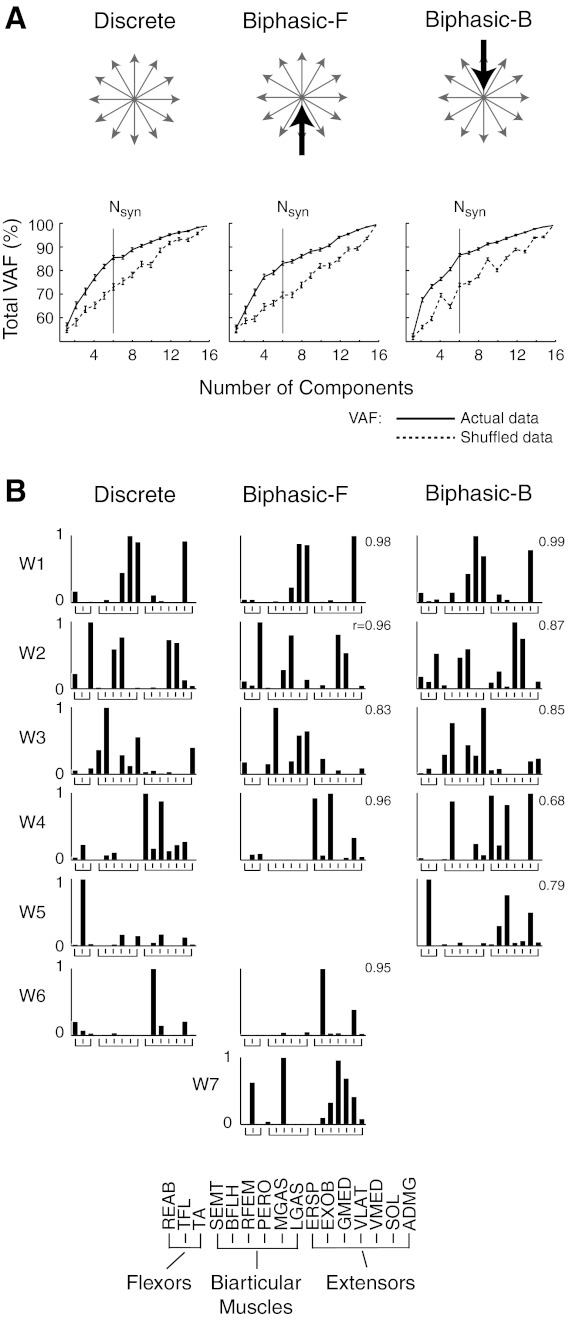
Example of selection and consistency of muscle synergies across perturbation types. A: comparison of total variability accounted for (VAF) by muscle synergies extracted using actual versus shuffled data. Error bars represent the estimated 95% confidence intervals of VAF. For the subject shown (subject 12), six muscle synergies were identified in all perturbation types. At the chosen number of muscle synergies (N_syn), the total VAF was, on average, 7.3 confidence intervals higher than muscle synergies extracted from shuffled data. Biphasic-F, biphasic forward; Biphasic-B, biphasic backward. B: consistency of muscle synergy structure across perturbation types. In this subject, the same six muscle synergies (W₁–W₆) were identified in different perturbation types. One muscle synergy was only found in forward biphasic perturbations. The following muscles were identified: rectus abdominis (REAB), tensor fascia lata (TFL), TA, semitendinosus (SEMT), long head of the biceps femoris (BFLH), rectus femoris (RFEM), peroneus longus (PERO), MGAS, lateral gastrocnemius (LGAS), erector spinae (ERSP), external oblique (EXOB), gluteus medius (GMED), VLAT, vastus medialis (VMED), soleus (SOL), and adductor magnus (ADMG).

Across all subjects, 64 of 71 (90%) muscle synergies extracted from discrete perturbations were found to have highly consistent spatial structure compared with muscle synergies extracted from biphasic perturbations (0.65 < r < 0.99, r = 0.87 ± 0.10; Fig. 4B). Because muscle synergies were consistent across perturbation types, we used muscle synergies extracted from discrete perturbations to reconstruct EMGs over all perturbation types and directions, generating temporal patterns of recruitment. Individual muscle synergies extracted from discrete perturbations also yielded high total and muscle VAF in biphasic perturbations (Table 1, discrete).

Muscle synergy structure and tuning direction were consistent across subjects (Fig. 5). Twelve different muscle synergies were identified across all subjects; 5 of 12 muscle synergies were consistent in at least 9 of 12 subjects. W₁ was identified in all 12 subjects (Fig. 5A); W₁ was composed mainly of calf muscles (MGAS, LGAS, and SOL) and was tuned to forward-rightward CoM acceleration directions (Fig. 5B). W₂ was identified in 11 subjects and composed mainly of quadriceps muscles (RFEM, VLAT, and VMED; Fig. 5C). In 8 of 11 subjects, W₂ had two local maxima, reflecting two preferred tuning directions, largely to backward CoM acceleration directions (forward platform directions), but also, to a lesser extent, in forward CoM acceleration directions (Fig. 5D, solid traces). In 3 of 11 subjects, W₂ was only tuned in response to backward CoM acceleration directions (Fig. 5D, shaded traces).

Fig. 5.

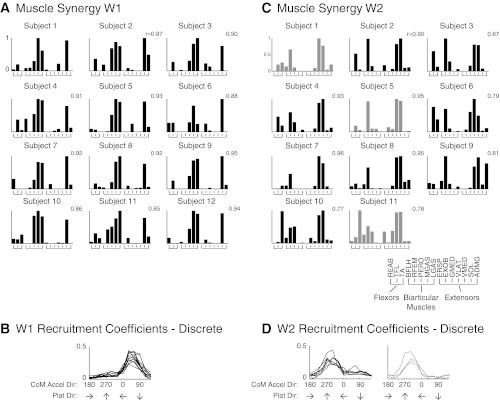
Consistency of muscle synergy structure and tuning across subjects. A: W₁ was consistently identified in all 12 subjects (r = 0.90 ± 0.03). B: W₁ had a preferred tuning direction in all subjects during backward-leftward perturbations (forward-rightward CoM acceleration directions). C: W₂ was identified in 11 of 12 subjects (r = 0.87 ± 0.08). D: for 8 of 11 subjects, W₂ had 2 preferred tuning directions (solid traces); 3 of 11 subjects had 1 preferred tuning direction (shaded traces). The shaded muscle synergies in C correspond to the shaded tuning curves in D.

Muscle Synergy Tuning Across Perturbation Types

For all subjects, the preferred tuning direction of each muscle synergy was similar across perturbation types, but the magnitude and breadth of tuning varied when plotted with respect to platform direction. Across all subjects, 63 of 71 (89%) muscle synergies had preferred tuning directions that were within 30° of each other across perturbation types. For example, in subject 6, muscle synergies W₁–W₄ had similar preferred tuning directions but higher recruitment in discrete versus biphasic perturbations (Fig. 6). W₃ was more broadly tuned in discrete perturbations; conversely, W₁ was more broadly tuned in forward biphasic perturbations. While some muscle synergies (i.e., W₁ and W₃) had a single preferred tuning direction, others (i.e., W₂ and W₄–W₆) had a second peak in tuning that also varied in magnitude across perturbation types.

Fig. 6.

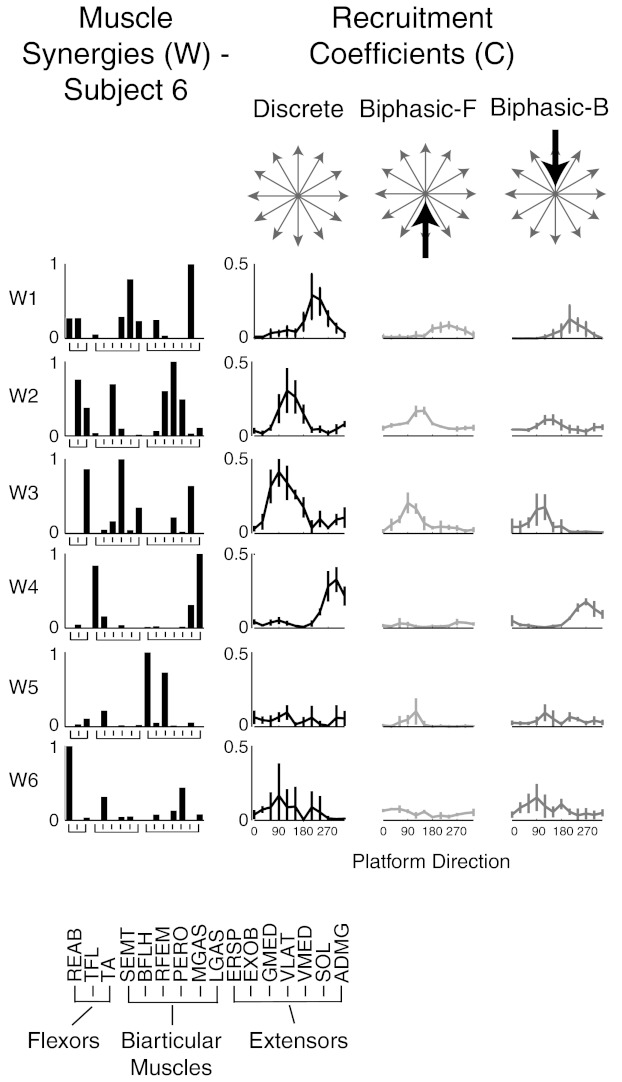
Muscle synergy tuning curves across perturbation types with respect to platform acceleration direction. Muscle synergies extracted from discrete perturbations are shown for a representative subject (subject 6). Averages and SDs of muscle synergy recruitment across trials were plotted with respect to platform perturbation direction. The peak magnitude, or preferred tuning direction, of muscle synergies was similar across perturbation types, although the magnitude of muscle synergy recruitment varied.

Differences in the breadth of muscle synergy tuning curves were largely resolved when data were plotted with respect to CoM (and not perturbation) acceleration direction (Fig. 7). For example, in subject 8, W₁ was more broadly tuned in forward biphasic perturbations and more narrowly tuned in backward biphasic perturbations when plotted with respect to platform direction. Peak tuning direction differed by ∼30° between discrete (Fig. 7B, black traces) and biphasic (Fig. 7B, green and purple traces) perturbations. However, when plotted against CoM acceleration direction, W₁ tuning curves became more similar in breadth across perturbation types (Fig. 7C) and peak tuning directions were more aligned. Remaining differences in the magnitude of muscle synergy recruitment reflected differences in CoM acceleration magnitude in discrete and biphasic. For example, in subject 8, the magnitude of W₁ recruitment in the peak tuning direction of 60° was smallest in backward biphasic perturbations, where the CoM acceleration in that direction was also smallest (Fig. 7D).

Fig. 7.

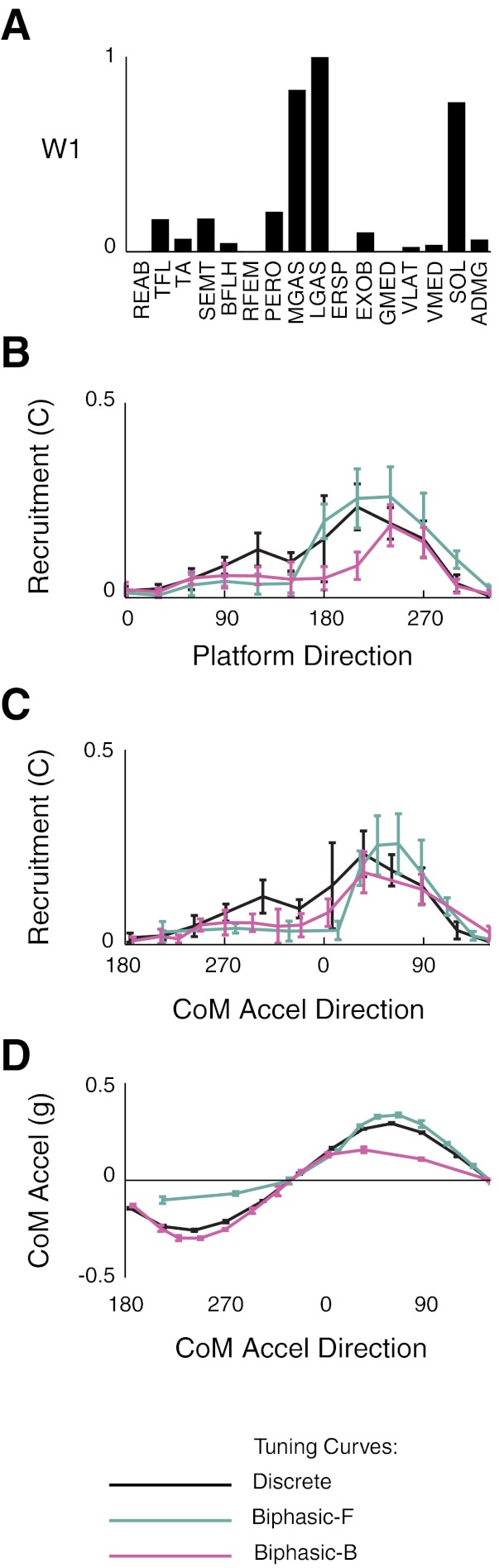
Tuning of muscle synergies to platform versus CoM acceleration direction. A: W₁ for subject 8. B: muscle synergy tuning versus platform direction. Compared with discrete perturbations, muscle synergy tuning was broader in forward biphasic perturbations and narrower in backward biphasic perturbations. C: muscle synergy tuning versus CoM acceleration direction. Muscle synergy tuning was more consistently tuned across perturbation types when plotted as a function of CoM acceleration direction versus platform direction. Note that CoM acceleration direction is the opposite of platform direction. D: projection of the CoM acceleration vector along the preferred tuning direction (60°) across perturbation directions. The reduced magnitude of muscle synergy recruitment in forward-biphasic perturbations (red) can be attributed to the reduced CoM acceleration in that direction.

Muscle Synergy Recruitment Is Well Reconstructed by Delayed CoM Feedback

Temporal patterns of muscle synergy recruitment in the preferred tuning direction could be equally well reconstructed in both discrete and biphasic perturbations by delayed feedback based on the projection of CoM kinematics along that direction (Fig. 8). For example, in subject 6, W₂ had a single burst along a forward-leftward (120°) discrete perturbation that caused the CoM to accelerate in the backward-rightward (300°) direction. In biphasic perturbations, this same muscle synergy was recruited at a very low magnitude during forward premovements that accelerated the body backward but was then further recruited when the perturbation changed direction, causing the CoM to accelerate along the preferred direction of W₂. Note that W₂ was not recruited in backward premovements where the CoM accelerated in the backward direction. Over all subjects, 53 of 71 muscle synergies (75%) were well reconstructed in their preferred tuning direction (r² = 0.68 ± 0.18, median r² = 0.71, VAF: 87 ± 6%, median VAF: 88%). Time delays were between 90 and 120 ms for all reconstructions, consistent with postural delays described in the literature (Horak et al. 1989; Horak and Macpherson 1996). The feedback gains used for a given muscle synergy across subjects were reasonably consistent, with coefficients of variation ranging from 0.05 to 1.22 (median coefficient of variation: 0.40). Moreover, if a particular muscle synergy was found to be dominated by one kinematic variable (e.g., velocity feedback), this was also true across subjects. For the 18 muscle synergies that were not well reconstructed, 17 muscle synergies had major contributions of muscles that had actions at the hip and trunk (ERSP, EXOB, REAB, and GMED; e.g., Fig. 8, W₅).

Fig. 8.

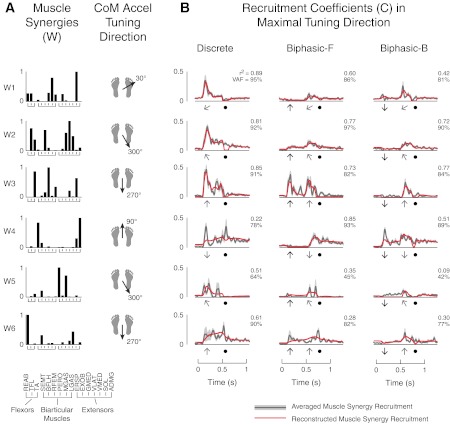
Example of feedback model reconstruction of muscle synergies in their preferred tuning direction. A: muscle synergy structure and preferred tuning direction with respect to CoM acceleration. Data are shown for the same subject as shown in Fig. 6 (subject 6). B: reconstructions of muscle synergy recruitment in the preferred tuning direction. The dark shaded lines and light shaded regions indicate averaged muscle synergy recruitment patterns and 1 SD, respectively. Red lines are feedback model reconstructions. Black arrows indicate the time and direction of premovement, shaded arrows indicate time and direction of movement, and solid circles indicate platform deceleration. Numbers indicate r² (top) and VAF (bottom) values for reconstructions. Average muscle synergy recruitment patterns for W₁–W₄ were well reconstructed across discrete and biphasic perturbations.

CoM Feedback Predicts Muscle Synergy Recruitment Across Changing Perturbation Directions

We were able to predict variations in the temporal recruitment patterns of each well-reconstructed muscle synergy across the remaining 11 perturbation directions using a fixed set of feedback gains based on differences in CoM kinematics along the preferred direction for each perturbation type. For example, in subject 1, muscle synergy W₁ was maximally tuned to the 60° CoM acceleration direction, corresponding to 240° perturbations, from which feedback gains (k_d, k_v, and k_a) were found (Fig. 9, B–D, red traces). The same gains predicted changes in both the magnitude and temporal recruitment patterns of that muscle synergy across other perturbation directions (Fig. 9, B–D, blue traces). Specifically, the magnitude decreased in adjacent perturbation directions (180–330°) and was predicted to be inhibited in perturbations in the opposite direction (0–150°) until the deceleration of the platform (Fig. 9B, solid circles). For biphasic perturbations, W₁ was predicted to be inhibited during forward premovements (Fig. 9C), predicted to be recruited in backward premovements (Fig. 9D), and predicted to have varying temporal recruitment patterns during the second, multidirectional perturbations (Fig. 9, C and D).

Fig. 9.

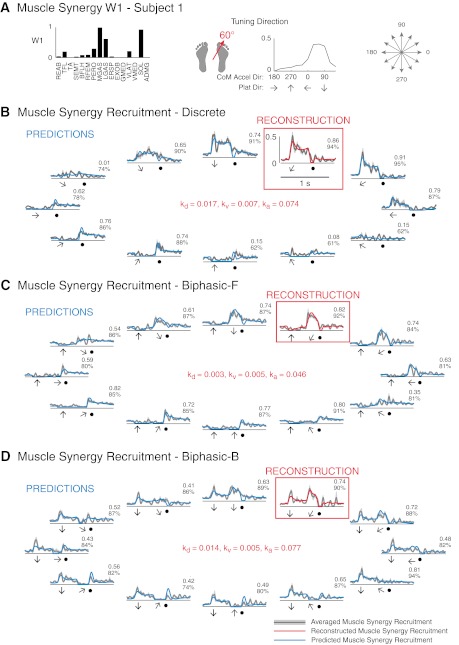
Predictions of muscle synergy recruitment patterns across directions based on feedback gains identified from reconstructions in one preferred tuning direction. A: W₁ in subject 1, which had one preferred CoM acceleration tuning direction. B: CoM feedback reconstruction and predictions of discrete perturbations. Note that CoM acceleration direction is opposite platform direction. C: CoM feedback reconstruction and predictions of forward biphasic perturbations. D: CoM feedback reconstruction and predictions of backward biphasic perturbations. Numbers indicate r² (top) and VAF (bottom) values for predictions. Black arrows indicate the time and direction of premovement, shaded arrows indicate time and direction of movement, and solid circles indicate platform deceleration.

For well-reconstructed muscle synergies with a single preferred tuning direction, goodness of fit was quantified for predictions of muscle synergy recruitment across all subjects, directions, and perturbation types (r² = 0.37 ± 0.28, median r² = 0.35, VAF = 65 ± 27%, median VAF = 74%). Although the majority of the predictions were not considered well predicted by our established criteria, predictions of muscle synergy quiescence are subject to error in both r² and VAF, as actual data during quiescent periods are noisy and of low magnitude (cf. Fig. 9B, 150° and 330° perturbations). Predictions of well-reconstructed muscle synergies with double tuning directions had similar goodness of fit values across subjects, directions, and perturbation types (r² = 0.36 ± 0.28, median r² = 0.33, VAF = 62 ± 28%, median VAF = 73%).

For muscle synergies that had two preferred tuning directions, identified feedback gains in the secondary tuning direction predicted muscle synergy recruitment in directions nearly opposite to the primary tuning direction (Fig. 10). In the example shown in Fig. 10A, W₂ had a large CoM acceleration tuning at 300° and a smaller but distinct tuning at 90°. Predictions of W₂ recruitment based on CoM tuning in 300° matched actual recruitment patterns in perturbations eliciting CoM kinematics near the preferred tuning direction (Fig. 10B, 30–180°, red/blue traces). However, recruitment in opposing directions (210–0°) was not predicted. This secondary recruitment pattern could be predicted using feedback gains derived from reconstructions in the secondary tuning direction of 90° (Fig. 10B, orange/green traces). The differences in the feedback gain magnitudes for the two tuning direction demonstrate that W₂ was responsive to backward CoM acceleration and position and forward CoM velocity.

Fig. 10.

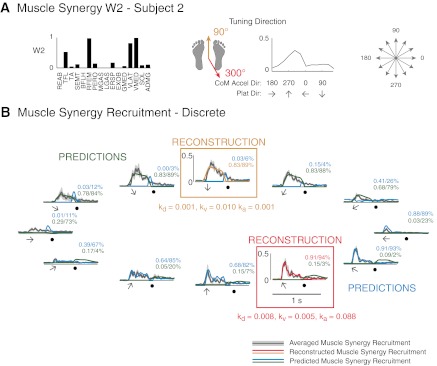
Predictions of muscle synergy recruitment patterns across directions based on feedback gains identified from reconstructions in two preferred tuning directions. A: W₂ in subject 2, which had two preferred CoM acceleration tuning directions. B: feedback model reconstruction and predictions of discrete perturbations. Muscle synergy recruitment was reconstructed in two directions (red/orange traces). Feedback gains identified from reconstructions were used to predict recruitment in all other perturbation directions (blue/green traces). Note that CoM acceleration direction is opposite platform direction. Numbers indicate r² (top) and VAF (bottom) values for predictions. Shaded arrows indicate time and direction of movement, and solid circles indicate platform deceleration.

Therefore, we combined predictions from one half of the directions using one set of feedback gains and the other half of the directions using the other set of feedback gains. Across all subjects and directions, predictions of muscle synergy recruitment in discrete perturbations improved when using two sets of feedback gains (r² = 0.47 ± 0.26, median r² = 0.49, VAF = 71 ± 19%, median VAF = 76%) compared with one set of feedback gains (r² = 0.30 ± 0.30, median r² = 0.20, VAF = 50 ± 32%, median VAF = 60%). Predictions in biphasic perturbations using two sets of feedback gains were not quantified because no single prediction could account for the entire time course of the recruitment pattern due to the changing platform direction.

We further predicted the directional tuning of muscle synergies based on one set of feedback gains identified for each preferred tuning direction. Using a cosine tuning principle, muscle synergy recruitment was predicted by the projection of CoM kinematics in the preferred direction, and the level of prediction was similar across all subjects and muscle synergies (r² = 0.62 ± 0.28, median r² = 0.73, VAF = 78 ± 18%, median VAF = 83%). For example, in subject 1, feedback gains identified from the preferred tuning direction predicted the directional tuning of muscle synergy W₁ over all directions (Fig. 11, top). Muscle synergy W₂ in subject 2 required two sets of feedback gains (cf. Fig. 10) to predict the tuning peaks in the forward and backward directions.

Fig. 11.

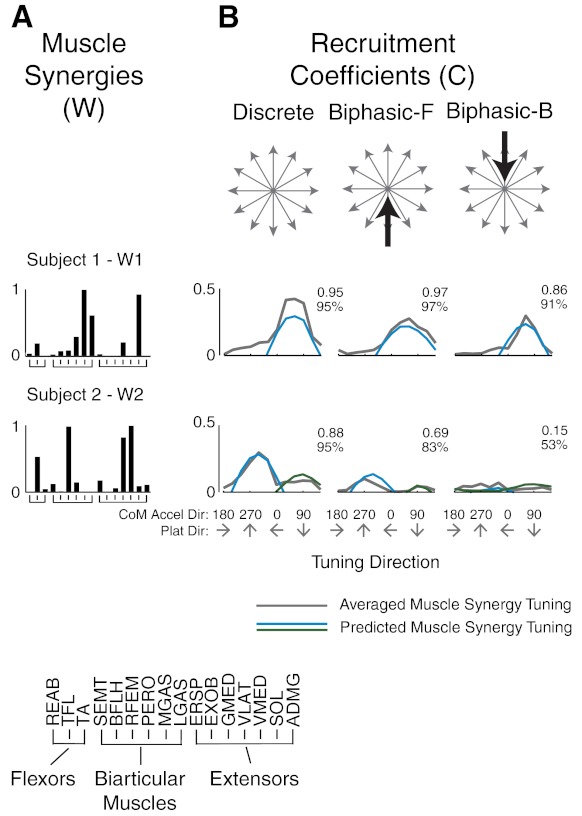
Predicted directional tuning curves for muscle synergy recruitment. A: W₁ in subject 1 (Fig. 9) and W₂ in subject 2 (Fig. 10). B: measured (gray) and predicted (blue and green) muscle synergy tuning curves. Numbers indicate r² (top) and VAF (bottom) values for predictions. Note that double-tuned muscle synergies required predicted tuning curves based on each tuning direction to be half-wave rectified and then concatenated.

DISCUSSION

Summary

Our results demonstrate that during perturbations to standing balance, the temporal recruitment of spatially fixed muscle synergies can be robustly predicted by error between the desired and actual state of the CoM, which we hypothesize to be the task-level goal for standing balance control. Our work demonstrates that the temporal structure of motor outputs is constrained by task-relevant error of CoM kinematics, whereas the spatial structure is constrained by a small set of directionally tuned muscle synergies. Moreover, despite differences in the mechanics of the body in the sagittal and frontal planes (Winter 1995), a common sensorimotor feedback transformation based on the on error between the desired state and the actual state of the CoM robustly reconstructed and predicted the recruitment of muscle synergies. Because the errors were based on the projection of CoM kinematics in a given direction, muscle synergies were predicted to have cosine tuning functions. These predictions were robust to biphasic perturbations where the prior movement of the body as well as the effects of the perturbation affected the required response to maintain balance. Taken together, our work supports a hierarchical and low-dimensional organization of the neuromotor system whereby temporal commands based on task-level variables recruit muscle synergies that coordinate muscles in a way to achieve that goal. This organization may reflect a general mechanism for motor control that allows the nervous system to transform motor intention to action.

The Temporal Structure of Motor Commands Is Determined by Task-Level Goals

Our results support the idea that the temporal structure of task-level motor commands is independent from mechanisms that allow those tasks to be executed (Bernstein 1967). Because CoM kinematics are abstract task-level variables, they must be estimated by integrating proprioceptive, visual, and vestibular information (Green et al. 2005; Horak and Macpherson 1996; Peterka 2002), presumably in the brain stem and higher neural centers. Previous work in balance control has shown that muscle synergies are directionally tuned and produce consistent spatial patterns of motor outputs that function to move the CoM in specific directions (Chvatal et al. 2011; Ting and Macpherson 2005; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2007, 2010). In contrast to previous studies, we were able to reconstruct the fine temporal features of muscle synergy recruitment in multiple perturbation directions and during perturbations that change direction. Temporal and spatial features of muscle synergy recruitment were predicted using one or two sets of feedback gains for each muscle synergy, based on cosine tuning functions centered on the preferred recruitment directions. The robustness of the predictions was surprising as the dynamics of the body differ greatly in frontal and sagittal planes (Bingham et al. 2011). However, our results confirm those of prior results in postural control demonstrating that different components of activity in the same muscle are independently tuned to pitch versus roll perturbations (Gruneberg et al. 2005).

Task-level commands may both activate and inhibit the recruitment of muscle synergies, as periods of both muscle synergy recruitment and quiescence were robustly predicted. In our model, the inhibition of a muscle synergy occurs when the sum of the weighted CoM kinematic signals is negative. The resulting temporal recruitment signal is then half-wave rectified such that negative commands become zero. This is consistent with a neuronal summation mechanism of synaptic inputs of task-level variables that inhibits the membrane potential below the spiking threshold. Thus, temporal recruitment of muscle synergies may be defined and constrained by the achievement of desired task-level goals.

Furthermore, the robustness of the sensorimotor feedback transformation to predict muscle synergy recruitment across dynamic states indicates that temporal motor commands reflect task-relevant error as opposed to sensory inflow. Previously, correlations between task-level variables and muscle activity, but not muscle stretch, were found across different discrete perturbation types (Allum et al. 2003; Carpenter et al. 1999; Diener et al. 1983; Gollhofer et al. 1989; Nashner 1976). Similarly, we have previously shown that the same muscle synergy could be recruited in response to different perturbations that induce stretch in different muscles but require the CoM to be moved in the same direction (Chvatal et al. 2011; Torres-Oviedo et al. 2006). Here, we further demonstrate that the evoked response to a perturbation reflects the task-level goal (e.g., CoM kinematics) and not simply the sensory inflow due to the perturbation (Kutch and Valero-Cuevas 2012). For example, in double-tuned muscle synergies, the secondary tuning direction was typically opposite to the primary tuning direction. It is highly unlikely that the local biomechanical effects of the perturbation could account for the evoked muscle activity in both tuning directions. Furthermore, our novel biphasic perturbations could perturb the body in a direction orthogonal to the direction of ongoing body motion. Thus, a direct response to the sensory inflow of the most recent perturbation would be insufficient to maintain postural stability (Mergner 2010; Pai and Patton 1997; Pai et al. 1998; van der Kooij and de Vlugt 2007). We showed that muscle synergy recruitment (and not simply muscle activity) could be recruited by task-level error feedback that integrates both the actual and desired state of the body under dynamic, multidirectional conditions imposed by biphasic perturbations. Similarly, during target jumps in a multidirectional reaching task, temporally fixed synergies are modulated as a function of both the initial and desired movement direction (d'Avella et al. 2011).

There may be interactions between task-level sensorimotor feedback and biomechanical factors that modulated the apparent feedback gains identified. The robustness of our predictions across directions was surprising because changes in feedback gains are necessary to maintain postural stability in the sagittal versus frontal planes due to biomechanical differences (Bingham et al. 2011); such changes appear to be resolved by the cosine tuning function. However, feedback gains were different during biphasic versus discrete perturbation sets, which could be due to the fact that the acceleration magnitude in the preferred tuning direction could be either lower or higher in biphasic perturbations (depending on the direction of the second perturbation), although the total displacement and peak velocities were matched in both sets. The variations in feedback gains were consistent with model predictions and experimental results suggesting that the feasible range of feedback gains to maintain stability are larger when perturbation accelerations are smaller (Bingham et al. 2011). These variations could also be due to differences in the sensory signals encoding body motion, such as the history- and time-dependent properties of muscle spindles and other sensory organs (Campbell and Moss 2002, 2000; Getz et al. 1998; Haftel et al. 2004; Nichols and Cope 2004).

Muscle synergies may be flexibly recruited in balance control based on multiple task-level variables. We found that some muscle synergies were recruited by more than one direction of CoM motion, suggesting that they are recruited by more than one task-level command. For example, quadriceps muscle synergies often had two preferred tuning directions and required two separate sensorimotor transformations based on CoM kinematics to predict recruitment in forward and backward directions. The primary recruitment of the quadriceps muscle synergy is consistent with its function of moving the CoM forward (Chvatal et al. 2011), whereas the secondary recruitment may provide stability to the limb (Neptune et al. 2009). There were also a few muscle synergies dominated by trunk muscles that were not well reconstructed by CoM feedback and have been found to be highly variable in their recruitment across various postural perturbation studies (Chvatal et al. 2011; Safavynia and Ting 2012; Torres-Oviedo and Ting 2007, 2010). Although we did not record from enough muscles to explicitly study muscle coordination at the trunk, it is possible that they are recruited to maintain the vertical orientation of the body, which may be a concurrent or secondary task-level goal for balance (Kluzik et al. 2005; Macpherson et al. 1997; Massion 1994).

Hierarchical Framework for Motor Control

We propose a hierarchical framework where the temporal and spatial structure of motor outputs are distinct, allowing for the separation of motor goals from their implementation across body segments with different biomechanical properties. Similarly, the spinal central pattern generator for locomotion has been demonstrated to have independent circuits governing the locomotor rhythm and the spatial coordination of muscles. This hierarchical arrangement allows for flexibility between the desired timing of movement and the specific muscles involved in generating the movement (McCrea and Rybak 2008). Likewise, in the cerebral cortex, neurons encoding the desired motor goal have been demonstrated to be independent of the muscles that are used to generate the motion (Grafton and Hamilton 2007; Rizzolatti et al. 1987). Such flexibility would be supported by a hierarchical structure where different muscle synergies could be recruited to achieve a common, task-level goal. This flexibility has been demonstrated in balance control, where different muscle synergies can be used to recover balance by using either ankle or hip torque predominantly (Torres-Oviedo and Ting 2007). Alternatively, different neural pathways may recruit a common set of muscle synergies in different tasks that share similar task-level goals. For example, the same set of muscle synergies for walking can be recruited during both voluntary and reactive modifications to locomotor muscle activity (Chvatal and Ting 2012). Similarly, in acute frog preparations, the same muscle synergies are recruited in different behaviors mediated by cortical, midbrain, or spinal circuits (Hart and Giszter 2004; Roh et al. 2011).

The proposed hierarchical framework may represent a common principle of motor control across motor tasks and levels of the nervous system. The recruitment of muscle synergies has been shown to be modulated by task variables across tasks, such as walking speed for locomotion (Chvatal and Ting 2012; Clark et al. 2010), CoM for balance control (Chvatal et al. 2011; Torres-Oviedo et al. 2006), and speed and direction for reaching movements (d'Avella et al. 2006, 2008, 2011). Muscle synergies have also been hypothesized to be encoded across the neuraxis, including the spinal cord for locomotion and primitive movements (Bizzi et al. 1991; Drew et al. 2008; Kargo et al. 2010; Roh et al. 2011; Saltiel et al. 2001), brain stem for postural control (Chvatal et al. 2011; Torres-Oviedo et al. 2006; Torres-Oviedo and Ting 2007), and motor cortex for grasping (d'Avella et al. 2008; Overduin et al. 2008). Accordingly, task-level variables are also encoded at multiple levels of the neuraxis. For example, pyramidal neurons in the motor cortex have been shown to respond to task-level variables such as end-point force, velocity, movement direction, and hand location (Georgopoulos et al. 1986; Sergio and Kalaska 1997). Neurons in the reticular formation have been shown to respond to task-level changes in postural equilibrium (Stapley and Drew 2009). Moreover, limb orientation can be encoded across the neuraxis, including reticular formation (Deliagina et al. 2008), the motor cortex (Scott and Kalaska 1997), and the dorsal spinocerebellar tract (Poppele et al. 2002). Therefore, the recruitment of muscle synergies that specify spatial coordination of muscles by task-level variables is plausible given the known structure and function of the nervous system, allowing abstract task-level goals to be flexibly transformed into appropriate muscular patterns that achieve those goals.

GRANTS

This work was supported by National Institutes of Health (NIH) Grant R01-NS-058322 (to L. H. Ting). S. A. Safavynia was supported by a Medical Scientist Training Program Fellowship (NIH Grant 5-T32-GM08169-24).

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

AUTHOR CONTRIBUTIONS

Author contributions: S.A.S. conception and design of research; S.A.S. performed experiments; S.A.S. analyzed data; S.A.S. and L.H.T. interpreted results of experiments; S.A.S. prepared figures; S.A.S. drafted manuscript; S.A.S. and L.H.T. edited and revised manuscript; S.A.S. and L.H.T. approved final version of manuscript.