Structural learning in feedforward and feedback control

Abstract

For smooth and efficient motor control, the brain needs to make fast corrections during the movement to resist possible perturbations. It also needs to adapt subsequent movements to improve future performance. It is important that both feedback corrections and feedforward adaptation need to be made based on noisy and often ambiguous sensory data. Therefore, the initial response of the motor system, both for online corrections and adaptive responses, is guided by prior assumptions about the likely structure of perturbations. In the context of correcting and adapting movements perturbed by a force field, we asked whether these priors are hard wired or whether they can be modified through repeated exposure to differently shaped force fields. We found that both feedback corrections to unexpected perturbations and feedforward adaptation to a new force field changed, such that they were appropriate to counteract the type of force field that participants had experienced previously. We then investigated whether these changes were driven by a common mechanism or by two separate mechanisms. Participants experienced force fields that were either temporally consistent, causing sustained adaptation, or temporally inconsistent, causing little overall adaptation. We found that the consistent force fields modified both feedback and feedforward responses. In contrast, the inconsistent force field modified the temporal shape of feedback corrections but not of the feedforward adaptive response. These results indicate that responses to force perturbations can be modified in a structural manner and that these modifications are at least partly dissociable for feedback and feedforward control.

the human motor system is capable of dealing with highly unpredictable environments. When a movement misses its target, the brain quickly corrects the ongoing movement (Goodale et al. 1986; Pelisson et al. 1986) and adapts the next motor command to prevent further errors (Donchin et al. 2003). Because sensory feedback is very noisy, the motor system has to rely on structural assumptions (Wolpert et al. 2011) about the nature of the perturbation. These assumptions result in a good first guess of how to respond, even in the absence of detailed information about the perturbation.

Structural assumptions become visible, for example, when adapting to state-dependent forces that occur during reaching (Shadmehr and Mussa-Ivaldi 1994). In a series of elegant studies, Sing et al. [2009; see also Wei et al. (2010)] perturbed reaches with either velocity- or position-dependent forces that pushed the arm orthogonally to the actual movement direction. After a single force-field trial, they found that the temporal shape of the adaptive response was a mixture of positively correlated velocity- and position-dependent forces, even for purely velocity- or position-dependent force fields. This tendency can be understood as arising from the structural assumption that forces with velocity and position dependence, acting in the same direction, are more likely than forces in which the two are negatively correlated (Fig. 1).

Fig. 1.

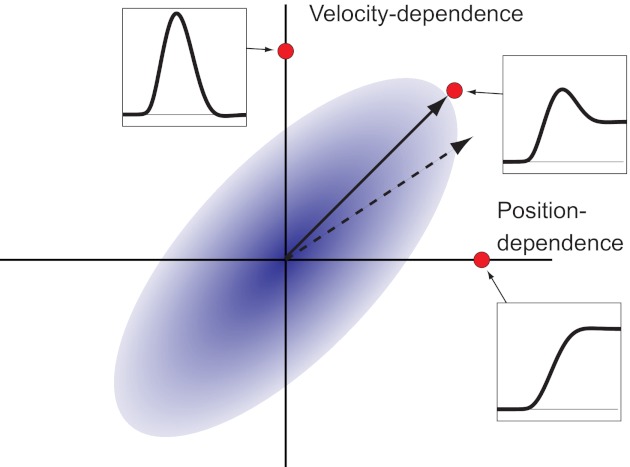
The effect of structural learning on the prior assumptions of the temporal shape of force fields. Possible perturbing forces are shown as points in coefficient space, with the x-axis indicating the strength and direction of the position-dependent component, whereas the y-axis indicates the strength and direction of the velocity-dependent component. The initial adaptation to any force field is biased toward the diagonal in the position/velocity coefficient space (solid arrow) (Sing et al. 2009). This bias indicates that the motor system relies on a prior probability distribution (blue cloud), which indicates that force fields with position and velocity components in the same direction are more likely than perturbations with components in opposite directions. We hypothesize that after repeated exposure to a position-dependent force field (independent of the direction of this force field), the response should now be biased toward the position-dependent axis. This indicates that prior assumption of the motor system has changed; i.e., structural learning has occurred.

However, it has not yet been shown whether these assumptions are hard wired or can be modified by prior experience. We first hypothesized that these structural assumptions during adaptation can be modified by exposing participants to a specific temporal shape of perturbation. For example, through repeated exposure to position-dependent force fields, we should be able to increase the propensity of the system to adapt to position-dependent forces. This would imply that structural assumptions are not hard wired (Sing et al. 2009) but are malleable by environmental dynamics. Structural learning has been demonstrated for adaptation to visuomotor mappings (Braun et al. 2009b, 2010a) and recently, also for force fields acting in different spatial directions (Kobak and Mehring 2012). Here, we test for the first time the mechanisms of structural learning of different temporal shapes of dynamic perturbations.

Given that the feedforward adaptive response can be structurally modified, we then asked whether structural learning also influences feedback mechanisms within the movement. Previous studies have shown that feedback gains can be modulated in size (Franklin and Wolpert 2008; Liu and Todorov 2007) and spatial direction (Braun et al. 2009b). We examine here whether such modification can also occur in the temporal shape of the response. Finally, having shown that structural learning occurs in both feedforward adaptation and feedback mechanisms, we considered whether this is caused by a single representational change or whether they are dissociable. We exploited the fact that feedforward and feedback mechanisms are differentially affected by the temporal characteristics of perturbations across trials (Gonzalez-Castro et al. 2008). We show that temporally consistent forces, which lead to adaptation, modulate both feedforward and feedback responses. However, forces that vary randomly trial by trial and do not lead to adaptation modify feedback but not feedforward responses. This demonstrates for the first time that structural learning in feedforward commands and feedback adaptation is driven by distinct signals.

MATERIALS AND METHODS

Participants.

All participants were self-described right-handed volunteers (18 male, 18 female, mean age 25 years), 12 of which participated in experiment 1 (five male, mean age 25), 12 in experiment 2 (five male, mean age 25), and 12 in experiment 3 (eight male, mean age 26). No participant from one experiment took part in either of the other two experiments. Experimental and consent procedures were approved by the University College London Ethics Committee.

General method.

Participants sat in front of a virtual environmental setup with their head on a forehead rest. They made 15-cm reaching movements to a single target with their right hand while holding onto a robotic device. This device recorded the position of the hand with a sampling frequency of 200 Hz. A monitor displayed a white square (0.5 cm × 0.5 cm) indicating the start position and a white 1-cm-wide target square. The screen was viewed via a mirror, such that participants did not have direct vision of their arm but received continuous and calibrated visual feedback of their hand position via a 0.3-cm diameter white cursor circle.

To start a trial, participants moved the cursor into the start box. When the target appeared 15 cm from the start position, participants were instructed to move the cursor to the target in the straight-ahead direction. Movements had to have a peak speed between 55 cm/s and 80 cm/s. Furthermore, the movement needed to stop within 800 ms at a distance of <0.65 cm from the center of the target. If all of these criteria were met, the target turned red and exploded, and participants scored a point. If the movement was not fast enough or was not completed within 800 ms, the target turned blue or pink; if participants moved too fast, the target turned yellow; if participants moved at the right speed but stopped the movement too far from the target, the target turned green. However, all trials were included in the analysis, and only trials where participants moved less than one-half of the distance to the target or showed a large deviation (>80°) in the initial movement direction were excluded. In experiment 2, we excluded the data from one participant whose baseline (pre-exposure) channel responses were very small and went in the opposite direction in coefficient space to the rest of the subjects. In experiment 3, we excluded the data from one participant who had <60% valid trials compared with >90% for the remaining subjects.

During parts of the experiment, participants were exposed to a dynamic force field, exerted orthogonally to the actual movement direction. The force (N) could depend on the position of the hand (in cm, relative to the start), the velocity (cm/s), or both (Fig. 2A)

$$\left[\begin{array}{c}Forc{e}_x\\ Forc{e}_y\end{array}\right]=C_p*s_1*\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right]*\left[\begin{array}{c}Positio{n}_x\\ Positio{n}_y\end{array}\right]+C_v*s_2*\left[\begin{array}{cc}0& 1\\ -1& 0\end{array}\right]*\left[\begin{array}{c}Velocit{y}_x\\ Velocit{y}_y\end{array}\right]$$

Fig. 2.

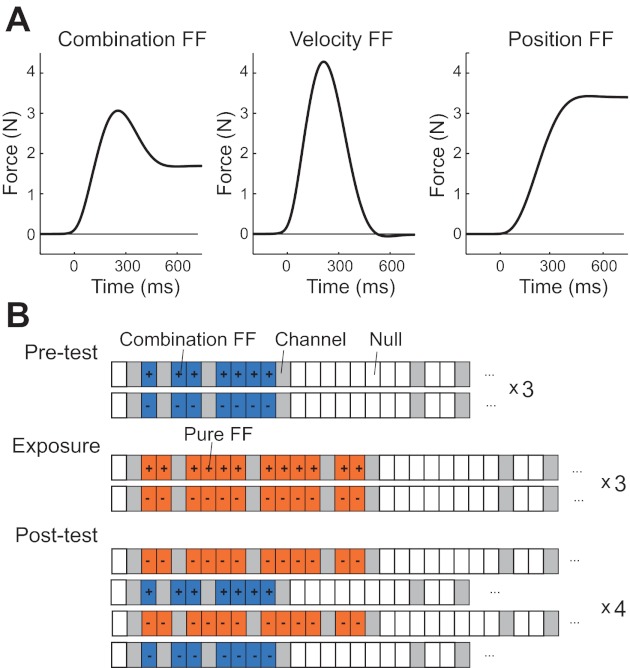
Methods for experiment 1. A: 3 different kinds of force fields (FF). In all cases, the force is orthogonal to the actual movement direction. The combination force field is a mixture of both position- and velocity-dependent force fields. The position-dependent force field increases monotonically with the y-position of the hand. The velocity-dependent force field is proportional to the y-velocity of the arm. B: the experiment consisted of a pretest phase with 6 short blocks of adaptation (2 blocks shown) to the combination force field (blue). The direction of the force alternated on each block from rightward (+) to leftward (−). Force channel trials (gray) were used to monitor adaptation. This was followed by an exposure phase, with 6 blocks of adaptation to pure velocity- or position-dependent force fields (orange), alternating left/right across blocks. Finally, in the post-test phase, subjects adapted in short blocks to the combination or pure force field, which alternated in type across blocks. These blocks were counterbalanced for direction, such that sometimes, a rightward block was followed by a leftward block and sometimes by a rightward block and vice versa.

The position-dependent force field [position component (C_P) = ±1, velocity component (C_V) = 0] pushed the hand either to the left or the right and increased monotonically from the start of the movement (Fig. 2A). The velocity-dependent force field (C_P = 0, C_V = ±1) acted either in a clockwise or counter-clockwise direction relative to the movement direction and reached its highest force at peak velocity. A positive combination force field (C_P = ±0.5, C_V = ±0.5) was simply a linear mixture of a velocity- and position-dependent force field acting in the same direction (positively correlated). We chose the coefficients s₁ (0.225 N/cm) and s₂ (0.075 N/cm) to achieve a peak force of ∼4 N on force-field trials.

To probe the state of the adaptation response, we used force-channel trials throughout the three experiments. During these trials, the robot applied a spring-like force in the x-direction (6,000 N/m), which forced the hand onto a 0° trajectory from the starting position. The force in the y-direction was always zero. To reduce vibration, we also applied a small, viscous damping force (75 Ns/m). If participants expected to be pushed by a force field, then they would exert a compensatory force into the wall of the channel during the movement. Therefore, the force produced in a channel is commonly thought to be a valid readout of the feedforward motor command (Joiner and Smith 2008; Scheidt et al. 2000; Smith et al. 2006).

We also used force channels to probe the feedback responses. On such trials, we presented a target to the right or left of the midline (±14°) and constrained the hand to a 0° trajectory, while the cursor was rotated to move directly to the target. To prevent participants from anticipating these force channels, we also added trials with targets to the left and right of the midline but without force channels (proportion of channel to nonchannel trials is outlined for each experiment below). Consequently, on trials without force channels, participants moved straight to these targets. On trials with force channels, they exerted a reactive force against the channel to resist the unexpected positional perturbation that pushed their hand away from the target. Because we considered the whole response from the beginning to the end of the movement, the response is determined by the stiffness of the arm (Burdet et al. 2000), fast- and long-latency reflexes, and a voluntary feedback response (Hammond 1956). We chose this particular way of introducing a positional perturbation (rather than presenting the target straight and tilting the channel), in order that the arm movements for testing feedforward and feedback control were physically identical throughout the three experiments.

Experiment 1.

In the first experiment, we tested the hypothesis that the exposure to a position- or a velocity-dependent force field would change the adaptation of the feedforward command to a positive combination force field. We tested participants on two separate days. Half of the participants was exposed to a velocity-dependent force field on the first and a position-dependent force field on the second. For the other half of the participants, this sequence was reversed.

Each day started with practice blocks that did not include force fields. On the 1st day, there were two practice blocks, and on the 2nd day, there was a single practice block. This was followed by the pretest to determine a baseline of how participants adapted to a combination force field. During this pretest, participants carried out six short blocks consisting of 23 trials each (Fig. 2B). Each of these short adaptation blocks started with a channel trial to probe the state of the arm. In the next 10 trials, the participants learned to adapt to a combination force field, within which three trials were force channels. The trial then ended with 13 null trials containing two further channel trials. The force field alternated in direction between adaptation blocks. During the pretest and post-test phases, where the subjects adapted to the combination force field, participants received visual feedback via a cursor on all trials. The sign of the combination force field alternated between clockwise and counter-clockwise during these six pretest blocks.

To induce structural learning, participants were then exposed to short adaptation blocks, in which they adapted either to a velocity- or position-dependent force field (on separate days; Fig. 2B). During this exposure phase, participants were not given visual feedback during the movement, such that we could ensure that structural learning was caused by proprioceptive information rather than by the observation of a certain visual trajectory. Each block consisted of 30 trials; the first trial was a channel trial, followed by 16 trials of the combination force field, of which four were channel trials. Finally, the block ended with 13 null trials, of which two were channel trials. Again, the force field alternated in direction between blocks. To allow for recalibration of the visuomotor mapping, we provided visual feedback after the end of the movement and on the way back to the starting position.

Finally, the post-test consisted of six blocks of the combination force field (see pretest). To ensure that the effects of the exposure phase would not be washed out too quickly, we alternated the combination force fields with blocks of the force field that participants had experienced in the exposure phase (velocity- or position-dependent force field). The blocks were identical to those in the previous phases of the experiment and were counterbalanced for direction. That is, a clockwise combination force field was equally, often preceded by a clockwise as well as by a counter-clockwise position/velocity-dependent force field. This allowed us to distinguish the contribution of structural learning (which should be identical for the two directions) and savings for a certain direction (which should only be present if the direction of the immediately preceding force field was identical to the following one).

Experiment 2.

In experiment 2, we tested the idea that structural learning would not only change the adaptation of feedforward commands but also feedback control. For this, we used exactly the same exposure procedure as in experiment 1 with repeated adaptation to a position- or velocity-dependent force field (on separate days). However, in the pre- and post-test, instead of probing the adaptation to a combination force field, we presented targets either ±7° or ±14° from straight ahead (0°). A third of the trials at each angle was chosen randomly as channel trials, during which the hand was forced to deviate from the intended movement direction. This meant that subjects could not change their feedforward command in expectation that they may get a channel. The reaction force against the channel could be taken as a measurement of the feedback corrective response to the perturbation. During these trials, the visual cursor feedback was rotated around the start position so that it moved directly to the presented target. To allow for a strong comparison, the direction of the targets was chosen so that the force response would match the channel force that participants exerted when adapting (and de-adapting) to the combination force field in experiment 1. Specifically, we chose 7° targets to produce a compensatory force, which would match the magnitude of the force produced in the third channel trial of experiment 1, and 14° targets to match the fourth channel trial in experiment 1.

Experiment 3.

In experiment 3, we tested whether the structural learning observed in the first two experiments resulted from the same or from different mechanisms. We used the fact that the temporal consistency of a force field during the exposure phase influences the strength of the adaptive response to a later perturbation (Gonzalez-Castro et al. 2008). We hypothesized that adaptation to a temporally consistent force field would lead to structural learning in feedforward adaptation. In contrast, a temporally inconsistent force field leads to large movement error but to small adaptive changes, as it is continually changing. This force field should therefore preferentially modulate the feedback response.

We used a similar design as in the previous experiments. In experiment 3, however, we exposed participants only to position-dependent force fields, which could either be consistent or inconsistent. In one session, participants experienced a consistent force field. During each of these exposure blocks (see Fig. 6A), participants performed 25 trials in the following order: one null, one channel, 12 force field, one channel, and 10 null. The direction of the force field again alternated between blocks. In the other session, participants were exposed to an inconsistent force field. We used exactly the same numbers of null, channel, and force field (to the left and right) trials but randomized the sequence of the trials until the correlation of the force-field direction of neighboring trials was below −0.3 (Gonzalez-Castro et al. 2008). This resulted in an effective lag-1 correlation of −0.37 for the inconsistent compared with 0.8 for the consistent force-field blocks (see Fig. 6A). The sequence of the consistent and inconsistent session was counterbalanced across participants.

Fig. 6.

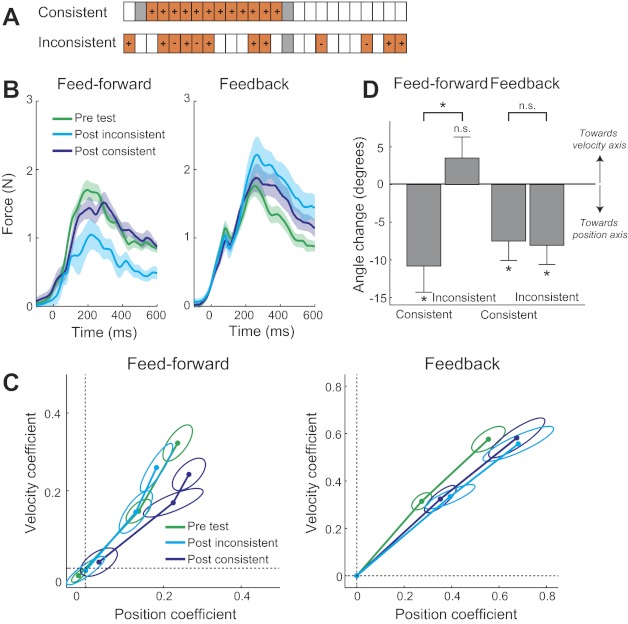
Experiment 3 shows dissociation of structural learning in feedforward and feedback control, depending on the temporal consistency of the exposure phase. A: the exposure blocks consisted of trials with a position-dependent force field (orange), whose direction (+ or −) was consistent over 12 trials or inconsistent, resulting in a negative lag-1 autocorrelation. Channel trials (gray) were interspersed randomly. Participants were tested both on adaptation to a combination force field (feedforward control) and reaction to titled channels (feedback control). B: average force trace exerted in the channel for the pretest (green), post-test after inconsistent exposure (light blue), and post-test after consistent exposure (dark blue) in the feedforward and feedback conditions. C: the regression coefficients, presented as in Figs. 4B and 5C, indicated a change in response toward a position-dependent force field. D: the change in the angle in coefficient space from pretest to post-test indicates structural learning. A negative number indicates a change of the angle toward the position axis. For feedforward adaptation, a modulation toward the position-dependent force field was only found for the consistent force field. For feedback control, modulation is found for both cases. There was a significant interaction of consistency and block type (*P < 0.05); n.s., not significant.

In the pre- and post-test, we tested both feedforward adaptation to a combination force field as well as the feedback response to randomly presented 0° channels when reaching to tilted targets. Hence, the six pretest blocks consisted of 24 trials, with 12 for the adaptation to the combination force field and 12 for reaching to tilted targets. The 12 trials of the adaptation to the combination force field were made up of: one null, one channel, one force field, one channel, two force fields, one channel, and finally, five null trials. In the remaining 12 trials, targets were presented randomly at 0° (four trials), ±7° (four trials), or ±14° (four trials) from straight ahead. For 25% randomly selected trials of each of these conditions, the hand movement was constrained by a 0° channel (as in experiment 2). We counterbalanced the order of these combined blocks, such that half of the subjects performed blocks for testing the feedforward adaptation before blocks for testing the feedback response, with the sequence reversed for the other half. In the post-test phase, we alternated the pure force field and the combination force field/tilted channel blocks following the same pattern as in the previous two experiments.

Analysis.

For all three experiments, we were primarily interested in the force with which participants pressed into the force channel. To quantify the strength and time course of the force responses, we regressed the x-force (F_X) of each individual trial from 300 ms before movement start until movement end against the y-position (P_Y) and the y-velocity (V_Y) of the same trial: F_x − F̄ = b₁s₁P_y + b₂s₂V_y + ϵ. Before the regression, we subtracted a common baseline (F̄) from each trial, which was calculated from the average force profile of the channel trials, where the target was at 0°, and the channel forced the hand on a 0° trajectory. These trials came from the practice blocks, the pre-exposure channels for the tilted target experiments, and the pre-adaptation and postwashout channels in the combination forcefield experiments. The position and velocity traces were scaled by factors s₁ (0.225 N/cm) and s₂ (0.075 N/cm) to convert them into units of force. This multiple regression model therefore did not contain an intercept. The velocity and position traces were scaled, such that the two resultant regression coefficients (b₁ and b₂) expressed the adaptation relative to the strength of the position- and velocity-dependent force fields. Therefore, a regression coefficient of one indicates a force that is exactly equal and opposite to the imposed force field; i.e., it implies that the system fully adapted to the force field. As there was no significant difference between the left- and right-acting force fields, we sign-reversed the regression coefficients for leftward force fields and then averaged over the left/right trials of the same condition. These regression coefficients are plotted throughout the paper in (position, velocity) coefficient space. The origin represents no adaptive response; full adaptation to the pure velocity- or position-dependent force fields would be evidenced by position/velocity regression coefficients of (0,1) and (1,0), whereas full adaptation to the combination force field would correspond to regression coefficients of (0.5,0.5). In polar coordinates, the radius of the point defined by the regression coefficients indicates the size of the response, whereas the angle determines the balance between position- and velocity-dependent components. We quantified changes from pre- to post-test by calculating the difference in the angles. This was done for the third and fourth channel trials in experiment 1, both 7° and 14° channels in experiment 2, and the third channel trial for the feedforward case and 7° targets for the feedback case in experiment 3.

RESULTS

Structural learning of feedforward motor commands.

In the first experiment, we tested whether repeated exposure to a position- or velocity-dependent force field modulates the internal structural assumption that the motor system has about the forces acting on the arm during a perturbation. This hypothesis makes two predictions: first, repeated adaptation to a single type of force field (position- or velocity-dependent) should allow participants to adapt faster and more directly to the same type of force field. Secondly, we predicted that the exposure should bias the adaption to a different type of force field (combination between position- and velocity-dependent) toward the temporal shape of the field experienced in the exposure phase.

To test the first prediction, we examined the structural learning in the adaptation to the exposure force field. For this analysis, we pooled the data from the adaptation phases across experiments 1 and 2 (n = 23). The force traces were regressed against position and velocity (see materials and methods) and the resulting regression coefficients plotted in coefficient space. A purely position-dependent force trace would have the temporal shape of the y-position of a movement (Fig. 2A), and a purely velocity-dependent force trace would look like the y-velocity. In coefficient space, such a position-dependent response would lie on the x-axis and a velocity-dependent response on the y-axis.

Our data, however, shows that when exposed to two trials of a position-dependent force field, participants produced the appropriate position-dependent force but also an additional velocity-dependent component [t(22) = 20.348, P < 0.001]. The converse was true after two trials of a velocity-dependent force field [t(22) = 8.198, P < 0.001] (Sing et al. 2009).

Structural learning of the respective temporal shape of the force field should allow participants to adapt faster and more directly to the appropriate type of force field. This should be the case despite the fact that the force field alternated direction from block to block. Because each participant completed 14 adaptation blocks, we could investigate how the adaptation of these force fields changed across the course of the experiment. For the position-dependent force field, channel trials were significantly more biased toward the position component during the last third of the experiment compared with the first third of the experiment. To quantify the balance between position- and velocity-dependent adaptation, we calculated the angle of the second channel trial in coefficient space. From the beginning to the end of the experiment, the angle of the adaptive response changed toward the position axis by 9.17° [Fig. 3; t(22) = 2.662, P = 0.014]. For the velocity-dependent force field, the mean angle tended to change toward the velocity axis by 11.46°, although this effect was not statistically significant [t(22) = −1.760, P = 0.092]. Thus our results show that there is a measurable effect of structural learning, such that after repeated exposure to a force field, this type of force field is easier/quicker to learn. This effect cannot be due to savings of the just previously experienced force field, as the direction of the force perturbation alternated from adaptation run to adaptation run.

Fig. 3.

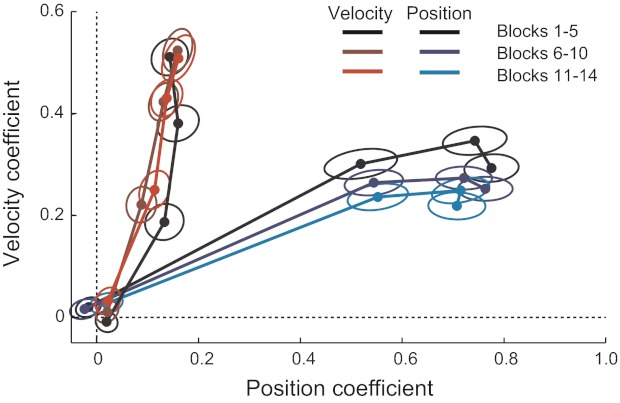
Change in the adaptation to a pure position- and velocity-dependent force field in experiments 1 and 2. Each point indicates the shape of the force response in a channel trial plotted in coefficient space. The evolution of learning after 0, 2, 6, and 10 trials of the exposure to a force field is shown. As the experiment progressed, the initial response became more position dependent and less velocity dependent. This demonstrates the effect of structural learning, such that once they experience a position-dependent force field for the first time, subsequent adaptation to such a force field was faster and more direct. No significant effect was observed for the velocity-dependent force field.

To test the second prediction, we analyzed participants' responses to a combination force field before and after exposure to either velocity- or position-dependent force fields. We predicted that after exposure to a position-dependent force field, the learning of a combination force field (independent of the particular direction) should show a larger position-dependent component (Fig. 1). In turn, after exposure to a velocity-dependent force field, the initial adaptive response should show a larger velocity-dependent component.

The forces that participants produced in the channel trials during adaptation to the combination force field are shown in Fig. 4A. The force traces were clearly modulated by the prior exposure to different types of force fields. After experiencing a position-dependent force field, participants exerted more force against the channel at the end of the movement, consistent with what they learned during the exposure phase. These changes can be seen clearly in the traces in Fig. 4D, which show the difference between the pre- and postchannel forces in the velocity and position conditions. After exposure to the velocity-dependent force field, participants exerted more force in the middle of the movement, consistent with what was learned in adapting to the velocity-dependent force field. The regression coefficients of the adaptation response (Fig. 4B) show that the initial adaptive response was changed by the force field experienced during the exposure phase. The change in the angle in coefficient space reflects the modulation seen in the force traces. After adaptation to a position-dependent force field, the line is more directed toward the position axis and after a velocity-dependent force field, more toward the velocity axis. To quantify the change of the initial adaptation response, we calculated the change in angle from pretest to post-test, averaged over the third and fourth channel trials. This analysis indicated that there was indeed a significant change after experiencing a position-dependent force field [t(11) = 6.632, P < 0.001] of −10.89°. For the velocity-dependent force field, the change (−0.57°) was not significant [t(11) = −0.347, P = 0.735]. However, the directional change in the two exposure conditions was significantly different from each other [t(11) = 5.842, P < 0.001]. Thus as hypothesized, the adaptive response to a combination force field can be modulated by repeatedly experiencing a force field with a particular temporal shape.

Fig. 4.

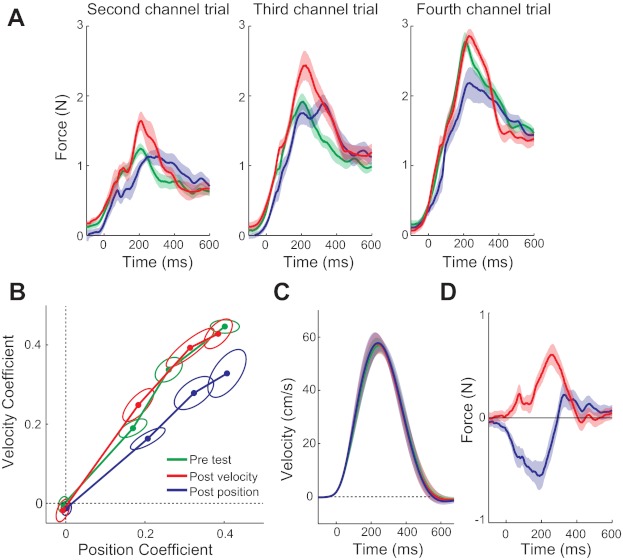
Results of experiment 1: adaptation to the combination force field before and after exposure to either a position- or a velocity-dependent force field. The channel response was measured before adaptation and at 3 time points during adaptation. A: the force that participants exert in the 2nd, 3rd, and 4th channel trials is shown for the pretest (green), after exposure to a position-dependent force field (blue), and after exposure to a velocity-dependent force field (red). After exposure to a position-dependent force field, participants exert lower forces at peak velocity and relatively higher forces in the end of the movement. After exposure to a velocity-dependent force field, the forces at peak velocity increase, but the forces in the end of the movement decreased. B: the same results plotted in coefficient space. We regressed the force traces against the position and velocity of that trial and plotted the regression coefficients for position (x-axis) against the regression coefficients for velocity (y-axis). Results are flipped and averaged across leftward- and rightward-directed force fields. The 95% confidence ellipses for the mean across participants are shown around each point. C: the velocity trajectories in the direction of movement during channel trials for the 3 conditions are shown, averaged over participants, and the shading indicates the SE across participants. D: the difference between the pre-exposure channel force and the postexposure channel force for the 2 exposure conditions is shown here. The differences have been averaged over channel trials 2–4 and clearly show the structure-specific change in the force exerted in the channel.

We had to consider that the change may not have been caused by structural learning but by the memory for a particular force field experienced immediately before. Such savings in adaptation (Smith et al. 2006; Zarahn et al. 2008) differ from structural learning in that they only facilitate memory of a specific point in coefficient space (i.e., leftward position-dependent force field) rather than a whole submanifold (purely position-dependent forces in general). For blocks where the previous position- or velocity-dependent force field was in the same direction as the combination force field, such savings could indeed produce the observed bias. For blocks in which the two force fields were in opposite directions, however, possible savings should have been overridden through interference from the opposing force field (Krakauer et al. 2005). Therefore, we split our data, depending on whether the direction of the force field changed from the preceding exposure block to the test block. We found that the change in angle in coefficient space remained significantly different between the two exposure conditions, no matter whether the previous block was in the same [t(11) = 5.044, P < 0.001] or opposite [t(11) = 3.609, P = 0.004] direction. Therefore, direction-specific savings could not explain the observed effect alone. In summary, this first experiment demonstrates that prior experience can modulate the feedforward adaptive response to a combination force field by biasing it toward the temporal shape of the force field experienced before.

Structural learning of feedback responses.

In the second experiment, we tested the hypothesis that exposure to a force field also changes the shape of the feedback response to unpredictable positional perturbations. We used a similar design as in experiment 1. However, in the pre- and post-test, participants reached to a target that was randomly presented at 0°, ±7°, and ±14°, and we probed feedback responses by randomly inserting channel trials in which the hand was forced to move in a 0° trajectory (Fig. 5A).

Fig. 5.

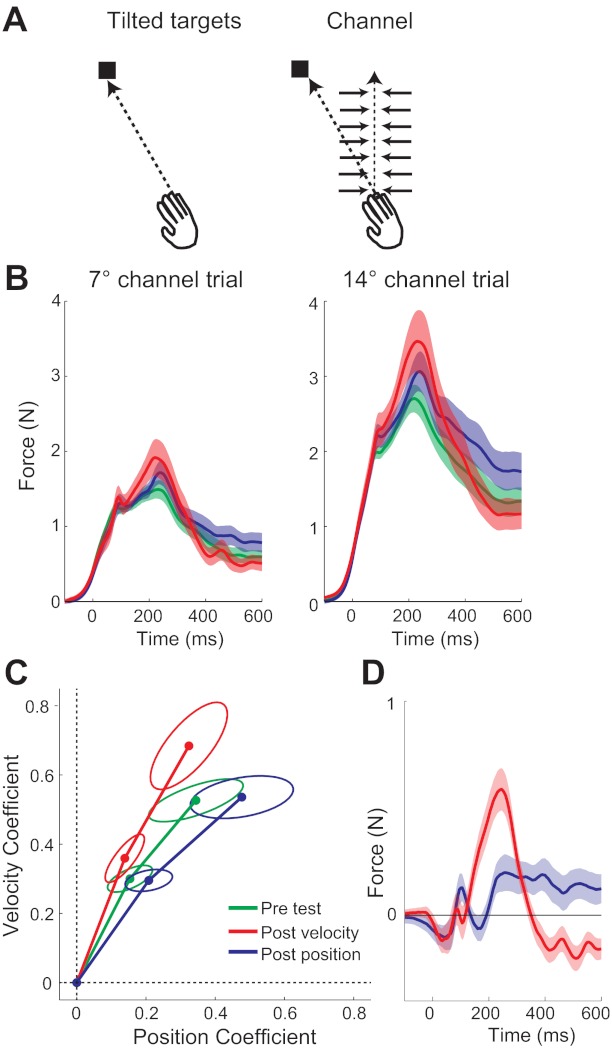
Results from experiment 2. A: we measured channel responses, caused by feedback mechanisms reacting to the force channel, which is at an angle to the intended movement direction. This was achieved by letting people reach to a target that was displaced laterally from straight ahead. On channel trials, the target still appeared at an eccentric angle, while the hand was constrained to move straight ahead in a force channel. During these channel trials, the cursor was rotated to move directly to the target. B: lateral force exerted into the channel for the 7° and 14° channel trials showed stronger position components after exposure to a position-dependent force field (blue trace) and stronger velocity components after exposure to a velocity-dependent force field (red). The force profile in the pretest phase (green trace) had the same stereotypical position/velocity profile. C: regression coefficients from the same time series show the same changes, with the lines shifting toward the axis of the force field experienced in the exposure phase. The ellipses indicate the 95% confidence interval for the between-participants mean. D: the differences between the pre-exposure channel force and the postexposure channel force for the 2 exposure conditions are shown here. These have been averaged over the 7° and 14° channels, and once more, the structure-specific change in the channel force can be seen clearly.

The force response of participants in the channel showed a similar mixture of position and velocity as seen for the adaptation to a combination force field (Fig. 5B). The force profile in the pretest phase had the same stereotypical position/velocity profile. Furthermore, the magnitude of the pretest 14° response in coefficient space (0.34,0.53) roughly matched the coefficients in the fourth channel trial of adaptation in experiment 1 (0.43,0.44). During the post-test, the overall size of the force response was increased. This can be seen in coefficient space (Fig. 5C), and the response to the 14° channel trials were further from the origin than in the pretest, both after exposure to a position [t(10) = −2.639, P = 0.025]- and a velocity [t(10) = 3.276, P = 0.008]-dependent force field. Thus over the course of the experiment, participants increased how much they responded to an unpredictable positional perturbation.

Importantly, we found that the temporal shape of the forces that participants exerted in the channel trials was modulated by the type of force field that they had experienced previously. Following adaptation to the position-dependent force field, we found a relative reduction in the velocity-dependent part and an increase in the position-dependent part of the feedback response. Conversely, after velocity-dependent force-field exposure, there was a relative increase in the velocity-dependent peak and a decrease in the position-dependent component. These effects can once more be seen when the responses are plotted in coefficient space (Fig. 5C). The post-test lines in coefficient space were rotated toward the axis of the force field experienced previously, as we had seen in experiment 1. We quantified these changes in coefficient space by the angle between the pre- and the post-test points, averaged over the 7° and 14° channels. The angle of the response changed significantly, both after a position-dependent force field −9.2° [toward the position axis; t(10) = 5.138, P < 0.001] and by +5.7° (toward the velocity axis) after a velocity-dependent force field [t(10) = −3.588, P = 0.005]. Once again, these changes were also significantly different across the two exposure conditions [t(10) = 9.074, P < 0.001]. This change can also be seen in the difference force traces (Fig. 5D), where after a position-dependent exposure, participants exerted more force at the end of the trial and after a velocity-dependent exposure, more in the middle of the trial.

To summarize, experiment 2 showed that the temporal shape of the feedback response to a channel trial deviating the hand from a target could also be shaped by prior exposure to a velocity- and position-dependent force field.

Do feedforward and feedback responses share the same mechanism?

Given that we observed similar structural learning effects for both feedforward and feedback responses, we asked whether these two modulations stem from a change of a single internal representation. This single structural assumption (or prior belief) about the shape of force perturbations would then shape both types of responses (Wagner and Smith 2008). Alternatively, the structural assumptions for feedforward and feedback control may be partly separate, and each of them may be modified by different signals from the environment.

Previous research has shown that feedforward adaptation rates increase in consistent environments, in which the perturbation on trial N is positively correlated with the perturbation on trial N-1 (Burge et al. 2008). Similarly, feedforward adaptation rates decrease when adjacent trials are negatively correlated (Gonzalez-Castro et al. 2008). We hypothesized that the temporal characteristics of the perturbation should not only influence the size of the adaptation gain but also how much structural learning it would induce. Specifically, we predicted that the direction of the feedforward adaptation should be more influenced by a consistent than by an inconsistent (or slightly anticonsistent) force field. In contrast, the relative direction of feedback responses should be modulated by perturbations in the movement, independent of whether these are consistent or whether they change direction randomly between trials, as both would necessitate a feedback correction.

We therefore exposed participants to a position-dependent force field with different temporal characteristics and then tested feedforward adaptation to the combination force field and feedback responses in the tilted channels. The exposure phase on one session was consistent, such that the participants experienced the force field in the same direction for 12 trials. In the other session, the force field was inconsistent, such that each trial was randomly assigned to a rightward force field, a leftward force field, or a null field (Fig. 6A).

We predicted that the consistent exposure would modulate both responses as in experiments 1 and 2, whereas the inconsistent would mostly modulate only the feedback response. As in the previous two experiments, we regressed the channel forces (Fig. 6B) against position and velocity and plotted the regression coefficients in coefficient space (Fig. 6C). Following consistent force-field exposure, the channel responses for adaptation to a combination force field were modulated toward the position axis by −10.9° [t(10) = 3.110, P = 0.011]. A similar −7.5° change of the angle of the pretest line to the post-test line in coefficient space was observed for feedback responses [t(10) = 2.918, P = 0.015; Fig. 6C]. This change can also be seen in the average force trace as an increase of the late component (Fig. 6B). These results therefore replicate the findings of experiments 1 and 2, demonstrating structural learning effects in both domains after exposure to a consistent force field.

When the exposure phase was temporally inconsistent, no modulation of feedforward adaptation was found, with the post-test line in coefficient space (Fig. 6C) lying almost exactly on top of the pretest line. The change in angle from pre- to post-test (Fig. 6D) was not significantly different from zero [t(10) = −1.260, P = 0.236]. Furthermore, the pre- to post-test angle change of the inconsistent exposure condition was significantly different than the consistent exposure condition [t(10) = 3.174, P = 0.010]. This indicates that the structural learning in the feedforward adaptation only occurs when the exposure is temporally consistent. In contrast, the change for the feedback response was equally strong (−8.0°) after inconsistent as after consistent exposure; no significant difference between these conditions in the angle change was found [t(10) = −0.265, P = 0.796]. Finally, a two-way ANOVA revealed a significant interaction of condition (consistent or inconsistent exposure) and block type (force field or tilted channels) on the angle change in coefficient space [F(1,10) = 14.484, P = 0.003]. Therefore, our final experiment clearly demonstrates that structural learning mechanisms for feedforward and feedback responses differ in the way that they are influenced by the temporal consistency of the environment.

DISCUSSION

The motor system has prior assumptions about the likely shape of a perturbation. This feature allows the motor system to immediately produce a “best guess” response to any unexpected error. Such structural assumptions can be found for visual motor adaptation, in which the motor system interprets ambiguous errors preferentially as visual rotations (Turnham et al. 2011). Similarly, for dynamic force fields, the motor system has a bias toward forces in which position- and velocity-dependent components act in the same direction (Sing et al. 2009). Here, we show that these priors are not hard wired but can be modulated by repeated exposure to a specific shape of perturbation through a process of structural learning (Braun et al. 2009a, b). Such updating of the structural priors allows the motor system to take into account the statistics of prior perturbations (Astrom 1995; Braun et al. 2010b; Wolpert et al. 2011).

We found that this modulation was independent of whether the preceding force field acted in the same or in a different direction than the tested force field. Therefore, our results cannot be explained by savings in relearning for a single force field (a single point in coefficient space), as such savings can be interfered with through the presentation of the opposite perturbation (Krakauer et al. 2005). Our results, however, would be consistent with a motor system that can show savings for multiple points in coefficient space. Indeed, such mechanisms would be similar to structural learning, where there is “savings” for a whole submanifold in coefficient space.

It is important that the observed modulation occurred during both feedforward adaptation and in feedback corrections. Braun et al. (2009b) showed previously that structural learning effects could be seen both in corrective feedback responses and in feedforward adaptation to three-dimensional (3D) visual rotations during reaching. Furthermore, structural learning has also been shown recently after adaptation to force fields that acted either horizontally or vertically in 3D space (Kobak and Mehring 2012). However, in these studies, the structure was defined by the spatial axis along which the perturbation occurred and could therefore be caused by the general upregulation of the responsiveness of certain muscle groups. Here, we used position- and velocity-dependent force fields and show that structural learning also occurs based on the temporal shape of the perturbation. Our findings demonstrate that the motor system takes advantage of the previously learned temporal structures and applies them to novel perturbations to facilitate adaptation as well as online corrections.

Such structural learning has also been explored in cognitive studies and is referred to as “learning to learn”, in which subjects extract common features during example tasks, leading to facilitation in subsequent learning of similar tasks (Duncan 1960; Griffiths and Tenenbaum 2005; Halford et al. 1998). Learning to learn has also been observed in motor tasks such as a visuomotor rotation task (Welch et al. 1993) and a treadmill task (Mulavara et al. 2009). Hence, such feature extraction may be a universal technique that the brain exploits to facilitate learning (Braun et al. 2009b; Wolpert et al. 2011).

A number of previous studies have shown that the size of feedback responses can be modulated through prior experience. For example, the size of feedback response increases when participants are exposed to large, unpredictable target displacements during movements (Liu and Todorov 2007). Similarly, the exposure to large errors introduced by a force field leads to an increased responsiveness of the system to rapid visual displacements of the cursor (Franklin and Wolpert 2008). Our results indicate that prior experience can also alter the temporal shape of such feedback responses rather than simply change their overall gain: prior exposure to a force field led to a rotation of the response in coefficient space toward the axis of the force field experienced. In contrast, a simple change in the overall gain of the response would only increase the length of the line.

Furthermore, our results demonstrate that the priors for feedforward and feedback control can be modulated—at least partly—independently. We found that the temporal consistency of the exposure phase modulated the two types of responses differentially. It has been shown that exposure to a visual shift with strong, positive autocorrelation (high consistency) increases adaptation rates (Burge et al. 2008). Similarly, force fields, which are anticorrelated from one trial to the next (inconsistent), lead to a reduced adaptive response (Gonzalez-Castro et al. 2008). In contrast, random inconsistent perturbations appear to increase the gain of feedback responses (Liu and Todorov 2007). Here, we show that this difference extends to structural learning of the temporal shape of different responses. For feedforward adaptation, we observed a modulation of the shape of the adaptive response after a consistent, but not after an inconsistent, force field. This suggests that the motor system holds separate priors for perturbations that require adaptive changes compared with corrective responses and that these two are sensitive to signals with different temporal statistics.

Such a view contrasts with models that propose that the motor system uses the feedback response as a template for adaptation of the feedforward motor command (Kawato 1999; Thoroughman and Shadmehr 1999). If this were the case, then a change in the feedback response should lead to a correlated change in the feedforward adaptation. For inconsistent force fields in experiment 3, however, we found a systematic change in the feedback response without an equivalent change in adaptation. These results therefore argue against an obligatory coupling of feedback response and feedforward adaptation but rather imply that the structural assumptions are (at least partially) independent.

The relationship between mechanisms of feedforward and feedback control is still a matter of debate, however. Consistent with our view of partially independent systems is the observation that participants adapt to visual motor rotations at similar speeds whether or not online corrections were allowed (Tseng et al. 2007). The same paper also shows that cerebellar patients are strongly impaired in both online correction and adaption but that the adaptation deficit persists unaltered even if the need for feedback corrections is removed, again arguing for the partial independence of these two processes. Some authors have even proposed that the two cerebral hemispheres may play differential roles in feedforward adaptation and feedback corrections, respectively (Mutha et al. 2011a, b). In contrast, other authors have emphasized that the two share most likely a common neural substrate (Pruszynski et al. 2011; Scott 2004). It has also been shown that feedback mechanisms use knowledge acquired during adaptation of the feedforward response (Wagner and Smith 2008). Furthermore, there are clear correlations between priors that determine the distribution of feedback corrections and the priors that determine the distribution of feedforward adaptation across multiple effectors (White and Diedrichsen 2010).

Being able to learn a separate prior assumption about the shape of perturbations, depending on whether they demand only an immediate feedback response or also subsequent adaption of the feedforward response, may be a good strategy for the motor system. Perturbations that require an adaptive or only a corrective response commonly arise from different sources. Examples of perturbations that require adaption are changes in the biomechanics through fatigue or changes in the visual motor calibration due to a new pair of glasses. These changes are consistent over time. On the other hand, perturbations that merely require an online correction for a single movement are those that arise from random and quickly fluctuating sources. Examples would be the unpredictable forces induced by sudden accelerations of a train, ship, or car while traveling. The temporal shape of such perturbations may be very different from those that indicate longer-lasting changes. Therefore, it seems sensible for the motor system to update two sets of priors, as they may have different origins and require different responses.

In agreement with previous studies, our data demonstrate that the prior assumptions that the motor system uses to respond to perturbations can be modulated by repeated exposure to a perturbation with a specific structure. Hence, the prior assumption is not hard wired but can be updated to reflect the structure of the perturbations experienced (Braun et al. 2009b). This feature allows the motor system to improve its initial response to an error flexibly by exploiting similarities in previously experienced errors. Interestingly, our results indicate that whereas this process happens for both feedforward and feedback responses, it does so, at least partly, independently for the two. This in turn suggests that the motor system can have separate internal assumptions for these responses, reflecting the fact that the two are often driven by perturbations originating from different sources in our environment.

GRANTS

Support for this research was funded by a Bupa Medical Research Grant to N. Yousif and a Biotechnology and Biological Sciences Research Council research grant (BB/E009174/1) to J. Diedrichsen.

DISCLOSURES

The authors declare no potential conflicts of interest, financial or otherwise.

AUTHOR CONTRIBUTIONS

Author contributions: N.Y. and J.D. designed research; N.Y. performed research; N.Y. and J.D. analyzed data; N.Y. and J.D. wrote the paper.