Abstract
The excited state structure of [Cu(1)[(1,10-phenanthroline-N,N’) bis(triphenylphosphine)] cations in their crystalline [BF4] salt has been determined at both 180 and 90K by single-pulse time-resolved synchrotron experiments with the modified polychromatic Laue method. The two independent molecules in the crystal show distortions on MLCT excitation which differ in magnitude and direction, a difference attributed to a pronounced difference in the molecular environment of the two complexes. As the excited states differ, the decay of the emission is bi-exponential with two strongly different lifetimes, the longer lifetime, assigned to the more restricted molecule, becoming more prevalent as the temperature increases. Standard deviations in the current Laue study are very much lower than those achieved in a previous monochromatic study of a Cu(I) 2,9 dimethyl-phenanthroline substituted complex (J. Am. Chem. Soc. 2009, 131, 6566), but the magnitude of the shifts on excitation is similar, indicating that lattice restrictions dominate over the steric effect of the methyl substitution. Above all the study illustrates emphatically that molecules in solids have physical properties different from those of isolated molecules and that their properties depend on the specific molecular environment. This conclusion is relevant for the understanding of the properties of molecular solid state devices which are increasingly used in current technology.
1. Introduction
Electron injection from molecular sensitizers absorbed on semiconductor surfaces to the underlying substrate have become an increasingly important subject due to their relevance for the mode of operation of photovoltaic cells. The precise geometry of the binding modes of the sensitizers to the underlying substrate has now become accessible in the case of Ti/O nanoparticles aligned periodically in the crystalline nanoparticle phase.1-2 As a first step towards time-resolved studies of structural changes occurring on photo-excitation of electron donors absorbed on nanoparticles, we have previously studied the excited state structure of the Cu(I) complex [Cu(I)(2,9-dimethyl 1,10-phenanthroline)(1,2-bis(diphenylphosphino)ethane)][PF6] (1) by monochromatic time-resolved methods.3 The complex of which the changes on excitation are described in the current article, [Cu(1)[(1,10-phenanthroline-N,N’) bis(triphenylphosphine) [BF4] (2), lacks the dimethyl substitution which interferes with the expected flattening, and is therefore expected to undergo a larger rearrangement upon formal oxidation of the Cu(I) atom on photo-induced metal-to-ligand-charge-transfer (MLCT).4-6 Cu(I) based chromophores have been proposed as promising and economically advantageous photosensitizers in photovoltaic cells.7
The monochromatic methods employed in our earlier studies suffer from two pronounced disadvantages. They require use of a stroboscopic technique in which a diffraction from a large number of pump-probe cycles is accumulated on the detector. This means that the excited state structure is recorded at a considerably higher temperature than the ground state structure due to the rapid sequence of laser pulses to which the sample crystal must be exposed. In the polychromatic Laue technique this is not the case because of the higher photon flux resulting from the increase in bandwidth. As a result with the ‘pink’ Laue method (ΔE/E ~8%) a diffraction pattern can be collected from a single, or at most a few 70 ps-length X-ray pulses. We have redesigned the Laue method for time-resolved applications to eliminate many of its conventional disadvantages.8 The result is a significant decrease in the excited state positional standard deviations of the more strongly scattering atoms from typically 0.02-0.05 Å in the most recent monochromatic studies to 0.006-0.008Å achieved in our recent Laue experiments.8
In the time-resolved Laue study of (2) described here a spatial resolution of 0.002-0.004Å is achieved at 90K for the excited state Cu atoms and 0.004-0.007Å for the lighter atoms in the excited-state structure. Like (1), (2) crystallizes with two independent molecules in the asymmetric unit, which allows analysis of the effect of the crystalline environment on the molecular changes.
2. Experimental and theoretical methods
2.1 Data collection
Time-resolved intensity data were collected at the 14-ID beamline at the BioCARS station at the Advanced Photon Source at an undulator setting of 15keV. To select the optimal laser power short 10° φ scans were performed at different laser powers. Correlation plots between the resulting response ratios are shown in Fig. 1. As expected, an increase in laser power leads to a larger response. Full data collections were performed at two different temperatures. In the first, at 180K, 35 ps pulses from a Ti:sapphire laser tuned to a wavelength of 390 nm were used as the pump source with a pump-probe delay of 100 ps. Laser power varied between 0.6 and 1.1 mJ/mm2/pulse. The second set was performed at 90 K with 4 ns pulses of a Nd:YAG laser tuned to a wavelength of 420nm with a pump-probe delay time of 2 ns and a laser power of 1.6 mJ/mm2/pulse. The longer delay time causes a spot extension on the ON frames9 which is effectively taken care of by a new non-profile fitting spot-integration procedure to be described elsewhere. To maximize the number of weak reflections observed in both sets, the pump-probe cycle was repeated three times for each frame before detector read-out. Δφ values of 1° and 2° were used. Laser-OFF and Laser-ON frames were collected in immediate succession to minimize the effect of long range fluctuations in the beam’s position or intensity. The ON/OFF pump-probe cycle was repeated ten times for each frame to allow subsequent statistical background estimation and filtering of the intensities. Further details are as described in reference 8. Specific information on each of the 12 data sets collected is given in Table S1.
Fig. 1.
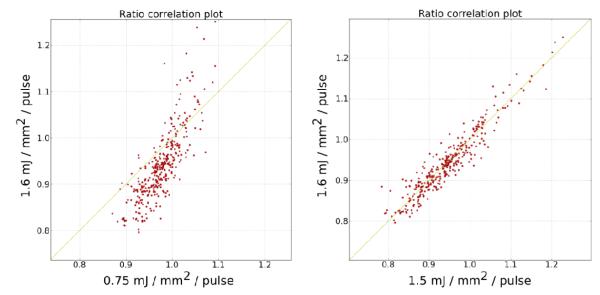
Correlation plots between the ratios of 10° data sets at different laser exposure collected at 90K. The yellow line has a 45° slope. Only data observed on all 10 repeated frames were included.
2.2 Data processing
The intensities from the Laue experiment were integrated and indexed by the newly developed LaueUtil toolkit,10 which includes both rapid orientation matrix determination suitable for intermediate size unit cell crystals and the novel spot integration technique. The integration method does not use profile-fitting techniques, nor does it require initial knowledge of the sample’s cell dimensions as it is based on statistical analysis of the intensities of all the pixels on successive frames in the φ scans. hkl indices are assigned subsequently using the orientation matrix from LaueUtil. After statistical analysis of the ten repeated ON/OFF pair measurements of each frame, ratios were averaged with the program SORTAV.11 Details are given in Table S1. Results of different runs were examined by correlation similar to those depicted in Fig. 1.
Crystallographic information on (2) is summarized in Table 1. Cell dimensions did not change as a result of the laser exposure, a result attributed to the low conversion percentages. Bond distances and selected angles are listed in Table S2.
Table 1.
Crystallographic information for [Cu(I)(phen)(PPh3)2][BF4] (2). First line 180K, second line 90K.
| Top line 180K. Lower line 90K. | |||||||
|---|---|---|---|---|---|---|---|
| Space group |
a | b | c | α | β | γ | V |
| P-1, Z′=2 | 17.472(2) | 19.393(2) | 12.834(1) | 80.579(2 | 84.560(2) | 106.466(2) | 4067.8 (6) |
| P-1, Z′=2 | 17.356(1) | 19.263(1) | 12.773(1) | 80.452(2) | 84.386(2) | 106.019(2) | 4000.9(5) |
2.3 Collection of monochromatic data
The RATIO method12 uses monochromatic intensities for reference. They are multiplied by the synchrotron-determined ON/OFF ratios to obtain reliable ION intensities, used for generation of photodifference maps such as shown in Fig 2. The monochromatic data were collected with Mo K radiation on a rotating anode generator equipped with a Bruker-Apex II area detector. At both temperatures five omega scans were collected each covering a 180° range with a step size of 0.5°. Bruker software was used for data collection and integration,13 while the data were merged with the program SORTAV.11 Refinements were performed with SHELX14 combined with a WinGX15 graphical overlay. Crystallographic information in listed Table 1.
Fig. 2.
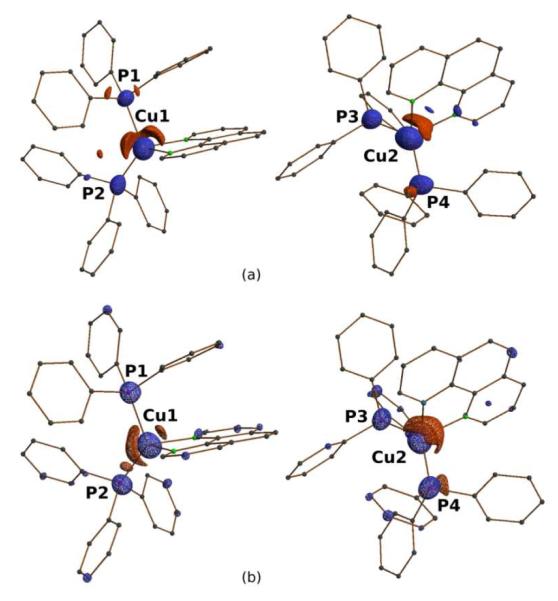
Photodifference maps with isosurfaces of ±0.25 eÅ−3 (red positive, blue negative) at 180K (a) and 90K (b). Cu(1) and Cu(2) are on the right and the left side of each of the graphs respectively. Calculated with XDGRAPH of the XD program set.21
2.4 Measurement of emission lifetimes at different temperatures
Luminescence measurements were performed on a ~150×200×400 ×m single crystal of (2) in a Displex cryogenic cooler equipped with a shroud specially constructed for low-temperature emission spectroscopy. A vacuum chamber with quartz windows attached to the cryostat was evacuated to ~10−7 bar. The crystal was cooled to the desired temperature and excited with λex=366 nm light from a N2-dye laser pulses with a 1 Hz repeat frequency. The emission spectrum was passed through an Oriel grating monochromator, recorded with a Hamamatsu photomultiplier tube and processed by a DSO-2102S computer-based digital oscilloscope with 100MHz sampling rate.
2.5 Theoretical calculations
Gaussian0916 was used for all reported calculations. Isolated molecule QM calculations were performed with a number of basis sets and with both the BP86 and B3LYP functionals. Cartesian xyz coordinate files were generated using Mercury 2.3.17 C-H bond lengths were extended to the standard lengths of 1.083 Å and 1.074 Å for aromatic and aliphatic carbons respectively, as derived from neutron diffraction experiments.18 QM/MM calculations were performed with the ONIOM module of Gaussian09, both without and with embedded charges on the crystalline shell surrounding the central molecule. The structure of the shell was kept fixed at the geometry as determined by X-ray diffraction. The UFF (Universal Force Field)19 force field as available in Gaussian09 was used for the MM region. As the surrounding shell was not varied in the calculation only the non-bonded interaction parameters of the atoms lining the cavity affect the results of the calculation. Hirshfeld charges from LANL2DZ-BP86 calculations were used for the Coulombic interactions of the surrounding shell with the central molecule in the QM/MM calculations.
3. Photocrystallographic Analysis
3.1 Photodifference maps
As Fourier maps must be based on datasets of maximum completeness to be meaningful, merging of all collected data sets is indicated. To accomplish this individual sets were scaled according to the average values of the response ratios ∣<η>∣ in each set, where η is defined as (ION-IOFF)/IOFF8,20. The photodifference maps based on all independent reflections from the data sets collected at each of the temperatures are shown in Fig. 2. Isosurfaces are drawn at ±0.25 e/Å3 to highlight the Cu displacements. The agreement between the 180K and the 90K results supports the validity of the experimental methods used. At both temperatures a displacement of the Cu(1) atom roughly within the Cu-P-P plane and away from its associated phenanthroline ligand is evident, as well as a pronounced displacement of Cu(2) towards the phenanthroline ligand to which it is ligated. The two independent molecules clearly show a different response to the excitation.
3.2 Least-squares refinement
The excites state structures were refined with the program LASER, which is based on the refinement of the response to light exposure, defined as η = (ION-IOFF)/IOFF=RON/OFF-1.22 The refinement procedure is based on a random spatial distribution of the excited state species in the crystal. Formation of domains sufficiently large to change the scattering formalism would lead to very different calculated intensities and in some cases a second set of reflections.23 No evidence for domain formation was found in the current study or any of our previous studies. The LASER program allows for simultaneous refinement of up to six data sets on the same structure. The variables in the refinement are, for each data set, the temperature scale factor, and the excited-state conversion percentage, plus the excited state structural parameters, including rigid body motions, for the combined data. The program calculates agreement-factors suitable for refinements based on the response ratios.24 Only data with ∣η∣/σ(η)>1 were used in the current refinement. The detailed refinement strategy is described in the supplementary material. Agreement factors and other information on the refinement are listed in Table S3.
3.3 Analysis of temperature differences due to laser exposure
An initial estimate of the temperature increase due to the laser exposure can be obtained from a photo-Wilson plot.23,25 The plot for the merged data collected at 90K is shown in Fig. 3.
Fig. 3.
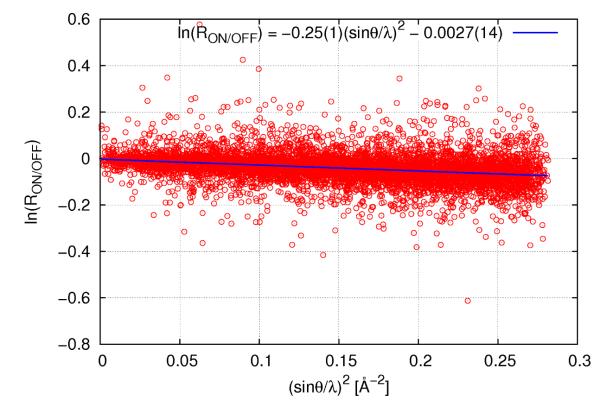
Photo-Wilson plot for 90 K data.
The slope of the plot corresponds to twice the isotropic increase of the average Debye-Waller factor 2 ΔB. The slope in fig. 3 corresponds to ΔB =0.125Å2 from which an estimate of the relative temperature increase, expressed as a temperature scale factor kB, can be obtained. kB is included as a variable in the refinement procedure with the program LASER,22 which leads to a second estimate of the temperature increase. Observed and least-squares refined values of kB for each of the 6 data sets collected at each temperature, listed in Table 2, agree well. The refined values tend to be somewhat larger, especially at 180K. The difference is attributed to the omission of the reflections with ∣η∣/σ(η)<1 from the least squares refinement, while the Photo-Wilson plots are based on all observed reflections. As shown in Fig. S1, the temperature scale factors correlate with the excited state occupancy from the least-squares refinement, as expected as both are a result of the laser exposure. Both sets indicate the temperature increase to be larger at 90K than at 180K, possibly due to a temperature dependence of the thermal conductivity of the crystals.26 Even at 90K the increase in temperature in the classical limit (B proportional to T) is not more than about 10°, except for data set 90-1.
Table 2.
Experimental and refined temperature scale factors, average response ratios and refined excited state occupancies for each of the 12 data sets collected at 180K and 90K.
| Temperature scale factor refinements | |||||
|---|---|---|---|---|---|
| kB Wilson Plot | <∣η_all∣> | kB refined | <∣ η_laser∣>* | ES- occupancy |
|
| 180-1 | 1.013 | 0.025 | 1.032 | 0.044 | 0.014 |
| 180-2 | 1.014 | 0.028 | 1.033 | 0.047 | 0.019 |
| 180-3 | 1.061 | 0.048 | 1.063 | 0.064 | 0.035 |
| 180-4 | 1.034 | 0.037 | 1.050 | 0.054 | 0.025 |
| 180-5 | 1.055 | 0.042 | 1.063 | 0.064 | 0.044 |
| 180-6 | 1.052 | 0.049 | 1.067 | 0.072 | 0.035 |
| 90-1 | 1.235 | 0.048 | 1.193 | 0.092 | 0.071 |
| 90-2 | 1.125 | 0.043 | 1.138 | 0.072 | 0.051 |
| 90-3 | 1.098 | 0.040 | 1.137 | 0.073 | 0.050 |
| 90-4 | 1.198 | 0.048 | 1.186 | 0.092 | 0.051 |
| 90-5 | 1.133 | 0.042 | 1.165 | 0.082 | 0.053 |
| 90-6 | 1.085 | 0.033 | 1.087 | 0.059 | 0.042 |
with ∣η∣/σ(η)>1
4. Structural response to excitation
Absolute values of the maximal shifts of the core Cu, P and N atoms on excitation, listed in Table 3, range up to 0.140(13) Å for P at 180K and 0.098(4) Å for Cu at 90K. Except for Cu(2) the shifts are considerably larger at the higher temperature at which the crystals are softer, as evident also from the increase in the Atomic Displacement Parameters.
Table 3.
Absolute values of the shift of the Cu, P and N atoms on excitation (in Å*10−3). Top: 180K; Lower: 90K.
| Cu(1) | P(1) | P(2) | N(1) | N(2) | Cu(2) | P(3) | P(4) | N(3) | N(4) |
|---|---|---|---|---|---|---|---|---|---|
| 37(5) | 64(13) | 96(11) | 77(7) | 79(6) | 94(5)) | 93(13)) | 140(13) | 71(6) | 56(6) |
| 27(3) | 29 (6) | 65(6) | 43(5) | 28(4) | 98(4) | 57(6) | 75(7) | 64(5) | 42(5) |
Specific information on the Cu coordination environment is provided by the changes in bond lengths and dihedral angles at the Cu atoms. Bond length changes are summarized in Table 4. In accordance with the maxima in the photodifference map, the changes at Cu differ drastically for the two independent molecules. For Cu(2) in the less confined molecule (labeled B) the Cu-N bonds shorten by ~0.04Å, whereas the Cu-P distances lengthen significantly, though the shifts are considerably smaller than calculated for the isolated molecule as further discussed in the next section. For Cu(1) (in the molecule labeled A) the changes in the bond lengths on excitation from the least-squares refinement are not significant, although the individual atom shifts are significant and clearly visible in the photodifference maps in a direction opposite to those at Cu(2). Bond-angle changes around Cu, listed in the last two rows of table 4, are generally significant, but again much larger for Cu(2).
Table 4.
Experimental changes in Cu coordination-bond lengths (Å) and angles (°) on excitation. Top:180K; Lower: 90K. Significant changes in bold.
| GS bond lengths/angles (Å, °) | Change on excitation | ||||||
|---|---|---|---|---|---|---|---|
| Cu(1)-P(1) | 2.300(1) 2.2924(2) |
Cu(1)-P(2) | 2.246(1) 2.2406(2) |
Cu(1)-P(1) | 0.029(12) −0.012(5) |
Cu(1)-P(2) | −0.016(16) 0.009(7) |
| Cu(2)-P(3) | 2.238(1) 2.2334(2) |
Cu(2)-P(4) | 2.235(1) 2.2288(2) |
Cu(2)-P(3) | −0.017(14) 0.014(6) |
Cu(2)-P(4) |
0.038(14)
0.038(6) |
| Cu(1)-N(1) | 2.078(2) 2.0738(2) |
Cu(1)-N(2) | 2.136(2) 2.1306(2) |
Cu(1)-N(1) | −0.021(9) −0.010(5) |
Cu(1)-N(2) | −0.022(9) −0.010(5) |
| Cu(2)-N(3) | 2.078(2) 2.0731(2) |
Cu(2)-N(4) | 2.075(2) 2.0695(2) |
Cu(2)-N(3) |
−0.039(8)
−0.043(6) |
Cu(2)-N(4) |
−0.037(7)
−0.042(6) |
| P2-Cu1-P1 | 124.835(1) 125.835(1) |
P3-Cu2-P4 | 128.280(1) 127.961(1) |
P2-Cu1-P1 |
−1.670(8)
−1.010(3) |
P3-Cu2-P4 |
−6.598(9))
−4.700(4) |
| N(1)- Cu(1)-N(2) |
81.102(1) 81.213(1) |
N3- Cu2-N4 | 80.533(1) 80.676(1) |
N1-Cu1-N2 |
1.001(7)
0.447(3) |
N3-Cu2-N4 |
1.838(13)
2.071(4) |
The earlier results from a monochromatic time-resolved study on the Cu(I)(dmp)(dmpe)+ 1) 3 agree qualitatively on the elongation of the Cu-P bonds, but are not conclusive on the Cu-N distance changes due to much poorer accuracy than achieved in the current study.
The distortion of the Cu-coordination environment from perfect mm symmetry, with the mirror planes coinciding with the P-Cu-P and N-Cu-N planes, can be quantified by the flattening, rocking and wagging distortions, as described by Dobson et al.27 and illustrated in Fig. 4. The coordination environments of the Cu(1) and Cu(2) centers are already quite distinct in the ground state and respond differently to the electronic excitation as described in Table 5. The flattening distortion, expected because of the formal oxidation of the Cu(I) atom on excitation, is barely observable for Cu(1) but significant for Cu(2). However, as described in the next section, both distortions are much smaller than calculated for the isolated molecule and expected in solution. As observed in the 2,9 methyl substituted Cu(I)(dmp)(dmpe)+ cation (1) rocking and wagging distortions are also much less than those calculated for the isolated molecule.
Fig. 4.
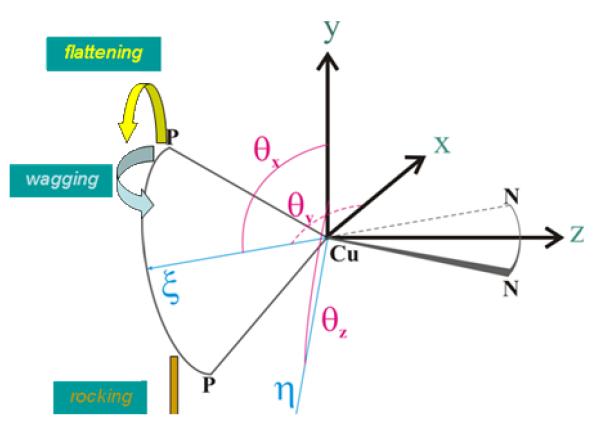
Definition of the flattening, wagging and rocking distortions of the Cu(I) coordination sphere.
Table 5.
Distortion angles as defined in Fig. 4. Top 180K; lower 90K. GS=ground state; ES=excited state. Significant changes on excitation are in bold.
| Cu(1)-GS | Cu(1)-ES | Δ | Cu(2)-GS | Cu(2)-ES | Δ | |
|---|---|---|---|---|---|---|
| Rocking- angle |
75.16(1) 75.22(1) |
74.1(6) 75.6(3) |
1.1(6) −0.4(3) |
88.85(1) 88.72(1) |
90.2(7) 89.6(3) |
−1.4(7) −0.9(3) |
| Wagging- angle |
90.77(1) 91.39(1) |
93.6(7) 91.4(3) |
2.8(7) 0.0(3) |
94.66(1) 95.33(1) |
93.1(8) 94.3(4) |
−1.6(8) −1.0(4) |
| Flattening- angle |
96.60(1) 97.25(1) |
99.7(6) 98.1(3) |
3.1(6) 0.9(3) |
96.75(1) 96.95(1) |
101.2(5) 99.7(2) |
4.5(5)
2.8(2) |
5. The effect of the crystalline environment
An important conclusion to be drawn from the experimental results is the different behavior of the two independent molecules in the crystal. This is evident from the shifts on excitation (Table 3), the bond length changes (Table 4) and the flattening angles (Table 5). The Cu(2) atom moves towards the phenanthroline ligand with a C-N shortening of ~0.04Å and away from P(4), whereas the shifts for Cu(1) are much smaller and within the experimental errors. Examination of the packing of the two molecules reveals a pronounced difference. Whereas molecule A is π-stacked with a center of symmetry-related neighbor, forming a π-stacked chain with alternating phenanthroline and phenyl ligands, no such interaction exists for molecule B, as illustrated in Fig. 5. The distortions around the Cu atoms at 90K are illustrated in Fig. 6. Those of Cu(1) are very small, whereas those of Cu(2) are clearly visible.
Fig. 5.
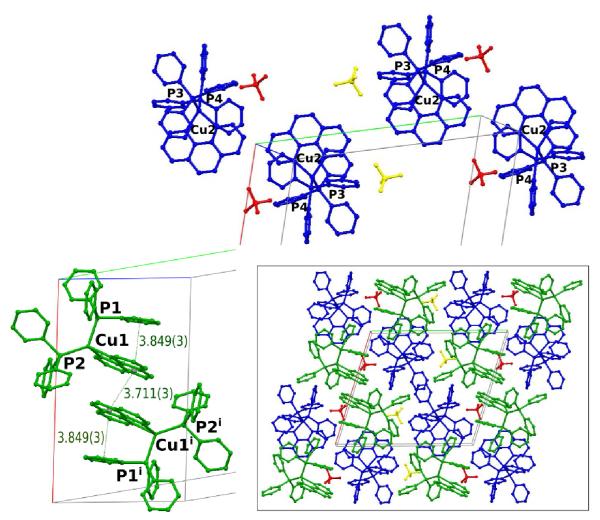
Comparison of the crystal-packing of the two independent molecules in the cell. (top in blue): The packing of molecules B. (lower left in green): The π-stacking of molecules A. (lower right): Combined packing of all molecules in the crystal.
Fig. 6.

Comparison of the crystal-packing of the two independent molecules in the cell. (a): Molecule A, (b) molecule B.
The effect of the lattice is even more evident when the observed distortions are compared with those calculated for the isolated molecule for which we calculate a flattening of ~31°, (B3LYP, 6-31G*) compared with 3-5° observed in the present case. Interestingly, there is very little difference between the flattening distortions observed in this study and those in the 2,9-dimethyl substituted complex (1), suggesting that the dramatic influence of packing restrictions override those of the methyl substitution.
In previous studies we have estimated the constraining effect of the lattice by QM/MM methods in which the central molecule is treated quantummechanically, but the effect of the surrounding crystal is introduced by treating the molecule-lattice interactions by force-field atom-atom potential functions.8,28 Application of this method accounted almost quantitatively for differences between the observed and calculated Rh-Rh shortening in a binuclear rhodium complex.8
We have not been able to reproduce the experimental results with this method in the present case. While a reduction in the distortions is predicted, they are underestimated and the calculations failed to reproduce the pronounced difference between the two sites, at least when B3LYP-DFT methods were used with several different basis sets. This is possibly due to the effect of dispersion forces, which are poorly accounted for in the DFT calculations, but important in π-π stacking observed here. This effect will be investigated in future calculations.
6. Time-resolved emission spectroscopy
Lifetime measurements were made at 50, 90 and 180K. Results at 90 and 180 K are shown in Fig. 7. At all temperatures a significantly superior fit was obtained with a bi-exponential decay as illustrated in the figure. Fitting constants indicate one short lifetime of ~12 ×s at 90K and a longer lifetime of ~116 ×s at the same temperature, with pre-exponential factors of 0.06 and 0.15 respectively. At 180K the two lifetimes are reduced to 8 and 72 ×s with pre-exponential factors of 0.026 and 0.144 respectively, indicating that the longer lifetime becomes relatively more dominant at the higher temperature. Full information is given Table S5 and Fig. S2. Interestingly, although the individual bond length changes at Cu(1) are not significant, they are consistently larger at 180K than at 90K, which is not the case for Cu(2). This suggest that longer lifetime is associated with the luminescence of complex with Cu(1) at its center, which is more confined in the crystal. This is in agreement with earlier conclusions of McMillin et al.29 that a smaller structural change of the Cu-phenanthroline complexes on excitation leads to a longer lifetime of the excited species, in accordance with the energy gap law,30-32 as a less relaxed excited state will have a higher energy. We conclude that the observed bi-exponential decay is to be attributed to the co-existence of two chemically identical, but structurally distinct molecules in the crystalline environment which show large difference in distortion on excitation.
Fig. 7.
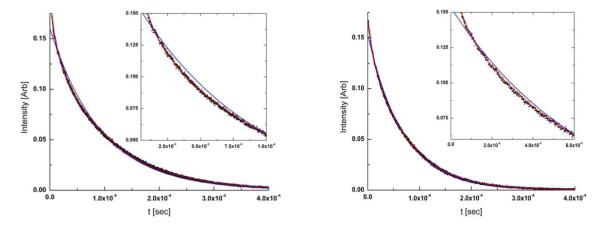
Time-dependence of the emission decay of (2) at 90K (left) and 180K (right). The red and blue lines represent the single exponential and bi-exponential fits to the data points (black) respectively. The inserts show the region with the largest differences between the two fits.
7. Conclusions
The modified Laue method for collection of time-resolved synchrotron data leads to structural information of significantly higher accuracy than achieved in an earlier monochromatic study of a related solid. Although the previously investigated complex (1) is dimethyl-substituted in the 2,9 positions of the phenanthroline ligand, which inhibits the expected flattening on photo-oxidation of the Cu atom, while (2) is not, flattening distortions of both complexes are very similar and very much less than calculated for the isolated molecule, indicating the dominant effect of the crystalline environment. Both complexes crystallize with two molecules in the asymmetric unit and in both cases the two independent molecules show different distortions on excitation. In the current study in one of the molecules the Cu-N distances contract, whereas the dominant motion of Cu in the second molecule is towards one of the phosphorus atoms. The observed bi-exponential decay of the emission is attributed to the different distortions of the two molecules. In accordance with the energy gap law the longer lifetime is assigned to molecule (1) which undergoes a smaller distortion on excitation. The QM/MM treatment of the effect of the molecular surroundings significantly underestimates the reduction in the flattening, in contrast to earlier results on binuclear rhodium compounds, but does confirm the difference betweent he two independent molecules in the crystal.
Above all the study illustrates emphatically that molecules in solids have physical properties different from those of isolated molecules and that their properties depend on the specific molecular environment. This conclusion is relevant for the understanding of the properties of molecular solid state devices which are increasingly used in current technology.
Supplementary Material
Acknowledgements
Support of this work by the U.S. National Science Foundation (CHE0843922) is gratefully acknowledged. We are grateful to Prof. Marius Schmidt of the University of Wisconsin at Milwaukee for use of the Nd-YAG laser. The BioCARS Sector 14 is supported by the National Institutes of Health, National Center for Research Resources, under grant number RR007707. The time-resolved facility at Sector 14 was funded in part through a collaboration with Philip Anfinrud (NIH/NIDDK). The Advanced Photon Source is supported by the U.S. Department of Energy, Office of Basic Energy Sciences, under Contract No.W-31-109-ENG-38.
Footnotes
Supporting Information Description of the refinement strategy. Tables specifying sample size and laser power used, crystallographic information, bond lengths and changes in the copper coordination on excitation. This information is available free of charge via the Internet at http://pubs.acs.org
References
- (1).Benedict JB, Coppens P. J. Am. Chem. Soc. 2010;132:2938. doi: 10.1021/ja909600w. [DOI] [PubMed] [Google Scholar]
- (2).Benedict JB, Freindorf R, Trzop E, Cogswell J, Coppens P. J. Am. Chem. Soc. 2010;132:13669. doi: 10.1021/ja106436y. [DOI] [PubMed] [Google Scholar]
- (3).Vorontsov II, Graber T, Kovalevsky AY, Novozhiliva IV, Gembicky M, Chen Y-S, Coppens P. J. Am. Chem. Soc. 2009;131:6566. doi: 10.1021/ja900921p. [DOI] [PubMed] [Google Scholar]
- (4).Kirchhoff JR, McMillin DR, Robinson WR, Powell DR, McKenzie AT, Chen S. Inorg. Chem. 1985;24:3928. [Google Scholar]
- (5).Everly RM, Ziessel R, Suffert J, McMillin DR. Inorg. Chem. 1991;30:559. [Google Scholar]
- (6).Cuttell DG, Kuang S-M, Fanwick PE, McMillin DR, Walton RA. J. Am. Chem. Soc. 2002;124:6. doi: 10.1021/ja012247h. [DOI] [PubMed] [Google Scholar]
- (7).Bessho T, Constable EC, Graetzel M, Redondo AH, Housecroft CE, Kylberg W, Nazeeruddin MK, Neuburger M, Schaffner S. Chem. Commun. 2008:3717. doi: 10.1039/b808491b. [DOI] [PubMed] [Google Scholar]
- (8).Makal A, Trzop E, Sokolow JD, Kalinowski J, Benedict J, Coppens P. Acta Cryst. 2011;A67:319. doi: 10.1107/S0108767311011883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Benedict JB, Makal A, Sokolow JD, Trzop E, Scheins S, Henning R, Graber T, Coppens P. Chem. Commun. 2011;47:1704. doi: 10.1039/c0cc04997b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Kalinowski J, Makal A, Coppens P. J.Appl.Cryst. 2011;44:1182. doi: 10.1107/S0021889811038143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Blessing RH. J. Appl. Cryst. 1997;30:421. [Google Scholar]
- (12).Coppens P, Pitak M, Gembicky M, Messerschmidt M, Scheins S, Benedict J, Adachi S-I, Sato T, Nozawa S, Ichiyanagi K, Chollet M, Koshihara S-Y. J. Synchrotron Rad. 2009;16:226. doi: 10.1107/S0909049508040892. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (13).Bruker AXS. Madison, WI: 1999. [Google Scholar]
- (14).Sheldrick GM. Acta Cryst. 2008;A64:112. [Google Scholar]
- (15).Farrugia LJ. J. Appl. Cryst. 1999;32:837. [Google Scholar]
- (16).Frisch M. J. e. a., Gaussian I., editors. Pittsburgh, PA: 2009. [Google Scholar]
- (17).Macrae CF, Bruno IJ, Chisholm JA, Edgington PR, McCabe P, Pidcock E, Rodriguez-Monge L, Taylor R, Van de Streek J, Wood PA. J. Appl. Cryst. 2008;41:466. [Google Scholar]
- (18).Allen FH, Watson DG, Brammer L, Orpen AG, Taylor R. International Tables for Crystallography. Second ed Vol. C. Kluwer Academic Publishers; Dordrecht Boston: 2009. [Google Scholar]
- (19).Rappe AK, Casewit CJ, Colwell KS, Goddard WA, III, Skiff WM. J. Am. Chem. Soc. 1992;114:10024. [Google Scholar]
- (20).Coppens P. Synchrotron Radiation Crystallography. Academic Press Limited; London: 1992. [Google Scholar]
- (21).Volkov A, Macchi P, Farrugia LJ, Gatti C, Mallinson PR, Richter T, Koritsanszky T. 2006.
- (22).Vorontsov I, Pillet S, Kaminski R, Schmokel M, Coppens P. J. Appl. Cryst. 2010;43:1129. [Google Scholar]
- (23).Vorontsov II, Coppens P. J. Synchr. Rad. 2005;12:488. doi: 10.1107/S0909049505014561. [DOI] [PubMed] [Google Scholar]
- (24).Coppens P, Kaminski R, Schmoekel MS. Acta Cryst. 2010;A66:626. doi: 10.1107/S0108767310021227. [DOI] [PubMed] [Google Scholar]
- (25).Schmøkel M, Kaminski R, Benedict JB, Coppens P. Acta Cryst. 2010;A66:632. doi: 10.1107/S0108767310029429. [DOI] [PubMed] [Google Scholar]
- (26).Michalski D, White MA. J. Chem. Phys. 1997;106:6202. [Google Scholar]
- (27).Dobson JF, Green BE, Healy PC, Kennard CHL, Pakawatchai C, White AH. Aust. J. Chem. 1984;37:649. [Google Scholar]
- (28).Kaminski R, Schmøkel MS, Coppens P. J. Phys. Chem. Lett. 2010;1:2349. [Google Scholar]
- (29).Eggleston MK, McMillin DR, Koenig KS, Pallenberg A. J. Inorg. Chem. 1997;36:172. [Google Scholar]
- (30).Caspar JV, Kober EM, Sullivan BP, Meyer TJ. J. Am. Chem. Soc. 1982;104:630. [Google Scholar]
- (31).Caspar JV, Meyer TJ. J. Phys. Chem. 1983;87:952. [Google Scholar]
- (32).Freed KF, Jortner JJ. Chem. Phys. 1970;52:6272. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


