Patterns of inspiratory phase-dependent activity in the in vitro respiratory network

Abstract

Mechanistic descriptions of rhythmogenic neural networks have often relied on ball-and-stick diagrams, which define interactions between functional classes of cells assumed to be reasonably homogenous. Application of this formalism to networks underlying respiratory rhythm generation in mammals has produced increasingly intricate models that have generated significant insight, but the underlying assumption that individual cells within these network fall into distinct functional classes has not been rigorously tested. In the present study we used multiunit extracellular recording in the in vitro pre-Bötzinger complex to identify and characterize the rhythmic activity of 951 cells. Inspiratory phase-dependent activity was estimated for all cells, and the data set as a whole was analyzed with principal component analysis, nonlinear dimensionality reduction, and hierarchical clustering techniques. None of these techniques revealed categorically distinct functional cell classes, indicating instead that the behavior of these cells within the network falls along several continua of spiking behavior.

rhythmic activity is ubiquitous in neural systems, from the slow rhythm generated by the suprachiasmatic nuclei that synchronizes mammalian circadian cycles (Dibner et al. 2010), to the broad frequency spectra covered by various oscillations generated within cortical networks (Buzsaki and Draguhn 2004; Tort et al. 2010; Wang 2010). Many of the underlying rules of rhythm generation have been established in neural circuits that generate rhythmic motor behaviors (Goulding 2009; Grillner 2006; Marder and Calabrese 1996). These motor activities are typically reciprocal in nature (e.g., expiration and inspiration, extension and flexion, protraction and retraction) and are often described by ball-and-stick¹ schematics that assume specific connectivity (sticks) between different types of cells or cell populations (balls). In these models each cell possesses functionally discrete properties firing in distinct phases with respect to a given global activity pattern (Guertin 2009; Selverston 2010). Ball-and-stick representations have been particularly powerful in invertebrate neuronal networks (Antonsen and Edwards 2003), because the firing and connectivity properties of physiologically and anatomically identified individual neurons could be reproducibly characterized across different individuals of the same species (Jing et al. 2010; Katz et al. 2010; Marder and Calabrese 1996; Newcomb et al. 2012; Ramirez, 1998; White and Nusbaum 2011). One of the many important lessons learned from these small invertebrate networks is that even in the case of a truly identified neuron, electrophysiological measures of single-cell properties do not suffice to uniquely specify a neuron (Brookings et al. 2012). This has very important implications for mammalian rhythm-generating networks. Despite the increased availability of molecularly identified mammalian neurons (Bouvier et al. 2010; Crone et al. 2012; Goulding, 2009; Gray et al. 2010; Grossmann et al. 2010), it continues to be very difficult to reproducibly identify individual neurons. Instead, investigations have often relied on categorizing physiological cell types on the basis of their phase-dependent firing patterns (Dougherty and Kiehn 2010a, 2010b; Kiehn 2006, 2011; Kwan et al. 2009; Morris et al. 2010; Richter 1982), but this approach does not necessarily identify a physiologically homogeneous class of neurons, let alone identify a single neuron.

Despite these caveats ball-and-stick schematics have also been applied to mammalian networks, and it seems that these models have become increasingly popular. In the respiratory and locomotor networks, catalogs of 5–20 different firing patterns and their hypothesized connections have been incorporated into increasingly complex models of rhythm generation with the idea that they can potentially explain how these networks generate rhythmicity (Molkov et al. 2010; Ogilvie et al. 1992; Rubin et al. 2009; Rybak et al. 1997a, 1997b, 1997c, 2007, 2008; Sherwood et al. 2011; Smith et al. 2007). Yet, despite the reliance of current models on the concept of different physiological categories, the quantitative basis for these categories has not been rigorously established, nor have the criteria that specify inclusion into one or another cell class been described in detail.

In the present study we show for the isolated mammalian respiratory network that although it is possible to qualitatively identify different firing patterns matching several of the traditionally described categories, these firing patterns vary along several continua that span and include the traditionally defined categories.

METHODS

Experimental procedures.

Transverse medullary brain stem slices were taken from CD1 mice, postnatal days (P)6–9, as described previously (Ramirez et al. 1996; Viemari and Ramirez 2006). This age range was chosen to reduce heterogeneity from neurodevelopmental changes known to affect respiratory rhythm generation in these mice. In accordance with protocols approved by the Institutional Animal Care and Use Committee at the University of Chicago, animals were deeply anesthetized with ether and rapidly decapitated. The brain stem was isolated in ice-cold, oxygenated (95% O₂-5% CO₂) artificial cerebrospinal fluid (aCSF) containing (in mM) 128 NaCl, 3 KCl, 1.5 CaCl₂, 1 MgCl₂, 24 NaHCO₃, 0.5 NaH₂PO₄, and 30 d-glucose (pH 7.4). The brain stem was then glued to an agar block on the mounting plate of a Leica Vibratome with the rostral end up and the ventral face toward the blade. Serial slices proceeded until visual landmarks became clear. The cut of the rostral face of the experimental slice was typically 530 μm caudal to the opening of the fourth ventricle. From this position slices of between 600 and 620 μm were taken, and histological characterizations have confirmed that these slices contain the pre-Bötzinger complex (pre-BötC; not shown). This slice was transferred directly to the recording chamber, where it was superfused with aCSF at a typical rate of 10 ml/min and allowed to equilibrate to experimental temperature (33–35°C). Robust population activity was initiated by raising the extracellular potassium concentration from 3 to 8 mM in two steps over 60 min.

Extracellular recording.

The basic recording and analysis methods are summarized in Fig. 1. Extracellular neural activity from the transverse medullary slice was recorded on up to 16 channels using custom-made multielectrodes. These were created by twisting nichrome microwire (25-μm inner diameter, Formvar-insulated Nichrome; A-M Systems) into tight bundles that were then sealed with epoxy, cut, and gold-plated at the tips. The geometry and arrangement of the individual wires was therefore random within the multielectrode probe, which was roughly 200 μm in diameter. Neural signals were amplified 1,000 times and band-pass filtered from 250 to 7,500 Hz with a custom analog amplifier. These filter settings were selected to reduce the effects of low-frequency components on thresholding used for spike detection and to include high-frequency waveform features that could aid spike sorting. The signals were then sampled (at 20 kHz), digitized, and saved using a Digidata 1322A data acquisition system and AxoScope software (Molecular Devices). To reduce superimposition of waveforms from presumptive single units on multiple channels, resulting signals were preprocessed using independent component analysis (FastICA; http://www.cis.hut.fi/projects/ica/fastica/). After preprocessing, action potential waveforms from distinct neurons were typically present on from one to three channels. These waveforms were detected and sorted using Offline Sorter (Plexon) with manual cluster cutting in tetrode-based feature spaces. Care was taken to follow nonstationarities in waveform shapes in assigning spikes to separate units, and auto- and cross-correlation histograms were examined as a check on sorting results (Lewicki 1998). To generate an integrated population activity waveform, signals from multiple channels were averaged, rectified, and digitally low-pass filtered at 30 Hz. With the exception of spike detection and sorting, all signal processing and statistical analyses were done in MATLAB (The MathWorks) using custom applications.

Fig. 1.

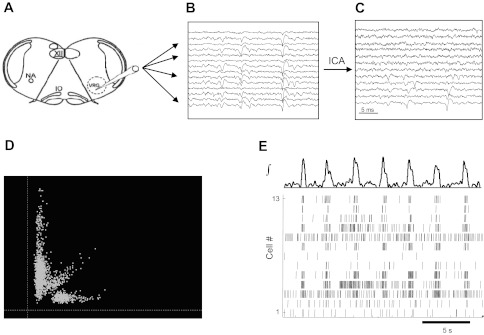
Schematic of multielectrode recording and analysis of in vitro rhythmic activity. A transverse medullary slice (A) shows the localization of the ventral respiratory group (VRG; presumptive pre-Bötzinger complex) and the placement of the twisted multiwire electrode. NA, nucleus ambiguus; IO, inferior olive; XII, hypoglossus nucleus. Multiple signals are recorded (B), and cross talk is reduced using independent component analysis (ICA; C). Extracellular spikes are detected and sorted in principal component analysis (PCA) feature space (D), identifying action potential times for individual neurons (E) in relation to the ongoing population activity (shown at top).

Intracellular recordings.

Inspiratory pre-BötC neurons (1 neuron per slice) were recorded using the blind patch-clamp recording method, after first being identified in the cell-attached mode, which revealed their discharge pattern in phase with population activity as described previously (Peña and Ramirez 2002; Tryba et al. 2008; Viemari and Ramirez 2006). Experiments were then performed in whole cell configuration with the neuron recorded in current clamp at the zero current potential. The patch electrodes were pulled from filamented borosilicate glass tubes (G150F-4; Warner Instruments) and filled with a solution containing 140 mM K-gluconic acid, 1 mM CaCl₂·6H₂O, 10 mM EGTA, 2 mM MgCl₂·6H2O, 4 mM Na₂ATP, and 10 mM HEPES.

Quantitative analysis.

The integrated population activity waveform for each experiment was characterized by a combination of four metrics of burst shape and timing variability: variance of interburst intervals, variance of burst peak amplitudes, burst shape variability, and signal-to-noise ratio. Slow baseline nonstationarity was eliminated by subtracting a highly smoothed version of the signal, estimated by low-order polynomial regression. A threshold was set interactively for each recording based on the signal noise power during intraburst intervals. The resulting detected bursts were screened for artifacts and false detections, and the burst onset time was defined from the remaining waveforms as the time of threshold crossing. For the purposes of this study, no effort was made to distinguish high-amplitude bursts, or fictive sighs (Lieske et al. 2000), from other bursts, although such bursts were observed in many recordings.

The relationship between the activity of individual neurons and the phase of the fictive inspiratory rhythm was determined by various analyses of the firing times of action potentials relative to the onset of each population burst (as defined above). Peri-burst firing rate histograms, for example, were generated by counting the number of occurrences of spikes from a given cell within small time bins relative to burst onset. These counts were then normalized by the bin width and the number of bursts recorded to provide a measure of the average firing rate for a given cell relative to the inspiratory phase. For other types of analysis, the behavior of each cell relative to the population activity was characterized by the estimation of instantaneous firing rate functions. In this case, a single vector of burst-centered spike times was created, and the instantaneous firing rate was generated by a summation of Gaussian kernel functions, each centered on the time of one action potential. Compared with histogram estimation, which imposes arbitrary boundaries based on the selection of the number of time bins and produces a discontinuous function, kernel rate estimation can generate a function of arbitrarily fine smoothness, avoiding the imposition of ad hoc boundaries within the data. Instead, kernel estimation requires the specification of a smoothing parameter (in the Gaussian case, the sigma width parameter of the kernel function), which determines the level of temporal detail discernible in the rate estimate. The nominal smoothing width was 0.03 s.

Principal component analysis (PCA) was used to inspect low-dimensional reconstructions of data sets representing firing rate functions. PCA is a method for finding orthogonal projections of a data set that maximally capture the variance in the data. These projections are ordered according to the amount of data variance captured so that by selecting the first few projections, a faithful but reduced representation of the data can be derived. Reduction of large data sets to two or three dimensions allows visualization of structure within the full data set that may otherwise remain obscure. For this study, PCA was implemented using the singular value decomposition function in MATLAB.

Intracellular recordings obtained from in vitro slice experiments in our laboratory with the use of nearly identical experimental methods (Viemari and Ramirez 2006) were analyzed for comparison with extracellular data. Action potential and population burst times were extracted from 61 recordings (duration 290 ± 113 s) and used to estimate burst-triggered firing rate functions by using the same computational methods described above for extracellular recordings. These estimated rate-functions were then projected into the same PCA subspace as the extracellularly estimated functions.

Several additional data dimensionality reduction techniques were also applied as an alternative to PCA. These methods (isomap, Laplacian eigenmap, and local linear embedding) all are attempts to capture nonlinear manifolds within high-dimensional data by relaxing the constraint on fitting the global data variance (Belkin and Niyogi 2003; Roweis and Saul 2000; Tenenbaum et al. 2000). In some cases these methods may find structure within the data that global, linear methods such as PCA may miss. In addition to the number of dimensions used in the reduced space, these algorithms require specification of a neighborhood parameter that defines the number of data points nearest to a given data point that are to be considered local to that point. All three of these algorithms were applied using MANI (http://www.math.ucla.edu/∼wittman/mani/) for MATLAB. Each algorithm was run with a data reduction dimension of 2 or 3 and several neighborhood values between 3 and 10.

Hierarchical clustering of burst-triggered firing rate functions was implemented with standard MATLAB routines. First, Euclidian distances between all pairs of data vectors (constructed from kernel estimation as described above) were calculated. Next, agglomerative clustering (using the Ward method) was applied to successively combine first single vectors, then groups of vectors, into a binary tree structure in which the within-group variance is minimized at each branch in the tree. Results of this analysis were visualized with a dendrogram, a diagram in which the lengths of individual branches represent the dissimilarity between the groups those branches subsume.

RESULTS

Classification of burst-triggered rate functions.

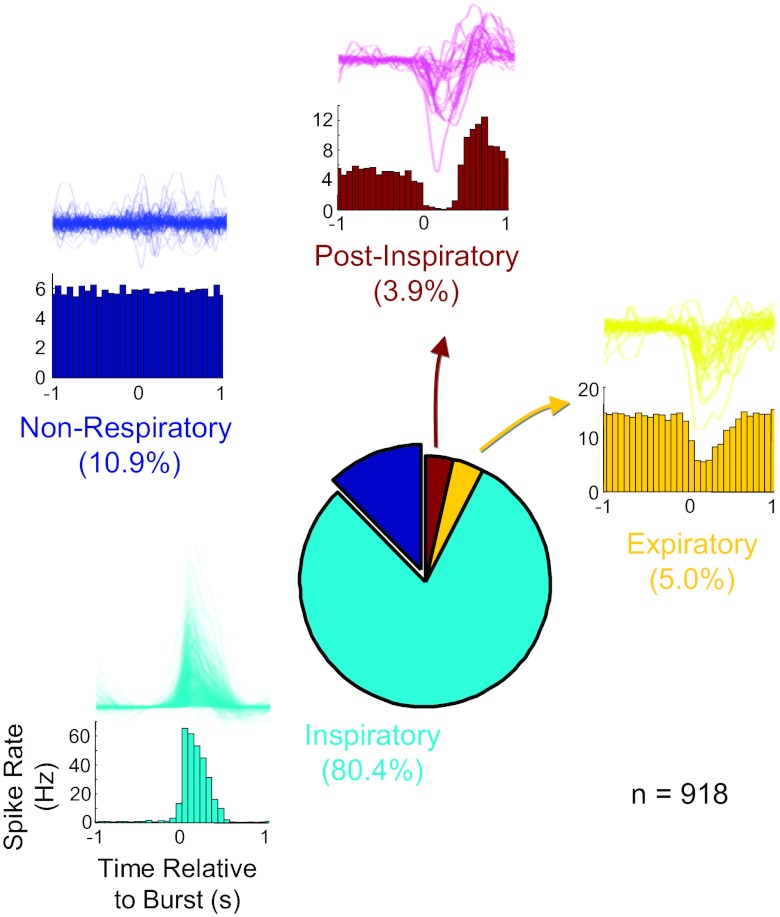
Of a total of 951 identified cells from 77 experiments (and an equal number of slices), peri-burst histograms from 918 cells with 30 or more recorded spikes in control conditions were generated by compiling spike times relative to each burst onset as defined by the time of threshold crossing of the rising phase of the integrated population waveform. Qualitative examination of these histograms (30 time bins between 1 s before and 1 s after the burst) revealed a mix of burst-related firing signatures in the recorded cell population (Fig. 2). The most common pattern (n = 738; 80.4%) was an inspiratory discharge, where spiking in the individual cell was in phase with population bursts. Presumptively nonrespiratory cells, in which firing was not related to population activity and which typically fired tonically throughout all fictive respiratory phases, were also abundant (n = 100; 10.9%). Neurons with a relatively tonic firing rate that was suppressed during the population burst, characteristic of expiratory neurons, comprised 4.8% of the total (46 of 951 neurons), whereas 3.7% of the neurons (34 of 951) showed inhibition during fictive inspiration with a marked postinhibitory rebound during postinspiration. These neurons have previously been described as postinspiratory neurons in vitro and in vivo (Ramirez et al. 1997). Because the purpose of this analysis was only to provide contrast with a more quantitative approach (to be presented below), no effort was made to further subdivide cell firing patterns into finer categories such as incrementing or decrementing.

Fig. 2.

Prevalence of 4 traditionally defined firing patterns from 77 in vitro multiunit recording experiments (n = 918 cells). For each cell type, histograms (bottom) illustrate the population burst-triggered firing pattern for example cells in that class, and the population of burst-triggered firing rate functions for each class is shown as a density plot (top).

Because it is possible that qualitative inspection of burst-related firing patterns may either miss true subcategories of discharge types or, conversely, arbitrarily divide a continuum of morphology into perceptually salient but ultimately physiologically indistinguishable classes, we used quantitative analyses of the firing pattern data to determine if these neural signatures could be considered as naturally separable classes. Peri-burst spike times were used to generate estimates of a smooth instantaneous firing rate function for each cell using Gaussian kernel smoothing (with a kernel sigma of 0.03 s). To focus further analysis on the shape rather than the amplitude of these functions, each was demeaned and normalized by its peak-to-peak amplitude. These functions were then sampled from 0.5 s before to 0.7 s after the population burst onset time at a temporal resolution of 4 ms (Fig. 3B illustrates a density cloud of the normalized waveforms for all cells). In this way, each waveform was represented by a vector of 301 values, meaning that the entire population can be considered as a group of points in a 301-dimensional space. PCA was used to project this cloud of points into a low-dimensional subspace, preserving maximal variance (application of this technique to synthetic data representing 50 waveforms in each of 2 classes illustrates how PCA can reveal structure in high-dimensional data sets; Fig. 3A). This allowed visual inspection to determine whether this population could be easily characterized by set of distinct subgroups or was more consistent with a continuum of firing patterns. Projection of the data onto the first 3 principal eigenvectors accounted for 85% of the total variance in the data set, indicating that this compact representation was relatively faithful to the complete data. Figure 3C illustrates the resulting point cloud in three dimensions with shadow projections on the three axis planes. There are perhaps two or three diffuse point clouds with only weak, poorly separated concentrations of points.

Fig. 3.

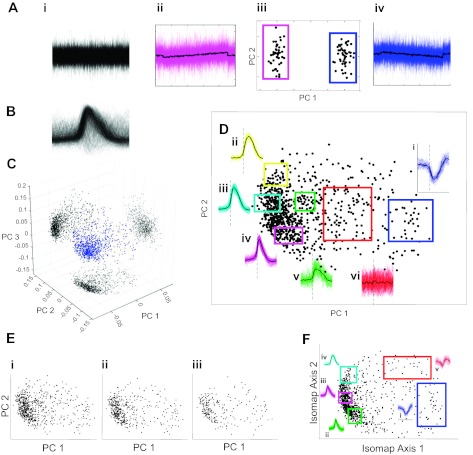
Analysis of cycle-triggered rate functions using dimensionality reduction techniques. A: an illustrative example of PCA applied to synthetic data with 2 subtly distinct waveform classes buried in high-amplitude Gaussian noise. Projection of the original high-dimensional data (i) onto the first 2 PCA dimensions (PC 1 and PC 2) shows distinct clusters (iii) from which the original waveform classes can be perfectly recovered (ii and iv). B: density plot showing all data waveforms demeaned and normalized to unit peak-to-peak amplitude. C: point cloud of waveforms in 3 primary PCA dimensions with shadow projections on axis planes. D: the features captured by the first 2 dimensions of PCA are illustrated with examples from various regions in this space (i–vi). E: additional PCAs of more selective subsets of waveforms (i–iii) show similar weak clustering. F: a globally nonlinear dimensionality reduction algorithm (isomap) identifies a similar feature space to PCA.

PCA can provide a parsimonious description of high-dimensional data, but the resulting dimensions are linear combinations of the original data vectors, meaning they are difficult to interpret in the context used here. To illustrate the variation in waveforms captured by PCA, Fig. 3D shows the subsets of rate functions represented by discrete regions of the first two dimensions of the PCA space. The dense point cloud at the left of the scatter plot represents most of what would be considered inspiratory waveforms with a transition from bottom to top along the second principal component dimension from narrow waveforms (Fig. 3Div) to more linear decrementing shapes (Fig. 3Diii) and more rounded bell-shaped waveforms with somewhat later onset latency (Fig. 3Dii). Along the primary axis from left to right, weakly modulated (Fig. 3Dv), nonrespiratory (Fig. 3Dvi), and finally a somewhat distinct cloud of expiratory (Fig. 3Di) waveforms is apparent.

Because it seeks projections that capture maximum data variance, PCA is susceptible to the influence of outliers within the sample. It is also possible that relatively distinct clusters of points are obscured by intermediate points from high-variance waveforms generated by poorly estimated firing rate functions or from burst-triggered firing rate functions that are poorly defined because of timing jitter in the detection of the burst onset in the population activity. To address these possibilities, three subsamples of the full data set were taken by using successively more stringent standards for selecting waveforms for inclusion in the PCA. For Fig. 3Ei, the experiments in which the quality of the integrated population activity waveform was in the lowest 25% for all experiments were eliminated. In addition, no cells were included in this subset, from which there were fewer than 100 action potentials used to estimate the firing rate function. This left 688 of the original set of rate functions, from which the first two PCA projections are shown. For Fig. 3Eii, only the experiments with the top 50% quality population waveforms were included, and the 437 cells from those experiments with 300 or more spikes were used in the PCA. For Fig. 3Eiii, only the experiments within the highest quartile of population regularity were selected, from which cells that fired more than 500 spikes are shown in PCA coordinates. Spatial clustering in the projections of these more exclusive data subsets remained weak, suggesting that the smear of data points in the initial analysis is not the result of experimental variability.

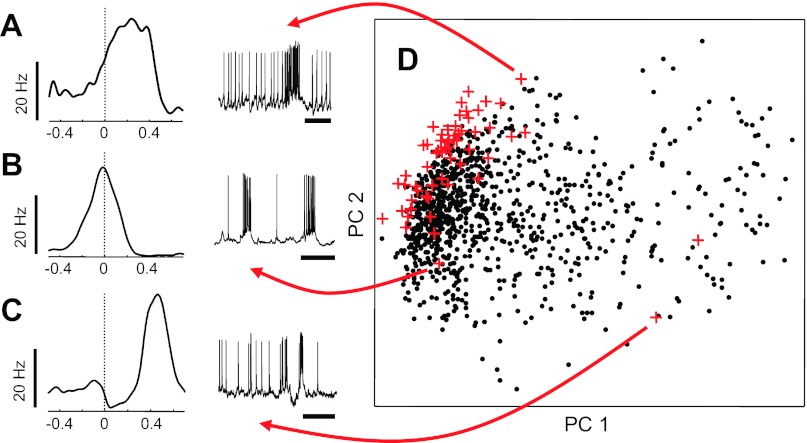
To confirm that findings from extracellular multielectrode experiments were not the result of artifacts of the recording or spike-sorting process, intracellular data from 61 recordings done in our laboratory were analyzed using only spike timing and population burst timing information to estimate burst-triggered firing rate functions (Fig. 4, A–C, left; sample inspiratory bursts, right). These estimated rate functions were then projected into the same principal component subspace as the extracellularly estimated functions (Fig. 3D, red crosses). The rate functions from these intracellular recordings showed a similar spatial distribution, perhaps with a bias toward more robustly inspiratory units (a selection bias of the intracellular recordings, where nonrespiratory cells were discarded before a whole cell patch configuration was achieved, after ongoing spiking activity was monitored in cell-attached mode).

Fig. 4.

Intracellularly recorded burst-triggered firing patterns. A–C: samples of firing rate functions from intracellular recordings (left; sample membrane potential traces, right) are morphologically similar to those estimated from multielectrode extracellular recordings. D: rate functions from 61 intracellular recordings (red crosses) shown along the primary PC axes against the field of points from Fig. 3D.

The lack of clear clustering in the PCAs may also be a result of the approach itself. Since PCA works to maximize the variance of linear projections of the data in a global way, it may fail to capture local regularities in the data that occur on nonlinear manifolds. In an effort to detect such regularities, a topologically local approach that is capable, in principle at least, of detecting such regularities was applied to the same firing rate data as used for PCA. The full data set was reduced to three dimensions using the isomap algorithm (Tenenbaum et al. 2000) with a neighborhood parameter of 10. The first two resulting dimensions are shown in Fig. 3F, where only weak and indistinct concentrations of points are visible. The callouts of representative waveform sets from the two-dimensional space show that despite its drastically different assumptions, the isomap algorithm identifies axes of variability that are similar to those produced by PCA. Analyses with different parameter values and other nonlinear manifold methods (local linear embedding and Laplacian eigenmaps) produced similar results, as did PCA repeated with rate functions estimated using histogram methods (data not shown).

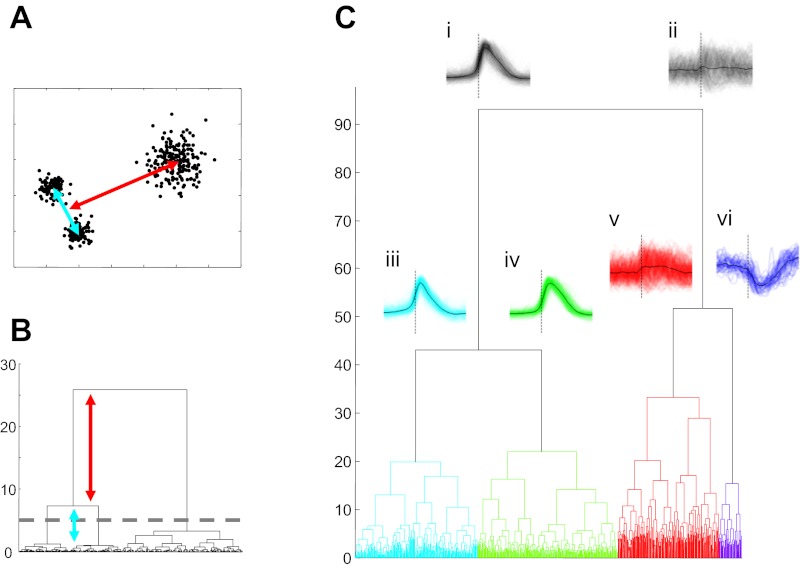
To further clarify potential structure in the burst-triggered firing rate function data, we applied a hierarchical clustering method to the same data set. This method attempts to find subsets in which data vectors are as similar as possible while making the groups as distinct from each other as possible. The results of hierarchical clustering algorithms can be displayed in a dendrogram, a diagram in which similar data points/groups are linked by vertically short branches and more distinct clusters are indicated by long vertical lines (Fig. 5, A and B). Thus long vertical branches indicate relatively natural groupings within the data, and the number of such appropriate groups is suggested by a threshold behavior from long vertical branches to indistinguishable clusters of short branches (although from a theoretical point of view, there is nothing to prevent successively splitting resulting groupings until only individual data points remain). Figure 5C illustrates the dendrogram produced by hierarchical clustering of the full burst-triggered firing rate function data set used for the basic PCA described above. The result of the first-order split in the data is shown, where a division between waveforms with inspiratory patterns (Fig. 5Ci) and those with expiratory or nonrespiratory waveforms (Fig. 5Cii) is evident. The second-order division of the respiratory group (Fig. 5, Ciii and Civ) produces a group of waveforms with a sharp onset and a group with more rounded shapes. The noninspiratory group is split at the second-order branch into a variable and nonrespiratory set (Fig. 5Cv) and a class with clear expiratory (or possibly postinspiratory) waveforms (Fig. 5Cvi). Further splitting of these classes is possible but is not as compelling as these initial divisions.

Fig. 5.

Hierarchical cluster analysis applied to cycle-triggered rate functions. A and B: hierarchical groupings in synthetic data (A) can be revealed by a dendrogram (B), which illustrates relationships between groups of data points. C: application of this technique to burst-triggered firing rate functions shows a primary but weak division between inspiratory and noninspiratory waveforms (i and ii) and a secondary bifurcation into sharp (iii) vs. more rounded inspiratory waveforms (iv) and weakly or unmodulated firing patterns (v) vs. clear expiratory cells (vi).

Characterization of simultaneously recorded firing patterns.

Whereas the previous analysis investigated the variability in the shapes of firing rate functions as a population across experiments, it did not establish the potential temporal relationships between these functions within single experiments. Figure 6A characterizes the population burst-related activity of 11 cells recorded simultaneously through 150 population bursts in 275 s of baseline recording. The central panel is a spike raster plot where individual ticks represent individual spike times from different cells (in 11 separate blocks) relative to the onset times of each population burst (designated as t = 0, with each successive population burst cycle plotted along the ordinate axis within each block). Each tick is also color coded for instantaneous spike rate (defined as the inverse of the interspike interval ending with that spike) on a heat map scale from 0 to 55 Hz. As illustrated in Fig. 6, a variety of firing rate patterns is present within this experiment. Weakly modulated cells with low baseline activity rates (e.g., cells 1 and 2) are present, as are those with strong expiratory phase activity as well as more robust inspiratory bursting. Estimated firing rate functions shown in Fig. 6B illustrate some of these differences. Also evident in the raster plots, and in the comparison plots in Fig. 6C, are onset timing differences between the average burst-triggered firing rates. In this experiment, for example, cell 9 tends to fire before cell 8, and cell 5 typically precedes cell 7. In Fig. 6D, the timing differences between cells are characterized statistically by a nonparametric comparison of median spike times for all cells during the period from 0.4 s before to 0.6 s after the burst onset. In a point process series, the median (or mean) characterizes the center of mass of the spike time density. Within Fig. 6D, statistically significant different median spike times (α = 0.05; Kruskal-Wallis test corrected for multiple comparisons using the Bonferroni method) between all possible pairs of cells are shown, with significance indicated by an asterisk within the grid (statistically significant onset differences for cell 6 are also depicted in Fig. 6A at left). In this experiment, 68% of possible pairs have distinguishable onset times. Thus statistically significant differences in the median firing times in the early part of the population burst are present between most pairs of cells. The histogram in Fig. 6F shows the significance percentage distribution for all 77 experiments, indicating that onset timing differences are common between simultaneously recorded cells. Figure 6E summarizes the simultaneous spiking behavior from 10 experiments in cycle-triggered rasters. The presence of firing patterns with a variety of shapes is evident in the texture of these rasters (percentages of statistically distinguishable pairs are listed below each).

Fig. 6.

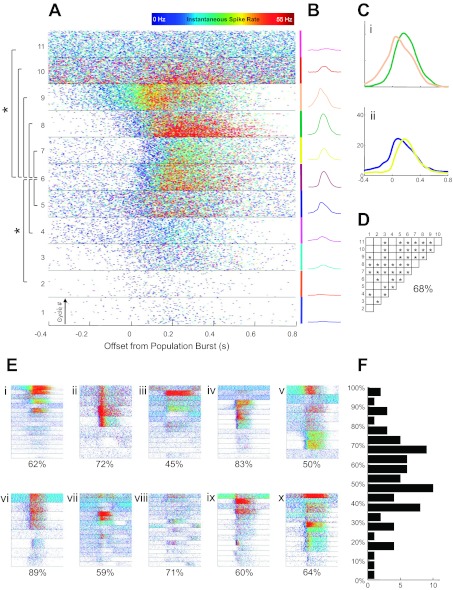
Cycle-by-cycle spiking behavior of 11 simultaneously recorded neurons across 150 population bursts. A: each block shows spike times of a different neuron relative to burst onset with successive cycles stacked in the block and the instantaneous spike rate coded as a heat map from between 0 and 55 Hz (top). B: cycle-triggered rate function estimates are shown corresponding to blocks in A, with each cell given a distinct color. C: onset timing differences are illustrated between cells 8 and 9 (i) and between cells 5 and 7 (ii). D: significantly different median onset times between all cell pairs are indicated in the grid, where 68% of pairs were statistically distinguishable. E: cycle-triggered rastergrams from 10 other experiments (i–x) including percentages of statistically significant pairs. F: distribution of such percentages over the entire data set of 77 slice experiments.

DISCUSSION

Characterization of the typical firing behavior of single neurons with respect to the respiratory cycle has been central to models of respiratory rhythm generation (Molkov et al. 2010; Rubin et al. 2009; Rybak et al. 2007; Smith et al. 2007). Categorization of this behavior into different types has provided the substrate for understanding rhythmogenesis as arising from antagonistic pools of neurons with characteristic firing patterns. The simplest of these models is the half-center oscillator, where two mutually inhibitory populations can produce a two-phase rhythm (Brown 1911; Getting 1989; Sharp et al. 1996). However, it must be emphasized that the original half-center concept only works with neurons that possess certain intrinsic membrane properties that facilitate transitions from one to the other phase; otherwise such a network configuration will not generate rhythmic activity on the basis of reciprocal inhibitory connectivity alone (Sharp et al. 1996; Skinner et al. 1994). Moreover, this network configuration can generate not only rhythmicity but also many different activity states, including synchrony (Belykh and Shilnikov 2008; Jalil et al. 2010, 2012; Sharp et al. 1996; Wang and Rinzel 1994). Subsequent classification systems in a variety of animal models and preparation types have grown more and more diverse, as have the complexity of the interactions proposed between these physiological classes (Abdala et al. 2009; Rybak et al. 2007; Smith et al. 2007). Undoubtedly, neurons with varying patterns of respiratory modulation do exist, and decades of experimental evidence suggest that these prototypical classes correspond to physiologically relevant functional differences within the network (Bianchi et al. 1995; Duffin 2004; Richter 1982). However, little effort has been made so far to establish a mathematical foundation for these categories that might provide a more nuanced substrate for further functional and modeling studies.

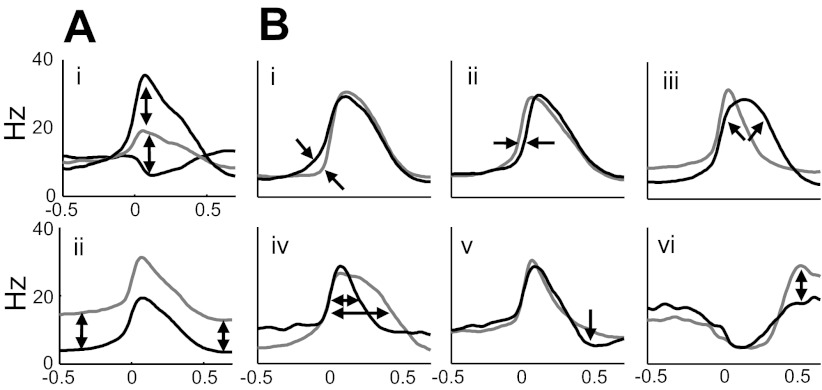
Because the pre-BötC can be physiologically defined by the presence of a variety of firing patterns within a confined area (Lieske et al. 2000; Ramirez et al. 1997) and is accessible in the slice to functional/pharmacological manipulation, we have focused this initial quantitative analysis of cellular firing patterns on this preparation. There is evidence for only weak clustering of these patterns into mathematically distinct classes. Instead, respiratory phase-related firing rate functions lay along several continua of variability, including the strength of activity during the expiratory phase, the degree of firing rate change during the inspiratory burst, and several features of the timing and shape (Fig. 7A). Two dimensions of variation in these data are obvious without any special statistical analysis: modulation of burst amplitude (including inhibition of baseline firing rates; Fig. 7Ai) and variation in the mean firing rate outside of the inspiratory burst phase (Fig. 7Aii). To uncover more subtle regularities in the shapes of the estimated waveforms, these two features were normalized out of the data for the analyses illustrated in the previous figures. The remaining variation in shape and timing are illustrated qualitative and diagrammatically in Fig. 7B with the use of smoothed example waveforms from the current database. The strength of spiking activity preceding the population burst has been addressed in earlier studies and has been hypothesized to indicate cells with a role in driving the population bursts (Ramirez and Viemari 2005). Waveform features indicative of this activity are clearly present in this data set, as well (characterized by Fig. 7Bi). Firing patterns with notably earlier and later onset latency to the population were also apparent in these data (as in Fig. 7Bii) and even occurred within the same recording. As with the preburst ramp onset mentioned above, earlier initiation of a cell's burst phase has been hypothesized to play a role in rhythmogenesis (Butera et al. 1999; Ramirez et al. 2004; Rekling et al. 1996). A range of roundedness of burst shape (Fig. 7Biii) has also been seen in these data, and these are again consistent with some prototypical waveforms seen previously (Richter 1982). The width of the inspiratory burst peak varied, as well (Fig. 7Biv), although this feature might be thought of as part of the continuum of shapes leading to the rounded burst in Fig. 7Biii. Relative decreases in activity can also be indicative of a neuron's burst signature, with some exhibiting relatively little postburst depression (Fig. 7Bv). Conversely, in those neurons presumably inhibited during the inspiration burst, a range of postinhibitory rebound can be seen (Fig. 7Bvi). Clearly, these features are not independent, and understanding their covariance relationships is an area for future analysis.

Fig. 7.

Schematic illustration of variation in modulation amplitude, baseline firing rate, and timing features of rate functions. A shows variation in modulation amplitude and baseline firing rate in unnormalized rate functions, whereas B shows shape and timing features that distinguish normalized rate functions: i, presence or absence of a “preinspiratory” ramp onset; ii, pure onset timing difference; iii, sharp or rounded burst envelope; iv, burst width; v, postinspiratory spike-rate depression; and vi, postinhibitory rebound.

It is tempting to hypothesize about the physiological significance of these dimensions of variability in the context of synaptic or intrinsic cellular properties, although ultimately the observations made here are nonmechanistic. Modeling studies have routinely presupposed, for example, that heterogeneity in cell response can be generated by endowing individual cells with a statistical distribution of intrinsic currents following parameters established from current-clamp studies (e.g., Rybak et al. 2003; for an interesting exception see Golowasch et al. 2002, where mean values of measured current densities failed to reproduce the experimentally observed behavior). Large-scale parameter search studies modeled on neurons within the stomatogastric ganglion of the crab have also established that whole cell behavior derives from relatively smooth manifolds in the parameter space of intrinsic conductances (Prinz et al. 2003, 2004). Within the respiratory network, some authors have proposed that intrinsic bursting behavior in some cells is not the result of a quantitatively distinct subclass of intrinsic conductance distributions, but rather stems from threshold behavior in the space of persistent sodium and leak current densities (Del Negro et al. 2002). Similarly, some have hypothesized that burst onset timing of individual cells within the respiratory network derives from the particular distribution of synaptic and intrinsic properties of each cell (Butera et al. 1999). Their model also suggests that the timing of the inspiratory burst onset for a given cell is a relatively invariant feature of that cell. The data presented in this article generally support the concept of a continuous distribution of intrinsic and synaptic properties resulting in a relatively continuous distribution of cellular behavior, and the burst timing data presented herein also confirm (although obviously not for the first time) the existence of a variety of burst onset latencies in the mean behavior of cells within the same network. The variability in burst onset timing for individual cells is addressed in a companion paper (Carroll and Ramirez 2012).

Limitations of the current approach.

The use of the medullary slice preparation for this analysis of burst-triggered rate function variability (including timing) may limit the scope of the analysis in the sense that this network may not contain the full range of firing patterns that have been documented in less reduced respiratory network preparations. While admitting the central and autorhythmic character of the pre-BötC, recent models have placed it in the context of a larger network containing pools of mutually antagonistic neurons that interact to produce a three-phase rhythm (Rybak et al. 2008). It is entirely possible, therefore, that analysis of recordings from a larger variety of structures along the rostrocaudal axis of the brain stem would reveal more robust and distinct differences between cellular firing patterns than could be shown here. However, because the pre-BötC does have cells with a variety of firing patterns in an experimentally accessible preparation, it provides an excellent starting point for a more quantitatively rigorous description of cellular behavior within the wider respiratory network.

The process of clustering high-dimensional data sets containing mixtures of subpopulation samples drawn from potentially arbitrary probability distributions does not yet have a strong statistical foundation. Thus the existence of natural classes within large data sets is, outside of the most obvious cases, largely in the eye of the beholder. In this study, we have used a collection of standard dimension reduction techniques to look for evidence of discrete substructures within the data, and we have found this evidence weak. However, there is always the possibility that some other analytical approach may be more sensitive to the existence of such substructures within the population.

Conclusion.

The analyses presented in this article have provided a reasonable quantitative outline of the range of variation in cycle-triggered firing rate waveforms within the in vitro pre-Bötzinger complex network. The present finding of a continuous distribution of firing rate behavior is consistent with an assumed graded distribution of intrinsic currents, likely determined by both developmental and activity-dependent factors. However, these data contradict a dominant model in the field of central respiratory control that views different participants in the network as possessing categorically distinct behaviors that determine each cell's role in specific phases of the rhythm. This model likely stems from conceptual foundations inspired by studies of invertebrate rhythm generators, where anatomically and physiologically identified cell types are abundant and more consistent with ball-and-stick representations. It is our hope that this more quantitative description of physiological behavior can provide a basis for a more in-depth understanding of the relationship between these waveform features and the physiological/functional roles of the cells within the respiratory network. This will be particularly important for neurons located in different areas of the wider respiratory network.

GRANTS

This study was supported by National Institutes of Health Grants R01 HL107084-01, R01 HL/NS60120, and P01 HL090544 Project 3.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the authors.

AUTHOR CONTRIBUTIONS

M.S.C. and J.-M.R. conception and design of research; M.S.C. and J.C.V. performed experiments; M.S.C. analyzed data; M.S.C. and J.-M.R. interpreted results of experiments; M.S.C. prepared figures; M.S.C. drafted manuscript; M.S.C. and J.-M.R. edited and revised manuscript; M.S.C., J.C.V., and J.-M.R. approved final version of manuscript.